はじめに
Matplotlibライブラリを利用して、2次元の格子(直方体の立体)を作成します。
【前の内容】
【目次】
3次元格子の作図
ここまでで、Matplotlibライブラリを利用して、2次元空間(平面)上に長方形と平行四辺形の格子のグラフを作成しました。
今回は、3次元空間上に直方体の格子のグラフを作成します。「2次元格子の作図【Matplotlib】 - からっぽのしょこ」の記事も参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
曲面の描画
まずは、3次元空間に曲面や平面を作成して、axes.plot_wireframe()の基本的な使い方を確認します。
x軸・y軸の値を作成して、z軸の値を計算します。
# x軸・y軸の値を作成 x = np.arange(start=-2.5, stop=2.6, step=0.5) y = np.arange(start=-2.0, stop=2.1, step=0.5) print(x) print(y) print(x.shape) print(y.shape) # 格子点を作成 X, Y = np.meshgrid(x, y) print(X[0]) print(Y[0]) print(X.shape) print(Y.shape) # z軸の値を計算 #Z = X**2 + Y**2 Z = 0.2 * X + 0.3 * Y print(Z[0]) print(Z.shape)
[-2.5 -2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. 2.5]
[-2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. ]
(11,)
(9,)
[-2.5 -2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. 2.5]
[-2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.]
(9, 11)
(9, 11)
[10.25 8. 6.25 5. 4.25 4. 4.25 5. 6.25 8. 10.25]
(9, 11)
x軸・y軸の値をx, yとして作成します。
x, yの格子状の点(全ての組み合わせ)をnp.meshgrid()で作成してX, Yとします。np.meshgrid()に2つの1次元配列を渡すと、2つの2次元配列を返します。出力される配列は、全て同じ形状です。2つの配列が出力されるので、2つのオブジェクトで受け取ります。
X, Yを使ってz軸の値を計算してZとします。2乗和と線形結合
とします。
X, Y, Zを用いて、曲面図を作成します。
# 曲面を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.plot_wireframe(X, Y, Z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') #fig.suptitle('$z = x^2 + y^2$', fontsize=20) fig.suptitle('$z = 0.2 x + 0.3 y$', fontsize=20) plt.show()
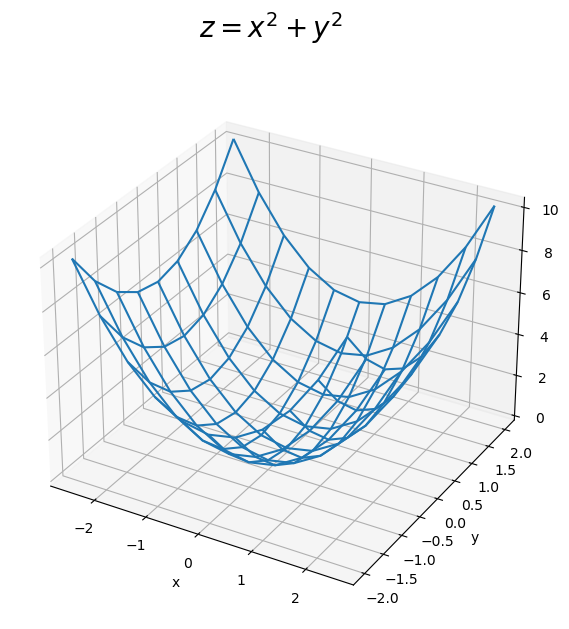
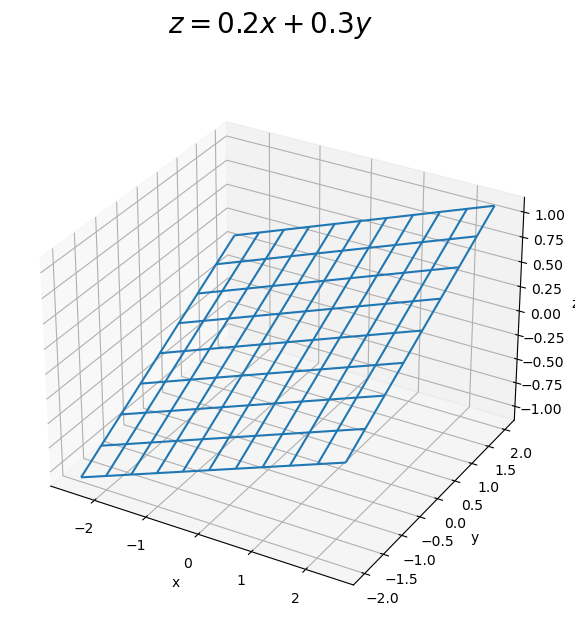
axes.plot_wireframe()で3次元の曲面や平面を描画できます。
3次元格子の描画
では、3次元の格子(直方体の立体)の作図方法を確認します。
x軸・y軸・z軸の値を作成します。
# 各軸の値を作成 x = np.arange(start=-4.0, stop=4.1, step=2) y = np.arange(start=0.0, stop=6.1, step=2) z = np.arange(start=1.0, stop=5.1, step=2) print(x) print(y) print(z) print(x.shape) print(y.shape) print(z.shape) # 格子点を作成 X, Y, Z = np.meshgrid(x, y, z) print(X[0]) print(Y[0]) print(Z[0]) print(X.shape) print(Y.shape) print(Z.shape)
[-4. -2. 0. 2. 4.]
[0. 2. 4. 6.]
[1. 3. 5.]
(5,)
(4,)
(3,)
[[-4. -4. -4.]
[-2. -2. -2.]
[ 0. 0. 0.]
[ 2. 2. 2.]
[ 4. 4. 4.]]
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
[[1. 3. 5.]
[1. 3. 5.]
[1. 3. 5.]
[1. 3. 5.]
[1. 3. 5.]]
(4, 5, 3)
(4, 5, 3)
(4, 5, 3)
x軸・y軸・z軸の値x, y, zを作成して、格子状の点X, Y, Zを作成します。np.meshgrid()に3つの1次元配列を渡すと、3つの3次元配列を返すので、3つのオブジェクトで受け取ります。全て同じ形状の配列です。
X, Y, Zを用いて、散布図を作成してプロット位置を確認します。
# 3D格子点を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.scatter(X, Y, Z) # 格子点 ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('Axes.scatter(X, Y, Z)', fontsize=20) ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 #ax.view_init(elev=0, azim=270) # xz面 #ax.view_init(elev=0, azim=0) # yz面 plt.show()
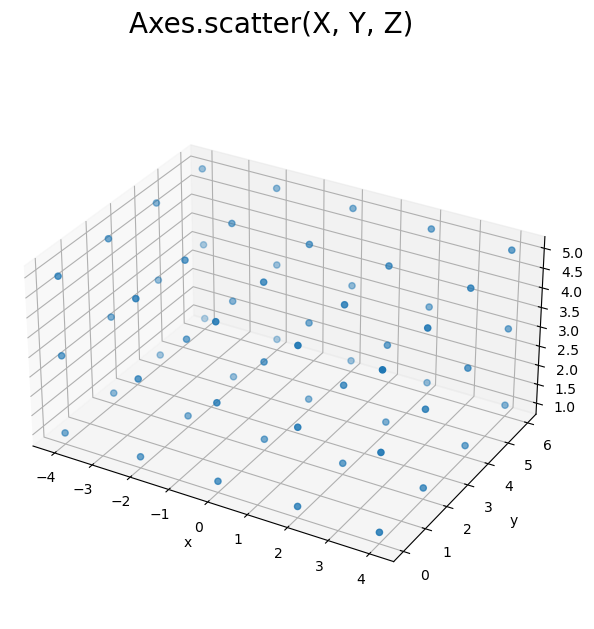
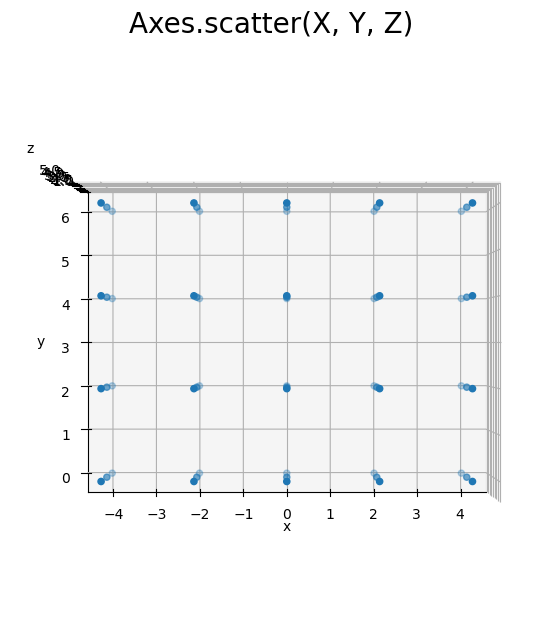
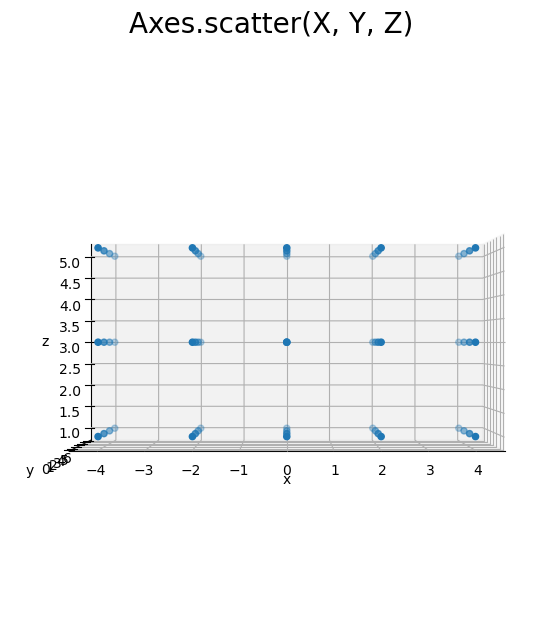
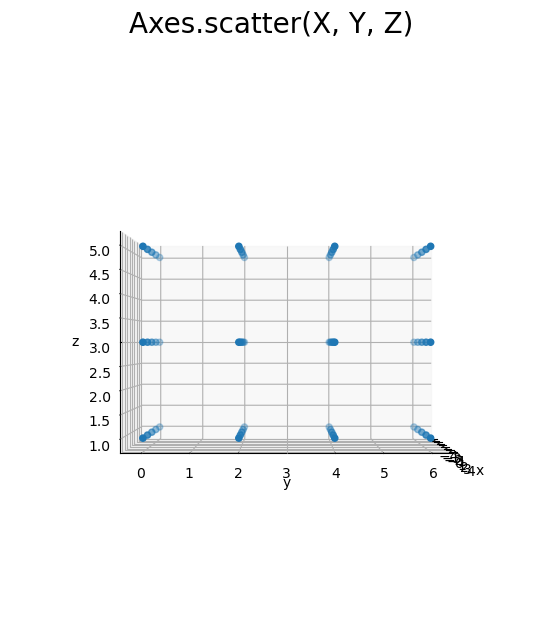
横・奥・縦それぞれに等間隔の点が直方体に並びます。面ごとに見ると長方形に並びます。x, y, zの値の間隔(step引数の値)に対応します。
隣り合う点を繋ぐ直線を引くと格子になります。
ただし、ax.plot_wireframe()は2次元配列しか扱えないので、3次元配列を指定するとエラーになります。
ValueError: Argument Z must be 2-dimensional.
そこで、3次元配列X, Y, Zからそれぞれ1つの次元(配列の軸)を取り出して、曲面図(平面)を描画してみます。
# 平面を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.plot_wireframe(X[0], Y[0], Z[0]) ax.set_xticks(ticks=x) ax.set_yticks(ticks=y) ax.set_zticks(ticks=z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('Axes.plot_wireframe(X[0], Y[0], Z[0])', fontsize=20) ax.set_aspect('equal') plt.show()
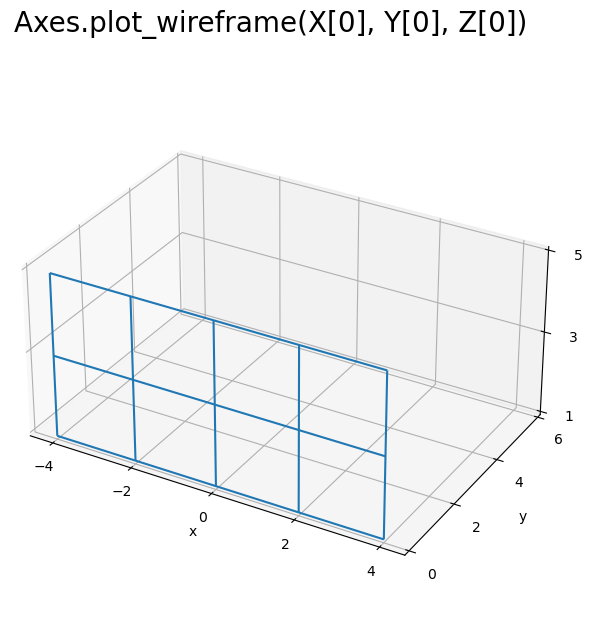
3次元空間上に、2次元(平面)の格子を1つ描画できました。
X, Y, Zの1つ目の次元(0番目の軸)に関して、for文で繰り返し平面を描画します。
# 2D格子を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.scatter(X, Y, Z) # 格子点 for i in range(len(y)): ax.plot_wireframe(X[i], Y[i], Z[i], alpha=0.5) # xz軸方向の平面 ax.set_xticks(ticks=x) ax.set_yticks(ticks=y) ax.set_zticks(ticks=z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('Axes.plot_wireframe(X[i], Y[i], Z[i])', fontsize=20) ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 plt.show()
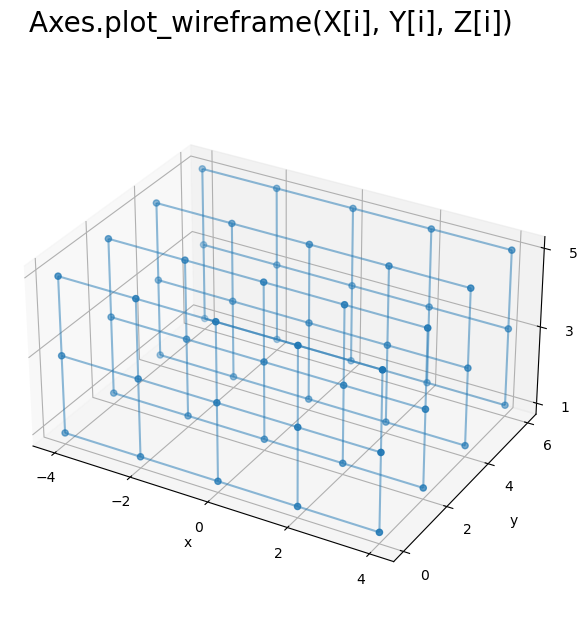
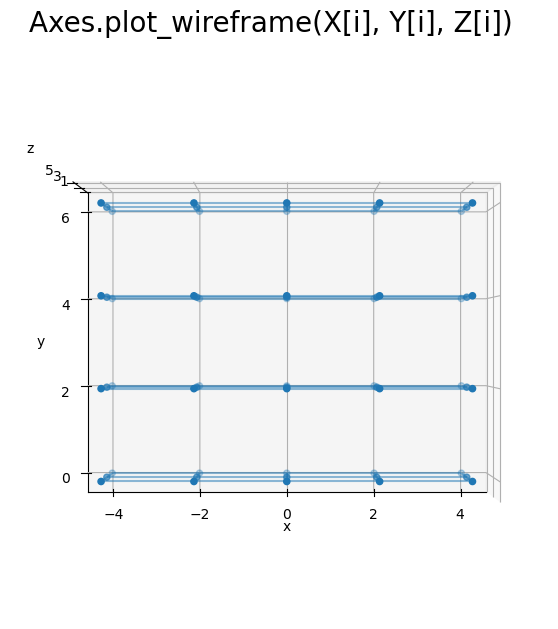
yの要素数(X, Y, Zの0番目の軸の要素数len(X)やX.shape[0])に応じて、x軸とz軸に広がる平面を描画できました。
同様に、X, Y, Zの2つ目の次元(1番目の軸)に関して平面を描画します。
# 2D格子を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.scatter(X, Y, Z) # 格子点 for i in range(len(x)): ax.plot_wireframe(X[:, i], Y[:, i], Z[:, i], alpha=0.5) # yz軸方向の平面 ax.set_xticks(ticks=x) ax.set_yticks(ticks=y) ax.set_zticks(ticks=z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('Axes.plot_wireframe(X[:, i], Y[:, i], Z[:, i])', fontsize=20) ax.set_aspect('equal') #ax.view_init(elev=0, azim=270) # xz面 plt.show()

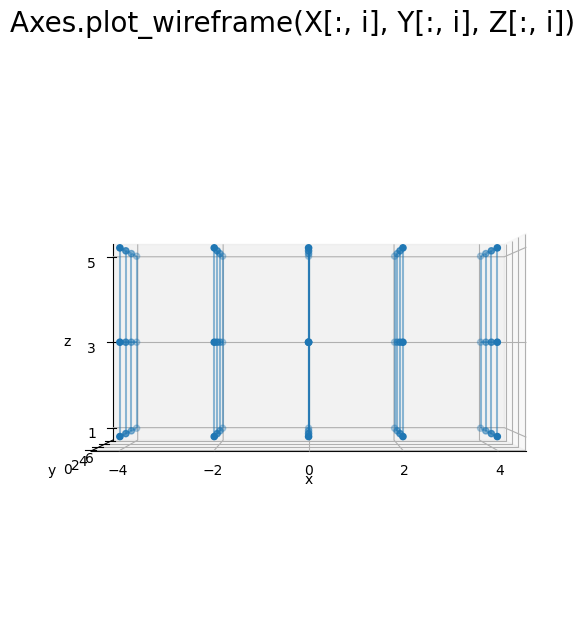
xの要素数(X, Y, Zの1番目の軸の要素数len(X[0])やX.shape[1])に応じて、y軸とz軸に広がる平面を描画できました。
X, Y, Zの3つ目の次元(2番目の軸)に関して平面を描画します。
# 2D格子を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.scatter(X, Y, Z) # 格子点 for i in range(len(z)): ax.plot_wireframe(X[:, :, i], Y[:, :, i], Z[:, :, i], alpha=0.5) # xy軸方向の平面 ax.set_xticks(ticks=x) ax.set_yticks(ticks=y) ax.set_zticks(ticks=z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('Axes.plot_wireframe(X[:, :, i], Y[:, :, i], Z[:, :, i])', fontsize=20) ax.set_aspect('equal') #ax.view_init(elev=0, azim=270) # xz面 plt.show()

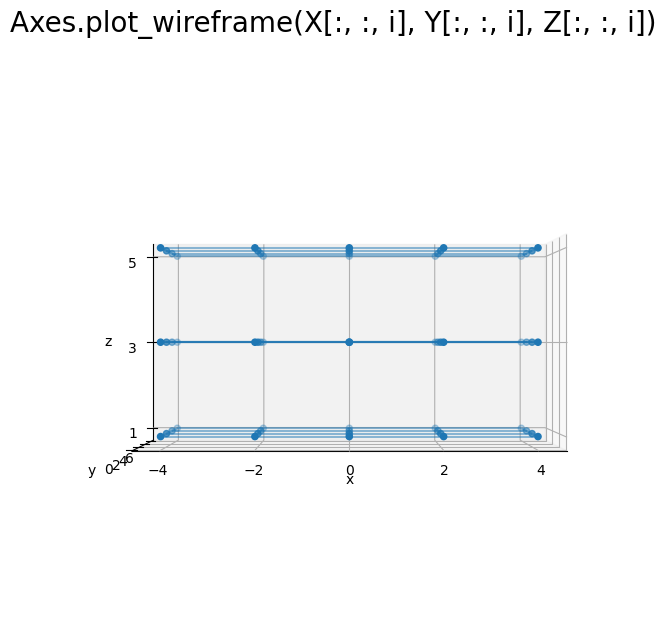
zの要素数(X, Y, Zの2つ目の軸の要素数len(X[0, 0])やX.shape[2])に応じて、x軸とy軸に広がる平面を描画できました。
X, Y, Zの全ての次元に関してそれぞれ平面を描画します。
# 3D格子を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) ax.scatter(X, Y, Z) # 格子点 for i in range(len(y)): # 凡例用に1つだけラベルを設定 if i == 0: label_text = '$a e_1 + b e_2 + c e_3$' else: label_text = '' ax.plot_wireframe(X[i], Y[i], Z[i], alpha=0.5, label=label_text) # xz軸方向の平面 for i in range(len(x)): ax.plot_wireframe(X[:, i], Y[:, i], Z[:, i], alpha=0.5) # yz軸方向の平面 #for i in range(len(z)): # ax.plot_wireframe(X[:, :, i], Y[:, :, i], Z[:, :, i], alpha=0.5) # xy軸方向の平面 ax.set_xticks(ticks=x) ax.set_yticks(ticks=y) ax.set_zticks(ticks=z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('3D grid', fontsize=20) ax.legend() ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 #ax.view_init(elev=0, azim=270) # xz面 #ax.view_init(elev=0, azim=0) # yz面 plt.show()
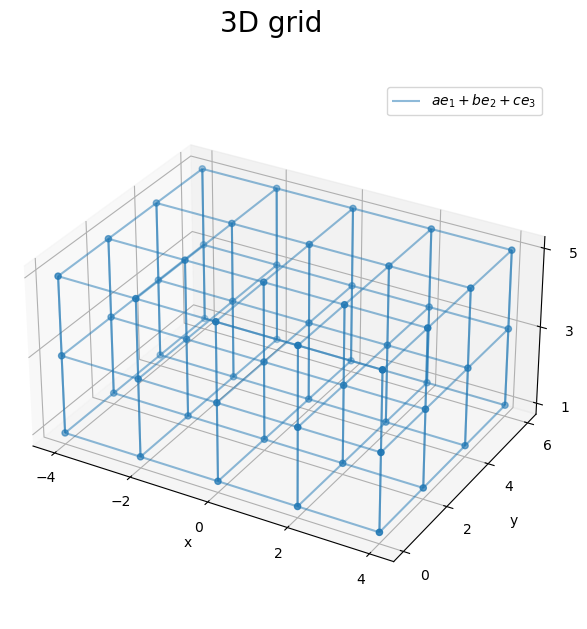
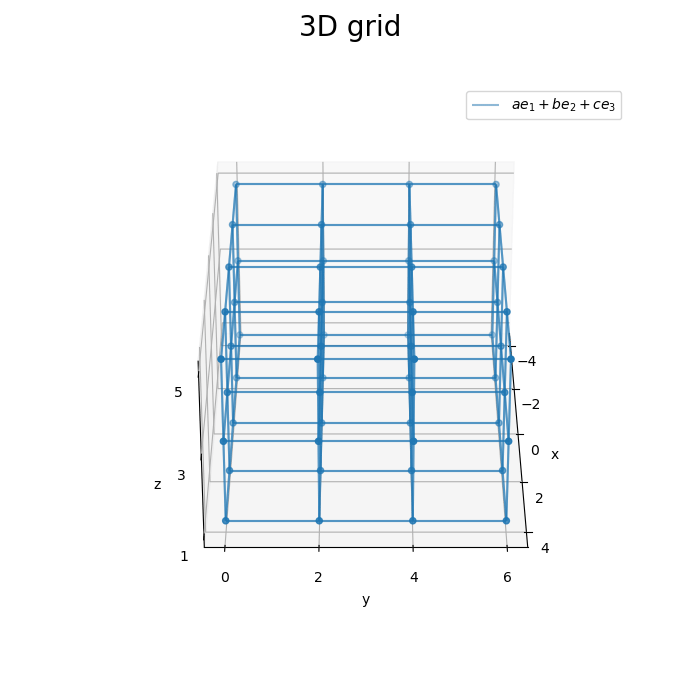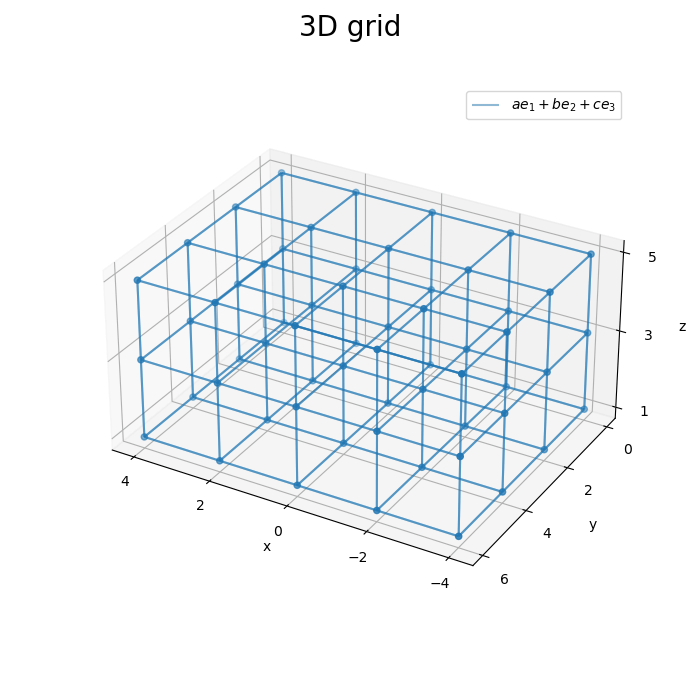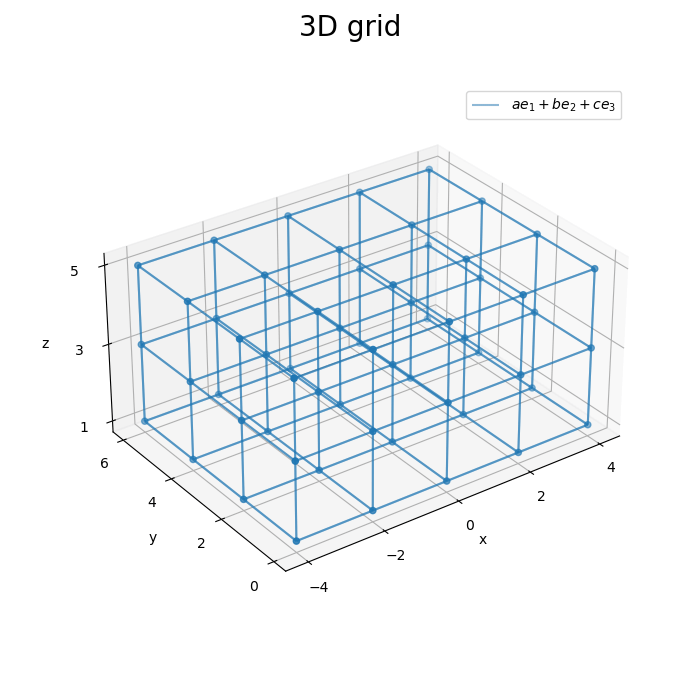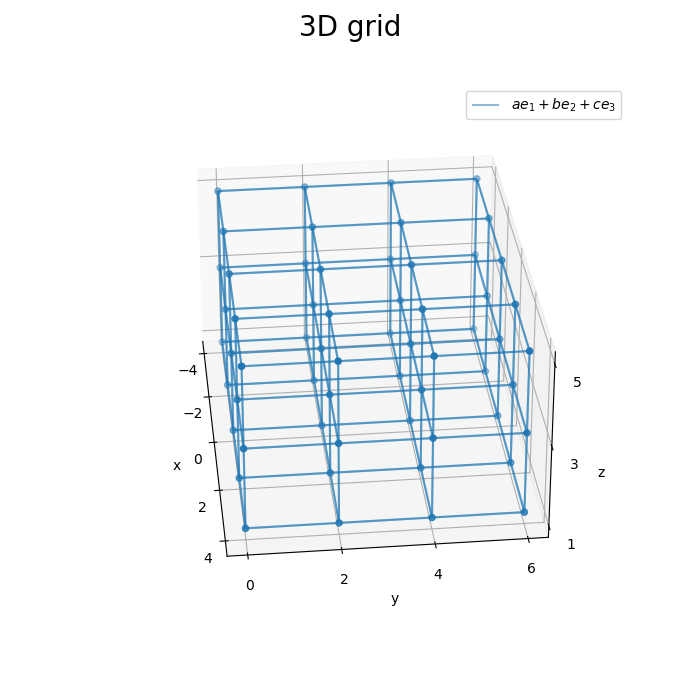
3方向の平面を組み合わせることで、3次元格子を描画できました。
x軸・y軸・z軸それぞれと平行な直線で立体が構成されるので、2方向の面を組み合わせれば、3次元格子を描画できます。
凡例を1つだけ表示するために、1つ目の平面の描画時のみlabel引数に文字列を指定します。if文を使って、初回(iが0のとき)以外は空の文字列''を指定します。(この例で表示している数式については気にしないでください。)
グラフを回転させて確認します。
・作図コード(クリックで展開)
# フレーム数を指定 frame_num = 60 # 水平方向の角度として利用する値を作成 h_n = np.linspace(start=0.0, stop=360.0, num=frame_num+1)[:frame_num] # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('3D grid', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の角度を取得 h = h_n[i] # 3D格子を作図 ax.scatter(X, Y, Z) # 格子点 for i in range(len(y)): # 凡例用に1つだけラベルを設定 label_text = '$a e_1 + b e_2 + c e_3$' if i == 0 else '' ax.plot_wireframe(X[i], Y[i], Z[i], alpha=0.5, label=label_text) # xz軸方向の平面 for i in range(len(x)): ax.plot_wireframe(X[:, i], Y[:, i], Z[:, i], alpha=0.5) # yz軸方向の平面 for i in range(len(z)): ax.plot_wireframe(X[:, :, i], Y[:, :, i], Z[:, :, i], alpha=0.5) # xy軸方向の平面 ax.set_xticks(ticks=x) ax.set_yticks(ticks=y) ax.set_zticks(ticks=z) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.legend() ax.set_aspect('equal') ax.view_init(elev=30, azim=h) # 表示角度 # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=150) # gif画像を保存 ani.save('grid360_3d.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。
if文を1行処理する記法を使っています。
3次元配列X, Y, Zの全ての次元を(1次元配列x, y, zを)同じ要素数にしておくと、1つのfor文で処理できます。
# 各軸の値を作成 x = np.arange(start=-2.0, stop=2.1, step=2) print(x.shape) # 格子点を作成 X, Y, Z = np.meshgrid(x, x, x) print(X.shape) print(Y.shape) print(Z.shape) # 3Dグリッド線を作図 fig, ax = plt.subplots(figsize=(7, 7), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(len(X)): # 凡例用に1つだけラベルを設定 label_text = '$a e_1 + b e_2 + c e_3$' if i == 0 else '' ax.plot_wireframe(X[i], Y[i], Z[i], label=label_text) # xz軸方向の平面 ax.plot_wireframe(X[:, i], Y[:, i], Z[:, i]) # yz軸方向の平面 ax.plot_wireframe(X[:, :, i], Y[:, :, i], Z[:, :, i]) # xy軸方向の平面 ax.set_xticks(ticks=x) ax.set_yticks(ticks=x) ax.set_zticks(ticks=x) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.suptitle('3D grid', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
(3,)
(3, 3, 3)
(3, 3, 3)
(3, 3, 3)
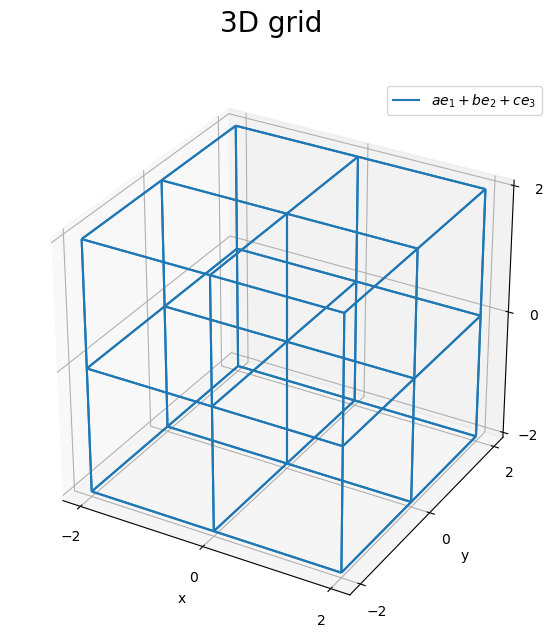
以上で、3次元の格子のグラフを作成できました。次は、傾いた3次元の格子のグラフを作成します。
おわりに
別記事にて格子を描画したかったのですが、素直なやり方ではできなかったのでメモです。
ax.plot_wireframe()は曲面を描画する関数だから、レイヤが重なるような立体は扱えないんですね(?)。近頃は球を描いてたので、できそうな気がしてました。
【次の内容】