はじめに
PythonのMatplotlibライブラリを使ってグラフを動かそうシリーズです。
この記事では、全ての方向に移動する2次元のランダムウォークのアニメーションを作成します。
【前の内容】
【他の内容】
【目次】
2次元ランダムウォークの作図:全方向移動
平面上の全ての方向(360°)に移動するランダムウォーク(random walk)のアニメーションを作成します。
利用するライブラリを読み込みます。
# 利用するモジュール import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import numpy as np
全方向移動の確認
まずは、平面上を移動する処理を確認します。
円周の座標計算やラジアンについては「円周の作図【Matplotlib】 - からっぽのしょこ」を参照してください。
・作図コード(クリックで展開)
単位円の円周上の点の座標を計算します。
# フレーム数を指定 frame_num = 101 # 点用のラジアンを作成 point_t_vec = np.linspace(start=0, stop=2*np.pi, num=frame_num+1)[:frame_num+1] # 1周期分 print(point_t_vec[:5].round(2)) # 単位円周上の点の座標を計算 point_x_vec = np.cos(point_t_vec) point_y_vec = np.sin(point_t_vec) print(point_x_vec[:5].round(2)) print(point_y_vec[:5].round(2))
[0. 0.06 0.12 0.19 0.25]
[1. 1. 0.99 0.98 0.97]
[0. 0.06 0.12 0.19 0.25]
フレーム数 frame_num を指定して、frame_num 個の点の座標を作成します。
から
の値
を作成して、x軸の値を
、y軸の値を
で計算します。
は円周率で、
np.pi で扱えます。
ノルム目盛線(円周)の描画用の値を作成します。
# グラフサイズを設定 axis_size = 1.5 # 目盛間隔を設定 tick_val = 0.5 # 円周の半径を作成 circle_r_vec = np.arange(start=tick_val, stop=axis_size*np.sqrt(2), step=tick_val) print(circle_r_vec) # 円周用のラジアンを作成 circle_t_vec = np.linspace(start=0, stop=2*np.pi, num=361) circle_t_arr = circle_t_vec[np.newaxis, :].repeat(repeats=len(circle_r_vec), axis=0) # ノルムごとに複製 print(circle_t_arr[:, :5].round(2)) # ノルム目盛線の座標を計算 circle_x_arr = circle_r_vec[:, np.newaxis] * np.cos(circle_t_arr) circle_y_arr = circle_r_vec[:, np.newaxis] * np.sin(circle_t_arr) print(circle_x_arr[:, :5].round(2)) print(circle_y_arr[:, :5].round(2))
[0.5 1. 1.5 2. ]
[[0. 0.02 0.03 0.05 0.07]
[0. 0.02 0.03 0.05 0.07]
[0. 0.02 0.03 0.05 0.07]
[0. 0.02 0.03 0.05 0.07]]
[[0.5 0.5 0.5 0.5 0.5]
[1. 1. 1. 1. 1. ]
[1.5 1.5 1.5 1.5 1.5]
[2. 2. 2. 2. 2. ]]
[[0. 0.01 0.02 0.03 0.03]
[0. 0.02 0.03 0.05 0.07]
[0. 0.03 0.05 0.08 0.1 ]
[0. 0.03 0.07 0.1 0.14]]
グラフサイズ axis_size と目盛の間隔 tick_val を指定して、目盛線の間隔に応じた半径の円周の座標を作成します。
角度目盛線(中心を通る斜線)の描画用のデータフレームを作成します。
# 半円(範囲π)における目盛数を指定 tick_num = 6 # 目盛番号を作成 diag_i_vec = np.arange(stop=tick_num) print(diag_i_vec) # 傾き用のラジアンを作成 diag_t_vec = diag_i_vec/tick_num * np.pi print(diag_t_vec.round(2)) # 目盛線の傾きを計算 diag_a_vec = np.tan(diag_t_vec) print(diag_a_vec.round(2))
[0 1 2 3 4 5]
[0. 0.52 1.05 1.57 2.09 2.62]
[ 0.00000000e+00 5.80000000e-01 1.73000000e+00 1.63312394e+16
-1.73000000e+00 -5.80000000e-01]
半円における目盛数 tick_num を指定して、目盛線の角度(円周上の点に対応する偏角) t を用いて目盛線の傾き a を作成します。
作成した点を描画します。
# グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(6, 6), facecolor='white') fig.suptitle('unit circle', fontsize=20) # 作図処理を定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 点の座標を取得 t = point_t_vec[i] x = point_x_vec[i] y = point_y_vec[i] # ラベル用の文字列を作成 coord_label = '$t = {:.2f}\pi, (x, y) = ({:.2f}, {:.2f})$'.format(t/np.pi, x, y) # 単位円周上の点を作図 ax.plot(circle_x_arr.T, circle_y_arr.T, color='gray', linewidth=0.5) # ノルム目盛線 for tick_i in range(tick_num): ax.axline(xy1=[0, 0], slope=diag_a_vec[tick_i], color='gray', linewidth=0.5) # 角度目盛線 ax.plot([0, x], [0, y], linewidth=2) # 動径 ax.scatter(x, y, s=100) # 円周上の点 ax.set_xlabel('$x = \cos t$') ax.set_ylabel('$y = \sin t$') ax.set_title(coord_label, loc='left') ax.grid() ax.set_aspect('equal') # 動画を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # 動画を書出 ani.save(filename='UnitCircle.gif', dpi=250)
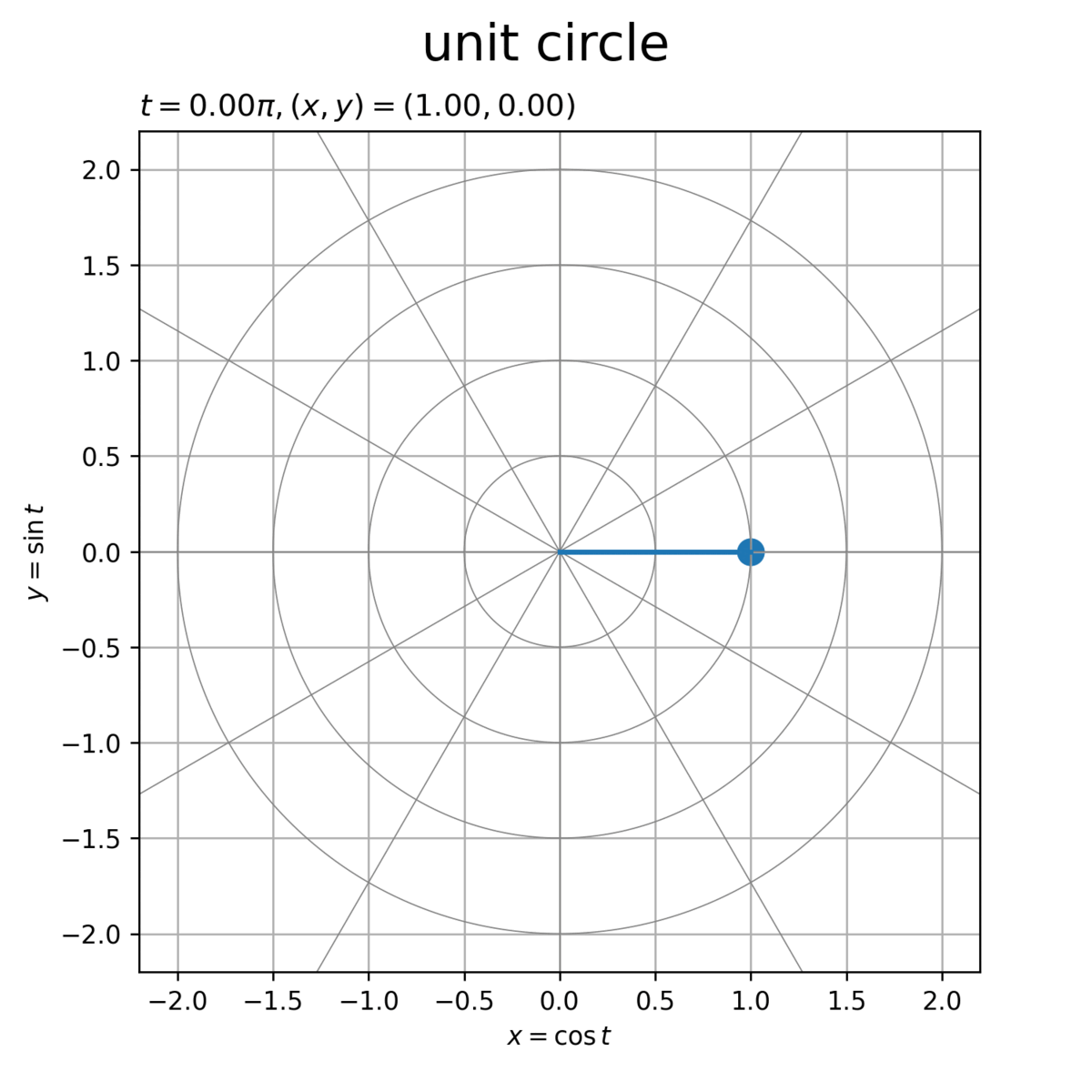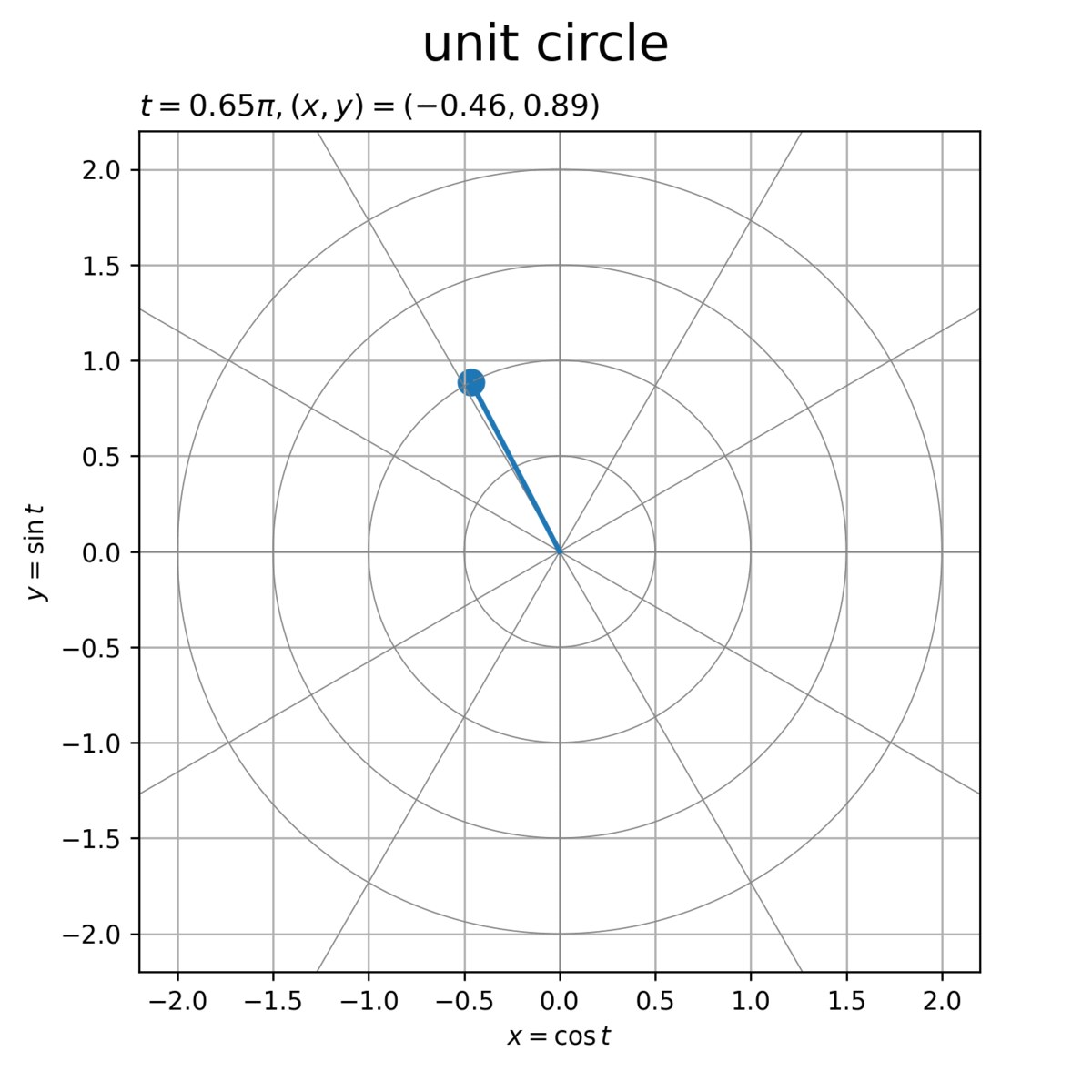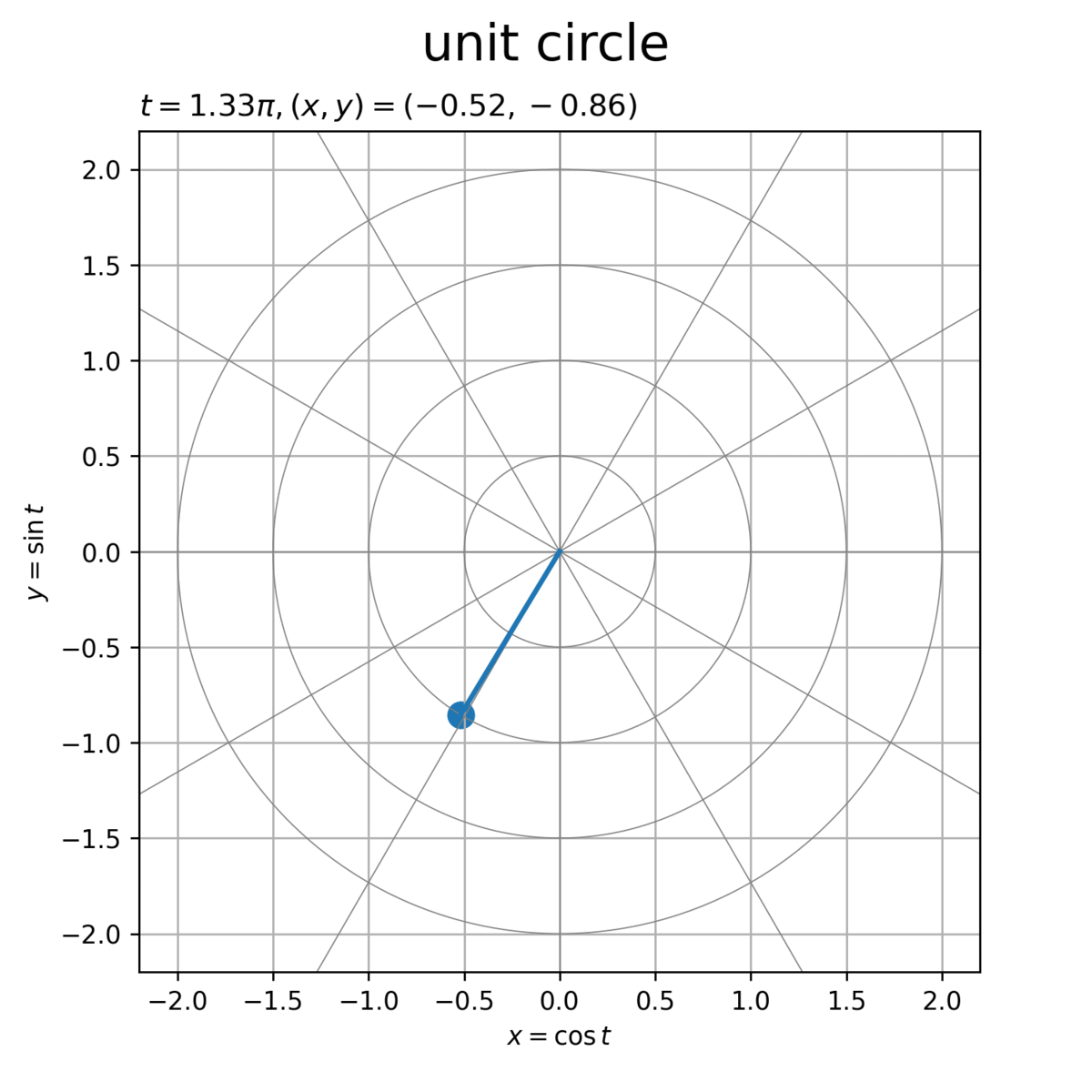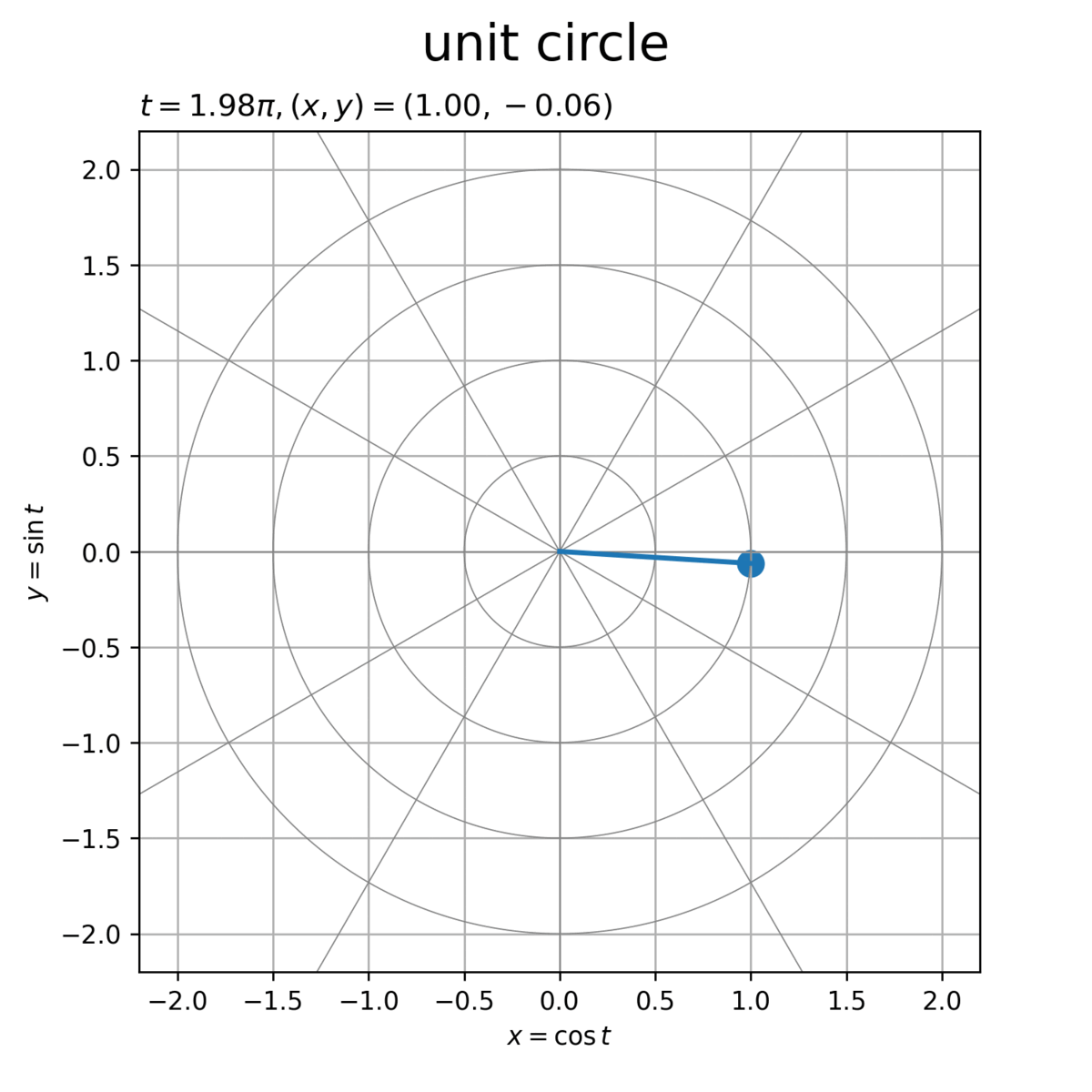
ラジアン(弧度法の角度) を用いて、単位円(半径が1)の円周上の点の座標
は、次の式で得られます。
は円周率です。
つまり、 から
の乱数を生成して座標を計算すると、現在の位置(円の中心)からランダムな方向に距離(ノルム)1の移動を表せます。
1サンプル
次は、1つのサンプルを描画します。
試行回数を指定して、移動量の計算用の値をランダムに生成します。
# 試行回数を指定 max_iter = 100 # 乱数を生成 random_vec = 2*np.pi * np.random.uniform(low=0, high=1, size=max_iter) # ラジアン print(random_vec[:5]) print(random_vec.shape)
[2.63964576 1.4487027 1.95752954 1.72786531 0.13066734]
(100,)
から
の一様乱数を
np.random.uniform()で生成します。 は円周率で、
np.pi で扱えます。最小値の引数 low に 0、最大値の引数 high に 1 を指定して、2*pi を掛けます。または、high 引数に 2*pi を指定します。
この例では原理的な処理が分かりやすいように、0 から 1 の乱数に 2*np.pi を掛けることで から
の乱数を作成しています。
移動量に応じた座標を計算します。
# 試行ごとに集計 x_vec = np.cumsum( np.hstack([0, np.cos(random_vec)]) # 初期値を追加 ) y_vec = np.cumsum( np.hstack([0, np.sin(random_vec)]) # 初期値を追加 ) print(x_vec[:5]) print(x_vec.shape) print(y_vec[:5]) print(y_vec.shape)
[ 0. -0.87664751 -0.75485699 -1.1320219 -1.28844585]
(101,)
[0. 0.48113319 1.47368901 2.39983513 3.38752514]
(101,)
乱数を用いてx座標を np.cos()、y座標を np.sin() で計算します。
初期値(スタート地点・0回目の結果)を 0 として追加して、各試行までの和(累積和)を np.cumsum() で計算します。
点の推移のグラフを作成します。
# 余白サイズを指定 margin_rate = 0.1 # グラフサイズを設定 axis_size = np.ceil(np.max([np.abs(x_vec), np.abs(y_vec)])) axis_size = np.ceil(axis_size * (1+margin_rate)) # 余白を追加 # 目盛間隔を設定 tick_val = 2.5 # ノルム目盛線の座標を作成 circle_r_vec = np.arange(start=tick_val, stop=axis_size*np.sqrt(2), step=tick_val) circle_t_vec = np.linspace(start=0, stop=2*np.pi, num=361) circle_t_arr = circle_t_vec[np.newaxis, :].repeat(repeats=len(circle_r_vec), axis=0) circle_x_arr = circle_r_vec[:, np.newaxis] * np.cos(circle_t_arr) circle_y_arr = circle_r_vec[:, np.newaxis] * np.sin(circle_t_arr) # 半円(範囲π)における目盛数を指定 tick_num = 6 # 目盛線の傾きを作成 diag_i_vec = np.arange(stop=tick_num) diag_t_vec = diag_i_vec/tick_num * np.pi diag_a_vec = np.tan(diag_t_vec)
# 2Dランダムウォークを作図 fig, ax = plt.subplots(figsize=(8, 8), dpi=250, facecolor='white') ax.plot(circle_x_arr.T, circle_y_arr.T, color='gray', linewidth=0.5) # ノルム目盛線 for tick_i in range(tick_num): ax.axline(xy1=[0, 0], slope=diag_a_vec[tick_i], color='gray', linewidth=0.5) # 角度目盛線 ax.axhline(y=0, color='red', linestyle='dashed') # 初期値 ax.axvline(x=0, color='red', linestyle='dashed') # 初期値 ax.plot(x_vec, y_vec) # 軌跡 ax.scatter(x_vec[max_iter], y_vec[max_iter], s=100, color='blue', zorder=10) # 最終地点 ax.set_xlim(xmin=-axis_size, xmax=axis_size) ax.set_ylim(ymin=-axis_size, ymax=axis_size) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('iteration: {}, $(x, y) = ({:.2f}, {:.2f})$'.format(max_iter, x_vec[max_iter], y_vec[max_iter]), loc='left') fig.suptitle('Random Walk', fontsize=20) ax.grid() ax.set_aspect('equal') plt.show()
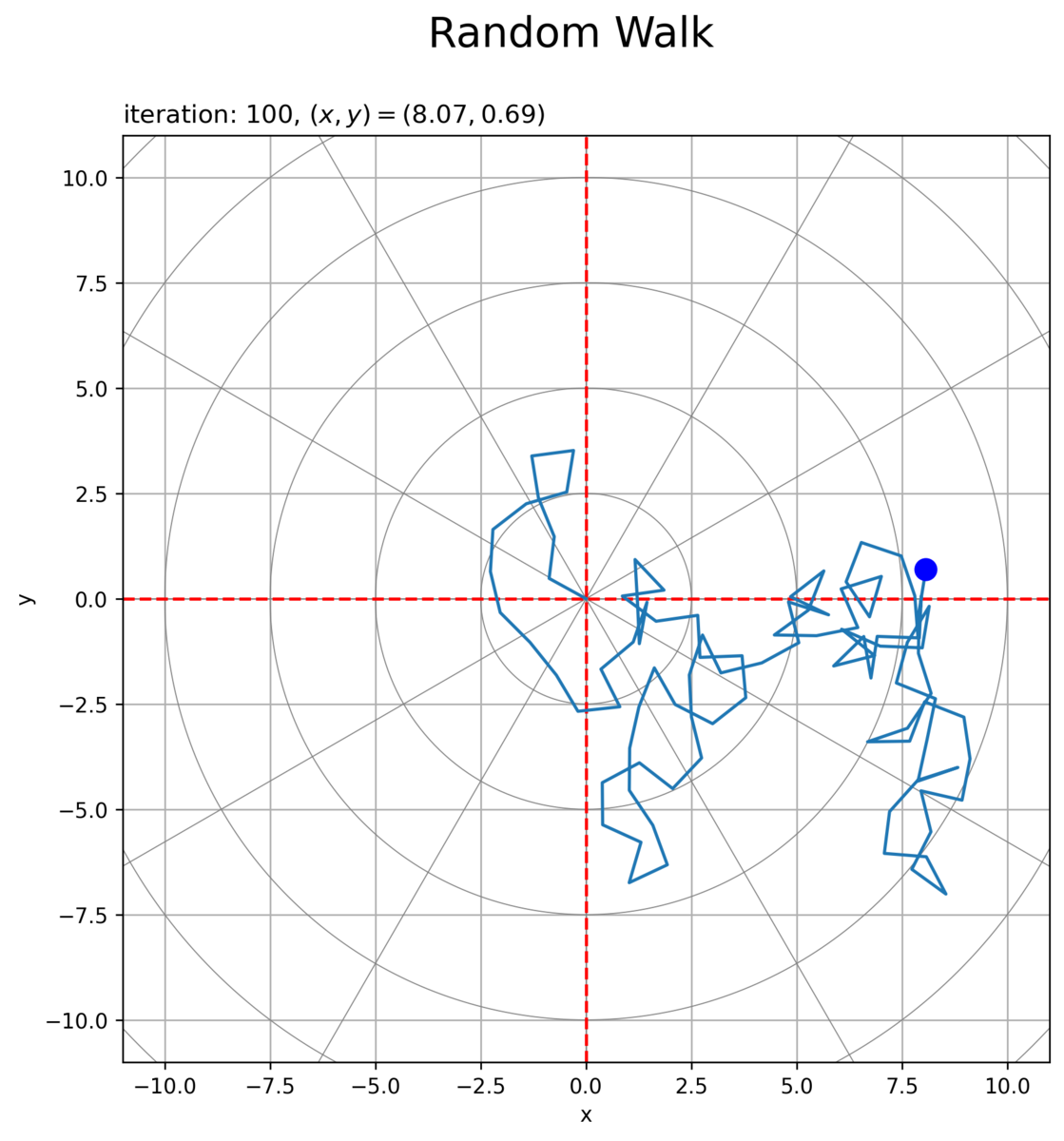
点の推移のアニメーションを作成します。
# グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white') fig.suptitle('Random Walk', fontsize=20) # 作図処理を定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 2Dランダムウォークを作図 ax.plot(circle_x_arr.T, circle_y_arr.T, color='gray', linewidth=0.5) # ノルム目盛線 for tick_i in range(tick_num): ax.axline(xy1=[0, 0], slope=diag_a_vec[tick_i], color='gray', linewidth=0.5) # 角度目盛線 ax.axhline(y=0, color='red', linestyle='dashed') # 初期値 ax.axvline(x=0, color='red', linestyle='dashed') # 初期値 ax.plot(x_vec[:i+1], y_vec[:i+1]) # 軌跡 ax.scatter(x_vec[i], y_vec[i], s=100, color='blue', zorder=10) # 現在地点 ax.set_xlim(xmin=-axis_size, xmax=axis_size) ax.set_ylim(ymin=-axis_size, ymax=axis_size) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('iteration: {}, $(x, y) = ({:.2f}, {:.2f})$'.format(i, x_vec[i], y_vec[i]), loc='left') ax.grid() ax.set_aspect('equal') # 動画を作成 ani = FuncAnimation(fig=fig, func=update, frames=max_iter+1, interval=100) # 動画を書出 ani.save(filename='2d_360_xy_1.gif', dpi=250)
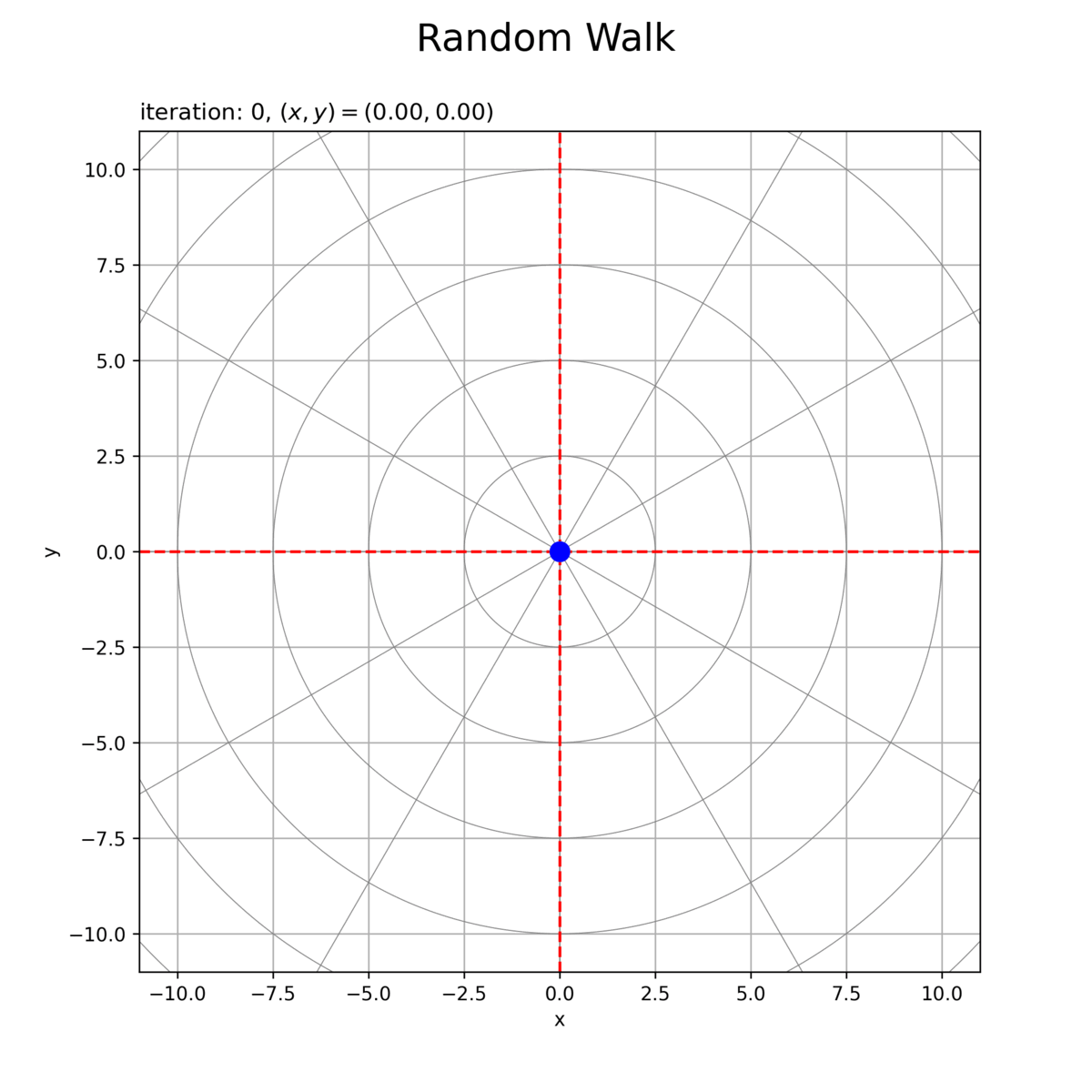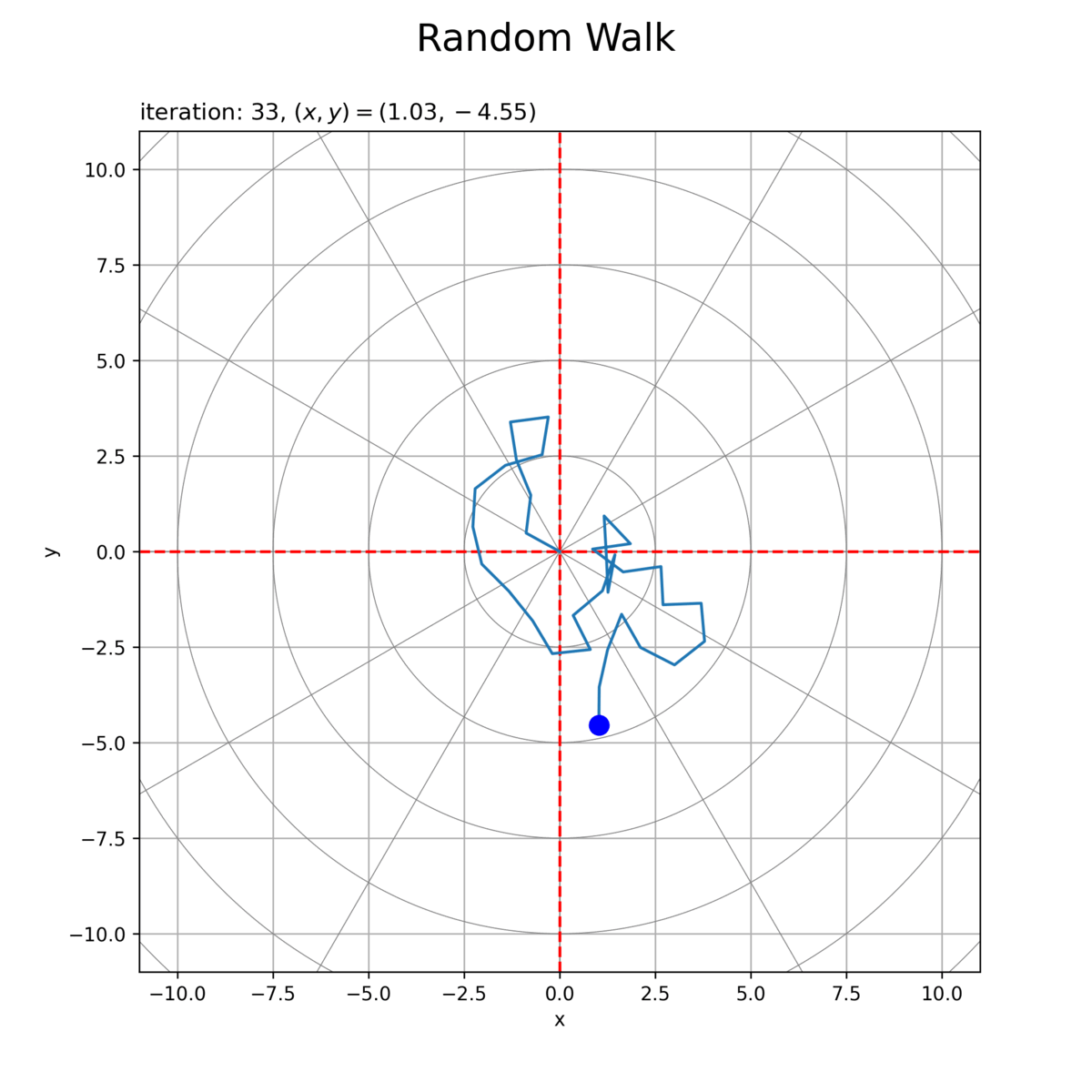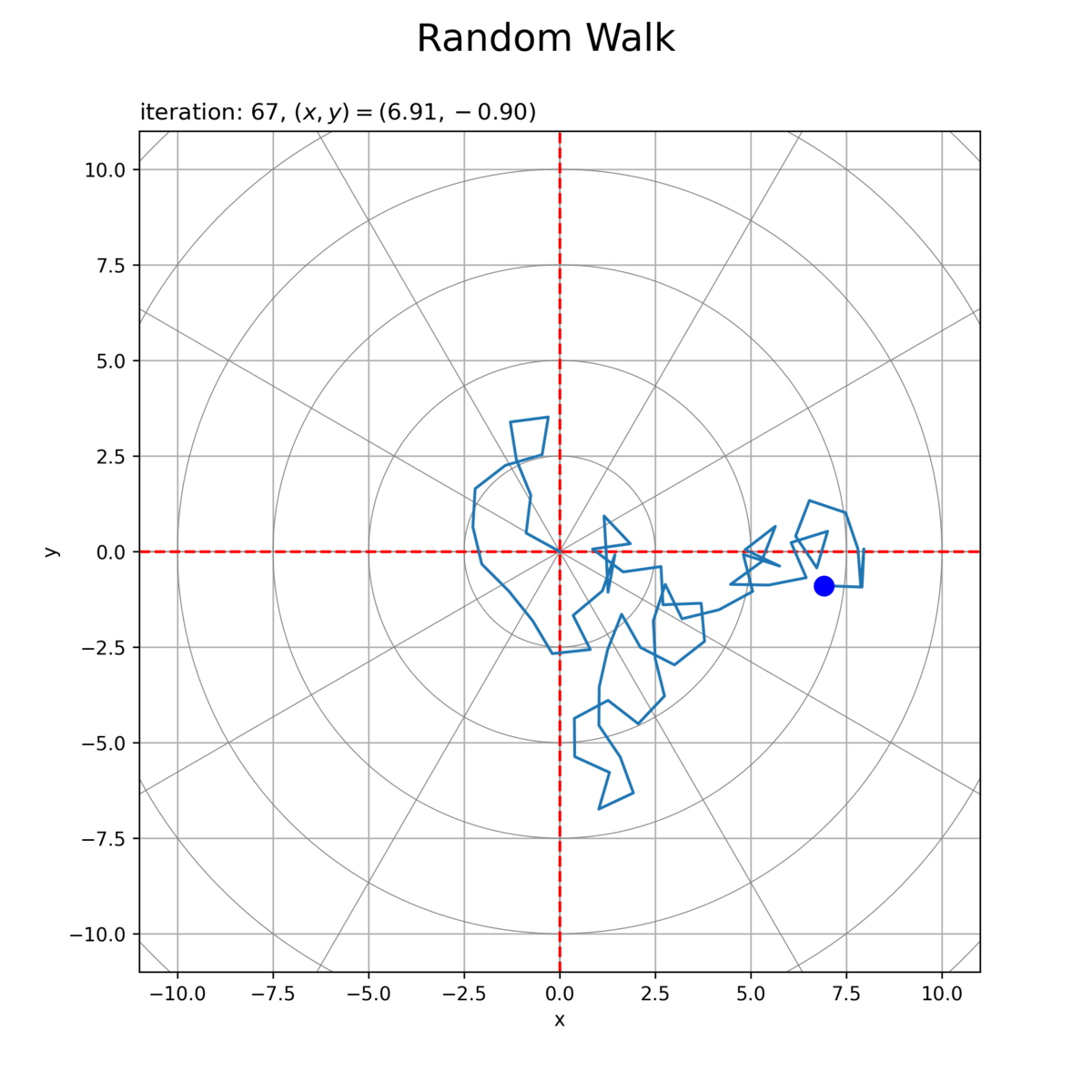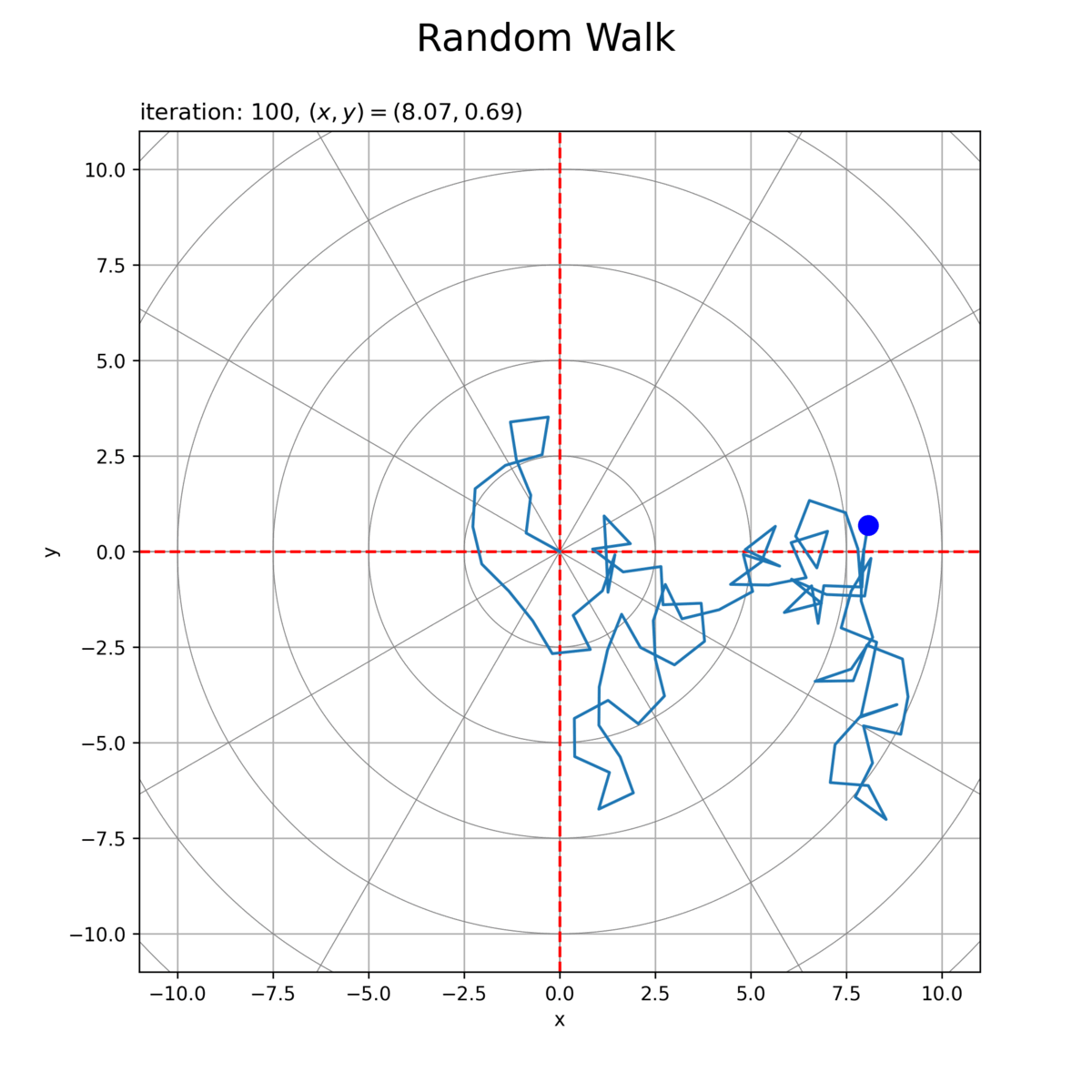
初期値(期待値)を破線で示します。また、初期値(原点)からの移動距離(ノルム)を円状の目盛線、移動方向(偏角)を放射状の目盛線で確認できます。
試行回数軸を追加したグラフを作成します。
# 最終値を取得 x = x_vec[max_iter] y = y_vec[max_iter] # 余白サイズを指定 margin_rate = 0.1 # グラフサイズを設定 axis_size = np.max([np.abs(x_vec), np.abs(y_vec)]) axis_size = np.ceil(axis_size * (1+margin_rate)) # 余白を追加 axis_i_min = -max_iter * margin_rate axis_i_max = max_iter * (1+margin_rate) # 矢サイズを指定 alr = 1.5 # 2Dランダムウォークを作図 fig, ax = plt.subplots(figsize=(10, 10), dpi=250, facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(axis_i_min, [-axis_size, 0], [0, -axis_size], 0, [2*axis_size, 0], [0, 2*axis_size], arrow_length_ratio=alr/(2*axis_size), color='black', linewidth=1) # x・y軸線 ax.quiver(axis_i_min, [axis_size, 0], [0, -axis_size], axis_i_max-axis_i_min, 0, 0, arrow_length_ratio=alr/max_iter, color='black', linewidth=1, linestyle=['dashed']*2+['solid']*4) # 面ごとのi軸線 ax.quiver(axis_i_min, 0, 0, axis_i_max-axis_i_min, 0, 0, arrow_length_ratio=alr/max_iter, color='black', linewidth=1) # i軸線 ax.plot(x_vec, y_vec, zs=axis_i_min, zdir='x', color='C0', linewidth=1, linestyle='dashed') # xy面の軌跡 ax.plot(np.arange(max_iter+1), x_vec, zs=-axis_size, zdir='z', color='C0', linewidth=1, linestyle='dashed') # ix面の軌跡 ax.plot(np.arange(max_iter+1), y_vec, zs=axis_size, zdir='y', color='C0', linewidth=1, linestyle='dashed') # iy面の軌跡 ax.scatter([axis_i_min, max_iter, max_iter], [x, x, axis_size], [y, -axis_size, y], s=100, fc='none', ec='blue') # 面ごとの最終地点 ax.quiver(max_iter, x, y, [axis_i_min-max_iter, 0, 0], [0, 0, axis_size-x], [0, -axis_size-y, 0], arrow_length_ratio=0, color='gray', linestyle='dotted') # 点の目盛線 ax.plot(np.arange(max_iter+1), x_vec, y_vec) # 軌跡 ax.scatter(max_iter, x, y, s=100, color='blue') # 最終地点 ax.margins(x=0.0, y=0.0, z=0.0) # (機能しない?のでlimで謎小細工) ax.set_xlim(xmin=axis_i_min+axis_i_max*0.025, xmax=axis_i_max) ax.set_ylim(ymin=-axis_size/1.05, ymax=axis_size/1.05) ax.set_zlim(zmin=-axis_size/1.05, zmax=axis_size/1.05) ax.set_xlabel('iteration') ax.set_ylabel('x') ax.set_zlabel('y') ax.set_title('iteration: {}, $(x, y) = ({:.2f}, {:.2f})$'.format(max_iter, x, y), loc='left') fig.suptitle('Random Walk', fontsize=20) ax.set_box_aspect((2, 1, 1)) #ax.view_init(elev=0, azim=0) # 表示アングル plt.show()
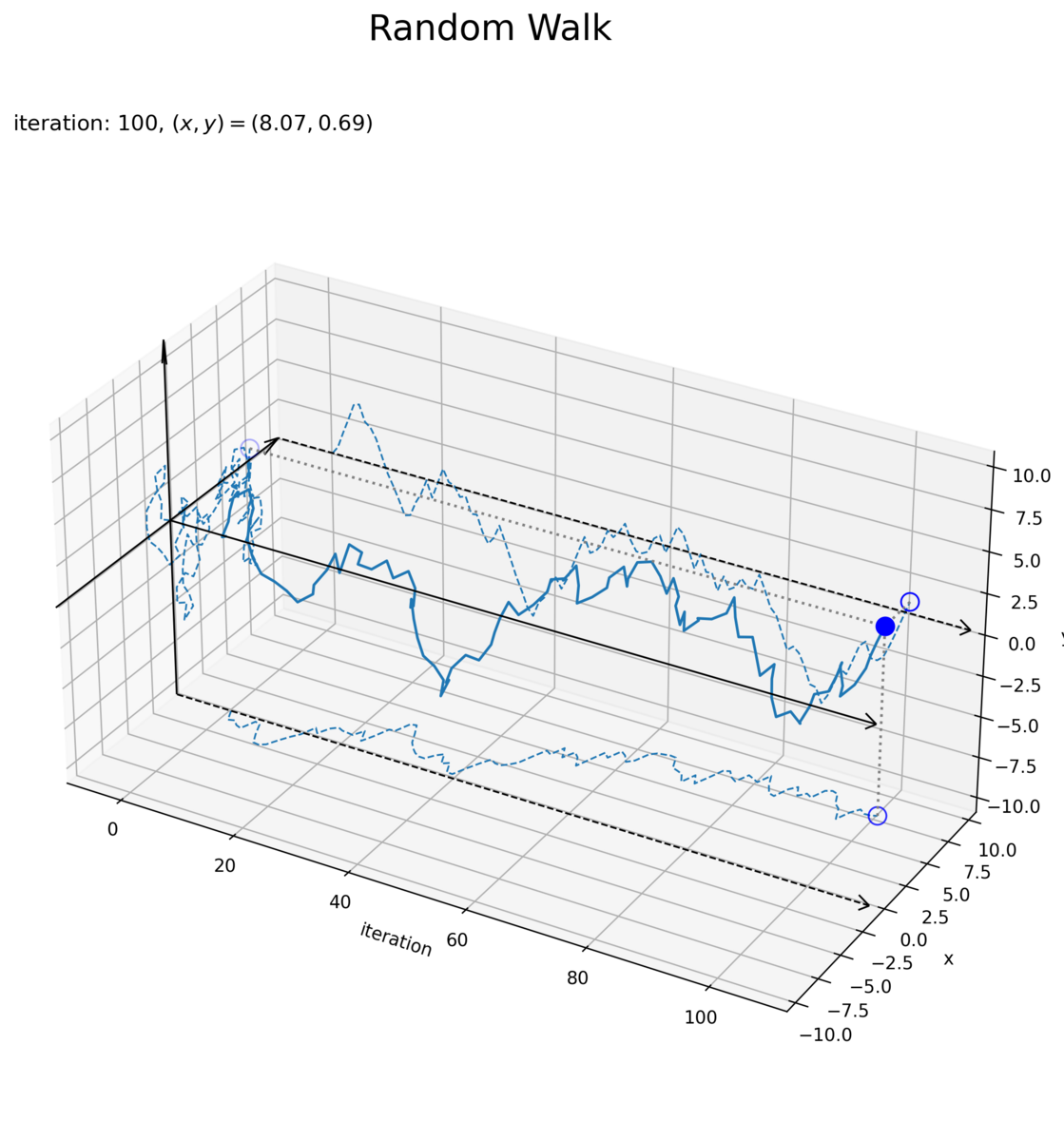
各軸線の最小値・最大値(各方向のグラフサイズ)は Axes.set_*lim() に指定した値に余白(マージン)が追加されます。よって、axis_size の位置にプロットすると側面や底面からズレます。マージン率(マージンを含めた全体のサイズは (最大値 - 最小値) * 1.05 らしい)を0にできればいいのですがやり方が分からなかったので、回避策としてごにょごにょしています(まっとうなやり方を教えてください)。コードの分かりやすさを優先するのであれば 1/1.05 と +axis_i_max*0.025 を外してください。
点の軌道(実線)と軸ごとの軌道(破線)が近いと分かりづらいので margin_rate で調整しています。
試行回数軸を追加したアニメーションを作成します。
# 余白サイズを指定 margin_rate = 0.1 # グラフサイズを設定 axis_size = np.max([np.abs(x_vec), np.abs(y_vec)]) axis_size = np.ceil(axis_size * (1+margin_rate)) # 余白を追加 axis_i_min = -max_iter * margin_rate axis_i_max = max_iter * (1+margin_rate) # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(10, 10), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Random Walk', fontsize=20) # 矢サイズを指定 alr = 1.5 # 作図処理を定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 現在値を取得 x = x_vec[i] y = y_vec[i] # 2Dランダムウォークを作図 ax.quiver(axis_i_min, [-axis_size, 0], [0, -axis_size], 0, [2*axis_size, 0], [0, 2*axis_size], arrow_length_ratio=alr/(2*axis_size), color='black', linewidth=1) # x・y軸線 ax.quiver(axis_i_min, [axis_size, 0], [0, -axis_size], axis_i_max-axis_i_min, 0, 0, arrow_length_ratio=alr/max_iter, color='black', linewidth=1, linestyle=['dashed']*2+['solid']*4) # 面ごとのi軸線 ax.quiver(axis_i_min, 0, 0, axis_i_max-axis_i_min, 0, 0, arrow_length_ratio=alr/max_iter, color='black', linewidth=1) # i軸線 ax.plot(x_vec[:i+1], y_vec[:i+1], zs=axis_i_min, zdir='x', color='C0', linewidth=1, linestyle='dashed') # xy面の軌跡 ax.plot(np.arange(i+1), x_vec[:i+1], zs=-axis_size, zdir='z', color='C0', linewidth=1, linestyle='dashed') # ix面の軌跡 ax.plot(np.arange(i+1), y_vec[:i+1], zs=axis_size, zdir='y', color='C0', linewidth=1, linestyle='dashed') # iy面の軌跡 ax.scatter([axis_i_min, i, i], [x, x, axis_size], [y, -axis_size, y], s=100, fc='none', ec='blue') # 面ごとの最終地点 ax.quiver(i, x, y, [axis_i_min-i, 0, 0], [0, 0, axis_size-x], [0, -axis_size-y, 0], arrow_length_ratio=0, color='gray', linestyle='dotted') # 点の目盛線 ax.plot(np.arange(i+1), x_vec[:i+1], y_vec[:i+1]) # 軌跡 ax.scatter(i, x, y, s=100, color='blue') # 現在地点 ax.margins(x=0.0, y=0.0, z=0.0) # (機能しない?のでlimで謎小細工) ax.set_xlim(xmin=axis_i_min+axis_i_max*0.025, xmax=axis_i_max) ax.set_ylim(ymin=-axis_size/1.05, ymax=axis_size/1.05) ax.set_zlim(zmin=-axis_size/1.05, zmax=axis_size/1.05) ax.set_xlabel('iteration') ax.set_ylabel('x') ax.set_zlabel('y') ax.set_title('iteration: {}, $(x, y) = ({:.2f}, {:.2f})$'.format(i, x, y), loc='left') ax.set_box_aspect((2, 1, 1)) #ax.view_init(elev=0, azim=0) # 表示アングル # 動画を作成 ani = FuncAnimation(fig=fig, func=update, frames=max_iter+1, interval=100) # 動画を書出 ani.save(filename='2d_360_ixy_1.gif', dpi=250)
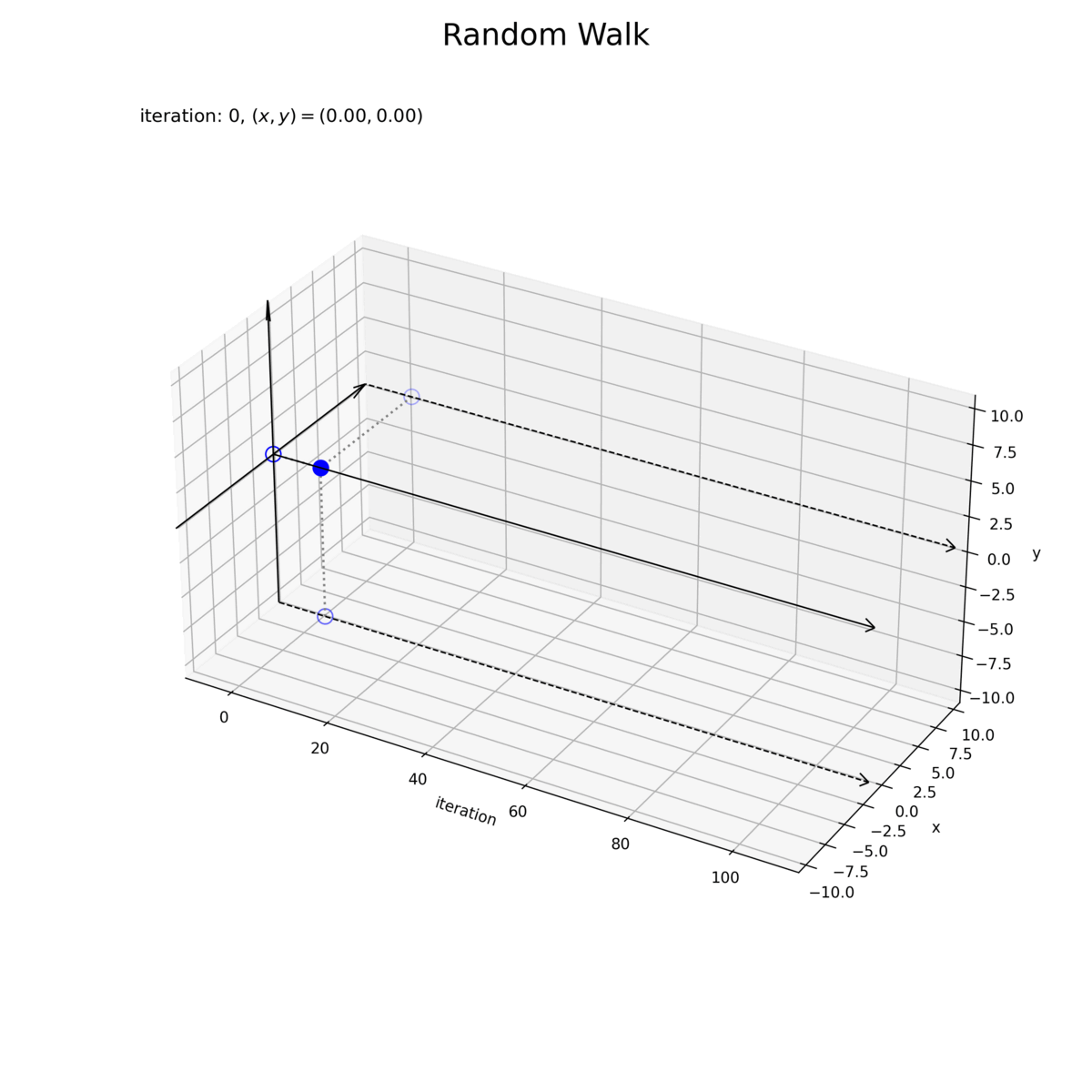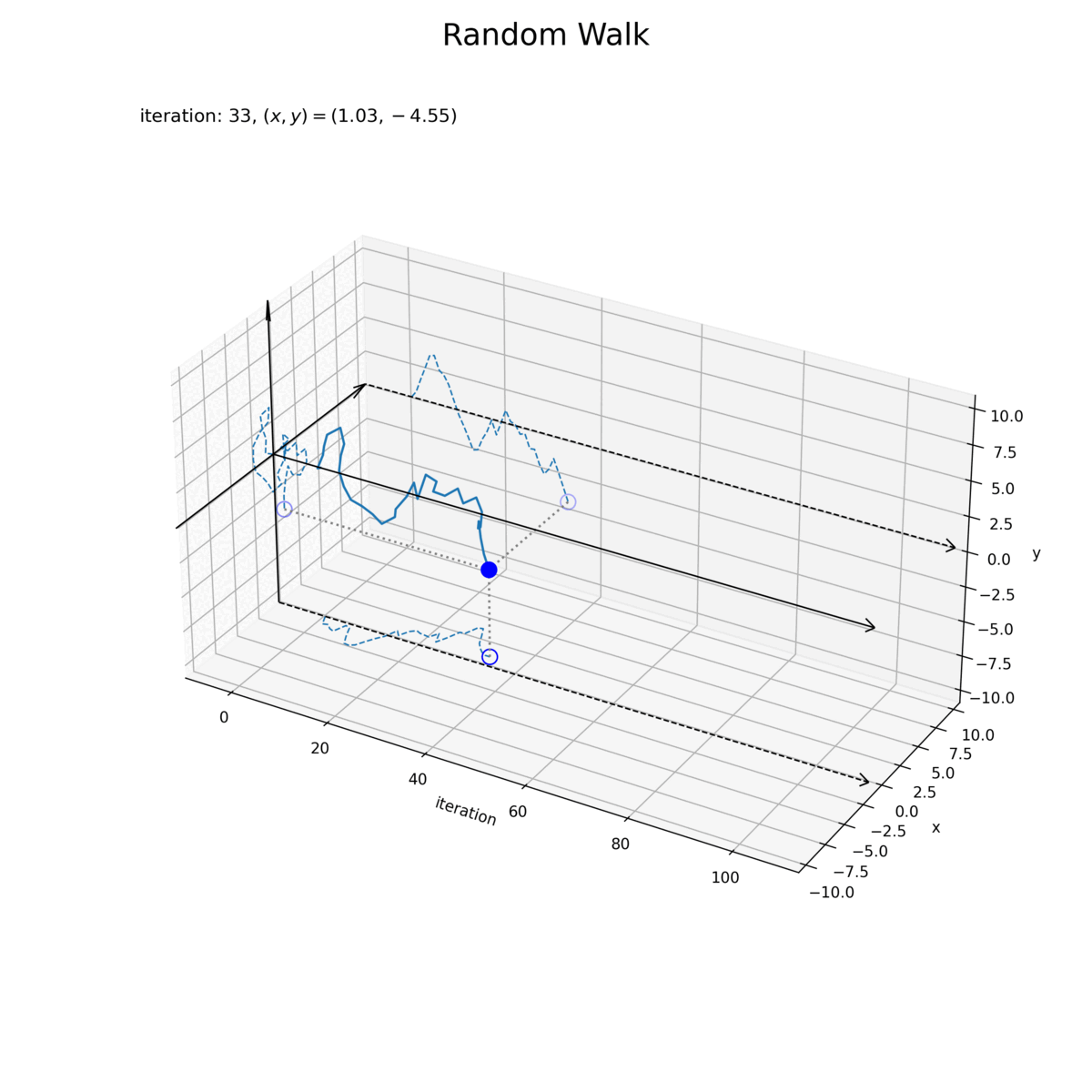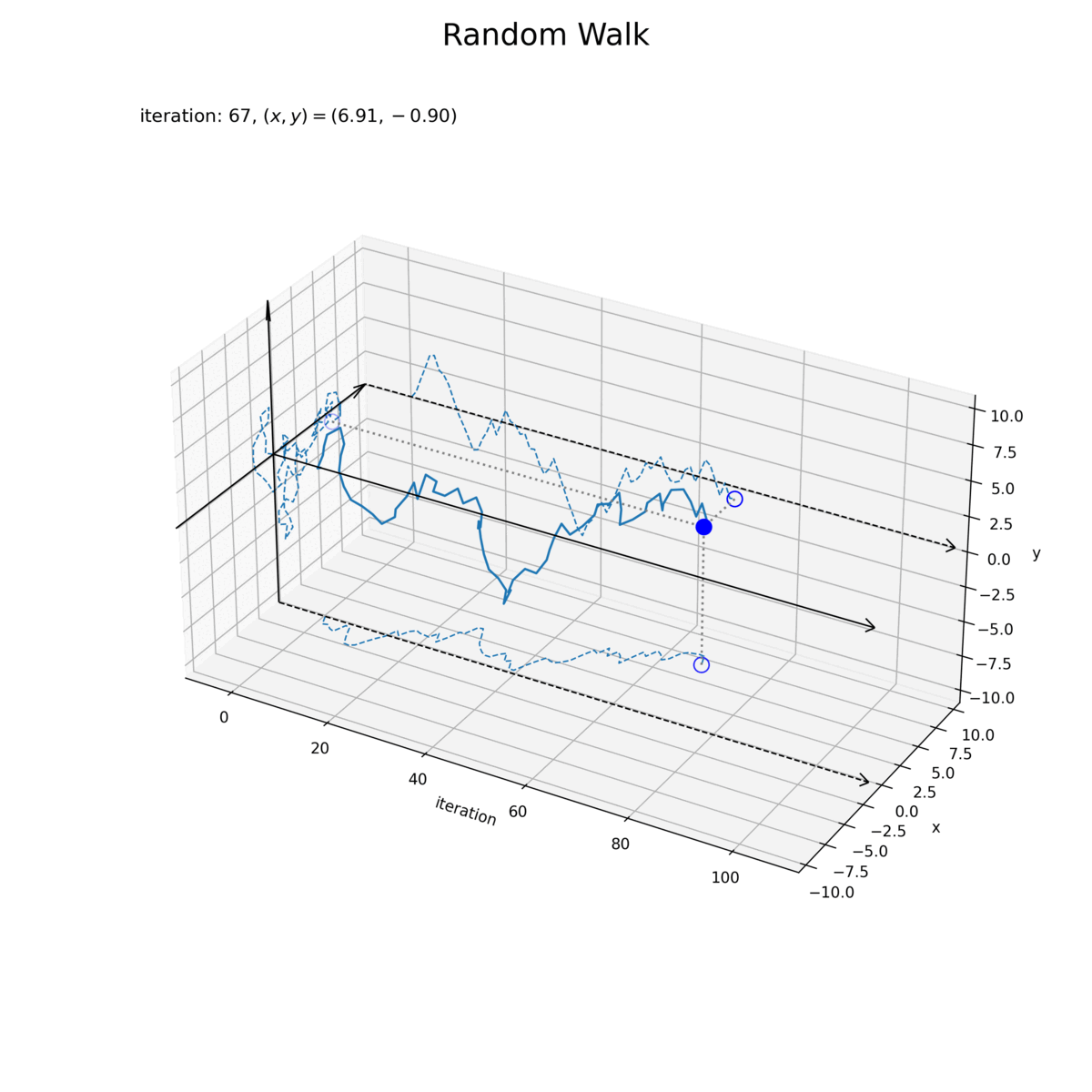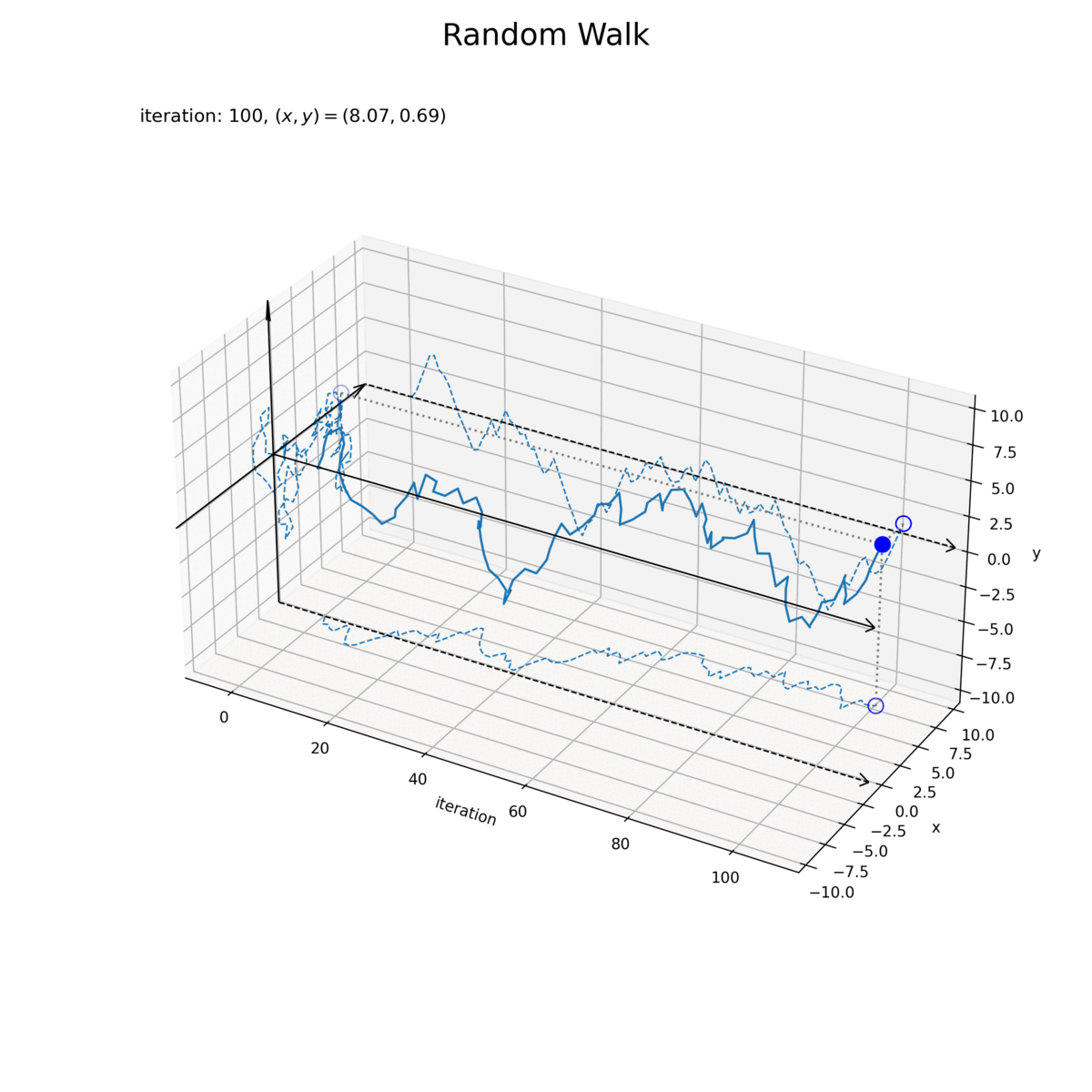
試行回数(時間)の変化を横軸で表します。また、試行回数ごとの各軸、両軸の変化をそれぞれ側面に描画しています。
試行回数と各軸のグラフは、1次元ランダムウォークのように推移していますが、1つの軸に注目すると距離(ノルム)が1以下で変化するので、異なる図です。
複数サンプル
続いて、複数のサンプルを並べて描画します。
作図コードについては「RandomWalk_2d_360.py at anemptyarchive/matplotlib · GitHub」を参照してください。
・座標軸のみ
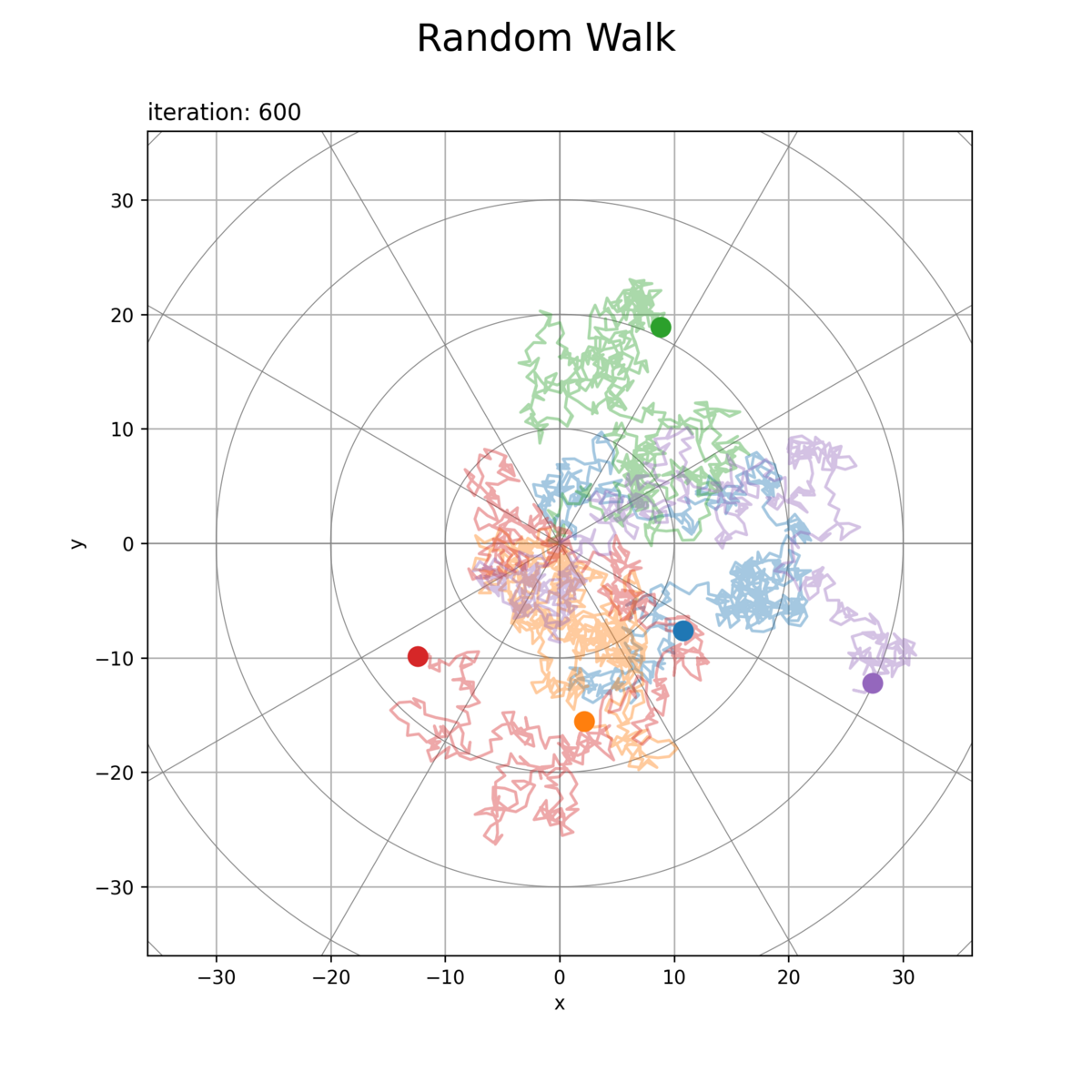
等確率で移動する場合、初期値が期待値になりますが分散を持ち(散らばり)ます。
・サンプル軸あり
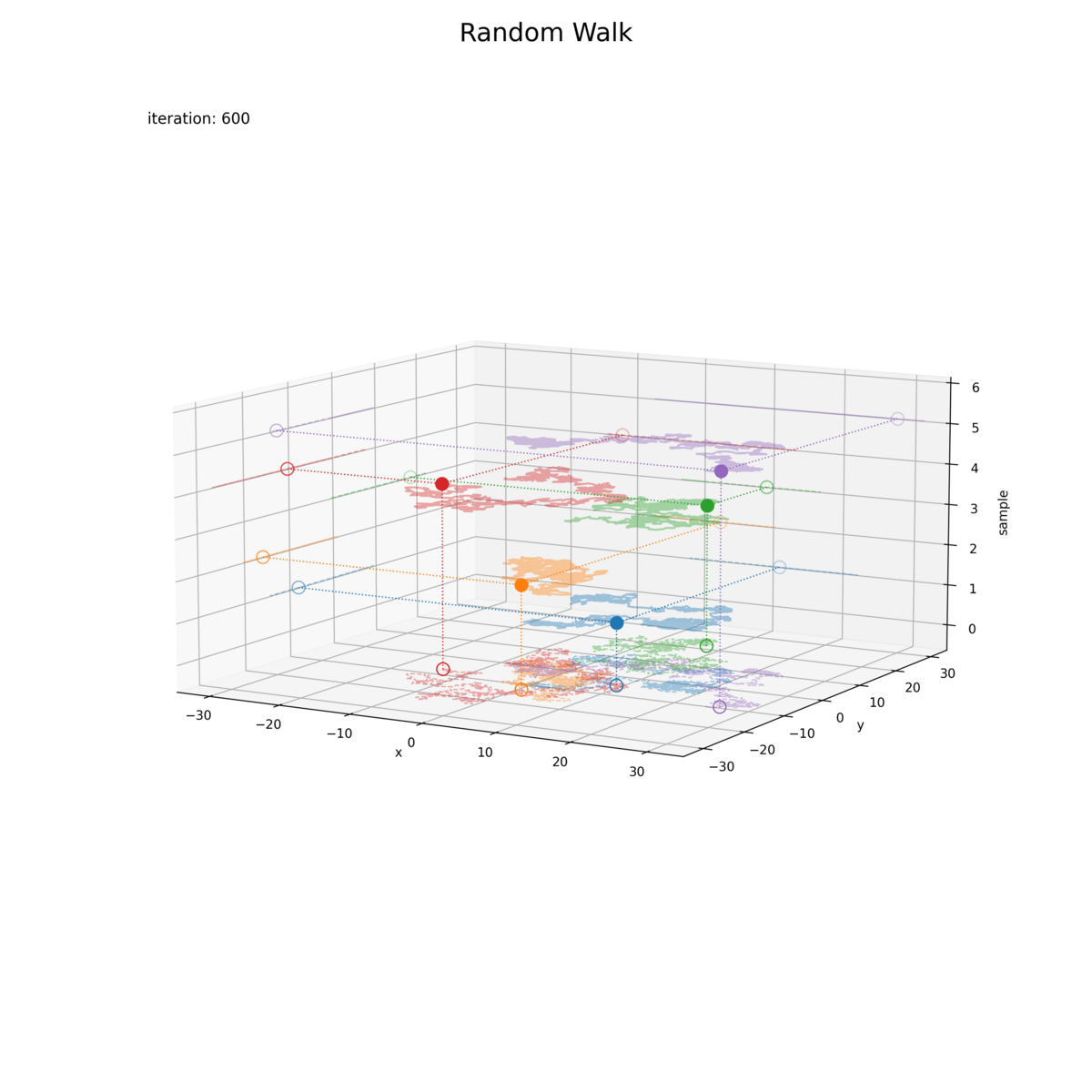
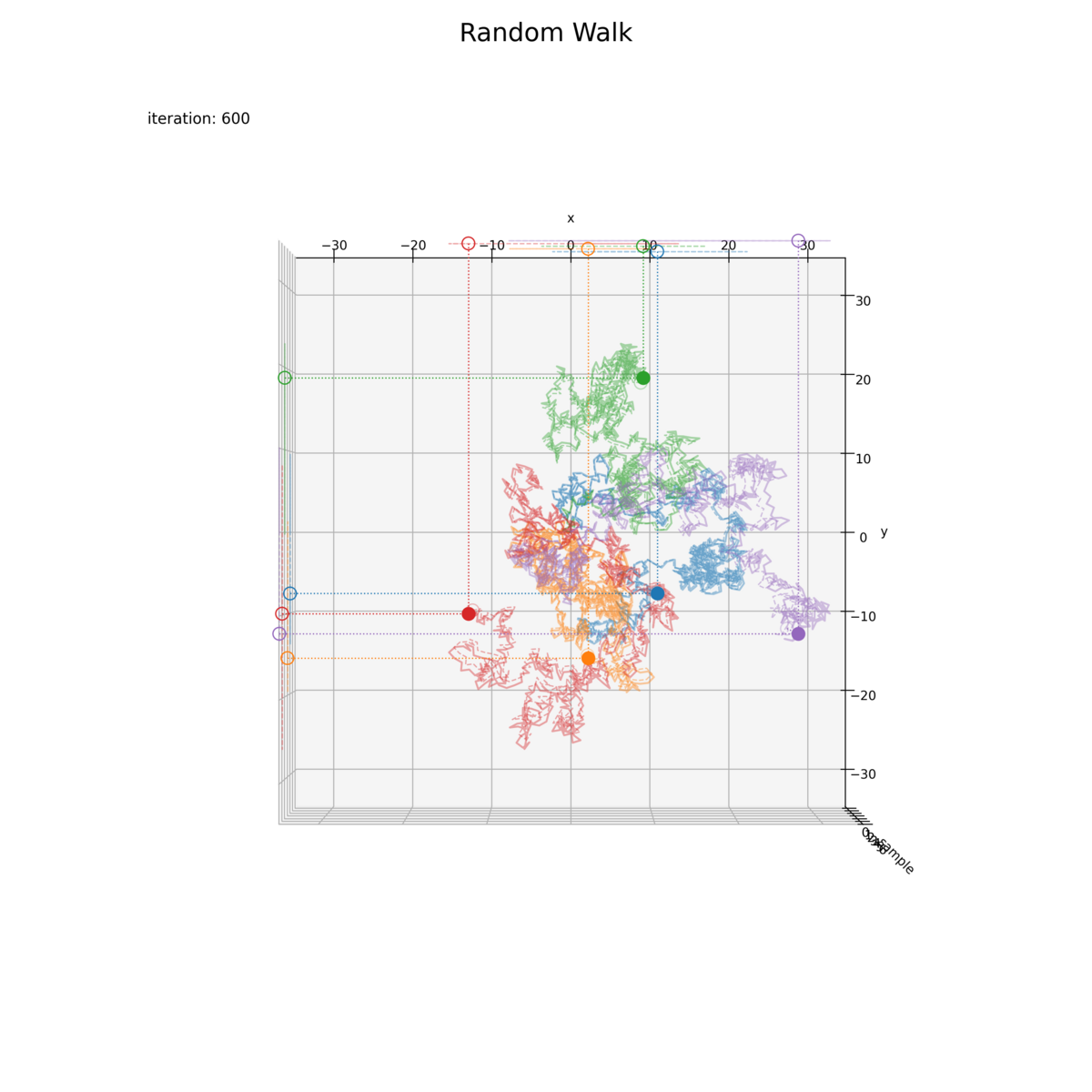
サンプルごとに縦に並べています。
・試行回数(時間)軸あり
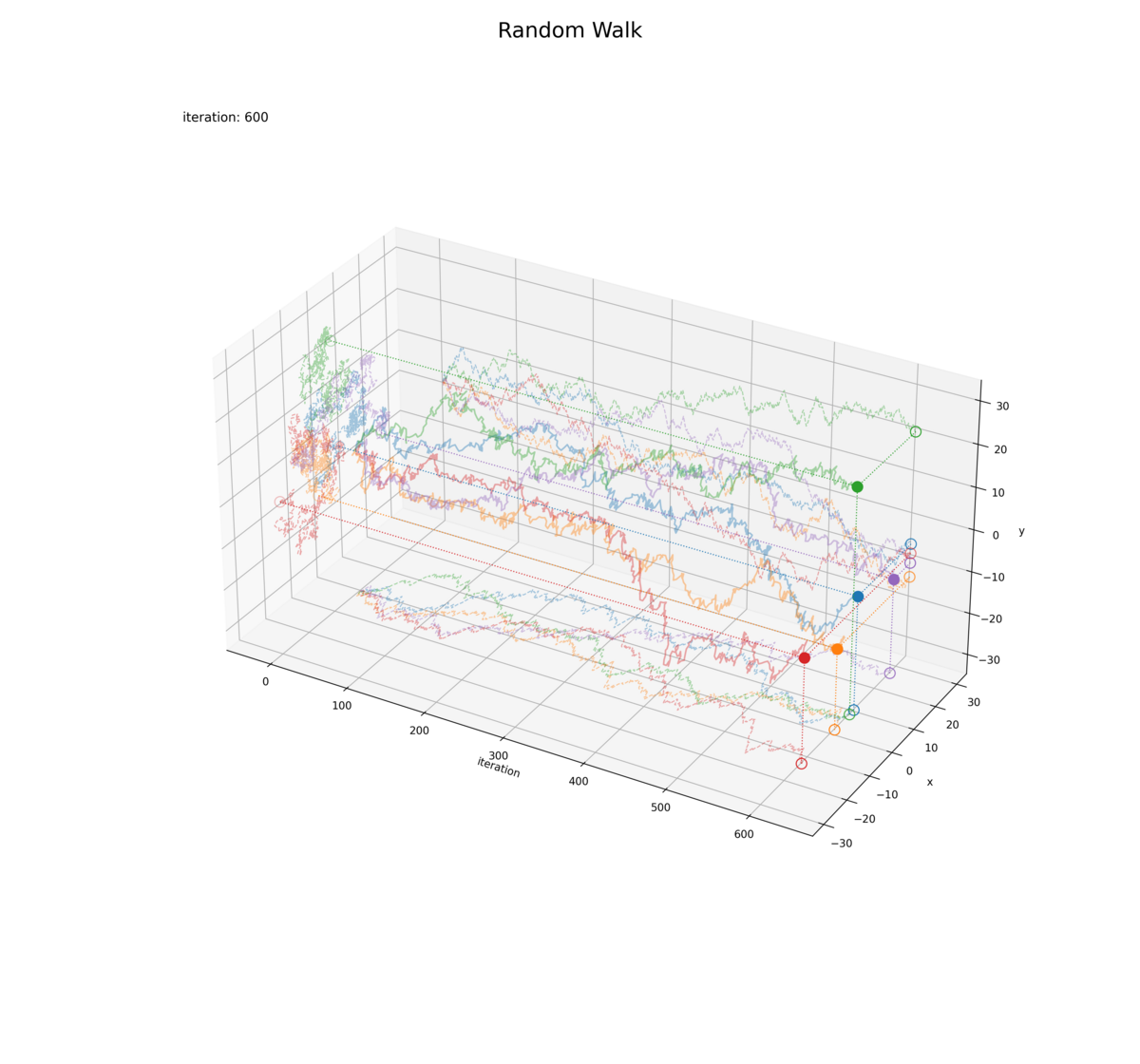
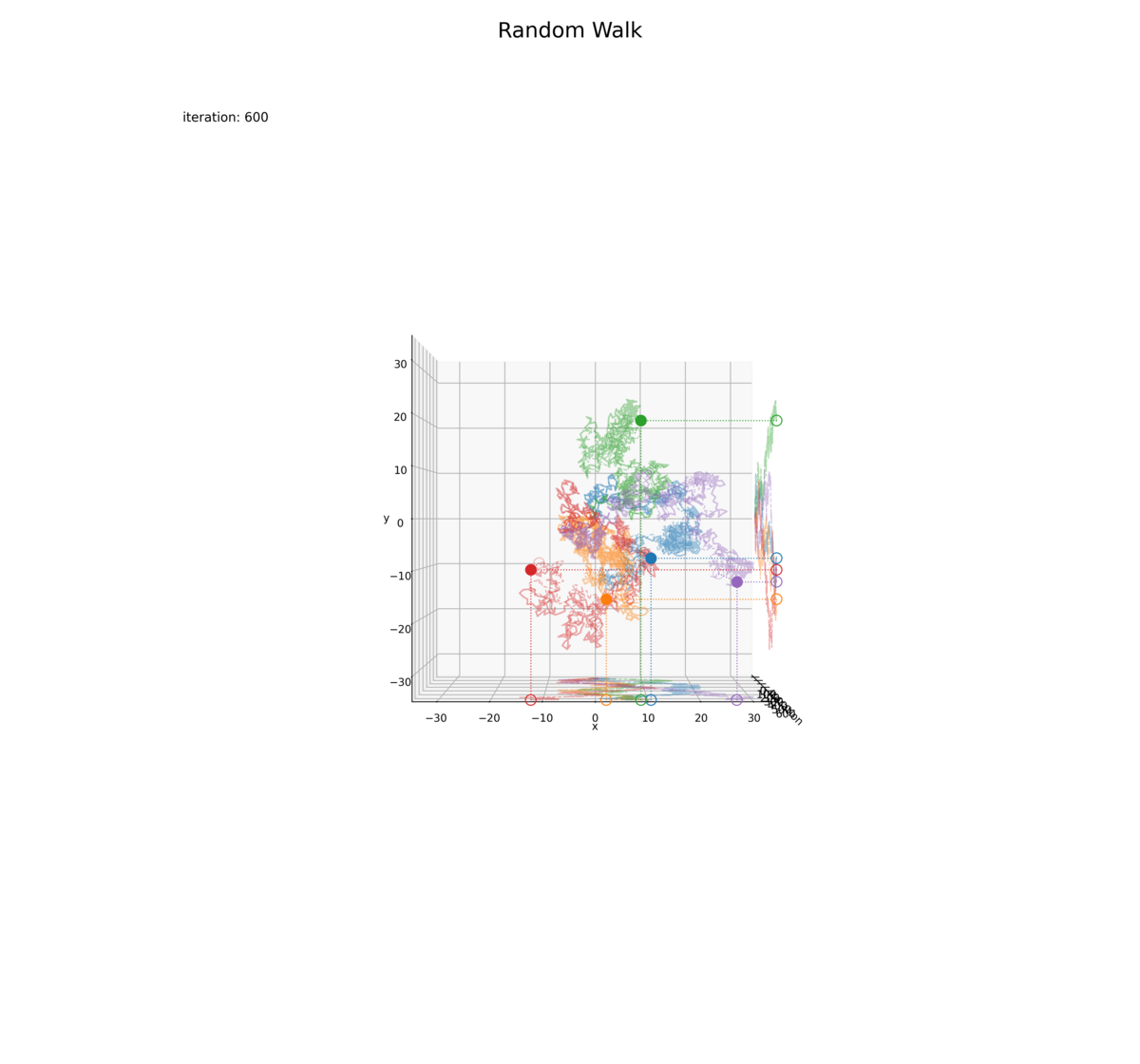
回数が増えると分散が大きくなるのを確認できます。
この記事では、全ての方向に移動する2次元ランダムウォークを扱いました。次の記事では、格子状に移動する3次元ランダムウォークを扱います。
おわりに
ここまではR版でもやりました。次からがPython版でやりたかった3次元編です。という想定でしたが、次の記事での図よりもこっちの記事の最後の3次元図の出来ばえに大満足しています。3Dプロットを作りたいがために思い付きで時間軸を加えたようなものですが、手を動かして遊んでると色々閃くものですね。見切り発車だったけど全部やって良かった。
R版も含めたランダムウォークシリーズでこの記事がたぶんサビです。
【次の内容】