はじめに

　Matplotlibライブラリを利用して、球面のグラフを作成します。

【前の内容】

【目次】

はじめに
球面の作図
おわりに

球面の作図

　Matplotlibライブラリを利用して、3次元空間上に球面(spherical surface)のグラフを作成します。また、球面座標系(spherical coordinate system)をグラフで確認します。

　利用するライブラリを読み込みます。

# 利用ライブラリ
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

座標の計算

　まずは、球面上の点の座標計算を確認します。

　角度と半径を指定して、球面上の点(ノルムが指定した半径になる3次元ベクトル)を計算します。

# 半径を指定
r = 14.0

# 度数法の角度を指定
t = 45.0
u = 180.0

# 弧度法の角度(ラジアン)を計算
t *= np.pi / 180.0
u *= np.pi / 180.0
print(t)
print(u)

# 球面上の点の座標を計算
x = r * np.sin(t) * np.cos(u)
y = r * np.sin(t) * np.sin(u)
z = r * np.cos(t)

# 座標を格納
p = np.array([x, y, z])
print(p)
print(np.linalg.norm(p))

0.7853981633974483
3.141592653589793
[-9.89949494e+00  1.21233848e-15  9.89949494e+00]
14.0

　度数法における角度を $\theta^{\circ}$ 、弧度法における角度(ラジアン)を $\theta$ で表すことにします。度数法と弧度法は $\theta = \frac{2 \pi}{360^{\circ}} \theta^{\circ}$ 、 $\theta^{\circ} = \frac{360}{2 \pi} \theta$ の関係です。つまり、 $\theta^{\circ} = 0^{\circ}$ のとき $\theta = 0$ 、 $\theta^{\circ} = 180^{\circ}$ のとき $\theta = \pi$ 、 $\theta^{\circ} = 360^{\circ}$ のとき $\theta = 2 \pi$ です。
　 $\pi$ は円周率で、np.piで扱えます。

　半径を $r$ 、垂直方向の角度(z軸とのなす角)を $\theta$ 、水平方向の角度(y軸とのなす角)を $\phi$ とします。オブジェクト名はr, t, uとします。
　半径が $r$ の曲面上の点(ノルムが $r$ の3次元ベクトル)を $\mathbf{p} = (x, y, z)$ とすると、x軸・y軸・z軸の座標は、次の式で計算できます。

$\displaystyle \begin{cases} x = r \sin \theta \cos \phi \\ y = r \sin \theta \sin \phi \\ z = r \cos \theta \end{cases} \tag{1}$

　直交座標系の座標を $(x, y, z)$ 、球面座標系の座標を $(r, \theta, \phi)$ で表します。
　式(1)は、球面座標系から直交座標系への変換式です。

　 $\mathbf{p}$ のユークリッドノルム $\|\mathbf{p}\| = \sqrt{x^2 + y^2 + z^2}$ は $r$ になります。ユークリッドノルムは、np.linalg.norm()で計算できます。

　あるいは、3次元ベクトルを指定して、球面上の点(ノルムが指定した半径になるベクトル)に変換します。

# ベクトルを指定
p = np.array([10.0, 17.0, 12.0])
#p = np.array([x, y, z]) # 確認用
print(np.linalg.norm(p))

# 半径を指定
r = 14.0

# ノルムをrに変換(球面上の座標を計算)
p *= r / np.linalg.norm(p)
print(p)
print(np.linalg.norm(p))

23.08679276123039
[ 6.06407315 10.30892435  7.27688777]
14.000000000000002

　任意の3次元ベクトル $\tilde{\mathbf{p}} = (\tilde{x}, \tilde{y}, \tilde{z})$ を指定して、ノルムで割り正規化(ノルムを1に変換)します。さらに、半径 $r$ を掛けるとノルムが $r$ のベクトルになります。

$\displaystyle \mathbf{p} = r \frac{ \tilde{\mathbf{p}} }{ \|\tilde{\mathbf{p}}\| } = r \frac{ \tilde{\mathbf{p}} }{ \sqrt{\tilde{x}^2 + \tilde{y}^2 + \tilde{z}^2} }$

　この計算により、3次元空間上の点 $\tilde{\mathbf{p}}$ と角度 $\theta, \phi$ が同じである球面上の点(ベクトル $\tilde{\mathbf{p}}$ と同じ方向であるノルムが $r$ のベクトル) $\mathbf{p}$ が得られます。ベクトルのスカラ倍なのでベクトルの向きは変わりません。

　球面上の点から半径と角度を計算します。

# 半径を計算
r = np.linalg.norm(p)
print(r)

# 垂直方向の角度(ラジアン)を計算
t = np.arccos(p[2] / np.linalg.norm(p))
print(t)

# 水平方向の角度(ラジアン)を計算
sgn_y = 1.0 if p[1] >= 0.0 else -1.0
u = sgn_y * np.arccos(p[0] / np.linalg.norm(p[[0, 1]]))
print(u)

# 度数法の角度を計算
t *= 180.0 / np.pi
u *= 180.0 / np.pi
print(t)
print(u)

14.000000000000002
1.0242056113903688
1.039072259536091
58.68265888628425
59.53445508054013

　半径 $r$ と2方向の角度 $\theta, \phi$ は、次の式で計算できます。

$\displaystyle \begin{align*} &\begin{cases} r = \|\mathbf{p}\| = \sqrt{x^2 + y^2 + z^2} \\ \theta = \arccos \Bigl( \frac{z}{\|\mathbf{p}\|} \Bigr) = \arccos \Bigl( \frac{z}{\sqrt{x^2 + y^2 + z^2}} \Bigr) \\ \phi = \mathrm{sgn}(y) \arccos \Bigl( \frac{x}{\sqrt{x^2 + y^2}} \Bigr) \\ \end{cases} \tag{2}\\ &\mathrm{sgn}(y) = \begin{cases} 1 & (y \geq 0) \\ -1 & (y < 0) \end{cases} \end{align*}$

　 $\arccos x$ は逆コサイン関数(コサイン関数 $\cos x$ の逆関数)で、np.arccos()で計算できます。y軸の値 $y$ の符号を $\mathrm{sgn}(y)$ で表しています。
　式(2)は、直交座標系から曲面座標系への変換式です。

　ここでは、2通りの座標計算方法を確認しました。以降は、1つ目の方法を用います。

球面の描画

　次は、球面全体の座標を計算して、球面のグラフを作成します。

　1周期分のラジアンを作成して、球面上の座標を計算します。周期については「2変数と各軸の値の関係」で確認します。

# 半径を指定
r = 1.0

# ラジアンを作成
t = np.linspace(start=0.0, stop=2.0*np.pi, num=81)
u = np.linspace(start=0.0, stop=2.0*np.pi, num=81)
print(t[:5])
print(len(t))

# 格子点を作成
T, U = np.meshgrid(t, u)
print(T[:3, :3].round(2))
print(U[:3, :3].round(2))
print(T.shape)
print(U.shape)

# 球面の座標を計算
X = r * np.sin(T) * np.cos(U)
Y = r * np.sin(T) * np.sin(U)
Z = r * np.cos(T)
print(X[:3, :3].round(2))
print(Y[:3, :3].round(2))
print(Z[:3, :3].round(2))

[0.         0.07853982 0.15707963 0.23561945 0.31415927]
81
[[0.   0.08 0.16]
 [0.   0.08 0.16]
 [0.   0.08 0.16]]
[[0.   0.   0.  ]
 [0.08 0.08 0.08]
 [0.16 0.16 0.16]]
(81, 81)
(81, 81)
[[0.   0.08 0.16]
 [0.   0.08 0.16]
 [0.   0.08 0.15]]
[[0.   0.   0.  ]
 [0.   0.01 0.01]
 [0.   0.01 0.02]]
[[1.   1.   0.99]
 [1.   1.   0.99]
 [1.   1.   0.99]]

　 $0 \leq \theta \leq 2 \pi$ 、 $0 \leq \phi \leq 2 \pi$ の範囲のラジアンt, uを作成して、格子状の点(全ての組み合わせ)T, Uをnp.meshgrid()で作成します。
　 $\theta, \phi$ の範囲(最大値と最小値の差)が $2 \pi$ であれば、他の値であっても同じグラフになります。また、片方の角度の範囲が $\pi$ でも球面を描画できます。
　T, Uを用いて、座標の計算式(1)を計算して、x軸・y軸・z軸の値をそれぞれX, Y, Zとします。

　色付け用の配列を作成します。また確認のため、点ごとにノルムを計算します。

# 3つの軸の値を結合
XYZ = np.stack([X.flatten(), Y.flatten(), Z.flatten()], axis=1)
print(XYZ[:5])
print(XYZ.shape)
print(np.linalg.norm(XYZ, axis=1)[:5])

[[0.         0.         1.        ]
 [0.0784591  0.         0.99691733]
 [0.15643447 0.         0.98768834]
 [0.23344536 0.         0.97236992]
 [0.30901699 0.         0.95105652]]
(6561, 3)
[1. 1. 1. 1. 1.]

　色付けやノルムの計算用に、X, Y, Zをそれぞれ1列として結合した配列XYZを作成します。
　np.linalg.norm()のaxix引数に1を指定して行(点)ごとにノルムを計算すると、どの点も値がrになるのを確認できます。

　球面のグラフを作成します。

# タイトル用の文字列(座標の計算式)を作成
coord_label = '$x = r\ \\sin \\theta\ \cos \phi$\n'
coord_label += '$y = r\ \\sin \\theta\ \sin \phi$\n'
coord_label += '$z = r\ \\cos \\theta$'

# 球面を作図
fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.plot_wireframe(X, Y, Z, alpha=0.5) # くり抜き曲面
#ax.plot_surface(X, Y, Z, cmap='jet', alpha=0.5) # 塗りつぶし曲面
#ax.scatter(X, Y, Z, c=Z, cmap='viridis', alpha=0.5) # 散布図:(z軸の値により色付け)
#ax.scatter(X, Y, Z, color=(XYZ+r)*0.5/r, alpha=0.5) # 散布図:(xyz座標の値により色付け)
ax.contour(X, Y, Z, cmap='jet', zdir='z', offset=-r) # 等高線
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('$r=' + str(r) + '$\n' + coord_label, loc='left')
fig.suptitle('spherical surface', fontsize=20)
ax.set_aspect('equal')
plt.show()

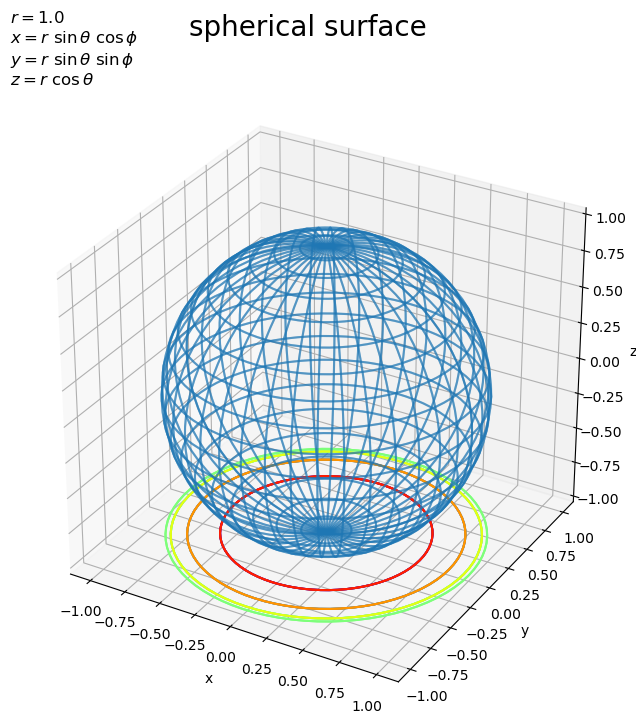
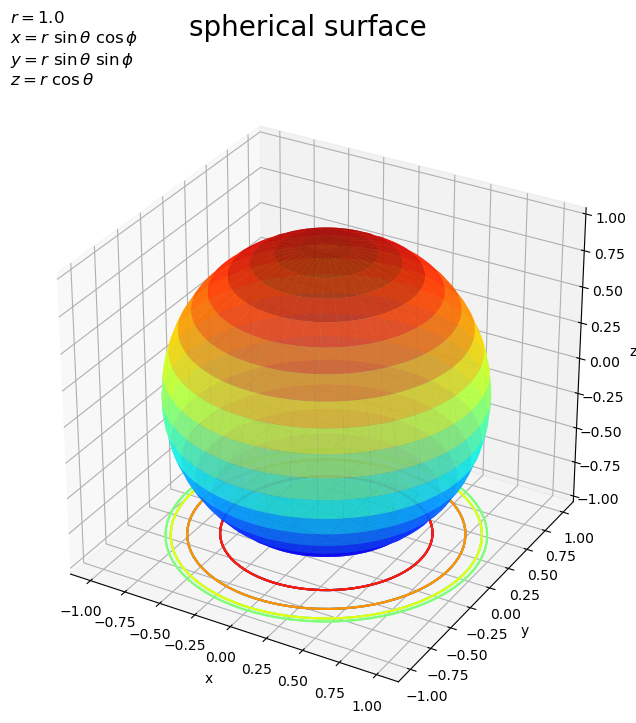
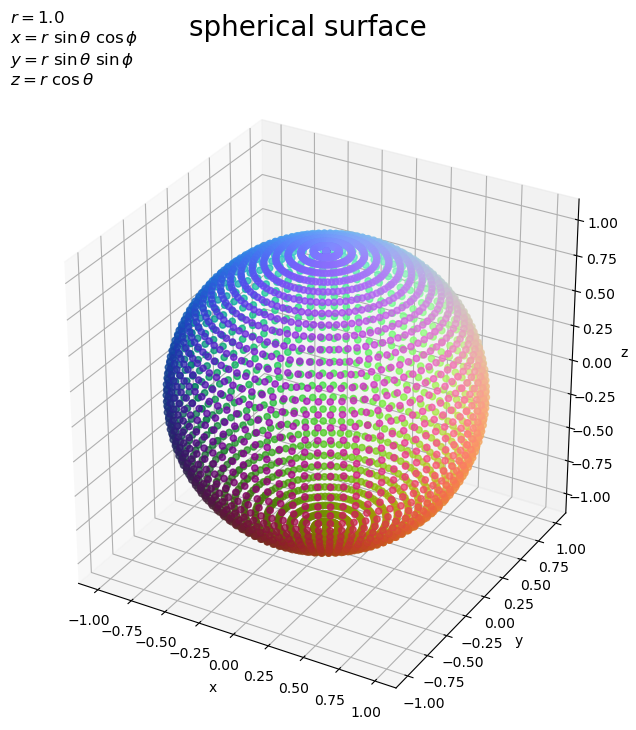
　Axes.plot_wireframe()で曲面図、Axes.plot_surface()で塗りつぶしの曲面図、Axes.scatter()で散布図として球面を描画できます。
　参考として、底面(z軸の最小値 $z = -r$ の面)にax.contour()で等高線図を描画しています。zdir引数に'x'や'y'を指定すると側面に描画できます。デフォルトは'z'で、底面に描画します。offset引数に値を指定して、描画位置を指定できます。

　綺麗な球面を描画するには、Axes.set_aspect('equal')を使ってアスペクト比を1に設定します。

　cmap引数にカラーマップ名を指定して、z軸の値などに応じてグラデーションで色付けられます。
　散布図に関して、color引数に「各点の座標 $(x, y, z)$ を正規化した値をRGB値」として指定して、点ごとの座標に応じて色付けられます。各軸の値は最小値が $-r$ 、最大値が $r$ です。そこで、各点に $r$ を足すことで $0$ から $2 r$ の値になり、さらに $2 r$ で割ることで $0$ から $1$ の値に変換できます。x軸の値が大きい( $x$ が $r$ に近く $y, z$ が $0$ に近い)ほど赤色、y軸の値が大きいほど緑色、z軸の値が大きいほど青色に近い色になります。

　グラフを回転させて確認します。

・作図コード(クリックで展開)

# フレーム数を指定
frame_num = 59

# 表示角度として利用する値を作成
v_n = np.linspace(start=30.0, stop=30.0, num=frame_num+1)[:frame_num]
h_n = np.linspace(start=0.0, stop=360.0, num=frame_num+1)[:frame_num]

# グラフオブジェクトを初期化
fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
fig.suptitle('spherical surface', fontsize=20)

# 作図処理を関数として定義
def update(i):
    
    # 前フレームのグラフを初期化
    plt.cla()

    # i番目の角度を取得
    v = v_n[i]
    h = h_n[i]
    
    # 球面を作図
    ax.scatter(X, Y, Z, color=(XYZ+r)*0.5/r, alpha=0.5) # 散布図:(xyz座標の値により色付け)
    ax.quiver([0, 0, 0], [0, 0, 0], [0, 0, 0], 
              [1, 0, 0], [0, 1, 0], [0, 0, 1], 
              color='black', lw=2, arrow_length_ratio=0.0, zorder=-50) # x,y,z軸
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    ax.set_title('$r=' + str(r) + '$\n' + coord_label, loc='left')
    ax.set_aspect('equal')
    ax.view_init(elev=v, azim=h) # 表示角度

# gif画像を作成
ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100)

# gif画像を保存
ani.save('sphere_3d.gif')

　作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。

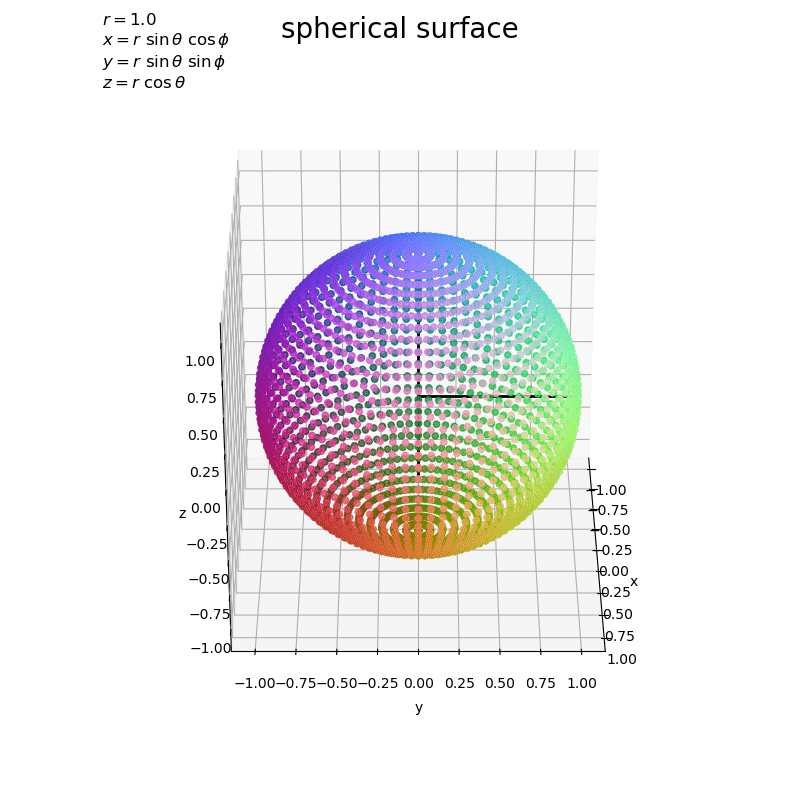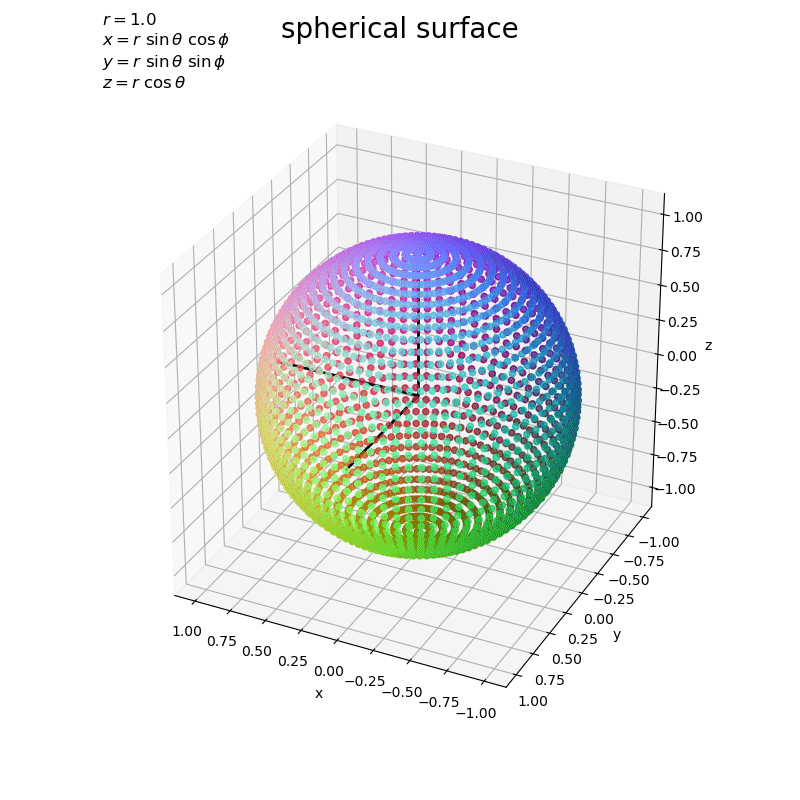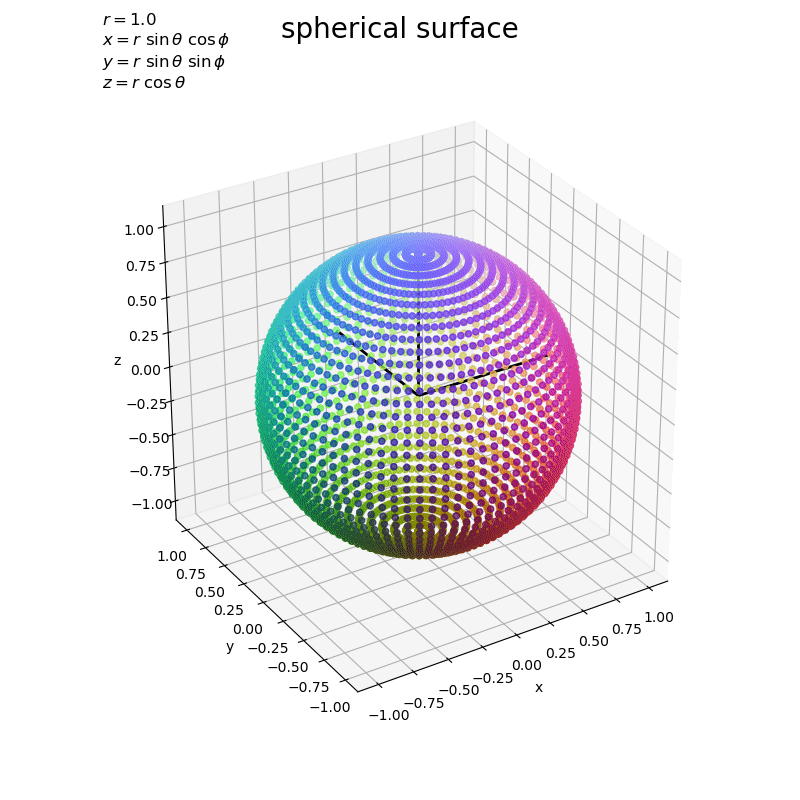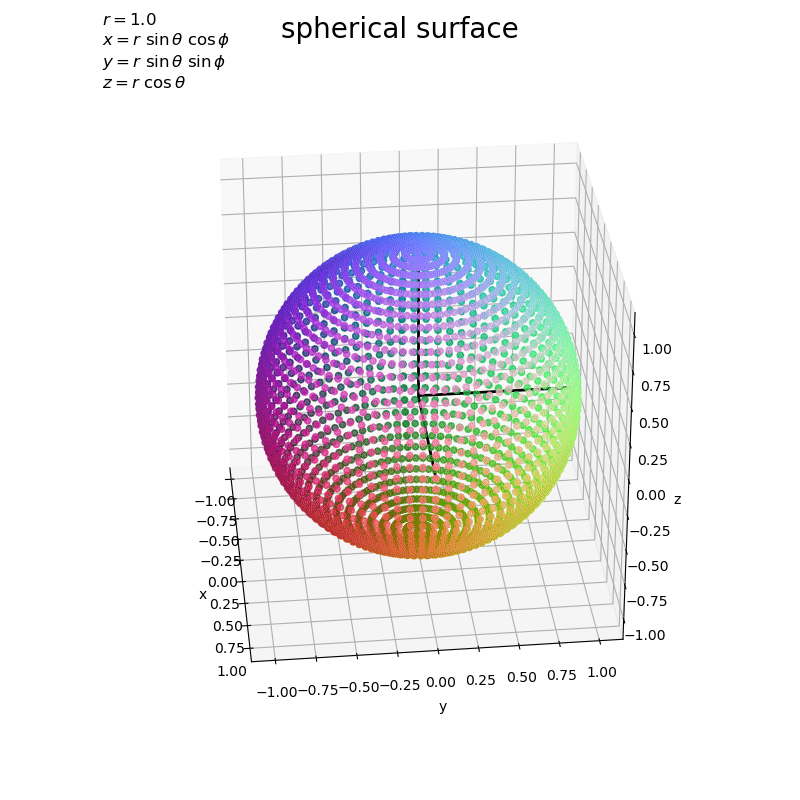
　x軸・y軸・z軸を黒色の線分として描画しています。
　球面は、原点からの距離(ノルム)が $r$ の点なのが分かります。

　以上で、球面を描画できました。次からは、2つの変数(角度)と3つの軸の値の関係を確認します。

2変数と各軸の値の関係

　2つの角度とx軸・y軸・z軸それぞれの値の関係をグラフで確認します。

　1周期分以上のラジアンを作成して、球面の座標を計算します。

# 半径を指定
r = 1.0

# ラジアンを作成
t = np.linspace(start=-2.0*np.pi, stop=2.0*np.pi, num=200)
u = np.linspace(start=-2.0*np.pi, stop=2.0*np.pi, num=200)
print(t[:5])
print(len(t))

# 格子点を作成
T, U = np.meshgrid(t, u)
print(T.shape)
print(U.shape)

# 球面の座標を計算
X = r * np.sin(T) * np.cos(U)
Y = r * np.sin(T) * np.sin(U)
Z = r * np.cos(T)
print(X[:3, :3].round(2))
print(Y[:3, :3].round(2))
print(Z[:3, :3].round(2))

[-6.28318531 -6.22003772 -6.15689013 -6.09374253 -6.03059494]
200
(200, 200)
(200, 200)
[[0.   0.06 0.13]
 [0.   0.06 0.13]
 [0.   0.06 0.12]]
[[0.   0.   0.  ]
 [0.   0.   0.01]
 [0.   0.01 0.02]]
[[1.   1.   0.99]
 [1.   1.   0.99]
 [1.   1.   0.99]]

　「球面の描画」のときと同様にして、球面の座標を計算します。ただしこの例では、周期性が分かるように、ラジアン $\theta, \phi$ の範囲をそれぞれ $-2 \pi$ から $2 \pi$ とします。

　 $\theta$ 軸・ $\phi$ 軸のラジアン目盛用の配列を作成します。グラフ自体には不要な処理です。

# 半円の目盛の数(分母の値)を指定
denom = 3.0

# 目盛の通し番号(分子の値)を作成
tick_vals = np.arange(start=-2.0*denom, stop=2.0*denom+0.1)
print(tick_vals[:5])

# 目盛用のラジアンを計算
tick_rad_vals = tick_vals / denom * np.pi
print(tick_rad_vals[:5].round(2))

# 目盛ラベルを作成
tick_label_vals = [
    '$' + ('-' if nomer < 0.0 else '') + '\\frac{' + str(abs(nomer)) + '}{' + str(int(denom)) + '} \pi$' for nomer in tick_vals.astype('int16')
]
print(tick_label_vals[:3])

[-6. -5. -4. -3. -2.]
[-6.28 -5.24 -4.19 -3.14 -2.09]
['$-\\frac{6}{3} \\pi$', '$-\\frac{5}{3} \\pi$', '$-\\frac{4}{3} \\pi$']

　軸目盛ラベルを $\frac{i}{n} \pi$ の形で表示することにします。この例では2周期分を描画するので、 $i$ を $-2 n$ から $2 n$ の整数 $i = -2 n, -2 (n-1), \dots , -1, 0, 1, \dots, 2 (n-1), 2 n$ とします。 $n$ をdenom、 $i$ をtick_valsとして値を指定します。
　軸目盛の座標用のラジアン $t = \frac{i}{n} \pi$ を計算してtick_rad_valsとします。

　 $\theta, \phi$ と $x$ の関係のグラフを作成します。

# x軸の値を曲面で作図
fig, ax = plt.subplots(figsize=(12, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.plot_surface(T, U, X, cmap='jet', alpha=0.8)
ax.contour(T, U, X, cmap='jet', zdir='z', offset=-r)
ax.set_xticks(ticks=tick_rad_vals, labels=tick_label_vals) # θ目盛ラベル
ax.set_yticks(ticks=tick_rad_vals, labels=tick_label_vals) # φ目盛ラベル
ax.set_xlabel('$\\theta$')
ax.set_ylabel('$\phi$')
ax.set_zlabel('$x$')
ax.set_title('$r=' + str(r) + '$', loc='left')
fig.suptitle('$x = r\ \\sin \\theta\ \cos \phi$', fontsize=20)
ax.set_aspect('equal')
plt.show()

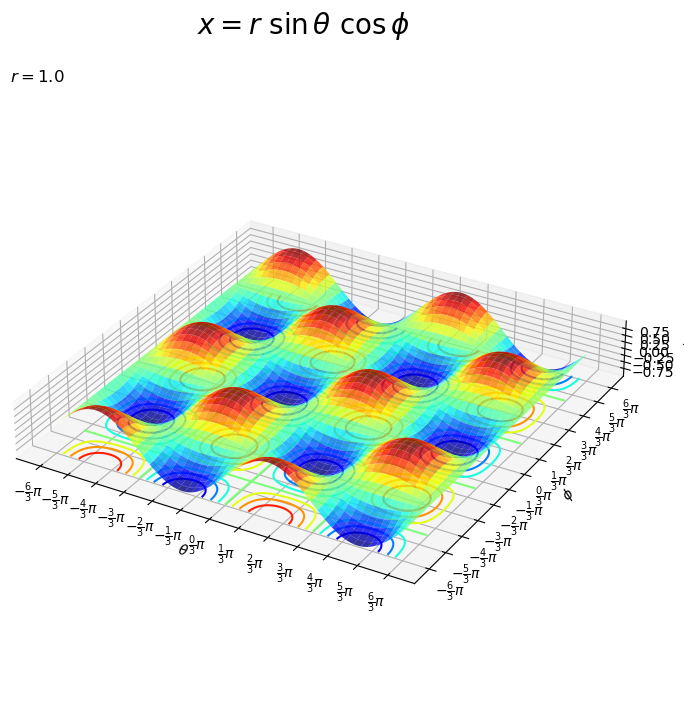
　 $\theta, \phi$ それぞれで $t, t + 2 \pi$ の $x$ の値が一致するのが分かります。それぞれの軸で $2 \pi$ ごとに周期的に推移します。

　 $\theta, \phi$ と $y$ の関係のグラフを作成します。

# y軸の値を曲面で作図
fig, ax = plt.subplots(figsize=(12, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.plot_surface(T, U, Y, cmap='jet', alpha=0.8)
ax.contour(T, U, Y, cmap='jet', zdir='z', offset=-r)
ax.set_xticks(ticks=tick_rad_vals, labels=tick_label_vals) # θ目盛ラベル
ax.set_yticks(ticks=tick_rad_vals, labels=tick_label_vals) # φ目盛ラベル
ax.set_xlabel('$\\theta$')
ax.set_ylabel('$\phi$')
ax.set_zlabel('$y$')
ax.set_title('$r=' + str(r) + '$', loc='left')
fig.suptitle('$y = r\ \\sin \\theta\ \\sin \phi$', fontsize=20)
ax.set_aspect('equal')
plt.show()

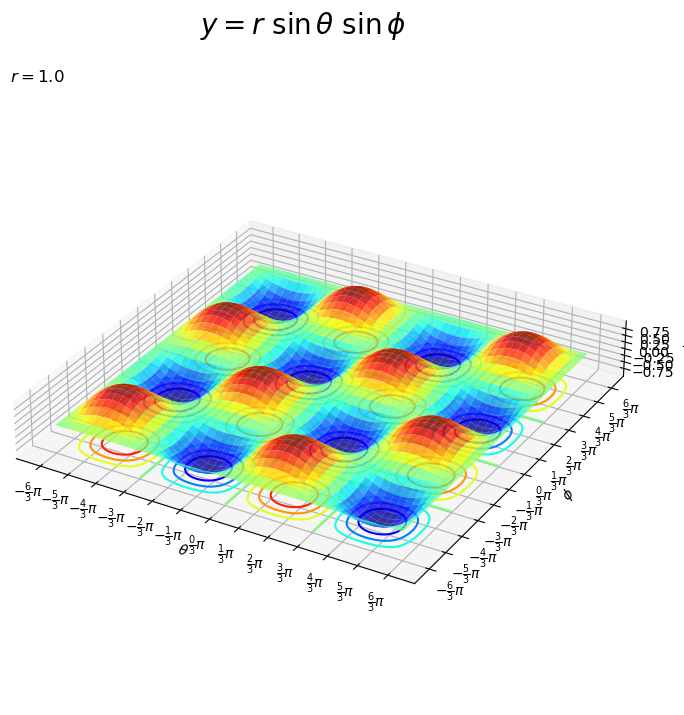
　こちらも $2 \pi$ ごとに周期します。

　 $\theta, \phi$ と $z$ の関係のグラフを作成します。

# z軸の値を曲面で作図
fig, ax = plt.subplots(figsize=(12, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.plot_surface(T, U, Z, cmap='jet', alpha=0.8)
ax.contour(T, U, Z, cmap='jet', zdir='z', offset=-r)
ax.set_xticks(ticks=tick_rad_vals, labels=tick_label_vals) # θ目盛ラベル
ax.set_yticks(ticks=tick_rad_vals, labels=tick_label_vals) # φ目盛ラベル
ax.set_xlabel('$\\theta$')
ax.set_ylabel('$\phi$')
ax.set_zlabel('$z$')
ax.set_title('$r=' + str(r) + '$', loc='left')
fig.suptitle('$z = r\ \\cos \\theta$', fontsize=20)
ax.set_aspect('equal')
plt.show()

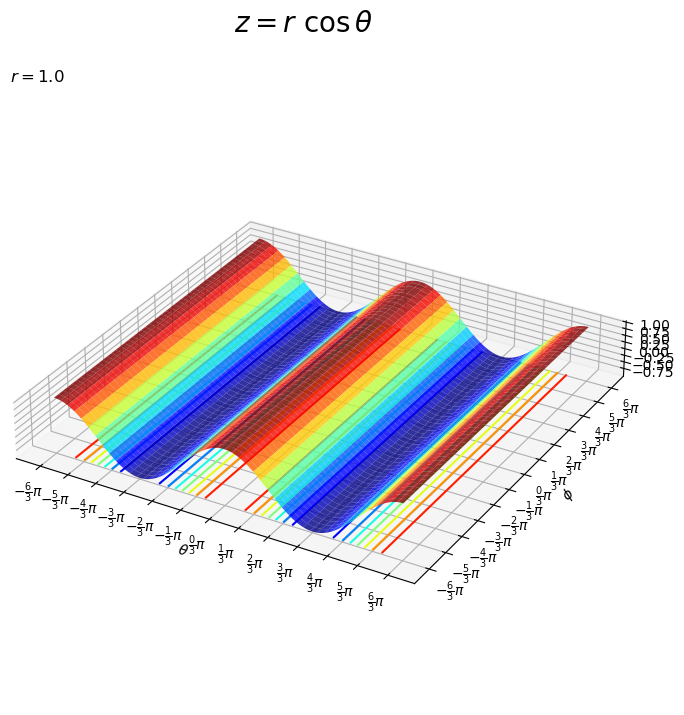
　 $z$ は $\phi$ と無関係なので、 $\theta$ の値によってのみ変化します。 $\theta$ について $2 \pi$ ごとに周期します。

　ここでは、2変数(角度)と3つの軸それぞれの値の関係を確認しました。次は、全ての軸の値との関係を確認します。

2変数と座標の関係

　最後に、球面上に2変数(角度)に関する軸目盛を描画して、変数と座標の関係をグラフで確認します。

　球面の座標を計算します。

# ラジアンを作成
t = np.linspace(start=0.0, stop=0.5*np.pi, num=50)
u = np.linspace(start=0.0, stop=0.5*np.pi, num=50)
print(t[:5])
print(len(t))

# 格子点を作成
T, U = np.meshgrid(t, u)
print(T.shape)
print(U.shape)

# 半径を指定
r = 1.0

# 球面の座標を計算
X = r * np.sin(T) * np.cos(U)
Y = r * np.sin(T) * np.sin(U)
Z = r * np.cos(T)

[0.         0.03205707 0.06411414 0.0961712  0.12822827]
50
(50, 50)
(50, 50)

　「球面の描画」のときと同様にして、球面の座標を計算します。ただしこの例では、目盛が見えやすいように、 $x \geq 0, y \geq 0, z \geq 0$ と $x \leq 0, y \leq 0, z \leq 0$ の範囲のみを描画します。そのため、ラジアン $\theta, \phi$ の範囲をそれぞれ $0$ から $\frac{\pi}{2}$ とします。

　 $\theta$ 軸・ $\phi$ 軸目盛用の配列を作成します。

# 半円の目盛の数(分母の値)を指定
denom = 3.0

# 目盛の通し番号(分子の値)を作成
tick_vals = np.arange(stop=2.0*denom)
print(tick_vals)

# 目盛用のラジアンを計算
tick_rad_vals = tick_vals / denom * np.pi
print(tick_rad_vals.round(2))

# 目盛用の座標を計算
tick_rsin_vals = r * np.sin(tick_rad_vals)
tick_rcos_vals = r * np.cos(tick_rad_vals)
print(tick_rsin_vals.round(2))
print(tick_rcos_vals.round(2))

[0. 1. 2. 3. 4. 5.]
[0.   1.05 2.09 3.14 4.19 5.24]
[ 0.    0.87  0.87  0.   -0.87 -0.87]
[ 1.   0.5 -0.5 -1.  -0.5  0.5]

　「2変数と各軸の値の関係」のときと同様にして、ラジアン目盛用の値を作成します。この例では1周期分を描画するので、 $i$ を $0$ から $2 n$ の整数 $i = 0, 1, \dots, 2 n$ とします。
　さらに、軸目盛用のラジアンtick_rad_valsを用いて、目盛の描画位置の座標を計算します。

　 $\phi = \frac{\pi}{2}$ のときの $0 \leq \theta \leq 2 \pi$ に対する値(曲面上の直線・球の断面の円)が、 $\theta$ 軸線に対応します。
　 $\sin \frac{\pi}{2} = 1, \cos \frac{\pi}{2} = 0$ なので、座標の計算式(1)は $x = r \sin \phi, y = \cos \phi, z = 0$ になります。

　同様に、 $\theta = 0$ のときの $0 \leq \phi \leq 2 \pi$ に対する値が、 $\phi$ 軸線に対応します。
　 $\sin 0 = 0, \cos 0 = 1$ なので、座標の計算式(1)は $x = 0, y = r \sin \theta, z = r \cos \theta$ になります。

　 $\theta$ 軸と $\phi$ 軸の目盛の座標は共通の値になりました。
　そこで、固定しない場合の $\theta, \phi$ の値を共通のラジアンtick_rad_valsとしておき、r倍したサイン関数の値をtick_rsin_vals、r倍したコサイン関数の値をtick_rcos_valsとして、それぞれの軸目盛の描画に使います。

　 $\theta$ 軸・ $\phi$ 軸線用の配列を作成します。

# 軸線用のラジアンを作成
axis_rad_vals = np.linspace(start=0.0, stop=2.0*np.pi, num=100)

# 軸線用の座標を計算
axis_rsin_vals = r * np.sin(axis_rad_vals)
axis_rcos_vals = r * np.cos(axis_rad_vals)

　軸目盛の座標のときと同様にして、軸線の座標を計算します。
　軸線用のラジアン $0 \leq t \leq 2 \pi$ をaxis_rad_valsとして、 $r \sin t$ と $r \cos t$ を計算してaxis_***_valsとします。

　なす角 $\theta, \phi$ の角マークと角ラベル用の配列を作成します。

# 角マーク用のラジアンを作成
angle_rad_vals = np.linspace(start=0.0, stop=1.0/denom*np.pi, num=50)

# 角マーク用の座標を計算
d = 0.1
angle_rsin_vals = d * np.sin(angle_rad_vals)
angle_rcos_vals = d * np.cos(angle_rad_vals)

# 角ラベル用の座標を計算
d = 0.15
angle_rsin = d * np.sin(0.5/denom*np.pi)
angle_rcos = d * np.cos(0.5/denom*np.pi)

　この例では、なす角 $\theta, \phi$ を示すために、それぞれ軸目盛1つ分の角マークを表示することにします。
　そこで、角マーク用のラジアン $0 \leq t \leq \frac{\pi}{n}$ をangle_rad_valsとして、円弧の座標 $r \sin t$ と $r \cos t$ を計算してangle_***_valsとします。

　角ラベルは、角マークの中点に表示することにします。
　そこで、 $r \sin \frac{\pi}{2 n}$ と $r \cos \frac{\pi}{2 n}$ を計算してangle_***とします。

　球面上に2つの変数(角度)軸を重ねて表示したグラフを作成します。

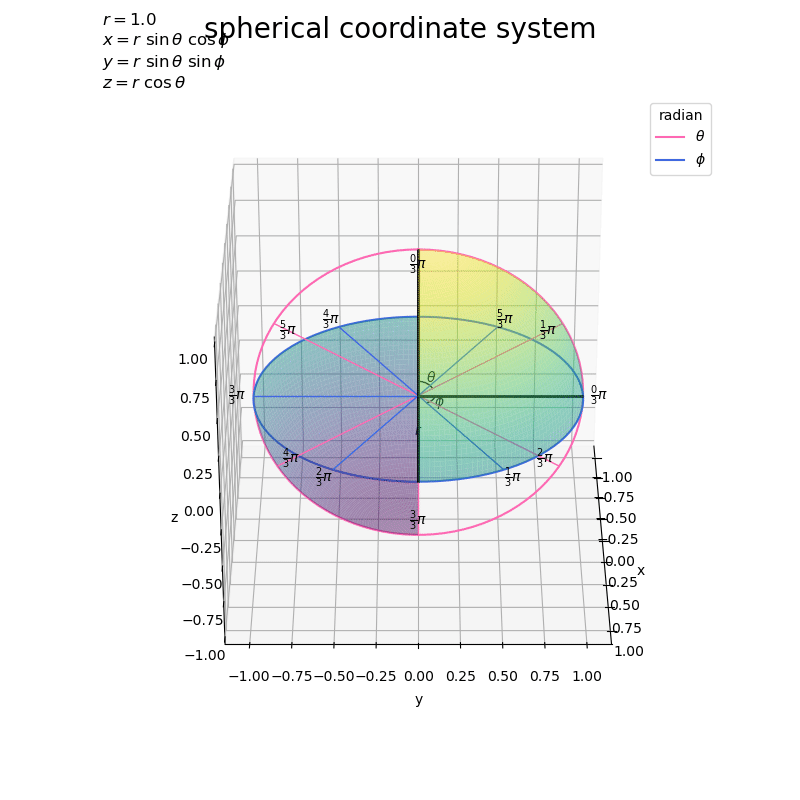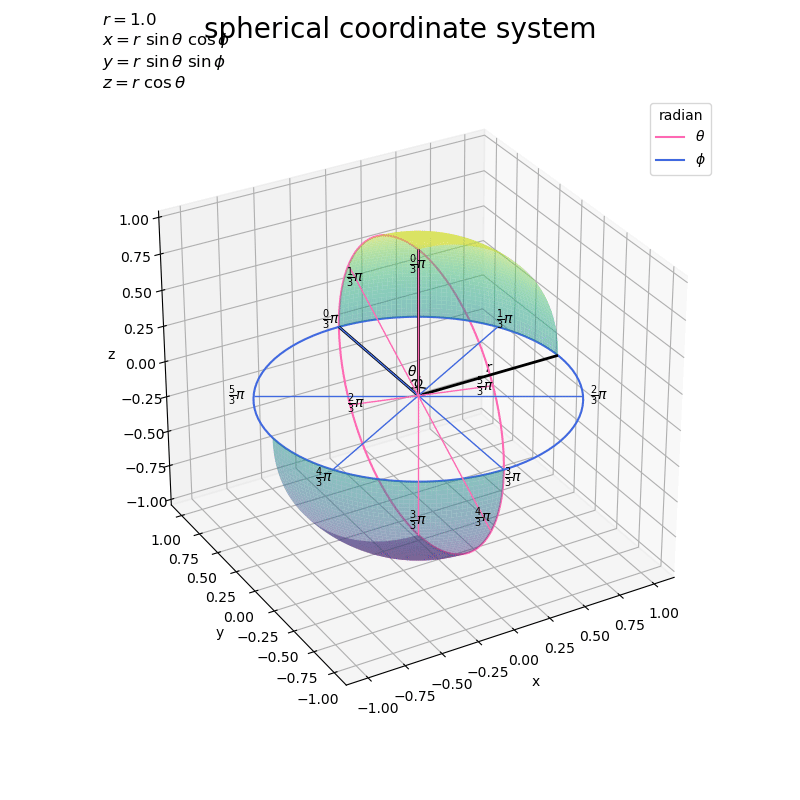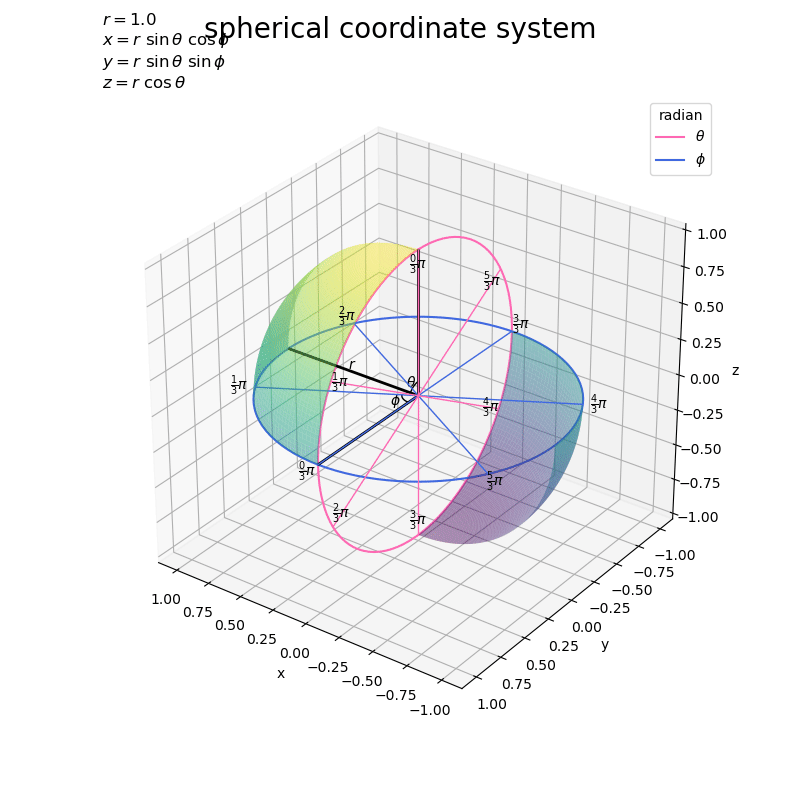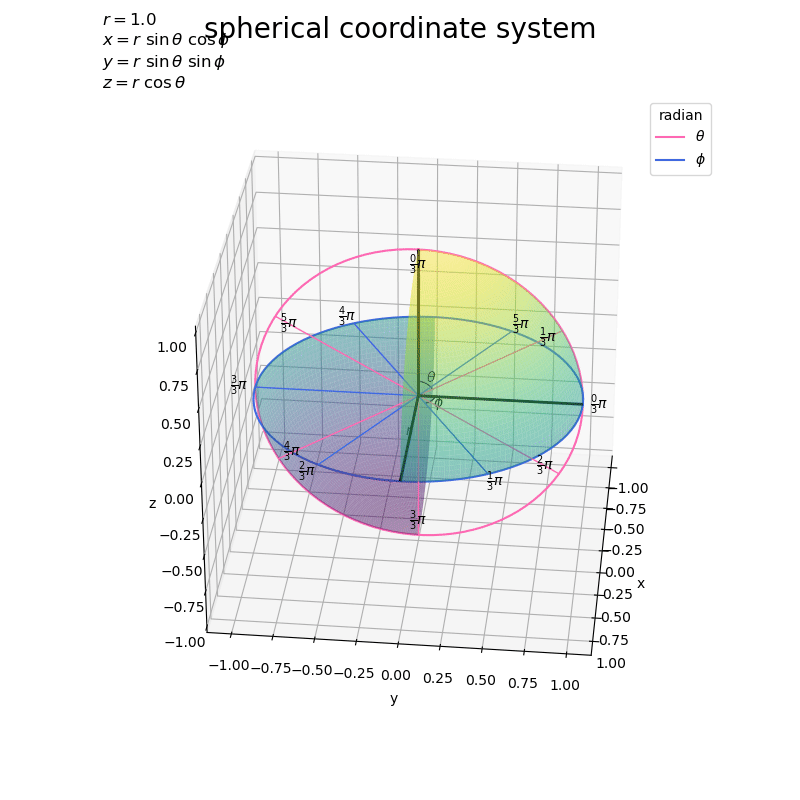
# タイトル用の文字列(座標の計算式)を作成
coord_label = '$x = r\ \\sin \\theta\ \cos \phi$\n'
coord_label += '$y = r\ \\sin \\theta\ \sin \phi$\n'
coord_label += '$z = r\ \\cos \\theta$'

# 球面上の変数(ラジアン)目盛を作図
fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.plot_surface(X, Y, Z, 
                cmap='viridis', vmin=-r, vmax=r, alpha=0.5, zorder=50) # 第1象限
ax.plot_surface(-X, -Y, -Z, 
                cmap='viridis', vmin=-r, vmax=r, alpha=0.5, zorder=50) # 第3象限
ax.plot(np.zeros_like(axis_rad_vals), axis_rsin_vals, axis_rcos_vals, 
        color='hotpink', label='$\\theta$', zorder=0) # θ軸
ax.plot(axis_rsin_vals, axis_rcos_vals, np.zeros_like(axis_rad_vals), 
        color='royalblue', label='$\phi$', zorder=0) # φ軸
ax.quiver(*np.repeat([[0, 0, 0]], repeats=len(tick_rad_vals), axis=0).T, 
          np.zeros_like(tick_rad_vals), tick_rsin_vals, tick_rcos_vals, 
          color='hotpink', lw=1, ls='-', arrow_length_ratio=0.0, zorder=-100) # θ目盛線
ax.quiver(*np.repeat([[0, 0, 0]], repeats=len(tick_rad_vals), axis=0).T, 
          tick_rsin_vals, tick_rcos_vals, np.zeros_like(tick_rad_vals), 
          color='royalblue', lw=1, ls='-', arrow_length_ratio=0.0, zorder=-100) # φ目盛線
for i in range(len(tick_vals)):
    d = 0.9
    ax.text(0.0, tick_rsin_vals[i]*d, tick_rcos_vals[i]*d, 
            s='$\\frac{' + str(int(tick_vals[i])) + '}{' + str(int(denom)) + '} \pi$', 
            ha='center', va='center', zorder=100) # θ目盛ラベル
    d = 1.1
    ax.text(tick_rsin_vals[i]*d, tick_rcos_vals[i]*d, 0.0, 
            s='$\\frac{' + str(int(tick_vals[i])) + '}{' + str(int(denom)) + '} \pi$', 
            ha='center', va='center', zorder=100) # φ目盛ラベル
ax.quiver([0, 0, 0], [0, 0, 0], [0, 0, 0], 
          [1, 0, 0], [0, 1, 0], [0, 0, 1], 
          color='black', lw=2, arrow_length_ratio=0.0, zorder=-50) # x,y,z軸
ax.plot(np.zeros_like(angle_rad_vals), angle_rsin_vals, angle_rcos_vals, 
        color='black', lw=1, zorder=-100) # θの角マーク
ax.plot(angle_rsin_vals, angle_rcos_vals, np.zeros_like(angle_rad_vals), 
        color='black', lw=1, zorder=-100) # φの角マーク
ax.text(0.0, angle_rsin, angle_rcos, 
        s='$\\theta$', ha='center', va='center', zorder=-100) # θの角ラベル
ax.text(angle_rsin, angle_rcos, 0.0, 
        s='$\phi$', ha='center', va='center', zorder=-100) # φの角ラベル
ax.text(0.5*r, 0.0, 0.0, 
        s='$r$', ha='center', va='bottom', zorder=-100) # 半径rラベル
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('$r=' + str(r) + '$\n' + coord_label, loc='left')
fig.suptitle('spherical coordinate system', fontsize=20)
ax.legend(title='radian')
ax.set_aspect('equal')
#ax.view_init(elev=90, azim=270) # xy面
#ax.view_init(elev=0, azim=0) # yz面
plt.show()

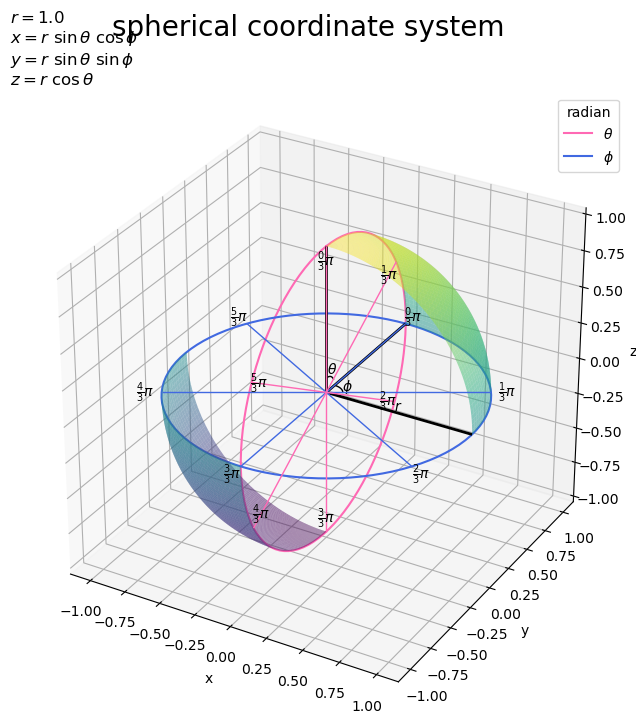
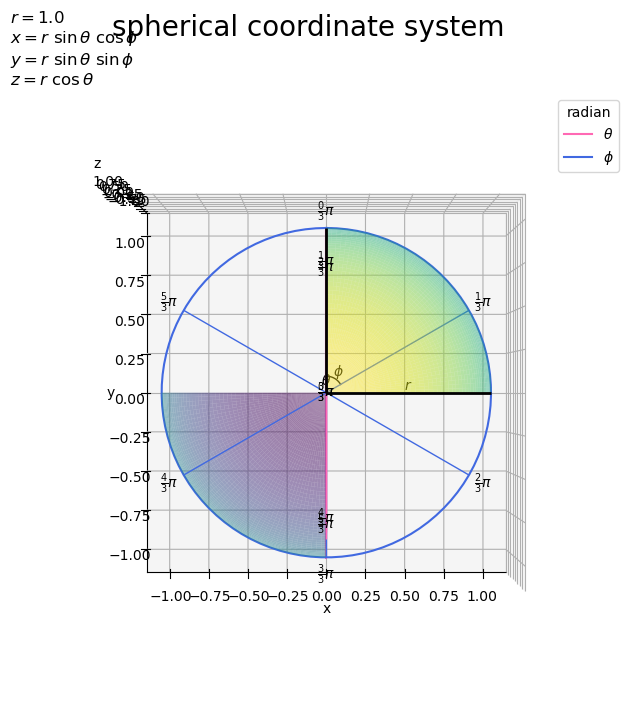
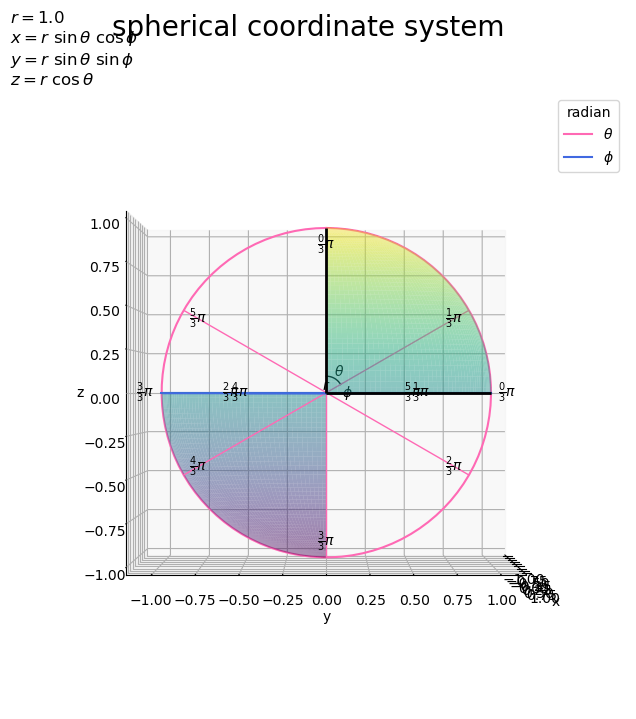
　軸目盛線をAxes.quiver()で描画します。第1・2・3引数に始点の座標、第4・5・6引数にベクトルのサイズ(移動量)を指定します。また、矢のサイズの引数arrow_length_ratioに0を指定して、線分を描画します。
　始点は原点です。配列の前に*を付けてアンパック(展開)して座標を指定しています。

　目盛ラベルや角ラベルをAxes.text()で描画します

　xz面を見ると、z軸線から時計回りの角度(なす角)が $\theta$ に対応しているのが分かります。同様に、xy面を見ると、y軸線から時計回りの角度が $\phi$ に対応しているのが分かります。反時計回りの角度は負の値で表現できます。

　グラフを回転させたアニメーションで確認します。

・作図コード(クリックで展開)

# フレーム数を指定
frame_num = 60

# 表示角度として利用する値を作成
h_n = np.linspace(start=0.0, stop=360.0, num=frame_num+1)[:frame_num]

# グラフオブジェクトを初期化
fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', 
                       subplot_kw={'projection': '3d'})
fig.suptitle('spherical coordinate system', fontsize=20)

# 作図処理を関数として定義
def update(i):
    
    # 前フレームのグラフを初期化
    plt.cla()

    # i番目の角度を取得
    h = h_n[i]
    
    # 球面上の変数(ラジアン)目盛を作図
    ax.plot_surface(X, Y, Z, 
                    cmap='viridis', vmin=-r, vmax=r, alpha=0.5, zorder=50) # 第1象限
    ax.plot_surface(-X, -Y, -Z, 
                    cmap='viridis', vmin=-r, vmax=r, alpha=0.5, zorder=50) # 第3象限
    ax.plot(np.zeros_like(axis_rad_vals), axis_rsin_vals, axis_rcos_vals, 
            color='hotpink', label='$\\theta$', zorder=0) # θ軸
    ax.plot(axis_rsin_vals, axis_rcos_vals, np.zeros_like(axis_rad_vals), 
            color='royalblue', label='$\phi$', zorder=0) # φ軸
    ax.quiver(*np.repeat([[0, 0, 0]], repeats=len(tick_rad_vals), axis=0).T, 
              np.zeros_like(tick_rad_vals), tick_rsin_vals, tick_rcos_vals, 
              color='hotpink', lw=1, ls='-', arrow_length_ratio=0.0, zorder=-100) # θ目盛線
    ax.quiver(*np.repeat([[0, 0, 0]], repeats=len(tick_rad_vals), axis=0).T, 
              tick_rsin_vals, tick_rcos_vals, np.zeros_like(tick_rad_vals), 
              color='royalblue', lw=1, ls='-', arrow_length_ratio=0.0, zorder=-100) # φ目盛線
    for i in range(len(tick_vals)):
        d = 0.9
        ax.text(0.0, tick_rsin_vals[i]*d, tick_rcos_vals[i]*d, 
                s='$\\frac{' + str(int(tick_vals[i])) + '}{' + str(int(denom)) + '} \pi$', 
                ha='center', va='center', zorder=100) # θ目盛ラベル
        d = 1.1
        ax.text(tick_rsin_vals[i]*d, tick_rcos_vals[i]*d, 0.0, 
                s='$\\frac{' + str(int(tick_vals[i])) + '}{' + str(int(denom)) + '} \pi$', 
                ha='center', va='center', zorder=100) # φ目盛ラベル
    ax.quiver([0, 0, 0], [0, 0, 0], [0, 0, 0], 
              [1, 0, 0], [0, 1, 0], [0, 0, 1], 
              color='black', lw=2, arrow_length_ratio=0.0, zorder=-50) # x,y,z軸
    ax.plot(np.zeros_like(angle_rad_vals), angle_rsin_vals, angle_rcos_vals, 
            color='black', lw=1, zorder=-100) # θの角マーク
    ax.plot(angle_rsin_vals, angle_rcos_vals, np.zeros_like(angle_rad_vals), 
            color='black', lw=1, zorder=-100) # φの角マーク
    ax.text(0.0, angle_rsin, angle_rcos, 
            s='$\\theta$', ha='center', va='center', zorder=-100) # θの角ラベル
    ax.text(angle_rsin, angle_rcos, 0.0, 
            s='$\phi$', ha='center', va='center', zorder=-100) # φの角ラベル
    ax.text(0.5*r, 0.0, 0.0, 
        s='$r$', ha='center', va='bottom', zorder=-100) # 半径rラベル
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    ax.set_title('$r=' + str(r) + '$\n' + coord_label, loc='left')
    ax.legend(title='radian')
    ax.set_aspect('equal')
    ax.view_init(elev=30, azim=360.0-h) # 表示角度

# gif画像を作成
ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100)

# gif画像を保存
ani.save('sphere_axis_3d.gif')

　この記事では、球面のグラフを作成しました。次の記事では、球面上の2点を繋ぐ線分のグラフを作成します。

おわりに

　雰囲気で使ってた曲面座標系とやらに踏み込んでみました。座標の計算式に微妙に違和感があったのですが、円のときと違って「y軸(とz軸)から時計回りに角度が大きくなる」んですね。それが分かっただけでも収穫でした。
　その角度(目盛)と座標の関係をどうグラフにしたものか試行錯誤してたのですが、中々格好良い図になったのではないでしょうか(見慣れただけかも)。

　なんだか最後にこの曲を聴くのがいい気がします。