はじめに
調べても分からなかったので自分なりにやってみる黒魔術シリーズです。もっといい方法があれば教えてください。
この記事では、3次元空間上の平面上の点の座標を計算します。
【目次】
3次元空間における3点を通る平面上の点を求めたい
「3次元空間における原点と2点を通る平面上の点を求めたい - からっぽのしょこ」では、原点と任意の2点を通る平面上の点について考えた。
この記事では、3次元空間において、任意の3点を通る平面(2つのベクトルに平行な平面)上の点に関して、x軸とy軸の値が与えられたときのz軸の値を計算したい。
検索したら色々出てきて分からなかったので、自分で考えてみた。もっといい方法があれば教えてほしい。
平面上の点の計算式の導出
まずは、3次元空間における平面上の点について、x軸とy軸の値が与えられたときのz軸の値の計算式を導出する。
任意の3点をとする。
点の座標を、それぞれ次の3次元ベクトルで表す。
ベクトルは、平行でなく、どちらも0ベクトルでないとする。
点を通る平面上の点を考える。
は、原点を
として
を用いて、次の式で表わせる。
点を通る平面は、ベクトル
によって張られる平面と言える。
平面上の点をとすると
は、実数(スカラ)
を係数として
の線形結合で表せる。
なので、
を用いて、次の式でも表せる。
また、この式をについて整理すると、次の式になる。
よって、点の座標を
とすると、各成分は次の式で表わせる。
平面上の点の座標(ベクトル
の成分)は、式(1')よりそれぞれ次の式で計算できる。
x軸の式(2)をそれぞれについて整理する。
同様に、y軸の式(3)を整理する。
に関する式について式(2')を式(3')に代入して、
について整理する。
の計算式が得られた。1行目から2行目では、両辺に
を掛けて分母を払った。
同様に、に関する式について式(2')を式(3')に代入して、
について整理する。
の計算式が得られた。1行目から2行目では、両辺に
を掛けて分母を払った。
の式(5)と
の式(6)をz軸の式(4)に代入して、式を整理する。
点のx軸とy軸の値が与えられたときのz軸の値の計算式が得られた。
(この式ってもっと綺麗な形にできますか?)
ちなみに、点が原点
のとき、この式は「原点と2点を通る平面上の点を求めたい」におけるz軸の値の計算式(7)になる。
平面上の点の計算の可視化
次は、3次元空間における線形結合(平面上の点の計算)と、x軸とy軸の値が与えられたときのz軸の値の計算をグラフで可視化する。
線形結合については「【Python】1.3:ベクトルの線形結合の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」も参照のこと。
利用するライブラリを読み込む。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
平面の計算
3次元ベクトルを指定する。
# 3次元ベクトルを指定 a = np.array([-2.0, 1.5, 1.0]) b = np.array([-2.0, -2.0, -2.0]) c = np.array([1.0, 2.0, -2.0]) #c = np.zeros(3) # 原点
を
a, b, cとして、それぞれ値を指定する。Pythonではインデックスが0から割り当てられるので、は
a[0]に対応することに注意する。
3次元空間におけるベクトルと
をグラフで確認する。
# グラフサイズ用の値を設定 x_min = np.floor(np.min([0.0, a[0], b[0], c[0]])) - 1 x_max = np.ceil(np.max([0.0, a[0], b[0], c[0]])) + 1 y_min = np.floor(np.min([0.0, a[1], b[1], c[1]])) - 1 y_max = np.ceil(np.max([0.0, a[1], b[1], c[1]])) + 1 z_min = np.floor(np.min([0.0, a[2], b[2], c[2]])) - 1 z_max = np.ceil(np.max([0.0, a[2], b[2], c[2]])) + 1 # 矢のサイズを指定 l = 0.4 # 基底ベクトルa,b,cを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(0, 0, 0, *a, color='red', linestyle='--', arrow_length_ratio=l/np.linalg.norm(a), label='$a=('+', '.join(map(str, a.round(2)))+')$') # ベクトルa ax.quiver(0, 0, 0, *b, color='blue', linestyle='--', arrow_length_ratio=l/np.linalg.norm(b), label='$b=('+', '.join(map(str, b.round(2)))+')$') # ベクトルb ax.quiver(*c, *-c, color='green', linestyle='--', arrow_length_ratio=l/np.linalg.norm(c), label='$-c=-('+', '.join(map(str, c.round(2)))+')$') # ベクトルc ax.quiver(*c, *a-c, color='red', arrow_length_ratio=l/np.linalg.norm(a-c), label='$a-c=('+', '.join(map(str, (a-c).round(2)))+')$') # ベクトルa-c ax.quiver(*c, *b-c, color='blue', arrow_length_ratio=l/np.linalg.norm(b-c), label='$b-c=('+', '.join(map(str, (b-c).round(2)))+')$') # ベクトルb-c ax.text(0, 0, 0, s='O', size=15, ha='right', va='center') # 原点ラベル ax.text(*a, s='A', size=15, ha='center', va='bottom') # 点aラベル ax.text(*b, s='B', size=15, ha='right', va='bottom') # 点bラベル ax.text(*c, s='C', size=15, ha='left', va='top') # 点cラベル ax.quiver([0, a[0], b[0], c[0]], [0, a[1], b[1], c[1]], [0, a[2], b[2], c[2]], [0, 0, 0, 0], [0, 0, 0, 0], [z_min, z_min-a[2], z_min-b[2], z_min-c[2]], color='gray', arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xlim(left=x_min, right=x_max) ax.set_ylim(bottom=y_min, top=y_max) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$O = (0, 0, 0)$', loc='left') fig.suptitle('$A = a, B = b, C = c$', fontsize=20) ax.legend() ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 #ax.view_init(elev=0, azim=270) # xz面 plt.show()

axes.quiver()でベクトルを描画する。第1・2・3引数に始点の座標、第4・5・6引数にベクトルのサイズ(移動量)を指定する。この例では、原点を始点とする。
配列a, b, cなどの前に*を付けてアンパック(展開)して座標を指定している。
arrow_length_ratio引数で矢のサイズ(全体に対する矢の割合)を指定できる。この例では、各ベクトルのノルムの逆数を指定することで、ベクトルのサイズに関わらず、全ての矢のサイズを統一している。
さらに、全てのベクトルで同じ値lを掛けることで、サイズを調整する。
係数を指定して、ベクトル
の線形結合(平面上の点
)を計算する。
# 係数を指定 alpha = 2.0 beta = -0.5 # 線形結合を計算:式(1) #p = c + alpha * (a - c) + beta * (b - c) p = (1.0 - alpha - beta) * c + alpha * a + beta * b print(p)
[-3.5 3. 4. ]
2つのベクトルのスカラー倍の和にを加える。
ベクトルの線形結合(ベクトル)をグラフで確認する。
・作図コード(クリックで展開)
# グラフサイズ用の値を設定 x_min = np.floor(np.min([a[0], b[0], c[0], alpha*(a-c)[0]+c[0], beta*(b-c)[0]+c[0], p[0]])) - 1 x_max = np.ceil(np.max([a[0], b[0], c[0], alpha*(a-c)[0]+c[0], beta*(b-c)[0]+c[0], p[0]])) + 1 y_min = np.floor(np.min([a[1], b[1], c[1], alpha*(a-c)[1]+c[1], beta*(b-c)[1]+c[1], p[1]])) - 1 y_max = np.ceil(np.max([a[1], b[1], c[1], alpha*(a-c)[1]+c[1], beta*(b-c)[1]+c[1], p[1]])) + 1 z_min = np.floor(np.min([a[2], b[2], c[2], alpha*(a-c)[2]+c[2], beta*(b-c)[2]+c[2], p[2]])) - 1 z_max = np.ceil(np.max([a[2], b[2], c[2], alpha*(a-c)[2]+c[2], beta*(b-c)[2]+c[2], p[2]])) + 1 # 矢のサイズを指定 l = 0.4 # ベクトルa-c,b-cの線形結合を作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(*c, *a-c, color='red', arrow_length_ratio=l/np.linalg.norm(a-c), label='$a-c=('+', '.join(map(str, (a-c).round(2)))+')$') # ベクトルa-c ax.quiver(*c, *b-c, color='blue', arrow_length_ratio=l/np.linalg.norm(b-c), label='$b-c=('+', '.join(map(str, (b-c).round(2)))+')$') # ベクトルb-c ax.quiver(*c, *alpha*(a-c), color='deeppink', arrow_length_ratio=l/np.linalg.norm(alpha*(a-c)), label='$\\alpha (a-c)=('+', '.join(map(str, (alpha*(a-c)).round(2)))+')$') # ベクトルα(a-c) ax.quiver(*c+beta*(b-c), *alpha*(a-c), color='deeppink', linestyle=':', arrow_length_ratio=0.0) # ベクトルα(a-c)の平行線 ax.quiver(*c, *beta*(b-c), color='deepskyblue', arrow_length_ratio=l/np.linalg.norm(beta*(b-c)), label='$\\beta (b-c)=('+', '.join(map(str, (beta*(b-c)).round(2)))+')$') # ベクトルβ(b-c) ax.quiver(*c+alpha*(a-c), *beta*(b-c), color='deepskyblue', linestyle=':', arrow_length_ratio=0.0) # ベクトルβ(b-c)の平行線 ax.quiver(*c, *p-c, color='purple', arrow_length_ratio=l/np.linalg.norm(p-c), label='$p-c=('+', '.join(map(str, (p-c).round(2)))+')$') # ベクトルp-c ax.text(*a, s='A', size=15, ha='center', va='bottom') # 点aラベル ax.text(*b, s='B', size=15, ha='right', va='bottom') # 点bラベル ax.text(*c, s='C', size=15, ha='left', va='top') # 点cラベル ax.text(*p, s='P', size=15, ha='center', va='bottom') # 点pラベル ax.quiver([a[0], b[0], c[0], alpha*(a-c)[0]+c[0], beta*(b-c)[0]+c[0], p[0]], [a[1], b[1], c[1], alpha*(a-c)[1]+c[1], beta*(b-c)[1]+c[1], p[1]], [a[2], b[2], c[2], alpha*(a-c)[2]+c[2], beta*(b-c)[2]+c[2], p[2]], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [z_min-a[2], z_min-b[2], z_min-c[2], z_min-alpha*(a-c)[2]-c[2], z_min-beta*(b-c)[2]-c[2], z_min-p[2]], color='gray', arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xlim(left=x_min, right=x_max) ax.set_ylim(bottom=y_min, top=y_max) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$\\alpha=' + str(alpha) + ', ' + '\\beta=' + str(beta) + ', ' + 'c=('+', '.join(map(str, c)) + ')$', loc='left') fig.suptitle('$p = (1-\\alpha-\\beta) c + \\alpha a + \\beta b$', fontsize=20) ax.legend(prop={'size': 9}) ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 #ax.view_init(elev=0, azim=270) # xz面 plt.show()

点から
移動、または点
から
移動した点が
になるのを確認できる。
ベクトルと平行な平面の座標を計算する。
# (平面の描画用の)係数を作成 alpha_vals = np.linspace(start=-1.0, stop=3.0, num=9) beta_vals = np.linspace(start=-1.5, stop=2.0, num=8) print(alpha_vals) print(beta_vals) # 格子状の点を作成 alpha_grid, beta_grid = np.meshgrid(alpha_vals, beta_vals) print(alpha_grid.shape) print(beta_grid.shape) # ベクトルa,bと平行な平面の座標を計算:式(1') x_grid = c[0] + alpha_grid * (a[0]-c[0]) + beta_grid * (b[0]-c[0]) y_grid = c[1] + alpha_grid * (a[1]-c[1]) + beta_grid * (b[1]-c[1]) z_grid = c[2] + alpha_grid * (a[2]-c[2]) + beta_grid * (b[2]-c[2]) #x_grid = (1.0 - alpha_grid - beta_grid) * c[0] + alpha_grid * a[0] + beta_grid * b[0] #y_grid = (1.0 - alpha_grid - beta_grid) * c[1] + alpha_grid * a[1] + beta_grid * b[1] #z_grid = (1.0 - alpha_grid - beta_grid) * c[2] + alpha_grid * a[2] + beta_grid * b[2]
[-1. -0.5 0. 0.5 1. 1.5 2. 2.5 3. ]
[-1.5 -1. -0.5 0. 0.5 1. 1.5 2. ]
(8, 9)
(8, 9)
係数の値を等間隔で作成して
alpha_vals, beta_valsとする。
alpha_vals, beta_valsの格子状の点(全ての組み合わせ)をnp.meshgrid()で作成してalpha_grid, beta_gridとする。
alpha_vals, beta_valsを用いて、成分ごとに線形結合(1')の計算を行う。
ベクトルによって張られる平面をグラフで確認する。
・作図コード(クリックで展開)
# グラフサイズ用の値を設定 x_min = np.floor(x_grid.min()) x_max = np.ceil(x_grid.max()) y_min = np.floor(y_grid.min()) y_max = np.ceil(y_grid.max()) z_min = np.floor(z_grid.min()) z_max = np.ceil(z_grid.max()) # 矢のサイズを指定 l = 0.6 # タイトル用の符号を設定 sgn_beta = '+' if beta >= 0.0 else '' # ベクトルa-c,b-cと平行な平面を作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) ax.plot_wireframe(x_grid, y_grid, z_grid, alpha=0.5, label='$c + \\alpha (a-c) + \\beta (b-c)$') # ベクトルa-c,b-cによる平面 ax.quiver(*c, *a-c, color='red', linewidth=3, arrow_length_ratio=l/np.linalg.norm(a-c), label='$a-c=('+', '.join(map(str, (a-c).round(2)))+')$') # ベクトルa-c ax.quiver(*c, *b-c, color='blue', linewidth=3, arrow_length_ratio=l/np.linalg.norm(b-c), label='$b-c=('+', '.join(map(str, (b-c).round(2)))+')$') # ベクトルb-c ax.quiver(*c, *alpha*(a-c), color='deeppink', arrow_length_ratio=l/np.linalg.norm(alpha*(a-c))) # ベクトルα(a-c) ax.quiver(*c+beta*(b-c), *alpha*(a-c), color='deeppink', linestyle=':', arrow_length_ratio=0.0) # ベクトルα(a-c)の平行線 ax.quiver(*c, *beta*(b-c), color='deepskyblue', arrow_length_ratio=l/np.linalg.norm(beta*(b-c))) # ベクトルβ(b-c) ax.quiver(*c+alpha*(a-c), *beta*(b-c), color='deepskyblue', linestyle=':', arrow_length_ratio=0.0) # ベクトルβ(b-c)の平行線 ax.quiver(*c, *p-c, color='purple', linewidth=3, arrow_length_ratio=l/np.linalg.norm(p-c), label='$p-c=('+', '.join(map(str, (p-c).round(2)))+')$') # ベクトルp-c ax.text(*a, s='A', size=15, ha='center', va='bottom') # 点aラベル ax.text(*b, s='B', size=15, ha='right', va='bottom') # 点bラベル ax.text(*c, s='C', size=15, ha='left', va='top') # 点cラベル ax.text(*p, s='P', size=15, ha='center', va='bottom') # 点pラベル ax.quiver([a[0], b[0], c[0], alpha*(a-c)[0]+c[0], beta*(b-c)[0]+c[0], p[0]], [a[1], b[1], c[1], alpha*(a-c)[1]+c[1], beta*(b-c)[1]+c[1], p[1]], [a[2], b[2], c[2], alpha*(a-c)[2]+c[2], beta*(b-c)[2]+c[2], p[2]], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [z_min-a[2], z_min-b[2], z_min-c[2], z_min-alpha*(a-c)[2]-c[2], z_min-beta*(b-c)[2]-c[2], z_min-p[2]], color='gray', arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xlim(left=x_min, right=x_max) ax.set_ylim(bottom=y_min, top=y_max) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$p=c+' + str(alpha) + '(a-c)' + sgn_beta + str(beta) + '(b-c)$\n' + '$c=('+', '.join(map(str, c)) + ')$', loc='left') fig.suptitle('linear combination of two vectors', fontsize=20) ax.legend(prop={'size': 9}) ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 #ax.view_init(elev=0, azim=270) # xz面 plt.show()



平面(水色のグリッド線)は、係数を変更したときの線形結合(点
)が取り得る座標を表す。
平面上の点の計算
点のx軸とy軸の値
を指定して、z軸の値
を計算する。
# x軸とy軸の値を指定 x = -5.0 y = 4.0 #x, y = p[0], p[1] # z軸の値を計算:式(7) tmp_a = a - c tmp_b = b - c z = (tmp_a[2]*tmp_b[1] - tmp_a[1]*tmp_b[2]) * (x - c[0]) z += (tmp_a[0]*tmp_b[2] - tmp_a[2]*tmp_b[0]) * (y - c[1]) z /= (tmp_a[0]*tmp_b[1] - tmp_a[1]*tmp_b[0]) z += c[2] # 座標を格納 p = np.array([x, y, z]) print(p)
[-5. 4. 6.57142857]
を
x, yとして値を指定する。先ほど計算したpの0番目の要素をx、1番目の要素をyとすると、z軸の値p[2]を計算できるのを確認できる。
式(7)によりを計算して
zとする。
x, y, zを配列に格納してpとする。
から係数
を計算する。
# 係数を計算:式(6)(5) alpha = (tmp_b[1]*(x - c[0]) - tmp_b[0]*(y - c[1])) / (tmp_a[0]*tmp_b[1] - tmp_a[1]*tmp_b[0]) beta = (tmp_a[0]*(y - c[1]) - tmp_a[1]*(x - c[0])) / (tmp_a[0]*tmp_b[1] - tmp_a[1]*tmp_b[0]) print(alpha) print(beta)
2.857142857142857
-0.8571428571428571
式(6)(5)により係数を計算してalpha, betaとする。
確認のため、求めた係数を用いて線形結合を計算する。
# 線形結合を計算:式(1) #p = c + alpha * (a - c) + beta * (b - c) p = (1.0 - alpha - beta) * c + alpha * a + beta * b print(p)
[-5. 4. 6.57142857]
値が変わらないのを確認できる。
ベクトルと平行な平面の座標を計算する。
# (平面の描画用の)係数の値を作成 alpha_min = np.min([-2.0, np.floor(alpha)]) alpha_max = np.max([2.0, np.ceil(alpha)]) beta_min = np.min([-2.0, np.floor(beta)]) beta_max = np.max([2.0, np.ceil(beta)]) alpha_vals = np.linspace(start=alpha_min, stop=alpha_max, num=int(2*(alpha_max-alpha_min)+1)) beta_vals = np.linspace(start=beta_min, stop=beta_max, num=int(2*(beta_max-beta_min)+1)) print(alpha_vals) print(beta_vals) # 格子状の点を作成 alpha_grid, beta_grid = np.meshgrid(alpha_vals, beta_vals) # ベクトルa,bと平行な平面の座標を計算:式(1') x_grid = c[0] + alpha_grid * (a[0]-c[0]) + beta_grid * (b[0]-c[0]) y_grid = c[1] + alpha_grid * (a[1]-c[1]) + beta_grid * (b[1]-c[1]) z_grid = c[2] + alpha_grid * (a[2]-c[2]) + beta_grid * (b[2]-c[2])
[-2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. 2.5 3. ]
[-2. -1.5 -1. -0.5 0. 0.5 1. 1.5 2. ]
先ほどと同様にして、平面の座標を計算する。こちらは、係数の範囲をいい感じに設定している。
平面上の点をグラフで確認する。
・作図コード(クリックで展開)
# グラフサイズ用の値を設定 x_min = np.floor(x_grid.min()) x_max = np.ceil(x_grid.max()) y_min = np.floor(y_grid.min()) y_max = np.ceil(y_grid.max()) z_min = np.floor(z_grid.min()) z_max = np.ceil(z_grid.max()) # 矢のサイズを指定 l = 0.6 # タイトル用の文字列を指定 form_label = 'z = ' form_label += '\\frac{(a_3-c_3) (b_2-c_2) - (a_2-c_2) (b_3-c_3)}{(a_1-c_1) (b_2-c_2) - (a_2-c_2) (b_1-c_1)} (x-c_1)' form_label += '+ \\frac{(a_1-c_1) (b_3-c_3) - (a_3-c_3) (b_1-c_1)}{(a_1-c_1) (b_2-c_2) - (a_2-c_2) (b_1-c_1)} (y-c_2)' form_label += '+c_3' # タイトル用の符号を設定 sgn_beta = '+' if beta >= 0.0 else '' # ベクトルa-c,b-cと平行な平面上の点を作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) ax.plot_wireframe(x_grid, y_grid, z_grid, alpha=0.5, label='$c + \\alpha (a-c) + \\beta (b-c)$') # ベクトルa-c,b-cによる平面 ax.scatter(*p, s=50, zorder=-100) # 点p ax.quiver(*c, *a-c, color='red', linewidth=3, arrow_length_ratio=l/np.linalg.norm(a-c), label='$a-c=('+', '.join(map(str, (a-c).round(2)))+')$') # ベクトルa-c ax.quiver(*c, *b-c, color='blue', linewidth=3, arrow_length_ratio=l/np.linalg.norm(b-c), label='$b-c=('+', '.join(map(str, (b-c).round(2)))+')$') # ベクトルb-c ax.quiver(*c, *alpha*(a-c), color='deeppink', arrow_length_ratio=l/np.linalg.norm(alpha*(a-c))) # ベクトルα(a-c) ax.quiver(*c+beta*(b-c), *alpha*(a-c), color='deeppink', linestyle=':', arrow_length_ratio=0.0) # ベクトルα(a-c)の平行線 ax.quiver(*c, *beta*(b-c), color='deepskyblue', arrow_length_ratio=l/np.linalg.norm(beta*(b-c))) # ベクトルβ(b-c) ax.quiver(*c+alpha*(a-c), *beta*(b-c), color='deepskyblue', linestyle=':', arrow_length_ratio=0.0) # ベクトルβ(b-c)の平行線 ax.quiver(*c, *p-c, color='purple', linewidth=3, arrow_length_ratio=l/np.linalg.norm(p-c), label='$p-c=('+', '.join(map(str, (p-c).round(2)))+')$') # ベクトルp-c ax.text(*a, s='A', size=15, ha='center', va='bottom') # 点aラベル ax.text(*b, s='B', size=15, ha='right', va='bottom') # 点bラベル ax.text(*c, s='C', size=15, ha='left', va='top') # 点cラベル ax.text(*p, s='P', size=15, ha='center', va='bottom') # 点pラベル ax.quiver([a[0], b[0], c[0], alpha*(a-c)[0]+c[0], beta*(b-c)[0]+c[0], p[0]], [a[1], b[1], c[1], alpha*(a-c)[1]+c[1], beta*(b-c)[1]+c[1], p[1]], [a[2], b[2], c[2], alpha*(a-c)[2]+c[2], beta*(b-c)[2]+c[2], p[2]], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [z_min-a[2], z_min-b[2], z_min-c[2], z_min-alpha*(a-c)[2]-c[2], z_min-beta*(b-c)[2]-c[2], z_min-p[2]], color='gray', arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xlim(left=x_min, right=x_max) ax.set_ylim(bottom=y_min, top=y_max) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$p=(x, y, z)=c+' + str(alpha.round(2)) + '(a-c)' + sgn_beta + str(beta.round(2)) + '(b-c)$\n' + '$c=('+', '.join(map(str, c)) + ')$', loc='left') fig.suptitle('$' + form_label + '$', fontsize=12) ax.legend(prop={'size': 9}) ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) # xy面 #ax.view_init(elev=0, azim=270) # xz面 plt.show()
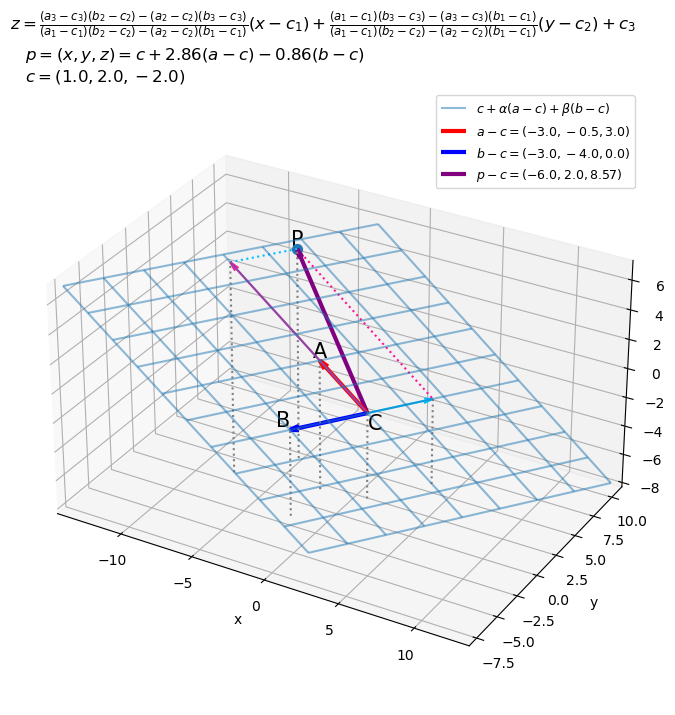
点とベクトル
が平面上の点であるのを確認できる。
グラフを回転させて確認する。
・作図コード(クリックで展開)
# フレーム数を指定 frame_num = 60 # 水平方向の角度として利用する値を作成 h_vals = np.linspace(start=0.0, stop=360.0, num=frame_num+1)[:frame_num] # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('$' + form_label + '$', fontsize=12) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の角度を取得 h = h_vals[i] # ベクトルa-c,b-cと平行な平面上の点を作図 ax.plot_wireframe(x_grid, y_grid, z_grid, alpha=0.5, label='$c + \\alpha (a-c) + \\beta (b-c)$') # ベクトルa-c,b-cによる平面 ax.scatter(*p, s=50, zorder=-100) # 点p ax.quiver(*c, *a-c, color='red', linewidth=3, arrow_length_ratio=l/np.linalg.norm(a-c), label='$a-c=('+', '.join(map(str, (a-c).round(2)))+')$') # ベクトルa-c ax.quiver(*c, *b-c, color='blue', linewidth=3, arrow_length_ratio=l/np.linalg.norm(b-c), label='$b-c=('+', '.join(map(str, (b-c).round(2)))+')$') # ベクトルb-c ax.quiver(*c, *alpha*(a-c), color='deeppink', arrow_length_ratio=l/np.linalg.norm(alpha*(a-c))) # ベクトルα(a-c) ax.quiver(*c+beta*(b-c), *alpha*(a-c), color='deeppink', linestyle=':', arrow_length_ratio=0.0) # ベクトルα(a-c)の平行線 ax.quiver(*c, *beta*(b-c), color='deepskyblue', arrow_length_ratio=l/np.linalg.norm(beta*(b-c))) # ベクトルβ(b-c) ax.quiver(*c+alpha*(a-c), *beta*(b-c), color='deepskyblue', linestyle=':', arrow_length_ratio=0.0) # ベクトルβ(b-c)の平行線 ax.quiver(*c, *p-c, color='purple', linewidth=3, arrow_length_ratio=l/np.linalg.norm(p-c), label='$p-c=('+', '.join(map(str, (p-c).round(2)))+')$') # ベクトルp-c ax.text(*a, s='A', size=15, ha='center', va='bottom') # 点aラベル ax.text(*b, s='B', size=15, ha='center', va='bottom') # 点bラベル ax.text(*c, s='C', size=15, ha='center', va='bottom') # 点cラベル ax.text(*p, s='P', size=15, ha='center', va='bottom') # 点pラベル ax.quiver([a[0], b[0], c[0], alpha*(a-c)[0]+c[0], beta*(b-c)[0]+c[0], p[0]], [a[1], b[1], c[1], alpha*(a-c)[1]+c[1], beta*(b-c)[1]+c[1], p[1]], [a[2], b[2], c[2], alpha*(a-c)[2]+c[2], beta*(b-c)[2]+c[2], p[2]], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [z_min-a[2], z_min-b[2], z_min-c[2], z_min-alpha*(a-c)[2]-c[2], z_min-beta*(b-c)[2]-c[2], z_min-p[2]], color='gray', arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xlim(left=x_min, right=x_max) ax.set_ylim(bottom=y_min, top=y_max) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$p=(x, y, z)=c+' + str(alpha.round(2)) + '(a-c)' + sgn_beta + str(beta.round(2)) + '(b-c)$\n' + '$c=('+', '.join(map(str, c)) + ')$', loc='left') ax.legend(prop={'size': 9}) ax.set_aspect('equal') ax.view_init(elev=30, azim=h) # 表示角度 # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('CPonPlane_3d.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。

以上で、3次元空間における任意の3点を通る平面上の点の計算を確認できた。
おわりに
軽く調べても見当たらなかったので自分なりにやってみたところ、とてもゴチャゴチャした式になりました。なるほどこりゃメンドいな。法線ベクトルがどうとかは読んでません。
見た目はおどろおどろしいですが、式をよく見るとから
を引いてるだけなので、
とでも置いてあげれば原点を通るときと同じ式(「導出」の最後の式)になるので、それほどでもないかもしれないと思ったり思わなかったりしたりしなかったり。
この記事は本などを読まずに我流で書いたので、変な表現や間違い・勘違いなどあると思います。教えてください。
投稿日に公開されたこの動画をぜひ聴きましょう。
One on まーちゃんシリーズは絶妙な組み合わせを供給してきてホントたまらんです。ありがとうございます、ごちそうさまです、おかわりをください。
線形結合って面白そうだなと思ったら線形代数の学び時です、知らんけど。このシリーズで一緒に学びましょう。