はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語でディリクレ分布の乱数を生成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
ディリクレ分布の乱数生成
ディリクレ分布(Dirichlet Distribution)の乱数を生成します。ディリクレ分布については「ディリクレ分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(MCMCpack) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
サンプリング
まずは、ディリクレ分布の乱数を生成します。
ディリクレ分布のパラメータ$\boldsymbol{\beta}$とデータ数$N$を設定します。この例では、三角図で可視化するため、次元数を$V = 3$とします。乱数の生成自体は次元数に関わらず行えます。
# パラメータを指定 beta_v <- c(4, 2, 3) # データ数(サンプルサイズ)を指定 N <- 10000
$V$次元ベクトル$\boldsymbol{\beta} = (\beta_1, \beta_2, \beta_3)$、$\beta_v > 0$の値を指定します。
ディリクレ分布に従う乱数を生成します。
# ディリクレ分布に従う乱数を生成 phi_nv <- MCMCpack::rdirichlet(n = N, alpha = beta_v) head(phi_nv); rowSums(phi_nv[1:5, ])
## [,1] [,2] [,3] ## [1,] 0.6498730 0.1085988 0.24152817 ## [2,] 0.5797410 0.3275577 0.09270128 ## [3,] 0.5655834 0.1104926 0.32392399 ## [4,] 0.4792222 0.1944610 0.32631686 ## [5,] 0.2566923 0.1355960 0.60771171 ## [6,] 0.2873406 0.3400511 0.37260827 ## [1] 1 1 1 1 1
ディリクレ分布の乱数は、MCMCpackパッケージのrdirichlet()で生成できます。データ数の引数nにN、パラメータの引数alphaにbeta_vを指定します。
生成した値(出力されるマトリクスの各行)をサンプル$\boldsymbol{\phi}_n = (\phi_{n,1}, \phi_{n,2}, \phi_{n,3})$とします。各行の和が1になります。
三角座標の準備
ディリクレ分布を三角図により可視化するために、三角座標を描画するための準備をします。詳しくは「ggplot2で三角グラフを作図したい - からっぽのしょこ」と「ggplot2で三角グラフの等高線を作図したい - からっぽのしょこ」を参照してください。
・作図用のコード(クリックで展開)
軸目盛の間隔を設定して、三角座標を描画するためのデータフレームを作成します。
# 軸目盛の位置を指定 axis_vals <- seq(from = 0, to = 1, by = 0.1) # 枠線用の値を作成 ternary_axis_df <- tibble::tibble( y_1_start = c(0.5, 0, 1), # 始点のx軸の値 y_2_start = c(0.5*sqrt(3), 0, 0), # 始点のy軸の値 y_1_end = c(0, 1, 0.5), # 終点のx軸の値 y_2_end = c(0, 0, 0.5*sqrt(3)), # 終点のy軸の値 axis = c("x_1", "x_2", "x_3") # 元の軸 ) # グリッド線用の値を作成 ternary_grid_df <- tibble::tibble( y_1_start = c( 0.5 * axis_vals, axis_vals, 0.5 * axis_vals + 0.5 ), # 始点のx軸の値 y_2_start = c( sqrt(3) * 0.5 * axis_vals, rep(0, times = length(axis_vals)), sqrt(3) * 0.5 * (1 - axis_vals) ), # 始点のy軸の値 y_1_end = c( axis_vals, 0.5 * axis_vals + 0.5, 0.5 * rev(axis_vals) ), # 終点のx軸の値 y_2_end = c( rep(0, times = length(axis_vals)), sqrt(3) * 0.5 * (1 - axis_vals), sqrt(3) * 0.5 * rev(axis_vals) ), # 終点のy軸の値 axis = c("x_1", "x_2", "x_3") |> rep(each = length(axis_vals)) # 元の軸 ) # 軸ラベル用の値を作成 ternary_axislabel_df <- tibble::tibble( y_1 = c(0.25, 0.5, 0.75), # x軸の値 y_2 = c(0.25*sqrt(3), 0, 0.25*sqrt(3)), # y軸の値 label = c("phi[1]", "phi[2]", "phi[3]"), # 軸ラベル h = c(3, 0.5, -2), # 水平方向の調整用の値 v = c(0.5, 3, 0.5), # 垂直方向の調整用の値 axis = c("x_1", "x_2", "x_3") # 元の軸 ) # 軸目盛ラベル用の値を作成 ternary_ticklabel_df <- tibble::tibble( y_1 = c( 0.5 * axis_vals, axis_vals, 0.5 * axis_vals + 0.5 ), # x軸の値 y_2 = c( sqrt(3) * 0.5 * axis_vals, rep(0, times = length(axis_vals)), sqrt(3) * 0.5 * (1 - axis_vals) ), # y軸の値 label = c( rev(axis_vals), axis_vals, rev(axis_vals) ), # 軸目盛ラベル h = c( rep(1.5, times = length(axis_vals)), rep(1.5, times = length(axis_vals)), rep(-0.5, times = length(axis_vals)) ), # 水平方向の調整用の値 v = c( rep(0.5, times = length(axis_vals)), rep(0.5, times = length(axis_vals)), rep(0.5, times = length(axis_vals)) ), # 垂直方向の調整用の値 angle = c( rep(-60, times = length(axis_vals)), rep(60, times = length(axis_vals)), rep(0, times = length(axis_vals)) ), # ラベルの表示角度 axis = c("x_1", "x_2", "x_3") |> rep(each = length(axis_vals)) # 元の軸 )
4つのデータフレームを使って以降の作図を行います。
乱数の可視化
続いて、生成した乱数のグラフを作成します。ディリクレ分布のグラフ作成については「【R】ディリクレ分布の作図 - からっぽのしょこ」を参照してください。
三角座標に変換してデータフレームに格納します。
# サンプルを三角座標に変換して格納 data_df <- tibble::tibble( y_1 = phi_nv[, 2] + 0.5 * phi_nv[, 3], # 三角座標のx軸の値 y_2 = sqrt(3) * 0.5 * phi_nv[, 3] # 三角座標のy軸の値 ) data_df
## # A tibble: 10,000 × 2 ## y_1 y_2 ## <dbl> <dbl> ## 1 0.229 0.209 ## 2 0.374 0.0803 ## 3 0.272 0.281 ## 4 0.358 0.283 ## 5 0.439 0.526 ## 6 0.526 0.323 ## 7 0.457 0.120 ## 8 0.451 0.444 ## 9 0.385 0.466 ## 10 0.553 0.112 ## # … with 9,990 more rows
2次元座標におけるx軸($y_1$軸)の値を$y_{n,1} = \phi_{n,2} + \frac{\phi_{n,3}}{2}$、y軸($y_2$軸)の値を$y_{n,2} = \frac{\sqrt{3} \phi_{n,3}}{2}$で計算して、データフレームに格納します。
作図用と計算用のディリクレ分布の確率変数の値$\boldsymbol{\phi}$を作成して、確率密度を計算します。
# 三角座標の値を作成 y_1_vals <- seq(from = 0, to = 1, length.out = 301) y_2_vals <- seq(from = 0, to = 0.5*sqrt(3), length.out = 300) # 格子点を作成 y_mat <- tidyr::expand_grid( y_1 = y_1_vals, y_2 = y_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 # 3次元変数に変換 phi_mat <- tibble::tibble( phi_2 = y_mat[, 1] - y_mat[, 2] / sqrt(3), phi_3 = 2 * y_mat[, 2] / sqrt(3) ) |> # 元の座標に変換 dplyr::mutate( phi_2 = dplyr::if_else(phi_2 >= 0 & phi_2 <= 1, true = phi_2, false = as.numeric(NA)), phi_3 = dplyr::if_else(phi_3 >= 0 & phi_3 <= 1 & !is.na(phi_2), true = phi_3, false = as.numeric(NA)), phi_1 = 1 - phi_2 - phi_3, phi_1 = dplyr::if_else(phi_1 >= 0 & phi_1 <= 1, true = phi_1, false = as.numeric(NA)) ) |> # 範囲外の値をNAに置換 dplyr::select(phi_1, phi_2, phi_3) |> # 順番を変更 as.matrix() # マトリクスに変換 # ディリクレ分布の確率密度を計算 dens_df <- tibble::tibble( y_1 = y_mat[, 1], # x軸の値 y_2 = y_mat[, 2], # y軸の値 density = MCMCpack::ddirichlet(x = phi_mat, alpha = beta_v), # 確率密度 ) |> dplyr::mutate( fill_flg = !is.na(rowSums(phi_mat)), density = dplyr::if_else(fill_flg, true = density, false = as.numeric(NA)) ) # 範囲外の値をNAに置換 dens_df
## # A tibble: 90,300 × 4 ## y_1 y_2 density fill_flg ## <dbl> <dbl> <dbl> <lgl> ## 1 0 0 0 TRUE ## 2 0 0.00290 NA FALSE ## 3 0 0.00579 NA FALSE ## 4 0 0.00869 NA FALSE ## 5 0 0.0116 NA FALSE ## 6 0 0.0145 NA FALSE ## 7 0 0.0174 NA FALSE ## 8 0 0.0203 NA FALSE ## 9 0 0.0232 NA FALSE ## 10 0 0.0261 NA FALSE ## # … with 90,290 more rows
三角座標を含めた2次元座標上の格子点を作成してy_matとします。
y_matを3次元座標上の点($\boldsymbol{\phi}$の点)に変換してphi_matとします。ただし、三角座標外の点については、総和が1の値($\boldsymbol{\phi}$を満たす値)にならないので欠損値NAに置き換えます。
ディリクレ分布の確率密度は、MCMCpackパッケージのddirichlet()で計算できます。確率変数の引数xにphi_mat、パラメータの引数alphaにbeta_vを指定します。
作図用の値y_matと、計算用の値x_matにより求めた確率密度をデータフレームに格納します。ただし、三角座標外の要素(phi_matの欠損値を含む行)については欠損値NAに置き換えます。
サンプルの散布図を確率分布の等高線図と重ねて作成します。
# パラメータラベル用の文字列を作成 param_text <- paste0( "list(", "beta==(list(", paste0(beta_v, collapse = ", "), "))", ", N==", N, ")" ) # サンプルの散布図を作成 ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_point(data = data_df, mapping = aes(x = y_1, y = y_2), color = "orange", alpha = 0.3) + # サンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = parse(text = param_text), color = "density", x = "", y = "")
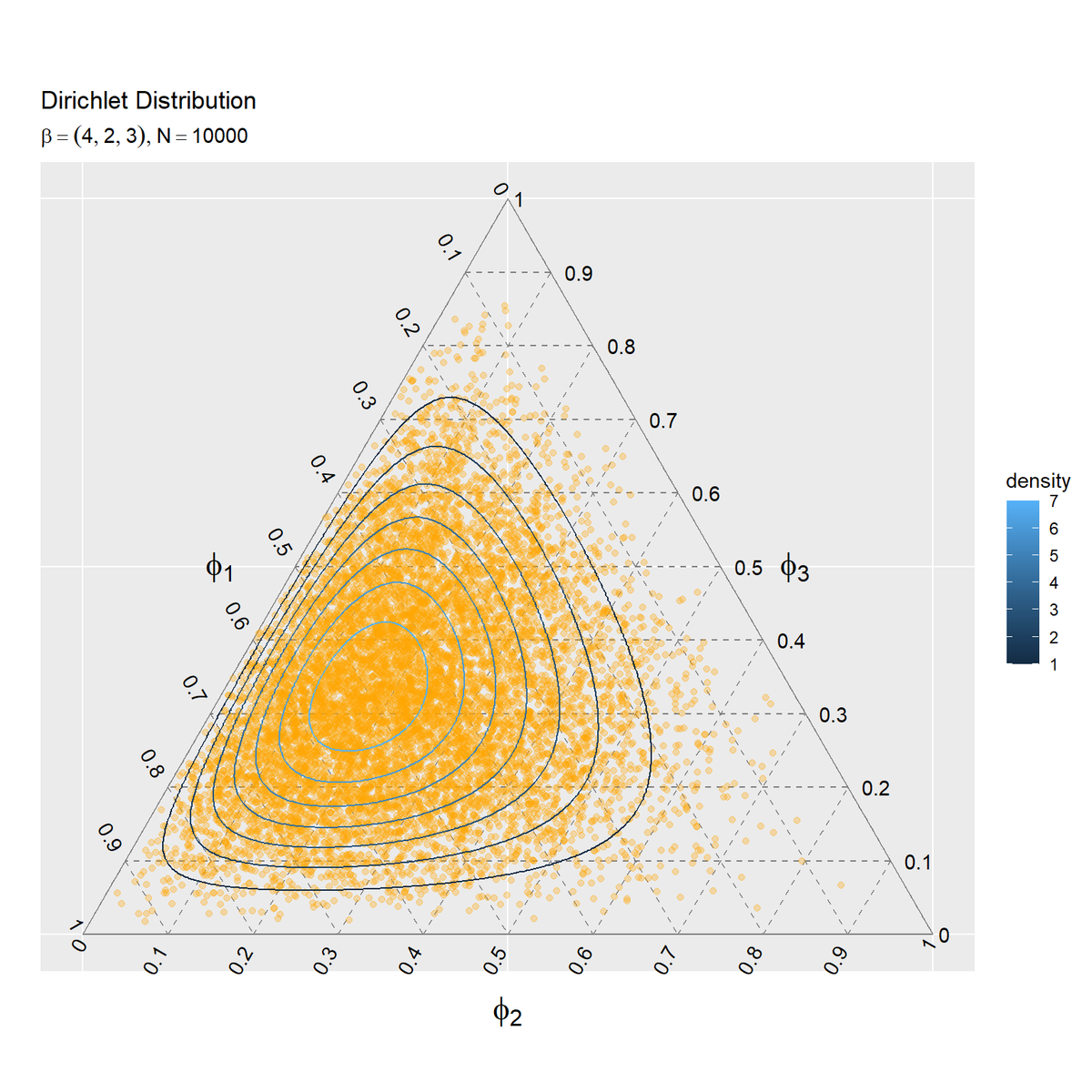
サンプルの度数のヒートマップを作成します。
# サンプルの度数のヒートマップを作成 ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_bin_2d(data = data_df, mapping = aes(x = y_1, y = y_2, fill = ..count..), alpha = 0.8) + # サンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 scale_color_distiller(palette = "Spectral") + # 等高線の色 scale_fill_distiller(palette = "Spectral") + # 塗りつぶしの色 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = parse(text = param_text), color = "density", fill = "frequency", x = "", y = "")
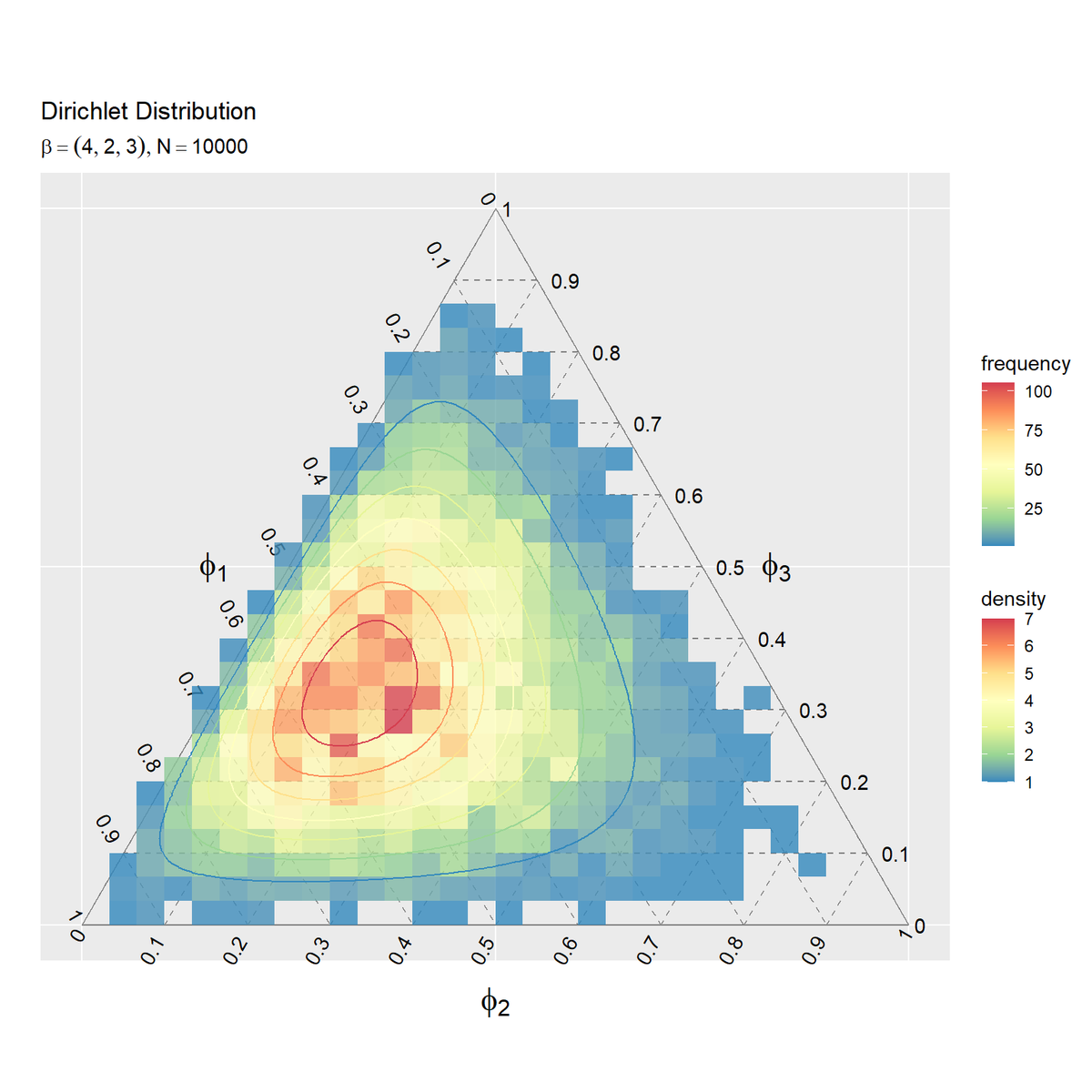
geom_bin_2d()で2次元の変数に対するヒートマップを描画できます。タイルの色の引数fillに..count..を指定すると度数、..density..を指定すると密度に応じて色付けされます。
密度の等高線図を作成します。
# サンプルの密度の等高線図を作成 ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_density_2d_filled(data = data_df, mapping = aes(x = y_1, y = y_2, fill = ..level..), alpha = 0.8) + # サンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 scale_color_viridis_c(option = "D") + # 等高線の色 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = parse(text = param_text), color = "density", fill = "density", x = "", y = "")
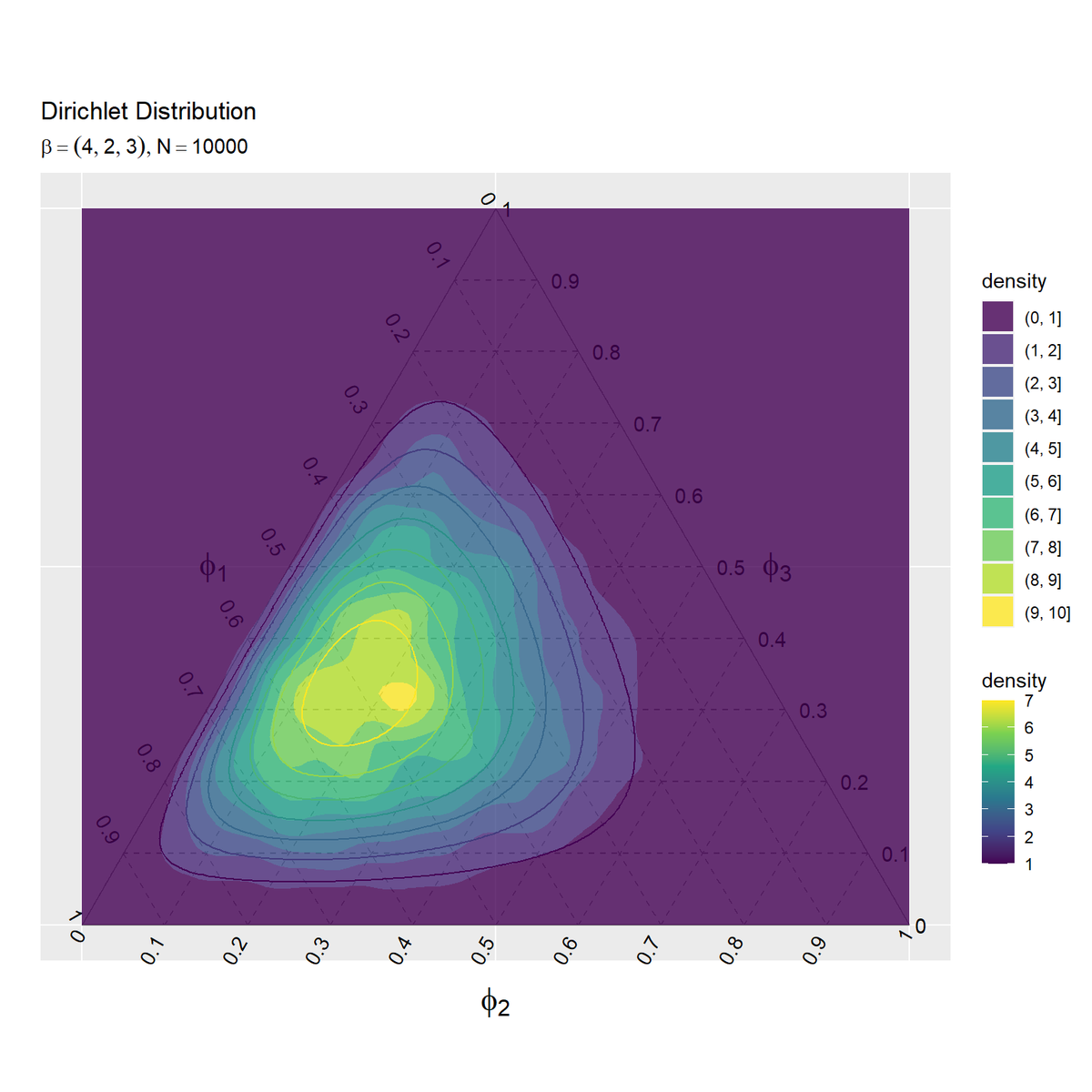
geom_density_2d_filled()で密度の等高線図を描画できます。
データ数が十分に増えると、ヒストグラムの形が分布の形に近付きます。
乱数と分布の関係をアニメーションで可視化
次は、サンプルサイズとヒストグラムの形状の関係をアニメーションで確認します。
1データずつ可視化
1データずつ乱数を生成するアニメーションを作成します。
・コード(クリックで展開)
データ数を指定して、サンプルを生成します。
# パラメータを指定 beta_v <- c(4, 2, 3) # データ数(フレーム数)を指定 N <- 100 # ディリクレ分布に従う乱数を生成 phi_nv <- MCMCpack::rdirichlet(n = N, alpha = beta_v) head(phi_nv)
## [,1] [,2] [,3] ## [1,] 0.3325355 0.24960432 0.4178602 ## [2,] 0.2857704 0.15698146 0.5572481 ## [3,] 0.4582656 0.18531630 0.3564181 ## [4,] 0.3497506 0.09792221 0.5523272 ## [5,] 0.4583167 0.25243550 0.2892478 ## [6,] 0.4128423 0.28524453 0.3019132
phi_nvのn番目の行を、n番目のデータ(n回目にサンプリングされた値)とみなします。アニメーションのn番目のフレームでは、n個のサンプルphi_nv[1:n, ]のグラフを描画します。
サンプルをデータフレームに格納します。
# サンプルを三角座標に変換して格納 anime_data_df <- tibble::tibble( n = 1:N, # データ番号 y_1 = phi_nv[, 2] + 0.5 * phi_nv[, 3], # 三角座標のx軸の値 y_2 = sqrt(3) * 0.5 * phi_nv[, 3], # 三角座標のy軸の値 parameter = paste0("beta=(", paste0(beta_v, collapse = ", "), "), n=", n) |> factor(levels = paste0("beta=(", paste0(beta_v, collapse = ", "), "), n=", 1:N)) # フレーム切替用ラベル ) anime_data_df
## # A tibble: 100 × 4 ## n y_1 y_2 parameter ## <int> <dbl> <dbl> <fct> ## 1 1 0.459 0.362 beta=(4, 2, 3), n=1 ## 2 2 0.436 0.483 beta=(4, 2, 3), n=2 ## 3 3 0.364 0.309 beta=(4, 2, 3), n=3 ## 4 4 0.374 0.478 beta=(4, 2, 3), n=4 ## 5 5 0.397 0.250 beta=(4, 2, 3), n=5 ## 6 6 0.436 0.261 beta=(4, 2, 3), n=6 ## 7 7 0.351 0.179 beta=(4, 2, 3), n=7 ## 8 8 0.235 0.356 beta=(4, 2, 3), n=8 ## 9 9 0.417 0.480 beta=(4, 2, 3), n=9 ## 10 10 0.443 0.270 beta=(4, 2, 3), n=10 ## # … with 90 more rows
サンプルphi_nvをデータフレームに格納して、フレーム切替用のラベルを作成します。ラベルが文字列型だと文字列の基準で順序が決まるので、因子型にしてサンプリング回数に応じたレベル(順序)を設定します。
このデータフレームは、各試行におけるサンプルを描画するのに使います。
サンプリング回数ごとに、それまでのサンプルを持つデータフレームを作成します。
# サンプルを複製して三角座標に変換して格納 anime_freq_df <- tidyr::expand_grid( frame = 1:N, # フレーム番号 n = 1:N # データ番号 ) |> # 全ての組み合わせを作成 dplyr::filter(n <= frame) |> # 各試行までのサンプルを抽出 dplyr::mutate( y_1 = phi_nv[n, 2] + 0.5 * phi_nv[n, 3], # 三角座標のx軸の値 y_2 = sqrt(3) * 0.5 * phi_nv[n, 3], # 三角座標のy軸の値 parameter = paste0("beta=(", paste0(beta_v, collapse = ", "), "), n=", frame) |> factor(levels = paste0("beta=(", paste0(beta_v, collapse = ", "), "), n=", 1:N)) # フレーム切替用ラベル ) anime_freq_df
## # A tibble: 5,050 × 5 ## frame n y_1 y_2 parameter ## <int> <int> <dbl> <dbl> <fct> ## 1 1 1 0.459 0.362 beta=(4, 2, 3), n=1 ## 2 2 1 0.459 0.362 beta=(4, 2, 3), n=2 ## 3 2 2 0.436 0.483 beta=(4, 2, 3), n=2 ## 4 3 1 0.459 0.362 beta=(4, 2, 3), n=3 ## 5 3 2 0.436 0.483 beta=(4, 2, 3), n=3 ## 6 3 3 0.364 0.309 beta=(4, 2, 3), n=3 ## 7 4 1 0.459 0.362 beta=(4, 2, 3), n=4 ## 8 4 2 0.436 0.483 beta=(4, 2, 3), n=4 ## 9 4 3 0.364 0.309 beta=(4, 2, 3), n=4 ## 10 4 4 0.374 0.478 beta=(4, 2, 3), n=4 ## # … with 5,040 more rows
フレーム番号とデータ番号(それぞれ1からNの整数)の全ての組み合わせをexpand_grid()で作成して、フレーム番号以下のデータ番号を抽出します。
データ番号をインデックスとして使って、x_ndから対応するサンプルを抽出します。
フレーム番号をデータ番号として、フレーム切替用のラベルを作成します。
このデータフレームは、ヒートマップなどのグラフを描画するのに使います。
サンプルの散布図のアニメーション(gif画像)を作成します。
# 散布図のアニメーションを作図 anime_freq_graph <- ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 geom_point(data = anime_freq_df, mapping = aes(x = y_1, y = y_2), color = "orange", alpha = 0.5) + # n個のサンプル geom_point(data = anime_data_df, mapping = aes(x = y_1, y = y_2), color = "orange", size = 3) + # n番目のサンプル gganimate::transition_manual(parameter) + # フレーム scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = "{current_frame}", color = "density", x = "", y = "") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N+10, end_pause = 10, fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにデータ数(サンプルサイズ)、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと指定した通りに動作しません。
サンプルの度数のヒートマップのアニメーションを作成します。
# 度数のヒートマップのアニメーションを作図 anime_freq_graph <- ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_bin_2d(data = anime_freq_df, mapping = aes(x = y_1, y = y_2, fill = ..count..), alpha = 0.8) + # n個のサンプル geom_point(data = anime_data_df, mapping = aes(x = y_1, y = y_2), color = "orange", size = 3) + # n番目のサンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 gganimate::transition_manual(parameter) + # フレーム scale_color_distiller(palette = "Spectral") + # 等高線の色 scale_fill_distiller(palette = "Spectral") + # 塗りつぶしの色 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = "{current_frame}", color = "density", fill = "frequency", x = "", y = "") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N+10, end_pause = 10, fps = 10, width = 800, height = 600)
サンプルの密度の等高線のアニメーションを作成します。
# 除去するフレーム数を指定 n_min <- 10 # (データが少ないと密度を計算できないため)最初のフレームを除去 tmp_data_df <- anime_data_df|> dplyr::filter(n > n_min) |> # 始めのデータを削除 dplyr::mutate( parameter = parameter |> as.character() |> (\(.){factor(., levels = unique(.))})() # レベルを再設定 ) tmp_freq_df <- anime_freq_df |> dplyr::filter(frame > n_min) |> # 始めのデータを削除 dplyr::mutate( parameter = parameter |> as.character() |> (\(.){factor(., levels = unique(.))})() # レベルを再設定 ) # 密度の等高線図のアニメーションを作図 anime_freq_graph <- ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_density_2d_filled(data = tmp_freq_df, mapping = aes(x = y_1, y = y_2, fill = ..level..), alpha = 0.8) + # n個のサンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 geom_point(data = tmp_data_df, mapping = aes(x = y_1, y = y_2), color = "orange", size = 3) + # n番目のサンプル gganimate::transition_manual(parameter) + # フレーム scale_color_viridis_c(option = "D") + # 等高線の色 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = "{current_frame}", color = "density", fill = "density", x = "", y = "") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N+10, end_pause = 10, fps = 10, width = 800, height = 600)
データが1つだと密度を計算できず、またデータが少ないと密度が大きくなり(z軸の最大値が大きくなり)アニメーション全体でのグラデーション(等高線)が分かりにくくなるので、始めのフレームに対応する行を取り除いておきます。
データフレームからデータを除いても、因子レベルの情報がアニメーションのフレームに影響してしまうので、因子の情報を再設定する必要があります。
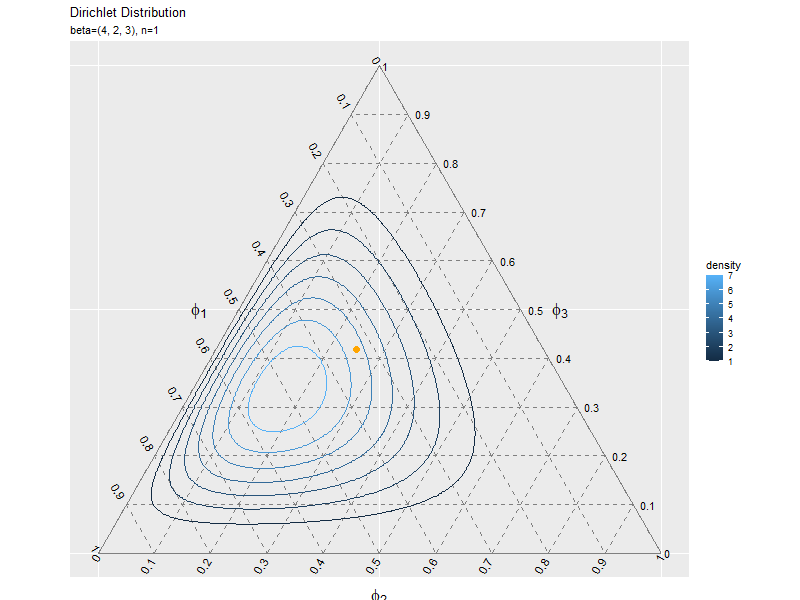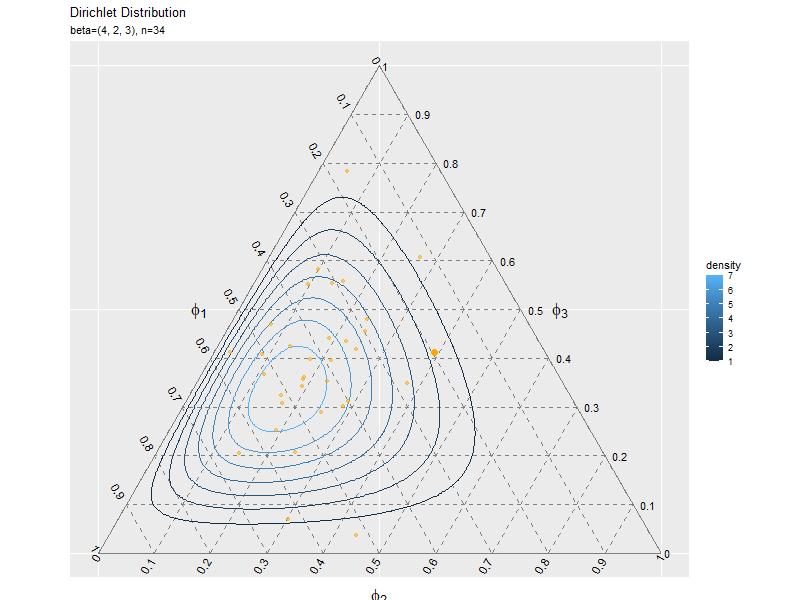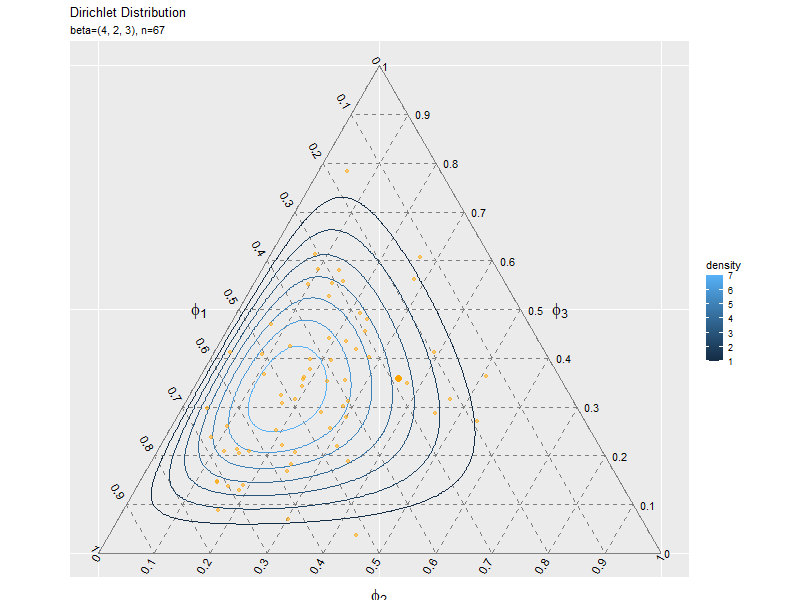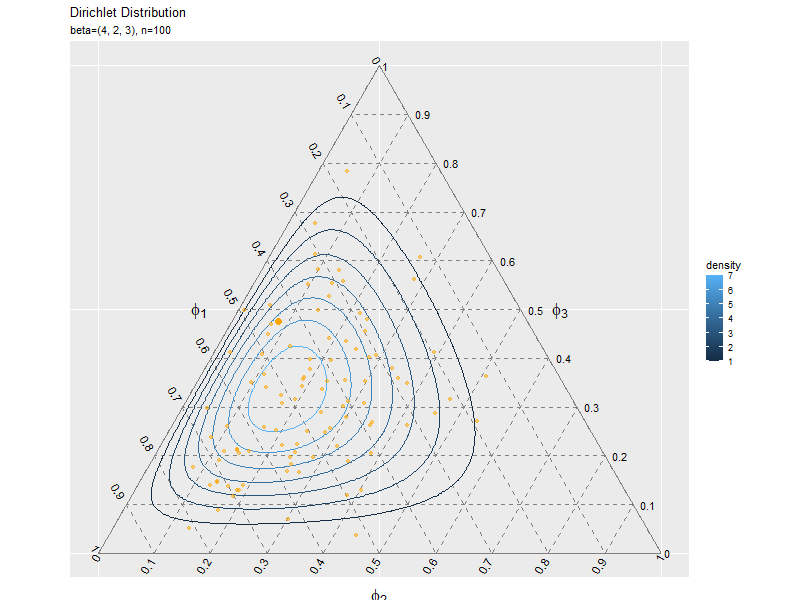
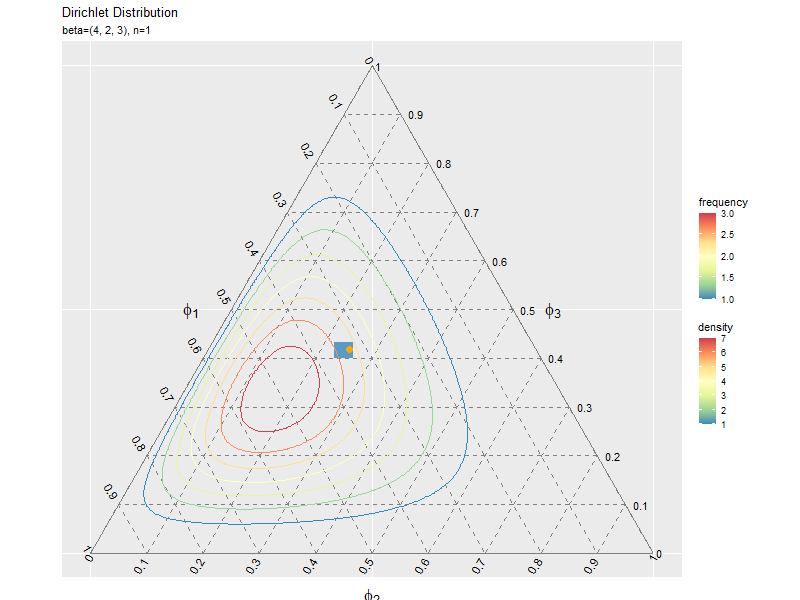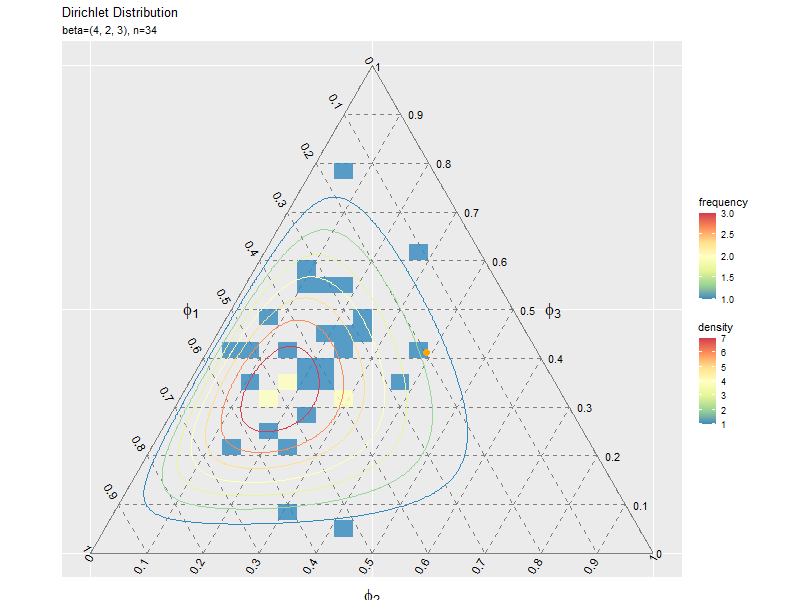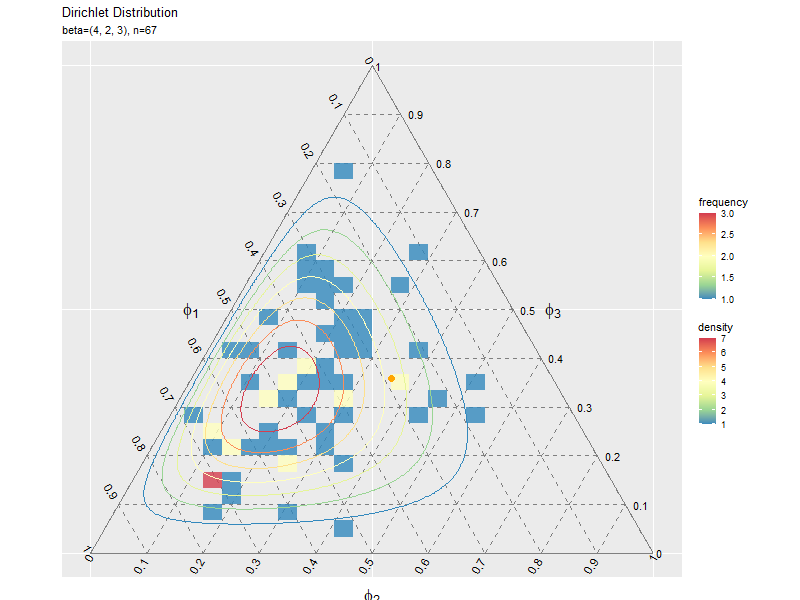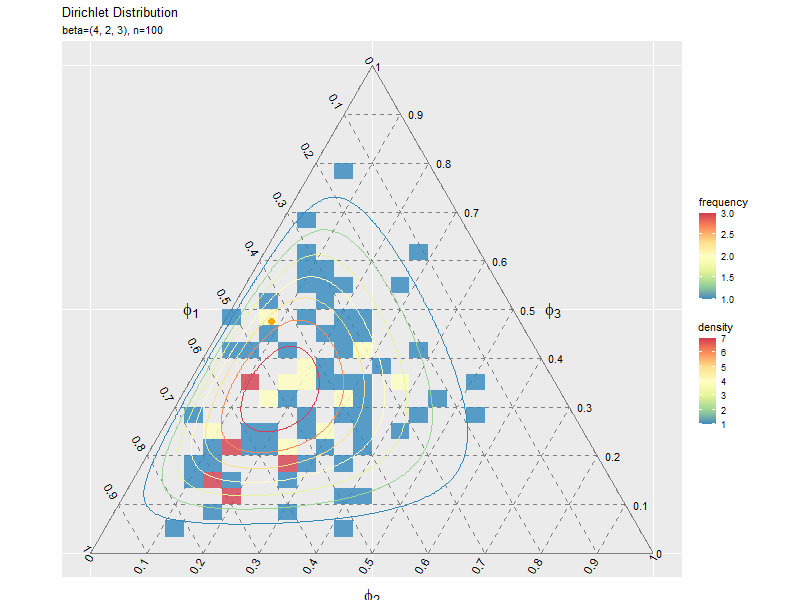
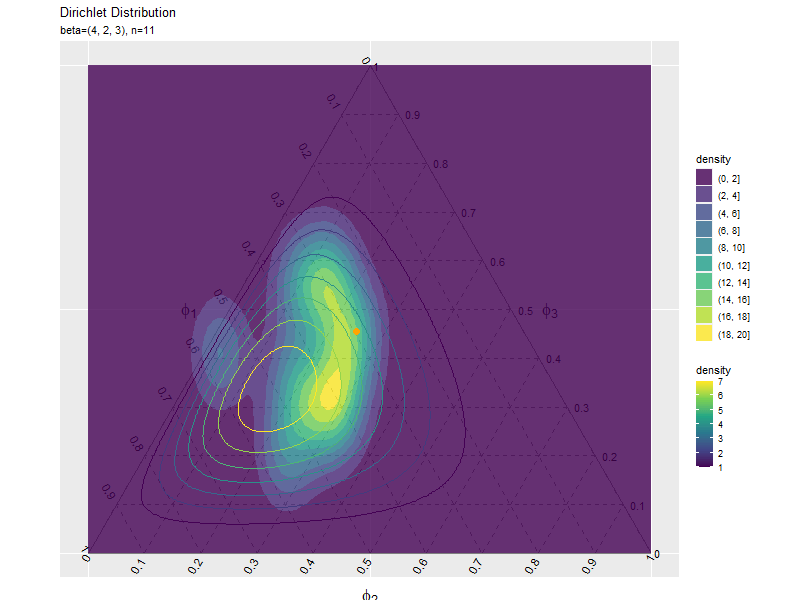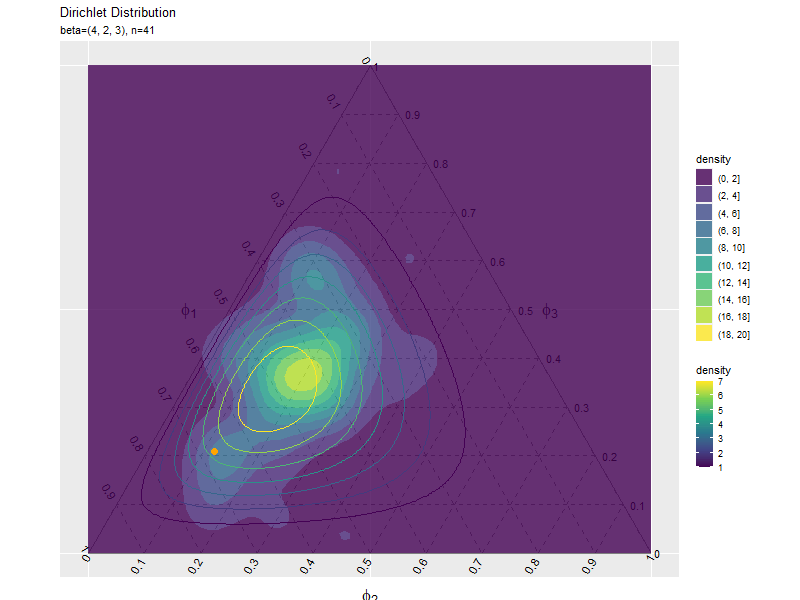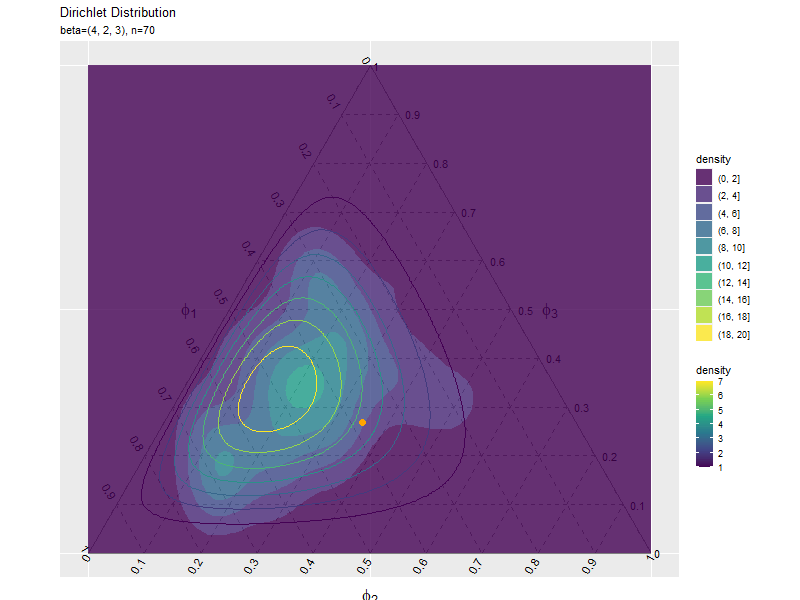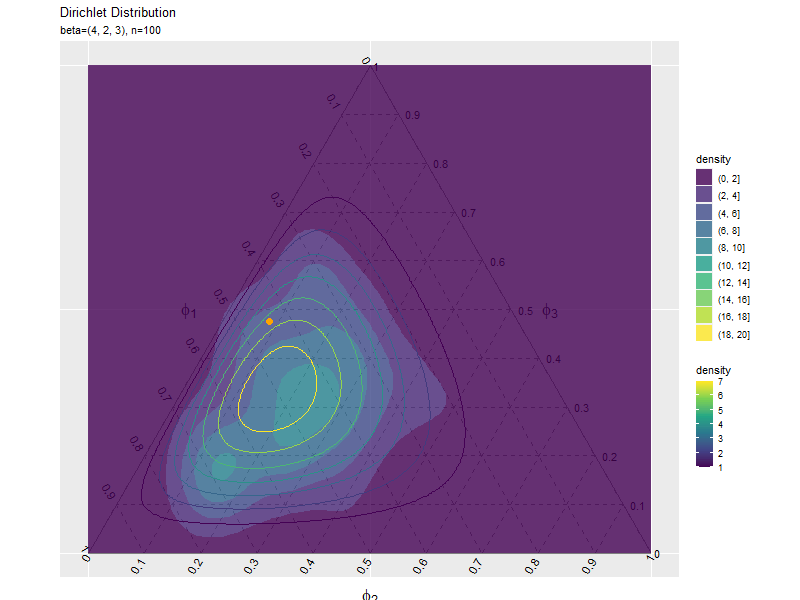
複数データずつ可視化
続いて、フレームごとに複数データを生成します。
・コード(クリックで展開)
データ数とフレーム数を指定します。
# パラメータを指定 beta_v <- c(4, 2, 3) # データ数を指定 N <- 10000 # フレーム数を指定 frame_num <- 100 # 1フレーム当たりのデータ数を計算 n_per_frame <- N %/% frame_num n_per_frame
## [1] 100
データ数Nとフレーム数frame_numを指定して、1フレーム当たりのデータ数n_per_frameを計算します。
サンプルを生成して、フレームごとにn_per_frame個ずつサンプルが増えるデータフレームを作成します。
# ディリクレ分布に従う乱数を生成 phi_nv <- MCMCpack::rdirichlet(n = N, alpha = beta_v) # サンプルを複製して三角座標に変換して格納 anime_freq_df <- tidyr::expand_grid( frame = 1:frame_num, # フレーム番号 n = 1:N # データ番号 ) |> # 全ての組み合わせを作成 dplyr::filter(n <= frame*n_per_frame) |> # 各フレームで利用するサンプルを抽出 dplyr::mutate( y_1 = phi_nv[n, 2] + 0.5 * phi_nv[n, 3], # 三角座標のx軸の値 y_2 = sqrt(3) * 0.5 * phi_nv[n, 3], # 三角座標のy軸の値 parameter = paste0("beta=(", paste0(beta_v, collapse = ", "), "), n=", frame*n_per_frame) |> factor(levels = paste0("beta=(", paste0(beta_v, collapse = ", "), "), n=", 1:frame_num*n_per_frame)) # フレーム切替用ラベル ) anime_freq_df
## # A tibble: 505,000 × 5 ## frame n y_1 y_2 parameter ## <int> <int> <dbl> <dbl> <fct> ## 1 1 1 0.420 0.147 beta=(4, 2, 3), n=100 ## 2 1 2 0.378 0.310 beta=(4, 2, 3), n=100 ## 3 1 3 0.319 0.206 beta=(4, 2, 3), n=100 ## 4 1 4 0.484 0.324 beta=(4, 2, 3), n=100 ## 5 1 5 0.455 0.349 beta=(4, 2, 3), n=100 ## 6 1 6 0.176 0.263 beta=(4, 2, 3), n=100 ## 7 1 7 0.466 0.413 beta=(4, 2, 3), n=100 ## 8 1 8 0.646 0.212 beta=(4, 2, 3), n=100 ## 9 1 9 0.503 0.647 beta=(4, 2, 3), n=100 ## 10 1 10 0.611 0.296 beta=(4, 2, 3), n=100 ## # … with 504,990 more rows
1データずつのときと同様に、作図用のデータを作成します。こちらは、フレームごとに「フレーム番号」掛ける「1フレーム当たりのデータ数」番目までのサンプルを抽出します。
散布図のアニメーションを作成します。
# 散布図のアニメーションを作図 anime_freq_graph <- ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_point(data = anime_freq_df, mapping = aes(x = y_1, y = y_2), color = "orange", alpha = 0.3) + # サンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 gganimate::transition_manual(parameter) + # フレーム scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = "{current_frame}", color = "density", x = "", y = "") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = frame_num+10, end_pause = 10, fps = 10, width = 800, height = 600)
1データずつのときと同様に処理します。
サンプルの度数のヒートマップのアニメーションを作成します。
# 度数のヒートマップのアニメーションを作図 anime_freq_graph <- ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_bin_2d(data = anime_freq_df, mapping = aes(x = y_1, y = y_2, fill = ..count..), alpha = 0.8) + # サンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 gganimate::transition_manual(parameter) + # フレーム scale_color_distiller(palette = "Spectral") + # 等高線の色 scale_fill_distiller(palette = "Spectral") + # 塗りつぶしの色 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = "{current_frame}", color = "density", fill = "frequency", x = "", y = "") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = frame_num+10, end_pause = 10, fps = 10, width = 800, height = 600)
サンプルの密度の等高線のアニメーションを作成します。
# 密度の等高線図のアニメーションを作図 anime_freq_graph <- ggplot() + geom_segment(data = ternary_axis_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50") + # 三角図の枠線 geom_segment(data = ternary_grid_df, mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end), color = "gray50", linetype = "dashed") + # 三角図のグリッド線 geom_text(data = ternary_ticklabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル geom_text(data = ternary_axislabel_df, mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 三角図の軸ラベル geom_density_2d_filled(data = anime_freq_df, mapping = aes(x = y_1, y = y_2, fill = ..level..), alpha = 0.8) + # サンプル geom_contour(data = dens_df, mapping = aes(x = y_1, y = y_2, z = density, color = ..level..)) + # 分布 gganimate::transition_manual(parameter) + # フレーム scale_color_viridis_c(option = "D") + # 等高線の色 scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸 scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(axis.ticks = element_blank(), panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "Dirichlet Distribution", subtitle = "{current_frame}", color = "density", fill = "density", x = "", y = "") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = frame_num+10, end_pause = 10, fps = 10, width = 800, height = 600)
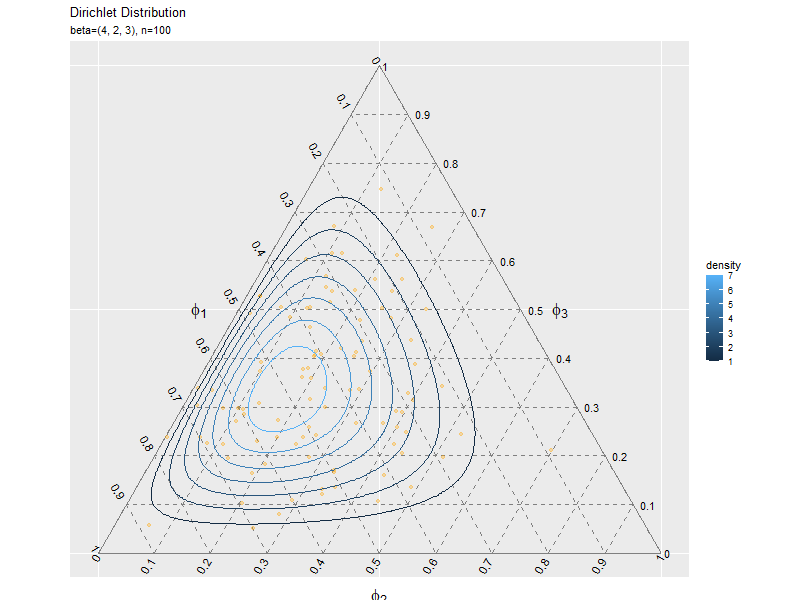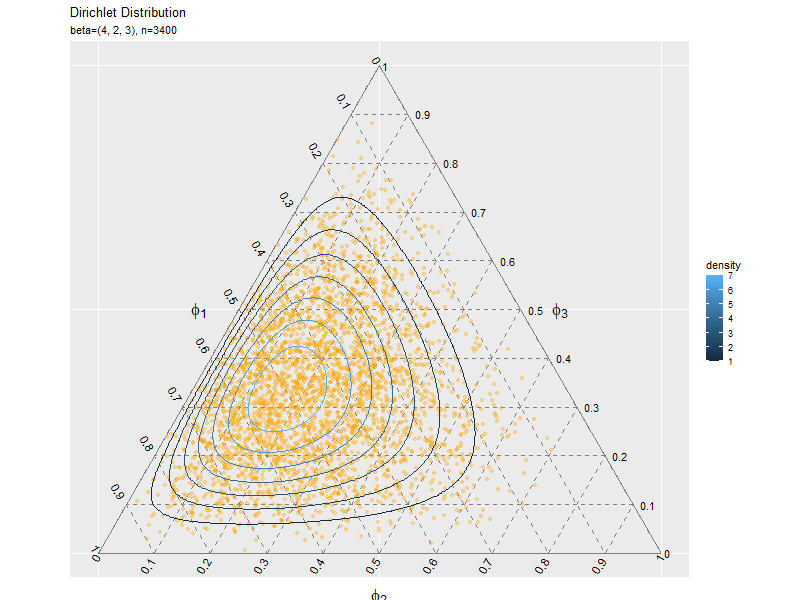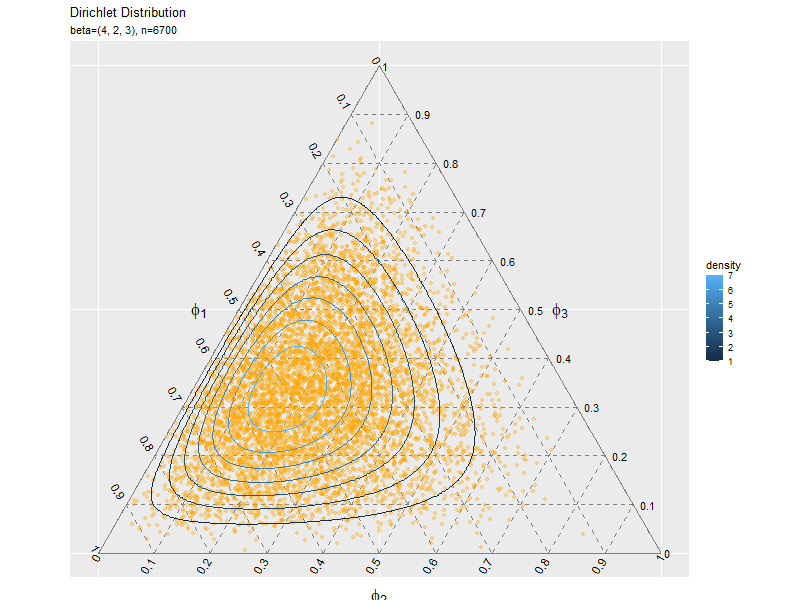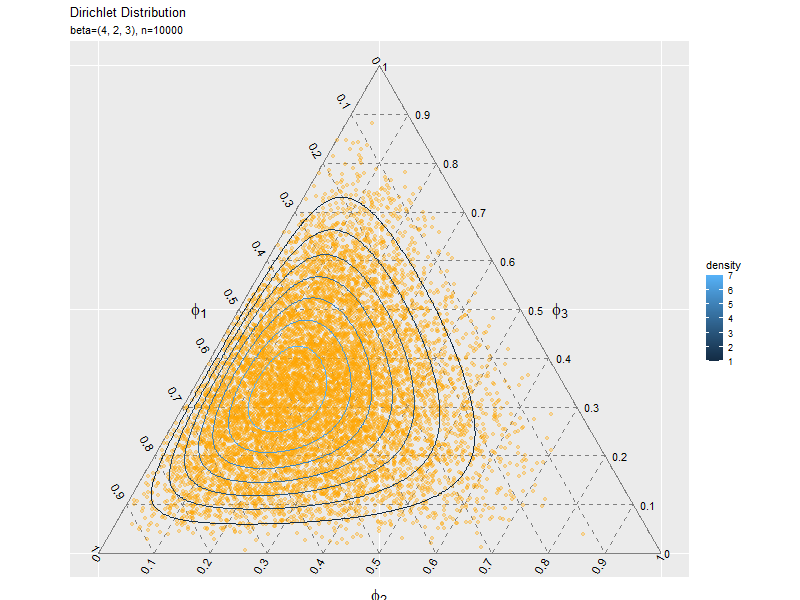
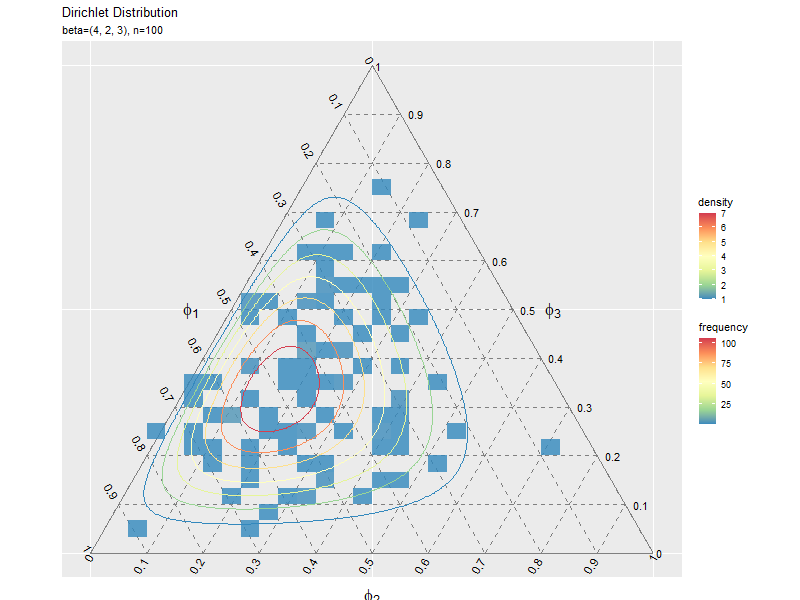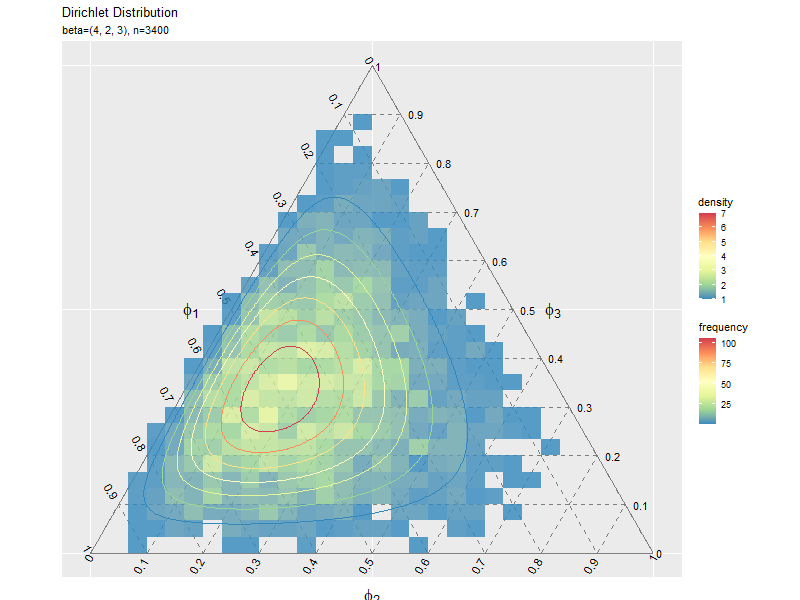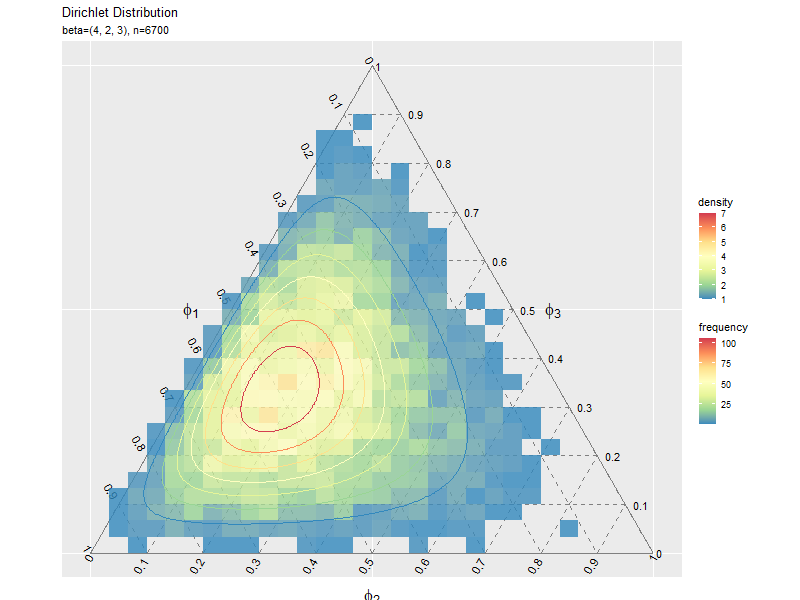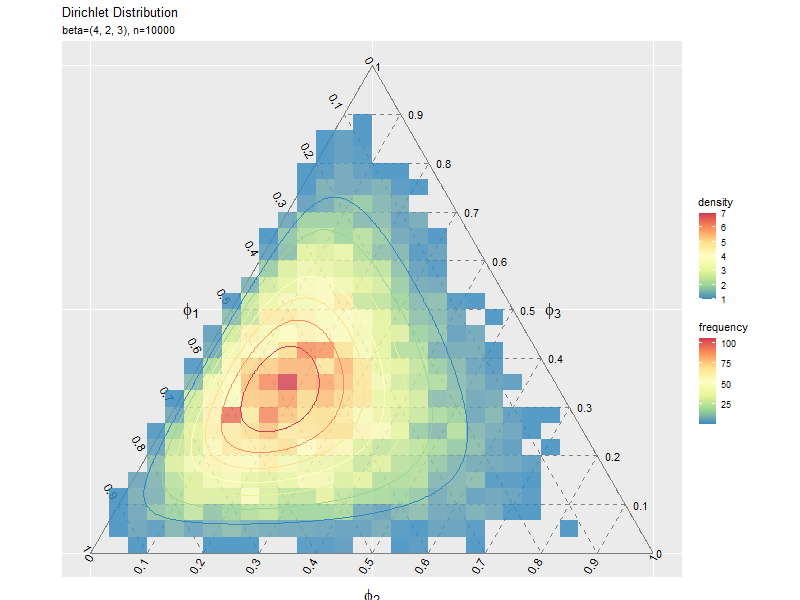
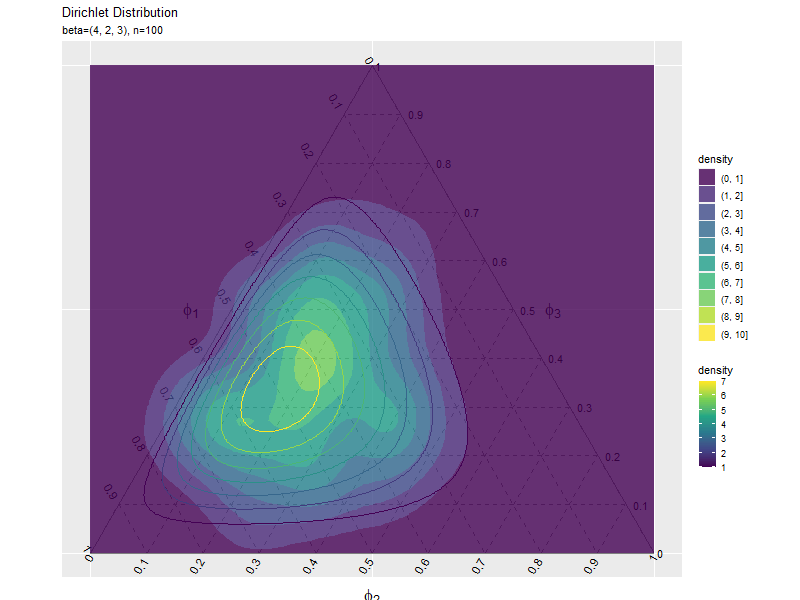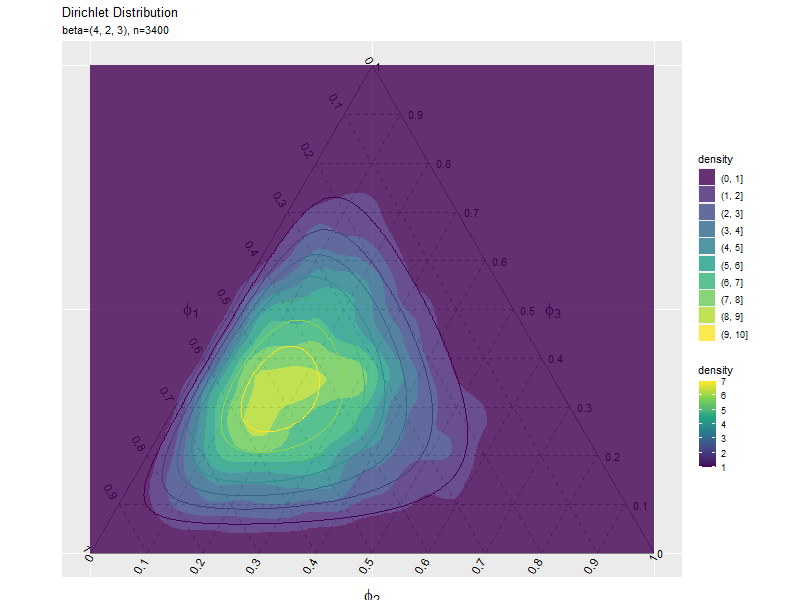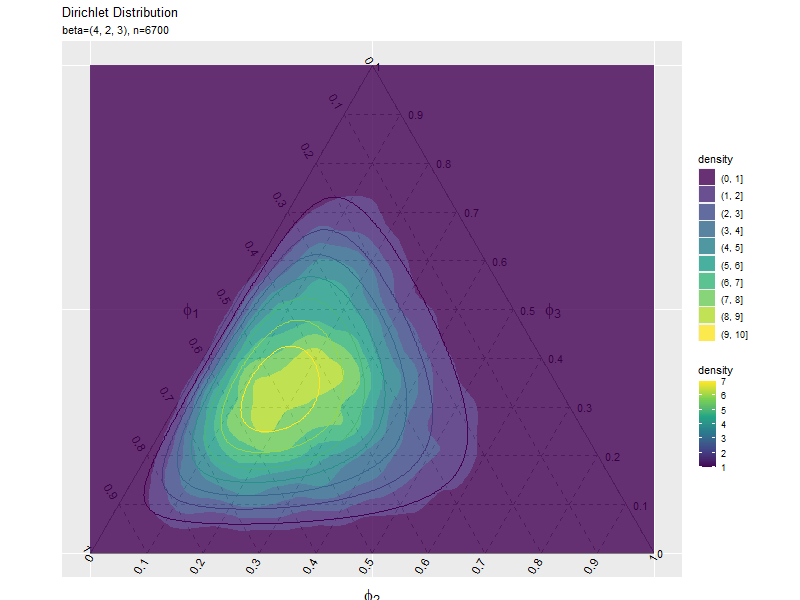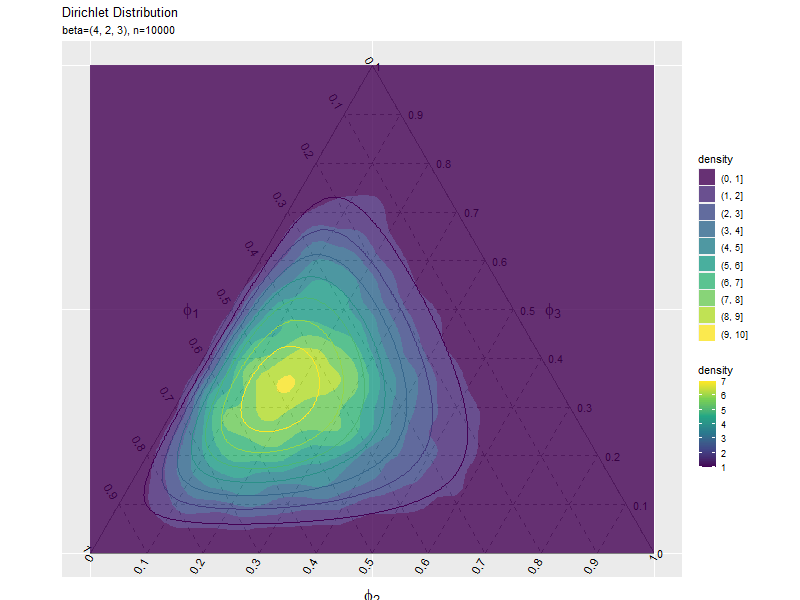
サンプルが増えるに従って、元の分布に近付くのを確認できます。
この記事では、ガウス分布の乱数生成を確認しました。次は、ガウス分布から確率分布を生成します。
参考文献
- 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.
おわりに
力及ばず密度のグラフで三角の外にも色が付いてしまったのが残念でした。上からグレーで塗りつぶそうかと思いましたが、これ以上コードが分かりにくくなってもしょうがないので諦めました。
【次の内容】