はじめに
素直なやり方ではできなかったのでむりくりなんとかする黒魔術シリーズです。もっといい方法があれば教えてください。
この記事では、Pythonで三角図を作成します。
【目次】
Matplotlibで三角グラフを作図したい
三角図や三角ダイアグラム(ternary diagram)などと呼ばれるグラフのアニメーションを作成したい。そこで、MatplotlibライブラリのAnimationモジュールを利用できるようにPyplotモジュールを利用して三角図を作成する。
利用するライブラリを読み込む。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
三角座標への変換式の確認
まずは、3次元座標上の点$\mathbf{x}$から三角座標(2次元座標)上の点$\mathbf{y}$に変換する計算式を確認する。
総和が1の3次元の変数(点)
に対して、次の式で2次元の変数(点)$\mathbf{y}$に変換できる。
$\mathbf{y}$は、正三角形の座標上の点になる。2次元座標上の点に変換することで、2次元のグラフで可視化できる。
総和が1でない定数の場合は、各成分(各次元の値)を総和(定数)で割り、総和が1になるように正規化することで、同様に計算(処理)できる。
この記事では、元の3次元の座標におけるx軸・y軸・z軸をそれぞれ$x_0$軸・$x_1$軸・$x_2$軸、変換後の2次元の座標におけるx軸・y軸をそれぞれ$y_0$軸・$y_1$軸と呼ぶことにする。Pythonのインデックスに合わせて添字を0から付けることにする。
三角図の座標
次は、三角図の基となる軸やグリッド線を用意する。
軸目盛用の値を設定する。
# 軸目盛の位置を指定 axis_vals = np.arange(start=0.0, stop=1.1, step=0.1) print(axis_vals)
[0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
3つの軸の目盛ラベルやグリッド線を描画する位置として、0から1の範囲の値をaxis_valsに指定する。
axis_valsを使って、描画に利用する配列を作成する。
正三角形の枠線(2次元座標上の$x_0$軸・$x_1$軸・$x_2$軸)を描画する用の配列を作成する。
# 軸線用の値を作成 axis_x = np.array([0.5, 0.0, 1.0]) axis_y = np.array([0.5*np.sqrt(3.0), 0.0, 0.0]) axis_u = np.array([-0.5, 1.0, -0.5]) axis_v = np.array([-0.5*np.sqrt(3.0), 0.0, 0.5*np.sqrt(3.0)]) print(axis_x) print(np.round(axis_y, 2)) print(axis_u) print(np.round(axis_v, 2))
[0.5 0. 1. ]
[0.87 0. 0. ]
[-0.5 1. -0.5]
[-0.87 0. 0.87]
3つの軸をそれぞれ線分として描画するため、各軸の始点の$y_0$軸・$y_1$軸の値をaxis_x・axis_y、始点と終点の$y_0$軸・$y_1$軸の変化量をaxis_u・axis_vとする。
グリッド線を描画する用の配列を作成する。
# グリッド線用の値を作成 grid_x = np.hstack([ 0.5 * axis_vals, axis_vals, 0.5 * axis_vals + 0.5 ]) grid_y = np.hstack([ 0.5 * axis_vals * np.sqrt(3.0), np.zeros_like(axis_vals), 0.5 * (1.0 - axis_vals) * np.sqrt(3.0) ]) grid_u = np.hstack([ 0.5 * axis_vals, 0.5 * (1.0 - axis_vals), -axis_vals ]) grid_v = np.hstack([ -0.5 * axis_vals * np.sqrt(3.0), 0.5 * (1.0 - axis_vals) * np.sqrt(3.0), np.zeros_like(axis_vals) ]) print(grid_x[:10]) print(np.round(grid_y[:10], 2)) print(grid_u[:10]) print(np.round(grid_v[:10], 2))
[0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45]
[0. 0.09 0.17 0.26 0.35 0.43 0.52 0.61 0.69 0.78]
[0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45]
[-0. -0.09 -0.17 -0.26 -0.35 -0.43 -0.52 -0.61 -0.69 -0.78]
$x_0$軸と$x_1$軸、$x_1$軸と$x_2$軸・$x_2$軸と$x_0$軸の対応する目盛を結ぶ線分(平行な線分)を描画するため、各グリッド線の始点の$y_0$軸・$y_1$軸の値をgrid_x・grid_y、始点と終点の$y_0$軸・$y_1$軸の変化量をgrid_u・grid_vとする。
作成した2つの配列を使って、三角図を作成する。
# 三角座標を作成 plt.figure(figsize=(10, 10), facecolor='white') # 図の設定 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.suptitle(t='Ternary Plot', fontsize=20) # 全体のタイトル plt.title(label='$x=(x_0, x_1, x_2)$', loc='left') # タイトル plt.show() # 描画
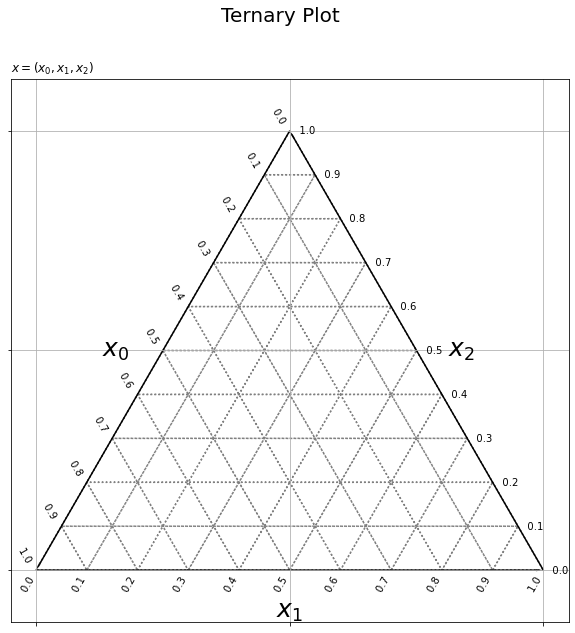
plt.quiver()で軸線とグリッド線を描画する。始点の値***_x, ***_yを第1・2引数、変化量***_u, ***_vを第3・4引数に指定して、線分を描画する。デフォルトでは調整された矢印が描画される。指定した値の通りに線を引く場合は、scale_units='xy'とscale=1を指定する。線分を描画する場合は、線の太さの引数widthと矢の太さの引数headwidthに同じ値を指定する。
plt.text()で目盛ラベルと軸ラベルを描画する。プロット位置の引数x, yと、表示する文字列の引数sに値を指定して、文字列を描画する。水平・垂直方向の調整用の引数ha, vaと、ラベルの表示角度の引数rotationを指定する。また、半角スペース' 'で微調整している。
目盛ラベルのプロット位置はgrid_x, grid_yと一致する。この例では、各軸の目盛ラベルとグリッド線が同じ角度になるように設定している。
ここまでで、三角図の座標を描画できた。続いて、グラフ全体の体裁を整える。
グラフ全体におけるx軸とy軸については、*ticks()で設定できる。主目盛(のラベルや補助線)の位置をticks引数に指定する。この例では、三角図の最小値・中央値・最大値とした。
正三角形になるようにplt.axis()に'equal'を指定して、アスペクト比を1に設定する。
各軸と対応するグリッド線の関係が分かりにくいので、色分けして確認する。
# 三角座標を作成:(軸の可視化) plt.figure(figsize=(10, 10), facecolor='white') # 図の設定 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec=np.repeat(['red', 'green', 'blue'], len(axis_vals)), linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc=['red', 'green', 'blue'], linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', c='red', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', c='green', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center', c='blue') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', c='red', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', c='green', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', c='blue', size=25) # 三角図のz軸ラベル plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.suptitle(t='Ternary Plot', fontsize=20) # 全体のタイトル plt.title(label='$x=(x_0, x_1, x_2)$', loc='left') # タイトル plt.show() # 描画
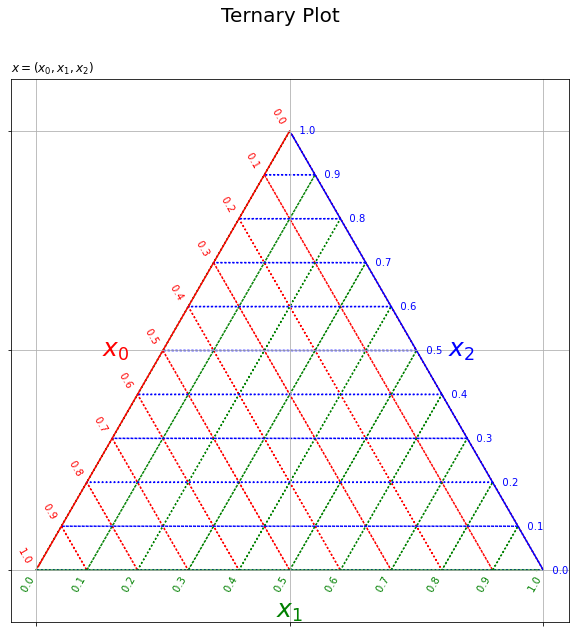
plt.quiver()の矢印の枠線の色の引数ec、plt.text()のテキストの色の引数cにそれぞれ色を指定する。軸線とグリッド線については3つの軸の値に対応するように色を複製して指定する必要がある。
以上で、三角図における座標を作成できた。次は、三角座標上にグラフを描画する。
散布図
三角座標上の散布図を作成する。
例として利用するために、一様分布の乱数を生成して正規化する。
# データ数を指定 N = 9 # 一様分布の乱数を生成 x_nk = np.random.rand(N*3).reshape((N, 3)) # 正規化 x_nk /= np.sum(x_nk, axis=1, keepdims=True) print(np.round(x_nk, 2)) print(np.sum(x_nk, axis=1))
[[0.43 0.05 0.52]
[0.23 0.26 0.51]
[0.38 0.29 0.33]
[0.25 0.53 0.22]
[0.56 0.33 0.11]
[0.48 0.12 0.39]
[0.76 0.16 0.07]
[0.23 0.36 0.41]
[0.3 0.37 0.32]]
[1. 1. 1. 1. 1. 1. 1. 1. 1.]
np.random.rand()でN×3個の一様乱数を生成して、N行3列の配列を作成する。各行が1つのサンプルに対応する。
行(サンプル)ごとに、総和で割ることで総和が1になるように正規化する。行ごとの和は、np.sum(axis=1)で計算できる。
あるいは、ディリクレ分布の乱数を生成する。
# ディリクレ分布のパラメータを指定 alpha_k = np.array([1.0, 1.0, 1.0]) # ディリクレ分布の乱数を生成 x_nk = np.random.dirichlet(alpha=alpha_k, size=N) print(np.round(x_nk, 2)) print(np.sum(x_nk, axis=1))
[[0.05 0.83 0.12]
[0.54 0.29 0.17]
[0.12 0.79 0.1 ]
[0.02 0.38 0.6 ]
[0.84 0.02 0.15]
[0.31 0.41 0.27]
[0.98 0.01 0.01]
[0.52 0.15 0.34]
[0.49 0.02 0.5 ]]
[1. 1. 1. 1. 1. 1. 1. 1. 1.]
ディリクレ分布の乱数(確率変数)は総和が1の値をとるので、正規化の必要がない。ディリクレ乱数は、np.random.dirichlet()で生成できる。パラメータの引数alphaに設定したパラメータalpha_k、サンプルサイズの引数sizeにNを指定する。
サンプルを三角座標に変換する。
# サンプルを三角座標に変換 y_n0 = x_nk[:, 1] + 0.5 * x_nk[:, 2] y_n1 = 0.5 * x_nk[:, 2] * np.sqrt(3.0) print(np.round(y_n0, 2)) print(np.round(y_n1, 2))
[0.89 0.37 0.84 0.68 0.09 0.55 0.02 0.31 0.27]
[0.11 0.15 0.08 0.52 0.13 0.24 0.01 0.29 0.43]
x_nkの各行をサンプル$\mathbf{x}_n = (x_{n,0}, x_{n,1}, x_{n,2})$として、$y_{n,0} = x_{n,1} + \frac{x_{n,2}}{2}$、$y_1 = \frac{\sqrt{3} x_{n,2}}{2}$で変換後の座標を計算する。
パラメータの値を数式で表示するための文字列を作成する。
# パラメータラベル用の文字列を作成 param_text = '$' + '\\alpha=('+', '.join([str(val) for val in alpha_k])+')' + ', x=(x_0, x_1, x_2)' + '$' print(param_text)
$\alpha=(1.0, 1.0, 1.0), x=(x_0, x_1, x_2)$
'$'で挟むとLaTeXコマンドを利用して数式を表示できる。
三角図上に散布図を描画する。
# 三角座標上の散布図を作成 plt.figure(figsize=(10, 10), facecolor='white') # 図の設定 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec=np.repeat(['red', 'green', 'blue'], len(axis_vals)), linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc=['red', 'green', 'blue'], linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', c='red', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', c='green', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center', c='blue') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', c='red', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', c='green', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', c='blue', size=25) # 三角図のz軸ラベル plt.scatter(x=y_n0, y=y_n1, c='orange', s=100) # サンプルの点 for n in range(N): plt.annotate(text='('+', '.join([str(np.round(val, 2)) for val in x_nk[n]])+')', xy=(y_n0[n], y_n1[n]+0.02), ha='center', va='bottom', c='orange', size=10, bbox=dict(boxstyle='round', fc='white', ec='orange', alpha=0.8)) # サンプルラベル plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.suptitle(t='Scatter Ternary Plot', fontsize=20) # タイトル plt.title(label=param_text, loc='left') # パラメータラベル plt.show() # 描画
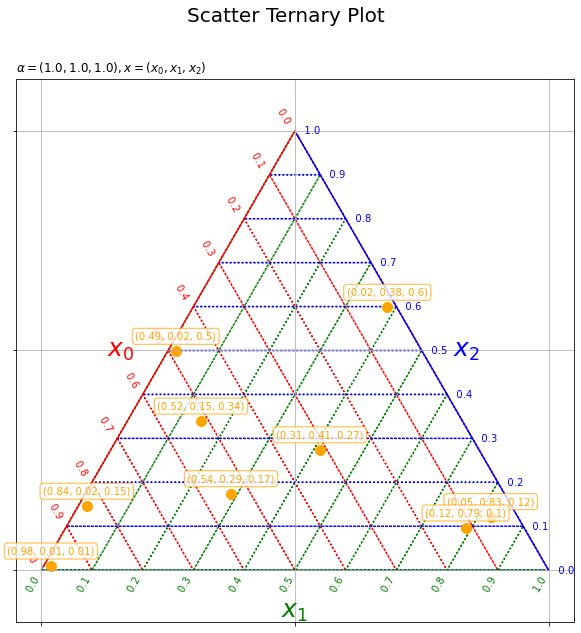
以上で、私が欲しいグラフが得られた。
散布図のアニメーション
最後に、散布図のアニメーション(gif画像)を作成して、三角図の座標について確認する。
3つの軸の方向を順番に点が移動するように値を指定する。
# 3次元変数の値を指定 x_0_vals = np.hstack([ np.arange(0.2, 0.401, step = 0.01), np.arange(0.2, 0.391, step = 0.01)[::-1], np.repeat(0.2, repeats = 19) ]).round(decimals=2) x_1_vals = np.hstack([ np.repeat(0.2, repeats = 21), np.arange(0.21, 0.401, step = 0.01), np.arange(0.21, 0.391, step = 0.01)[::-1] ]).round(decimals=2) x_2_vals = np.hstack([ np.arange(0.4, 0.601, step = 0.01)[::-1], np.repeat(0.4, repeats = 20), np.arange(0.41, 0.591, step = 0.01) ]).round(decimals=2) print(x_0_vals[:10]) print(x_1_vals[:10]) print(x_2_vals[:10]) # 三角座標に変換 y_0_vals = x_1_vals + 0.5 * x_2_vals y_1_vals = 0.5 * x_2_vals * np.sqrt(3.0) print(np.round(y_0_vals[:10], 2)) print(np.round(y_1_vals[:10], 2))
[0.2 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29]
[0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2]
[0.6 0.59 0.58 0.57 0.56 0.55 0.54 0.53 0.52 0.51]
[0.5 0.5 0.49 0.48 0.48 0.48 0.47 0.46 0.46 0.46]
[0.52 0.51 0.5 0.49 0.48 0.48 0.47 0.46 0.45 0.44]
散布図のときと同様に値を変換する。
三角図のアニメーションを作成する。
# フレーム数を設定 frame_num = len(x_0_vals) # 図を初期化 fig = plt.figure(figsize=(10, 10), facecolor='white') # 図の設定 fig.suptitle(t='Ternary Plot', fontsize=20) # タイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の値を取得 y_0 = y_0_vals[i] y_1 = y_1_vals[i] # 三角座標上の散布図を作成 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec=np.repeat(['red', 'green', 'blue'], len(axis_vals)), linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc=['red', 'green', 'blue'], linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', c='red', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', c='green', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center', c='blue') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', c='red', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', c='green', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', c='blue', size=25) # 三角図のz軸ラベル plt.scatter(x=y_0, y=y_1, c='orange', s=150) # サンプルの点 plt.annotate(text='('+str(x_0_vals[i])+', '+str(x_1_vals[i])+', '+str(x_2_vals[i])+')', xy=(y_0, y_1+0.03), ha='center', va='bottom', c='orange', size=15, bbox=dict(boxstyle='round', fc='white', ec='orange', alpha=0.8)) # サンプルラベル plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.title(label='$x=(x_0, x_1, x_2)$', loc='left') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('../figure/ternary_scatter.gif')
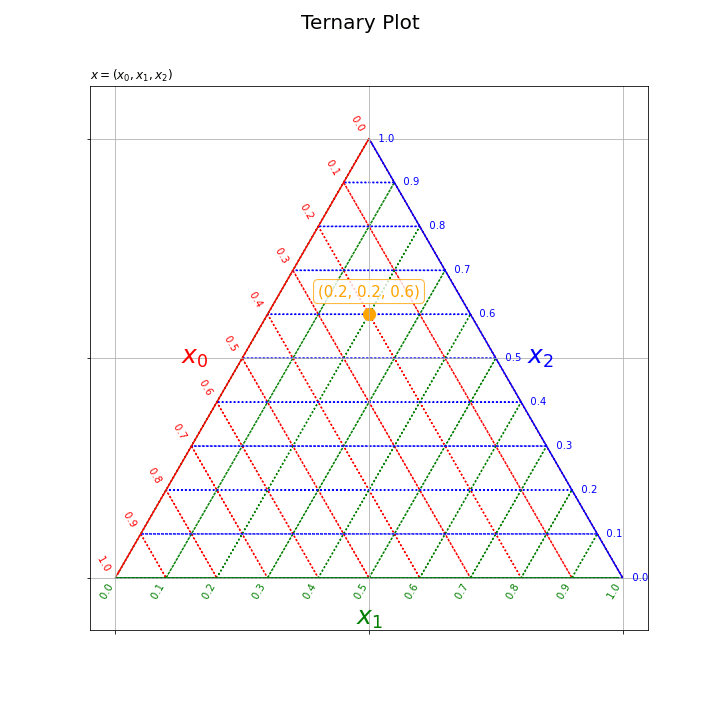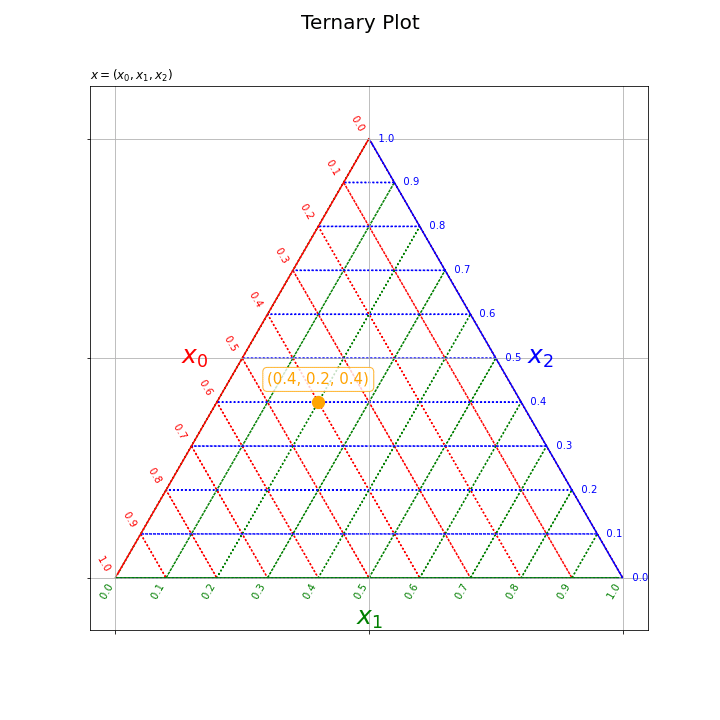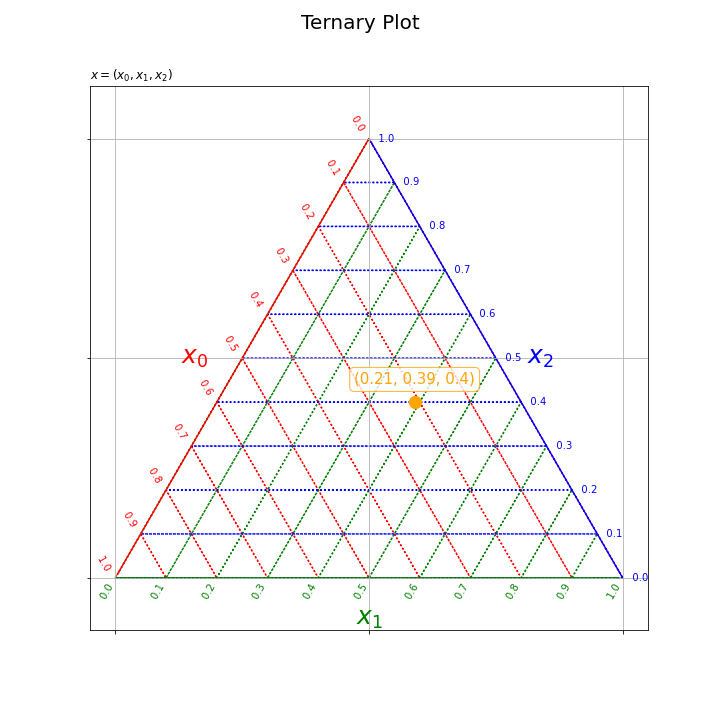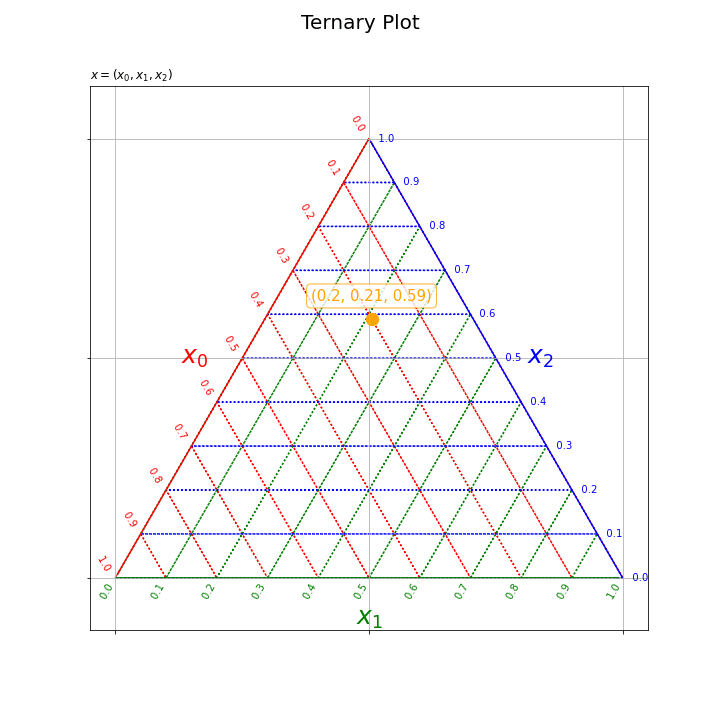
各フレームの作図処理を関数として定義して、FuncAnimation()を使ってアニメーション(gif画像)を作成する。
以上で、三角図上のデータ点と座標の関係を掴めた気がする。次は、等高線の作図を考える。
おわりに
実際に使うのであれば座標に関わる処理をまとめて関数化したらいいんだと思います。このシリーズでは調整しやすいように羅列しています。コピペした後に修正するのが大変でした。
線分を描くのってplt.quiver()でいいんでしょうか。そろそろPlotlyを覚える頃合い。
先日公開されたMVを聴きましょう。
ソロ活動が充実してきてよきかなよきかな。
【次の内容】