はじめに
R言語で三角関数の定義や公式を可視化しようシリーズのスピンオフです。
この記事では、sinh関数のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
sinh関数の可視化
双曲線関数の1つであるsinh関数(双曲線正弦関数・ハイパボリックサイン関数・hyperbolic sine function)をグラフで確認します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(patchwork) library(gganimate) library(magick)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
定義式の確認
まずは、sinh関数の定義式を確認します。
sinh関数は、次の式で定義されます。
$e^x$はネイピア数$e$を底とする自然指数関数です。
sinh関数曲線の作図
次に、sinh関数のグラフを作成します。
作図用の変数の値を作成します。
# 作図用の変数の値を指定 theta_vec <- seq(from = -5, to = 5, by = 0.01) head(theta_vec)
## [1] -5.00 -4.99 -4.98 -4.97 -4.96 -4.95
作図に利用する変数$\theta$の範囲と間隔を指定してtheta_vecとします。
・作図コード(クリックで展開)
sinh関数の曲線を描画するためのデータフレームを作成します。
# sinh曲線の描画用 sinh_df <- tibble::tibble( t = theta_vec, sinh_t = sinh(theta_vec) ) sinh_df
## # A tibble: 1,001 × 2 ## t sinh_t ## <dbl> <dbl> ## 1 -5 -74.2 ## 2 -4.99 -73.5 ## 3 -4.98 -72.7 ## 4 -4.97 -72.0 ## 5 -4.96 -71.3 ## 6 -4.95 -70.6 ## 7 -4.94 -69.9 ## 8 -4.93 -69.2 ## 9 -4.92 -68.5 ## 10 -4.91 -67.8 ## # … with 991 more rows
$\theta$の値と$\sinh \theta$の値をデータフレームに格納します。sinh関数はsinh()で計算できます。
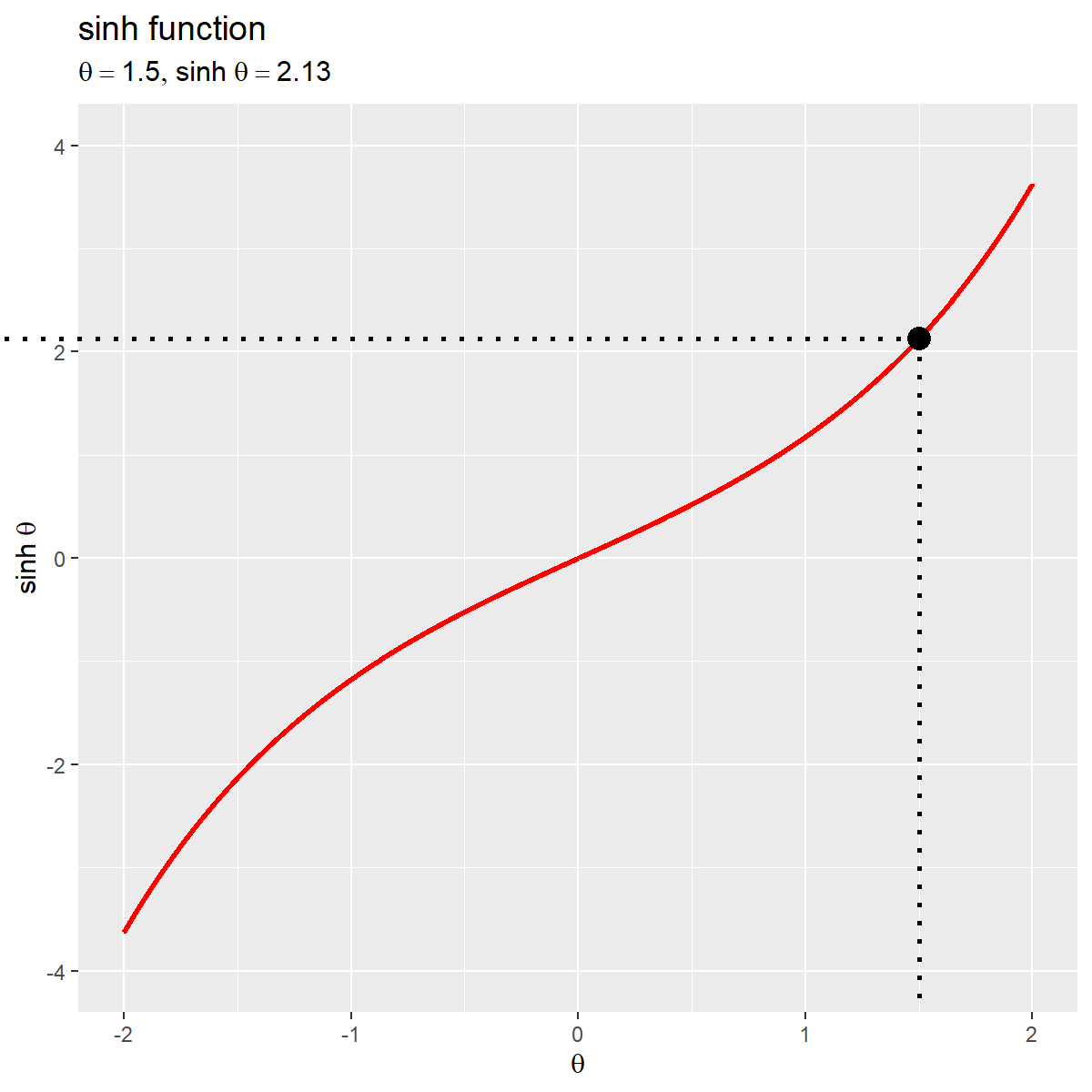
sinh関数のグラフを作成します。
# sinh関数曲線を作図 ggplot() + geom_line(data = sinh_df, mapping = aes(x = t, y = sinh_t), size = 1) + # sinh曲線 labs(title = "sinh function", x = expression(theta), y = expression(sinh~theta))
x軸を$\theta$、y軸を$\sinh \theta$として、geom_line()で折れ線グラフを描画します。

変数$\theta$の値が小さいほど$\sinh \theta$も小さく、大きいほど大きくなるのを確認できます。
双曲線の作図
続いて、sinh関数の可視化に利用する単位双曲線(unit hyperbola)のグラフを作成します。双曲線については「【R】双曲線の作図 - からっぽのしょこ」を参照してください。
・作図コード(クリックで展開)
作図に利用するデータフレームを作成します。
# 作図用の変数の値を指定 theta_vec <- seq(from = -2, to = 2, by = 0.002) # 双曲線の描画用 hyperbola_df <- tibble::tibble( t = c(theta_vec, theta_vec), sinh_t = c(sinh(theta_vec), sinh(theta_vec)), cosh_t = c(cosh(theta_vec), -cosh(theta_vec)), sign = rep(c("plus", "minus"), each = length(theta_vec))# 符号 ) # 軸の最大値を設定 axis_max <- hyperbola_df[["cosh_t"]] |> max() |> ceiling() # 漸近線の描画用 asymptote_df <- tibble::tibble( x = seq(from = -axis_max, to = axis_max, length.out = 100) |> rep(times = 2), y = rep(c(1, -1), each = 100) * x, slope = rep(c("plus", "minus"), each = 100) # 符号 ) # 正方形グリッドの描画用 square_df <- tibble::tibble( x = c(1, 1, -1, -1, 1), y = c(1, -1, -1, 1, 1) ) # 軸線の描画用 axis_df <- tibble::tibble( x_from = c(-axis_max, 0), y_from = c(0, -axis_max), x_to = c(axis_max, 0), y_to = c(0, axis_max), axis = c("x", "y") )
双曲線と補助線のグラフを作成します。
# 単位双曲線を作図 ggplot() + geom_segment(data = axis_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, group = "axis"), arrow = arrow(length = unit(10, units = "pt"))) + # 軸線 geom_path(data = square_df, mapping = aes(x = x, y = y), linetype = "dashed") + # 正方形グリッド geom_line(data = asymptote_df, mapping = aes(x = x, y = y, group = slope), linetype = "dashed") + # 漸近線 geom_path(data = hyperbola_df, mapping = aes(x = cosh_t, y = sinh_t, group = sign), size = 1) + # 双曲線 theme(legend.text.align = 0.5) + # 凡例の体裁:(凡例表示用) coord_fixed(ratio = 1, xlim = c(-axis_max, axis_max), ylim = c(-axis_max, axis_max)) + # 表示範囲 labs(title = "unit hyperbola", x = "x", y = "y")

このグラフ上に双曲線関数を描画します。
双曲線上のsinh関数の可視化
次は、単位双曲線上における双曲線関数(sinh・cosh)のグラフを作成します。
グラフの作成
変数を固定したsinh関数をグラフで確認します。
変数の値を設定します。
# 変数の値を指定 theta <- 1.5
変数$\theta$の値を指定します。
・作図コード(クリックで展開)
曲線上の点を描画するためのデータフレームを作成します。
# 曲線上の点の描画用 point_df <- tibble::tibble( t = theta, sinh_t = sinh(theta), cosh_t = cosh(theta) ) point_df
## # A tibble: 1 × 3 ## t sinh_t cosh_t ## <dbl> <dbl> <dbl> ## 1 1.5 2.13 2.35
sinh曲線上の点のx軸の値$\theta$とy軸の値$\sinh \theta$、単位双曲線上の点のx軸の値$\cosh \theta$とy軸の値$\sinh \theta$を格納します。
変数の値(の半分)を面積(塗りつぶし領域)として描画するためのデータフレームを作成します。
# 変数(面積)の描画用 variable_area_df <- tibble::tibble( x = seq(from = 0, to = cosh(theta), length.out = 50), sign = dplyr::if_else(theta >= 0, true = 1, false = -1), # 符号 curve = sign * sqrt(x^2 - 1), # x軸と双曲線上の線分 straight = sinh(theta)/cosh(theta) * x # 原点と曲線上の点の線分 ) |> dplyr::mutate( curve = dplyr::if_else(is.na(curve), true = 0, false = curve) ) # 双曲線の範囲外を0に置換 variable_area_df
## # A tibble: 50 × 4 ## x sign curve straight ## <dbl> <dbl> <dbl> <dbl> ## 1 0 1 0 0 ## 2 0.0480 1 0 0.0435 ## 3 0.0960 1 0 0.0869 ## 4 0.144 1 0 0.130 ## 5 0.192 1 0 0.174 ## 6 0.240 1 0 0.217 ## 7 0.288 1 0 0.261 ## 8 0.336 1 0 0.304 ## 9 0.384 1 0 0.348 ## 10 0.432 1 0 0.391 ## # … with 40 more rows
「原点と双曲線上の点を結ぶ線分」と「$0 \leq x < 1$の範囲のx軸線($y = 0$の直線)と$1 \leq x \leq \cosh \theta$の範囲の双曲線」の範囲を塗りつぶします。ただし、双曲線について、$\theta > 0$のときは$y > 0$の範囲を塗りつぶすため$y = \sqrt{x^2 - 1}$、$\theta < 0$のときは$y < 0$の範囲を塗りつぶすため$y = - \sqrt{x^2 - 1}$を使います。
x軸の値として$0$から$\cosh \theta$の範囲の値を作成してx列とします。
thetaの正負によって符号を変更してsign列としておき、双曲線を計算してcurve列とします。ただし、$0$から$1$の範囲がNaNになるので0に置き換えます。
原点と点$(\cosh \theta, \sinh \theta)$を結ぶ直線の傾きは$a = \frac{\sinh \theta}{\cosh \theta}$です。$y = a x$を計算してstraight列とします。
双曲線関数を直線として描画するためのデータフレームを作成します。
# 関数ラベルのレベルを指定 fnc_level_vec <- c("sinh", "cosh") # 双曲線関数の描画用 function_df <- tibble::tibble( x_from = c(0, cosh(theta), 0, 0), y_from = c(0, 0, 0, sinh(theta)), x_to = c(0, cosh(theta), cosh(theta), cosh(theta)), y_to = c(sinh(theta), sinh(theta), 0, sinh(theta)), fnc = c("sinh", "sinh", "cosh", "cosh") |> factor(levels = fnc_level_vec) # 色分け用 ) function_df
## # A tibble: 4 × 5 ## x_from y_from x_to y_to fnc ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0 0 0 2.13 sinh ## 2 2.35 0 2.35 2.13 sinh ## 3 0 0 2.35 0 cosh ## 4 0 2.13 2.35 2.13 cosh
関数を区別するためのfnc列の因子レベルをfnc_level_vecとして指定しておきます。因子レベルは、辺(線分)の描画順(重なり順)や色付け順に影響します。
各線分の始点の座標をx_from, y_from列、終点の座標をx_to, y_to列とします。
sinh関数は点$(\cosh \theta, \sinh \theta)$からx軸線への垂線、cosh関数は点$(\cosh \theta, \sinh \theta)$からy軸線への垂線に対応します。この例では、関数ごとの対応関係を分かりやすくするために、それぞれ平行移動した座標も描画します。
関数名をラベルとして描画するためのデータフレームを作成します。
# 双曲線関数ラベルの描画用 function_label_df <- tibble::tibble( x = c(0, 0.5*cosh(theta)), y = c(0.5*sinh(theta), 0), angle = c(90, 0), v = c(-0.5, 1), fnc = c("sinh", "cosh") |> factor(levels = fnc_level_vec), # 色分け用 fnc_label = c("sinh~theta", "cosh~theta") # 関数ラベル ) function_label_df
## # A tibble: 2 × 6 ## x y angle v fnc fnc_label ## <dbl> <dbl> <dbl> <dbl> <fct> <chr> ## 1 0 1.06 90 -0.5 sinh sinh~theta ## 2 1.18 0 0 1 cosh cosh~theta
関数を示す線分の中点に関数名を配置します。ギリシャ文字などの記号や数式を表示する場合は、expression()の記法を使います。
ラベルの表示角度をangle列、上下の表示位置をv列として値を指定します。
関数の値を表示するための文字列を作成します。
# 変数ラベルの描画用 function_label <- paste0( "list(", "theta==", theta, ", sinh~theta==", round(sinh(theta), digits = 2), ", cosh~theta==", round(cosh(theta), digits = 2), ")" ) function_label
## [1] "list(theta==1.5, sinh~theta==2.13, cosh~theta==2.35)"
等号は==、複数の(数式上の)変数を並べるにはlist(変数1, 変数2)とします。(プログラム上の)変数の値を使う場合は、文字列として作成しておきparse()のtext引数に渡します。
双曲線上に双曲線関数を重ねたグラフを作成します。
# 双曲線関数を作図 ggplot() + geom_segment(data = axis_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, group = "axis"), arrow = arrow(length = unit(10, units = "pt"))) + # 軸線 geom_line(data = asymptote_df, mapping = aes(x = x, y = y, group = slope), linetype = "dashed") + # 漸近線 geom_path(data = hyperbola_df, mapping = aes(x = cosh_t, y = sinh_t, group = sign), size = 1) + # 双曲線 geom_point(data = point_df, mapping = aes(x = cosh_t, y = sinh_t), size = 4) + # 双曲線上の点 geom_ribbon(data = variable_area_df, mapping = aes(x = x, ymin = curve, ymax = straight), fill = "#00A968", alpha = 0.5) + # 変数(面積) geom_text(mapping = aes(x = 0.5, y = 0.25*tanh(theta), label = "frac(theta, 2)"), parse = TRUE, size = 3) + # 変数ラベル geom_segment(data = function_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = fnc), size = 1) + # 双曲線関数直線 geom_text(data = function_label_df, mapping = aes(x = x, y = y, label = fnc_label, color = fnc, angle = angle, vjust = v), parse = TRUE, show.legend = FALSE) + # 双曲線関数ラベル coord_fixed(ratio = 1, xlim = c(-axis_max, axis_max), ylim = c(-axis_max, axis_max)) + # 表示範囲 labs(title = "hyperbolic functions", subtitle = parse(text = function_label), color = "function", x = expression(cosh~theta), y = expression(sinh~theta))
geom_segment()で線分を描画して、各関数の値を可視化します。
geom_ribbon()で原点から曲線上の点の範囲を塗りつぶして、変数の値を可視化します。
geom_label()でラベル(文字列)を描画します。この例では、変数ラベルを$(0.5, 0.25 \tanh \theta)$の位置に配置します。

双曲線上の点の座標は$(\cosh \theta, \sinh \theta)$なので、点のy軸の値がsinh関数の値に対応します。
アニメーションの作成
続いて、変数の値を変化させたアニメーションで確認します。
フレーム数を指定して、変数として用いる値を作成します。
# フレーム数を指定 frame_num <- 101 # 変数の値を作成 theta_i <- seq(from = -2, to = 2, length.out = frame_num) # 範囲を指定 head(theta_i)
## [1] -2.00 -1.96 -1.92 -1.88 -1.84 -1.80
フレーム数frame_numを指定して、frame_num個の$\theta$の値を作成します。
・作図コード(クリックで展開)
フレーム切替用のラベルとして使う文字列ベクトルを作成します。
# フレーム切替用ラベルを作成 frame_label_vec <- paste0( "θ = ", round(theta_i, digits = 2), ", sinh θ = ", round(sinh(theta_i), digits = 2), ", cosh θ = ", round(cosh(theta_i), digits = 2) ) head(frame_label_vec)
## [1] "θ = -2, sinh θ = -3.63, cosh θ = 3.76" ## [2] "θ = -1.96, sinh θ = -3.48, cosh θ = 3.62" ## [3] "θ = -1.92, sinh θ = -3.34, cosh θ = 3.48" ## [4] "θ = -1.88, sinh θ = -3.2, cosh θ = 3.35" ## [5] "θ = -1.84, sinh θ = -3.07, cosh θ = 3.23" ## [6] "θ = -1.8, sinh θ = -2.94, cosh θ = 3.11"
この例では、変数と関数の値をグラフに表示するために、フレームごとの値をフレーム切替用のラベル列として使います。
theta_iの値と対応する関数の値を文字列結合します。
曲線上の点を描画するためのデータフレームを作成します。
# 曲線上の点の描画用 anim_point_df <- tibble::tibble( t = theta_i, sinh_t = sinh(theta_i), cosh_t = cosh(theta_i), frame_label = factor(frame_label_vec, levels = frame_label_vec) # フレーム切替用ラベル ) anim_point_df
## # A tibble: 101 × 4 ## t sinh_t cosh_t frame_label ## <dbl> <dbl> <dbl> <fct> ## 1 -2 -3.63 3.76 θ = -2, sinh θ = -3.63, cosh θ = 3.76 ## 2 -1.96 -3.48 3.62 θ = -1.96, sinh θ = -3.48, cosh θ = 3.62 ## 3 -1.92 -3.34 3.48 θ = -1.92, sinh θ = -3.34, cosh θ = 3.48 ## 4 -1.88 -3.20 3.35 θ = -1.88, sinh θ = -3.2, cosh θ = 3.35 ## 5 -1.84 -3.07 3.23 θ = -1.84, sinh θ = -3.07, cosh θ = 3.23 ## 6 -1.8 -2.94 3.11 θ = -1.8, sinh θ = -2.94, cosh θ = 3.11 ## 7 -1.76 -2.82 2.99 θ = -1.76, sinh θ = -2.82, cosh θ = 2.99 ## 8 -1.72 -2.70 2.88 θ = -1.72, sinh θ = -2.7, cosh θ = 2.88 ## 9 -1.68 -2.59 2.78 θ = -1.68, sinh θ = -2.59, cosh θ = 2.78 ## 10 -1.64 -2.48 2.67 θ = -1.64, sinh θ = -2.48, cosh θ = 2.67 ## # … with 91 more rows
変数$\theta$と関数$\sinh \theta, \cosh \theta$の値をフレーム切替用のラベルとあわせて格納します。
変数の値(の半分)を面積(塗りつぶし領域)として描画するためのデータフレームを作成します。
# 変数(面積)の描画用 anim_variable_area_df <- tibble::tibble( t = theta_i, frame_label = factor(frame_label_vec, levels = frame_label_vec) # フレーム切替用ラベル ) |> dplyr::group_by(t, frame_label) |> # x軸の値の作成用 dplyr::summarise( x = seq(from = 0, to = cosh(t), length.out = 50), .groups = "drop" ) |> # フレームごとにx軸の値を作成 dplyr::mutate( sign = dplyr::if_else(t >= 0, true = 1, false = -1), # 符号 curve = sign * sqrt(x^2 - 1), # x軸と双曲線上の線分 curve = dplyr::if_else(is.na(curve), true = 0, false = curve), # 双曲線の範囲外を0に置換 straight = sinh(t)/cosh(t) * x # 原点と曲線上の点の線分 ) anim_variable_area_df
## # A tibble: 5,050 × 6 ## t frame_label x sign curve straight ## <dbl> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0 -1 0 0 ## 2 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.0768 -1 0 -0.0740 ## 3 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.154 -1 0 -0.148 ## 4 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.230 -1 0 -0.222 ## 5 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.307 -1 0 -0.296 ## 6 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.384 -1 0 -0.370 ## 7 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.461 -1 0 -0.444 ## 8 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.537 -1 0 -0.518 ## 9 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.614 -1 0 -0.592 ## 10 -2 θ = -2, sinh θ = -3.63, cosh θ = 3.76 0.691 -1 0 -0.666 ## # … with 5,040 more rows
変数の値とフレーム切替用のラベルを格納して、変数の値(フレーム)ごとに(t, frame_label列でグループ化して)、塗りつぶし範囲の曲線と直線(下限と上限)の値を計算します。
変数の値に応じてx軸の範囲($0 \leq x \leq \cosh \theta$)が変わるので、フレームごとにsummarise()でx列の値を作成して計算に使います。
変数ラベルを描画するためのデータフレームを作成します。
# 変数ラベルの描画用 anim_variable_label_df <- tibble::tibble( t = theta_i, x = 0.5, y = 0.25 * tanh(theta_i), frame_label = factor(frame_label_vec, levels = frame_label_vec) # フレーム切替用ラベル ) anim_variable_label_df
## # A tibble: 101 × 4 ## t x y frame_label ## <dbl> <dbl> <dbl> <fct> ## 1 -2 0.5 -0.241 θ = -2, sinh θ = -3.63, cosh θ = 3.76 ## 2 -1.96 0.5 -0.240 θ = -1.96, sinh θ = -3.48, cosh θ = 3.62 ## 3 -1.92 0.5 -0.239 θ = -1.92, sinh θ = -3.34, cosh θ = 3.48 ## 4 -1.88 0.5 -0.239 θ = -1.88, sinh θ = -3.2, cosh θ = 3.35 ## 5 -1.84 0.5 -0.238 θ = -1.84, sinh θ = -3.07, cosh θ = 3.23 ## 6 -1.8 0.5 -0.237 θ = -1.8, sinh θ = -2.94, cosh θ = 3.11 ## 7 -1.76 0.5 -0.236 θ = -1.76, sinh θ = -2.82, cosh θ = 2.99 ## 8 -1.72 0.5 -0.234 θ = -1.72, sinh θ = -2.7, cosh θ = 2.88 ## 9 -1.68 0.5 -0.233 θ = -1.68, sinh θ = -2.59, cosh θ = 2.78 ## 10 -1.64 0.5 -0.232 θ = -1.64, sinh θ = -2.48, cosh θ = 2.67 ## # … with 91 more rows
この例では、$x = 0.5$の位置に変数ラベルを配置します。塗りつぶし範囲のy軸の中点は$\frac{x \tanh \theta}{2}$で計算できます。
双曲線関数を直線として描画するためのデータフレームを作成します。
# 双曲線関数の描画用 anim_function_df <- tibble::tibble( x_from = c( rep(0, times = frame_num), cosh(theta_i), rep(0, times = frame_num), rep(0, times = frame_num) ), y_from = c( rep(0, times = frame_num), rep(0, times = frame_num), rep(0, times = frame_num), sinh(theta_i) ), x_to = c( rep(0, times = frame_num), cosh(theta_i), cosh(theta_i), cosh(theta_i) ), y_to = c( sinh(theta_i), sinh(theta_i), rep(0, times = frame_num), sinh(theta_i) ), fnc = c("sinh", "sinh", "cosh", "cosh") |> rep(each = frame_num) |> factor(levels = fnc_level_vec), # 色分け用 label_flag = c(TRUE, FALSE, TRUE, FALSE) |> rep(each = frame_num), # # 関数ラベル用 frame_label = frame_label_vec |> rep(times = 4) |> factor(levels = frame_label_vec) # フレーム切替用ラベル ) anim_function_df
## # A tibble: 404 × 7 ## x_from y_from x_to y_to fnc label_flag frame_label ## <dbl> <dbl> <dbl> <dbl> <fct> <lgl> <fct> ## 1 0 0 0 -3.63 sinh TRUE θ = -2, sinh θ = -3.63, cosh θ… ## 2 0 0 0 -3.48 sinh TRUE θ = -1.96, sinh θ = -3.48, cosh… ## 3 0 0 0 -3.34 sinh TRUE θ = -1.92, sinh θ = -3.34, cosh… ## 4 0 0 0 -3.20 sinh TRUE θ = -1.88, sinh θ = -3.2, cosh … ## 5 0 0 0 -3.07 sinh TRUE θ = -1.84, sinh θ = -3.07, cosh… ## 6 0 0 0 -2.94 sinh TRUE θ = -1.8, sinh θ = -2.94, cosh … ## 7 0 0 0 -2.82 sinh TRUE θ = -1.76, sinh θ = -2.82, cosh… ## 8 0 0 0 -2.70 sinh TRUE θ = -1.72, sinh θ = -2.7, cosh … ## 9 0 0 0 -2.59 sinh TRUE θ = -1.68, sinh θ = -2.59, cosh… ## 10 0 0 0 -2.48 sinh TRUE θ = -1.64, sinh θ = -2.48, cosh… ## # … with 394 more rows
「グラフの作成」と同様に、frame_num個の座標を格納します。
関数ラベルを描画する辺(線分)をlabel_flag列に指定しておきます。
関数名をラベルとして描画するためのデータフレームを作成します。
# 双曲線関数ラベルの描画用 anim_function_label_df <- anim_function_df |> dplyr::filter(label_flag) |> # ラベル付けする辺を抽出 dplyr::group_by(fnc, frame_label) |> # 中点の計算用 dplyr::summarise( x = median(c(x_from, x_to)), y = median(c(y_from, y_to)), .groups = "drop" ) |> # 線分の中点に配置 tibble::add_column( angle = rep(c(90, 0), each = frame_num), v = rep(c(-0.5, 1), each = frame_num), fnc_label = rep(c("sinh~theta", "cosh~theta"), each = frame_num) # 関数ラベル ) anim_function_label_df
## # A tibble: 202 × 7 ## fnc frame_label x y angle v fnc_label ## <fct> <fct> <dbl> <dbl> <dbl> <dbl> <chr> ## 1 sinh θ = -2, sinh θ = -3.63, cosh θ = 3.76 0 -1.81 90 -0.5 sinh~the… ## 2 sinh θ = -1.96, sinh θ = -3.48, cosh θ… 0 -1.74 90 -0.5 sinh~the… ## 3 sinh θ = -1.92, sinh θ = -3.34, cosh θ… 0 -1.67 90 -0.5 sinh~the… ## 4 sinh θ = -1.88, sinh θ = -3.2, cosh θ … 0 -1.60 90 -0.5 sinh~the… ## 5 sinh θ = -1.84, sinh θ = -3.07, cosh θ… 0 -1.53 90 -0.5 sinh~the… ## 6 sinh θ = -1.8, sinh θ = -2.94, cosh θ … 0 -1.47 90 -0.5 sinh~the… ## 7 sinh θ = -1.76, sinh θ = -2.82, cosh θ… 0 -1.41 90 -0.5 sinh~the… ## 8 sinh θ = -1.72, sinh θ = -2.7, cosh θ … 0 -1.35 90 -0.5 sinh~the… ## 9 sinh θ = -1.68, sinh θ = -2.59, cosh θ… 0 -1.29 90 -0.5 sinh~the… ## 10 sinh θ = -1.64, sinh θ = -2.48, cosh θ… 0 -1.24 90 -0.5 sinh~the… ## # … with 192 more rows
flag_label列がTRUEの列を取り出して、関数とフレームごとに(fnc, frame_label列でグループ化して)、中点の座標をmedian()で計算します。
単位双曲線上の双曲線関数のアニメーションを作成します。
# 双曲線関数のアニメーションを作図 anim <- ggplot() + geom_segment(data = axis_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, group = "axis"), arrow = arrow(length = unit(10, units = "pt"))) + # 軸線 geom_line(data = asymptote_df, mapping = aes(x = x, y = y, group = slope), linetype = "dashed") + # 漸近線 geom_path(data = hyperbola_df, mapping = aes(x = cosh_t, y = sinh_t, group = sign), size = 1) + # 双曲線 geom_point(data = anim_point_df, mapping = aes(x = cosh_t, y = sinh_t), size = 4) + # 双曲線上の点 geom_ribbon(data = anim_variable_area_df, mapping = aes(x = x, ymin = curve, ymax = straight), fill = "#00A968", alpha = 0.5) + # 変数(面積) geom_text(data = anim_variable_label_df, mapping = aes(x = x, y = y), label = "frac(theta, 2)", parse = TRUE, size = 3) + # 変数ラベル geom_segment(data = anim_function_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = fnc), size = 1) + # 双曲線関数直線 geom_text(data = anim_function_label_df, mapping = aes(x = x, y = y, label = fnc_label, color = fnc, angle = angle, vjust = v), parse = TRUE, show.legend = FALSE) + # 双曲線関数ラベル gganimate::transition_manual(frames = frame_label) + # フレーム coord_fixed(ratio = 1, xlim = c(-axis_max, axis_max), ylim = c(-axis_max, axis_max)) + # 表示範囲 labs(title = "hyperbolic functions", subtitle = "{current_frame}", color = "function", x = "x", y = "y") # gif画像を作成 gganimate::animate(plot = anim, nframes = frame_num, fps = 10, width = 600, height = 600)
gganimateパッケージを利用して、アニメーション(gif画像)を作成します。
transition_manual()のフレーム制御の引数framesにフレーム(変数)ラベル列frame_labelを指定して、グラフを作成します。
animate()のplot引数にグラフオブジェクト、nframes引数にフレーム数frame_numを指定して、gif画像を作成します。また、fps引数に1秒当たりのフレーム数を指定できます。

双曲線上の点とsinh曲線の関係の可視化
最後は、双曲線上におけるsinh関数の値(直線)と、sinh関数の曲線の関係をグラフで確認します。
グラフの作成
変数を固定したグラフで確認します。
・作図コード(クリックで展開)
双曲線上の点とsinh曲線上の点を結ぶ補助線(の半分)を描画するためのデータフレームを作成します。
# sinh曲線との対応用 l <- 0.5 segment_hyperbola_df <- tibble::tibble( x_from = cosh(theta), x_to = axis_max+l, y = sinh(theta) ) segment_hyperbola_df
## # A tibble: 1 × 3 ## x_from x_to y ## <dbl> <dbl> <dbl> ## 1 2.35 4.5 2.13
曲線上の点からy軸の反対側への垂線を引くように座標を指定します。
双曲線のグラフを作成します。
# 変数ラベルの描画用 hyperbola_label <- paste0( "list(", "theta==", theta, ", cosh~theta==", round(cosh(theta), digits = 2), ", sinh~theta==", round(sinh(theta), digits = 2), ")" ) # 双曲線関数を作図 hyperbola_graph <- ggplot() + geom_segment(data = axis_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, group = "axis"), arrow = arrow(length = unit(10, units = "pt"))) + # 軸線 geom_line(data = asymptote_df, mapping = aes(x = x, y = y, group = slope), linetype = "dashed") + # 漸近線 geom_path(data = hyperbola_df, mapping = aes(x = cosh_t, y = sinh_t, group = sign), size = 1) + # 双曲線 geom_point(data = point_df, mapping = aes(x = cosh_t, y = sinh_t), size = 4) + # 双曲線上の点 geom_ribbon(data = variable_area_df, mapping = aes(x = x, ymin = curve, ymax = straight), fill = "#00A968", alpha = 0.5) + # 変数(面積) geom_text(mapping = aes(x = 0.5, y = 0.25*tanh(theta), label = "frac(theta, 2)"), parse = TRUE, size = 3) + # 変数ラベル geom_segment(data = segment_hyperbola_df, mapping = aes(x = x_from, y = y, xend = x_to, yend = y), size = 1, linetype = "dotted") + # sinh曲線との対応線 geom_segment(data = function_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = fnc), size = 1) + # 双曲線関数直線 geom_text(data = function_label_df, mapping = aes(x = x, y = y, label = fnc_label, color = fnc, angle = angle, vjust = v), parse = TRUE, show.legend = FALSE) + # 双曲線関数ラベル scale_color_manual(breaks = c("sinh", "cosh"), values = c("red", "blue")) + coord_fixed(ratio = 1, clip = "off", xlim = c(-axis_max, axis_max), ylim = c(-axis_max, axis_max)) + # 表示範囲 labs(title = "hyperbola", subtitle = parse(text = hyperbola_label), color = "function", x = expression(cosh~theta), y = expression(sinh~theta)) hyperbola_graph

sinh曲線上の点と双曲線上の点を結ぶ補助線(の半分)を描画するためのデータフレームを作成します。
# 双曲線との対応用 d <- 1.1 l <- 0.6 segment_sinh_df <- tibble::tibble( x_from = c(theta, theta), y_from = c(sinh(theta), sinh(theta)), x_to = c(theta, min(theta_vec)-l), y_to = c(-axis_max*d, sinh(theta)) ) segment_sinh_df
## # A tibble: 2 × 4 ## x_from y_from x_to y_to ## <dbl> <dbl> <dbl> <dbl> ## 1 1.5 2.13 1.5 -4.4 ## 2 1.5 2.13 -2.6 2.13
曲線上の点からx軸とy軸への垂線を引くように座標を指定します。
sinh関数曲線のグラフを作成します。
# sinh曲線の描画用 sinh_df <- tibble::tibble( t = theta_vec, sinh_t = sinh(theta_vec) ) # 関数ラベルの描画用 sinh_label <- paste0( "list(", "theta==", theta, ", sinh~theta==", round(sinh(theta), digits = 2), ")" ) # sinh関数を作図 sinh_graph <- ggplot() + geom_line(data = sinh_df, mapping = aes(x = t, y = sinh_t), color = "red", size = 1) + # sinh曲線 geom_segment(data = segment_sinh_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to), size = 1, linetype = "dotted") + # 双曲線との対応線 geom_point(data = point_df, mapping = aes(x = t, y = sinh_t), size = 4) + #sinh曲線上の点 coord_cartesian(clip = "off", xlim = c(min(theta_vec), max(theta_vec)), ylim = c(-axis_max, axis_max)) + # labs(title = "sinh function", subtitle = parse(text = sinh_label), x = expression(theta), y = expression(sinh~theta)) sinh_graph
2つのグラフを並べて描画します。
# 並べて描画 patchwork::wrap_plots(hyperbola_graph, sinh_graph, guides = "collect")
patchworkパッケージのwrap_plots()を使ってグラフを並べます。
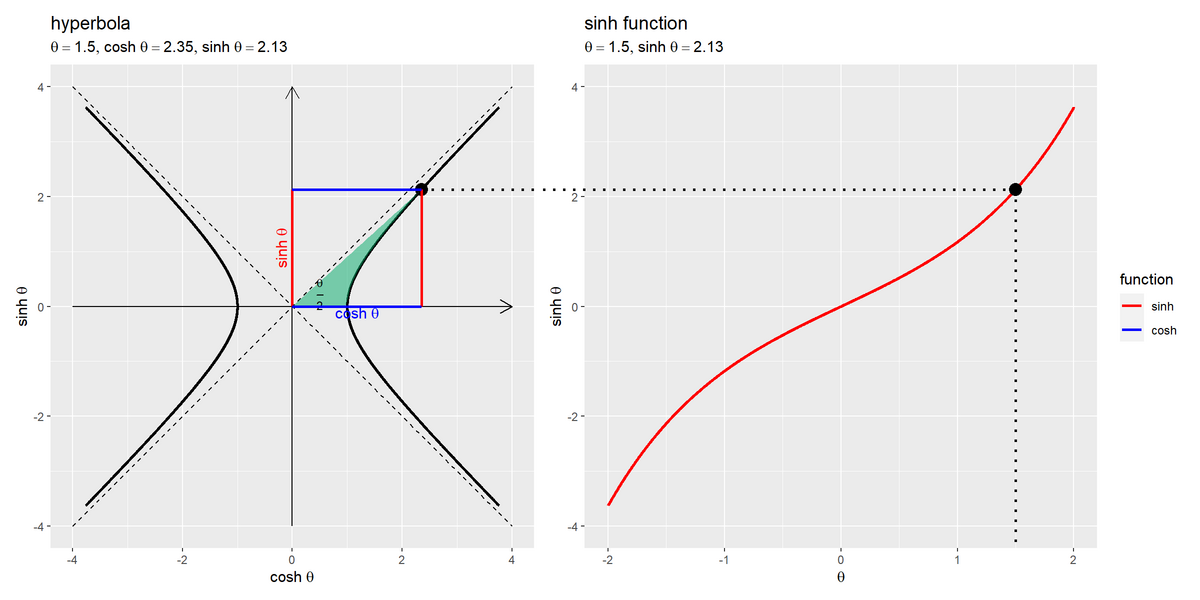
双曲線のグラフにおける高さがsinh関数の曲線に対応しているのを確認できます。
アニメーションの作成
続いて、変数の値を変化させたアニメーションで確認します。
フレーム数を指定して、変数として用いる値を作成します。
# フレーム数を指定 frame_num <- 101 # 変数の値を作成 theta_i <- seq(from = -2, to = 2, length.out = frame_num) # 範囲を指定 head(theta_i)
## [1] -2.00 -1.96 -1.92 -1.88 -1.84 -1.80
フレーム数frame_numを指定して、frame_num個の$\theta$の値を作成します。
・作図コード(クリックで展開)
theta_iから順番に値を取り出して作図し、グラフを書き出します。
# 一時保存フォルダを指定 dir_path <- "tmp_folder" # 関数ラベルのレベルを指定 fnc_level_vec <- c("sinh", "cosh") # 変数ごとに作図 for(i in 1:frame_num) { # i番目の値を取得 theta <- theta_i[i] # 曲線上の点の描画用 point_df <- tibble::tibble( t = theta, sinh_t = sinh(theta), cosh_t = cosh(theta) ) # 変数(面積)の描画用 variable_area_df <- tibble::tibble( x = seq(from = 0, to = cosh(theta), length.out = 50), sign = dplyr::if_else(theta >= 0, true = 1, false = -1), # 符号 curve = sign * sqrt(x^2 - 1), # x軸と双曲線上の線分 straight = sinh(theta)/cosh(theta) * x # 原点と曲線上の点の線分 ) |> dplyr::mutate( curve = dplyr::if_else(is.na(curve), true = 0, false = curve) ) # 双曲線の範囲外を0に置換 # 双曲線関数の描画用 function_df <- tibble::tibble( x_from = c(0, cosh(theta), 0, 0), y_from = c(0, 0, 0, sinh(theta)), x_to = c(0, cosh(theta), cosh(theta), cosh(theta)), y_to = c(sinh(theta), sinh(theta), 0, sinh(theta)), fnc = c("sinh", "sinh", "cosh", "cosh") |> factor(levels = fnc_level_vec) # 色分け用 ) # 双曲線関数ラベルの描画用 function_label_df <- tibble::tibble( x = c(0, 0.5*cosh(theta)), y = c(0.5*sinh(theta), 0), angle = c(90, 0), v = c(-0.5, 1), fnc = c("sinh", "cosh") |> factor(levels = fnc_level_vec), # 色分け用 fnc_label = c("sinh~theta", "cosh~theta") # 関数ラベル ) # sinh曲線との対応用 l <- 0.5 segment_hyperbola_df <- tibble::tibble( x_from = cosh(theta), x_to = axis_max+l, y = sinh(theta) ) # 変数ラベルの描画用 hyperbola_label <- paste0( "list(", "theta==", theta, ", cosh~theta==", round(cosh(theta), digits = 2), ", sinh~theta==", round(sinh(theta), digits = 2), ")" ) # 双曲線関数を作図 hyperbola_graph <- ggplot() + geom_segment(data = axis_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, group = "axis"), arrow = arrow(length = unit(10, units = "pt"))) + # 軸線 geom_line(data = asymptote_df, mapping = aes(x = x, y = y, group = slope), linetype = "dashed") + # 漸近線 geom_path(data = hyperbola_df, mapping = aes(x = cosh_t, y = sinh_t, group = sign), size = 1) + # 双曲線 geom_point(data = point_df, mapping = aes(x = cosh_t, y = sinh_t), size = 4) + # 双曲線上の点 geom_ribbon(data = variable_area_df, mapping = aes(x = x, ymin = curve, ymax = straight), fill = "#00A968", alpha = 0.5) + # 変数(面積) geom_text(mapping = aes(x = 0.5, y = 0.25*tanh(theta), label = "frac(theta, 2)"), parse = TRUE, size = 3) + # 変数ラベル geom_segment(data = segment_hyperbola_df, mapping = aes(x = x_from, y = y, xend = x_to, yend = y), linetype = "dotted") + # sinh曲線との対応線 geom_segment(data = function_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = fnc), size = 1) + # 双曲線関数直線 geom_text(data = function_label_df, mapping = aes(x = x, y = y, label = fnc_label, color = fnc, angle = angle, vjust = v), parse = TRUE, show.legend = FALSE) + # 双曲線関数ラベル scale_color_manual(breaks = c("sinh", "cosh"), values = c("red", "blue")) + coord_fixed(ratio = 1, clip = "off", xlim = c(-axis_max, axis_max), ylim = c(-axis_max, axis_max)) + # 表示範囲 labs(title = "hyperbola", subtitle = parse(text = hyperbola_label), color = "function", x = expression(cosh~theta), y = expression(sinh~theta)) # sinh曲線の描画用 sinh_df <- tibble::tibble( t = theta_vec, sinh_t = sinh(theta_vec) ) # 双曲線との対応用 d <- 1.1 l <- 0.6 segment_sinh_df <- tibble::tibble( x_from = c(theta, theta), y_from = c(sinh(theta), sinh(theta)), x_to = c(theta, min(theta_vec)-l), y_to = c(-axis_max*d, sinh(theta)) ) # 関数ラベルの描画用 sinh_label <- paste0( "list(", "theta==", theta, ", sinh~theta==", round(sinh(theta), digits = 2), ")" ) # sinh関数を作図 sinh_graph <- ggplot() + geom_line(data = sinh_df, mapping = aes(x = t, y = sinh_t), color = "red", size = 1) + # sinh曲線 geom_segment(data = segment_sinh_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to), linetype = "dotted") + # 双曲線との対応線 geom_point(data = point_df, mapping = aes(x = t, y = sinh_t), size = 4) + #sinh曲線上の点 coord_cartesian(clip = "off", xlim = c(min(theta_vec), max(theta_vec)), ylim = c(-axis_max, axis_max)) + # labs(title = "sinh function", subtitle = parse(text = sinh_label), x = expression(theta), y = expression(sinh~theta)) # 並べて描画 graph <- patchwork::wrap_plots(hyperbola_graph, sinh_graph, guides = "collect") # ファイルを書き出し file_path <- paste0(dir_path, "/", stringr::str_pad(i, width = nchar(frame_num), pad = "0"), ".png") ggplot2::ggsave(filename = file_path, plot = graph, width = 1200, height = 600, units = "px", dpi = 100) # 途中経過を表示 message("\r", i, " / ", frame_num, appendLF = FALSE) }
変数の値ごとに「グラフの作成」と同様に処理します。作成したグラフをggsave()で保存します。
sinh関数のアニメーションを作成します。
# gif画像を作成 paste0(dir_path, "/", stringr::str_pad(1:frame_num, width = nchar(frame_num), pad = "0"), ".png") |> # ファイルパスを作成 magick::image_read() |> # 画像ファイルを読込 magick::image_animate(fps = 1, dispose = "previous") |> # gif画像を作成 magick::image_write_gif(path = "sinh.gif", delay = 0.1) -> tmp_path # gifファイル書き出
全てのファイルパスを作成して、image_read()で画像ファイルを読み込んで、image_animate()でgif画像に変換して、image_write_gif()でgifファイルを書き出します。delay引数に1秒当たりのフレーム数の逆数を指定します。

双曲線上の点の高さに応じて推移するのを確認できます。
この記事では、sinh関数を可視化しました。次の記事では、cosh関数を可視化します。
おわりに
tanh関数に続いて双曲線関数シリーズ2つ目の記事ですが、シリーズ的にはこっちを1つ目とした方が流れがいいですね。残り4つもやるつもりです。
2023年2月22日は、モーニング娘。'23の横山玲奈さんの22歳のお誕生日です。(サムネの左上の方です)
よこにゃーん🐨
【次の内容】