はじめに

　この記事は、「R言語 Advent Calendar 2023」の13日目の記事です。

　この記事では、R言語を使ってパラノーマル分布のグラフを作成します(ネタ記事です)。

【他の記事一覧】

www.anarchive-beta.com

【この記事の内容】

はじめに
パラノーマル分布の作図
- ゴースト
  - 身体
  - 浮遊
  - 仮装
- メンダコ
おわりに

パラノーマル分布の作図

　正規分布(normal distribution)によって描くおばけ分布(paranormal distribution)のグラフを作成します。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)
library(gganimate)
library(ggstar)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要です。ただし、作図コードについてはパッケージ名を省略するので、 ggplot2 を読み込む必要があります。
　また、ネイティブパイプ演算子 |> を使います。magrittr パッケージのパイプ演算子 %>% に置き換えられますが、その場合は magrittr を読み込む必要があります。

ゴースト

　正規分布を使っておばけを描きます。
　正規分布については「【R】1次元ガウス分布の作図 - からっぽのしょこ」、cos関数や波の加工については「【R】cos関数の可視化 - からっぽのしょこ」を参照してください。

身体

　まずは段階を踏んで、おばけの身体を整形する処理を確認します。

　おばけの元となる正規分布を設定します。

# 標準偏差を指定
sgm <- 1

# ゴーストの元の座標
body_df <- tibble::tibble(
  # 身体を作成
  x = seq(from = -5, to = 5, length.out = 1001), 
  y = dnorm(x = x, mean = 0, sd = sgm), 
  y_bottom = 0
)
body_df

# A tibble: 1,001 × 3
       x          y y_bottom
   <dbl>      <dbl>    <dbl>
 1 -5    0.00000149        0
 2 -4.99 0.00000156        0
 3 -4.98 0.00000164        0
 4 -4.97 0.00000173        0
 5 -4.96 0.00000181        0
 6 -4.95 0.00000191        0
 7 -4.94 0.00000200        0
 8 -4.93 0.00000210        0
 9 -4.92 0.00000221        0
10 -4.91 0.00000232        0
# ℹ 991 more rows

　正規分布の確率密度を dnorm() で計算します。標準偏差( sd 引数)でフォルムを調整します。
　後のコードとの兼ね合いで、確率密度の下限を y_bottom 列として作成しておきます。

　おばけの目の位置を設定します。

# 目の位置を指定
eye_dist_x     <- 0.3
eye_relative_y <- 0.7

# ゴーストの目の座標
eye_df <- body_df |> 
  dplyr::select(x_med = x, y_max = y) |> 
  dplyr::filter(y_max == max(y_max)) |> # 頭上を抽出
  dplyr::reframe(
    sgn_x = c(-1, 1), .by = dplyr::everything()
  ) |> # 左右用に複製
  dplyr::mutate(
    # 目の位置を調整
    x = x_med + sgn_x*eye_dist_x, 
    y = y_max * eye_relative_y
  )
eye_df

# A tibble: 2 × 5
  x_med y_max sgn_x     x     y
  <dbl> <dbl> <dbl> <dbl> <dbl>
1     0 0.399    -1  -0.3 0.279
2     0 0.399     1   0.3 0.279

　確率密度の最大値の行を filter() で取り出して、reframe() で2行に複製して、左右の目のプロット位置(座標)を作成します。
　この例では、中心から左右への移動量 eye_dist_x、頭の先から下方向の割合 eye_relative_y を指定して、座標を計算します。

　おばけの元となる正規分布のグラフを作成します。

# ゴーストを作図
ggplot() + 
  geom_ribbon(data = body_df, 
              mapping = aes(x = x, ymin = y_bottom, ymax = y), 
              fill = "white", alpha = 0.8) + # 身体
  ggstar::geom_star(data = eye_df, 
                    mapping = aes(x = x, y = y),
                    starshape = "ellipse", fill = "black", size = 5) + # 目
  labs(title = "paranormal distribution", 
       x = "x", y = "density")

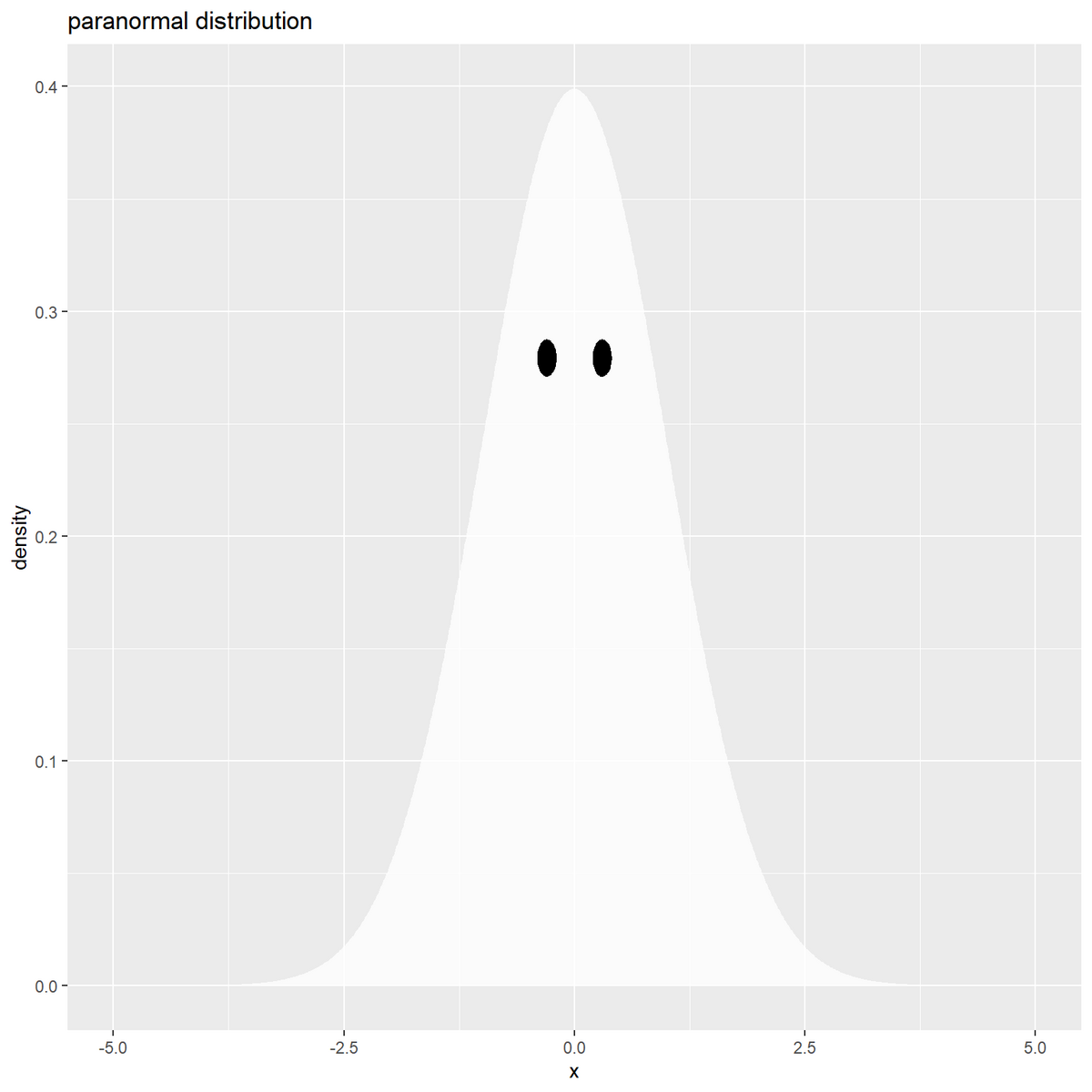
　身体として、geom_ribbon() で内側を塗りつぶした曲線を描画します。
　目として、ggstar パッケージの geom_star() で楕円を描画します。

　山の付け根を削除します。

# 身体の最小値を指定
y_min <- 0.05

# ゴーストの全体の座標
body_df <- tibble::tibble(
  # 身体を作成
  x = seq(from = -5, to = 5, length.out = 1001), 
  y = dnorm(x = x, mean = 0, sd = sgm)
) |> 
  dplyr::filter(
    # 胴を作成
    y >= y_min
  ) |> 
  dplyr::mutate(
    # 裾の形を指定
    y_bottom = y_min
  )
body_df

# A tibble: 407 × 3
       x      y y_bottom
   <dbl>  <dbl>    <dbl>
 1 -2.03 0.0508     0.05
 2 -2.02 0.0519     0.05
 3 -2.01 0.0529     0.05
 4 -2    0.0540     0.05
 5 -1.99 0.0551     0.05
 6 -1.98 0.0562     0.05
 7 -1.97 0.0573     0.05
 8 -1.96 0.0584     0.05
 9 -1.95 0.0596     0.05
10 -1.94 0.0608     0.05
# ℹ 397 more rows

　確率密度の下限 y_min を指定して、確率密度が y_min 以上の行を filter() で取り出します。

　先ほどのコードでグラフを作成します。

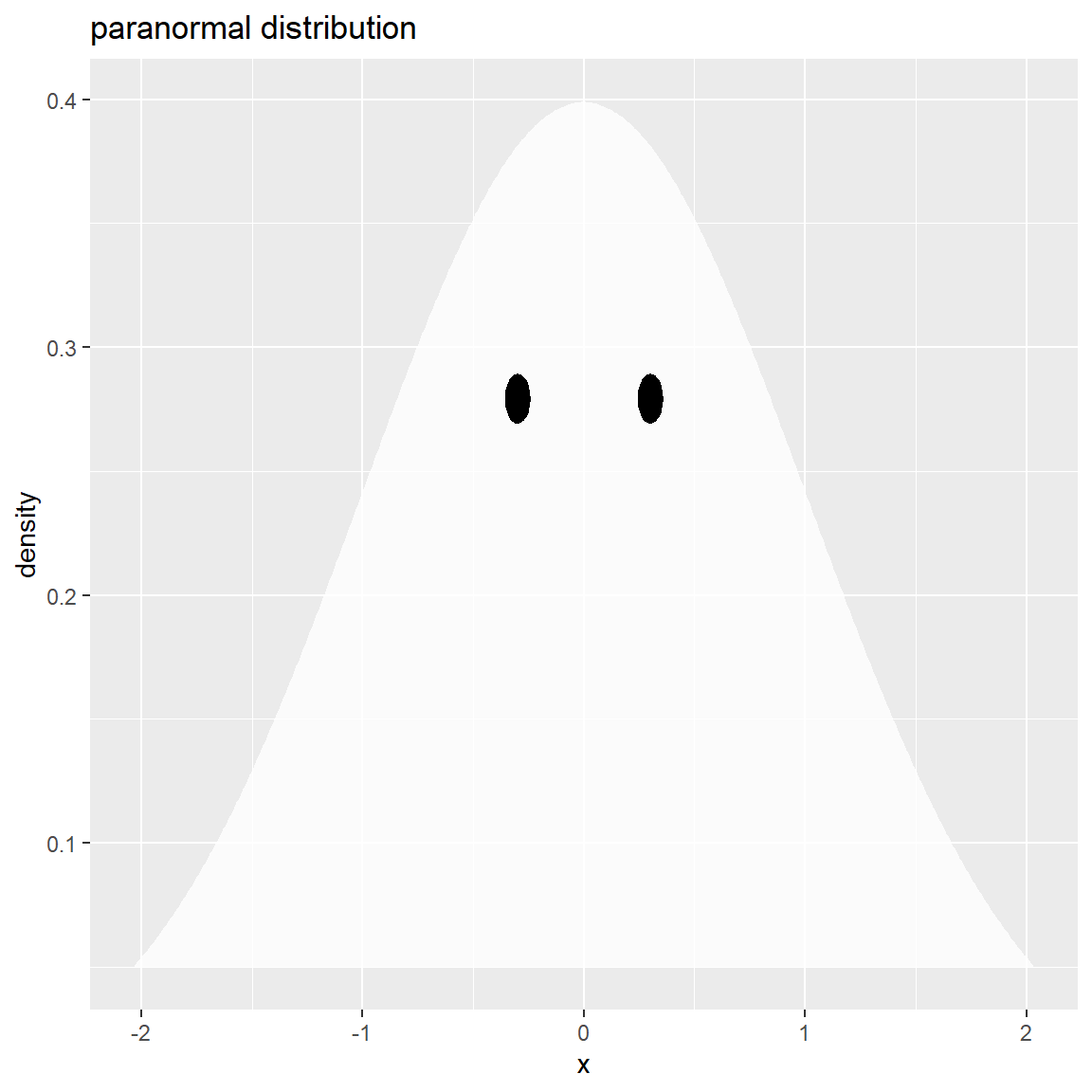
　正規分布の下部を y_min で切断しました。

　裾を作成します。

# ゴーストの全体の座標
body_df <- tibble::tibble(
  # 身体を作成
  x = seq(from = -5, to = 5, length.out = 1001), 
  y = dnorm(x = x, mean = 0, sd = sgm)
) |> 
  dplyr::filter(
    # 胴を作成
    y >= y_min
  ) |> 
  dplyr::mutate(
    # 裾の形を指定
    tmp_y    = (y - y_min), # 0以上の値
    y_bottom = y_min - tmp_y*0.1
  )
body_df

# A tibble: 407 × 4
       x      y    tmp_y y_bottom
   <dbl>  <dbl>    <dbl>    <dbl>
 1 -2.03 0.0508 0.000824   0.0499
 2 -2.02 0.0519 0.00186    0.0498
 3 -2.01 0.0529 0.00292    0.0497
 4 -2    0.0540 0.00399    0.0496
 5 -1.99 0.0551 0.00508    0.0495
 6 -1.98 0.0562 0.00618    0.0494
 7 -1.97 0.0573 0.00730    0.0493
 8 -1.96 0.0584 0.00844    0.0492
 9 -1.95 0.0596 0.00959    0.0490
10 -1.94 0.0608 0.0108     0.0489
# ℹ 397 more rows

　y 列は y_min 以上の値なので、y_min を引いて 0 以上の値( tmp_y 列)にします。両端が0に近く中心が最大値になります。
　山の大きさ(裾のたれ具合)は係数(この例だと 0.1 )で調整します。

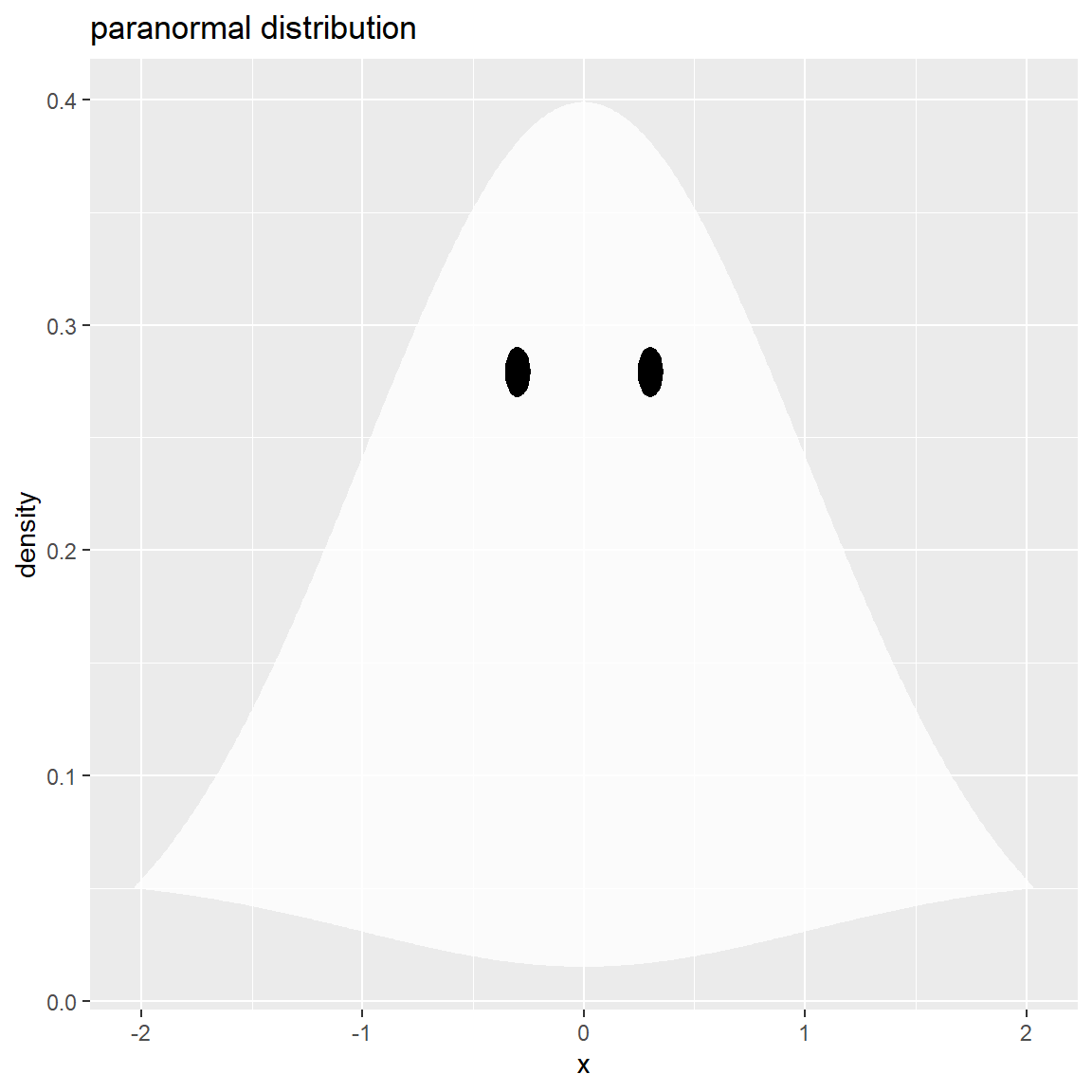
　裾が、身体部分を上下反転・縮小した形状になりました。

　裾を波打たせます。

# ゴーストの全体の座標
body_df <- tibble::tibble(
  # 身体を作成
  x = seq(from = -5, to = 5, length.out = 1001), 
  y = dnorm(x = x, mean = 0, sd = sgm)
) |> 
  dplyr::filter(
    # 胴を作成
    y >= y_min
  ) |> 
  dplyr::mutate(
    # 裾の形を指定
    tmp_y    = (y - y_min) * 0.2, # 0以上の値
    w        = tmp_y / max(tmp_y), # 0から1の値
    cos_x    = 0.01 * cos(15*x), 
    y_bottom = y_min - tmp_y + w*cos_x
  )
body_df

# A tibble: 407 × 6
       x      y    tmp_y       w      cos_x y_bottom
   <dbl>  <dbl>    <dbl>   <dbl>      <dbl>    <dbl>
 1 -2.03 0.0508 0.000165 0.00236  0.00569     0.0498
 2 -2.02 0.0519 0.000373 0.00534  0.00439     0.0497
 3 -2.01 0.0529 0.000584 0.00837  0.00300     0.0494
 4 -2    0.0540 0.000798 0.0114   0.00154     0.0492
 5 -1.99 0.0551 0.00102  0.0146   0.0000487   0.0490
 6 -1.98 0.0562 0.00124  0.0177  -0.00145     0.0487
 7 -1.97 0.0573 0.00146  0.0209  -0.00291     0.0485
 8 -1.96 0.0584 0.00169  0.0242  -0.00431     0.0482
 9 -1.95 0.0596 0.00192  0.0275  -0.00561     0.0479
10 -1.94 0.0608 0.00215  0.0309  -0.00678     0.0476
# ℹ 397 more rows

　tmp_y 列を最大値で割って 0 から 1 の値( w 列)にして、重みとして使います。
　コサイン関数 cos() で波線を作成して、重み付けしてy軸の下限の値に加えます。

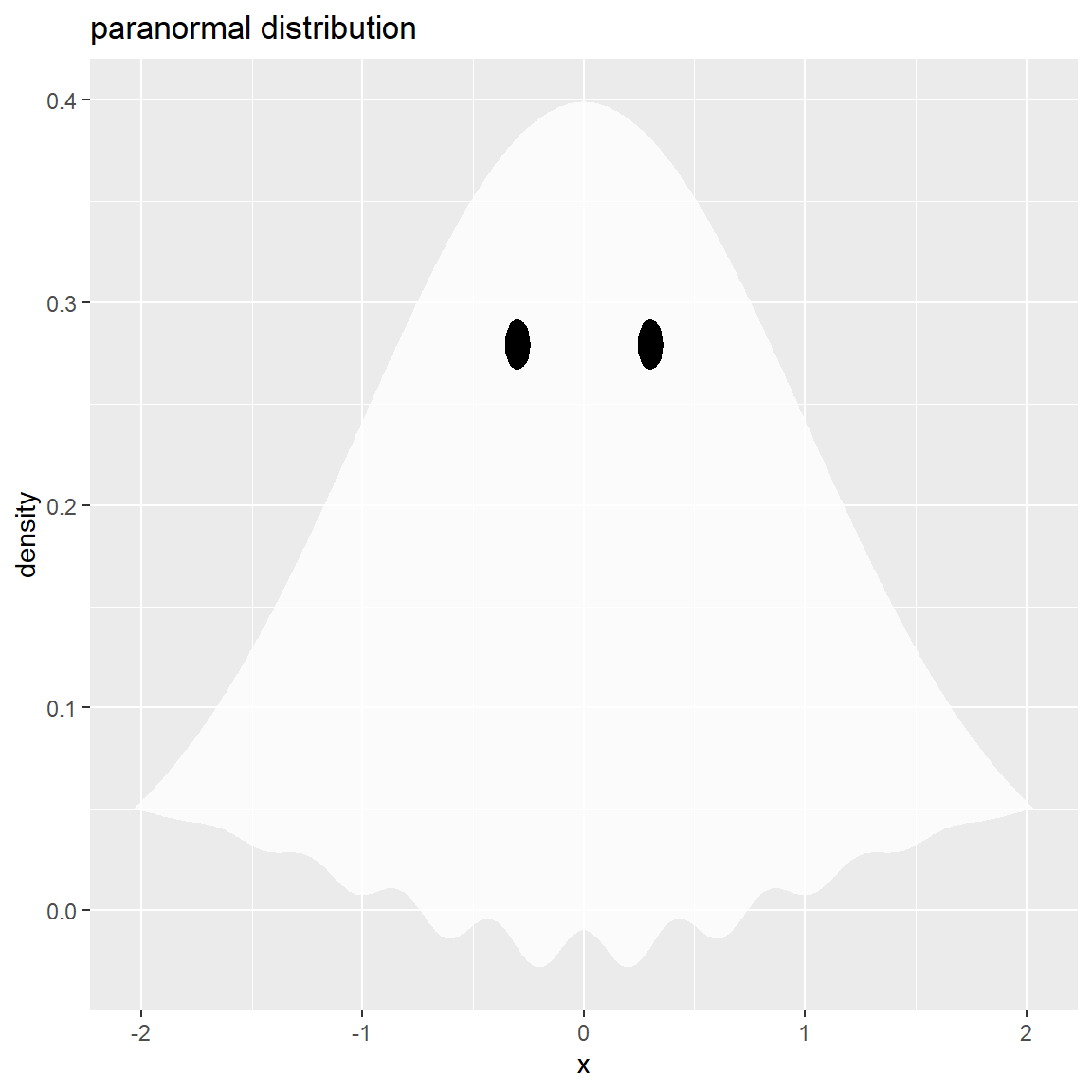
　裾が、波打った形状になりました。両端が0の重みを使って結合しているので、身体と裾の端が繋がり、波の振り幅も外側ほど穏やかになります。

　裾の形を整形します。

# ゴーストの全体の座標
body_df <- tibble::tibble(
  # 身体を作成
  x = seq(from = -5, to = 5, length.out = 1001), 
  y = dnorm(x = x, mean = 0, sd = sgm)
) |> 
  dplyr::filter(
    # 胴を作成
    y >= y_min
  ) |> 
  dplyr::mutate(
    # 裾の形を指定
    j = dplyr::row_number(x), 
    tmp_y    = (y - y_min) * 0.15, # 0以上の値
    w        = tmp_y / max(tmp_y), # 0から1の値
    cos1_x   = cos(15*x), 
    cos2_x   = 0.5 * cos(12.5*x + 0.5*pi), 
    cos3_x   = 0.1 * sqrt(j) * cos(5*x + 0.5*pi), 
    cos_x    = 0.01 * (cos1_x + cos2_x + cos3_x), 
    y_bottom = y_min - tmp_y + w*cos_x
  )
body_df |> 
  dplyr::select(!j) # 資料作成用に間引き

# A tibble: 407 × 9
       x      y    tmp_y       w   cos1_x   cos2_x  cos3_x     cos_x y_bottom
   <dbl>  <dbl>    <dbl>   <dbl>    <dbl>    <dbl>   <dbl>     <dbl>    <dbl>
 1 -2.03 0.0508 0.000124 0.00236  0.569    0.120   -0.0663  0.00622    0.0499
 2 -2.02 0.0519 0.000280 0.00534  0.439    0.0585  -0.0884  0.00409    0.0497
 3 -2.01 0.0529 0.000438 0.00837  0.300   -0.00387 -0.101   0.00195    0.0496
 4 -2    0.0540 0.000599 0.0114   0.154   -0.0662  -0.109  -0.000207   0.0494
 5 -1.99 0.0551 0.000762 0.0146   0.00487 -0.127   -0.112  -0.00235    0.0492
 6 -1.98 0.0562 0.000927 0.0177  -0.145   -0.187   -0.112  -0.00443    0.0490
 7 -1.97 0.0573 0.00110  0.0209  -0.291   -0.243   -0.109  -0.00643    0.0488
 8 -1.96 0.0584 0.00127  0.0242  -0.431   -0.296   -0.104  -0.00830    0.0485
 9 -1.95 0.0596 0.00144  0.0275  -0.561   -0.344   -0.0959 -0.0100     0.0483
10 -1.94 0.0608 0.00161  0.0309  -0.678   -0.386   -0.0859 -0.0115     0.0480
# ℹ 397 more rows

　複数の波を(コネコネしながら)重ね合わせます。

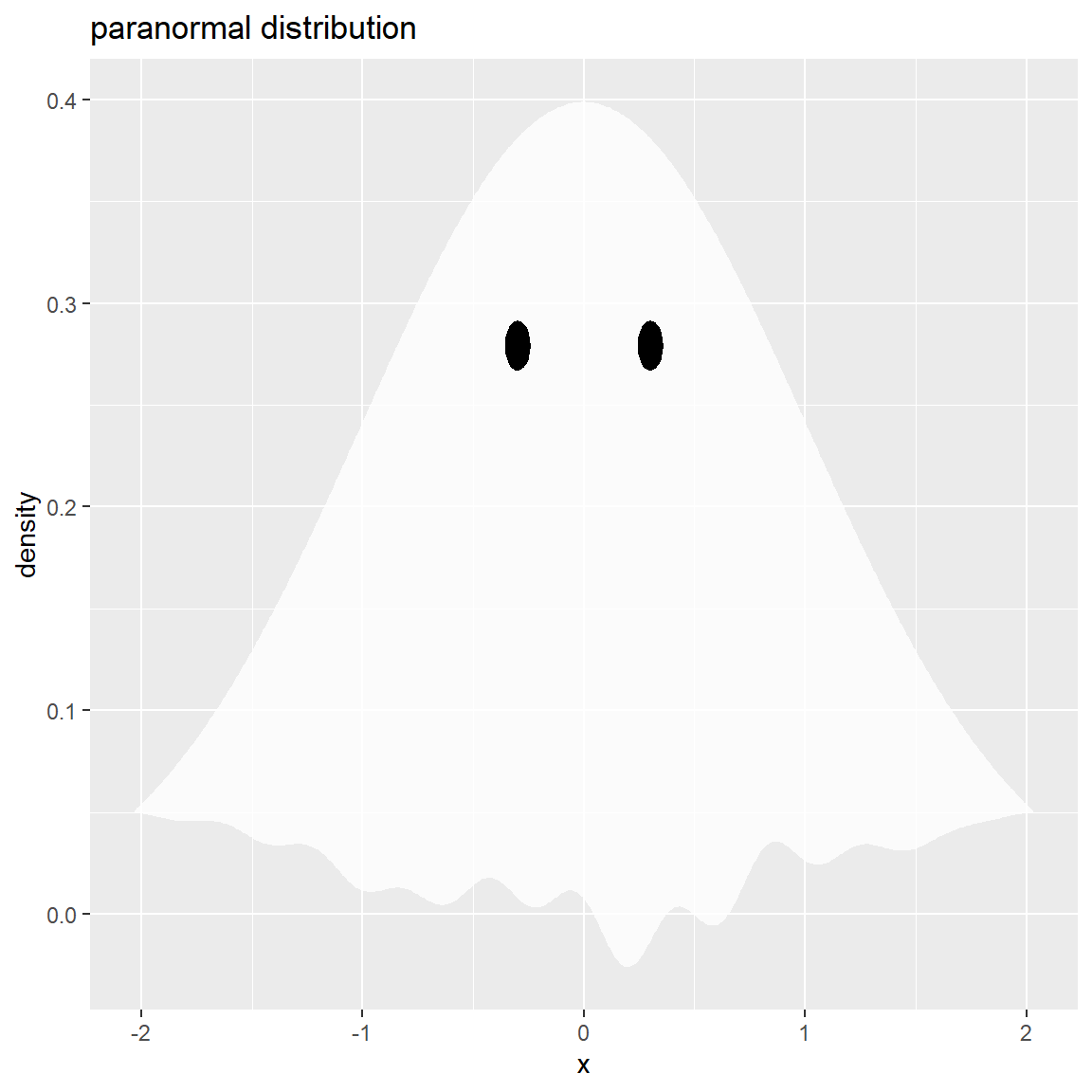
　満足な形状に設定できれば完成です。

　以上で、おばけを作図できました。

浮遊

　続いて、おばけを浮遊させます。
　浮遊の軌道については「【R】リサージュ曲線の可視化 - からっぽのしょこ」を参照してください。

　おばけの身体の描画用のデータフレームを作成します。

# フレーム数を指定
frame_num <- 100

# 身体の伸び縮み(ガワのフワフワ)用の標準偏差を指定
sgm_vals <- c(
  seq(from = 2, to = 2.2, length.out = floor(0.5*frame_num+1))[1:floor(0.5*frame_num)], 
  seq(from = 2.2, to = 2, length.out = ceiling(0.5*frame_num+1))[1:ceiling(0.5*frame_num)]
)

# 浮遊用のラジアンを作成
t_vals <- seq(from = 0, to = 2*pi, length.out = frame_num+1)[1:frame_num]

# 胴の縦サイズを指定
dens_lower <- 0.02

# 縦・横の移動量を指定
turn_dist_x <- 1.5
turn_dist_y <- 0.05

# 身体の座標を作成
body_df <- tidyr::expand_grid(
  i   = 1:frame_num, # フレーム番号
  var = seq(from = -5, to = 5, length.out = 1001)
) |> # フレームごとに複製
  dplyr::mutate(
    # 身体を作成
    sgm  = sgm_vals[i], 
    dens = dnorm(x = var, mean = 0, sd = sgm)
  ) |> 
  dplyr::filter(
    # 胴を作成
    dens >= dens_lower
  ) |> 
  dplyr::mutate(
    # 浮遊の軌道を作成
    t = t_vals[i], 
    x = var  + turn_dist_x * cos(t), 
    y = dens + turn_dist_y * sin(t)
  ) |> 
  dplyr::mutate(
    # 裾の形を指定
    j        = dplyr::row_number(x), 
    y_min    = min(y), 
    tmp_y    = (y - y_min) * 0.2, # 0以上の値
    w        = tmp_y / max(tmp_y), # 0から1の値
    cos1_x   = 1 * cos(5.5*x), 
    cos2_x   = 1.5 * cos(6*x + 0.5*pi), 
    cos3_x   = 0.1 * sqrt(j) * cos(3*x + 0.5*pi), 
    cos_x    = 0.002 * (cos1_x + cos2_x + cos3_x), 
    y_bottom = y_min - tmp_y + w*cos_x, 
    .by = i
  )
body_df |> 
  dplyr::select(i, var, dens, x, y, tmp_y, w, cos_x, y_bottom) # 資料作成用に間引き

# A tibble: 89,098 × 9
       i   var   dens     x      y     tmp_y       w    cos_x y_bottom
   <int> <dbl>  <dbl> <dbl>  <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
 1     1 -4.28 0.0202 -2.78 0.0202 0         0       -0.00413   0.0202
 2     1 -4.27 0.0204 -2.77 0.0204 0.0000434 0.00121 -0.00390   0.0202
 3     1 -4.26 0.0206 -2.76 0.0206 0.0000872 0.00243 -0.00367   0.0201
 4     1 -4.25 0.0209 -2.75 0.0209 0.000131  0.00366 -0.00344   0.0201
 5     1 -4.24 0.0211 -2.74 0.0211 0.000176  0.00490 -0.00319   0.0200
 6     1 -4.23 0.0213 -2.73 0.0213 0.000221  0.00616 -0.00294   0.0200
 7     1 -4.22 0.0215 -2.72 0.0215 0.000266  0.00742 -0.00269   0.0199
 8     1 -4.21 0.0218 -2.71 0.0218 0.000312  0.00869 -0.00242   0.0199
 9     1 -4.2  0.0220 -2.7  0.0220 0.000358  0.00997 -0.00214   0.0198
10     1 -4.19 0.0222 -2.69 0.0222 0.000404  0.0113  -0.00186   0.0198
# ℹ 89,088 more rows

　フレーム数 frame_num を指定して、軌道の座標計算用のラジアン(変数)などを作成します。
　フレーム番号( 1 から frame_num までの整数)と確率変数(x軸用)の値の全ての組み合わせを tidyr::expand_grid() で作成することで、フレームごとに変数列を複製して、「身体」のときと同様におばけの輪郭(上限と下限の座標)を作成します。
　確率変数を $v$ としてx座標を $x = v + A \cos(a \theta + \alpha)$ 、確率密度を $d$ としてy座標を $y = d + B \sin(b \theta + \beta)$ で計算(設定)します。リサージュ曲線の軌道を辿ります。

　おばけの目の描画用のデータフレームを作成します。

# 目の位置を指定
eye_dist_x <- 0.4
eye_dist_y <- 0.05

# 目の座標を作成
eye_df <- body_df |> 
  dplyr::select(i, x_med = x, y_max = y) |> 
  dplyr::filter(y_max == max(y_max), .by = i) |> # 頭上を抽出
  dplyr::reframe(
    sgn_x = c(-1, 1), .by = dplyr::everything()
  ) |> # 左右用に複製
  dplyr::mutate(
    # 目の位置を調整
    x = x_med + sgn_x*eye_dist_x, 
    y = y_max - eye_dist_y
  )
eye_df

# A tibble: 200 × 6
       i x_med y_max sgn_x     x     y
   <int> <dbl> <dbl> <dbl> <dbl> <dbl>
 1     1  1.5  0.199    -1  1.1  0.149
 2     1  1.5  0.199     1  1.9  0.149
 3     2  1.50 0.202    -1  1.10 0.152
 4     2  1.50 0.202     1  1.90 0.152
 5     3  1.49 0.205    -1  1.09 0.155
 6     3  1.49 0.205     1  1.89 0.155
 7     4  1.47 0.208    -1  1.07 0.158
 8     4  1.47 0.208     1  1.87 0.158
 9     5  1.45 0.210    -1  1.05 0.160
10     5  1.45 0.210     1  1.85 0.160
# ℹ 190 more rows

　フレームごとに「身体」のときと同様にして両目のプロット位置(座標)を作成します。

　おばけが浮遊するアニメーションを作成します。

# ゴーストのアニメーションを作図
anim <- ggplot() + 
  geom_ribbon(data = body_df, 
              mapping = aes(x = x, ymin = y_bottom, ymax = y), 
              fill = "white", color = "gray", alpha = 0.8) + # 身体
  ggstar::geom_star(data = eye_df,
                    mapping = aes(x = x, y = y),
                    starshape = "ellipse", fill = "black", size = 8) + # 目
  gganimate::transition_manual(frames = i) + # フレーム切替
  guides(x = "none", y = "none") + 
  labs(title = "paranormal distribution", 
       #subtitle = "frame: {current_frame}", 
       x = "", y = "")

# gif画像を作成
gganimate::animate(plot = anim, nframes = frame_num, fps = 100, width = 800, height = 800)

　gganimate パッケージを利用してアニメーション(gif画像)を作成します。
　transition_manual() のフレーム制御の引数 frames にフレーム番号列 i を指定します。
　animate() の plot 引数にグラフオブジェクト、nframes 引数にフレーム数 frame_num を指定して、gif画像を作成します。また、fps 引数に1秒当たりのフレーム数を指定できます。

　おばけの形状は、正規分布の標準偏差だけでなく、軌道の振り幅や図のサイズ( width, height 引数)の影響も受けます(思い通りの形状に設定するには色々と考慮して頑張る必要があります)。

仮装

　ハロウィンネタということで、t分布におばけのガワを着せます。
　t分布については「【R】1次元スチューデントのt分布の作図 - からっぽのしょこ」を参照してください。

　おばけの中身の描画用のデータフレームを作成します。

# 胴の横サイズを指定
var_lower <- 3.6

# 中身(ナカ)の身体の座標を作成
inner_body_df <- tidyr::expand_grid(
  i   = 1:frame_num, # フレーム番号
  var = seq(from = -5, to = 5, length.out = 1001)
) |> # フレームごとに複製
  dplyr::mutate(
    # 身体を作成
    dens = LaplacesDemon::dst(x = var, mu = 0, sigma = 2, nu = 2.5)
  ) |> 
  dplyr::filter(
    # 縦方向の胴の位置を作成
    dens >= dens_lower
  ) |> 
  dplyr::mutate(
    # 縦方向の浮遊の軌道を作成
    t = t_vals[i], 
    y = dens + turn_dist_y * sin(t), 
    # 裾の形を指定
    y_min    = min(y), 
    tmp_y    = (y - y_min) * 0.2, # 0以上の値
    y_bottom = y_min - tmp_y, 
    .by = i
  ) |> 
  dplyr::filter(
    # 横方向の胴の位置を作成
    var >= -var_lower, var <= var_lower
  ) |> 
  dplyr::mutate(
    # 横方向の浮遊の軌道を作成
    x = var  + turn_dist_x * cos(t)
  )
inner_body_df

# A tibble: 72,100 × 9
       i   var   dens     t      y  y_min   tmp_y y_bottom     x
   <int> <dbl>  <dbl> <dbl>  <dbl>  <dbl>   <dbl>    <dbl> <dbl>
 1     1 -3.6  0.0422     0 0.0422 0.0202 0.00441   0.0158 -2.1 
 2     1 -3.59 0.0425     0 0.0425 0.0202 0.00446   0.0157 -2.09
 3     1 -3.58 0.0427     0 0.0427 0.0202 0.00450   0.0157 -2.08
 4     1 -3.57 0.0429     0 0.0429 0.0202 0.00455   0.0157 -2.07
 5     1 -3.56 0.0432     0 0.0432 0.0202 0.00460   0.0156 -2.06
 6     1 -3.55 0.0434     0 0.0434 0.0202 0.00464   0.0156 -2.05
 7     1 -3.54 0.0437     0 0.0437 0.0202 0.00469   0.0155 -2.04
 8     1 -3.53 0.0439     0 0.0439 0.0202 0.00474   0.0155 -2.03
 9     1 -3.52 0.0441     0 0.0441 0.0202 0.00479   0.0154 -2.02
10     1 -3.51 0.0444     0 0.0444 0.0202 0.00484   0.0154 -2.01
# ℹ 72,090 more rows

　「浮遊」のときと同様に、データフレームを作成します。
　t分布の確率密度を LaplacesDemon パッケージの dst() で計算して、左右にはみ出る部分を取り除いておきます。

　おばけの中身の装飾用のデータフレームを作成します。

# 中身(ナカ)の頭上の2点の座標を作成
inner_top_df <- inner_body_df |> 
  dplyr::select(i, x_med = x, y_max = y) |> 
  dplyr::filter(y_max == max(y_max), .by = i) |> # 頭上を抽出
  dplyr::reframe(
    sgn_x = c(-1, 1), .by = dplyr::everything()
  ) |> # 左右用に複製
    dplyr::mutate(
      # 耳の角度を指定
      deg = -sgn_x * 40, 
      .by = i
    )
inner_top_df

# A tibble: 200 × 5
       i x_med y_max sgn_x   deg
   <int> <dbl> <dbl> <dbl> <dbl>
 1     1  1.5  0.181    -1    40
 2     1  1.5  0.181     1   -40
 3     2  1.50 0.184    -1    40
 4     2  1.50 0.184     1   -40
 5     3  1.49 0.187    -1    40
 6     3  1.49 0.187     1   -40
 7     4  1.47 0.190    -1    40
 8     4  1.47 0.190     1   -40
 9     5  1.45 0.193    -1    40
10     5  1.45 0.193     1   -40
# ℹ 190 more rows

　「浮遊」のときと同様に、データフレームを作成します。プロット位置については次の描画時に設定します。

　おばけが浮遊するアニメーションを作成します。

# 耳・目・口の位置を指定
ear_dist_x   <- 0.9
ear_dist_y   <- 0.015
eye_dist_x   <- 0.6
eye_dist_y   <- 0.04
mouth_dist_y <- 0.05

# ゴーストのアニメーションを作図
anim <- ggplot() + 
  geom_ribbon(data = inner_body_df, 
              mapping = aes(x =  x, ymin = y_bottom, ymax = y), 
              fill = "gray76") + # ナカの身体
  geom_text(data = inner_top_df, 
            mapping = aes(x = x_med+sgn_x*ear_dist_x, y = y_max-ear_dist_y, angle = deg), 
            label = "▲", color = "gray67", size = 15) + # ナカの耳
  geom_point(data = inner_top_df,
             mapping = aes(x = x_med+sgn_x*eye_dist_x, y = y_max-eye_dist_y),
             shape = "circle", color = "gray56", size = 8) + # ナカの目
  geom_text(data = inner_top_df, 
            mapping = aes(x = x_med, y = y_max-mouth_dist_y), 
            label = "x", color = "gray56", size = 8) + # ナカの口
  geom_ribbon(data = body_df, 
              mapping = aes(x = x, ymin = y_bottom, ymax = y), 
              fill = "white", color = "gray", alpha = 0.8) + # ガワの身体
  ggstar::geom_star(data = eye_df,
                    mapping = aes(x = x, y = y),
                    starshape = "ellipse", fill = "black", size = 8) + # ガワの目
  gganimate::transition_manual(frames = i) + # フレーム切替
  guides(x = "none", y = "none") + 
  labs(title = "paranormal distribution", 
       #subtitle = "frame: {current_frame}", 
       x = "", y = "")

# gif画像を作成
gganimate::animate(plot = anim, nframes = frame_num, fps = 100, width = 800, height = 800)

　諸々がはみ出ない(あるいは意図的に少しはみ出る)ように調整すれば完成です。

メンダコ

　ハロウィンネタをそのままアドカレネタに流用するのはなんなので、正規分布を使ってメンダコ(あるいはメンダコに化けたおばけ)を作成します。

　メンダコの身体の描画用のデータフレームを作成します。

# フレーム数を指定
frame_num <- 300

# 身体の伸び縮み(腕の開閉)用の標準偏差を指定
sgm_vals <- c(
  seq(from = 2, to = 2.5, length.out = 0.25*frame_num+1)[1:(0.25*frame_num)], 
  seq(from = 2.5, to = 2, length.out = 0.25*frame_num+1)[1:(0.25*frame_num)], 
  seq(from = 2, to = 2.5, length.out = 0.25*frame_num+1)[1:(0.25*frame_num)], 
  seq(from = 2.5, to = 2, length.out = 0.25*frame_num+1)[1:(0.25*frame_num)]
)

# 浮遊用のラジアンを作成
rad_vals <- seq(from = 0, to = 2*pi, length.out = frame_num+1)[1:frame_num]

# 身体の座標を作成
body_df <- tidyr::expand_grid(
  i   = 1:frame_num, # フレーム番号
  var = seq(from = -5, to = 5, length.out = 1001)
) |> # フレームごとに複製
  dplyr::mutate(
    # 身体を作成
    sgm = sgm_vals[i], 
    dens = dnorm(x = var, mean = 0, sd = sgm)
  ) |> 
  dplyr::filter(
    # 胴のサイズを指定
    dens >= 0.05
  ) |> 
  dplyr::mutate(
    # 浮遊の軌道を指定
    t = rad_vals[i], 
    x = var  + cos(t) * 5, 
    y = dens + sin(2*t) * 0.05, 
    # 裾用のラジアンを作成
    j = dplyr::row_number(var), 
    u = seq(from = 0, to = 2*pi, length.out = length(j))[j], 
    # 裾の形を指定
    y_min    = min(y), 
    tmp_y    = (y - y_min) * 0.2, # 0以上の値
    w        = tmp_y / max(tmp_y), # 0から1の値
    cos_u    = 0.01 * cos(4 * u), 
    y_bottom = y_min - tmp_y + w*cos_u, 
    .by = i
  )
body_df |> 
  dplyr::select(!c(sgm, t, y_min, tmp_y)) # 資料作成用に間引き

# A tibble: 214,572 × 10
       i   var   dens     x      y     j       u       w   cos_u y_bottom
   <int> <dbl>  <dbl> <dbl>  <dbl> <int>   <dbl>   <dbl>   <dbl>    <dbl>
 1     1 -3.32 0.0503  1.68 0.0503     1 0       0       0.01      0.0503
 2     1 -3.31 0.0507  1.69 0.0507     2 0.00946 0.00281 0.00999   0.0502
 3     1 -3.3  0.0511  1.7  0.0511     3 0.0189  0.00563 0.00997   0.0502
 4     1 -3.29 0.0516  1.71 0.0516     4 0.0284  0.00846 0.00994   0.0501
 5     1 -3.28 0.0520  1.72 0.0520     5 0.0379  0.0113  0.00989   0.0501
 6     1 -3.27 0.0524  1.73 0.0524     6 0.0473  0.0142  0.00982   0.0500
 7     1 -3.26 0.0528  1.74 0.0528     7 0.0568  0.0171  0.00974   0.0500
 8     1 -3.25 0.0533  1.75 0.0533     8 0.0662  0.0199  0.00965   0.0499
 9     1 -3.24 0.0537  1.76 0.0537     9 0.0757  0.0229  0.00955   0.0498
10     1 -3.23 0.0541  1.77 0.0541    10 0.0852  0.0258  0.00943   0.0498
# ℹ 214,562 more rows

　「浮遊」のときと同様にしてデータフレームを作成します。

　メンダコのヒレと目の描画用のデータフレームを作成します。

# 頭上の2点の座標を作成
top_df <- body_df |> 
  dplyr::select(i, x_med = x, y_max = y) |> 
  dplyr::filter(y_max == max(y_max), .by = i) |> # 頭上を抽出
  dplyr::reframe(
    sgn_x = c(-1, 1), .by = dplyr::everything()
  ) |> # 左右用に複製
  dplyr::mutate(
    t   = rad_vals[i], 
    deg = sgn_x * (asin(sin(6*t + 0.5*pi)) * 180/pi * 7/9 + 35), # 角度
    .by = i
  )
top_df

# A tibble: 600 × 6
       i x_med y_max sgn_x      t    deg
   <int> <dbl> <dbl> <dbl>  <dbl>  <dbl>
 1     1  5    0.199    -1 0      -105  
 2     1  5    0.199     1 0       105  
 3     2  5.00 0.201    -1 0.0209  -99.4
 4     2  5.00 0.201     1 0.0209   99.4
 5     3  5.00 0.202    -1 0.0419  -93.8
 6     3  5.00 0.202     1 0.0419   93.8
 7     4  4.99 0.204    -1 0.0628  -88.2
 8     4  4.99 0.204     1 0.0628   88.2
 9     5  4.98 0.205    -1 0.0838  -82.6
10     5  4.98 0.205     1 0.0838   82.6
# ℹ 590 more rows

　「浮遊」のときと同様にしてデータフレームを作成します。
　座標計算用のラジアンを用いて、頭のヒレの角度を作成します。ラジアン $t$ を $u = \arcsin(\sin t)$ で $0 \leq u \leq \pi$ の範囲のラジアン(弧度法の角度)に変換して、さらに $u^{\circ} = \frac{180^{\circ}}{\pi} u$ で度数法の角度に変換します。 $t$ または $u^{\circ}$ に値(この例でだと 0.5*pi, 35 )を加えて描画時の角度を調整できます。また、変換前の最大値で割って変換後の最大値を掛ける(この例だと 7/9 )ことで、角度の範囲を調整できます。

　メンダコが遊泳するアニメーションを作成します。

# ヒレ・目の位置を指定
fin_dist_x <- 0.8
fin_dist_y <- 0.01
eye_dist_x <- 0.8
eye_dist_y <- 0.05

# メンダコのアニメーションを作図
anim <- ggplot() + 
  ggstar::geom_star(data = top_df, 
                    mapping = aes(x = x_med+sgn_x*fin_dist_x, y = y_max-fin_dist_y, angle = deg), 
                    starshape = "thin triangle", fill = "tomato", color = "red", size = 20) + # ヒレ
  geom_ribbon(data = body_df, 
              mapping = aes(x = x, ymin = y_bottom, ymax = y), 
              fill = "tomato", color = "red") + # 身体
  geom_point(data = top_df, 
             mapping = aes(x = x_med+sgn_x*eye_dist_x, y = y_max-eye_dist_y), 
             shape = "circle filled", fill = "yellow", alpha = 0.9, size = 12) + # 目
  ggstar::geom_star(data = top_df, 
                    mapping = aes(x = x_med+sgn_x*eye_dist_x, y = y_max-eye_dist_y),
                    starshape = "rectangle", fill = "black", size = 6) + # 瞳
  gganimate::transition_manual(frames = i) + # フレーム切替
  guides(x = "none", y = "none") + 
  labs(title = "paranormal distribution", 
       #subtitle = "frame: {current_frame}", 
       x = "", y = "")

# gif画像を作成
gganimate::animate(plot = anim, nframes = frame_num, fps = 12, width = 1000, height = 500)

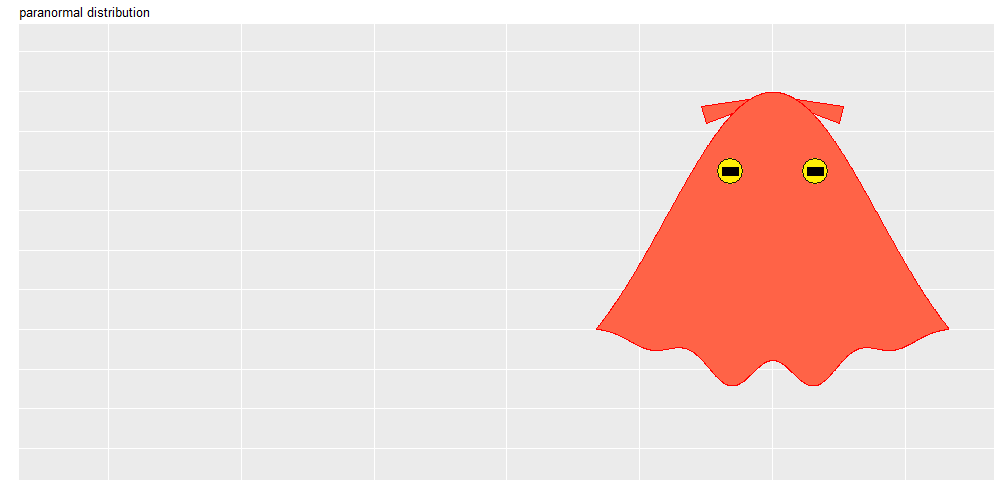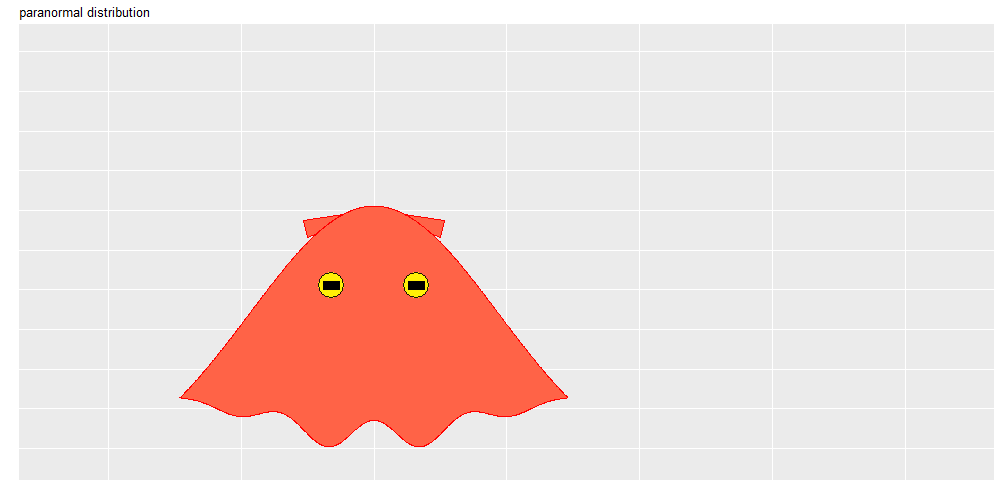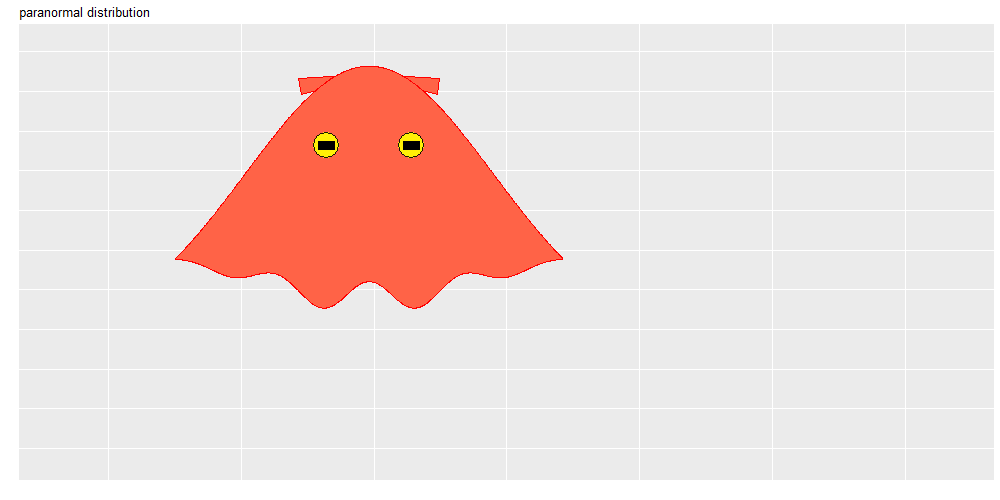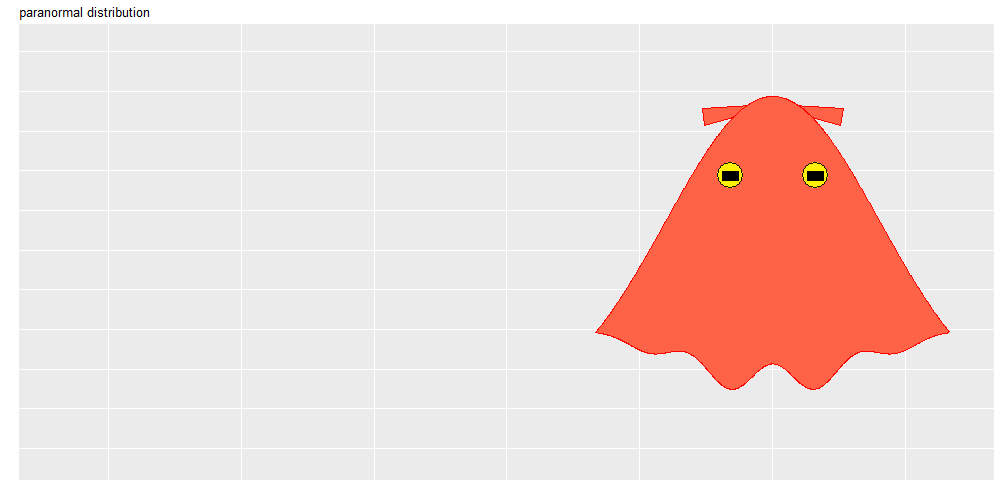
　メンダコの形状は、正規分布の標準偏差だけでなく、軌道の振り幅や図のサイズ( width, height 引数)の影響も受けます(思い通りの形状に設定するには色々と考慮して頑張る必要があります)。
　ヒレの角度は楕円(点)の中心を基準に傾きます。

　この記事では、パラノーマル分布(ネタ)を作成しました。

　Enjoy!

おわりに

　ハロウィンネタにガウス分布でゴーストを作りました。gaussならぬghost分布と言おうと思ってたのですが、normalを文字ってparanormal分布と呼ぶようでした。
　それが思いの外反応があったのでアドカレネタに流用しました。ネタ記事でいいのかというのは置いといて、ハロウィンネタをそのまま流用するのは流石になんなのでメンダコに化けてもらいました。という次第です。
　細かいところで微妙に苦労したのですが最近扱ってた内容(Rアドカレ11日目のネタなど)が使えて満足でした。

　最後まで読んでいただきありがとうございました。
　昨年までのアドカレも普段も真面目な記事を書いています。良ければ読んでみてください。

【他の内容】

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【R】パラノーマル分布の作図

はじめに

パラノーマル分布の作図

ゴースト

身体

浮遊

仮装

メンダコ

おわりに