はじめに
『トピックモデル』(MLPシリーズ)の勉強会資料のまとめです。各種モデルやアルゴリズムを「数式」と「プログラム」を用いて解説します。
本の補助として読んでください。
この記事では、混合ユニグラムモデル(混合カテゴリモデル)に対する周辺化ギブスサンプリングをPythonでスクラッチ実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
3.5 混合ユニグラムモデルの周辺化ギブスサンプリングの実装
混合ユニグラムモデル(mixture of unigram models)に対する周辺化ギブスサンプリング(collapsed Gibbs sampling)を実装する。
混合ユニグラムモデルについては「【Python】8.1:無限混合ユニグラムモデルの生成モデルの実装【青トピックモデルのノート】 - からっぽのしょこ」やアルゴリズム3.3を参照のこと。
利用するライブラリを読み込む。
# 利用ライブラリ import numpy as np from scipy.special import loggamma, digamma import matplotlib.pyplot as plt
文書データの簡易生成
まずは、混合ユニグラムモデルの生成モデルに従って、文書集合に対応するデータを生成する。
トイデータの作成については「生成モデルの実装」を参照のこと。
真の分布や真のトピックなど本来は得られない情報についてはオブジェクト名に true を付けて表す。
パラメータ類を設定して、文書集合を作成する。
# 文書数を指定 D = 100 # 語彙数を指定 V = 150 # トピック数を指定 true_K = 10 # ハイパーパラメータを指定 true_alpha = 1.0 # トピック分布 true_beta = 1.0 # 語彙分布 # トピック分布のパラメータを生成 true_theta_k = np.random.dirichlet( alpha=np.repeat(true_alpha, repeats=true_K), size=1 ).reshape(true_K) # 語彙分布のパラメータを生成 true_phi_kv = np.random.dirichlet( alpha=np.repeat(true_beta, repeats=V), size=true_K ) # 受け皿を初期化 w_dic = {} # 文書ごとの各単語の語彙 true_z_d = np.tile(np.nan, reps=D) # 各文書のトピック N_d = np.zeros(shape=D, dtype='int') # 各文書の単語数 N_dv = np.zeros(shape=(D, V), dtype='int') # 文書ごとの各語彙の単語数 # 文書データを生成 for d in range(D): # 文書ごと # トピックを生成 k = np.random.choice(a=np.arange(true_K), size=1, p=true_theta_k).item() # (カテゴリ乱数) # トピックを割当 true_z_d[d] = k # 単語数を生成 N_d[d] = np.random.randint(low=100, high=200, size=1) # 下限・上限を指定 # 受け皿を初期化 tmp_w_n = np.repeat(np.nan, repeats=N_d[d]) # 各単語の語彙 for n in range(N_d[d]): # 単語ごと # 語彙を生成 v = np.random.choice(a=np.arange(V), size=1, p=true_phi_kv[k]).item() # (カテゴリ乱数) # 語彙を割当 tmp_w_n[n] = v # 頻度をカウント N_dv[d, v] += 1 # データを記録 w_dic[d] = tmp_w_n.copy() # 途中経過を表示 print(f'document: {d+1}, words: {N_d[d]}, topic: {k+1}')
document: 1, words: 130, topic: 7
document: 2, words: 136, topic: 8
document: 3, words: 182, topic: 10
document: 4, words: 178, topic: 3
document: 5, words: 169, topic: 1
(省略)
document: 96, words: 164, topic: 7
document: 97, words: 152, topic: 1
document: 98, words: 109, topic: 9
document: 99, words: 161, topic: 7
document: 100, words: 156, topic: 7
文書ごとにトピックを割り当て、トピックに応じた単語を生成する。
文書データを確認する。
# 観測データを確認 print(N_dv[:5, :10]) print(N_dv.shape)
[[ 0 0 1 2 0 0 3 1 2 0]
[ 0 1 2 1 1 1 0 0 0 2]
[ 0 0 7 0 4 0 2 4 0 0]
[ 0 2 1 4 3 0 10 1 0 1]
[ 0 1 1 1 0 0 0 0 1 2]]
(100, 150)
文書集合 から得られる語彙の頻度データ
を用いてパラメータを推定する。
パラメータの推定
。
文書集合に関する値を設定する。
# 文書数を取得 D = N_dv.shape[0] print(D) # 語彙数を取得 V = N_dv.shape[1] print(V) # 各文書の単語数を取得 N_d = N_dv.sum(axis=1) print(N_d[:5])
100
150
[130 136 182 178 169]
文書数 、語彙数
、各文書の単語数
を取得する。
トピック数とハイパーパラメータの初期値を設定する。
# トピック数を指定 K = 9 # ハイパーパラメータの初期値を指定 alpha = 1.0 # トピック分布 beta = 1.0 # 語彙分布
トピック数 、トピック分布のハイパーパラメータ
、単語分布のハイパーパラメータ
を指定する。
。
# 各文書のトピックを初期化 z_d = np.tile(np.nan, reps=D) # 各トピックの割り当て文書数を初期化 D_k = np.zeros(shape=K) # 語彙ごとの各トピックの割り当て単語数を初期化 N_kv = np.zeros(shape=(K, V)) # 各トピックの割り当て単語数を初期化 N_k = np.zeros(shape=K)
各文書のトピック 、各トピックが割り当てられた文書数
、各トピックが割り当てられた語彙ごとの単語数
、各トピックが割り当てられた単語数
のオブジェクトを作成する。
試行回数を指定して、周辺化ギブスサンプリングによりパラメータを繰り返し更新する。
# 試行回数を指定 max_iter = 1000 # 初期値を記録 trace_z_lt = [z_d.copy()] trace_Dk_lt = [D_k.copy()] trace_Nkv_lt = [N_kv.copy()] trace_alpha_lt = [alpha] trace_beta_lt = [beta] # 崩壊型ギブスサンプリング for i in range(max_iter): # 繰り返し試行 for d in range(D): # 文書ごと if not np.isnan(z_d[d]): # (初回は不要) # 前ステップのトピックを取得 k = z_d[d].astype('int') # ディスカウント D_k[k] -= 1 N_kv[k] -= N_dv[d] N_k[k] -= N_d[d] # サンプリング確率を計算:式(3.27) log_prob_z_k = np.log(D_k + alpha) log_prob_z_k += loggamma(N_k + V*beta) log_prob_z_k -= loggamma(N_k + N_d[d] + V*beta) log_prob_z_k += loggamma(N_kv + N_dv[d] + beta).sum(axis=1) log_prob_z_k -= loggamma(N_kv + beta).sum(axis=1) prob_z_k = np.exp(log_prob_z_k - log_prob_z_k.min()) # (アンダーフロー対策) prob_z_k /= prob_z_k.sum() # 正規化 # トピックをサンプリング k = np.random.choice(a=np.arange(K), size=1, p=prob_z_k).item() # (カテゴリ乱数) # トピックを割当 z_d[d] = k # カウント D_k[k] += 1 N_kv[k] += N_dv[d] N_k[k] += N_d[d] # トピック分布のパラメータを更新:式(3.28) old_alpha = alpha alpha *= digamma(D_k + old_alpha).sum() - K * digamma(old_alpha) alpha /= K * digamma(D + K*old_alpha) - K * digamma(K*old_alpha) # 語彙分布のパラメータを更新:式(3.29) old_beta = beta beta *= digamma(N_kv + old_beta).sum() - K*V * digamma(old_beta) beta /= V * digamma(N_k + V*old_beta).sum() - K*V * digamma(V*old_beta) # 更新値を記録 trace_z_lt.append(z_d.astype('int').copy()) trace_Dk_lt.append(D_k.copy()) trace_Nkv_lt.append(N_kv.copy()) trace_alpha_lt.append(alpha) trace_beta_lt.append(beta) # 途中経過を表示 print(f'iteration: {i+1}, alpha = {alpha:.3f}, beta = {beta:.3f}')
iteration: 1, alpha = 1.085, beta = 1.018
iteration: 2, alpha = 1.196, beta = 1.031
iteration: 3, alpha = 1.295, beta = 1.041
iteration: 4, alpha = 1.394, beta = 1.050
iteration: 5, alpha = 1.481, beta = 1.057
(省略)
iteration: 996, alpha = 2.790, beta = 1.094
iteration: 997, alpha = 2.789, beta = 1.094
iteration: 998, alpha = 2.795, beta = 1.095
iteration: 999, alpha = 2.793, beta = 1.095
iteration: 1000, alpha = 2.792, beta = 1.094
解説はその内に書き足します…
推定結果の可視化
最後は、推定した文書データ・パラメータ・分布のグラフを作成する。
アニメーションの作図コードは「collapsed_Gibbs_sampling.py at anemptyarchive/Topic-Models-AO · GitHub」を参照のこと。
カラーマップを設定する。
# 作図用に変換 z_d = z_d.astype('int') # 配色の共通化用のカラーマップを作成 cmap = plt.get_cmap('tab10') # カラーマップの色数を設定:(カラーマップに応じて固定) color_num = 10
トピックごとに共通の配色をするために、カラーマップを指定して配色用のオブジェクト cmap を作成する。また、カラーマップで扱える色数を color_num とする。
この記事では、トピック番号 k に応じて色付けする。その際に、トピック番号を色数で割った整数部分 k % color_num を使うことで、トピック番号が色数を超える場合にカラーマップの配色がサイクルして割り当てられる。
トピックの作図
描画する文書の数を指定して、文書データとトピック集合のグラフを作成する。
# 描画する文書数を指定 #doc_num = D doc_num = 10 # グラフサイズを設定 u = 5 axis_Ndv_max = np.ceil(N_dv[:doc_num].max() /u)*u # u単位で切り上げ axis_Dk_max = np.ceil(D_k.max() /u)*u # u単位で切り上げ # サブプロットの列数を指定:(1 < 列数 < D+1) col_num = 3 row_num = np.ceil((doc_num+1) / col_num).astype('int') # 文書データを作図 fig, axes = plt.subplots(nrows=row_num, ncols=col_num, constrained_layout=True, figsize=(30, 20), dpi=100, facecolor='white') for d in range(doc_num): # サブプロットを抽出 r = d // col_num c = d % col_num ax = axes[r, c] # トピック番号を取得 k = z_d[d] # 語彙頻度を描画 ax.bar(x=np.arange(stop=V)+1, height=N_dv[d], color=cmap(k%color_num)) # 単語数 ax.set_ylim(ymin=0, ymax=axis_Ndv_max) ax.set_xlabel('vocabulary ($v$)') ax.set_ylabel('frequency ($N_{dv}$)') ax.set_title(f'iteration: {max_iter}, $d = {d+1}, k = {k+1}$', loc='left') ax.grid() # 残りのサブプロットを非表示 if c == col_num-1: # (最後の文書が右端の列の場合) r = row_num - 1 c = -1 for c in range(c+1, col_num-1): axes[r, c].axis('off') # トピックの割当を描画 ax = axes[row_num-1, col_num-1] ax.bar(x=np.arange(stop=K)+1, height=D_k, color=[cmap(k%color_num) for k in range(K)]) # 文書数 ax.set_ylim(ymin=0, ymax=axis_Dk_max) ax.set_xlabel('topic ($k$)') ax.set_ylabel('count ($D_k$)') ax.set_title(f'iteration: {max_iter}, $D = {D}$', loc='left') ax.grid() fig.supxlabel('document ($d$)') fig.supylabel('document ($d$)') fig.suptitle('document data (collapsed Gibbs sampling)', fontsize=20) plt.show()
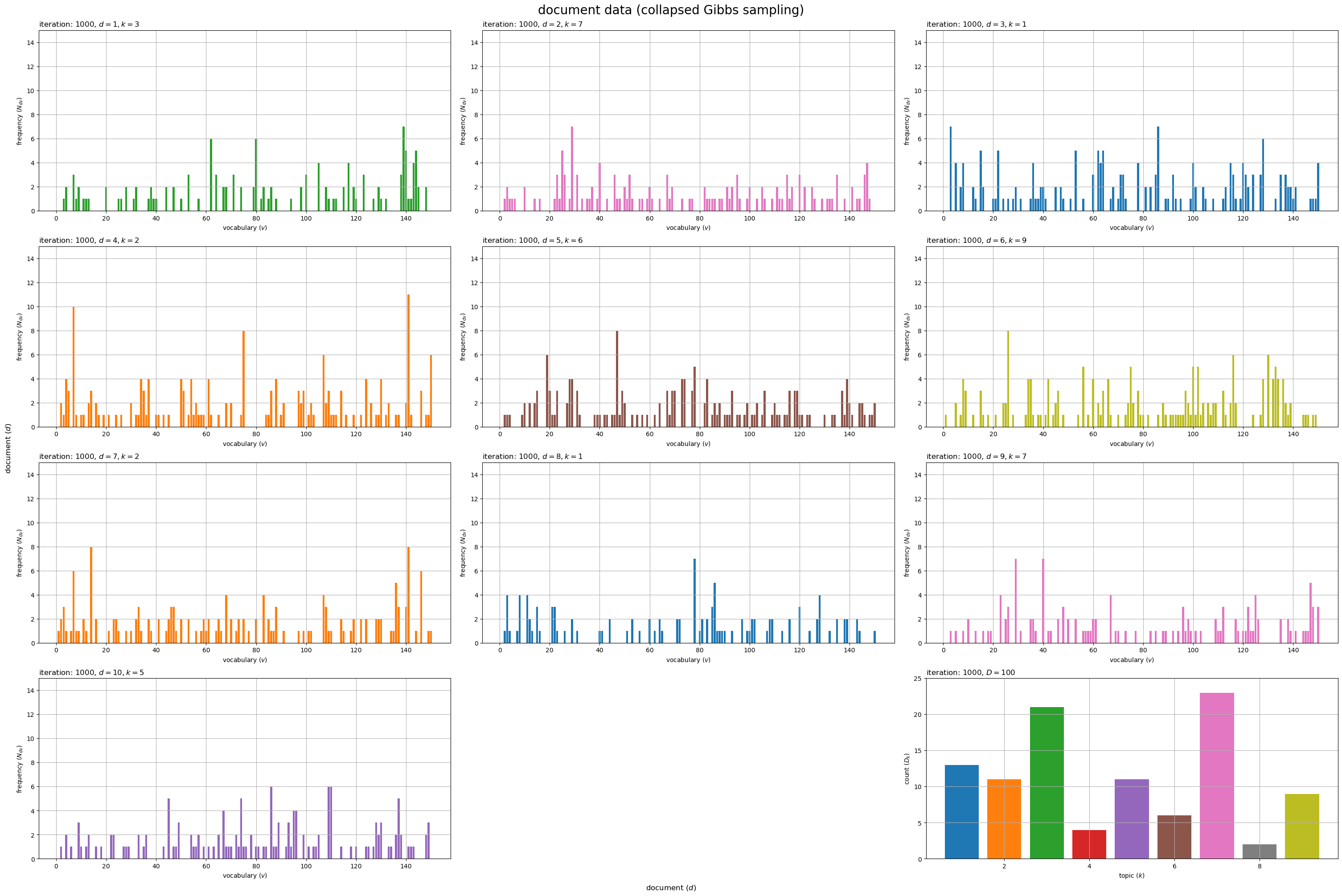
文書ごとに各語彙の出現回数 を棒グラフとして縦横に並べて描画する。各グラフは割り当てられたトピック
で色付けしている。
最後(右下)の図は、各トピックが割り当てられた文書数 を棒グラフで表している。
トピック集合の推移のアニメーションを作成する。
各文書に割り当てられたトピックの推移を確認できる。
分布の作図
トピック分布のパラメータを作成する。
# トピック分布を計算 theta_k = D_k + alpha theta_k /= theta_k.sum() # 正規化 print(theta_k.round(2)) # 0から1の値 print(theta_k.sum()) # 総和が1の値
[0.13 0.11 0.19 0.05 0.11 0.07 0.21 0.04 0.09]
1.0000000000000002
トピック分布のパラメータは、次の式で計算できる。
トピック分布のグラフを作成する。
# グラフサイズを設定 u = 0.1 axis_size = np.ceil(theta_k.max() /u)*u # u単位で切り上げ # トピック分布を作図 fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white') ax.bar(x=np.arange(stop=K)+1, height=theta_k, color=[cmap(k%color_num) for k in range(K)]) # 確率 ax.set_ylim(ymin=0, ymax=axis_size) ax.set_xlabel('topic ($k$)') ax.set_ylabel('probability ($\\theta_k$)') ax.set_title(f'iteration: {max_iter}, $\\alpha = {alpha:.2f}$', loc='left') fig.suptitle('topic distribution (collapsed Gibbs sampling)', fontsize=20) ax.grid() plt.show()
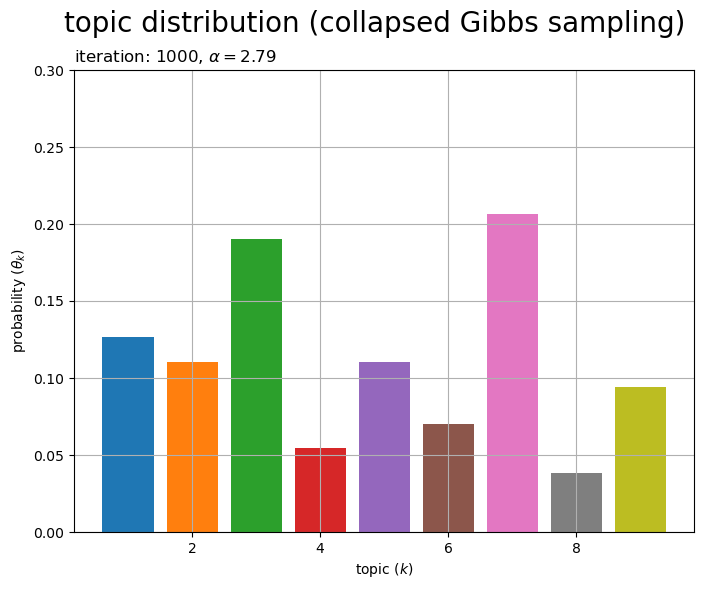
トピック分布 を棒グラフとして描画する。各トピックの割り当て確率
がバーに対応する。
各グラフの値(バーの高さ)の総和が1になる。
トピック分布の推移のアニメーションを作成する。
左図はトピック分布のハイパーパラメータ 、中図はハイパーパラメータ
と各トピックの割り当て文書数
の和(更新式の分子の値)、右図はトピック分布のパラメータ(更新式の分子を正規化した値)
である。
トピックが割り当てられた文書数の多少と割り当て確率の大小が対応するのを確認できる。
ハイパーパラメータが一様な場合、全てのトピックに一定の値を加えることで、割り当て確率が0にならないように機能している。
単語分布のパラメータを作成する。
# 語彙分布のパラメータを計算 phi_kv = N_kv + beta phi_kv /= phi_kv.sum(axis=1, keepdims=True) # 正規化 print(phi_kv.round(2)) # 0から1の値 print(phi_kv.sum(axis=1)) # 総和が1の値
[[0. 0.01 0.03 ... 0. 0.01 0.02]
[0.01 0.01 0.01 ... 0.01 0.01 0.02]
[0. 0. 0.02 ... 0.01 0. 0. ]
...
[0. 0. 0.01 ... 0.02 0. 0.02]
[0.01 0. 0. ... 0. 0. 0. ]
[0. 0. 0. ... 0.01 0. 0. ]]
[1. 1. 1. 1. 1. 1. 1. 1. 1.]
単語分布のパラメータは、次の式で計算できる。
描画するトピックの数を指定して、単語分布のグラフを作成する。
# 描画するトピック数を指定 #topic_num = K topic_num = 9 # グラフサイズを設定 u = 0.01 axis_size = np.ceil(phi_kv[:topic_num].max() /u)*u # u単位で切り上げ # サブプロットの列数を指定:(1 < 列数 < K) col_num = 3 row_num = np.ceil(topic_num / col_num).astype('int') # 語彙分布を作図 fig, axes = plt.subplots(nrows=row_num, ncols=col_num, constrained_layout=True, figsize=(30, 15), dpi=100, facecolor='white') for k in range(topic_num): # サブプロットを抽出 r = k // col_num c = k % col_num ax = axes[r, c] # 語彙分布を描画 ax.bar(x=np.arange(stop=V)+1, height=phi_kv[k], color=cmap(k%color_num)) # 確率 ax.set_ylim(ymin=0, ymax=axis_size) ax.set_xlabel('vocabulary ($v$)') ax.set_ylabel('probability ($\phi_{kv}$)') ax.set_title(f'iteration: {max_iter}, $k = {k+1}, \\beta = {beta:.2f}$', loc='left') ax.grid() # 残りのサブプロットを非表示 for c in range(c+1, col_num): axes[r, c].axis('off') fig.supxlabel('topic ($k$)') fig.supylabel('topic ($k$)') fig.suptitle('word distribution (collapsed Gibbs sampling)', fontsize=20) plt.show()
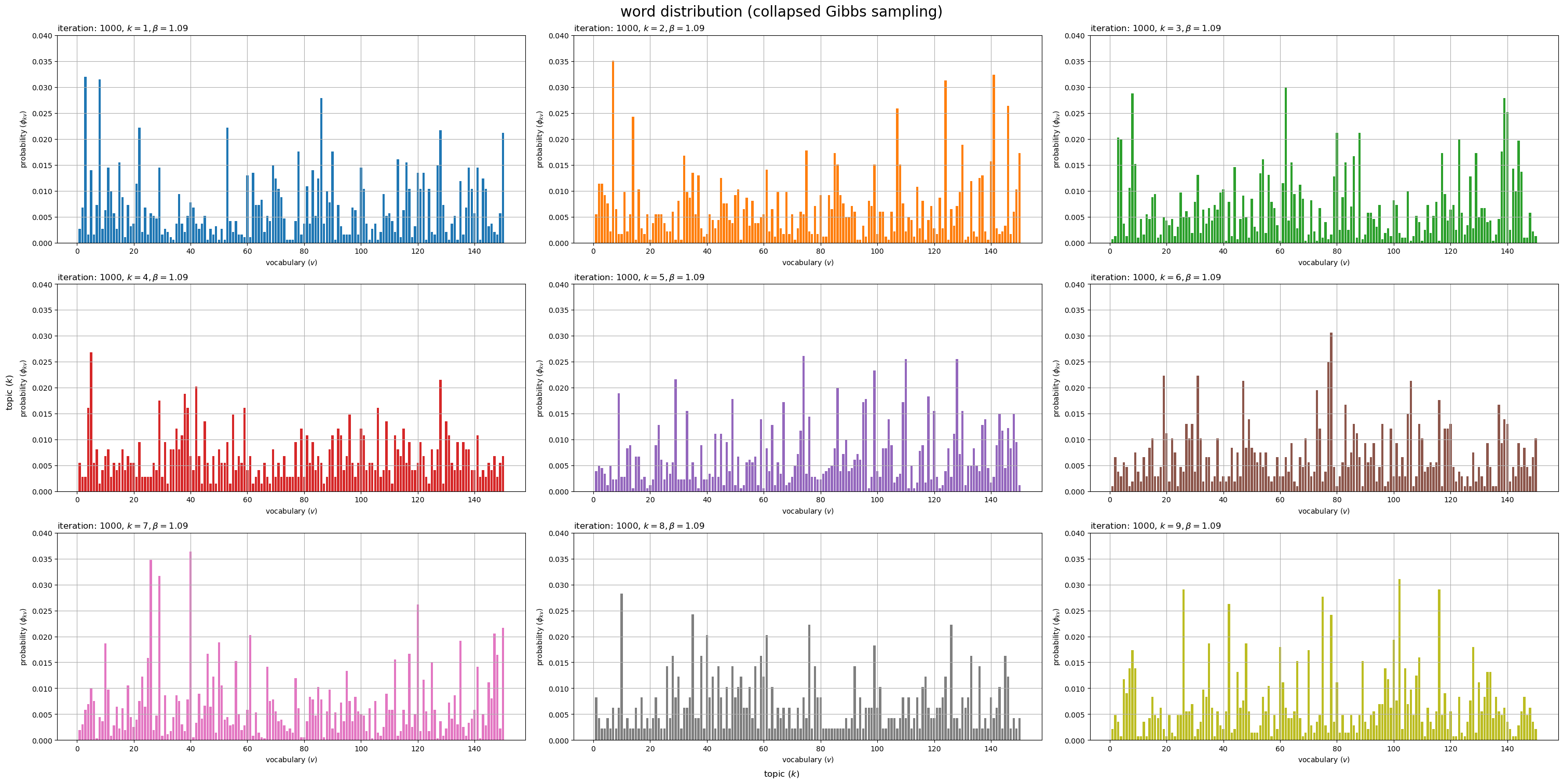
トピックごとの単語分布(語彙分布) をそれぞれ棒グラフとして縦横に並べて描画する。各トピックにおける各語彙の出現確率
がバーに対応する。
各グラフの値(バーの高さ)の総和が1になる。
単語分布の推移のアニメーションを作成する。
左上図は単語分布のハイパーパラメータ 、左側図はハイパーパラメータ
と各トピックの割り当て単語数
の和(更新式の分子の値)、右側図は単語分布のパラメータ(更新式の分子を正規化した値)
である。
トピックが割り当てられた単語数の多少と語彙の割り当て確率の大小が対応するのを確認できる。
ハイパーパラメータが一様な場合、全ての語彙に一定の値を加えることで、割り当て確率が0にならないように機能している。
パラメータの作図
トピック分布のハイパーパラメータの推移のグラフを作成する。
# 配列に変換 trace_alpha_i = np.array(trace_alpha_lt) # グラフサイズを設定 u = 5 axis_size = np.ceil(trace_alpha_i.max() /u)*u # u単位で切り上げ # ハイパーパラメータの推移を作図 fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white') ax.plot(np.arange(max_iter+1), trace_alpha_i) # 更新値 ax.set_ylim(ymin=0, ymax=axis_size) ax.set_xlabel('iteration') ax.set_ylabel('value ($\\alpha$)') fig.suptitle('hyperparameter of topic distribution (collapsed Gibbs sampling)', fontsize=20) ax.grid() plt.show()
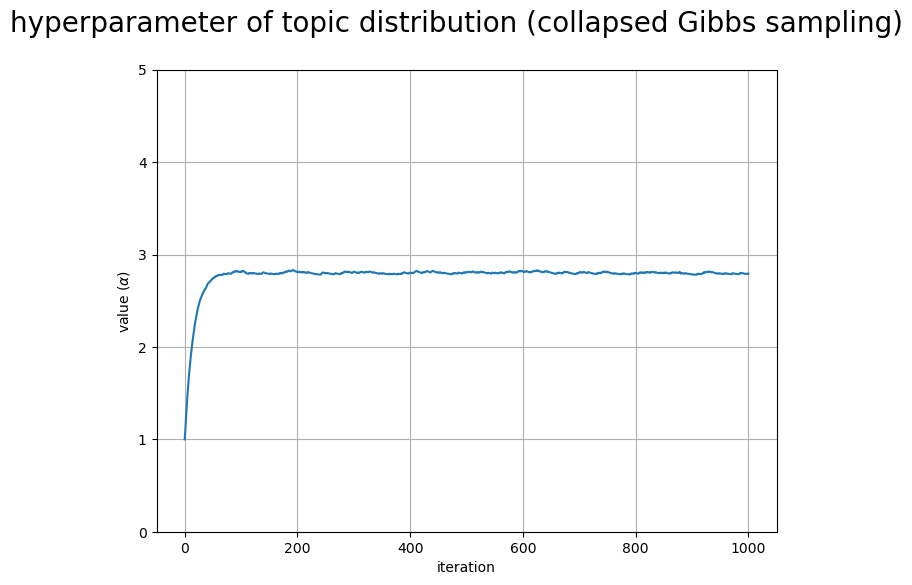
回目の更新値
の推移を折れ線グラフで示す。
単語分布のハイパーパラメータの推移のグラフを作成する。
# 配列に変換 trace_beta_i = np.array(trace_beta_lt) # グラフサイズを設定 u = 2 axis_size = np.ceil(trace_beta_i.max() /u)*u # u単位で切り上げ # ハイパーパラメータの推移を作図 fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white') ax.plot(np.arange(max_iter+1), trace_beta_i) # 更新値 ax.set_xlabel('iteration') ax.set_ylabel('value ($\\beta$)') fig.suptitle('hyperparameter of word distribution (collapsed Gibbs sampling)', fontsize=20) ax.set_ylim(ymin=0, ymax=axis_size) ax.grid() plt.show()
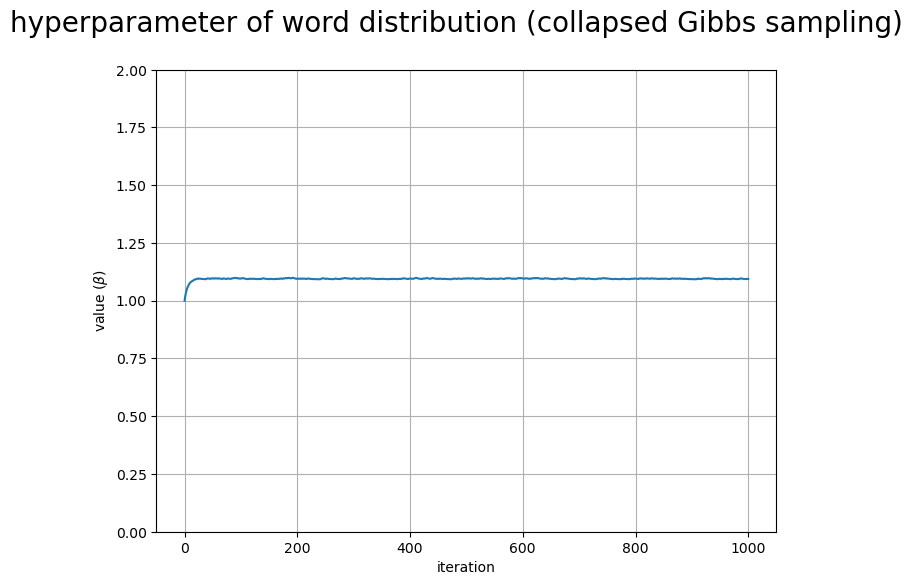
回目の更新値
の推移を折れ線グラフで示す。
トピック分布のパラメータの推移のグラフを作成する。
# 配列に変換 trace_theta_ik = np.array(trace_Dk_lt) trace_theta_ik += np.array(trace_alpha_lt).reshape((max_iter+1, 1)) trace_theta_ik /= trace_theta_ik.sum(axis=1, keepdims=True) # 正規化 # グラフサイズを設定 u = 0.5 axis_size = np.ceil(trace_theta_ik.max() /u)*u # u単位で切り上げ # パラメータの推移を作図 fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white') ax.plot(np.arange(max_iter+1), trace_theta_ik) # 更新値 ax.set_ylim(ymin=0, ymax=axis_size) ax.set_xlabel('iteration') ax.set_ylabel('probability ($\\theta_k$)') ax.set_title(f'$K = {K}$', loc='left') fig.suptitle('parameter of topic distribution (collapsed Gibbs sampling)', fontsize=20) ax.grid() plt.show()
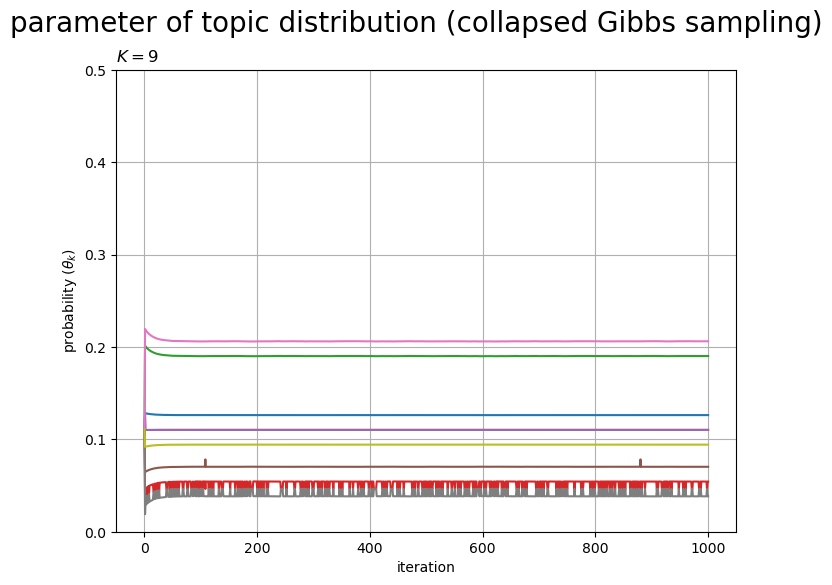
回目の
個の更新値
、
の推移を折れ線グラフで示す。
単語分布のパラメータの推移のグラフを作成する。
# 配列に変換 trace_phi_ikv = np.array(trace_Nkv_lt) trace_phi_ikv += np.array(trace_beta_lt).reshape((max_iter+1, 1, 1)) trace_phi_ikv /= trace_phi_ikv.sum(axis=2, keepdims=True) # 正規化 # 描画するトピック数を指定 #topic_num = K topic_num = 9 # グラフサイズを設定 u = 0.01 axis_size = np.ceil(trace_phi_ikv[:, :topic_num].max() /u)*u # u単位で切り上げ # サブプロットの列数を指定:(1 < 列数 < K) col_num = 3 row_num = np.ceil(topic_num / col_num).astype('int') # パラメータの推移を作図 fig, axes = plt.subplots(nrows=row_num, ncols=col_num, constrained_layout=True, figsize=(20, 15), dpi=100, facecolor='white') for k in range(topic_num): # サブプロットを抽出 r = k // col_num c = k % col_num ax = axes[r, c] # パラメータの推移を描画 ax.plot(np.arange(max_iter+1), trace_phi_ikv[:, k]) # 更新値 ax.set_ylim(ymin=0, ymax=axis_size) ax.set_xlabel('iteration') ax.set_ylabel('probability ($\\phi_{kv}$)') ax.set_title(f'$k = {k+1}, V = {V}$', loc='left') ax.grid() # 残りのサブプロットを非表示 for c in range(c+1, col_num): axes[r, c].axis('off') fig.supxlabel('topic ($k$)') fig.supylabel('topic ($k$)') fig.suptitle('parameter of word distribution (collapsed Gibbs sampling)', fontsize=20) plt.show()
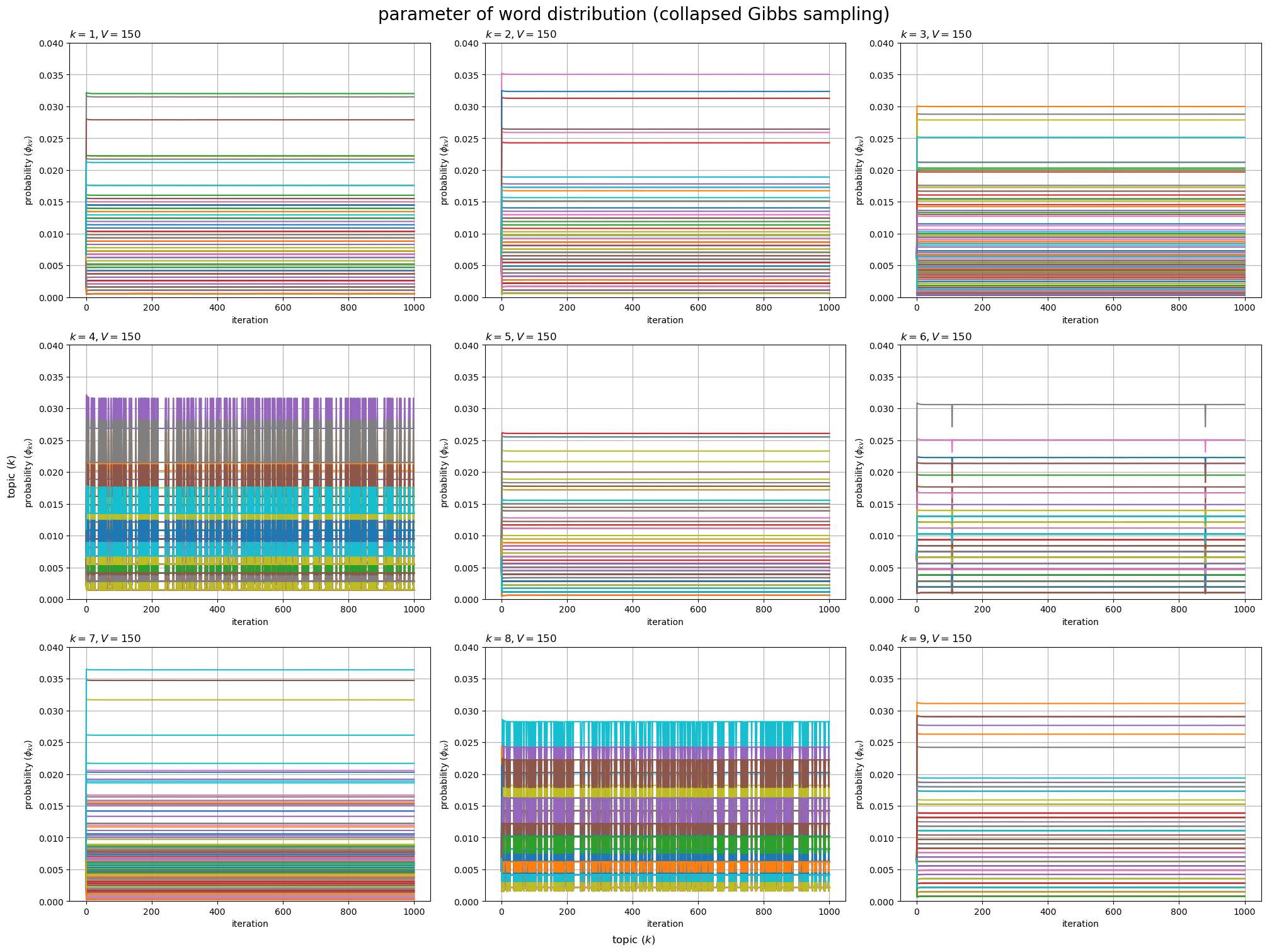
トピックごとに、 回目の更新値
個の更新値
、
の推移を折れ線グラフで示す。
ここまでの記事では、混合ユニグラムモデルに関するアルゴリズムを扱った。次からの記事では、トピックモデルを扱う。
参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
Python実装の執筆順で言うと、データ生成パートをいくつか書いていて、推論パートの1つ目の記事です。今後も本の順番通りにとはいかなそうです。
2024年4月17日は、カントリー・ガールズとJuice=Juiceの元メンバーの稲場愛香さんのソロデビュー日です!!!
デビューおめでとうございます!!!マルチな活躍が期待できる方です。皆さんよろしくお願いします。
【次節の内容】
つづく