はじめに

　調べても分からなかったので自分なりにやってみる黒魔術シリーズです。もっといい方法があれば教えてください。
　この記事は、「R言語 Advent Calendar 2023」の23日目の記事です。

　この記事では、Q-Qプロットを作成します。

【他の内容】

【目次】

はじめに
Q-Qプロットを作図したい
参考文献
おわりに

Q-Qプロットを作図したい

　サンプルと確率分布を比較する方法にQ-Qプロット(Q-Q plot・quantile-quantile plot)がある。正規分布の場合は正規Q-Qプロット(Normal Q-Q plot)とも呼ばれる。
　R言語ではベースプロットやggplot2パッケージに作図関数が用意されている。この記事では理論面の理解も兼ねて、正規Q-Qプロットをスクラッチで作図する。スクラッチと言っても、勿論ggplot2パッケージの通常の関数は使う。
　正規分布については「1次元ガウス分布の定義式 - からっぽのしょこ」を参照のこと。

　利用するパッケージを読み込む。

# 利用パッケージ
library(tidyverse)
library(gganimate)
library(patchwork)
library(magick)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージを読み込む必要はない。ただし、作図コードについてはパッケージ名を省略するので、ggplot2 を読み込む必要がある。
　また、ネイティブパイプ演算子 |> を使う。magrittr パッケージのパイプ演算子 %>% に置き換えられるが、その場合は magrittr を読み込む必要がある。

トイデータの作成

　まずは、作図に用いる正規分布の乱数(トイデータ)を作成する。

　パラメータを指定して、正規分布の乱数を作成する。

# サンプルサイズを指定
N <- 100

# 正規分布のパラメータを指定
mu    <- 10
sigma <- 5

# 正規分布の乱数を生成
sample_vec <- rnorm(n = N, mean = mu, sd = sigma)
head(sample_vec)

[1] 10.536088 13.709559 15.864429 11.126390  7.957008 16.418463

　サンプルサイズ $N$ 、平均パラメータ $\mu$ 、標準偏差パラメータ $\sigma$ を指定して、正規分布の乱数 $x_i$ を rnorm() で生成する。

・作図コード(クリックで展開)

　サンプルの描画用のデータフレームを作成する。

# サンプルを格納
sample_df <- tibble::tibble(
  i = 1:N,       # サンプル番号
  x = sample_vec # サンプル値
)
sample_df

# A tibble: 100 × 2
       i     x
   <int> <dbl>
 1     1 10.5 
 2     2 13.7 
 3     3 15.9 
 4     4 11.1 
 5     5  7.96
 6     6 16.4 
 7     7 13.7 
 8     8  8.93
 9     9 10.2 
10    10  9.15
# ℹ 90 more rows

　通し番号 $i$ とサンプル $x_i$ をデータフレームに格納する。

　生成分布の描画用のデータフレームを作成する。

# 変数の範囲を設定
axis_x_size <- (sample_df[["x"]] - mu) |> 
  abs() |> 
  max() |> 
  ceiling()

# 生成分布の確率密度を作成
theory_df <- tibble::tibble(
  x = seq(from = mu-axis_x_size, to = mu+axis_x_size, length.out = 1001), # 確率変数
  d = dnorm(x = x, mean = mu, sd = sigma) # 確率密度
)
theory_df

# A tibble: 1,001 × 2
       x       d
   <dbl>   <dbl>
 1 -4    0.00158
 2 -3.97 0.00161
 3 -3.94 0.00163
 4 -3.92 0.00166
 5 -3.89 0.00169
 6 -3.86 0.00171
 7 -3.83 0.00174
 8 -3.80 0.00177
 9 -3.78 0.00179
10 -3.75 0.00182
# ℹ 991 more rows

　生成されたサンプルの範囲の確率密度を dnorm() で計算する。

　サンプルのヒストグラムと生成分布の確率密度を重ねたグラフを作成する。

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "N == ", N, ", mu == ", mu, ", sigma == ", sigma, 
  ")"
)

# サンプルを作図
ggplot() + 
  geom_histogram(data = sample_df, 
                 mapping = aes(x = x, y = ..density..), 
                 bins = 50) + # サンプル
  geom_point(data = sample_df, 
             mapping = aes(x = x, y = -0.01), 
             size = 3, alpha = 0.1) + # サンプル
  geom_line(data = theory_df, 
            mapping = aes(x = x, y = d), 
            linewidth = 1) + # 確率密度
  labs(title = "Normal distribution: sample", 
       subtitle = parse(text = param_label), 
       x = "variable", y = "density")

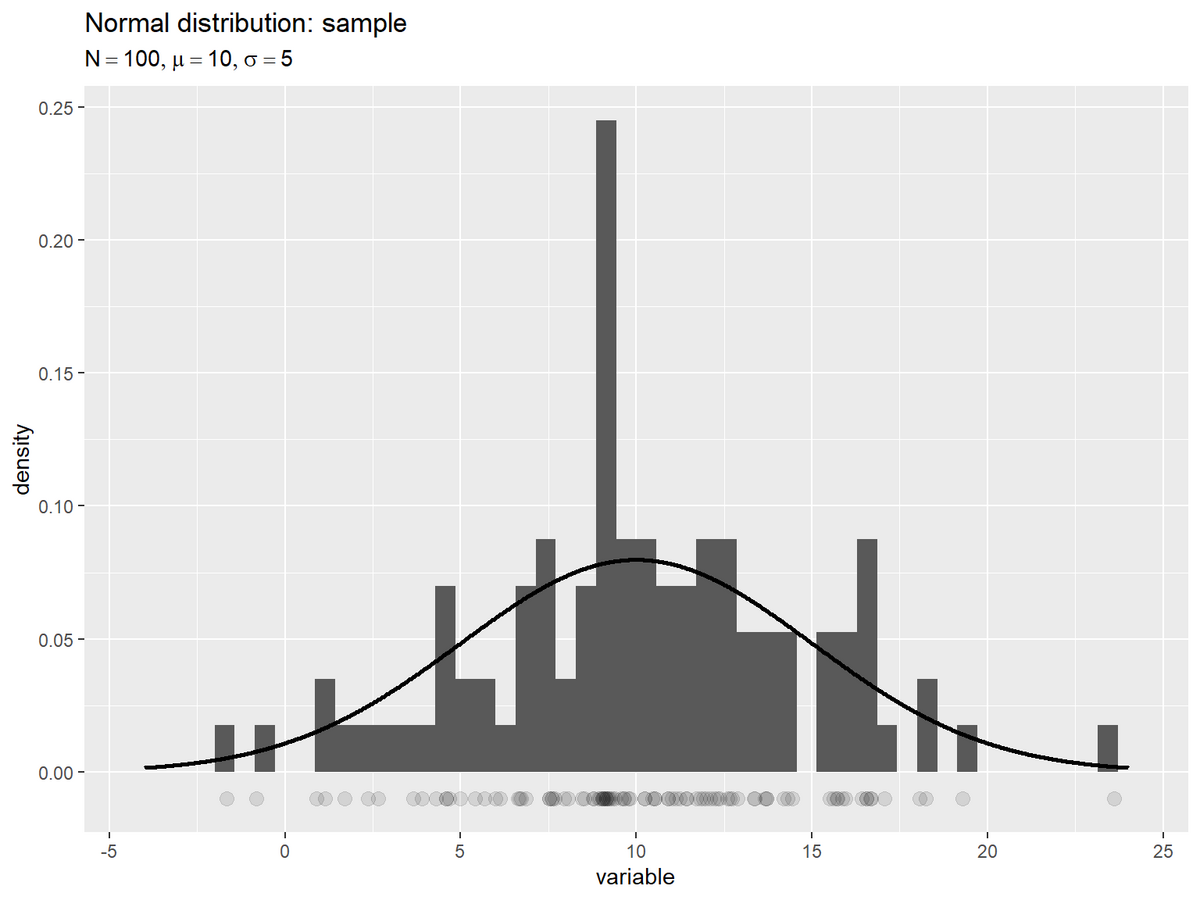
　ヒストグラムの形状が確率密度に従ってるように見えなくもないが、バーの数や幅によって形状が変わるなど、何とも言い難い。そこで、Q-Qプロットによって可視化する。

パッケージを使って作図

　続いて、組み込みまたはggplot2のQ-Qプロット作図関数を使ってグラフを作成する。

　ベースプロットの関数でQ-Qプロットを作成する。

# Q-Qプロットを作成
qqnorm(sample_vec) # サンプル値と理論値の対応点
qqline(sample_vec) # 理論値の線

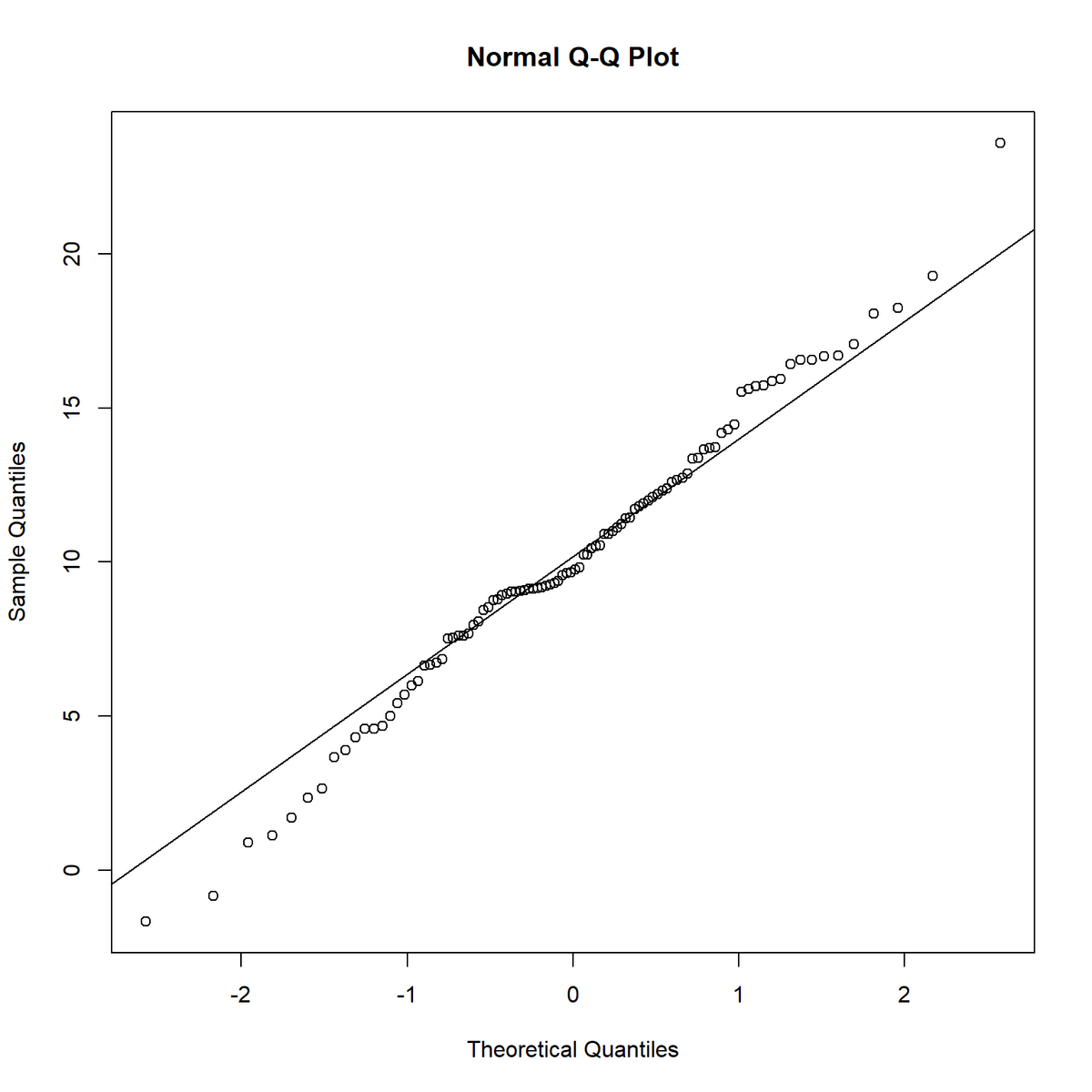
　qqnorm() で実測値と理論値の散布図、qqline() で理論値の直線を描画できる。

　ggplot2の関数でQ-Qプロットを作成する。

# サンプルを格納
sample_df <- tibble::tibble(
  x = sample_vec
)

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "N == ", N, ", mu == ", mu, ", sigma == ", sigma, 
  ")"
)

# Q-Qプロットを作成
ggplot(data = sample_df, 
       mapping = aes(sample = x)) + 
  stat_qq() + # サンプル値と理論値の対応点
  stat_qq_line(line.p = c(0.25, 0.75), fullrange = FALSE) + # 理論値の線
  labs(title = "Normal Q-Q Plot", 
       subtitle = parse(text = param_label), 
       x = "Theoretical Quantiles", 
       y = "Sample Quantiles")

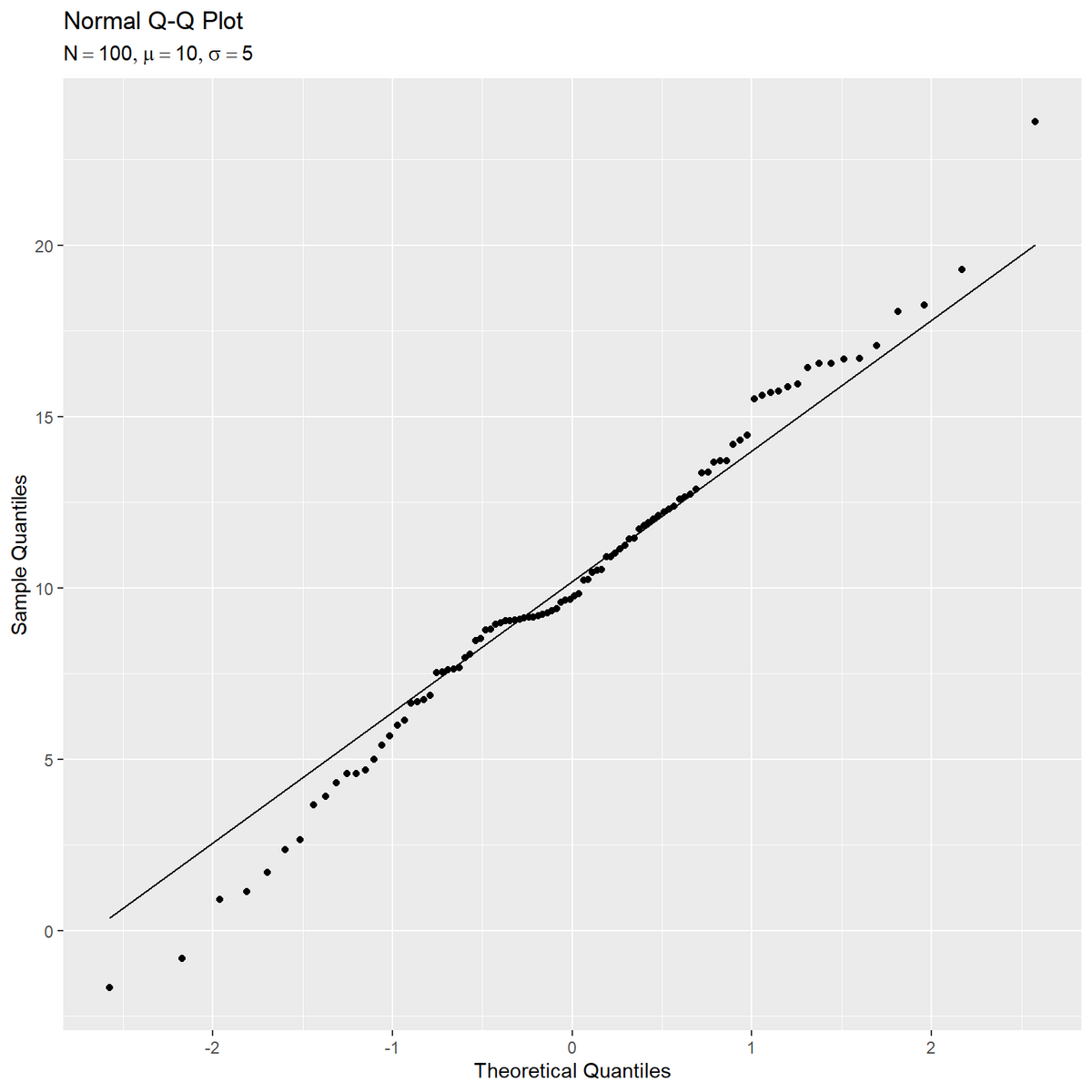
　stat_qq() で実測値と理論値の散布図、stat_qq_line() で理論値の直線を描画できる。geom_qq_band() で信頼区間を描画できるがこの記事では扱わない。

　軸などの意味については「サンプル値と理論値の変換」、作図関数や引数については「デフォルトと自作の対応」で確認する。

スクラッチで作図

　次は、専用の作図関数を使うと2行で描画できるQ-Qプロットを自作する。

　データ点の描画用のデータフレームを作成する。

# 理論値の計算用のパラメータを指定
mu_z    <- 0
sigma_z <- 1

# サンプルごとの理論値を作成
sample_df <- tibble::tibble(
  i   = 1:N, # 昇順のサンプル番号(分位番号)
  x   = sort(sample_vec), # サンプル(確率変数)
  p   = (i - 0.5) / N, # 分位番号 → パーセンタイル:(両端は0.5)
  #p   = i / (N + 1), # 分位番号 → パーセンタイル:(両端も1)
  q_x = qnorm(p = p, mean = mu, sd = sigma), # パーセンタイル → クォンタイル
  q_z = qnorm(p = p, mean = mu_z, sd = sigma_z) # パーセンタイル → クォンタイル
)
sample_df

# A tibble: 100 × 5
       i      x     p    q_x   q_z
   <int>  <dbl> <dbl>  <dbl> <dbl>
 1     1 -1.66  0.005 -2.88  -2.58
 2     2 -0.822 0.015 -0.850 -2.17
 3     3  0.906 0.025  0.200 -1.96
 4     4  1.13  0.035  0.940 -1.81
 5     5  1.70  0.045  1.52  -1.70
 6     6  2.36  0.055  2.01  -1.60
 7     7  2.66  0.065  2.43  -1.51
 8     8  3.66  0.075  2.80  -1.44
 9     9  3.91  0.085  3.14  -1.37
10    10  4.31  0.095  3.45  -1.31
# ℹ 90 more rows

　昇順に割り当てたサンプル番号を分位番号 $i = 1, \dots, N$ として、パーセンタイルを $p_i = (i - \frac{1}{2}) \frac{1}{N}$ または $p_i = \frac{i}{N + 1}$ で計算する。
　パーセンタイル(累積確率・左側確率) $p_i$ を用いて、クォンタイル(確率変数の値) $q_i$ を qnorm() で計算する。
　サンプル生成用のパラメータでもクォンタイルを計算しているが、通常は未知の値なので計算できない。

　理論値線の描画用のデータフレームを作成する。

# 理論値を作成
theory_df <- tibble::tibble(
  p   = seq(from = 0.001, to = 0.999, by = 0.001), # パーセンタイル
  q_x = qnorm(p = p, mean = mu, sd = sigma), # パーセンタイル → クォンタイル
  q_z = qnorm(p = p, mean = mu_z, sd = sigma_z) # パーセンタイル → クォンタイル
)
theory_df

# A tibble: 999 × 3
       p   q_x   q_z
   <dbl> <dbl> <dbl>
 1 0.001 -5.45 -3.09
 2 0.002 -4.39 -2.88
 3 0.003 -3.74 -2.75
 4 0.004 -3.26 -2.65
 5 0.005 -2.88 -2.58
 6 0.006 -2.56 -2.51
 7 0.007 -2.29 -2.46
 8 0.008 -2.04 -2.41
 9 0.009 -1.83 -2.37
10 0.01  -1.63 -2.33
# ℹ 989 more rows

　パーセンタイル(0から1の値)を作成して、サンプル生成用と理論値計算用のパラメータそれぞれでクォンタイルを計算する。ただし、正規分布の場合は0と1のとき発散するので除いておく。

　Q-Qプロットを作成する。

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "N == ", N, ", mu == ", mu, ", sigma == ", sigma, 
  ")"
)

# Q-Qプロットを作図
ggplot() + 
  geom_line(data = theory_df, 
            mapping = aes(x = q_z, y = q_x)) + # 理論値の線
  geom_point(data = sample_df, 
             mapping = aes(x = q_z, y = x)) + # サンプル値と理論値の対応点
  labs(title = "Normal Q-Q Plot", 
       subtitle = parse(text = param_label), 
       x = "Theoretical Quantiles", 
       y = "Sample Quantiles")

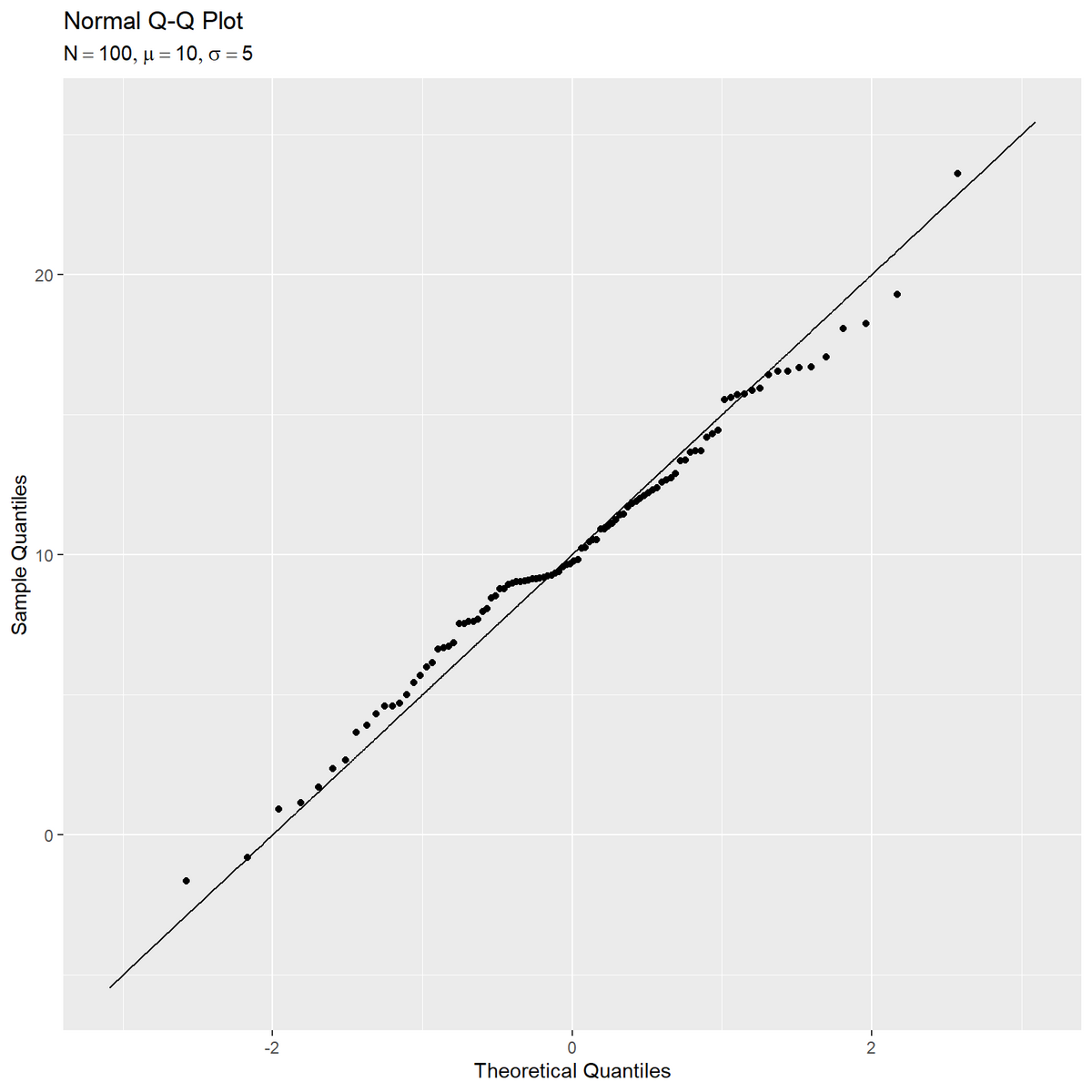
　直線の横軸は比較用の分布(理論値計算用のパラメータ)におけるクォンタイルの理論値、縦軸は生成分布(サンプル生成用のパラメータ)におけるクォンタイルの理論値である。
　散布図の横軸はクォンタイルの理論値、縦軸はクォンタイルの実測値(サンプル)である。

　または(理論値の直線上の点の座標ではなく)、理論値の直線の傾きと切片を作成する。

# 理論値線の傾き・切片を計算
a <- (sample_df[["q_x"]][N] - sample_df[["q_x"]][1]) / (sample_df[["q_z"]][N] - sample_df[["q_z"]][1])
b <- mu - a * mu_z
a; b

[1] 5
[1] 10

　サンプル生成用と理論値計算用のパラメータによるクォンタイルを $q^{(x)}_i, q^{(z)}_i$ で表すと、直線の傾きは $a = \frac{q^{(x)}_N - q^{(x)}_1}{q^{(z)}_N - q^{(z)}_1}$ で計算できる。
　生成用と計算用の平均パラメータを $\mu_x, \mu_z$ で表すと、点 $(\mu_z, \mu_z)$ は直線上の点であり $\mu_x = a \mu_z + b$ なので、直線の切片は $b = \mu_x - a \mu_z$ で計算できる。

　Q-Qプロットを作成する。

# グラフサイズを設定
axis_x_size <- (sample_df[["x"]] - mu) |> 
  abs() |> 
  max() |> 
  ceiling()
axis_z_size <- (sample_df[["q_z"]] - mu_z) |> 
  abs() |> 
  max() |> 
  ceiling()

# Q-Qプロットを作図
ggplot() + 
  geom_abline(slope = a, intercept = b) + # 理論値の線
  geom_point(data = sample_df, 
             mapping = aes(x = q_z, y = x)) + # サンプル値と理論値の対応点
  coord_cartesian(xlim = c(mu_z-axis_z_size, mu_z+axis_z_size), 
                  ylim = c(mu-axis_x_size, mu+axis_x_size)) + # 描画領域
  labs(title = "Normal Q-Q Plot", 
       subtitle = parse(text = param_label), 
       x = "Theoretical Quantiles", 
       y = "Sample Quantiles")

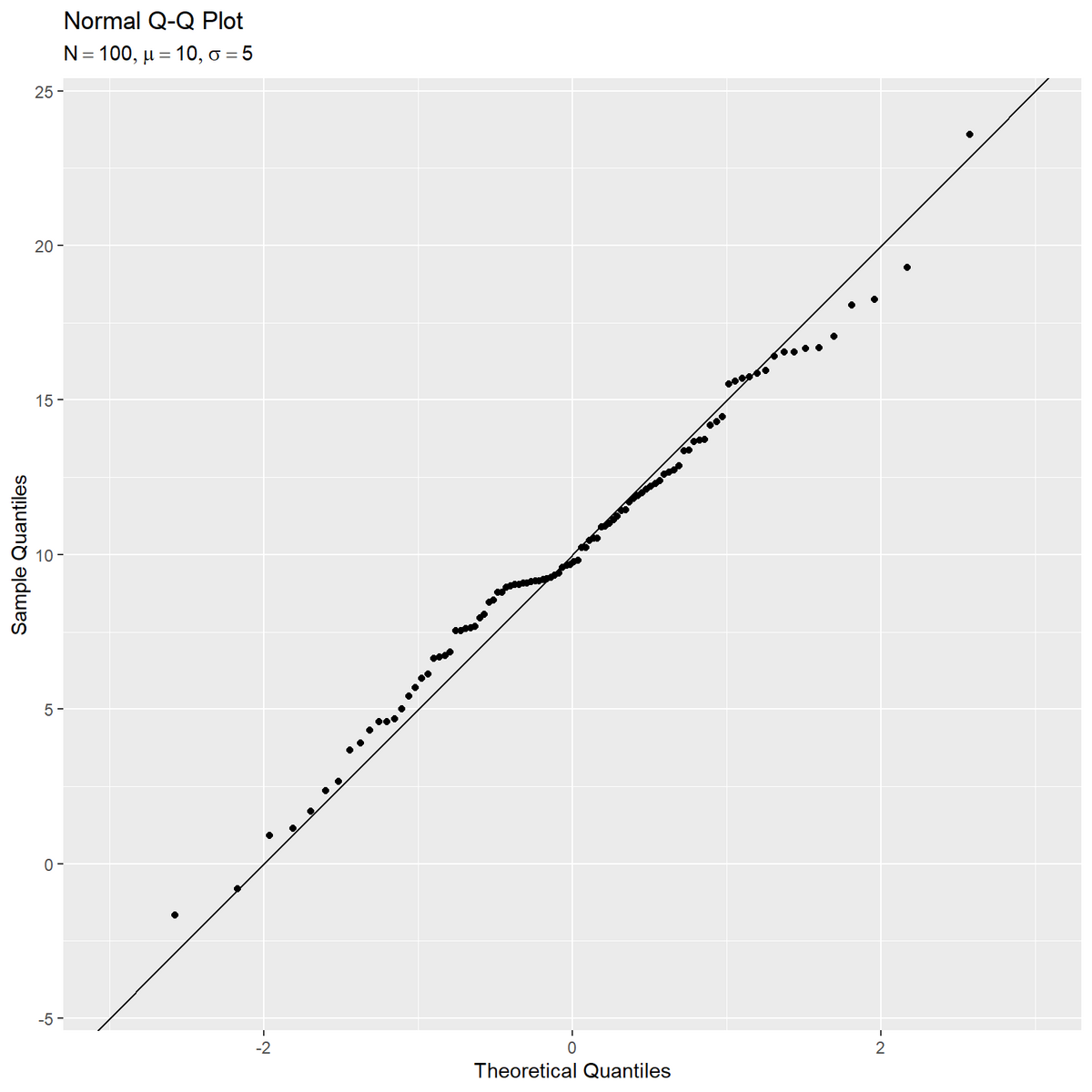
　こちらの方法だと、描画領域全体に直線を描画できる。

　全ての点が直線に近いほど理論値に近いことを意味し、サンプルが対象の分布(この例だと正規分布)に近いと考えられる。
　ただし通常は、生成分布のパラメータは未知の値なので理論値の直線は描画できない。疑似的に直線を引く方法は「理論値線の調整」で扱う。

　以上で、Q-Qプロットを作成できた。続いて、作図における理論的な過程を確認していく。

サンプル値と理論値の変換

　サンプル番号からクォンタイルの理論値への変換をグラフで確認する。

操作の確認

　x軸の値の変換で行う操作について1つずつグラフを作成する。

　サンプルを並べたグラフを作成する。

・作図コード(クリックで展開)

# サンプルを格納
sample_df <- tibble::tibble(
  i = 1:N,       # サンプル番号
  x = sample_vec # サンプル値
)

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "N == ", N, ", mu == ", mu, ", sigma == ", sigma, 
  ")"
)

# サンプルを作図
ggplot() + 
  geom_segment(data = sample_df, 
               mapping = aes(x = i, y = -Inf, xend = i, yend = x), 
               linetype = "dotted") + # 横軸の補助線
  geom_point(data = sample_df, 
             mapping = aes(x = i, y = x)) + # サンプル
  labs(title = "Normal distribution: sample", 
       subtitle = parse(text = param_label), 
       x = "sample number", y = "sample value")

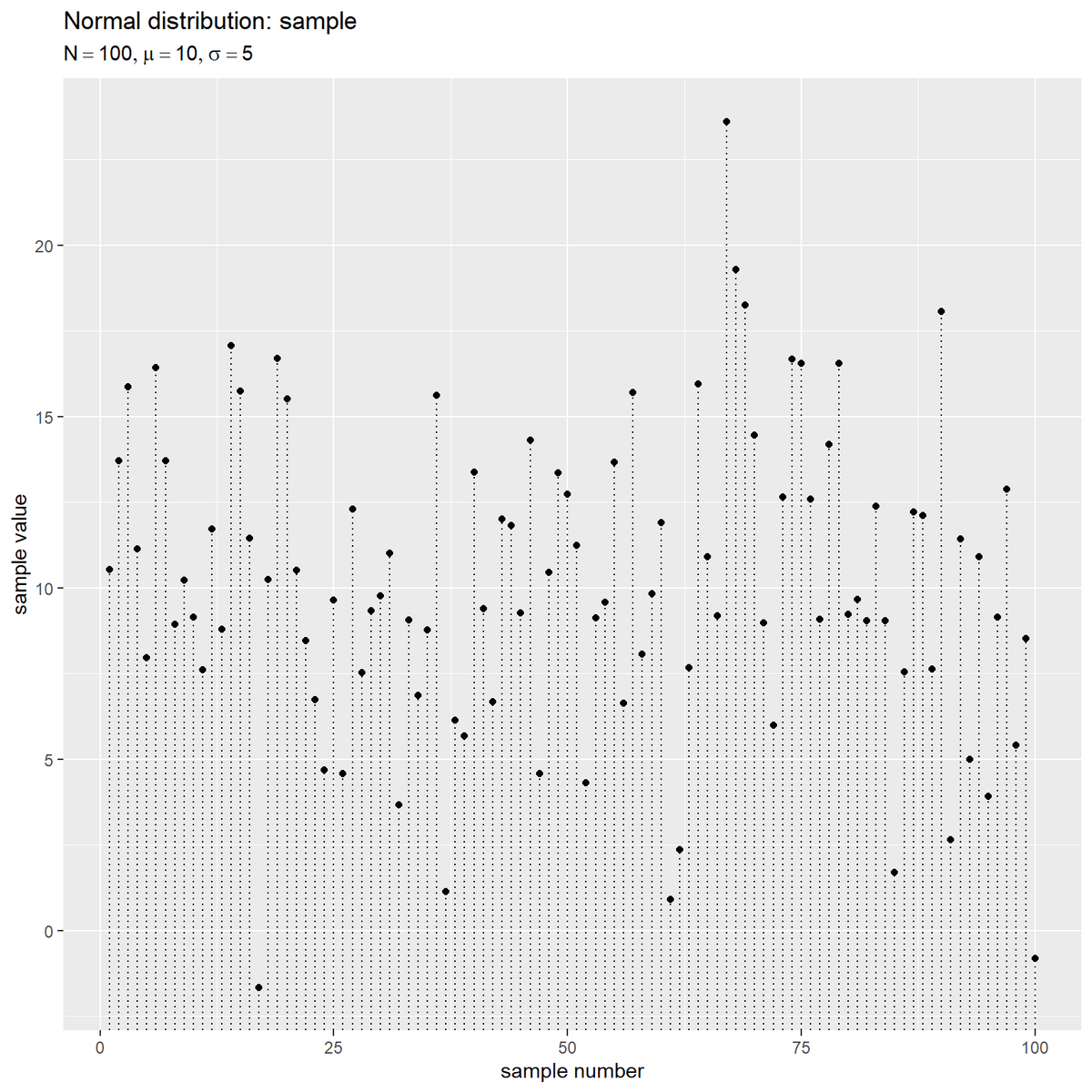
　サンプルに通し番号を割り当て、生成された順番に等間隔に点を並べる。

　サンプルを昇順に並べ替えたグラフを作成する。

・作図コード(クリックで展開)

# 理論値の計算用のパラメータを指定
mu_z    <- 0
sigma_z <- 1

# サンプルごとの理論値を作成
sample_df <- tibble::tibble(
  i   = 1:N, # 昇順のサンプル番号(分位番号)
  x   = sort(sample_vec), # サンプル(確率変数)
  p   = (i - 0.5) / N, # 分位番号 → パーセンタイル:(両端は0.5)
  #p   = i / (N + 1), # 分位番号 → パーセンタイル:(両端も1)
  q_z = qnorm(p = p, mean = mu_z, sd = sigma_z), # パーセンタイル → クォンタイル
  d_z = dnorm(x = q_z, mean = mu_z, sd = sigma_z)  # クォンタイル → 確率密度
)

# サンプルを作図
ggplot() + 
  geom_segment(data = sample_df, 
               mapping = aes(x = i, y = -Inf, xend = i, yend = x), 
               linetype = "dotted") + # 横軸の補助線
  geom_point(data = sample_df, 
             mapping = aes(x = i, y = x)) + # サンプル
  labs(title = "Normal distribution: sample", 
       subtitle = parse(text = param_label), 
       x = "sample number", 
       y = "sample value")

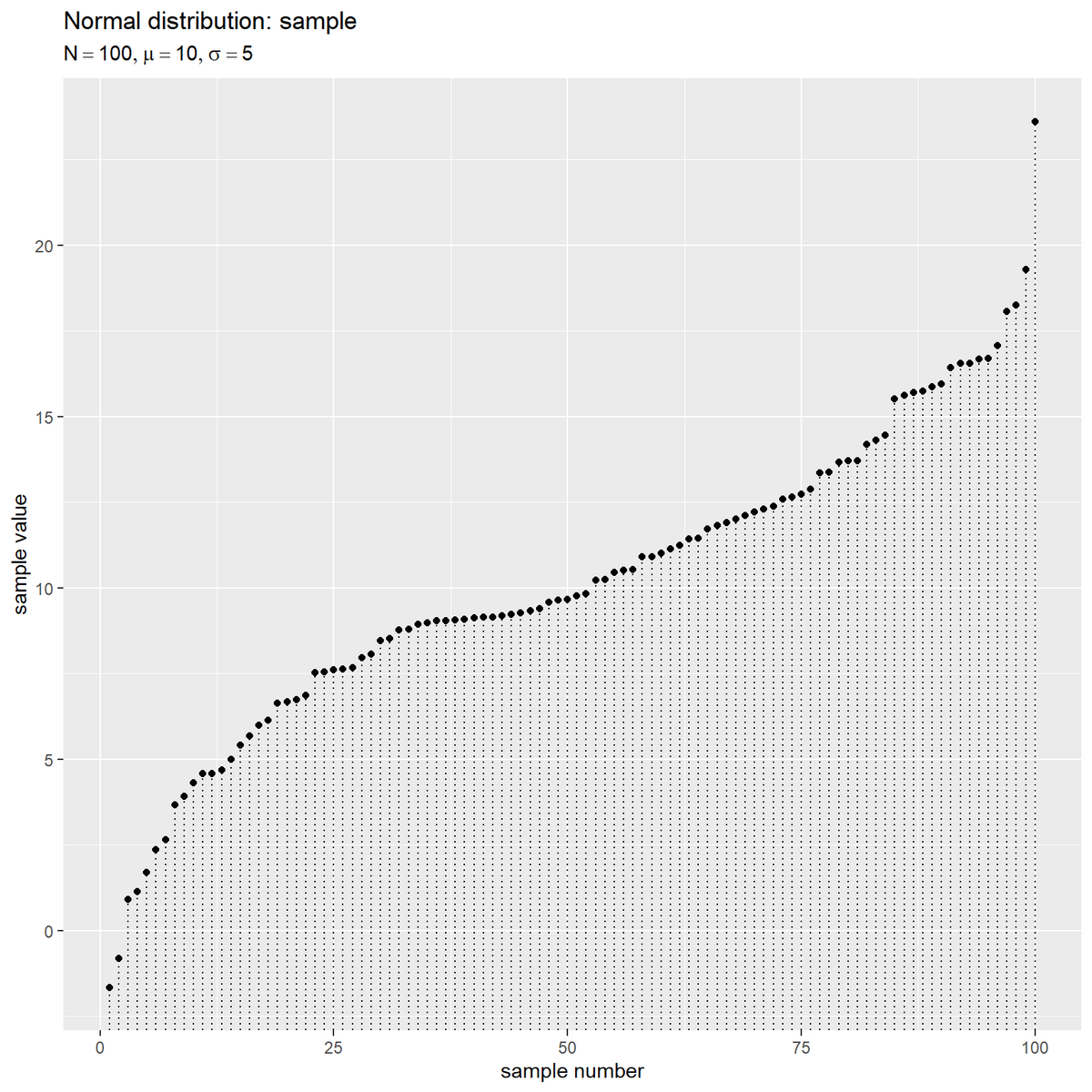
　昇順にサンプル番号を割り当て、昇順に等間隔に点を並べる。横方向に点が入れ替わっただけで、それぞれ縦方向には変化していない。
　サンプル番号 $i = 1, \dots, N$ を分位番号として扱う。

　サンプル番号をパーセンタイルに置き換えたグラフを作成する。

・作図コード(クリックで展開)

# サンプルを作図
ggplot() + 
  geom_segment(data = sample_df, 
               mapping = aes(x = p, y = -Inf, xend = p, yend = x), 
               linetype = "dotted") + # 横軸の補助線
  geom_point(data = sample_df, 
             mapping = aes(x = p, y = x)) + # サンプル
  labs(title = "Normal distribution: sample", 
       subtitle = parse(text = param_label), 
       x = "percentile", 
       y = "sample value")

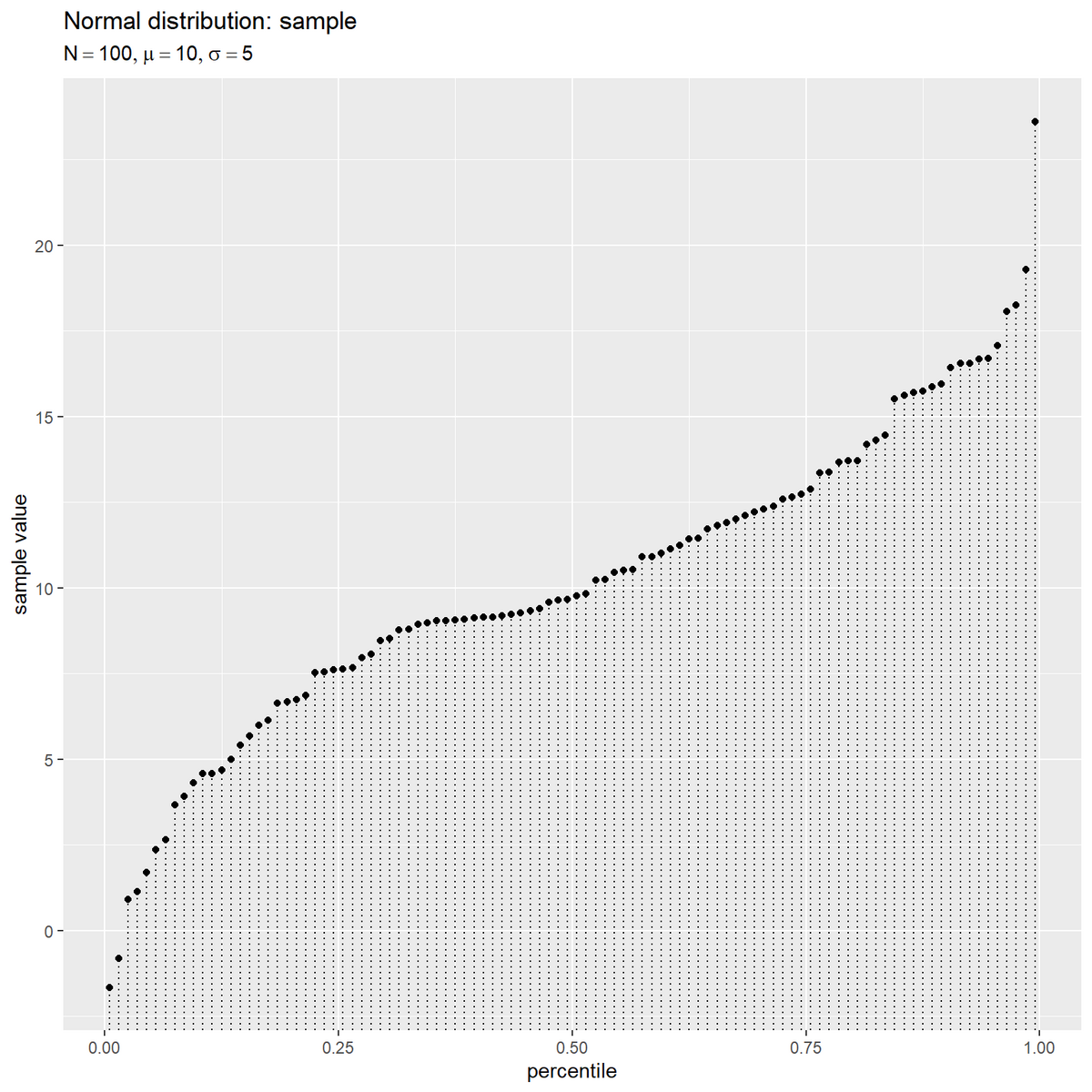
　サンプル番号に応じてパーセンタイルを割り当て、0から1の範囲で等間隔に点を並べる。
　パーセンタイルを $p_i = (i - \frac{1}{2}) \frac{1}{N}$ で計算すると、1番目の点からN番目の点の間が等間隔になり、0と1番目の点またN番目の点と1の間は他の間隔の半分になる。
　パーセンタイルを $p_i = \frac{i}{N + 1}$ で計算すると、0から1の全ての間隔が等しくなる。

　n 個のパーセンタイルを作成して、左端に 0 を右端に 1 を追加して、要素間の差を計算してみる。

# サンプルサイズを指定
n <- 4

# パーセンタイルを計算:(両端は0.5)
p_vec <- (1:n - 0.5) / n

# 差を計算
c(0, p_vec, 1); c(p_vec, 1) - c(0, p_vec)

[1] 0.000 0.125 0.375 0.625 0.875 1.000
[1] 0.125 0.250 0.250 0.250 0.125

　サンプル間の間隔が両端の間隔の倍になるのを確認できる。

# パーセンタイルを計算:(両端も1)
p_vec <- 1:n / (n + 1)

# 差を計算
c(0, p_vec, 1); c(p_vec, 1) - c(0, p_vec)

[1] 0.0 0.2 0.4 0.6 0.8 1.0
[1] 0.2 0.2 0.2 0.2 0.2

　全ての要素間の差が等しくなるのを確認できる。

　パーセンタイルをクォンタイルに置き換えたグラフを作成する。

・作図コード(クリックで展開)

# サンプルを作図
ggplot() + 
  geom_segment(data = sample_df, 
               mapping = aes(x = q_z, y = -Inf, xend = q_z, yend = x), 
               linetype = "dotted") + # 横軸の補助線
  geom_point(data = sample_df, 
             mapping = aes(x = q_z, y = x)) + # サンプル
  labs(title = "Normal distribution: sample", 
       subtitle = parse(text = param_label), 
       x = "quantile", 
       y = "sample value")

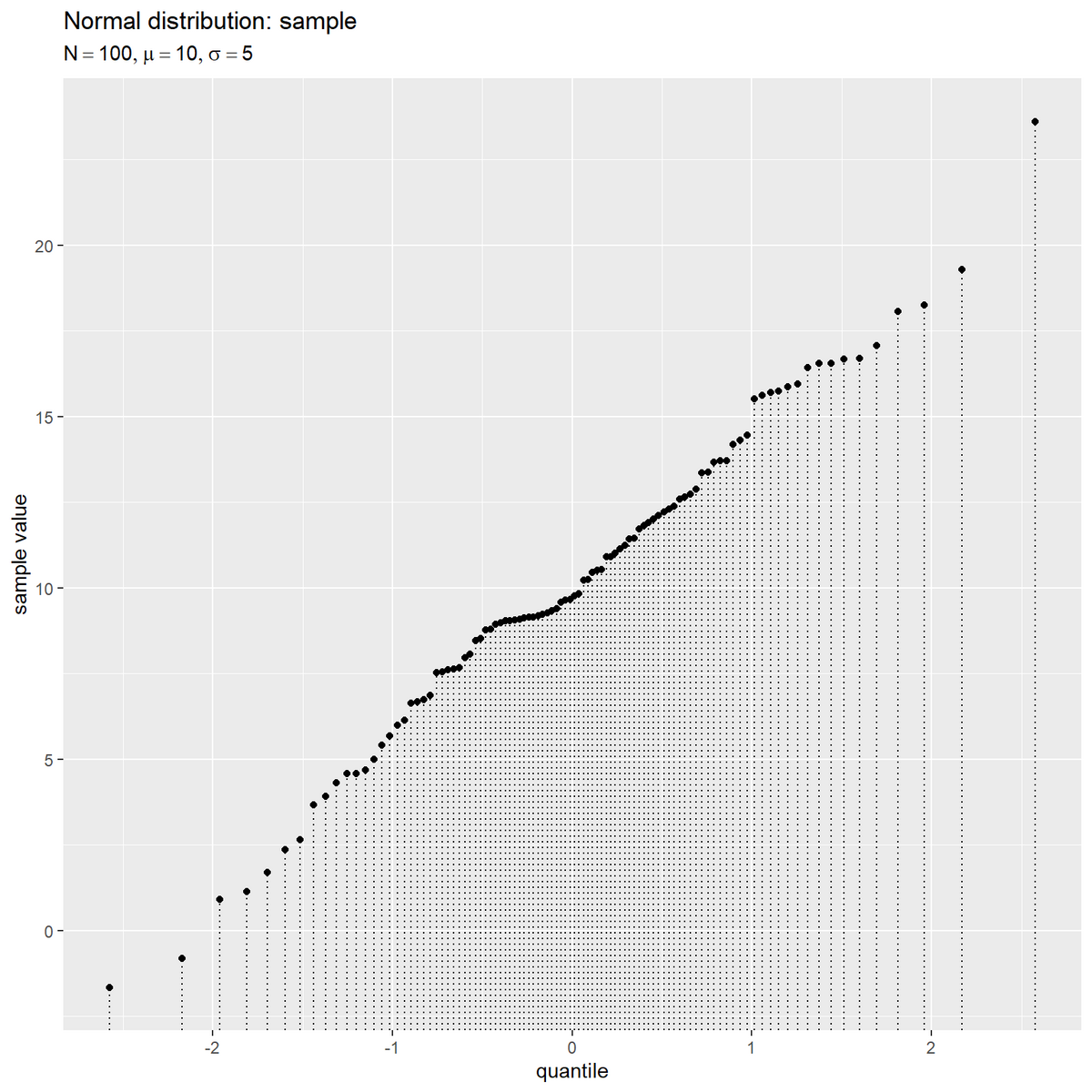
　パーセンタイルに応じてクォンタイルの理論値割り当て、点を並べる。
　横軸の値は、理論値計算用のパラメータに依存し、値自体は結果に影響しない。

　パーセンタイルとクォンタイルの変換は累積分布関数(の逆関数)に対応する。

・作図コード(クリックで展開)

# 理論値を作成
theory_df <- tibble::tibble(
  p   = seq(from = 0.001, to = 0.999, by = 0.001), # パーセンタイル
  q_z = qnorm(p = p, mean = mu_z, sd = sigma_z), # パーセンタイル → クォンタイル
  d_z = dnorm(x = q_z, mean = mu_z, sd = sigma_z) # クォンタイル → 確率密度
)

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "mu == ", mu_z, ", sigma == ", sigma_z, 
  ")"
)

# 累積分布確率を作図
ggplot() + 
  geom_segment(data = sample_df, 
               mapping = aes(x = q_z, y = -Inf, xend = q_z, yend = p), 
               linetype = "dotted") + # 横軸の補助線
  geom_segment(data = sample_df, 
               mapping = aes(x = -Inf, y = p, xend = q_z, yend = p), 
               linetype = "dotted") + # 縦軸の補助線
  geom_line(data = theory_df, 
            mapping = aes(x = q_z, y = p)) + # 累積確率
  geom_point(data = sample_df, 
             mapping = aes(x = q_z, y = p)) + # 曲線上の点
  labs(title = "Normal distribution: cumulative distribution function", 
       subtitle = parse(text = param_label), 
       x = "quantile", 
       y = "percentile")

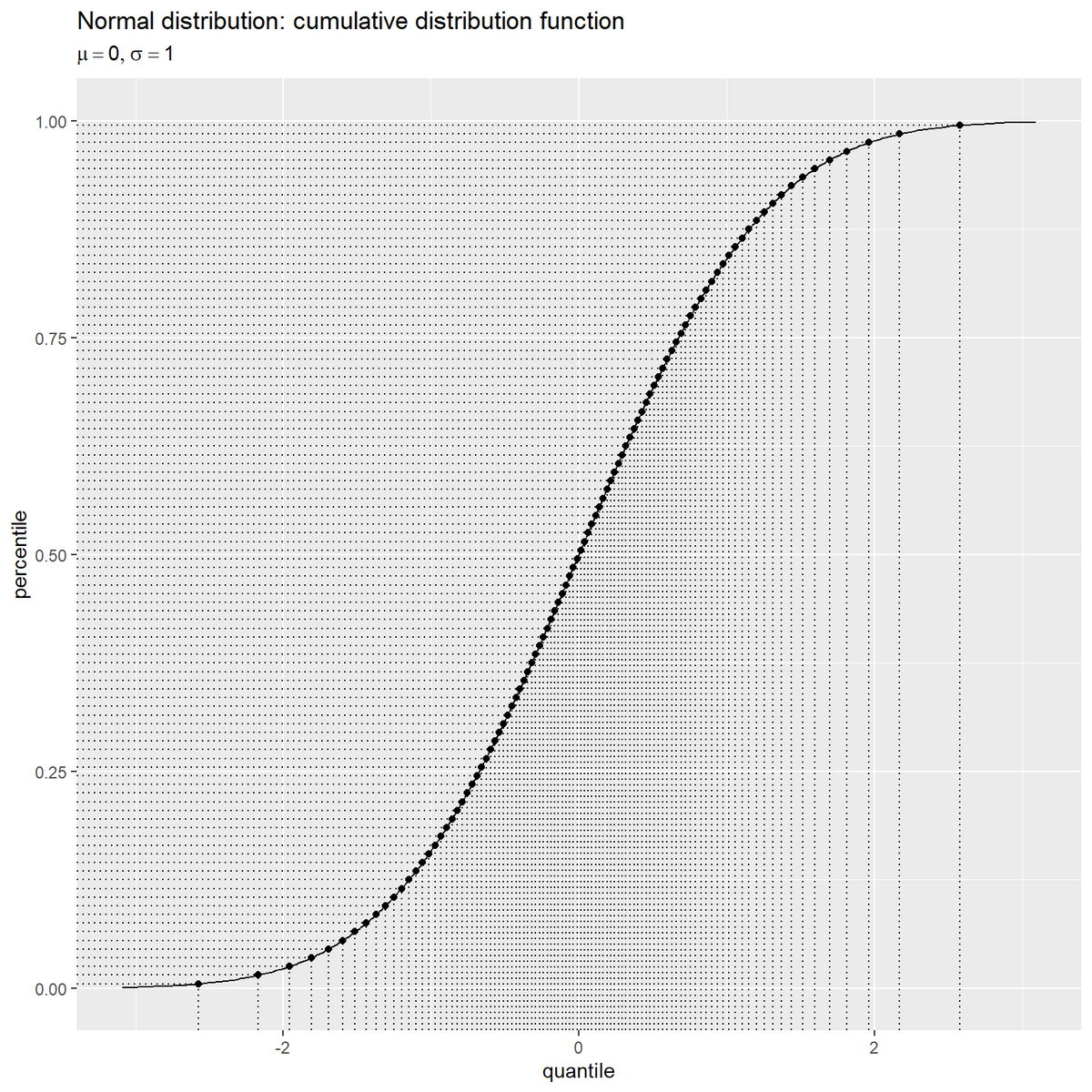
　横軸はクォンタイルで縦軸はパーセンタイル(累積確率)で、確率変数の値がクォンタイルの値以下になる確率を表す。
　等間隔のパーセンタイルが正規分布に応じた間隔に変換されるのを確認できる。
　累積分布関数については「【R】正規分布(ガウス分布)の確率密度関数と累積分布関数の関係の可視化 - からっぽのしょこ」を参照のこと。

対応の確認

　x軸の値の変換についてサンプルごとの対応を確認するアニメーションを作成する。
　作図コードについては「GitHub - anemptyarchive/Black-Magick/.../QQplot.R」を参照のこと。

　サンプル番号からクォンタイルの理論値への変換のアニメーションを作成する。

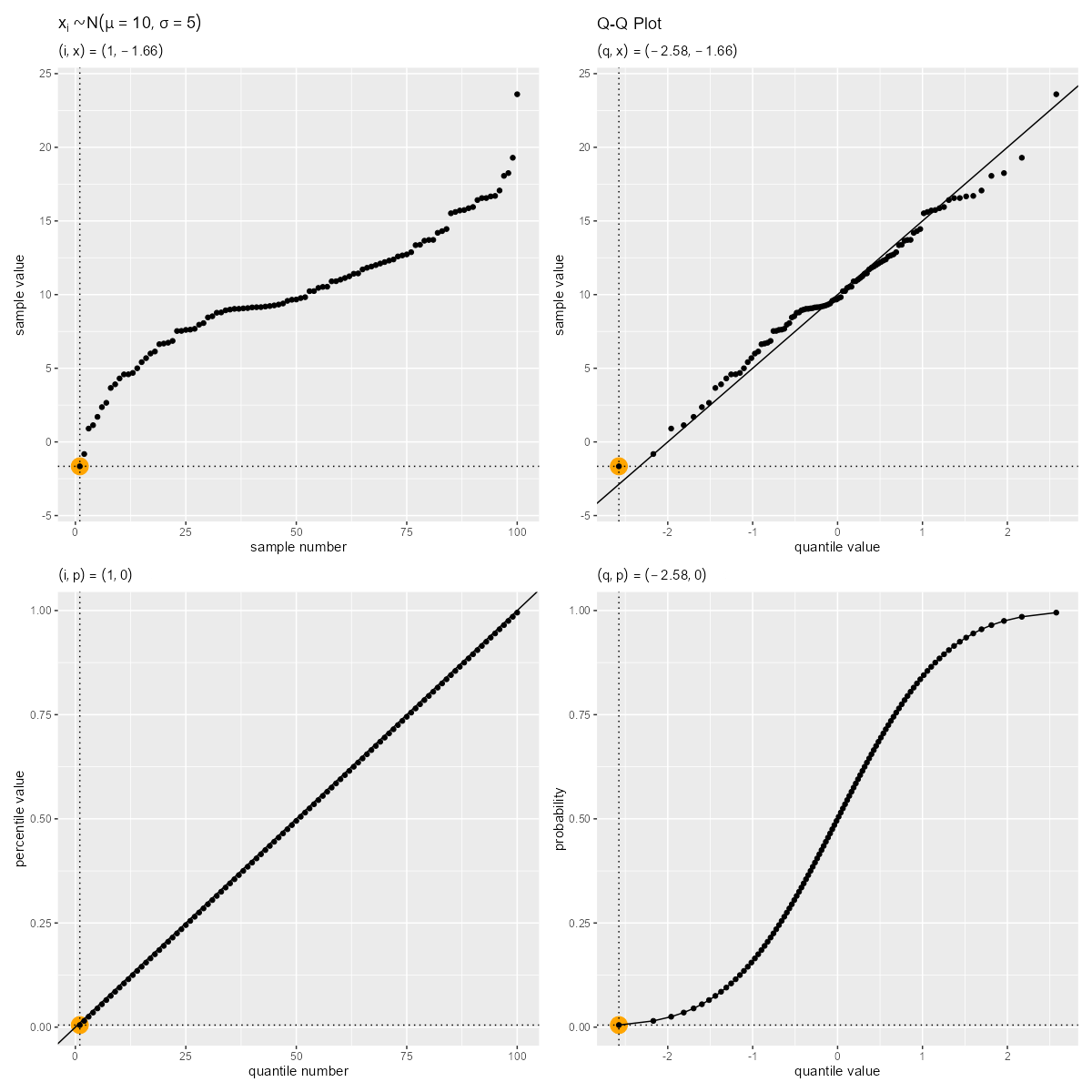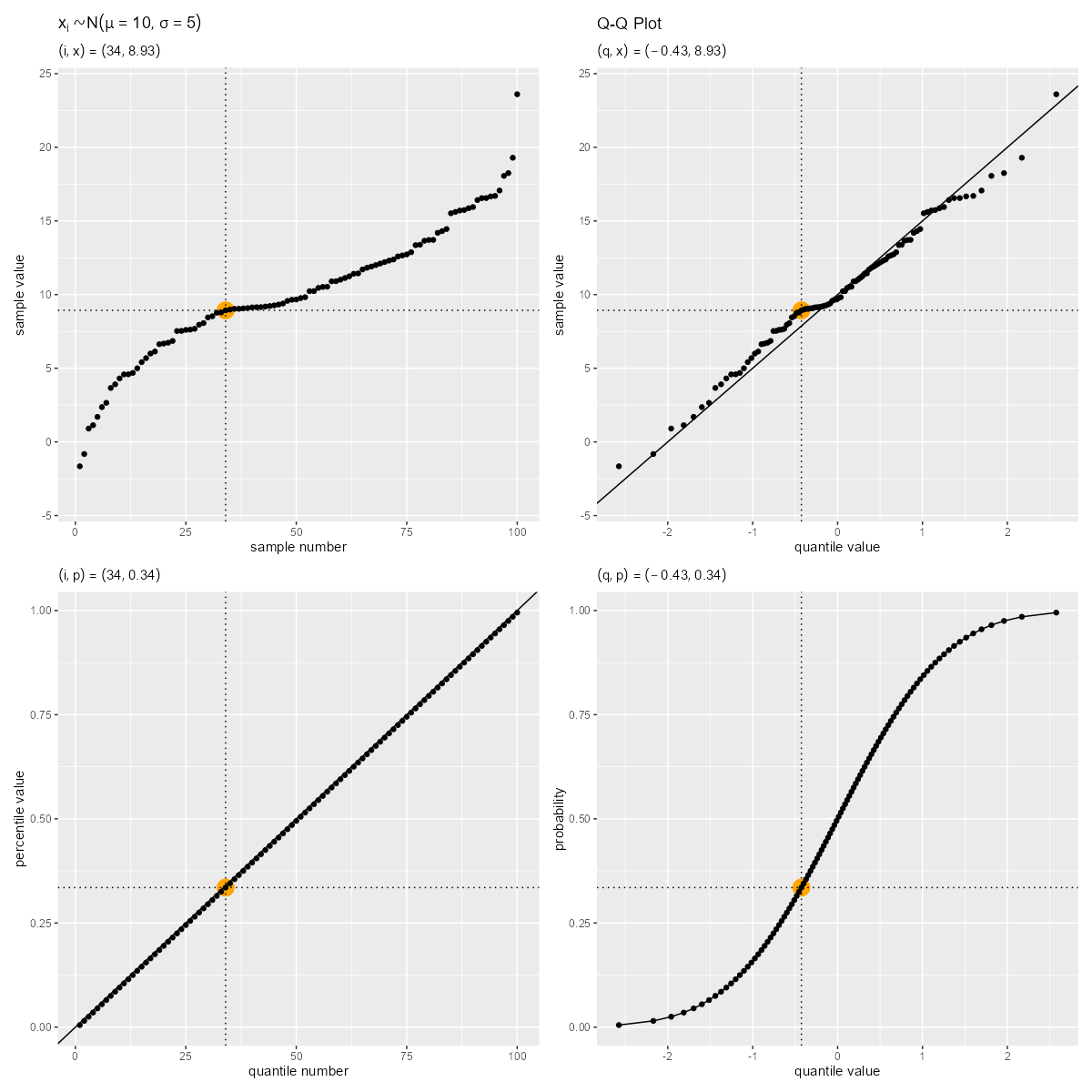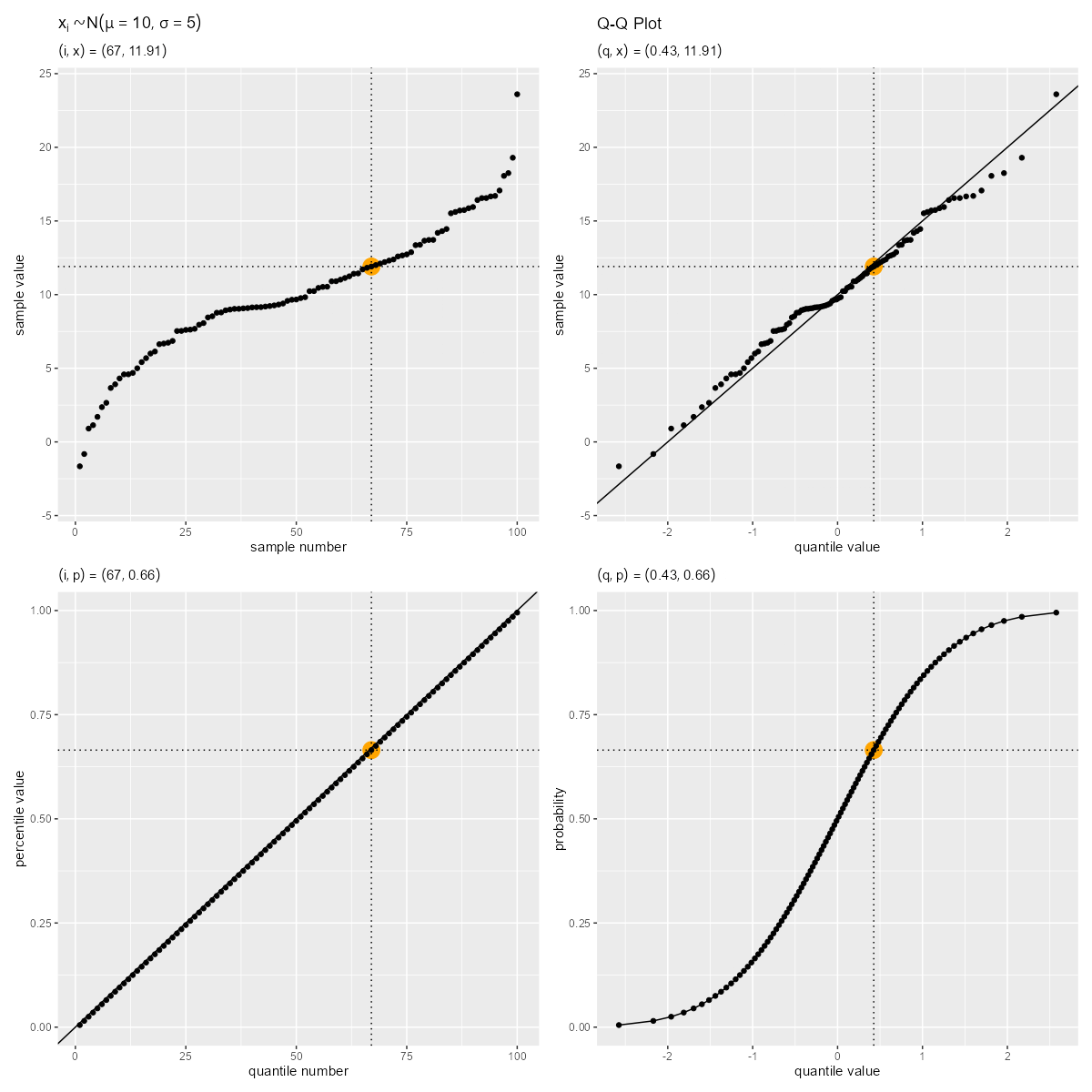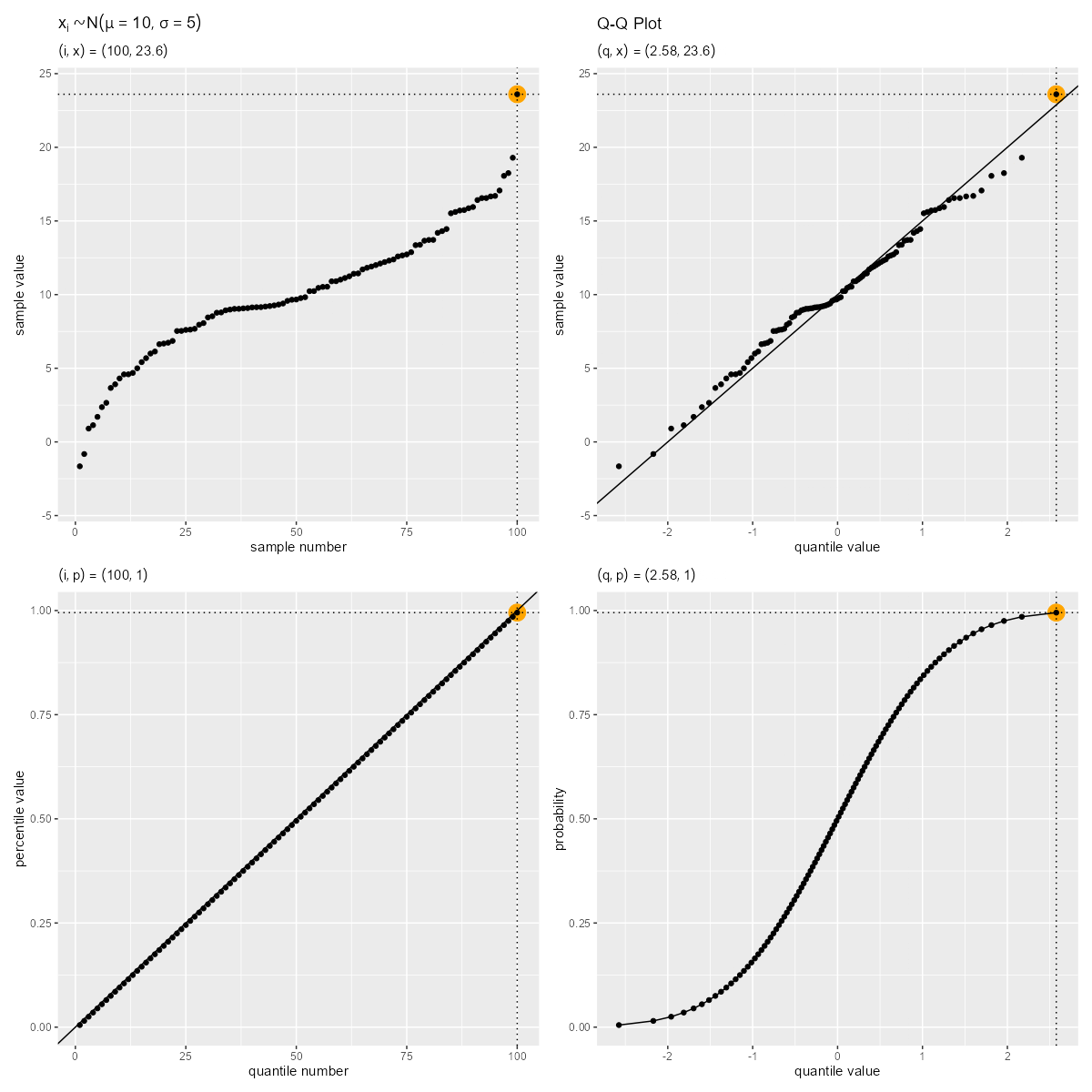
　右上の図がQ-Qプロットであり、左上の図から反時計回りに、軸の値が「サンプル番号・分位番号」→「パーセンタイル・累積確率」→「クォンタイル」に変換されているのサンプルごとに確認できる。

デフォルトと自作の対応

　自作したグラフと比較して、ggplot2のQ-Qプロット作図関数の引数の効果を確認する。

データ点の調整

　理論値の計算に関する引数について確認する。

　これまでの方法でグラフを作成する。

・作図コード(クリックで展開)

　サンプル値と理論値の描画用のデータフレームを作成する。

# 理論値の計算用のパラメータを指定
mu_z    <- 0
sigma_z <- 1

# サンプルごとの理論値を作成
sample_df <- tibble::tibble(
  i   = 1:N, # 昇順のサンプル番号(分位番号)
  x   = sort(sample_vec), # サンプル(確率変数)
  p   = (i - 0.5) / N, # 分位番号 → パーセンタイル:(両端は0.5)
  #p   = i / (N + 1), # 分位番号 → パーセンタイル:(両端も1)
  q_x = qnorm(p = p, mean = mu, sd = sigma), # パーセンタイル → クォンタイル
  q_z = qnorm(p = p, mean = mu_z, sd = sigma_z) # パーセンタイル → クォンタイル
)
sample_df

# A tibble: 100 × 5
       i      x     p    q_x   q_z
   <int>  <dbl> <dbl>  <dbl> <dbl>
 1     1 -1.66  0.005 -2.88  -2.58
 2     2 -0.822 0.015 -0.850 -2.17
 3     3  0.906 0.025  0.200 -1.96
 4     4  1.13  0.035  0.940 -1.81
 5     5  1.70  0.045  1.52  -1.70
 6     6  2.36  0.055  2.01  -1.60
 7     7  2.66  0.065  2.43  -1.51
 8     8  3.66  0.075  2.80  -1.44
 9     9  3.91  0.085  3.14  -1.37
10    10  4.31  0.095  3.45  -1.31
# ℹ 90 more rows

　「スクラッチで作図」のときのコードで、サンプル生成用と理論値計算用のパラメータそれぞれでクォンタイルを計算する。

　Q-Qプロットを作成する。

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "mu[x] == ", mu, ", sigma[x] == ", sigma, ", ", 
  "mu[z] == ", mu_z, ", sigma[z] == ", sigma_z, 
  ")"
)

# Q-Qプロットを作図
ggplot() + 
  stat_qq_line(data = sample_df, 
               mapping = aes(sample = x), 
               line.p = c(0.25, 0.75), fullrange = FALSE, 
               color = "blue", linewidth = 1) + # 理論値の線
  geom_line(data = sample_df, 
            mapping = aes(x = q_z, y = q_x), 
            color = "red", linewidth = 1) + # 理論値の線
  stat_qq(data = sample_df, 
          mapping = aes(sample = x, color = "stat_qq"), 
          size = 6) + # サンプル値と理論値の対応点
  geom_point(data = sample_df, 
             mapping = aes(x = q_z, y = x, color = "geom_point"), 
             size = 3) + # サンプル値と理論値の対応点
  scale_color_manual(breaks = c("stat_qq", "geom_point"), 
                     values = c("blue", "red"), 
                     name = "function") + # 凡例表示用
  labs(title = "Normal Q-Q Plot", 
       subtitle = parse(text = param_label), 
       x = "Theoretical Quantiles (z)", 
       y = "Sample Quantiles (x)")

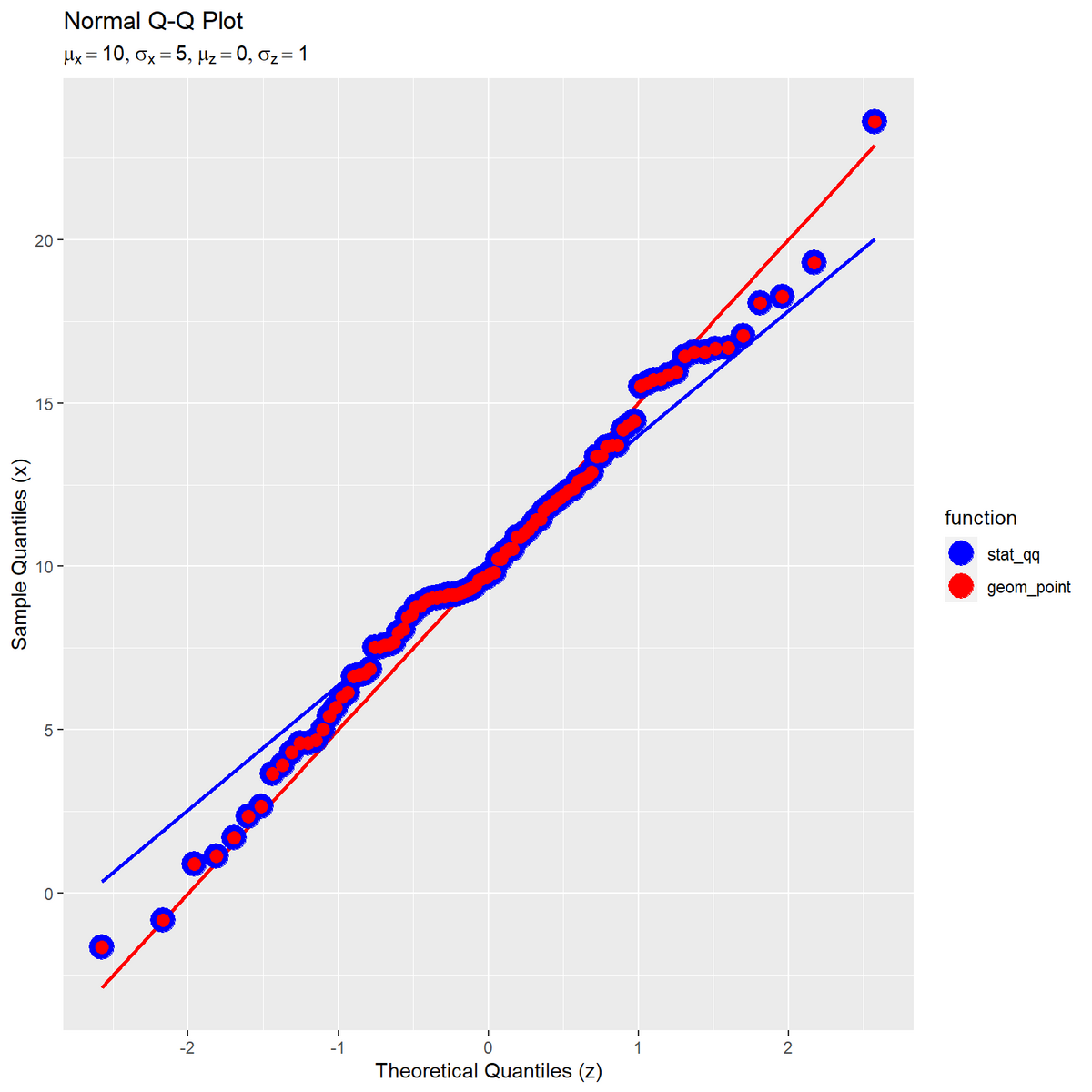
　ggplot2のQ-Qプロット用の関数を用いた点と一致した。直線は(基本的に)一致しない。

　続いて、生成用のパラメータを用いて両軸の理論値を計算しグラフを作成する。

・作図コード(クリックで展開)

　サンプル値と理論値の描画用のデータフレームを作成する。

# サンプルごとの理論値を作成
sample_df <- tibble::tibble(
  i = 1:N, # 昇順のサンプル番号(分位番号)
  x = sort(sample_vec), # サンプル(確率変数)
  p = (i - 0.5) / N, # 分位番号 → パーセンタイル:(両端は0.5)
  #p = i / (N + 1), # 分位番号 → パーセンタイル:(両端も1)
  q = qnorm(p = p, mean = mu, sd = sigma) # パーセンタイル → クォンタイル
)
sample_df

# A tibble: 100 × 4
       i      x     p      q
   <int>  <dbl> <dbl>  <dbl>
 1     1 -1.66  0.005 -2.88 
 2     2 -0.822 0.015 -0.850
 3     3  0.906 0.025  0.200
 4     4  1.13  0.035  0.940
 5     5  1.70  0.045  1.52 
 6     6  2.36  0.055  2.01 
 7     7  2.66  0.065  2.43 
 8     8  3.66  0.075  2.80 
 9     9  3.91  0.085  3.14 
10    10  4.31  0.095  3.45 
# ℹ 90 more rows

　これまでと同様にして、クォンタイルを計算する。

　Q-Qプロットを作成する。

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "mu == ", mu, ", sigma == ", sigma, 
  ")"
)

# Q-Qプロットを作図
ggplot() + 
  stat_qq_line(data = sample_df, 
               mapping = aes(sample = x), 
               distribution = qnorm, dparams = list(mean = mu, sd = sigma), 
               line.p = c(0.25, 0.75), fullrange = FALSE, 
               color = "blue", linewidth = 1) + # 理論値の線
  geom_line(data = sample_df, 
            mapping = aes(x = q, y = q), 
            color = "red", linewidth = 1) + # 理論値の線
  stat_qq(data = sample_df, 
          mapping = aes(sample = x, color = "stat_qq"), 
          distribution = qnorm, dparams = list(mean = mu, sd = sigma), 
          size = 6) + # サンプル値と理論値の対応点
  geom_point(data = sample_df, 
             mapping = aes(x = q, y = x, color = "geom_point"), 
             size = 3) + # サンプル値と理論値の対応点
  scale_color_manual(breaks = c("stat_qq", "geom_point"), 
                     values = c("blue", "red"), 
                     name = "function") + # 凡例表示用
  coord_fixed(ratio = 1) + 
  labs(title = "Normal Q-Q Plot", 
       subtitle = parse(text = param_label), 
       x = "Theoretical Quantiles", 
       y = "Sample Quantiles")

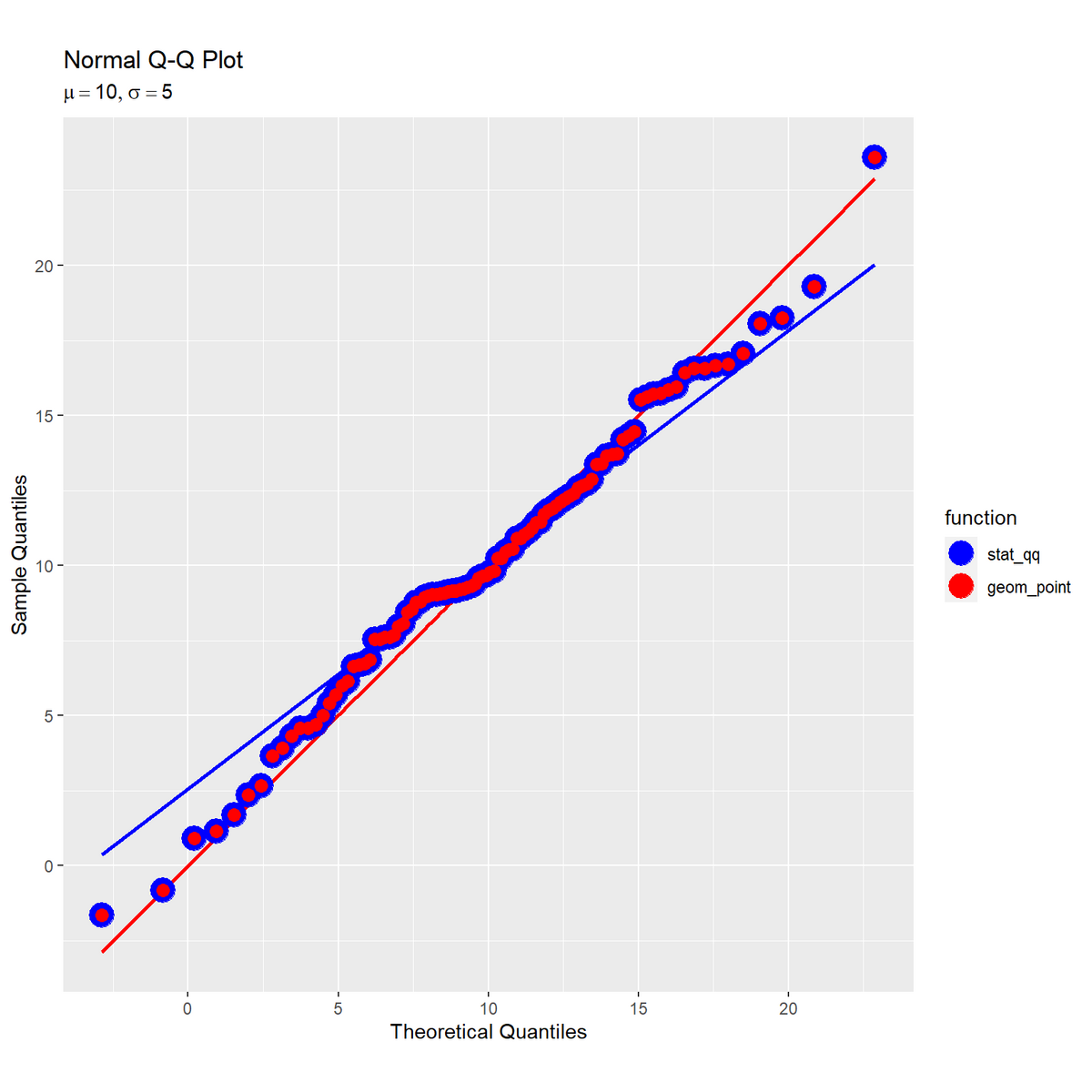
　stat_qq() と stat_qq_line() の distribution 引数に比較用の確率分布の分位数関数、dparams 引数にパラメータを指定できる。デフォルトは標準正規分布 qnorm(mean = 0, sd = 1) である。
　両軸のパラメータを統一すると、傾きが1で切片が0の直線になる。ただし通常は、生成分布のパラメータは未知の値なので計算できない。

　理論値計算用のパラメータによって横軸の値が変化するが、点や直線の相対的な配置は変わらず、結果がパラメータの影響を受けないのが分かる。

理論値線の調整

　直線の疑似的な計算に関する引数について確認する。

　2つのサンプルと疑似理論値線の関係のグラフを作成する。

・作図コード(クリックで展開)

　サンプル値と理論値の描画用のデータフレームを作成する。

# 理論値の計算用のパラメータを指定
mu_z    <- 0
sigma_z <- 1

# サンプルごとの理論値を作成
sample_df <- tibble::tibble(
  i   = 1:N, # 昇順のサンプル番号(分位番号)
  x   = sort(sample_vec), # サンプル(確率変数)
  p   = (i - 0.5) / N, # 分位番号 → パーセンタイル:(両端は0.5)
  #p   = i / (N + 1), # 分位番号 → パーセンタイル:(両端も1)
  q_x = qnorm(p = p, mean = mu, sd = sigma), # パーセンタイル → クォンタイル
  q_z = qnorm(p = p, mean = mu_z, sd = sigma_z) # パーセンタイル → クォンタイル
)
sample_df

# A tibble: 100 × 5
       i      x     p    q_x   q_z
   <int>  <dbl> <dbl>  <dbl> <dbl>
 1     1 -1.66  0.005 -2.88  -2.58
 2     2 -0.822 0.015 -0.850 -2.17
 3     3  0.906 0.025  0.200 -1.96
 4     4  1.13  0.035  0.940 -1.81
 5     5  1.70  0.045  1.52  -1.70
 6     6  2.36  0.055  2.01  -1.60
 7     7  2.66  0.065  2.43  -1.51
 8     8  3.66  0.075  2.80  -1.44
 9     9  3.91  0.085  3.14  -1.37
10    10  4.31  0.095  3.45  -1.31
# ℹ 90 more rows

　「スクラッチで作図」のときのコードで、サンプル生成用と理論値計算用のパラメータそれぞれでクォンタイルを計算する。

　2つのサンプルを指定して、疑似理論値の直線の傾きと切片を作成する。

# 基準とする2点のパーセンタイルを指定
p_k <- 0.25
p_l <- 0.75

# 基準とする2点のサンプル番号を設定:(両端は0.5の場合)
i_k <- floor(N * p_k + 0.5)
i_l <- ceiling(N * p_l + 0.5)

# 基準とする2点のサンプル番号を設定:(両端も1の場合)
#i_k <- floor((N + 1) * p_k)
#i_l <- ceiling((N + 1) * p_l)

# 疑似理論値線の傾き・切片を計算
a <- (sample_df[["x"]][i_l] - sample_df[["x"]][i_k]) / (sample_df[["q_z"]][i_l] - sample_df[["q_z"]][i_k])
b <- sample_df[["x"]][i_k] - a * sample_df[["q_z"]][i_k]
a; b

[1] 3.820076
[1] 10.24121

　2つのパーセンタイル $p_k, p_l$ を指定して、対応するサンプル番号 $k, l$ を計算する。計算式は、分位番号からパーセンタイルへの計算式に従う。
　2つのサンプル $x_k, x_l$ をクォンタイルの理論値とみなして、直線の傾きを $a = \frac{x_l - x_k}{q_l - q_k}$ 、切片を $b = x_k - a q_k$ で計算する。

　Q-Qプロットを作成する。

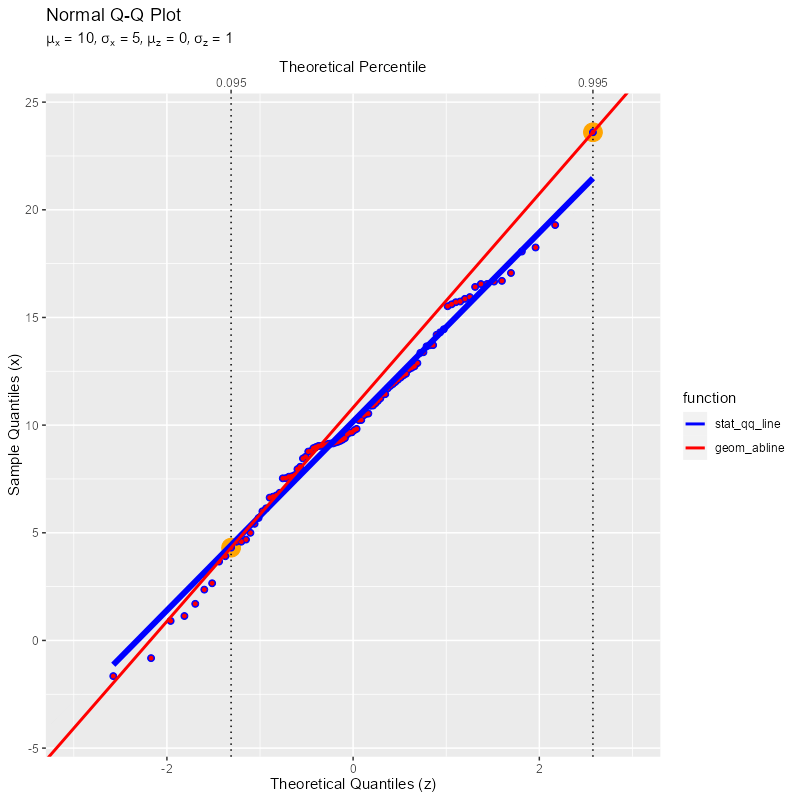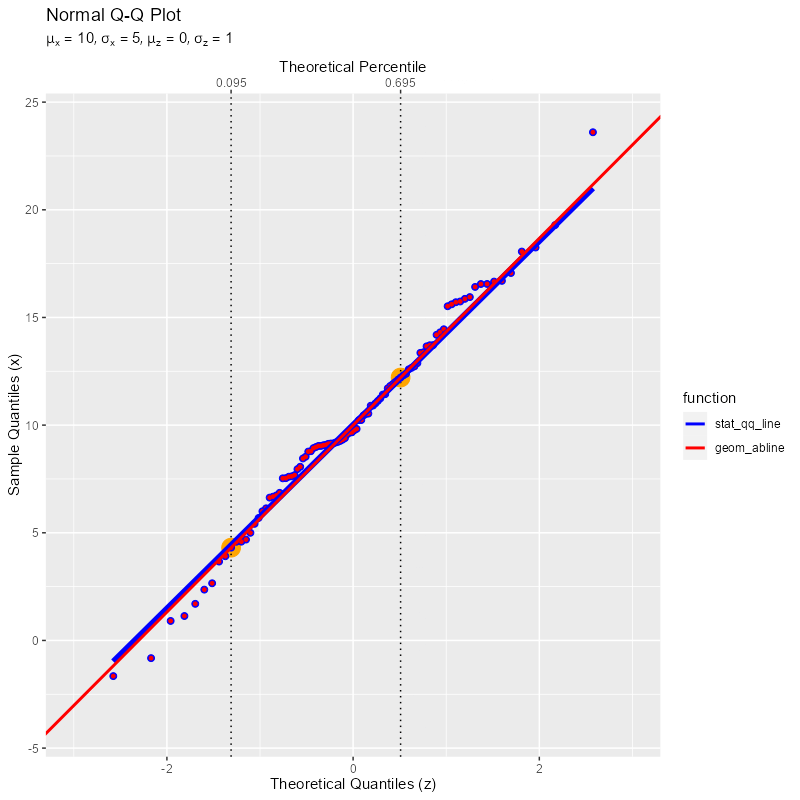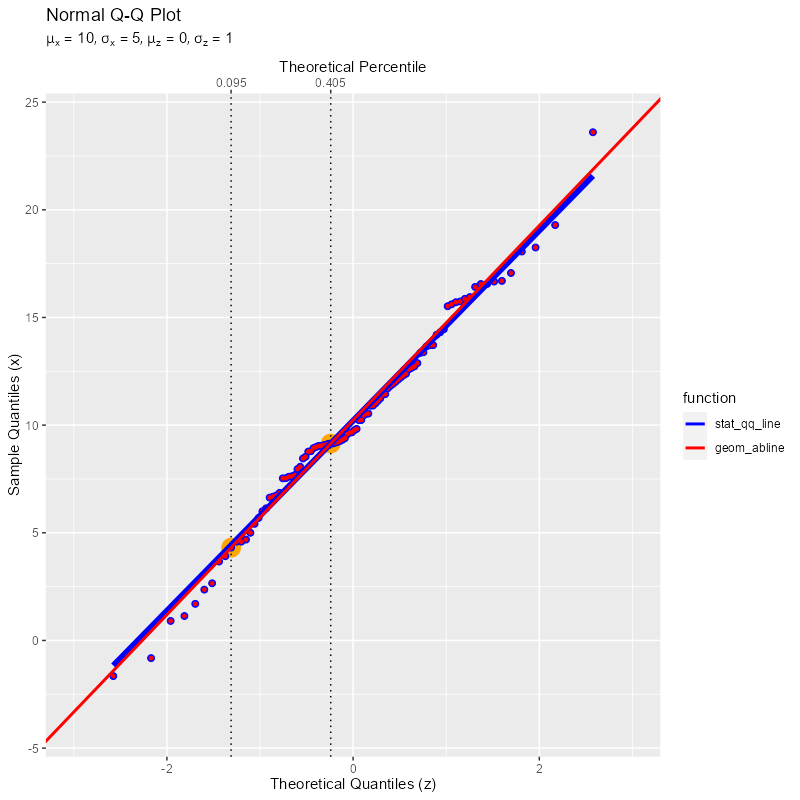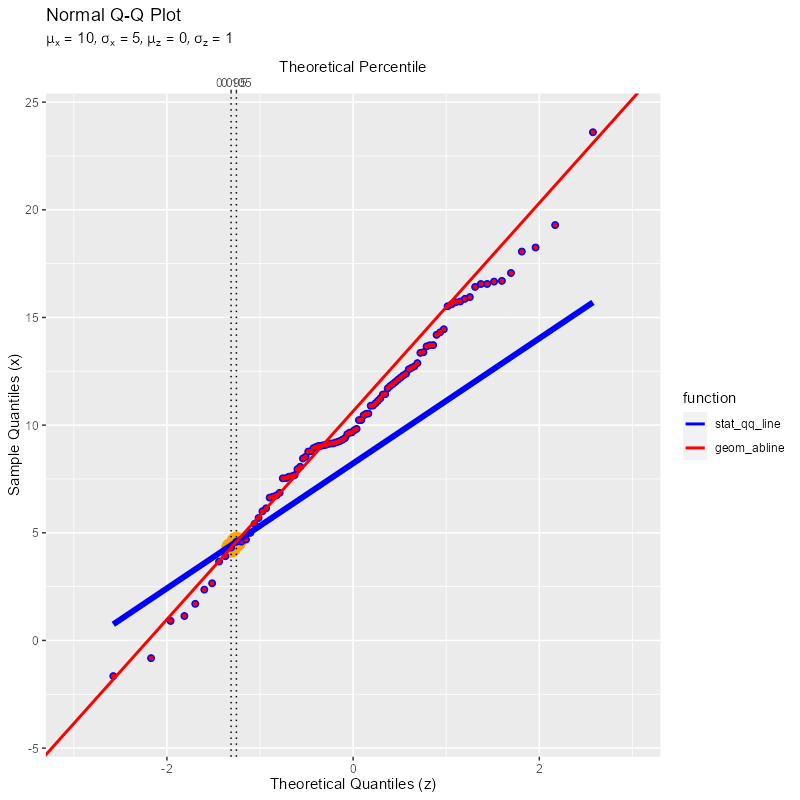
# 基準とす2点の理論値を作成
point_df <- sample_df |> 
  dplyr::filter(i %in% c(i_k, i_l)) # 基準とする2点を抽出

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "mu[x] == ", mu, ", sigma[x] == ", sigma, ", ", 
  "mu[z] == ", mu_z, ", sigma[z] == ", sigma_z, 
  ")"
)

# Q-Qプロットを作図
ggplot() + 
  geom_point(data = point_df, 
             mapping = aes(x = q_z, y = x), 
             color = "orange", size = 6) + # 基準とする2点
  stat_qq(data = sample_df, 
          mapping = aes(sample = x), 
          distribution = qnorm, dparams = list(mean = mu_z, sd = sigma_z), 
          color = "blue", size = 2) + # サンプル値と理論値の対応点
  geom_point(data = sample_df, 
             mapping = aes(x = q_z, y = x), 
             color = "red", size = 1) + # サンプル値と理論値の対応点
  stat_qq_line(data = sample_df, 
               mapping = aes(sample = x, color = "stat_qq_line"), 
               distribution = qnorm, dparams = list(mean = mu_z, sd = sigma_z), 
               line.p = c(p_k, p_l), fullrange = FALSE, 
               linewidth = 2) + # 理論値の線
  geom_abline(mapping = aes(slope = a, intercept = b, color = "geom_abline"), 
              linewidth = 1, show.legend = FALSE) + # 理論値の線
  scale_color_manual(breaks = c("stat_qq_line", "geom_abline"), 
                     values = c("blue", "red"), 
                     name = "function") + # 凡例表示用
  guides(color = guide_legend(override.aes = list(linewidth = 1))) + 
  labs(title = "Normal Q-Q Plot", 
       subtitle = parse(text = param_label), 
       x = "Theoretical Quantiles (z)", 
       y = "Sample Quantiles (x)")

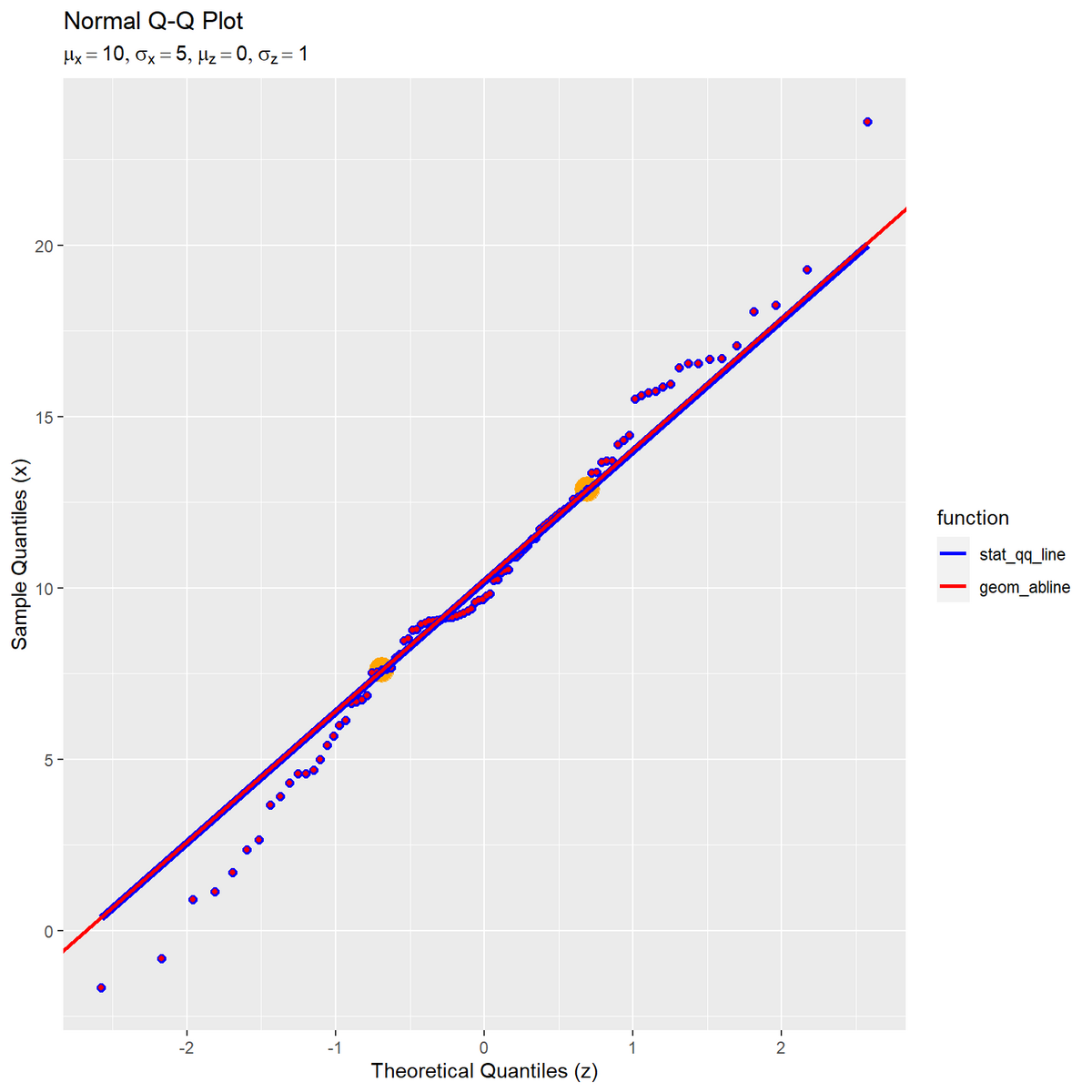
　ggplot2のQ-Qプロット用の関数を用いた直線と一致した(サンプル番号とパーセンタイルの変換処理の影響で(?)、微妙にズレることがあるがこれ以上は深入りしない)。

　2つのサンプルと疑似理論値線の関係のグラフを作成する。下限の点は固定し、上限の点を変化させる。
　作図コードについては「QQplot.R」を参照のこと。

　基準とする2点を通る直線が引かれているのを確認できる(両端の点ほど点間が広がるのでズレやすい)。

　この記事では、Q-Qプロットを作成した。

　Enjoy!

参考文献

小杉考司・紀ノ定保礼・清水裕士『数値シミュレーションで読み解く統計のしくみ～Rでためしてわかる心理統計』技術評論社,2023年.

おわりに

　読んでいた本で簡単に紹介されていたQ-Qプロットが気になって夜も眠れなくなったので自分なりに深掘りしてみました。
　パーセンタイルやクォンタイルなど、名称の段階で分かりにくくて苦労しました。

　コードを読んだ人がいればサンプルxが縦軸なことに困惑したことでしょう。私もとても混乱しました。sとかにしておけばよかった。

　ちなみにアドカレが1つ空いてたのでたこの記事で埋めたのであって遅刻したわけではないですよ。

　投稿日に公開された新曲をどうぞ♪

　これまでにない軸に世界観を拡げている感じがする。今がハマり時かもですよ？メリークリスマス❅

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【R】Q-Qプロットを作図したい【ggplot2】

はじめに

Q-Qプロットを作図したい

トイデータの作成

パッケージを使って作図

スクラッチで作図

サンプル値と理論値の変換

操作の確認

対応の確認

デフォルトと自作の対応

データ点の調整

理論値線の調整

参考文献

おわりに