はじめに

　円関数(三角関数)の定義や公式をR言語で可視化して理解しようシリーズの補足シリーズ(黄金比編)です。

　この記事では、黄金角の性質を確認します。

【前の内容】

www.anarchive-beta.com

【他の記事一覧】

www.anarchive-beta.com

【この記事の内容】

はじめに
黄金角の性質の可視化
- 黄金角の性質
- 円周上の点とsin曲線・cos曲線の関係
  - パラメータと座標の関係
参考書籍
おわりに

黄金角の性質の可視化

　黄金比(golden ratio)を用いて定義される黄金角(golden angle)の性質をグラフで確認します。
　黄金角については「【R】黄金角の定義の可視化 - からっぽのしょこ」を参照してください。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)
library(gganimate)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要です。ただし、作図コードについてはパッケージ名を省略するので、 ggplot2 を読み込む必要があります。
　また、ネイティブパイプ演算子 |> を使います。magrittr パッケージのパイプ演算子 %>% に置き換えられますが、その場合は magrittr を読み込む必要があります。

黄金角の性質

　黄金角の性質をグラフで確認します。
　円周の座標や度数法と弧度法の角度については「【R】円周の作図 - からっぽのしょこ」を参照してください。

　黄金角を作成します。

# 黄金角を計算
beta <- (3 - sqrt(5)) * pi
beta

[1] 2.399963

　黄金角 $(3 - \sqrt{5}) \pi$ を計算して、パラメータ $\beta$ とします。

・作図コード(クリックで展開)

　半径を指定して、円周の描画用のデータフレームを作成します。

# 半径を指定
r <- 1

# 円周の座標を作成
circle_df <- tibble::tibble(
  theta = seq(from = 0, to = 2*pi, length.out = 901), # ラジアン
  x     = r * cos(theta), 
  y     = r * sin(theta)
)
circle_df

# A tibble: 901 × 3
     theta     x       y
     <dbl> <dbl>   <dbl>
 1 0       1     0      
 2 0.00698 1.00  0.00698
 3 0.0140  1.00  0.0140 
 4 0.0209  1.00  0.0209 
 5 0.0279  1.00  0.0279 
 6 0.0349  0.999 0.0349 
 7 0.0419  0.999 0.0419 
 8 0.0489  0.999 0.0488 
 9 0.0559  0.998 0.0558 
10 0.0628  0.998 0.0628 
# ℹ 891 more rows

　 $0 \leq \theta \leq 2 \pi$ の範囲のラジアンを作成して、半径が $r$ の円周のx軸の値 $x = r \cos \theta$ 、y軸の値 $y = r \sin \theta$ を計算します。

　角度目盛の描画用のデータフレームを作成します。

# 半円における目盛数(分母の値)を指定
denom <- 6

# 角度目盛線の座標を作成
angle_axis_df <- tibble::tibble(
  i     = 0:(2*denom-1),  # 目盛位置番号(分子の値)
  theta = i / denom * pi, # 目盛値
  x     = r * cos(theta), 
  y     = r * sin(theta)
)
angle_axis_df

# A tibble: 12 × 4
       i theta         x         y
   <int> <dbl>     <dbl>     <dbl>
 1     0 0      1   e+ 0  0       
 2     1 0.524  8.66e- 1  5   e- 1
 3     2 1.05   5   e- 1  8.66e- 1
 4     3 1.57   6.12e-17  1   e+ 0
 5     4 2.09  -5   e- 1  8.66e- 1
 6     5 2.62  -8.66e- 1  5   e- 1
 7     6 3.14  -1   e+ 0  1.22e-16
 8     7 3.67  -8.66e- 1 -5   e- 1
 9     8 4.19  -5.00e- 1 -8.66e- 1
10     9 4.71  -1.84e-16 -1   e+ 0
11    10 5.24   5   e- 1 -8.66e- 1
12    11 5.76   8.66e- 1 -5.00e- 1

　「円周の作図」を参照してください。

黄金角と点の間隔の関係

　パラメータ(偏角の係数・点間の角度)として黄金角を用いて、円周上に点を配置します。

　点の数を指定して、円周上の点の描画用のデータフレームを作成します。

# 点数を指定
n <- 300

# 円周上の点の座標を作成
point_df <- tibble::tibble(
  i     = 1:n, # 点番号
  theta = i * beta, # ラジアン
  x     = r * cos(theta), 
  y     = r * sin(theta)
)
point_df

# A tibble: 300 × 4
       i theta       x      y
   <int> <dbl>   <dbl>  <dbl>
 1     1  2.40 -0.737   0.675
 2     2  4.80  0.0874 -0.996
 3     3  7.20  0.608   0.794
 4     4  9.60 -0.985  -0.174
 5     5 12.0   0.844  -0.537
 6     6 14.4  -0.260   0.966
 7     7 16.8  -0.461  -0.887
 8     8 19.2   0.939   0.343
 9     9 21.6  -0.924   0.382
10    10 24.0   0.424  -0.906
# ℹ 290 more rows

　 $n$ 個の点番号 $i = 1, \dots, n$ に応じて偏角を $\theta_i = i \beta$ として、円周上の点の座標 $x_i = r \cos \theta_i, y_i = r \sin \theta_i$ を計算します。

　円周上の点のグラフを作成します。

# ラベル用の文字列を作成
var_label <- paste0(
  "list(", 
  "r == ", r, ", ", 
  "theta == i * beta ~~ (i == list(1, ldots, n)), ", 
  "n == ", n, ", ", 
  "beta == ", round(beta/pi, digits = 2), " * pi, ", 
  "beta*degree == ", round(beta/pi*180, digits = 2), "*degree", 
  ")"
)

# 円周上の点を作図
ggplot() + 
  geom_segment(data = angle_axis_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = factor(i)), 
               color = "white") + # 角度目盛線
  geom_path(data = circle_df, 
            mapping = aes(x = x, y = y), 
            linewidth = 1) + # 円周
  geom_point(data = point_df, 
             mapping = aes(x = x, y = y, color = i), 
             size = 2.5) + # 円周上の点
  geom_path(data = point_df, 
            mapping = aes(x = x, y = y, color = i), 
            linewidth = 0.5) + # 円周上の点を結ぶ線分
  coord_fixed(ratio = 1) + 
  labs(title = "golden angle", 
       subtitle = parse(text = var_label), 
       color = expression(i),
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

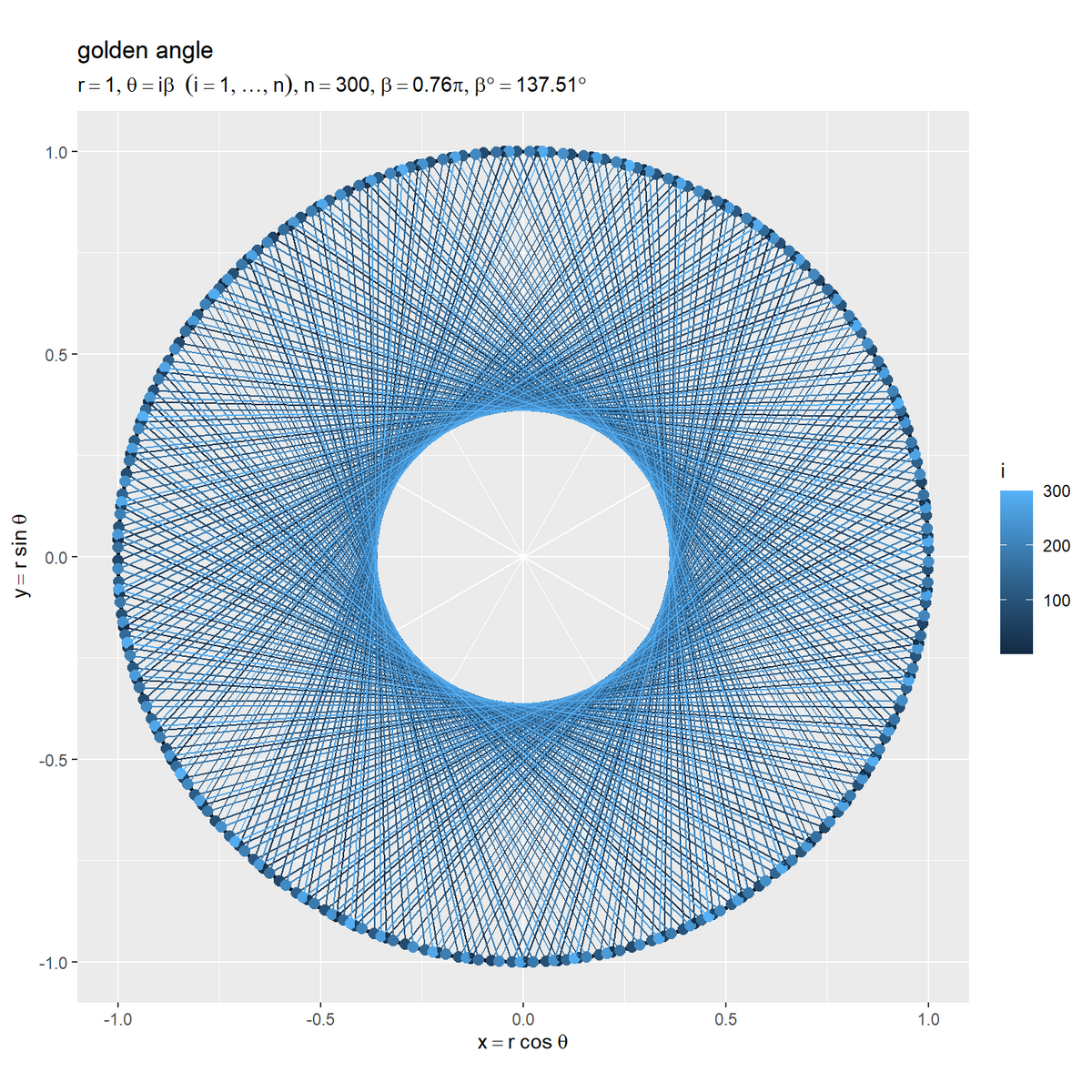
　黄金角 $\beta$ を係数として用いて偏角(x軸線の正の部分とのなす角)を $\theta_i = i \beta$ とし、 $i$ 番目の点の座標 $(x_i, y_i)$ を $x_i = r \cos \theta_i, y = r \sin \theta_i$ とすると、点が重ならないように円周上に配置されます。
　 $i$ 番目の点と $i+1$ 番目の点を結ぶ線分を表示しています。

　次からは、この性質を確認していきます。

パラメータと点の位置の関係

　点間の角度(パラメータ)と円周上の点の位置の関係を示すアニメーションを作成します。

・作図コード(クリックで展開)

　点間を補完して円周上を移動する点の描画用のデータフレームを作成します。

# 点数を指定
n <- 10

# 点間の補完数を指定
inter_num <- 10

# 点間を補完して変化する点の座標を作成
anim_point_df <- tibble::tibble(
  i     = 1:n, # 点番号
  theta = (i - 1) * beta # 各点のラジアン
) |> 
  dplyr::reframe(
    theta    = seq(from = theta, to = theta+beta, length.out = inter_num+1)[1:inter_num], # 次点間のラジアン
    inter_id = 1:inter_num, # 補完番号
    .by = dplyr::everything()
  ) |> # 次点間を補完
  dplyr::mutate(
    frame_i = (i - 1) * inter_num + inter_id, # フレーム番号
    x = r * cos(theta), 
    y = r * sin(theta), 
    var_label = paste0(
      "list(", 
      "r == ", r, ", ", 
      "theta == i * beta, ", 
      "n == ", n, ", ", 
      "i == ", i, ", ", 
      "beta == ", round(beta/pi, digits = 2), " * pi, ", 
      "beta*degree == ", round(beta/pi*180, digits = 2), "*degree, ", 
      "theta == ", round(theta/pi, digits = 2), " * pi", 
      ")"
    ) # 変数ラベル
  ) |> 
  dplyr::arrange(frame_i)
anim_point_df

# A tibble: 100 × 7
       i theta inter_id frame_i      x     y var_label                          
   <int> <dbl>    <int>   <dbl>  <dbl> <dbl> <chr>                              
 1     1 0            1       1  1     0     list(r == 1, theta == i * beta, n …
 2     1 0.240        2       2  0.971 0.238 list(r == 1, theta == i * beta, n …
 3     1 0.480        3       3  0.887 0.462 list(r == 1, theta == i * beta, n …
 4     1 0.720        4       4  0.752 0.659 list(r == 1, theta == i * beta, n …
 5     1 0.960        5       5  0.574 0.819 list(r == 1, theta == i * beta, n …
 6     1 1.20         6       6  0.362 0.932 list(r == 1, theta == i * beta, n …
 7     1 1.44         7       7  0.130 0.991 list(r == 1, theta == i * beta, n …
 8     1 1.68         8       8 -0.109 0.994 list(r == 1, theta == i * beta, n …
 9     1 1.92         9       9 -0.342 0.940 list(r == 1, theta == i * beta, n …
10     1 2.16        10      10 -0.556 0.831 list(r == 1, theta == i * beta, n …
# ℹ 90 more rows

　点番号 $i$ を格納して、偏角 $\theta_i = i \beta$ を計算します。ただし、偏角との関係が分かりやすいように、点番号を $0$ から $n-1$ の整数として用います。
　 $i$ 番目の点の偏角 $\theta_i$ と次の点の偏角 $\theta_{i+1} = \theta_i + \beta$ までの範囲のラジアン $\theta_i \leq \theta \lt \theta_{i+1}$ を reframe() で作成します。補完する数 inter_num を指定して、補完番号を inter_id 列とします。
　点番号と補完番号からフレーム番号を作成して、円周上の点の座標を計算します。フレーム数は点数掛ける補完数になります。

　1パラメータ分遅れて円周上を移動する点の描画用のデータフレームを作成します。

# パラメータ分遅れて変化する点の座標を作成
delay_point_df <- anim_point_df |> 
  dplyr::select(!c(x, y, var_label)) |> 
  dplyr::mutate(
    theta = theta - beta, # パラメータ分戻す
    x     = r * cos(theta), 
    y     = r * sin(theta)
  )
delay_point_df

# A tibble: 100 × 6
       i  theta inter_id frame_i      x      y
   <int>  <dbl>    <int>   <dbl>  <dbl>  <dbl>
 1     1 -2.40         1       1 -0.737 -0.675
 2     1 -2.16         2       2 -0.556 -0.831
 3     1 -1.92         3       3 -0.342 -0.940
 4     1 -1.68         4       4 -0.109 -0.994
 5     1 -1.44         5       5  0.130 -0.991
 6     1 -1.20         6       6  0.362 -0.932
 7     1 -0.960        7       7  0.574 -0.819
 8     1 -0.720        8       8  0.752 -0.659
 9     1 -0.480        9       9  0.887 -0.462
10     1 -0.240       10      10  0.971 -0.238
# ℹ 90 more rows

　円周上を移動する点のデータ anim_point_df を使って、各フレームの偏角 theta からパラメータ beta を引いて、円周上の点の座標を再度計算します。

　点間を補完しない円周上の点の描画用のデータフレームを作成します。

# 各点の座標を作成
current_point_df <- tibble::tibble(
  i     = 1:n, 
  theta = (i - 1) * beta, 
  x     = r * cos(theta), 
  y     = r * sin(theta)
) |> 
  tidyr::uncount(
    weights = inter_num, .id = "inter_id"
  ) |> # 補完フレーム分の点を複製
  dplyr::mutate(
    frame_i = (i - 1) * inter_num + inter_id
  ) |> # フレーム番号を補完フレームに対応
  dplyr::arrange(frame_i)
current_point_df

# A tibble: 100 × 6
       i theta     x     y inter_id frame_i
   <int> <dbl> <dbl> <dbl>    <int>   <dbl>
 1     1     0     1     0        1       1
 2     1     0     1     0        2       2
 3     1     0     1     0        3       3
 4     1     0     1     0        4       4
 5     1     0     1     0        5       5
 6     1     0     1     0        6       6
 7     1     0     1     0        7       7
 8     1     0     1     0        8       8
 9     1     0     1     0        9       9
10     1     0     1     0       10      10
# ℹ 90 more rows

　点番号に対応した円周上の点の座標を作成して、uncount() で補完数分に複製します。

　各フレームまでの点間を補完しない円周上の点の描画用のデータフレームを作成します。

# 過去の点の座標を作成
trace_point_df <- tibble::tibble(
  i     = 1:n, 
  theta = (i - 1) * beta, 
  x     = r * cos(theta), 
  y     = r * sin(theta)
) |> 
  dplyr::reframe(
    frame_i = i:n, .by = dplyr::everything()
  ) |> # 過去フレームの点を複製
  tidyr::uncount(
    weights = inter_num, .id = "inter_id"
  ) |> # 補完フレーム分の点を複製
  dplyr::mutate(
    frame_i = (frame_i - 1) * inter_num + inter_id
  ) |> # フレーム番号を補完フレームに対応
  dplyr::arrange(frame_i)
trace_point_df

# A tibble: 550 × 6
       i theta     x     y frame_i inter_id
   <int> <dbl> <dbl> <dbl>   <dbl>    <int>
 1     1     0     1     0       1        1
 2     1     0     1     0       2        2
 3     1     0     1     0       3        3
 4     1     0     1     0       4        4
 5     1     0     1     0       5        5
 6     1     0     1     0       6        6
 7     1     0     1     0       7        7
 8     1     0     1     0       8        8
 9     1     0     1     0       9        9
10     1     0     1     0      10       10
# ℹ 540 more rows

　点番号に対応した円周上の点の座標を作成して、reframe() で点番号以下のフレーム番号分に複製して、uncount() で補完数分に複製します。

　角ラベルの描画用のデータフレームを作成します。

# 角ラベルの座標を作成
d <- 0.15
angle_label_df <- anim_point_df |> 
  dplyr::select(!c(x, y, var_label)) |> 
  dplyr::mutate(
    theta = theta - 0.5*beta, # パラメータの半分戻す
    x     = d * cos(theta), 
    y     = d * sin(theta)
  )
angle_label_df

# A tibble: 100 × 6
       i  theta inter_id frame_i      x       y
   <int>  <dbl>    <int>   <dbl>  <dbl>   <dbl>
 1     1 -1.20         1       1 0.0544 -0.140 
 2     1 -0.960        2       2 0.0860 -0.123 
 3     1 -0.720        3       3 0.113  -0.0989
 4     1 -0.480        4       4 0.133  -0.0693
 5     1 -0.240        5       5 0.146  -0.0357
 6     1  0            6       6 0.15    0     
 7     1  0.240        7       7 0.146   0.0357
 8     1  0.480        8       8 0.133   0.0693
 9     1  0.720        9       9 0.113   0.0989
10     1  0.960       10      10 0.0860  0.123 
# ℹ 90 more rows

　移動する2点間の中点にラベルを表示することにします。
　円周上を移動する点のデータ anim_point_df を使って、各フレームの偏角 theta からパラメータ beta の半分を引いて、円周上の点の座標を再度計算します。ラベルの位置を d として調整します。

　角マークの描画用のデータフレームを作成します。

# 角マークの座標を作成
d <- 0.1
angle_arc_df <- anim_point_df |> 
  dplyr::select(!c(x, y, var_label)) |> 
  dplyr::reframe(
    theta = seq(from = theta, to = theta-beta, length.out = 100), .by = dplyr::everything()
  ) |> # パラメータ分戻した範囲のラジアンを作成
  dplyr::mutate(
    x = d * cos(theta), 
    y = d * sin(theta)
  )
angle_arc_df

# A tibble: 10,000 × 6
       i   theta inter_id frame_i      x        y
   <int>   <dbl>    <int>   <dbl>  <dbl>    <dbl>
 1     1  0             1       1 0.1     0      
 2     1 -0.0242        1       1 0.100  -0.00242
 3     1 -0.0485        1       1 0.0999 -0.00485
 4     1 -0.0727        1       1 0.0997 -0.00727
 5     1 -0.0970        1       1 0.0995 -0.00968
 6     1 -0.121         1       1 0.0993 -0.0121 
 7     1 -0.145         1       1 0.0989 -0.0145 
 8     1 -0.170         1       1 0.0986 -0.0169 
 9     1 -0.194         1       1 0.0981 -0.0193 
10     1 -0.218         1       1 0.0976 -0.0216 
# ℹ 9,990 more rows

　円周上を移動する点のデータ anim_point_df を使って、各フレームの偏角 theta からパラメータ beta 分戻した範囲のラジアンを reframe() で作成して、円周上の点の座標を再度計算します。

　円周上を移動する2点間の角度のアニメーションを作成します。

# 円周上の点のアニメーションを作図
anim <- ggplot() + 
  geom_segment(data = angle_axis_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = factor(i)), 
               color = "white") + # 角度目盛線
  geom_path(data = circle_df, 
            mapping = aes(x = x, y = y), 
            linewidth = 1) + # 円周
  geom_path(data = trace_point_df,
            mapping = aes(x = x, y = y, color = i),
            linewidth = 0.5) + # 過去の点間の線分
  geom_point(data = trace_point_df,
             mapping = aes(x = x, y = y, color = i),
             size = 4) + # 過去の点
  geom_segment(data = current_point_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y), 
               linewidth = 1) + # 現在の点との半径線
  geom_segment(data = delay_point_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y), 
               linewidth = 1, linetype = "dashed") + # 遅れて変化する点との半径線
  geom_segment(data = anim_point_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y), 
               linewidth = 1) + # 変化する点との半径線
  geom_point(data = anim_point_df, 
             mapping = aes(x = x, y = y, color = i), 
             size = 6) + # 変化する点
  geom_path(data = angle_arc_df, 
            mapping = aes(x = x, y = y)) + # 角マーク
  geom_text(data = angle_label_df, 
            mapping = aes(x = x, y = y), 
            label = "beta", parse = TRUE, size = 6) + # 角ラベル
  geom_text(data = anim_point_df, 
            mapping = aes(x = -Inf, y = Inf, label = var_label), 
            parse = TRUE, hjust = 0, vjust = -0.5) + # 変数ラベル
  gganimate::transition_manual(frames = frame_i) + # 
  coord_fixed(ratio = 1, clip = "off") + 
  labs(title = "golden angle", 
       subtitle = "", # (変数ラベルの表示用)
       color = expression(i),
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

# gif画像を作成
gganimate::animate(plot = anim, nframes = n*inter_num, fps = 10, width = 800, height = 800)

　gganimate パッケージを利用してアニメーション(gif画像)を作成します。
　transition_manual() のフレーム制御の引数 frames にフレーム番号列 frame_i を指定します。
　animate() の plot 引数にグラフオブジェクト、nframes 引数にフレーム数 frame_num を指定して、gif画像を作成します。また、fps 引数に1秒当たりのフレーム数を指定できます。
　gganimate を利用したフレーム切り替えでは、フレームに応じてサブタイトルを変更できますが expression() を使えないので、geom_text() を使って疑似的にサブタイトルの位置にパラメータラベルを表示します。coord_***() に clip = "off" を指定すると、描画領域外(余白領域)に描画できます。

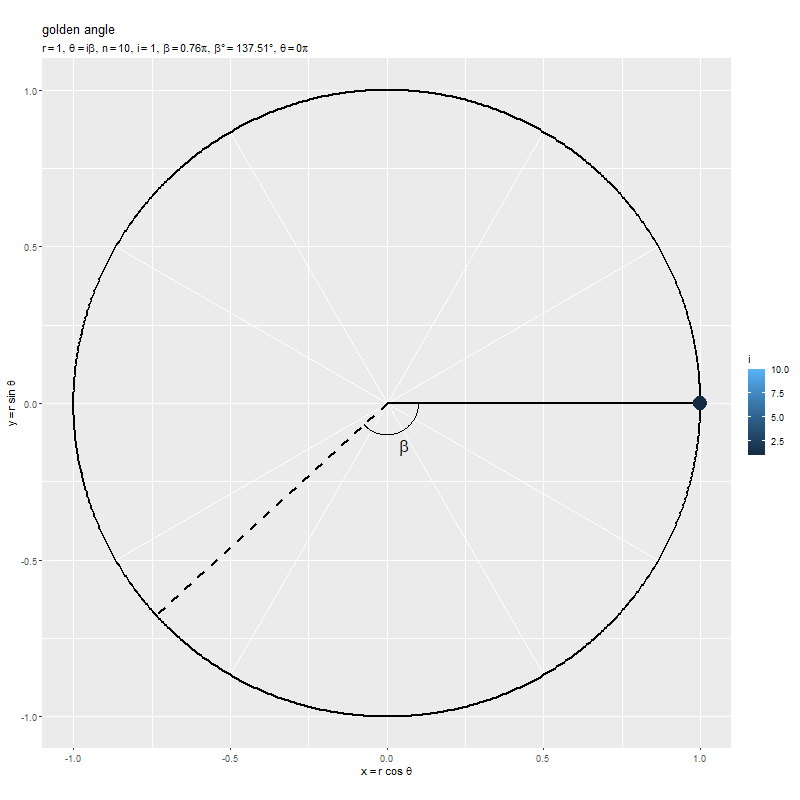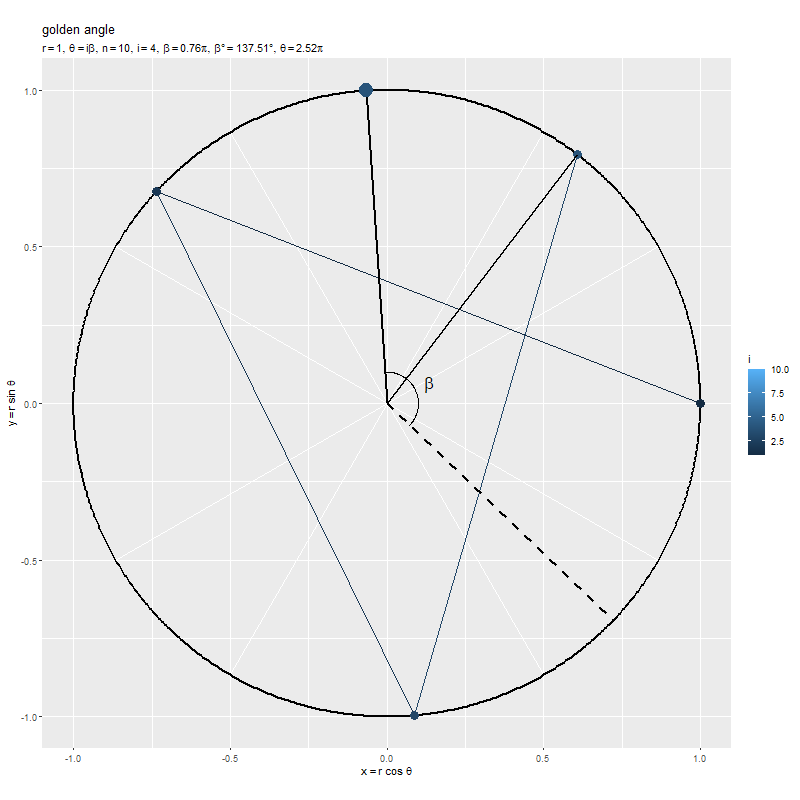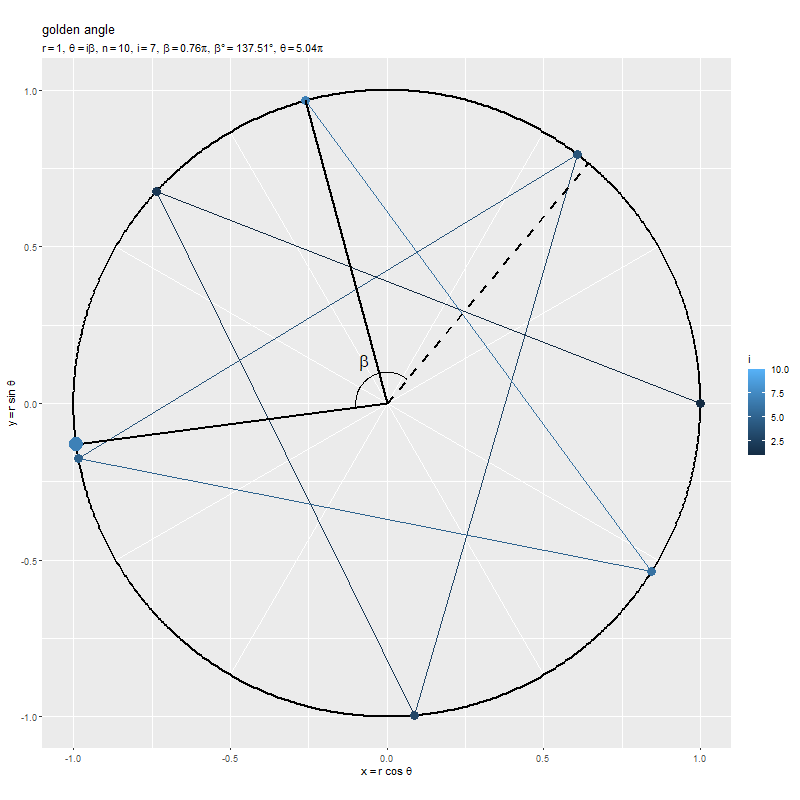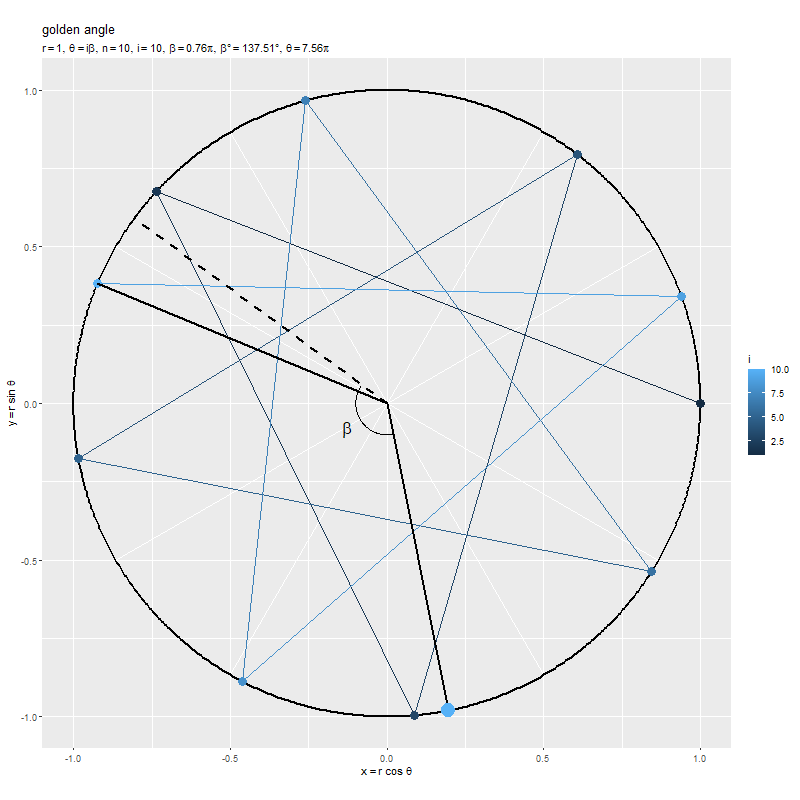
　隣り合う2点間の角度(偏角の差)が $\beta$ になるように、1つ前の点から左回りに $\beta$ 回転した位置に点が配置されていくのを確認できます。ただし、この例では偏角が分かりやすいように、最初の点がx軸線の正の部分上(偏角が $\theta_1 = 0$ )となるように、点の位置を1つ後にズラして $\theta_i = (i - 1) \beta$ としています。
　各点の偏角は $\theta_i = i \beta$ なので、1つ前の点との関係は $\theta_{i+1} = (i + 1) \beta = \theta_i + \beta$ となることからも、2点間の角度(偏角の差)が $\beta$ になるのが分かります。

変数と点の位置の関係

　点番号(変数)と円周上の点の位置の関係を示すアニメーションを作成します。

・作図コード(クリックで展開)

　点の描画用のデータフレームを作成します。

# 点数(フレーム数)を指定
n <- 100

# 円周上の点の座標を作成
trace_point_df <- tibble::tibble(
  frame_i = 1:n # フレーム番号
) |> 
  dplyr::reframe(
    i = 1:frame_i, .by = dplyr::everything()
  ) |> # 過去フレームの点を複製
  dplyr::mutate(
    theta = (i - 1) * beta, 
    x     = r * cos(theta), 
    y     = r * sin(theta)
  )
trace_point_df

# A tibble: 5,050 × 5
   frame_i     i theta       x      y
     <int> <int> <dbl>   <dbl>  <dbl>
 1       1     1  0     1       0    
 2       2     1  0     1       0    
 3       2     2  2.40 -0.737   0.675
 4       3     1  0     1       0    
 5       3     2  2.40 -0.737   0.675
 6       3     3  4.80  0.0874 -0.996
 7       4     1  0     1       0    
 8       4     2  2.40 -0.737   0.675
 9       4     3  4.80  0.0874 -0.996
10       4     4  7.20  0.608   0.794
# ℹ 5,040 more rows

　点数(フレーム数) n を指定して、フレーム番号を frame_i 列とします。
　フレームごとにフレーム番号までの点番号を reframe() で作成して、点の座標を計算します。

　変数ラベルの表示用のデータフレームを作成します。

# ラベル用の文字列を作成
anim_label_df <- tibble::tibble(
  frame_i = 1:n, 
  i       = frame_i, 
  theta   = (i - 1) * beta, 
  var_label = paste0(
    "list(", 
    "r == ", r, ", ", 
    "theta == i * beta, ", 
    "n == ", n, ", ", 
    "i == ", i, ", ", 
    "beta == ", round(beta/pi, digits = 2), " * pi, ", 
    "theta == ", round(theta/pi, digits = 2), " * pi", 
    ")"
  ), 
)
anim_label_df

# A tibble: 100 × 4
   frame_i     i theta var_label                                                
     <int> <int> <dbl> <chr>                                                    
 1       1     1  0    list(r == 1, theta == i * beta, n == 100, i == 1, beta =…
 2       2     2  2.40 list(r == 1, theta == i * beta, n == 100, i == 2, beta =…
 3       3     3  4.80 list(r == 1, theta == i * beta, n == 100, i == 3, beta =…
 4       4     4  7.20 list(r == 1, theta == i * beta, n == 100, i == 4, beta =…
 5       5     5  9.60 list(r == 1, theta == i * beta, n == 100, i == 5, beta =…
 6       6     6 12.0  list(r == 1, theta == i * beta, n == 100, i == 6, beta =…
 7       7     7 14.4  list(r == 1, theta == i * beta, n == 100, i == 7, beta =…
 8       8     8 16.8  list(r == 1, theta == i * beta, n == 100, i == 8, beta =…
 9       9     9 19.2  list(r == 1, theta == i * beta, n == 100, i == 9, beta =…
10      10    10 21.6  list(r == 1, theta == i * beta, n == 100, i == 10, beta …
# ℹ 90 more rows

　フレームごとに変数ラベル用の文字列を作成します。

　円周上の点のアニメーションを作成します。

# 円周上の点のアニメーションを作図
anim <- ggplot() + 
  geom_segment(data = angle_axis_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = factor(i)), 
               color = "white") + # 角度目盛線
  geom_path(data = circle_df, 
            mapping = aes(x = x, y = y), 
            linewidth = 1) + # 円周
  geom_point(data = trace_point_df, 
             mapping = aes(x = x, y = y, color = i), 
             size = 4) + # 円周上の点
  geom_path(data = trace_point_df, 
            mapping = aes(x = x, y = y, color = i), 
            linewidth = 0.5) + # 円周上の点を結ぶ線分
  geom_text(data = anim_label_df, 
            mapping = aes(x = -Inf, y = Inf, label = var_label), 
            parse = TRUE, hjust = 0, vjust = -0.5) + # 変数ラベル
  gganimate::transition_manual(frames = frame_i) + # 円周上の点を結ぶ線分
  coord_fixed(ratio = 1, clip = "off") + 
  labs(title = "golden angle", 
       subtitle = "", # (変数ラベルの表示用)
       color = expression(i),
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

# gif画像を作成
gganimate::animate(plot = anim, nframes = n, fps = 10, width = 800, height = 800)

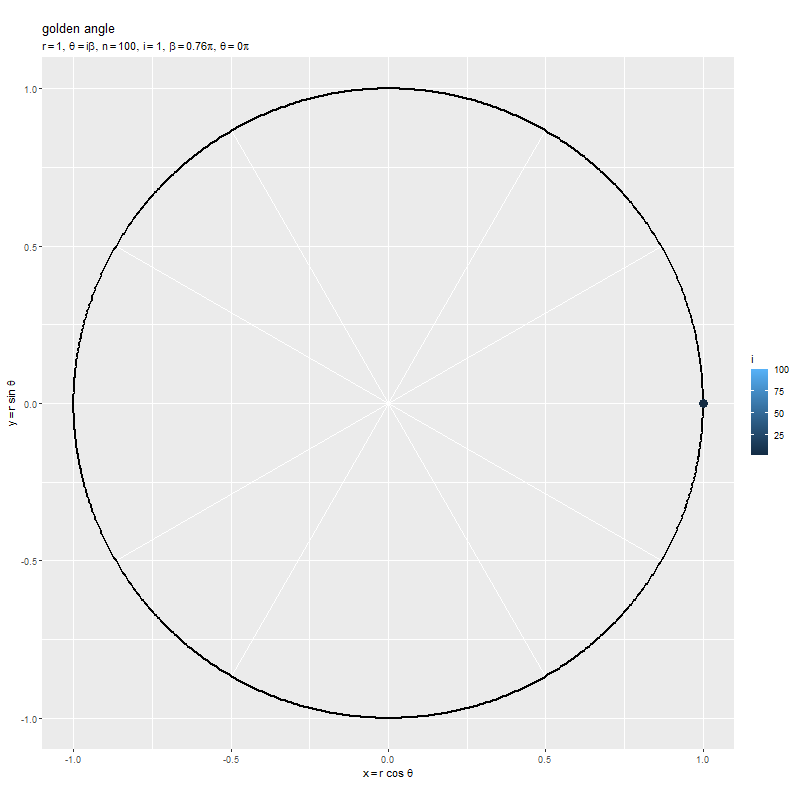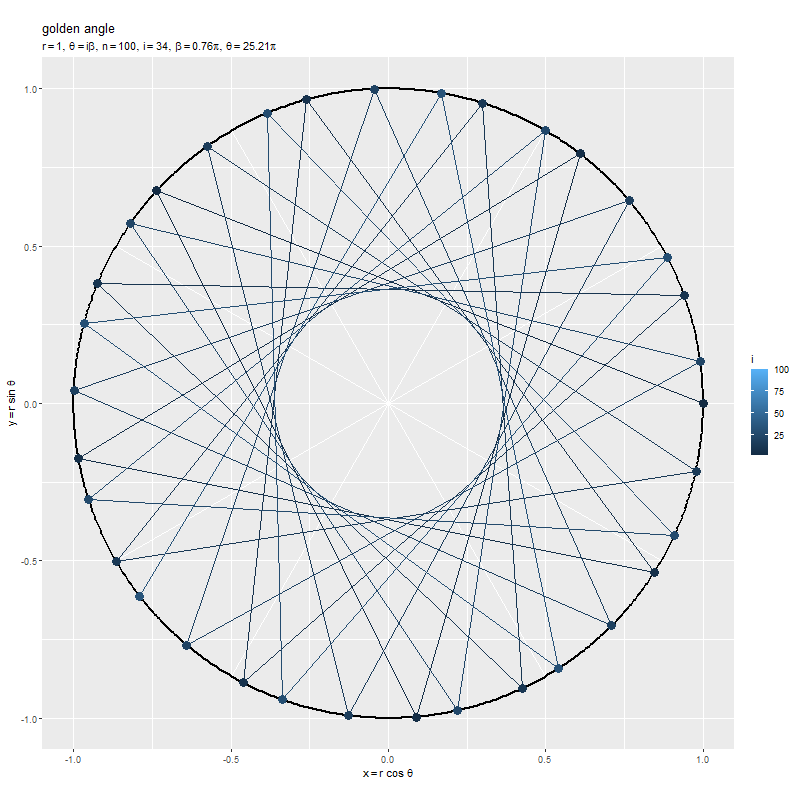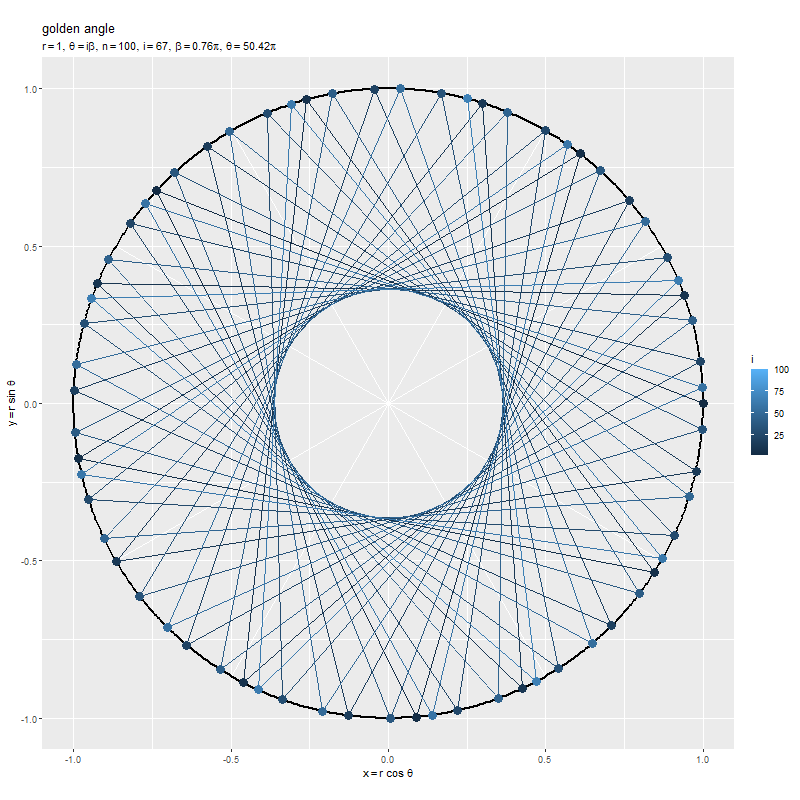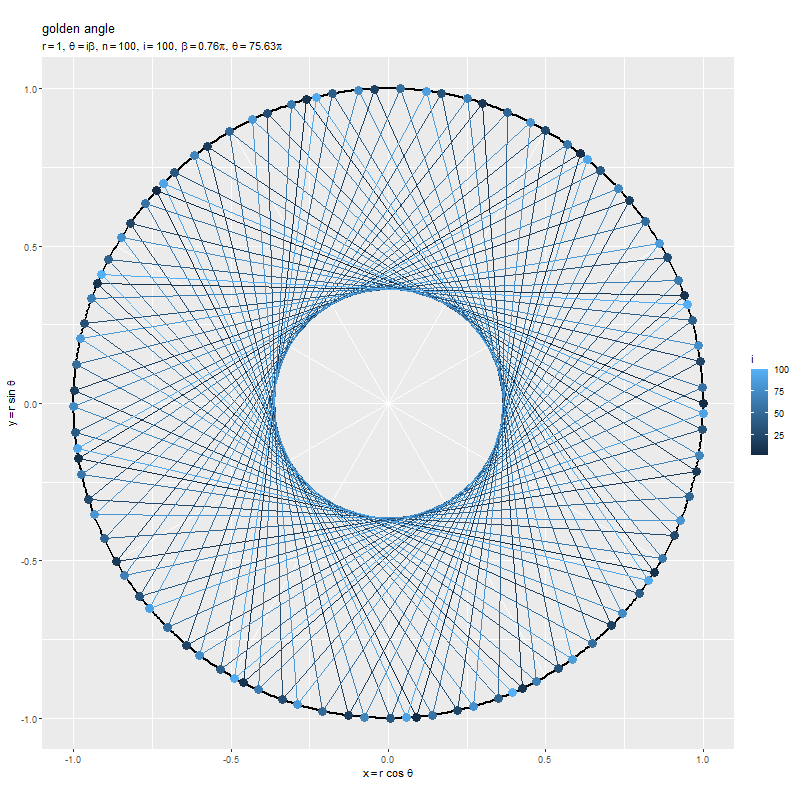
　点間の角度 $\beta$ を固定して、点(の数) $i$ を増やしていきます。
　黄金角を用いると、点が重ならないように円周上に配置されるのを確認できます。

パラメータと点の間隔の関係

　点間の角度(パラメータ)と円周上の点の散らばり具合の関係を示すアニメーションを作成します。

・作図コード(クリックで展開)

　フレーム数と点数を指定して、点の描画用のデータフレームを作成します。

# フレーム数を指定
frame_num <- 360

# 点間の角度の範囲を指定
# beta_deg_vals <- seq(from = 0, to = 360, length.out = frame_num+1)[1:frame_num] # 度数法の角度を作成
# beta_rad_vals <- beta_deg_vals/180 * pi # 弧度法の角度に変換
beta_rad_vals <- seq(from = 0, to = 2*pi, length.out = frame_num+1)[1:frame_num] # 弧度法の角度を作成
beta_deg_vals <- beta_rad_vals/pi * 180 # 度数法の角度に変換

# 点数を指定
n <- 100

# 円周上の点の座標を作成
anim_point_df <- tidyr::expand_grid(
  frame_i = 1:frame_num, # フレーム番号
  i       = 1:n # 点番号
) |> # フレームごとに点を複製
  dplyr::mutate(
    beta  = beta_rad_vals[frame_i], 
    theta = (i - 1) * beta, 
    x     = r * cos(theta), 
    y     = r * sin(theta)
  )
anim_point_df

# A tibble: 36,000 × 6
   frame_i     i  beta theta     x     y
     <int> <int> <dbl> <dbl> <dbl> <dbl>
 1       1     1     0     0     1     0
 2       1     2     0     0     1     0
 3       1     3     0     0     1     0
 4       1     4     0     0     1     0
 5       1     5     0     0     1     0
 6       1     6     0     0     1     0
 7       1     7     0     0     1     0
 8       1     8     0     0     1     0
 9       1     9     0     0     1     0
10       1    10     0     0     1     0
# ℹ 35,990 more rows

　フレーム数 frame_num を指定して、パラメータの値を frame_num 個作成します。 $2 \pi$ の倍数の範囲を frame_num + 1 個の等間隔に分割して最後の値を除くと、最後のフレームと最初のフレームのグラフが繋がります。
　点数 n を指定して、フレーム番号と点番号の全ての組み合わせを expand_grid() 作成することでフレームごとに点を複製して、点の座標を計算します。

　変数ラベルの表示用のデータフレームを作成します。

# ラベル用の文字列を作成
anim_label_df <- tibble::tibble(
  frame_i  = 1:frame_num, 
  beta_rad = beta_rad_vals, 
  beta_deg = beta_deg_vals, 
  var_label = paste0(
    "list(", 
    "r == ", r, ", ", 
    "theta == i * beta, ", 
    "n == ", n, ", ", 
    "beta == ", round(beta_rad/pi, digits = 2), " * pi, ", 
    "beta*degree == ", round(beta_deg, digits = 2), "*degree", 
    ")"
  )
)
anim_label_df

# A tibble: 360 × 4
   frame_i beta_rad beta_deg var_label                                          
     <int>    <dbl>    <dbl> <chr>                                              
 1       1   0             0 list(r == 1, theta == i * beta, n == 100, beta == …
 2       2   0.0175        1 list(r == 1, theta == i * beta, n == 100, beta == …
 3       3   0.0349        2 list(r == 1, theta == i * beta, n == 100, beta == …
 4       4   0.0524        3 list(r == 1, theta == i * beta, n == 100, beta == …
 5       5   0.0698        4 list(r == 1, theta == i * beta, n == 100, beta == …
 6       6   0.0873        5 list(r == 1, theta == i * beta, n == 100, beta == …
 7       7   0.105         6 list(r == 1, theta == i * beta, n == 100, beta == …
 8       8   0.122         7 list(r == 1, theta == i * beta, n == 100, beta == …
 9       9   0.140         8 list(r == 1, theta == i * beta, n == 100, beta == …
10      10   0.157         9 list(r == 1, theta == i * beta, n == 100, beta == …
# ℹ 350 more rows

　フレームごとに変数ラベル用の文字列を作成します。

　円周上の点のアニメーションを作成します。

# 円周上の点のアニメーションを作図
anim <- ggplot() + 
  geom_segment(data = angle_axis_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = factor(i)), 
               color = "white") + # 角度目盛線
  geom_path(data = circle_df, 
            mapping = aes(x = x, y = y), 
            linewidth = 1) + # 円周
  geom_point(data = anim_point_df, 
             mapping = aes(x = x, y = y, color = i), 
             size = 4) + # 円周上の点
  geom_path(data = anim_point_df, 
            mapping = aes(x = x, y = y, color = i), 
            linewidth = 0.5) + # 円周上の点を結ぶ線分
  geom_text(data = anim_label_df, 
            mapping = aes(x = -Inf, y = Inf, label = var_label), 
            parse = TRUE, hjust = 0, vjust = -0.5) + # 変数ラベル
  gganimate::transition_manual(frames = frame_i) + # 円周上の点を結ぶ線分
  coord_fixed(ratio = 1, clip = "off") + 
  labs(title = "golden angle", 
       subtitle = "", # (変数ラベルの表示用)
       color = expression(i),
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

# gif画像を作成
gganimate::animate(plot = anim, nframes = n, fps = 6, width = 800, height = 800)

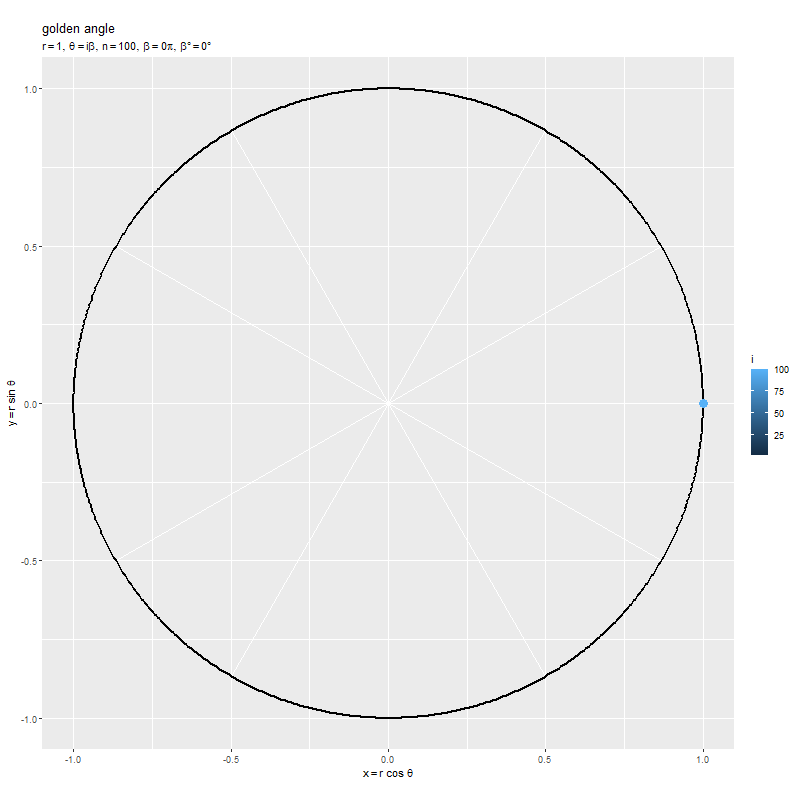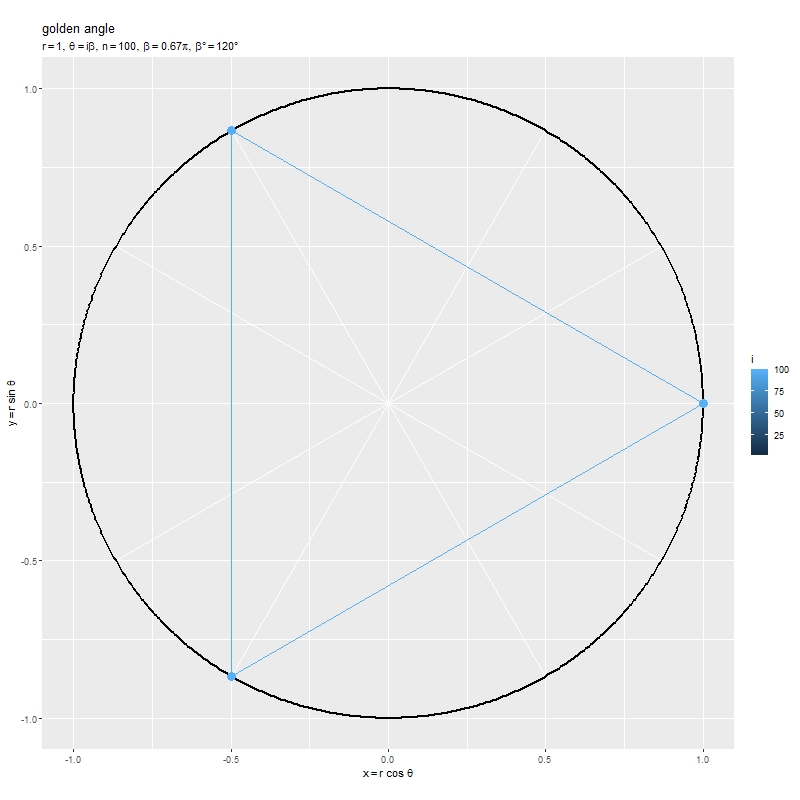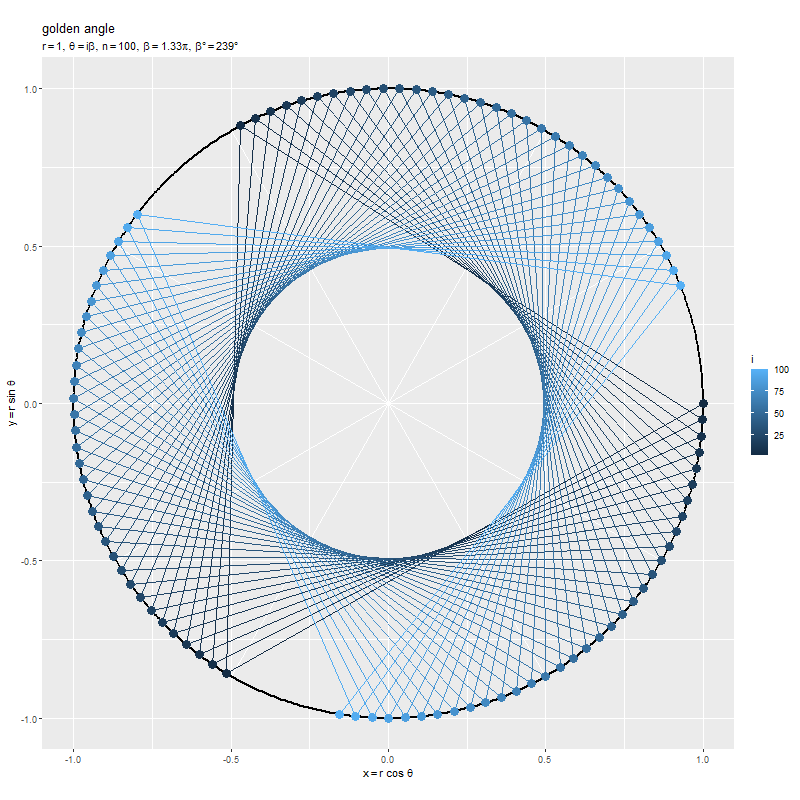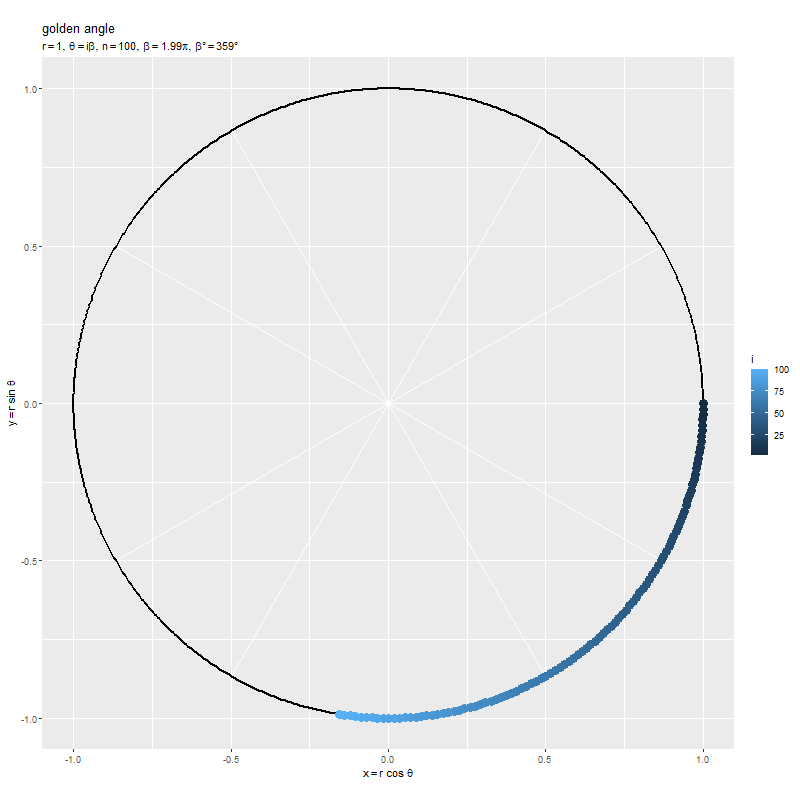
　点の数 $n$ を固定して、点間の角度 $\beta$ を大きくしていきます。
　円周上の点の周期は $2 \pi$ なので、 $\frac{2 \pi}{\theta_i}$ の余りが一致する点は重なります。また、点間の角度 $\beta$ が半周期 $\pi$ に近いほど次の番号の点が遠く(線分が長く・直径に近く)なり、 $0$ または $2 \pi$ に近いほどが近く(線分が短く)なるのを確認できます。

円周上の点とsin曲線・cos曲線の関係

　最後は、黄金角による円周上の点とsin関数・cos関数の曲線上の点のグラフを作成して、パラメータと座標の関係を確認します。
　作図コードについては「GitHub - anemptyarchive/Mathematics: 数学ノート」、作図の解説については「【R】cos関数の可視化 - からっぽのしょこ」などを参照してください。

パラメータと座標の関係

　パラメータに応じて変化するsin曲線・cos曲線上の点のアニメーションを作成します。

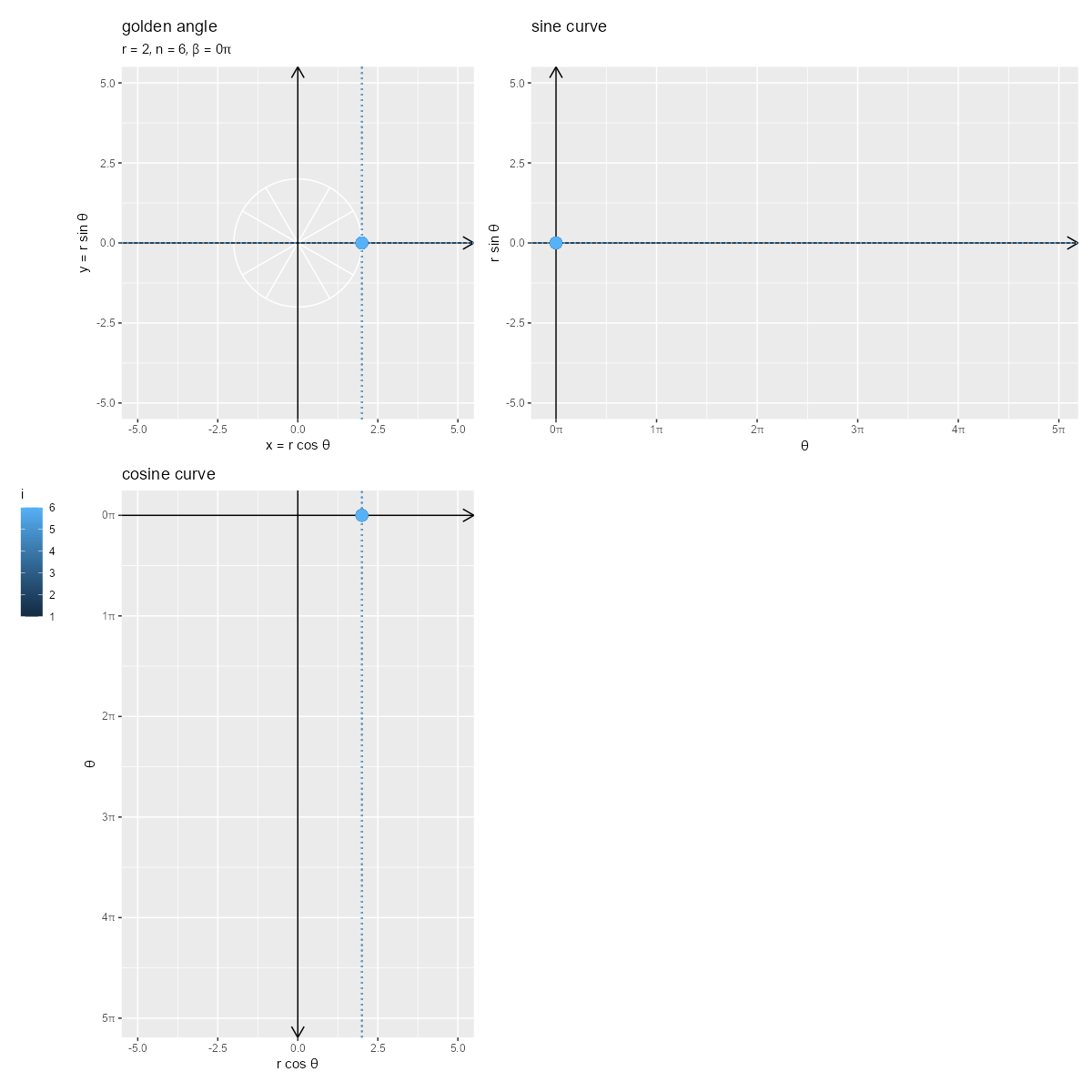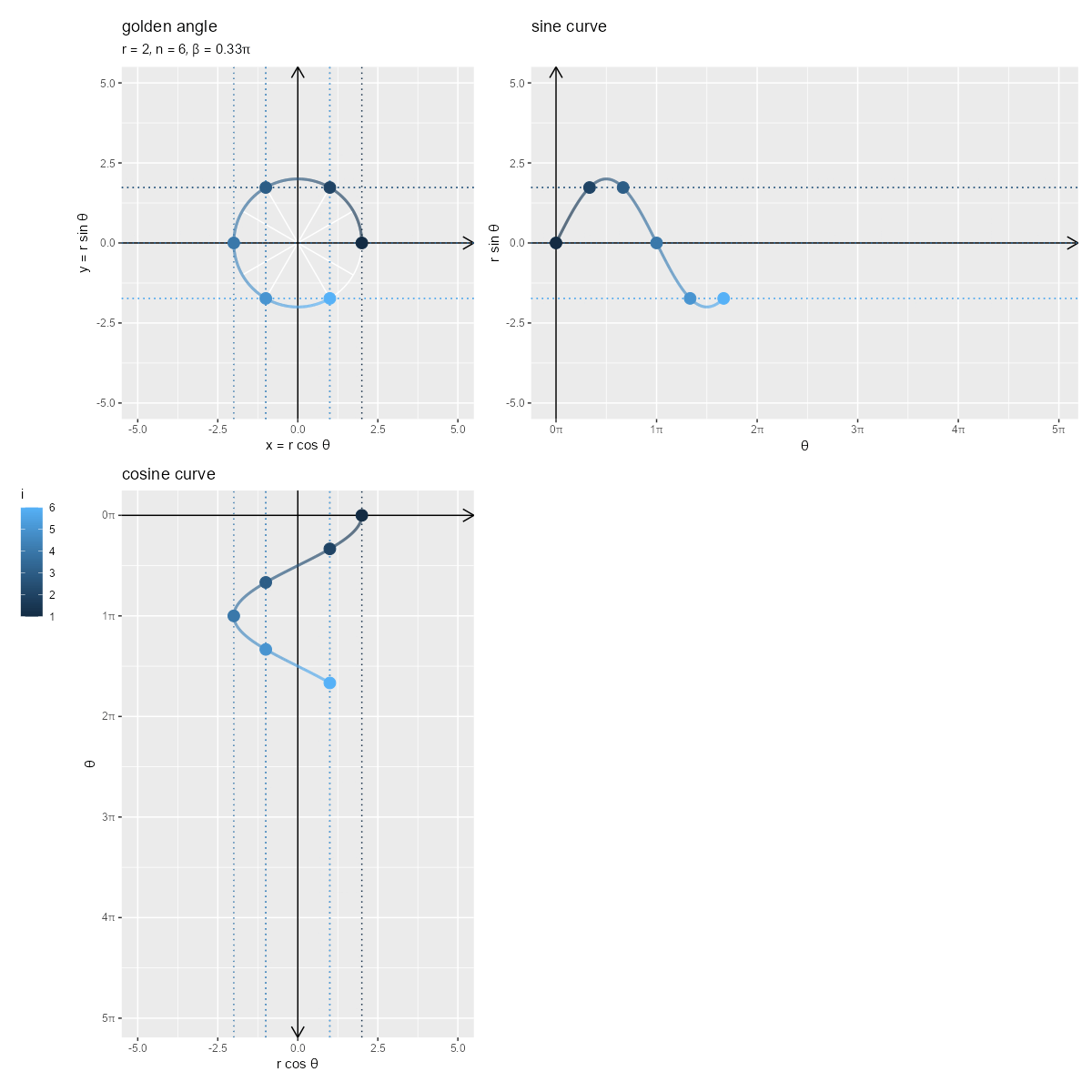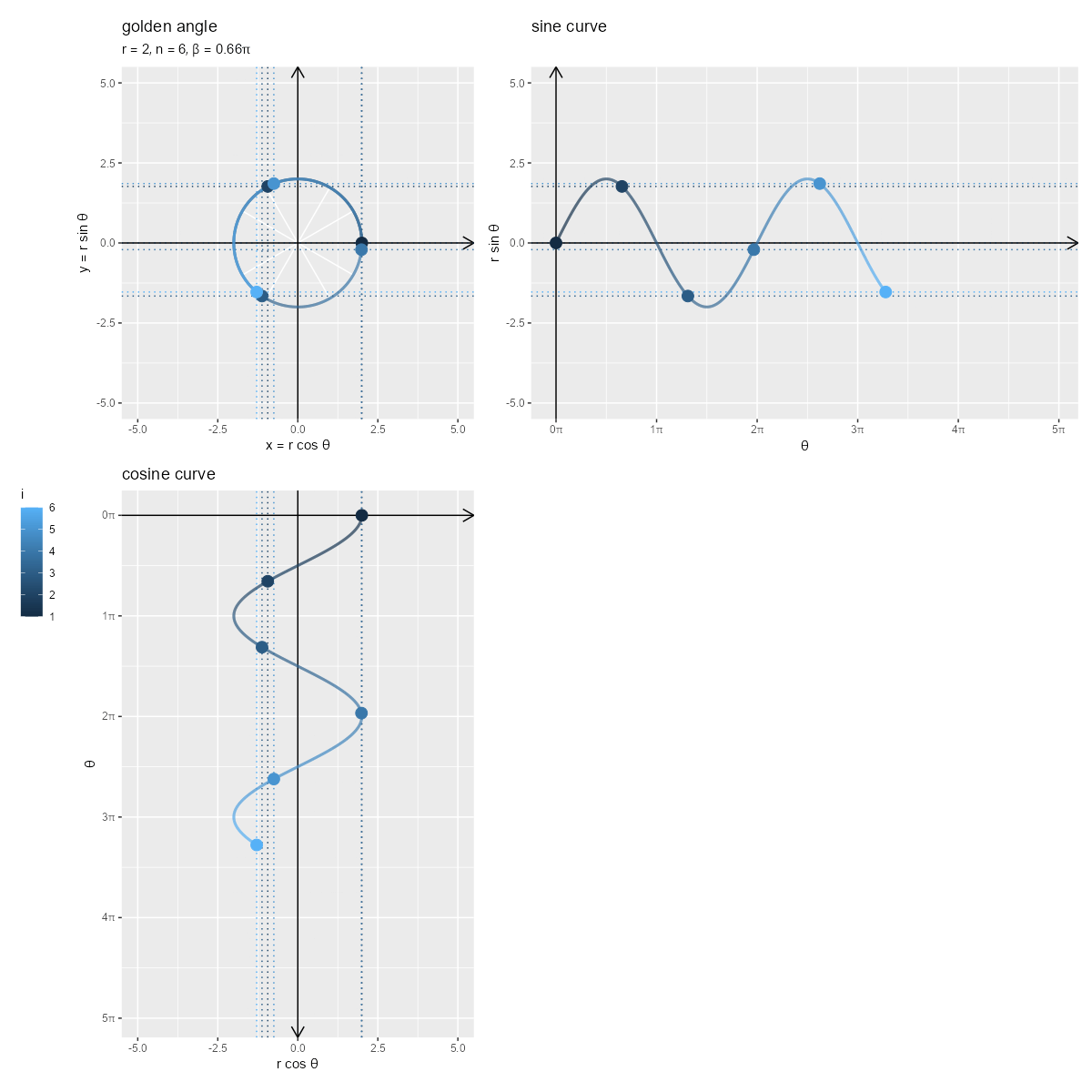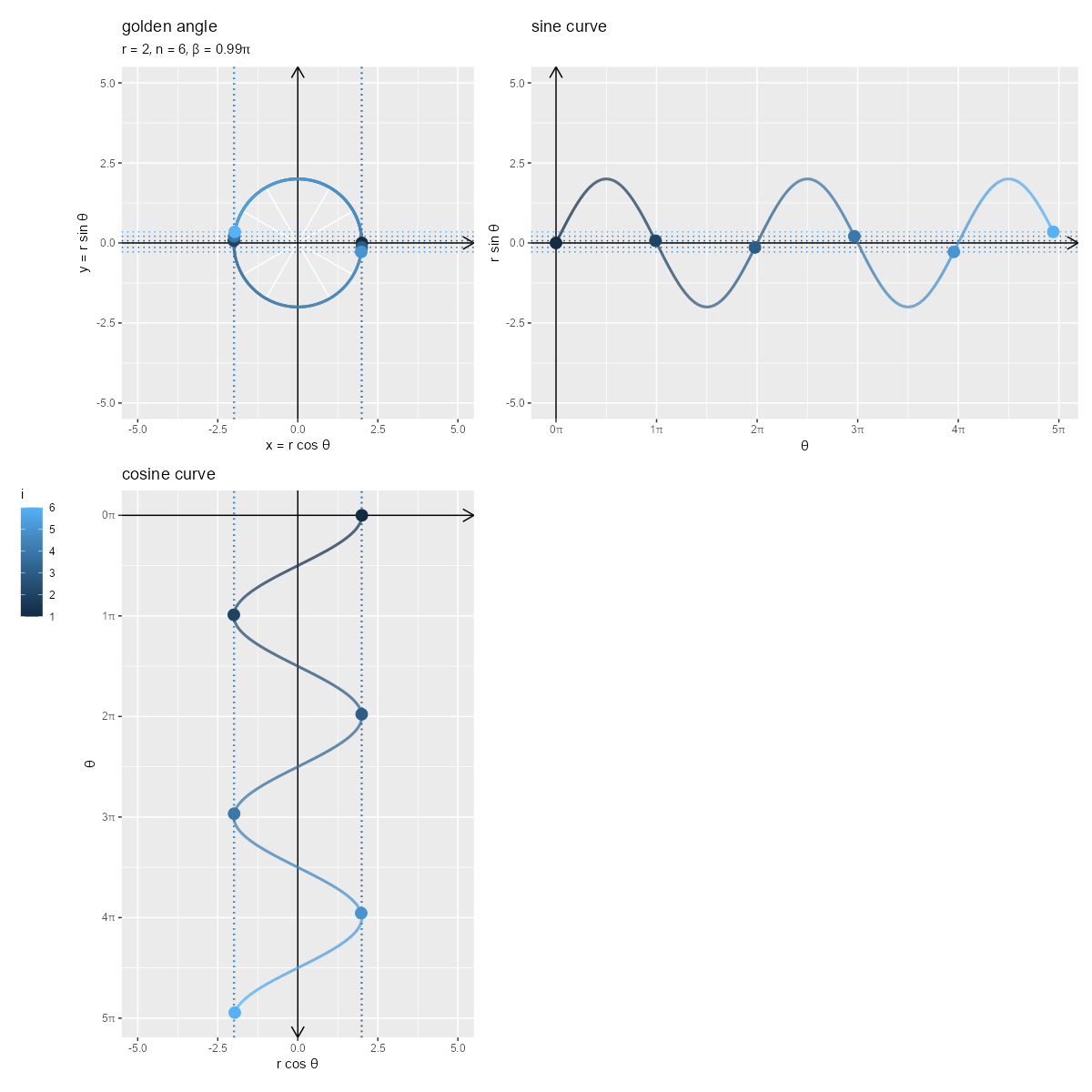
　円周上の点のx軸方向の変化とy軸方向の変化が、それぞれcos関数曲線上の点とsin関数曲線上の点に対応しているのを確認できます。
　点間の角度(ラジアン) $\beta$ が大きいほど偏角(ラジアン) $\theta$ の範囲が大きくなるので、曲線の範囲も広がります。

　ちなみに、点番号 $i$ に応じて中心から距離をとる(偏角 $\theta$ はそのまま距離 $r$ を変化させる)とフォーゲルの螺旋になります。

　この記事では、黄金角の性質をグラフで確認しました。次の記事では、黄金角を用いた螺旋をグラフで確認します。

参考書籍

『曲線と曲面（改訂版）－微分幾何的アプローチ－』梅原雅顕・山田光太郎,裳華房,2015年.

おわりに

　フィボナッチ数列について書いて黄金比についてはお茶を濁し、黄金角について書いてフェルマー螺旋に戻るつもりだったのですが、なんやかやで黄金比についても並行して書き始めました。それも複数記事になりそうです。内容的な繋がりと作業順が破綻しており、頭の中がとっ散らかって捗りません。が、年内にやっておきたいことがまだいくつかあるので、黄金比シリーズは今月中には終わらせたーい。

　2023年11月11日は、モーニング娘。'23の櫻井梨央さんの18歳のお誕生日です。

　まだ加入して1年半の新人とは思えないほど馴染んでいて末恐ろしい(誉め言葉)です。
　らいりーも然りですが、最近の若い人って表情が可愛いというよりも表情の変化も含めて可愛いという印象を受けます。これがショート動画世代ってことなのか。

【次の内容】

つづく

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【R】黄金角の性質の可視化

はじめに

黄金角の性質の可視化

黄金角の性質

黄金角と点の間隔の関係

パラメータと点の位置の関係

変数と点の位置の関係

パラメータと点の間隔の関係

円周上の点とsin曲線・cos曲線の関係

パラメータと座標の関係

参考書籍

おわりに