はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語で1次元ガウス分布(一変量正規分布)のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
1次元ガウス分布の作図
1次元ガウス分布(Gaussian Distribution)のグラフを作成します。ガウス分布については「1次元ガウス分布の定義式の確認 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、ガウス分布の定義式を確認します。
ガウス分布は、次の式で定義されます。
ここで、$\mu$は平均パラメータ、$\sigma$は標準偏差パラメータ、$\pi$は円周率です。$\sigma$の2乗を分散パラメータ$\sigma^2$、分散パラメータの逆数を精度パラメータ$\lambda = \frac{1}{\sigma^2}$と呼びます。
$x$は実数をとり、$\mu$は実数、$\sigma$は正の実数を満たす必要があります。
ガウス分布の期待値・分散・最頻値は、次の式で計算できます。詳しくはいつか書きます。
これらの計算を行いグラフを作成します。
グラフの作成
ggplot2パッケージを利用して、ガウス分布のグラフを作成します。ガウス分布の確率や統計量の計算については「【R】1次元ガウス分布の計算 - からっぽのしょこ」を参照してください。
ガウス分布のパラメータ$\mu, \sigma$を設定します。
# 平均パラメータを指定 mu <- 0 # 標準偏差パラメータを指定 sigma <- 1
平均パラメータ(実数)$\mu$と標準偏差パラメータ(正の実数)$\sigma$を計算します。
ガウス分布の確率変数がとり得る値$x$を作成します。
# xの値を作成 x_vals <- seq(from = mu - sigma*4, to = mu + sigma*4, length.out = 251)
実数$x$の値を作成してx_valsとします。この例では、muを中心に4倍を範囲とします。
$x$の値ごとの確率密度を計算します。
# ガウス分布を計算 dens_df <- tidyr::tibble( x = x_vals, # 確率変数 density = dnorm(x = x_vals, mean = mu, sd = sigma) # 確率密度 ) dens_df
## # A tibble: 251 × 2 ## x density ## <dbl> <dbl> ## 1 -4 0.000134 ## 2 -3.97 0.000152 ## 3 -3.94 0.000173 ## 4 -3.90 0.000196 ## 5 -3.87 0.000221 ## 6 -3.84 0.000251 ## 7 -3.81 0.000283 ## 8 -3.78 0.000320 ## 9 -3.74 0.000361 ## 10 -3.71 0.000406 ## # … with 241 more rows
ガウス分布の確率密度は、dnorm()で計算できます。確率変数の引数xにx_vals、平均の引数meanにmu、標準偏差の引数sdにsigmaを指定します。
x_valsと、x_valsの各要素に対応する確率密度をデータフレームに格納します。
ガウス分布のグラフを作成します。
# ガウス分布のグラフを作成 ggplot(data = dens_df, mapping = aes(x = x, y = density)) + # データ geom_line(color = "#00A968", size = 1) + # 折れ線グラフ labs( title = "Gaussian Distribution", subtitle = paste0("mu=", mu, ", sigma=", sigma), # (文字列表記用) #subtitle = parse(text = paste0("list(mu==", mu, ", sigma==", sigma, ")")), # (数式表記用) x = "x", y = "density" ) # ラベル
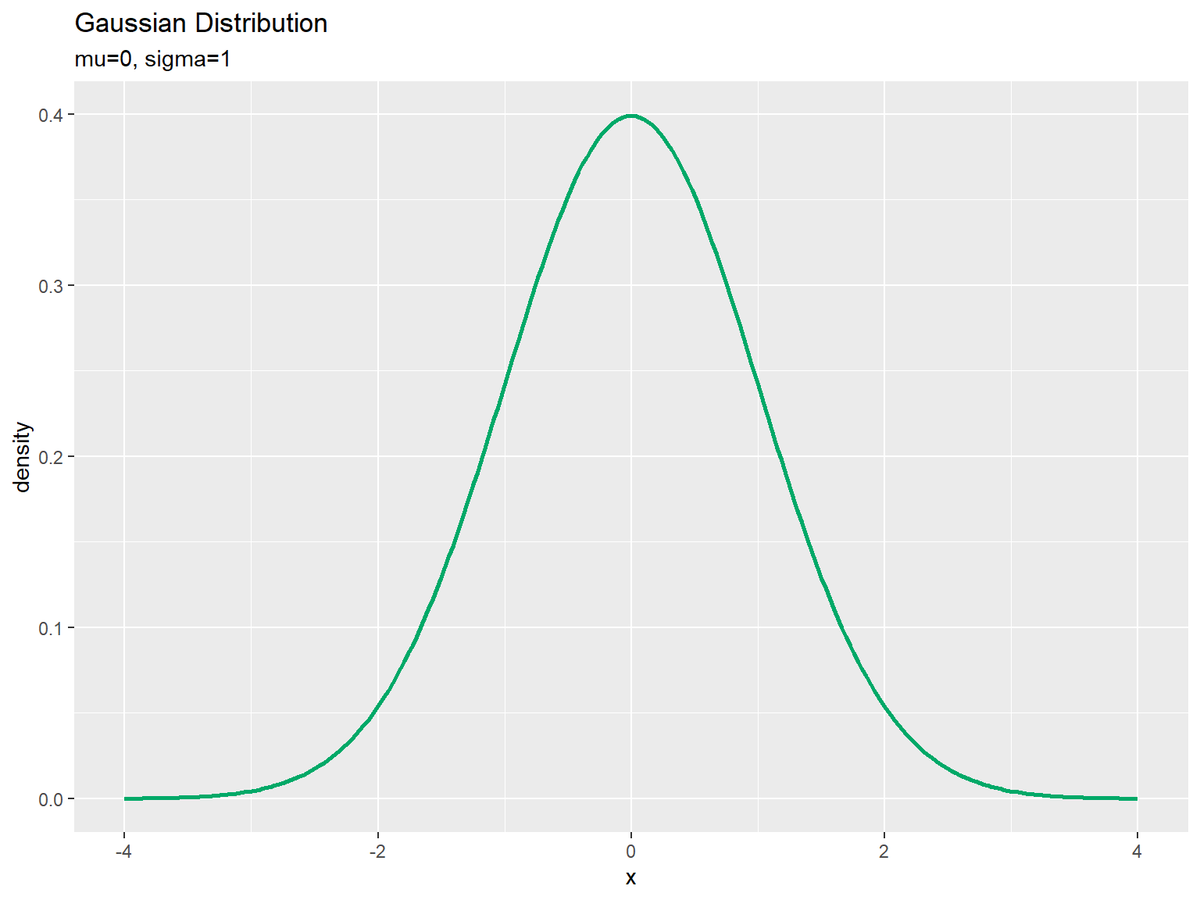
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
この分布に統計量の情報を重ねて表示します。
# 統計量を重ねたガウス分布のグラフを作成:線のみ ggplot(data = dens_df, mapping = aes(x = x, y = density)) + # データ geom_line(color = "#00A968", size = 1) + # 分布 geom_vline(xintercept = mu, color = "blue", size = 1, linetype = "dashed") + # 期待値 geom_vline(xintercept = mu-sigma, color = "orange", size = 1, linetype = "dotted") + # 期待値 - 標準偏差 geom_vline(xintercept = mu+sigma, color = "orange", size = 1, linetype = "dotted") + # 期待値 + 標準偏差 labs( title = "Gaussian Distribution", subtitle = parse(text = paste0("list(mu==", mu, ", sigma==", sigma, ")")), x = "x", y = "density" ) # ラベル
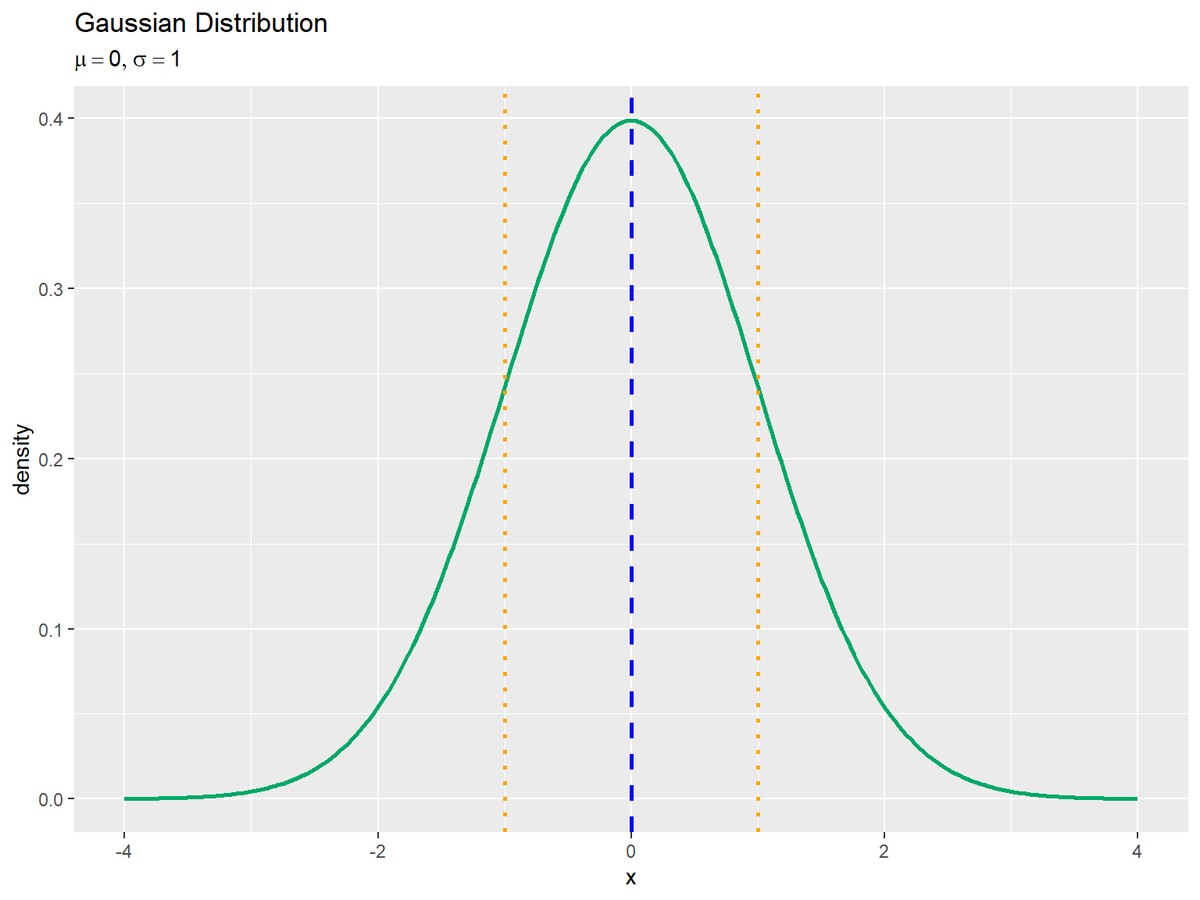
期待値・標準偏差(分散の平方根)を計算して、それぞれgeom_vline()で垂直線を引きます。標準偏差については期待値から足し引きした値を使います。
凡例を表示する場合は、垂直線を引く値をデータフレームにまとめます。
# 統計量を格納 stat_df <- tibble::tibble( statistic = c(mu, mu-sigma, mu+sigma), # 統計量 type = c("mean", "sd", "sd") # 色分け用ラベル ) stat_df
## # A tibble: 3 × 2 ## statistic type ## <dbl> <chr> ## 1 0 mean ## 2 -1 sd ## 3 1 sd
各統計量を区別するための文字列も格納します。期待値と標準偏差の差・和は同じラベルとします。
線の色や種類、凡例テキストを指定する場合は、設定用の名前付きベクトルを作成します。
# 凡例用の設定を作成:(数式表示用) color_vec <- c(mean = "blue", sd = "orange") linetype_vec <- c(mean = "dashed", sd = "dotted") label_vec <- c(mean = expression(E(x)), sd = expression(E(x) %+-% sqrt(V(x)))) color_vec; linetype_vec; label_vec
## mean sd ## "blue" "orange" ## mean sd ## "dashed" "dotted" ## expression(mean = E(x), sd = E(x) %+-% sqrt(V(x)))
各要素(設定)の名前をtype列の文字列と対応させて、設定(線の色・種類と数式用のテキスト)を指定します。
凡例付きのグラフを作成します。
# 統計量を重ねたガウス分布のグラフを作成:凡例付き ggplot() + geom_line(data = dens_df, mapping = aes(x = x, y = density), color = "#00A968", size = 1) + # 分布 geom_vline(data = stat_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1) + # 期待値 scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(色指定と数式表示用) scale_linetype_manual(values = linetype_vec, labels = label_vec, name = "statistic") + # 線の種類:(線指定と数式表示用) guides(color = guide_legend(override.aes = list(size = 0.5))) + # 凡例の体裁 theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Gaussian Distribution", subtitle = parse(text = paste0("list(mu==", mu, ", sigma==", sigma, ")")), x = "x", y = "density") # ラベル
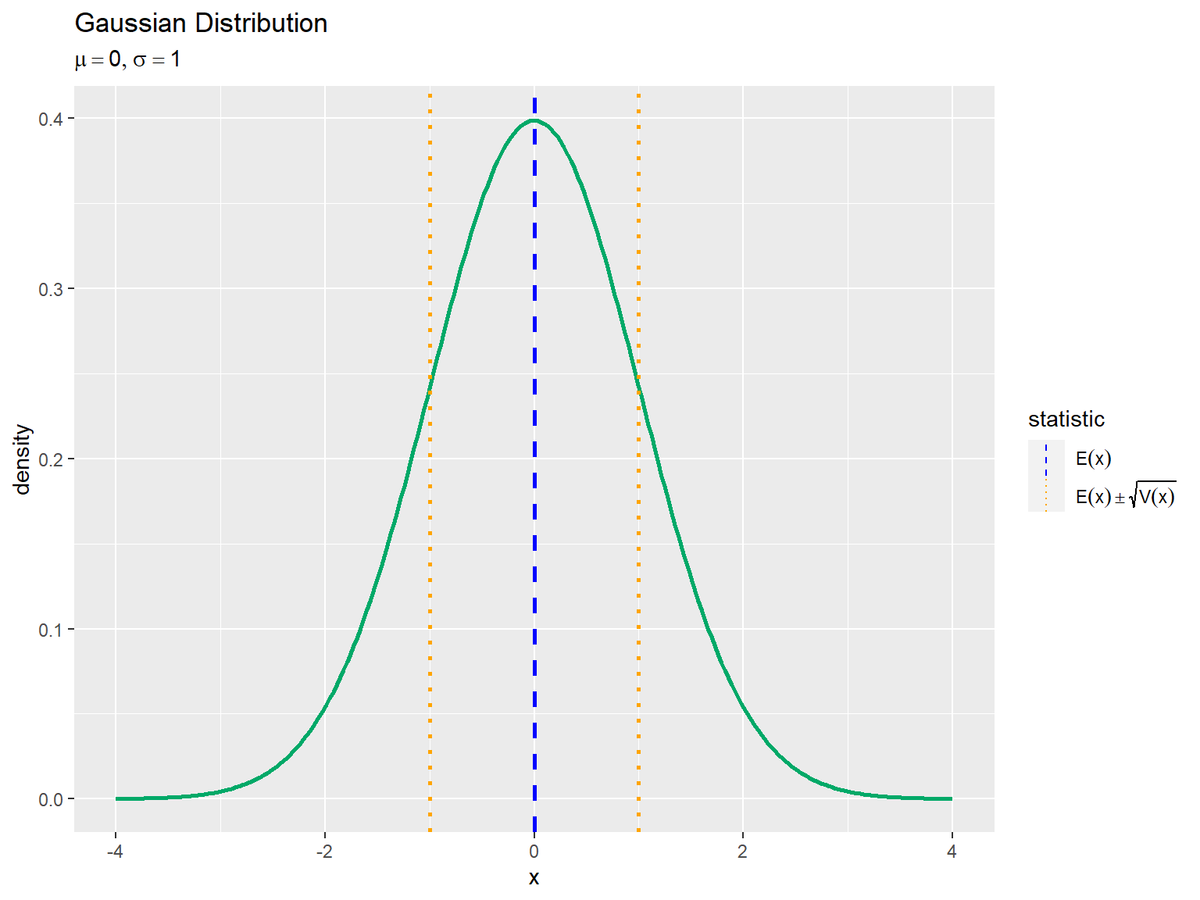
scale_color_manual()のvalues引数に線の色、scale_linetype_manual()のvalues引数に線の種類を指定します。凡例テキストを指定する場合は、それぞれのlabels引数に指定します。names引数は凡例ラベルです。
凡例テキストは、theme()のlegend.text.align引数に0を指定すると左寄せ、デフォルト(1)だと右寄せになります。
ガウス分布のグラフを描画できました。以降は、ここまでの作図処理を用いて、パラメータの影響を確認していきます。
パラメータと分布の関係を並べて比較
複数のパラメータのグラフを比較することで、パラメータの値と分布の形状の関係を確認します。
平均の影響
複数の$\mu$を指定し、$\sigma$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# 平均パラメータとして利用する値を指定 mu_vals <- c(-3.5, -2, -0.5, 1, 2.5, 4) # 標準偏差パラメータを指定 sigma <- 1 # xの値を作成 x_vals <- seq(from = min(mu_vals) - sigma*2, to = max(mu_vals) + sigma*2, length.out = 251) # パラメータごとにガウス分布を計算 res_dens_df <- tidyr::expand_grid( x = x_vals, mu = mu_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(mu, x) |> # パラメータごとに並べ替え dplyr::mutate( density = dnorm(x = x, mean = mu, sd = sigma), parameter = paste0("mu=", mu, ", sigma=", sigma) |> factor(levels = paste0("mu=", sort(mu_vals), ", sigma=", sigma)) # 色分け用ラベル ) # 確率密度を計算 res_dens_df
## # A tibble: 1,506 × 4 ## x mu density parameter ## <dbl> <dbl> <dbl> <fct> ## 1 -5.5 -3.5 0.0540 mu=-3.5, sigma=1 ## 2 -5.45 -3.5 0.0591 mu=-3.5, sigma=1 ## 3 -5.41 -3.5 0.0646 mu=-3.5, sigma=1 ## 4 -5.36 -3.5 0.0705 mu=-3.5, sigma=1 ## 5 -5.32 -3.5 0.0767 mu=-3.5, sigma=1 ## 6 -5.27 -3.5 0.0833 mu=-3.5, sigma=1 ## 7 -5.22 -3.5 0.0903 mu=-3.5, sigma=1 ## 8 -5.18 -3.5 0.0976 mu=-3.5, sigma=1 ## 9 -5.13 -3.5 0.105 mu=-3.5, sigma=1 ## 10 -5.09 -3.5 0.113 mu=-3.5, sigma=1 ## # … with 1,496 more rows
確率変数x_valsとパラメータmu_valsそれぞれの要素の全ての組み合わせをexpand_grid()で作成します。
組み合わせごとに確率密度を計算して、パラメータごとにラベルを作成します。ラベルは、グラフの設定や凡例テキストとして使います。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
凡例を数式で表示する場合は、expression()に対応した記法に変換します。
# 凡例用のラベルを作成:(数式表示用) label_vec <- res_dens_df[["parameter"]] |> stringr::str_replace_all(pattern = "=", replacement = "==") |> # 等号表示用の記法に変換 (\(.){paste0("list(", ., ")")})() |> # カンマ表示用の記法に変換 unique() |> # 重複を除去 parse(text = _) # expression関数化 names(label_vec) <- unique(res_dens_df[["parameter"]]) # ggplotに指定する文字列に対応する名前付きベクトルに変換 label_vec[1]
## expression(`mu=-3.5, sigma=1` = list(mu == -3.5, sigma == 1))
変換後の文字列のベクトルに対してnames()を使って、元の文字列を各要素の名前として設定します。
3行目の処理では、無名関数function()の省略記法\()を使って、(\(引数){引数を使った具体的な処理})()としています。直前のパイプ演算子を%>%にすると、行全体(\(引数){処理})()を{}の中の処理(この例だとpaste0("list(", ., ")"))に置き換えられます(置き換えられるように引数名を.にしています)。
res_prob_dfのparameter列の要素mu=-3.5, sigma=1と、変換後の文字列list(mu == -3.5, sigma == 1)が対応しています。
パラメータごとにグラフを作成します。
# パラメータごとにガウス分布を作図 ggplot(data = res_dens_df, mapping = aes(x = x, y = density, color = parameter)) + # データ geom_line(size = 1) + # 折れ線グラフ scale_color_hue(labels = label_vec) + # 線の色:(数式表示用) theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Gaussian Distribution", x = "x", y = "density") # ラベル
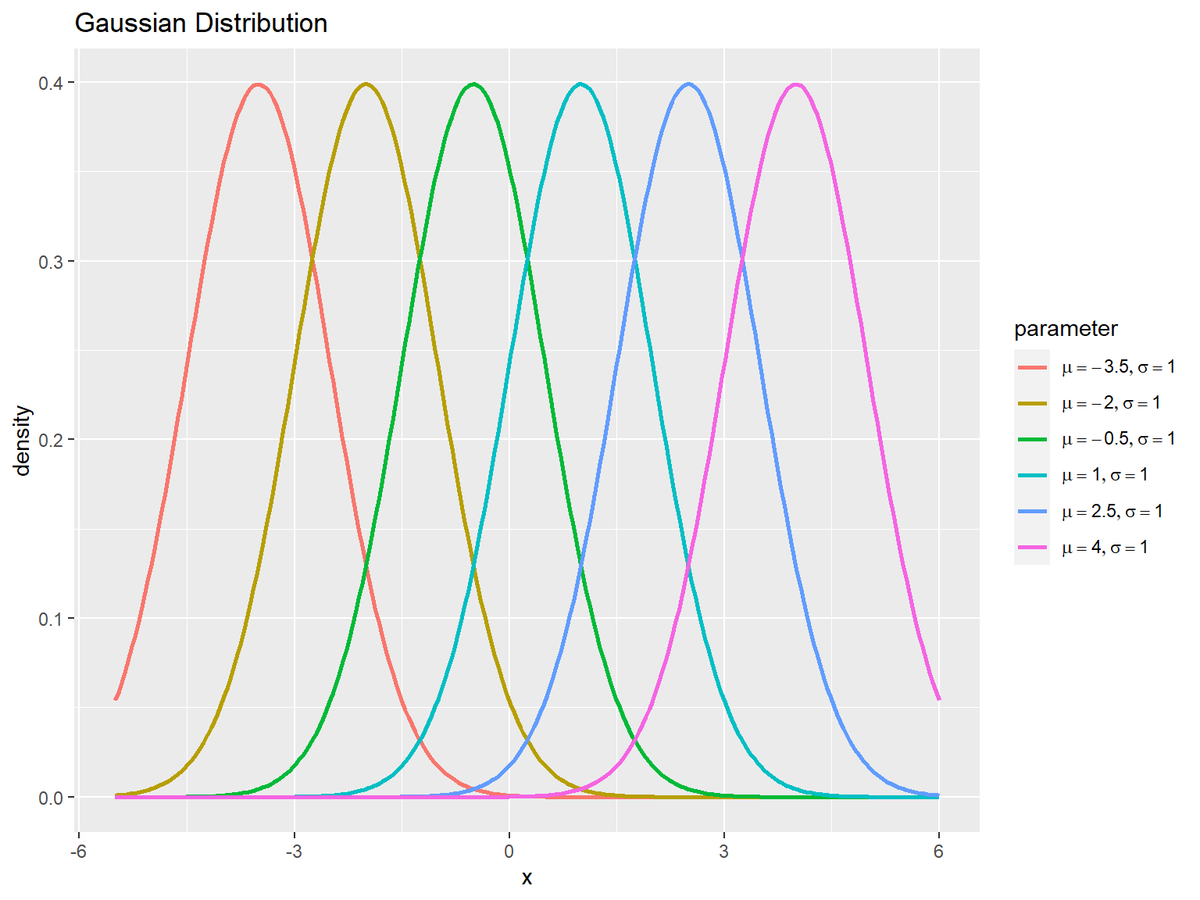
$\mu$が大きいほど山が右に移動します。
標準偏差の影響
続いて、$\mu$を固定し、複数の$\sigma$を指定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# 平均パラメータを指定 mu <- 0 # 標準偏差パラメータとして利用する値を指定 sigma_vals <- c(0.5, 1, 2, 4) # xの値を作成 x_vals <- seq(from = mu - max(sigma_vals)*1.5, to = mu + max(sigma_vals)*1.5, length.out = 250) # パラメータごとにガウス分布を計算 res_dens_df <- tidyr::expand_grid( x = x_vals, sigma = sigma_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(sigma, x) |> # パラメータごとに並べ替え dplyr::mutate( density = dnorm(x = x, mean = mu, sd = sigma), parameter = paste0("mu=", mu, ", sigma=", sigma) |> factor(levels = paste0("mu=", mu, ", sigma=", sort(sigma_vals))) # 色分け用ラベル ) # 確率密度を計算 res_dens_df
## # A tibble: 1,000 × 4 ## x sigma density parameter ## <dbl> <dbl> <dbl> <fct> ## 1 -6 0.5 4.29e-32 mu=0, sigma=0.5 ## 2 -5.95 0.5 1.36e-31 mu=0, sigma=0.5 ## 3 -5.90 0.5 4.26e-31 mu=0, sigma=0.5 ## 4 -5.86 0.5 1.32e-30 mu=0, sigma=0.5 ## 5 -5.81 0.5 4.07e-30 mu=0, sigma=0.5 ## 6 -5.76 0.5 1.24e-29 mu=0, sigma=0.5 ## 7 -5.71 0.5 3.75e-29 mu=0, sigma=0.5 ## 8 -5.66 0.5 1.12e-28 mu=0, sigma=0.5 ## 9 -5.61 0.5 3.33e-28 mu=0, sigma=0.5 ## 10 -5.57 0.5 9.78e-28 mu=0, sigma=0.5 ## # … with 990 more rows
x_valsとsigma_valsの全ての組み合わせを作成して、同様に処理します。
作図については同じコードで処理できます。
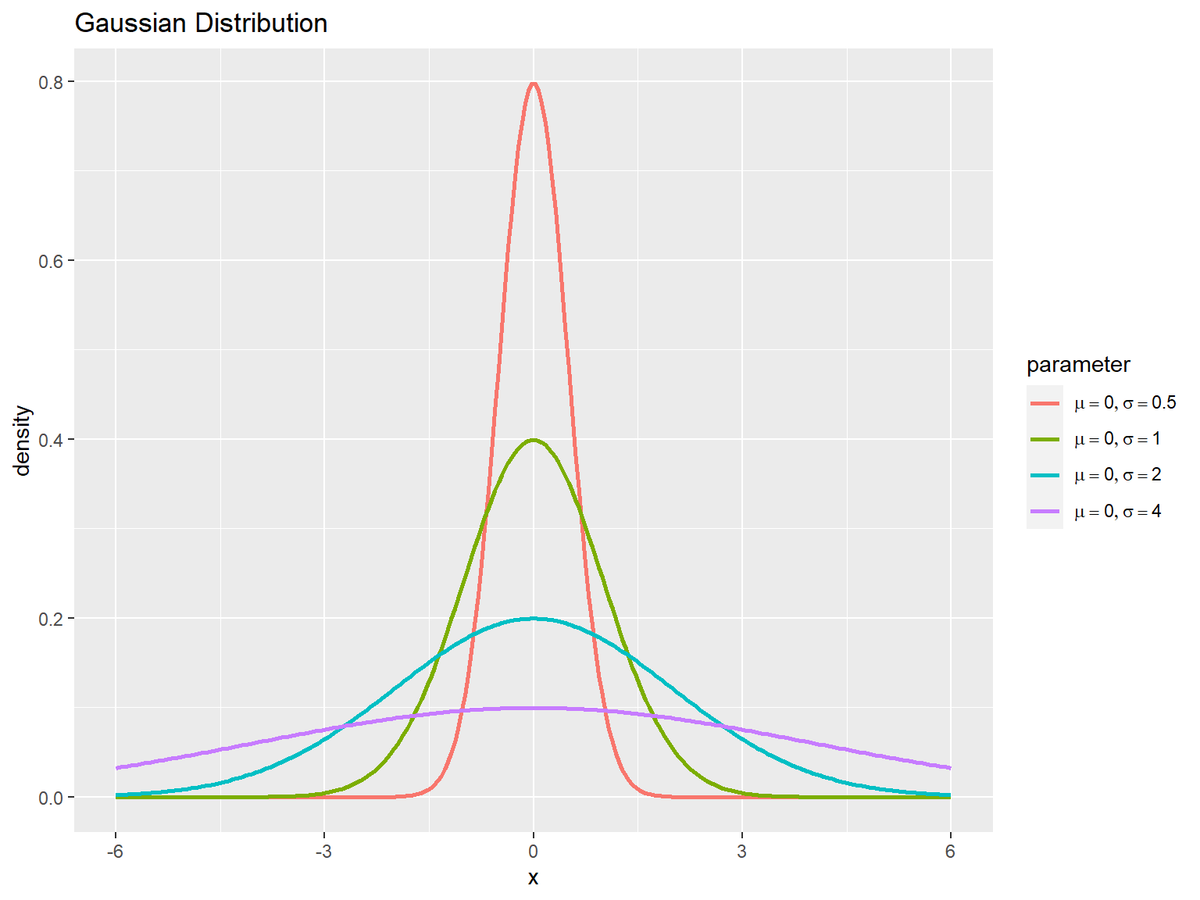
$\sigma$が小さいほど、山が細く高くなります。
精度の影響
$\mu$を固定し、$\sigma$の代わりに複数の$\lambda$を指定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# 平均パラメータを指定 mu <- 0 # 標準偏差パラメータとして利用する値を指定 lambda_vals <- c(0.25, 0.5, 1, 2, 4) # xの値を作成 sigma <- 1 / sqrt(min(lambda_vals)) x_vals <- seq(from = mu - sigma*3, to = mu + sigma*3, length.out = 250) # パラメータごとにガウス分布を計算 res_dens_df <- tidyr::expand_grid( x = x_vals, lambda = lambda_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(lambda, x) |> # パラメータごとに並べ替え dplyr::mutate( density = dnorm(x = x, mean = mu, sd = 1/sqrt(lambda)), parameter = paste0("mu=", mu, ", lambda=", lambda) |> factor(levels = paste0("mu=", mu, ", lambda=", sort(lambda_vals))) # 色分け用ラベル ) # 確率密度を計算 res_dens_df
## # A tibble: 1,250 × 4 ## x lambda density parameter ## <dbl> <dbl> <dbl> <fct> ## 1 -6 0.25 0.00222 mu=0, lambda=0.25 ## 2 -5.95 0.25 0.00238 mu=0, lambda=0.25 ## 3 -5.90 0.25 0.00256 mu=0, lambda=0.25 ## 4 -5.86 0.25 0.00275 mu=0, lambda=0.25 ## 5 -5.81 0.25 0.00295 mu=0, lambda=0.25 ## 6 -5.76 0.25 0.00316 mu=0, lambda=0.25 ## 7 -5.71 0.25 0.00338 mu=0, lambda=0.25 ## 8 -5.66 0.25 0.00362 mu=0, lambda=0.25 ## 9 -5.61 0.25 0.00388 mu=0, lambda=0.25 ## 10 -5.57 0.25 0.00415 mu=0, lambda=0.25 ## # … with 1,240 more rows
x_valsとlambda_valsの全ての組み合わせを作成して、同様に処理します。
作図については同じコードで処理できます。
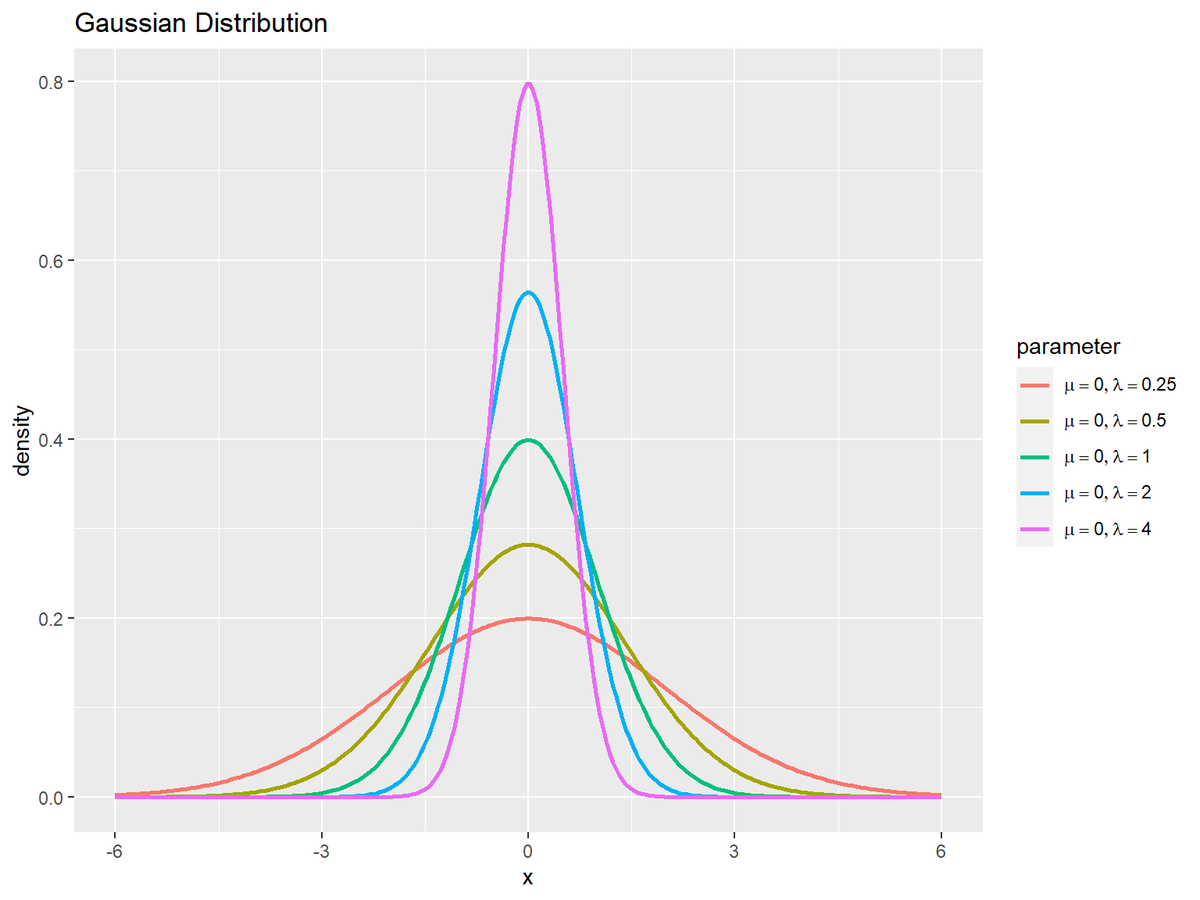
$\lambda$が大きいほど、山が細く高くなります。
パラメータと分布の形状の関係をアニメーションで可視化
前節では、複数のパラメータのグラフを並べて比較しました。次は、パラメータの値を少しずつ変化させて、分布の形状の変化をアニメーションで確認します。
平均の影響
$\mu$の値を変化させ、$\sigma$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# 平均パラメータとして利用する値を指定 mu_vals <- seq(from = -5, to = 5, by = 0.1) # (線の変化用) #mu_vals <- seq(from = -5, to = 5, by = 0.5) # (線の軌跡用) length(mu_vals) # フレーム数 # 標準偏差パラメータを指定 sigma <- 1 # xの値を作成 x_vals <- seq(from = min(mu_vals)-sigma, to = max(mu_vals)+sigma, length.out = 251) # パラメータごとにガウス分布を計算 anime_dens_df <- tidyr::expand_grid( x = x_vals, mu = mu_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(mu, x) |> # パラメータごとに並べ替え dplyr::mutate( density = dnorm(x = x, mean = mu, sd = sigma), parameter = paste0("mu=", round(mu, 2), ", sigma=", sigma) |> factor(levels = paste0("mu=", round(mu_vals, 2), ", sigma=", sigma)) # フレーム切替用ラベル ) # 確率密度を計算 anime_dens_df
## # A tibble: 25,351 × 4 ## x mu density parameter ## <dbl> <dbl> <dbl> <fct> ## 1 -6 -5 0.242 mu=-5, sigma=1 ## 2 -5.95 -5 0.254 mu=-5, sigma=1 ## 3 -5.90 -5 0.265 mu=-5, sigma=1 ## 4 -5.86 -5 0.277 mu=-5, sigma=1 ## 5 -5.81 -5 0.288 mu=-5, sigma=1 ## 6 -5.76 -5 0.299 mu=-5, sigma=1 ## 7 -5.71 -5 0.310 mu=-5, sigma=1 ## 8 -5.66 -5 0.320 mu=-5, sigma=1 ## 9 -5.62 -5 0.330 mu=-5, sigma=1 ## 10 -5.57 -5 0.340 mu=-5, sigma=1 ## # … with 25,341 more rows
値の間隔が一定になるようにmu_valsを作成します。パラメータごとにフレームを切り替えるので、mu_valsの要素数がアニメーションのフレーム数になります。
データフレームの変数名以外は「並べて比較」のときと同じ処理です。
ガウス分布のアニメーション(gif画像)を作成します。
# ガウス分布のアニメーションを作図 anime_dens_graph <- ggplot(data = anime_dens_df, mapping = aes(x = x, y = density)) + # データ geom_line(color = "#00A968", size = 1) + # 折れ線グラフ gganimate::transition_manual(parameter) + # フレーム labs(title = "Gaussian Distribution", subtitle = "{current_frame}", x = "x", y = "density") # ラベル # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(mu_vals), fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
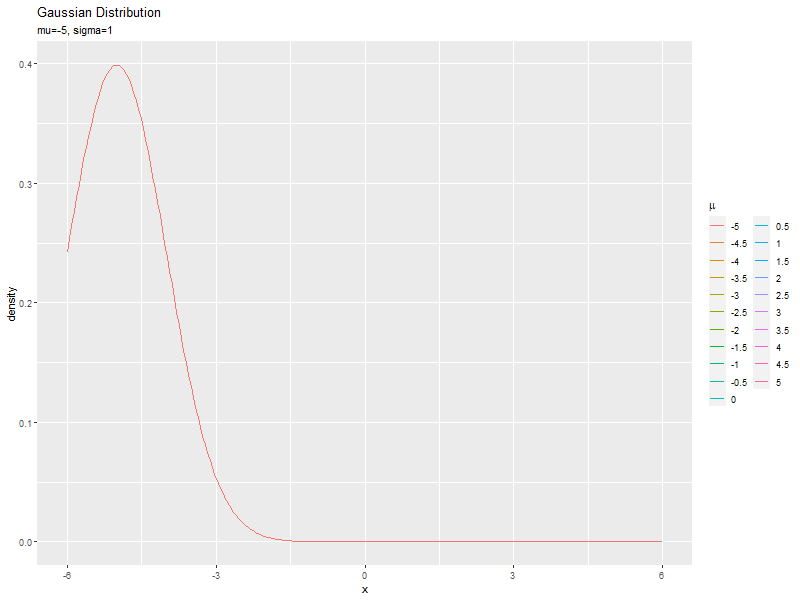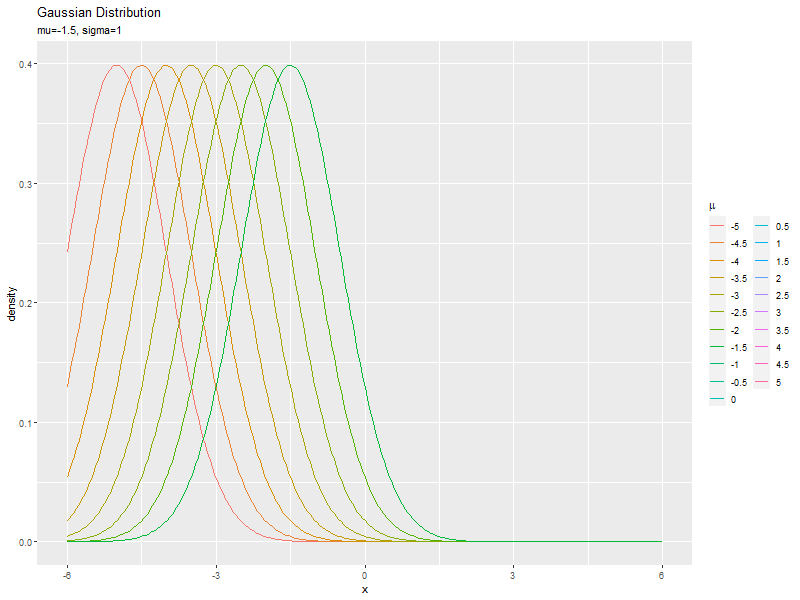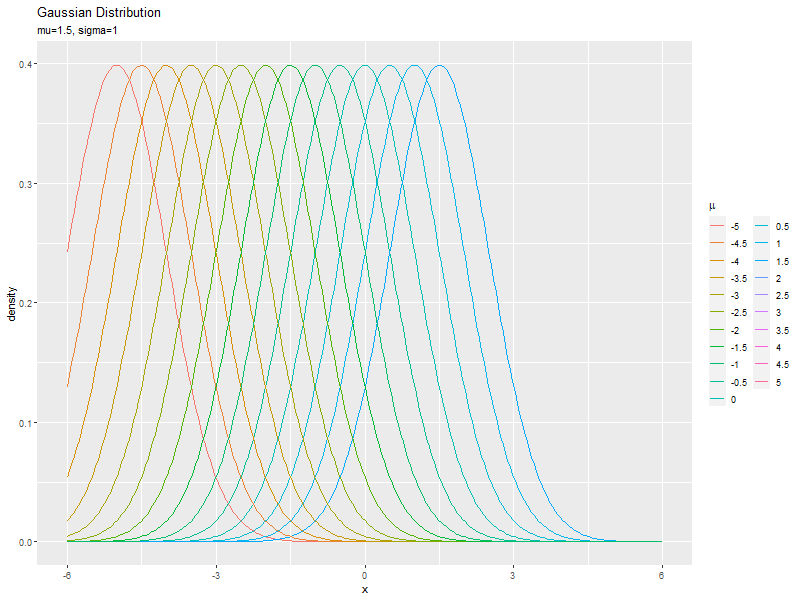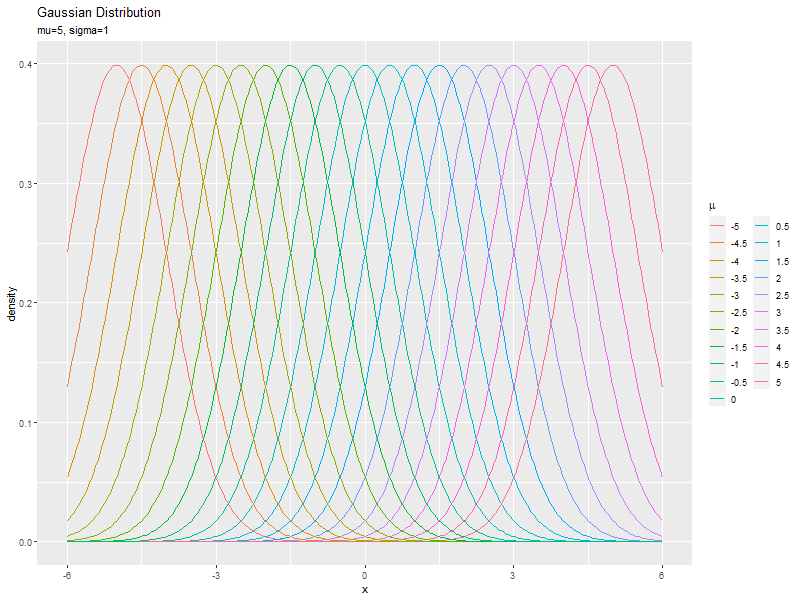
続いて、分布の変化の軌跡を描画するアニメーションを作成します。mu_valsの値の間隔を粗くしておきます。
# ガウス分布のアニメーションを作図 anime_dens_graph <- ggplot(data = anime_dens_df, mapping = aes(x = x, y = density, color = factor(mu), group = mu)) + # データ geom_line() + # 折れ線グラフ gganimate::transition_reveal(mu) + # フレーム labs(title = "Gaussian Distribution", subtitle = paste0("mu={frame_along}, sigma=", sigma), color = expression(mu), x = "x", y = "density") # ラベル # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(mu_vals)+10, end_pause = 10, fps = 10, width = 800, height = 600)
transition_reveal()を使ってフレームを切り替えると、過去フレームのグラフが表示され続けます。
animate()のend_pause引数を指定すると、最後のフレームでグラフが一時停止(最後のグラフを指定したフレーム数表示)します。
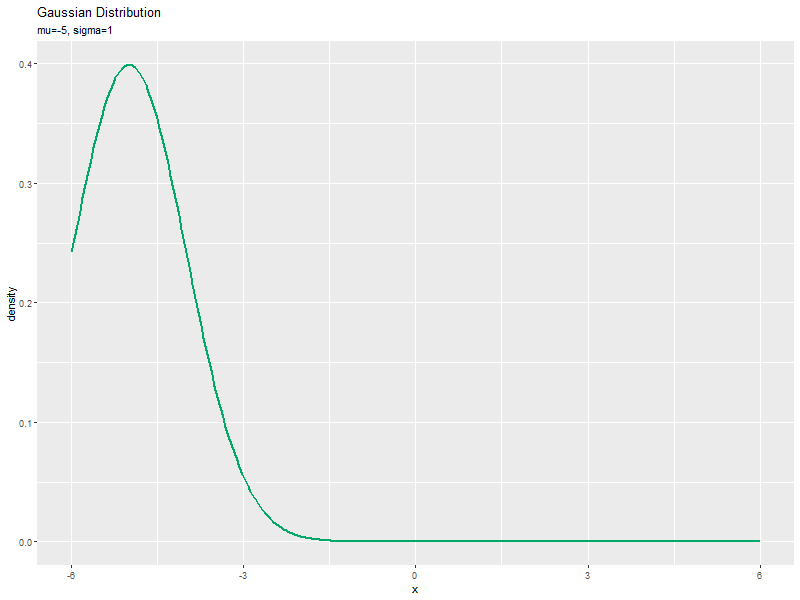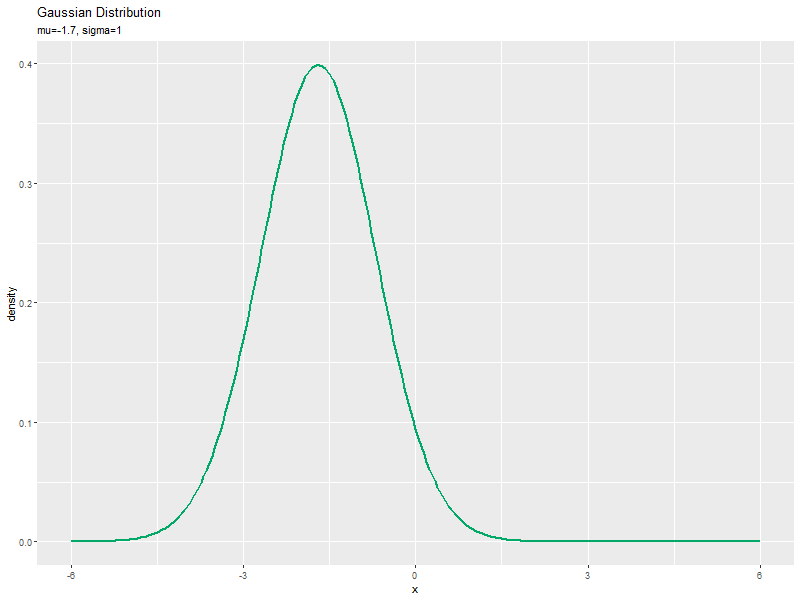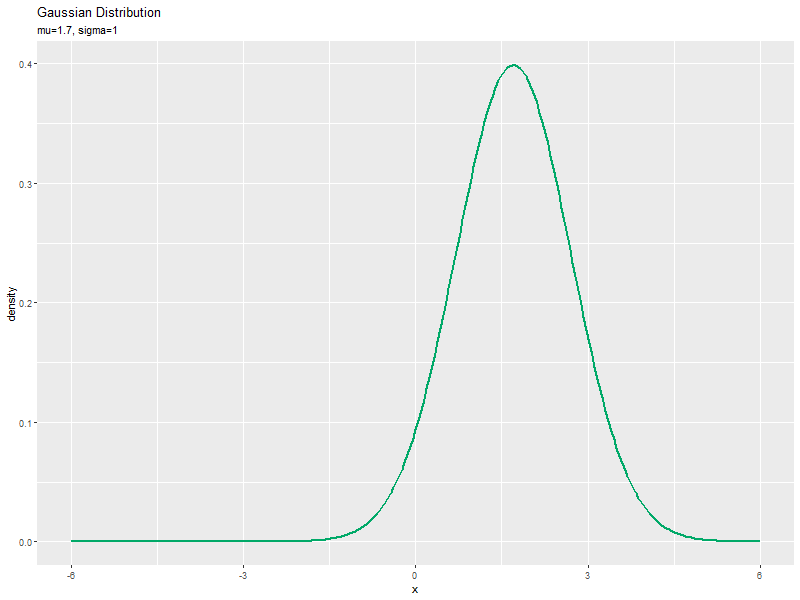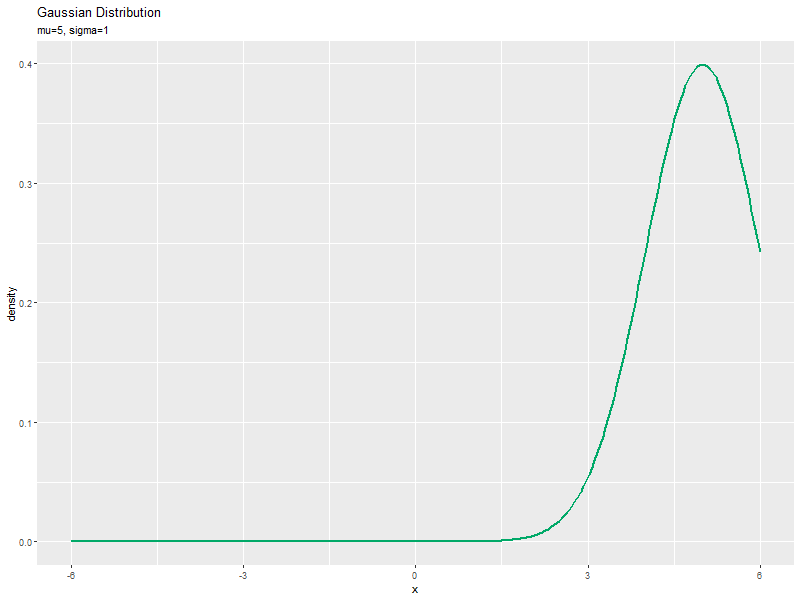
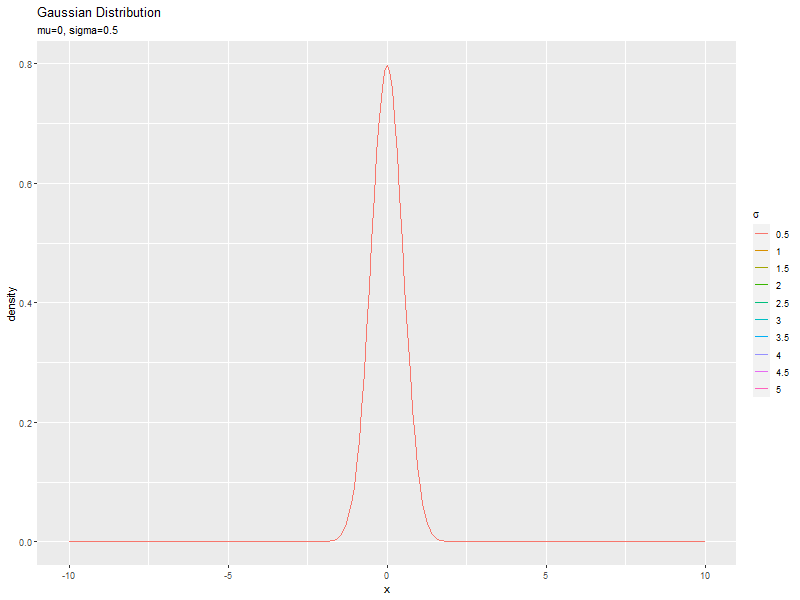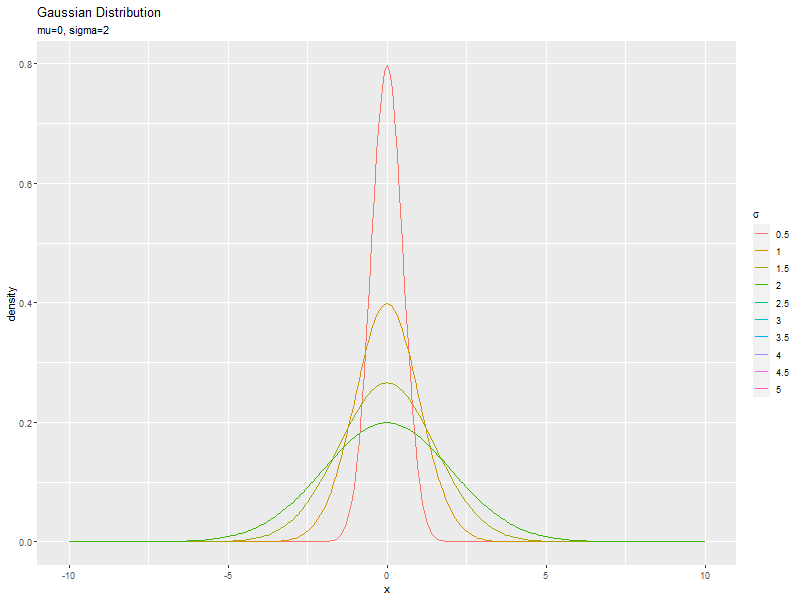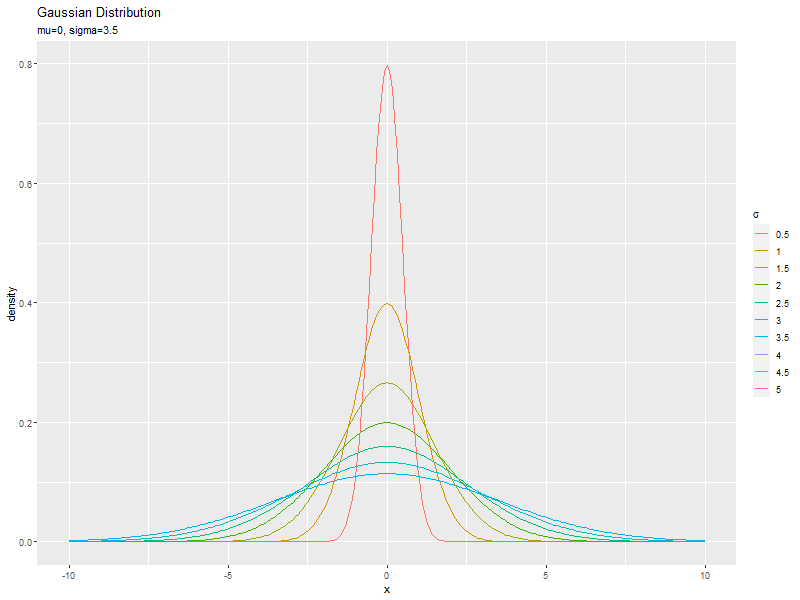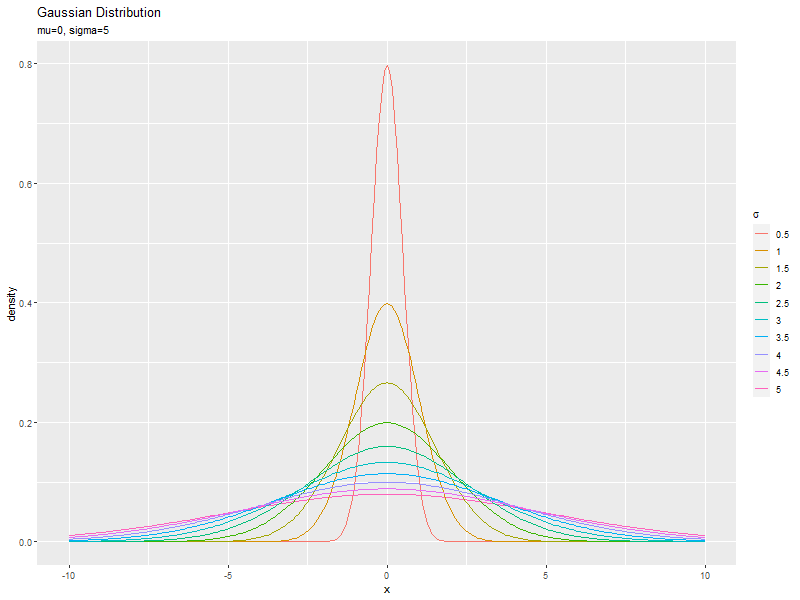
標準偏差の影響
続いて、$\mu$を固定し、$\sigma$の値を変化させて、それぞれ分布を計算します。
・作図コード(クリックで展開)
# 平均パラメータを指定 mu <- 0 # 標準偏差パラメータとして利用する値を指定 sigma_vals <- seq(from = 0.5, to = 5, by = 0.1) # (線の変化用) #sigma_vals <- seq(from = 0.5, to = 5, by = 0.5) # (線の軌跡用) length(sigma_vals) # フレーム数 # xの値を作成 x_vals <- seq(from = mu - max(sigma_vals)*2, to = mu + max(sigma_vals)*2, length.out = 251) # パラメータごとにガウス分布を計算 anime_dens_df <- tidyr::expand_grid( x = x_vals, sigma = sigma_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(sigma, x) |> # パラメータごとに並べ替え dplyr::mutate( density = dnorm(x = x, mean = mu, sd = sigma), parameter = paste0("mu=", mu, ", sigma=", round(sigma, 2)) |> factor(levels = paste0("mu=", mu, ", sigma=", round(sigma_vals, 2))) # フレーム切替用ラベル ) # 確率密度を計算 anime_dens_df
## # A tibble: 11,546 × 4 ## x sigma density parameter ## <dbl> <dbl> <dbl> <fct> ## 1 -10 0.5 1.10e-87 mu=0, sigma=0.5 ## 2 -9.92 0.5 2.67e-86 mu=0, sigma=0.5 ## 3 -9.84 0.5 6.31e-85 mu=0, sigma=0.5 ## 4 -9.76 0.5 1.45e-83 mu=0, sigma=0.5 ## 5 -9.68 0.5 3.26e-82 mu=0, sigma=0.5 ## 6 -9.6 0.5 7.12e-81 mu=0, sigma=0.5 ## 7 -9.52 0.5 1.52e-79 mu=0, sigma=0.5 ## 8 -9.44 0.5 3.15e-78 mu=0, sigma=0.5 ## 9 -9.36 0.5 6.39e-77 mu=0, sigma=0.5 ## 10 -9.28 0.5 1.26e-75 mu=0, sigma=0.5 ## # … with 11,536 more rows
「並べて比較」や「平均の影響」と同様に処理します。
「平均の影響」のコードで作図できます。フレーム数はsigma_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(sigma_vals), fps = 10, width = 800, height = 600)
続いて、分布の変化の軌跡を描画するアニメーションを作成します。sigma_valsの値の間隔を粗くしておきます。
# ガウス分布のアニメーションを作図 anime_dens_graph <- ggplot(data = anime_dens_df, mapping = aes(x = x, y = density, color = factor(sigma), group = sigma)) + # データ geom_line() + # 折れ線グラフ gganimate::transition_reveal(sigma) + # フレーム labs(title = "Gaussian Distribution", subtitle = paste0("mu=", mu, ", sigma={frame_along}"), color = expression(sigma), x = "x", y = "density") # ラベル # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(sigma_vals)+10, end_pause=10, fps = 10, width = 800, height = 600)
「平均の影響」のmuをsigmaに置き換えて処理します。
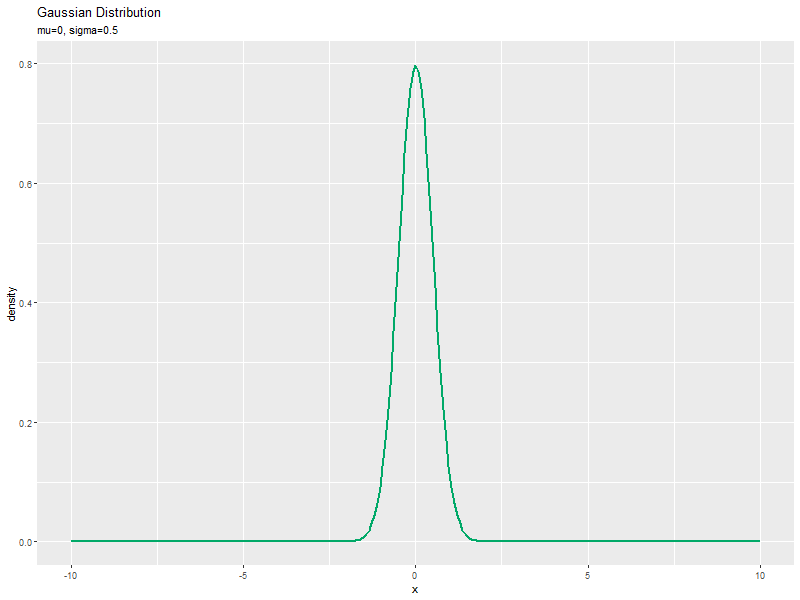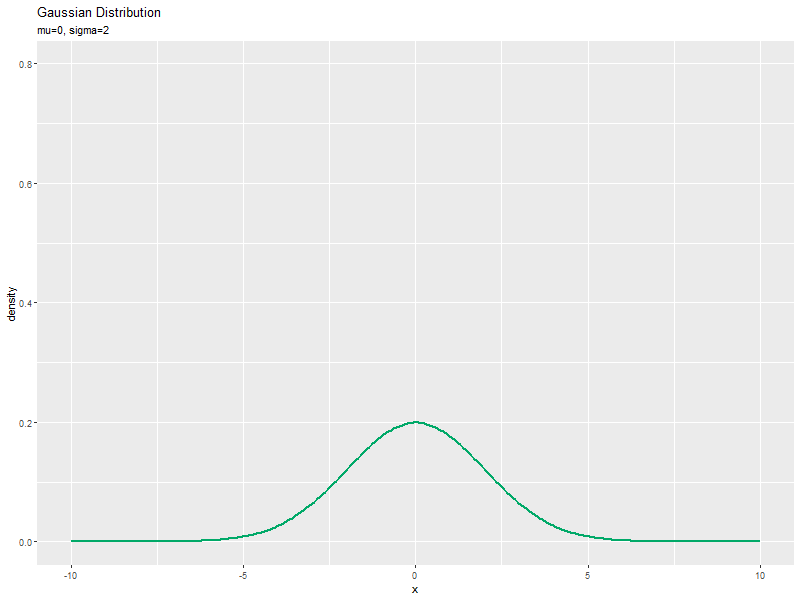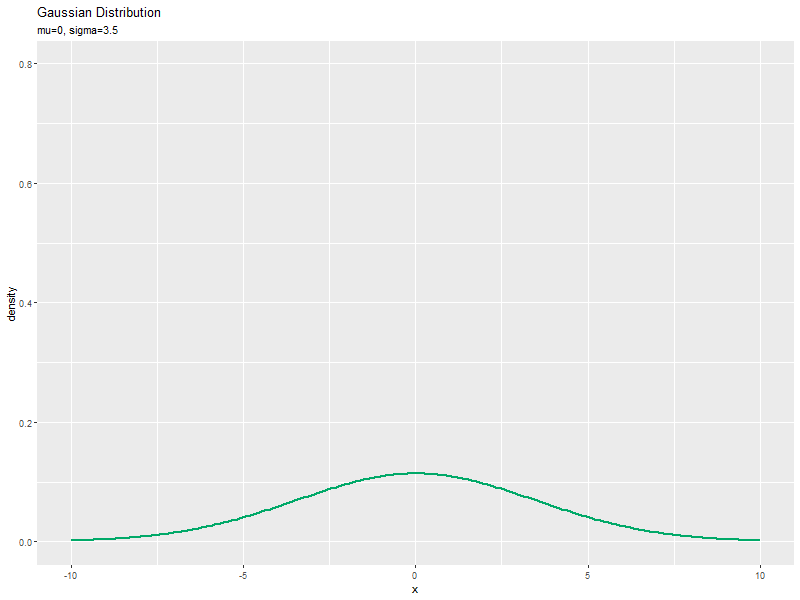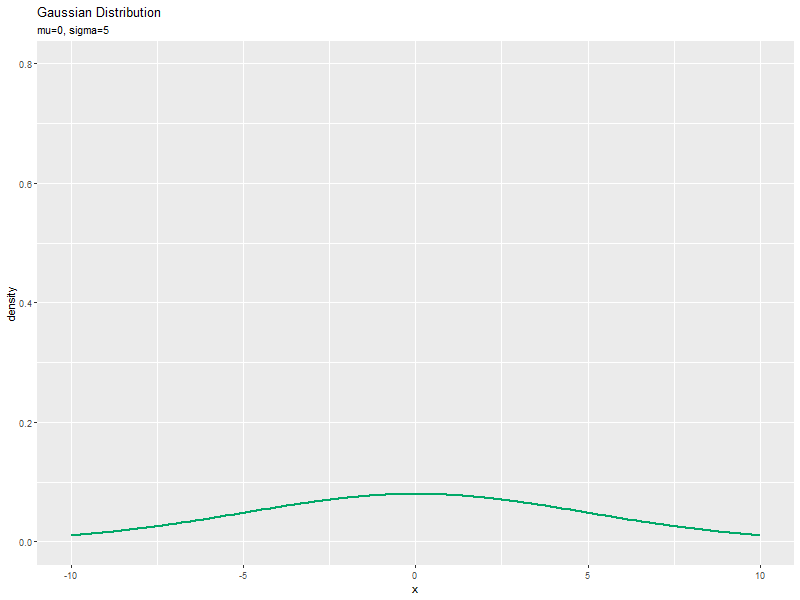
精度の影響
$\mu$を固定し、$\sigma$の代わりに$\lambda$の値を変化させて、それぞれ分布を計算します。
・作図コード(クリックで展開)
# 平均パラメータを指定 mu <- 0 # 標準偏差パラメータとして利用する値を指定 lambda_vals <- seq(from = 0.1, to = 10, by = 0.1) # (線の変化用) #lambda_vals <- seq(from = 0.5, to = 7.5, by = 0.5) # (線の軌跡用) length(lambda_vals) # フレーム数 # xの値を作成 sigma <- 1 / sqrt(min(lambda_vals)) x_vals <- seq(from = mu - sigma*2, to = mu + sigma*2, length.out = 250) # パラメータごとにガウス分布を計算 anime_dens_df <- tidyr::expand_grid( x = x_vals, lambda = lambda_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(lambda, x) |> # パラメータごとに並べ替え dplyr::mutate( density = dnorm(x = x, mean = mu, sd = 1/sqrt(lambda)), parameter = paste0("mu=", mu, ", lambda=", round(lambda, 2)) |> factor(levels = paste0("mu=", mu, ", lambda=", round(lambda_vals, 2))) # フレーム切替用ラベル ) # 確率密度を計算 anime_dens_df
## # A tibble: 25,000 × 4 ## x lambda density parameter ## <dbl> <dbl> <dbl> <fct> ## 1 -6.32 0.1 0.0171 mu=0, lambda=0.1 ## 2 -6.27 0.1 0.0176 mu=0, lambda=0.1 ## 3 -6.22 0.1 0.0182 mu=0, lambda=0.1 ## 4 -6.17 0.1 0.0188 mu=0, lambda=0.1 ## 5 -6.12 0.1 0.0194 mu=0, lambda=0.1 ## 6 -6.07 0.1 0.0200 mu=0, lambda=0.1 ## 7 -6.02 0.1 0.0206 mu=0, lambda=0.1 ## 8 -5.97 0.1 0.0212 mu=0, lambda=0.1 ## 9 -5.92 0.1 0.0219 mu=0, lambda=0.1 ## 10 -5.87 0.1 0.0226 mu=0, lambda=0.1 ## # … with 24,990 more rows
「並べて比較」や「平均の影響」と同様に処理します。
「平均の影響」のコードで作図できます。フレーム数はlambda_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(lambda_vals), fps = 10, width = 800, height = 600)
続いて、分布の変化の軌跡を描画するアニメーションを作成します。lambda_valsの値の間隔を粗くしておきます。
# ガウス分布のアニメーションを作図 anime_dens_graph <- ggplot(data = anime_dens_df, mapping = aes(x = x, y = density, color = factor(lambda), group = lambda)) + # データ geom_line() + # 折れ線グラフ gganimate::transition_reveal(lambda) + # フレーム labs(title = "Gaussian Distribution", subtitle = paste0("mu=", mu, ", lambda={frame_along}"), color = expression(lambda), x = "x", y = "density") # ラベル # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(lambda_vals)+10, end_pause=10, fps = 10, width = 800, height = 600)
「平均の影響」のmuをlambdaに置き換えて処理します。
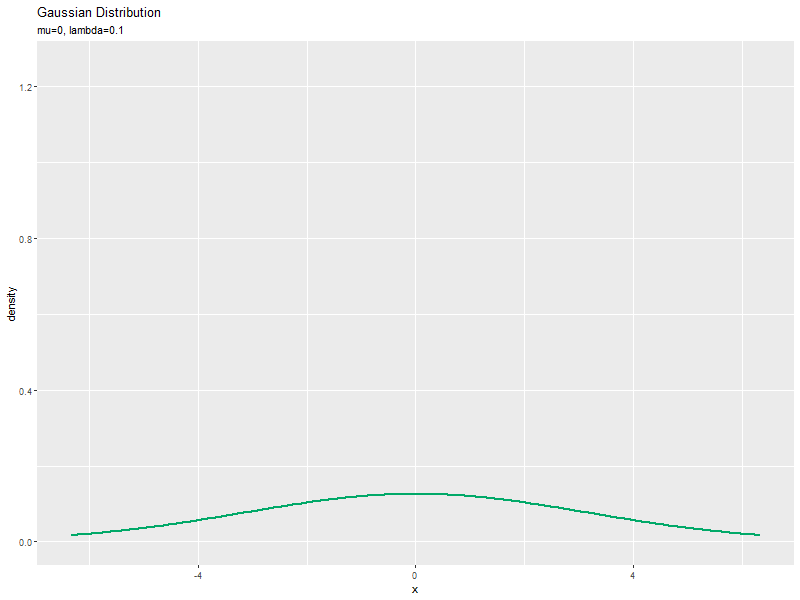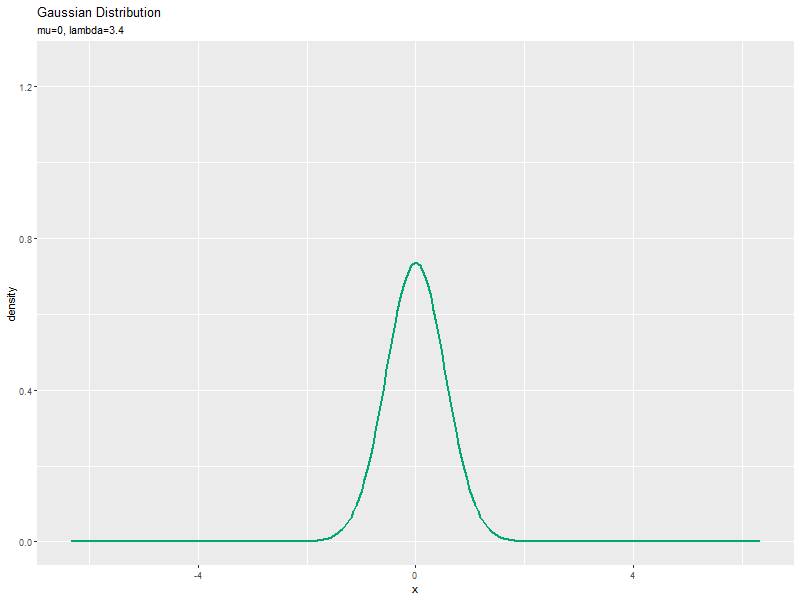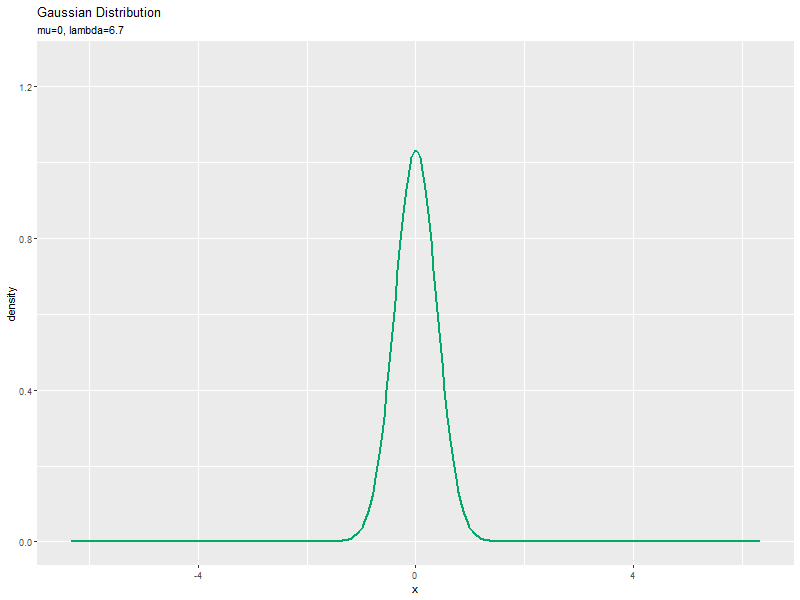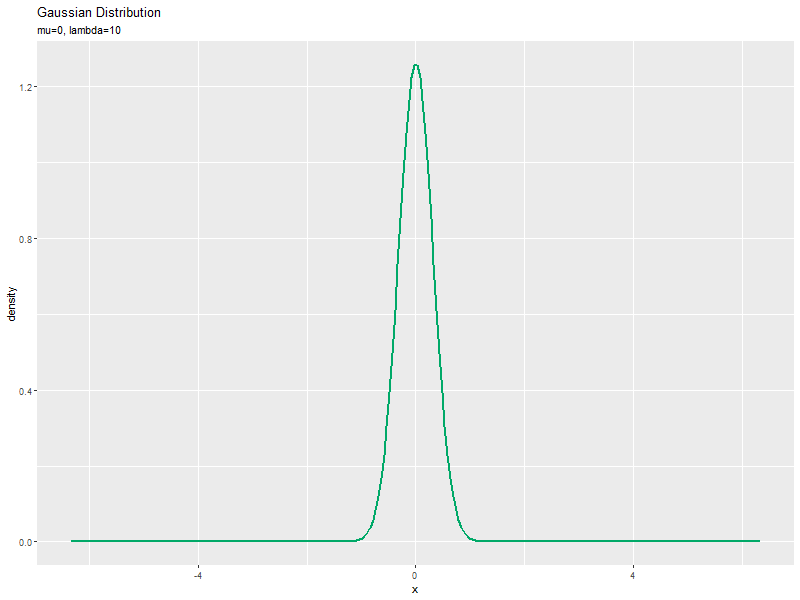
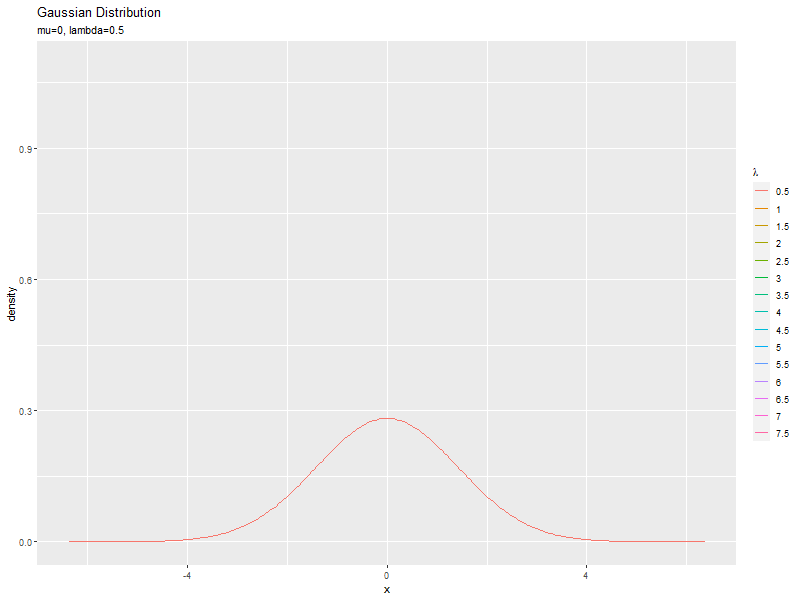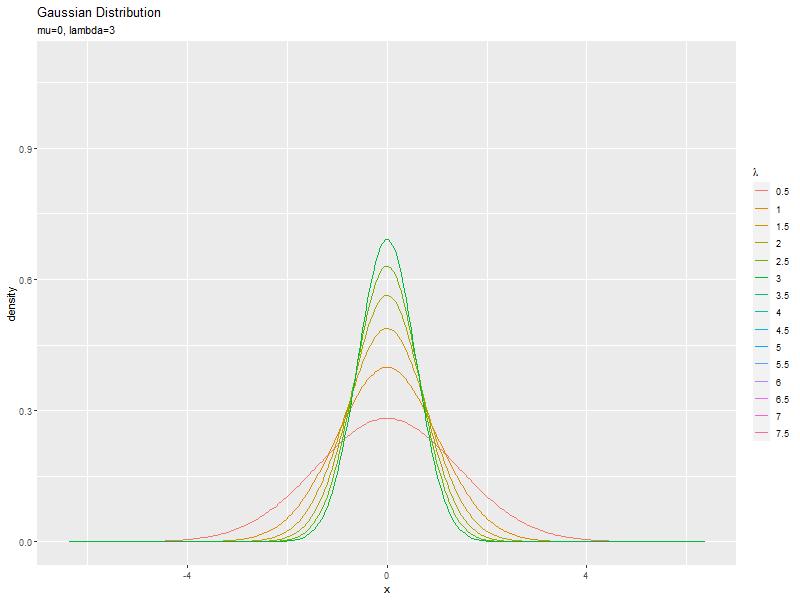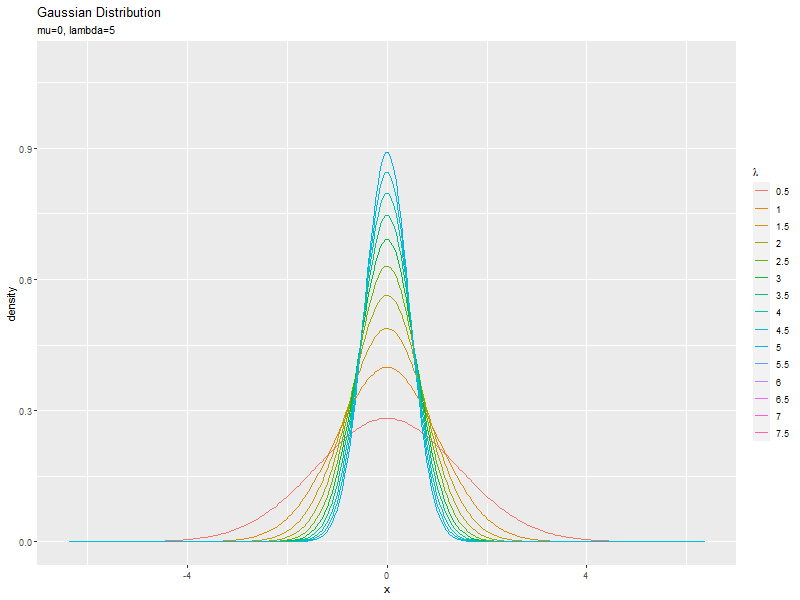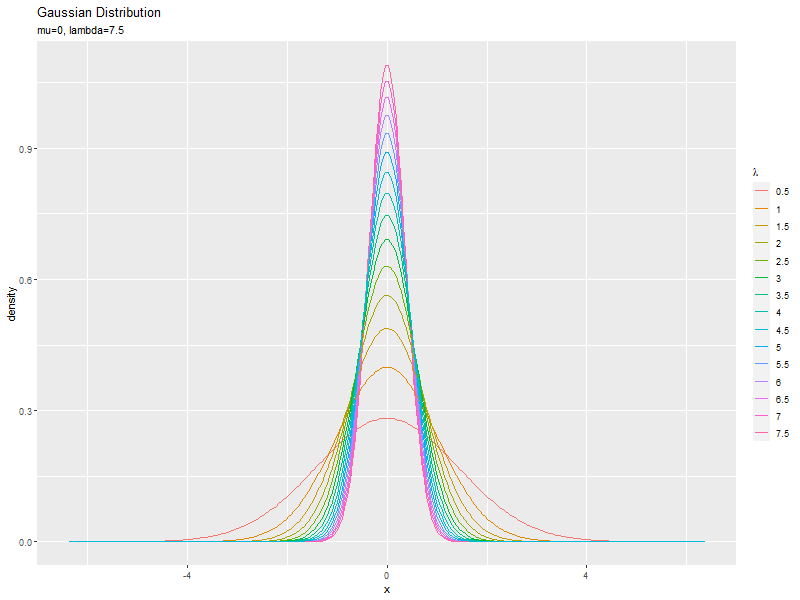
パラメータと統計量の関係をアニメーションで可視化
ここまでは、パラメータと分布の関係を確認しました。次は、パラメータと統計量と歪度・尖度の関係をアニメーションで確認します。
平均の影響
「パラメータと分布の形状の関係」と同様に、$\mu$の値を変化させ、$\sigma$を固定して、anime_dens_dfを作成します。
・作図コード(クリックで展開)
パラメータごとに統計量を計算します。
# パラメータごとに統計量を計算 anime_stat_df <- tibble::tibble( mean = mu_vals, # 期待値 sd = sigma, # 標準偏差 parameter = paste0("mu=", round(mu_vals, 2), ", sigma=", sigma) |> factor(levels = paste0("mu=", round(mu_vals, 2), ", sigma=", sigma)) # フレーム切替用のラベル ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !parameter, names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd")) # 期待値±標準偏差のカテゴリを統一 anime_stat_df
## # A tibble: 303 × 3 ## parameter type statistic ## <fct> <chr> <dbl> ## 1 mu=-5, sigma=1 mean -5 ## 2 mu=-5, sigma=1 sd -6 ## 3 mu=-5, sigma=1 sd -4 ## 4 mu=-4.9, sigma=1 mean -4.9 ## 5 mu=-4.9, sigma=1 sd -5.9 ## 6 mu=-4.9, sigma=1 sd -3.9 ## 7 mu=-4.8, sigma=1 mean -4.8 ## 8 mu=-4.8, sigma=1 sd -5.8 ## 9 mu=-4.8, sigma=1 sd -3.8 ## 10 mu=-4.7, sigma=1 mean -4.7 ## # … with 293 more rows
期待値・標準偏差・最頻値を計算して、さらに期待値から標準偏差を引いた値と足した値を求めます。
期待値・標準偏差の和と差・最頻値の4つの列をpivot_longer()でまとめます。列名がラベルになるので、標準偏差の和と差のラベルを統一します。
線と凡例の設定用の名前付きベクトルを作成します。
# 凡例用の設定を作成:(数式表示用) color_vec <- c(mean = "blue", sd = "orange") linetype_vec <- c(mean = "dashed", sd = "dotted") label_vec <- c(mean = expression(E(x)), sd = expression(E(x) %+-% sqrt(V(x))))
「グラフの作成」のときと同じ処理です。
統計量の情報を重ねたガンマ分布のアニメーション(gif画像)を作成します。
# 統計量を重ねた分布のアニメーションを作図 anime_dens_graph <- ggplot() + geom_line(data = anime_dens_df, mapping = aes(x = x, y = density), color = "#00A968", size = 1) + # 分布 geom_vline(data = anime_stat_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1) + # 統計量 gganimate::transition_manual(parameter) + # フレーム scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(色指定と数式表示用) scale_linetype_manual(values = linetype_vec, labels = label_vec, name = "statistic") + # 線の種類:(線指定と数式表示用) guides(color = guide_legend(override.aes = list(size = 0.5))) + # 凡例の体裁 theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Gaussian Distribution", subtitle = "{current_frame}") # ラベル # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(mu_vals), fps = 10, width = 800, height = 600) # (平均の影響の場合)
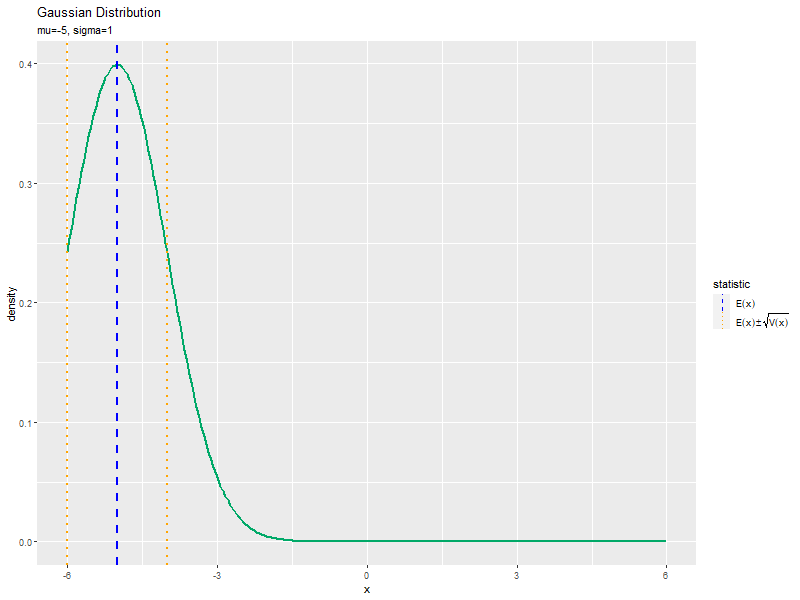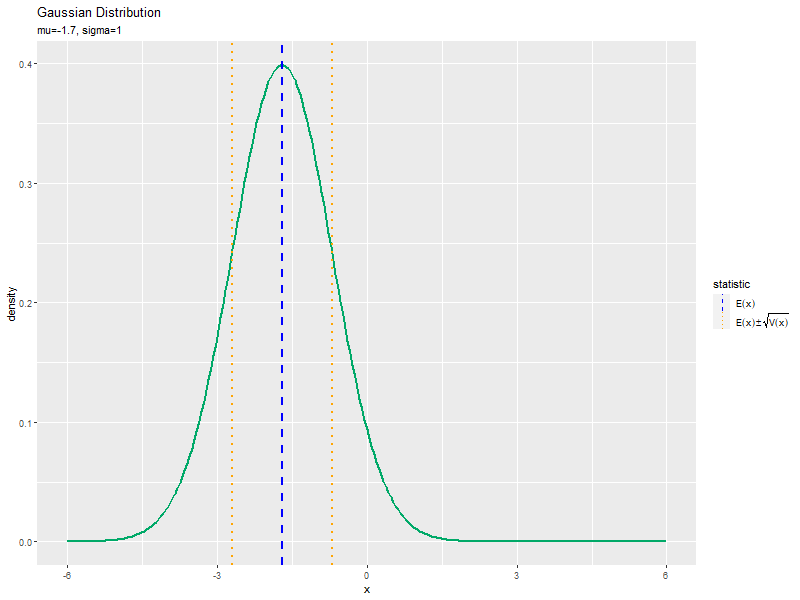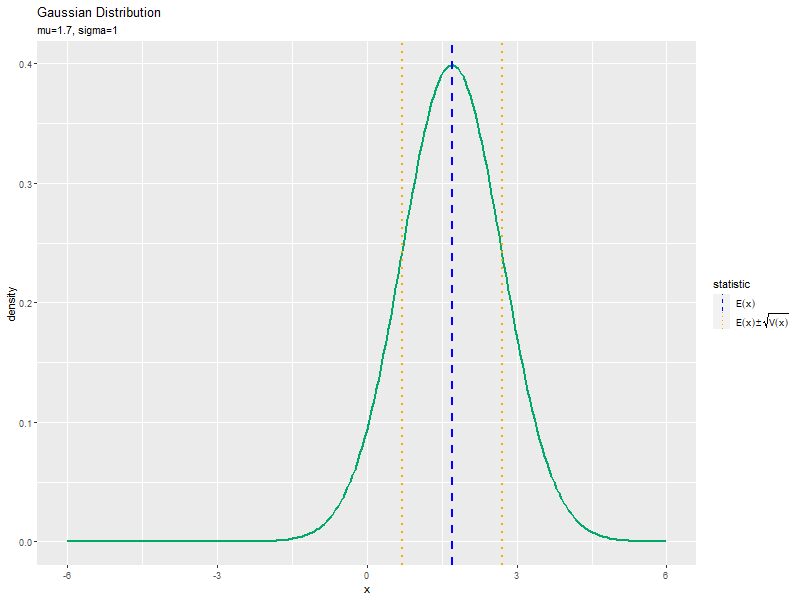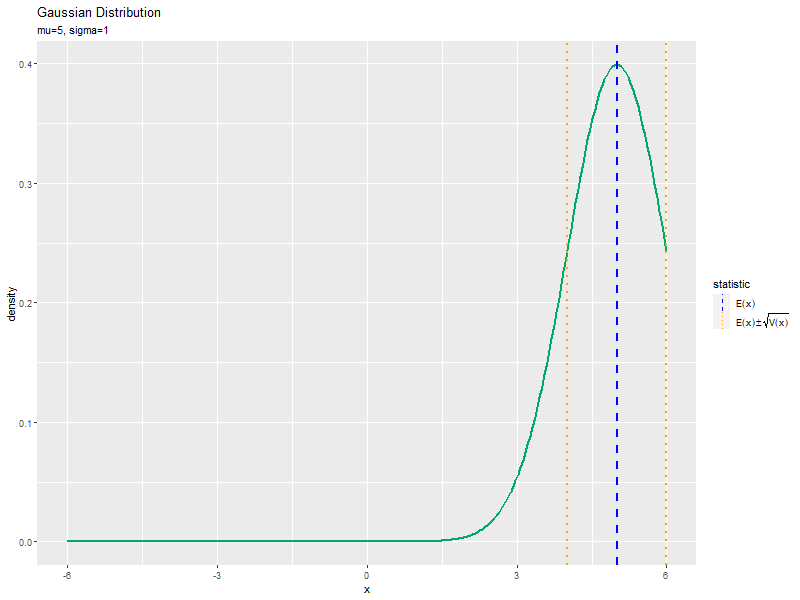
標準偏差の影響
$\mu$を固定し、$\sigma$の値を変化させて、anime_dens_dfを作成します。
・作図コード(クリックで展開)
パラメータごとに統計量を計算します。
# パラメータごとに統計量を計算 anime_stat_df <- tibble::tibble( mean = mu, # 期待値 sd = sigma_vals, # 標準偏差 parameter = paste0("mu=", mu, ", sigma=", round(sigma_vals, 2)) |> factor(levels = paste0("mu=", mu, ", sigma=", round(sigma_vals, 2))) # フレーム切替用のラベル ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !parameter, names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd")) # 期待値±標準偏差のカテゴリを統一 anime_stat_df
## # A tibble: 138 × 3 ## parameter type statistic ## <fct> <chr> <dbl> ## 1 mu=0, sigma=0.5 mean 0 ## 2 mu=0, sigma=0.5 sd -0.5 ## 3 mu=0, sigma=0.5 sd 0.5 ## 4 mu=0, sigma=0.6 mean 0 ## 5 mu=0, sigma=0.6 sd -0.6 ## 6 mu=0, sigma=0.6 sd 0.6 ## 7 mu=0, sigma=0.7 mean 0 ## 8 mu=0, sigma=0.7 sd -0.7 ## 9 mu=0, sigma=0.7 sd 0.7 ## 10 mu=0, sigma=0.8 mean 0 ## # … with 128 more rows
「平均の影響」のmu_valsをmu、sigmaをsigma_valsに置き換えるように処理します。
「平均の影響」のコードで作図できます。フレーム数はsigma_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(sigma_vals), fps = 10, width = 800, height = 600) # (標準偏差の影響の場合)
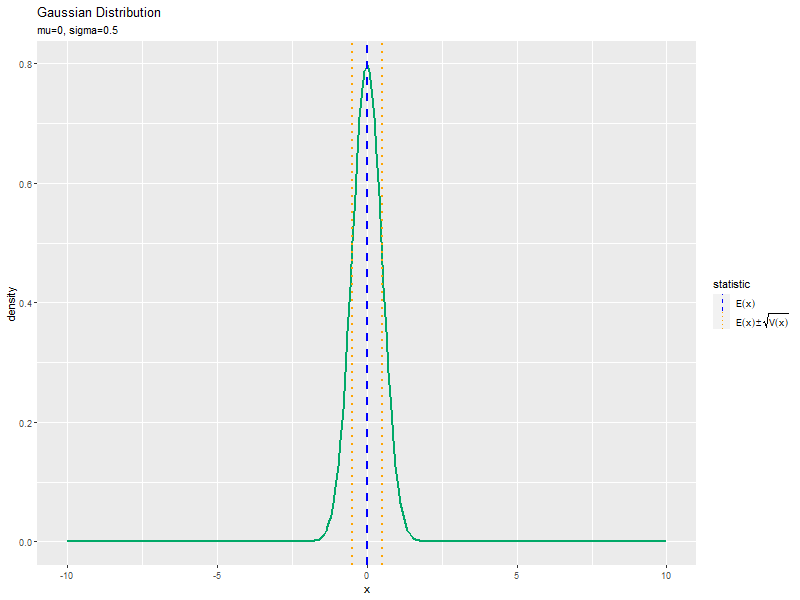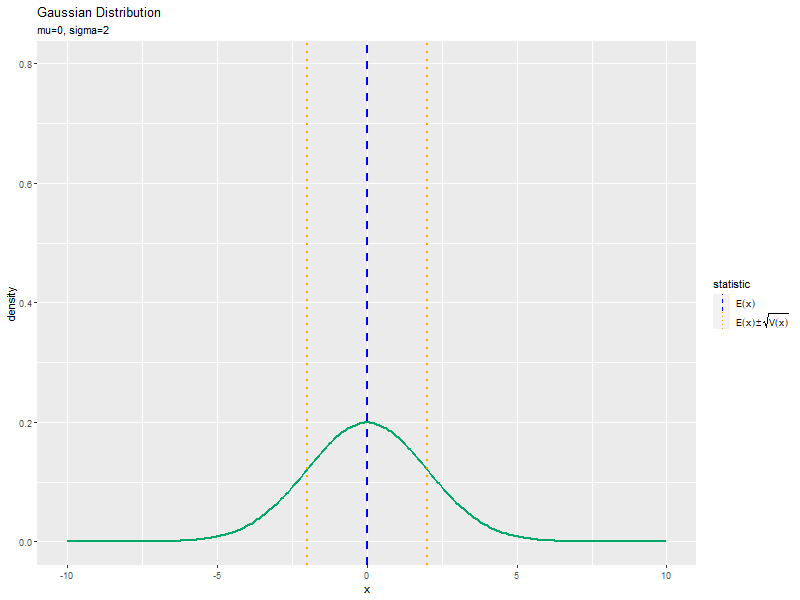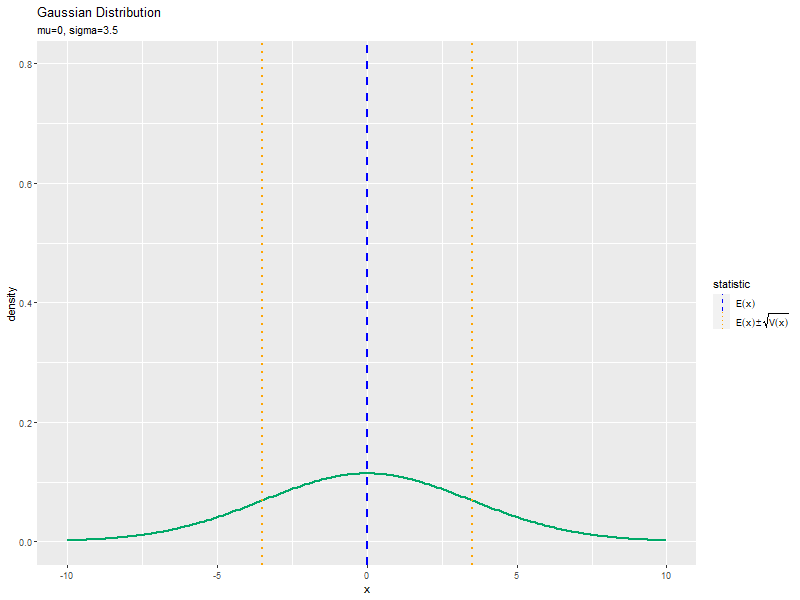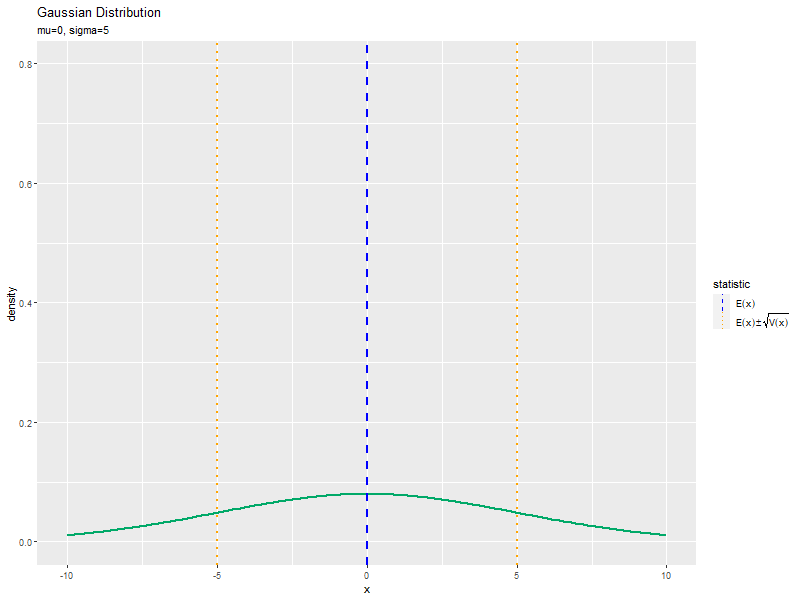
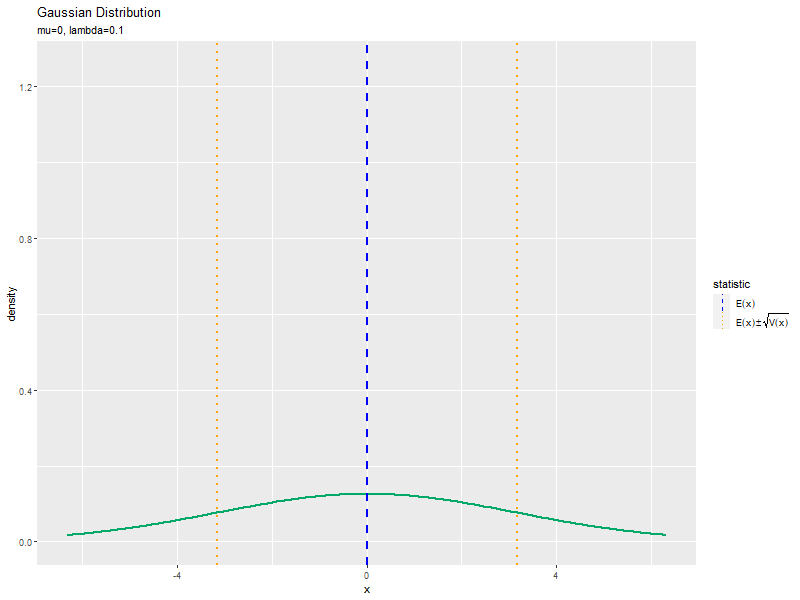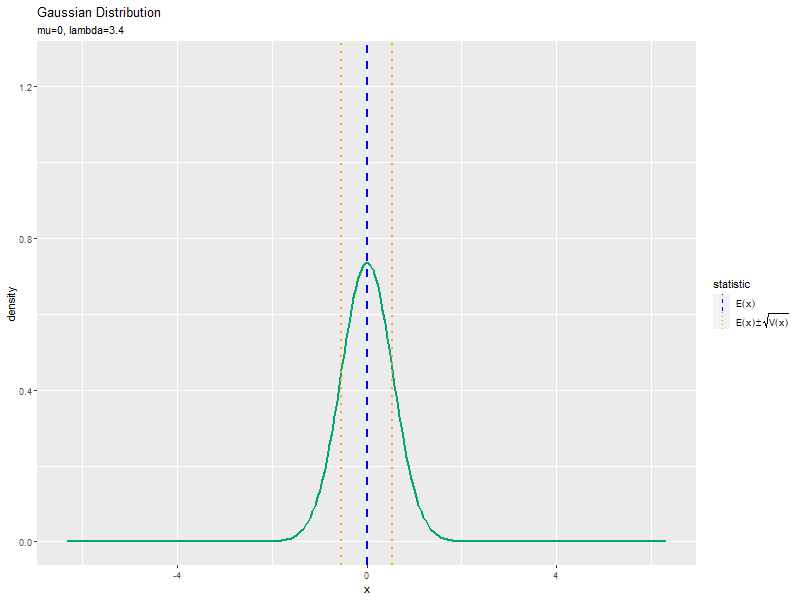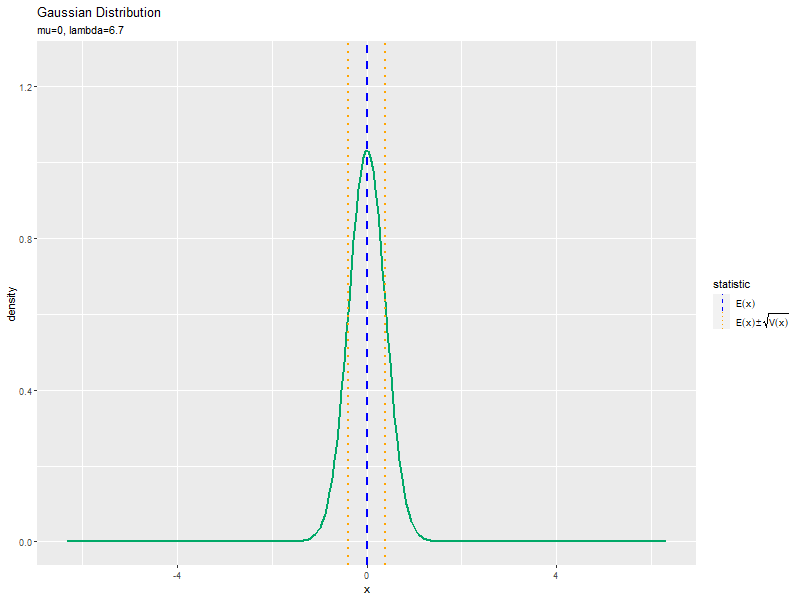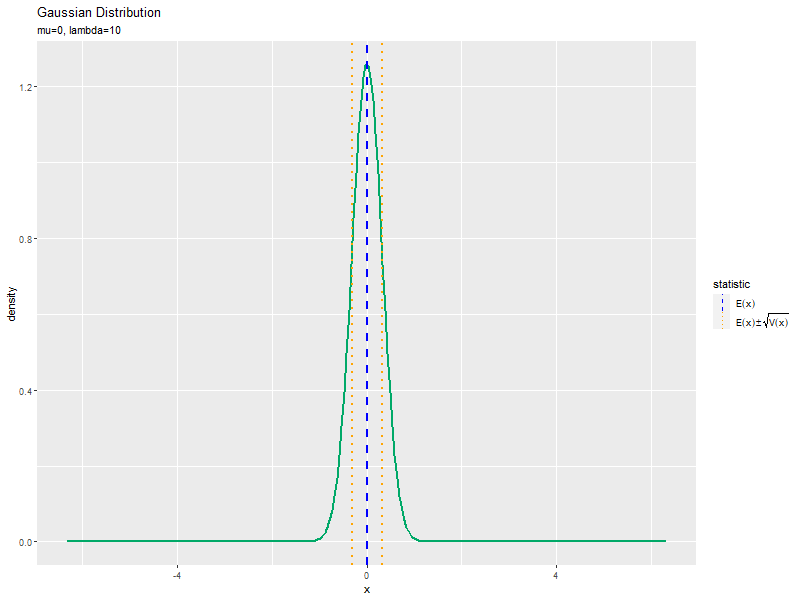
精度の影響
$\mu$を固定し、$\sigma$の代わりに$\lambda$の値を変化させて、anime_dens_dfを作成します。
・作図コード(クリックで展開)
パラメータごとに統計量を計算します。
# パラメータごとに統計量を計算 anime_stat_df <- tibble::tibble( mean = mu, # 期待値 sd = 1 / sqrt(lambda_vals), # 標準偏差 parameter = paste0("mu=", mu, ", lambda=", round(lambda_vals, 2)) |> factor(levels = paste0("mu=", mu, ", lambda=", round(lambda_vals, 2))) # フレーム切替用のラベル ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !parameter, names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd")) # 期待値±標準偏差のカテゴリを統一 anime_stat_df
## # A tibble: 300 × 3 ## parameter type statistic ## <fct> <chr> <dbl> ## 1 mu=0, lambda=0.1 mean 0 ## 2 mu=0, lambda=0.1 sd -3.16 ## 3 mu=0, lambda=0.1 sd 3.16 ## 4 mu=0, lambda=0.2 mean 0 ## 5 mu=0, lambda=0.2 sd -2.24 ## 6 mu=0, lambda=0.2 sd 2.24 ## 7 mu=0, lambda=0.3 mean 0 ## 8 mu=0, lambda=0.3 sd -1.83 ## 9 mu=0, lambda=0.3 sd 1.83 ## 10 mu=0, lambda=0.4 mean 0 ## # … with 290 more rows
「標準偏差の影響」のsigma_valsをlambda_valsに置き換えるように処理します。
「平均の影響」のコードで作図できます。フレーム数はlambda_valsの要素数です。
# 統計量を重ねた分布のアニメーションを作図 anime_dens_graph <- ggplot() + geom_line(data = anime_dens_df, mapping = aes(x = x, y = density), color = "#00A968", size = 1) + # 分布 geom_vline(data = anime_stat_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1) + # 統計量 gganimate::transition_manual(parameter) + # フレーム scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(色指定と数式表示用) scale_linetype_manual(values = linetype_vec, labels = label_vec, name = "statistic") + # 線の種類:(線指定と数式表示用) guides(color = guide_legend(override.aes = list(size = 0.5))) + # 凡例の体裁 theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Gaussian Distribution", subtitle = "{current_frame}") # ラベル # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(lambda_vals), fps = 10, width = 800, height = 600) # (精度の影響の場合)
この記事では、1次元ガウス分布の作図を確認しました。次は、乱数を生成します。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
ヒストグラムを描くときの頻度から密度に変換する計算をよく分かってない。
2022年1月30日は、Juice=Juiceの江端妃咲さんの15歳のお誕生日です!
若い、眩しい、キラキラ粒子が舞ってるのを感じる。
- 2022.07.31:加筆修正の際に記事を分割しました。
記事を分割したのにこの記事だけで文字数が元の記事全体の1.5倍ある。
【次の内容】