からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

トップ > 攻略ノート > 【R】第7講：正規分布の性質【統計学入門(小島)のノート】

【R】第7講：正規分布の性質【統計学入門(小島)のノート】

攻略ノート 攻略ノート-統計学入門(小島) 統計学 確率分布 確率分布-ガウス分布(正規分布) R

はじめに

　『完全独習 統計学入門』の学習ノートです。本に載っている計算や表、グラフをR言語で再現します。本とあわせて読んでください。
　この記事では、R言語で正規分布の性質を確認します。

【前の節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

第7講 身長、コイン投げなど最もよく見られる分布、正規分布

　正規分布の性質を確認します。より詳しくは「1次元ガウス分布の定義式 - からっぽのしょこ」を参照してください。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)

　この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
　また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。

7-1 最もよく見かけるデータ分布

　まずは、標準正規分布のグラフを作成します。

　正規分布のパラメータを指定します。

# パラメータを指定
mu    <- 0
sigma <- 1

　標準正規分布は、平均パラメータが \mu = 0、標準偏差パラメータが \sigma = 1の正規分布です。mu, sigmaとして値を指定します。
　値を変更すると、任意の(標準でない)正規分布のグラフを作成できます。

棒グラフで可視化

　正規分布の棒グラフを作成します。

　区間ごとの確率を計算します。

# 階級の幅を指定
x_width <- 0.1

# (離散値的な)確率変数の値を指定
x_vec = seq(from = -5, to = 5.1, by = x_width)

# 各値より大きい確率を計算
prob_vec <- pnorm(q = x_vec, mean = mu, sd = sigma, lower.tail = FALSE)
head(x_vec); head(prob_vec)

## [1] -5.0 -4.9 -4.8 -4.7 -4.6 -4.5
## [1] 0.9999997 0.9999995 0.9999992 0.9999987 0.9999979 0.9999966

　この例では、0.1間隔の区間における確率を描画することにします。

　そこで、確率変数(x軸)の値を0.1間隔で作成して、各値より大きい値をとる確率 p(X > x)を計算します。
　正規分布の累積確率( x以下の値をとる確率) p(X \leq x)はpnorm()で計算できます。確率変数の引数qに0.1間隔の値x_vec、平均の引数meanに0、標準偏差の引数sdに1を指定します。lower.tail引数にFALSEを指定すると、第1引数に指定した値より大きい値をとる確率を返します。

　作図用のデータフレームを作成します。

# 区間ごとの確率を計算
prob_df <- tibble::tibble(
  x = x_vec[-length(x_vec)] + 0.5*x_width, 
  probability = prob_vec[-length(x_vec)] - prob_vec[-1]
)
prob_df

## # A tibble: 101 × 2
##        x probability
##    <dbl>       <dbl>
##  1 -4.95 0.000000193
##  2 -4.85 0.000000314
##  3 -4.75 0.000000507
##  4 -4.65 0.000000812
##  5 -4.55 0.00000129 
##  6 -4.45 0.00000201 
##  7 -4.35 0.00000313 
##  8 -4.25 0.00000481 
##  9 -4.15 0.00000731 
## 10 -4.05 0.0000110  
## # … with 91 more rows

　階級の下限(バーの左端)がx_vecの値になるように、階級の幅x_widthの半分を足した(各バーの中心をx_widthの半分だけ右にズラした)値をx軸の値とします。
　階級の幅(バーの横幅)がx_widthである区間ごとの確率 p(x_i \leq X \lt x_{i-1})になるように、prob_vec[i] - prob_vec[i-1]を計算してy軸の値とします。

　パラメータをタイトルに表示する用の文字列を作成します。作図自体には不要な処理です。

# タイトル用の文字列を作成
param_label <- paste0(
  "list(mu==", mu, ", sigma==", sigma, ")"
)
param_label

## [1] "list(mu==0, sigma==1)"

　expression()の記法に従い指定します。

　棒グラフとして、標準正規分布を作図します。

# 正規分布を棒グラフで作図
ggplot() + 
  geom_bar(data = prob_df, mapping = aes(x = x, y = probability), 
           stat = "identity", width = x_width, fill = "#00A968") + # 相対度数
  labs(title = "standard normal distribution", 
       subtitle = parse(text = param_label), 
       x = "x", y = "probability")

標準正規分布の棒グラフ

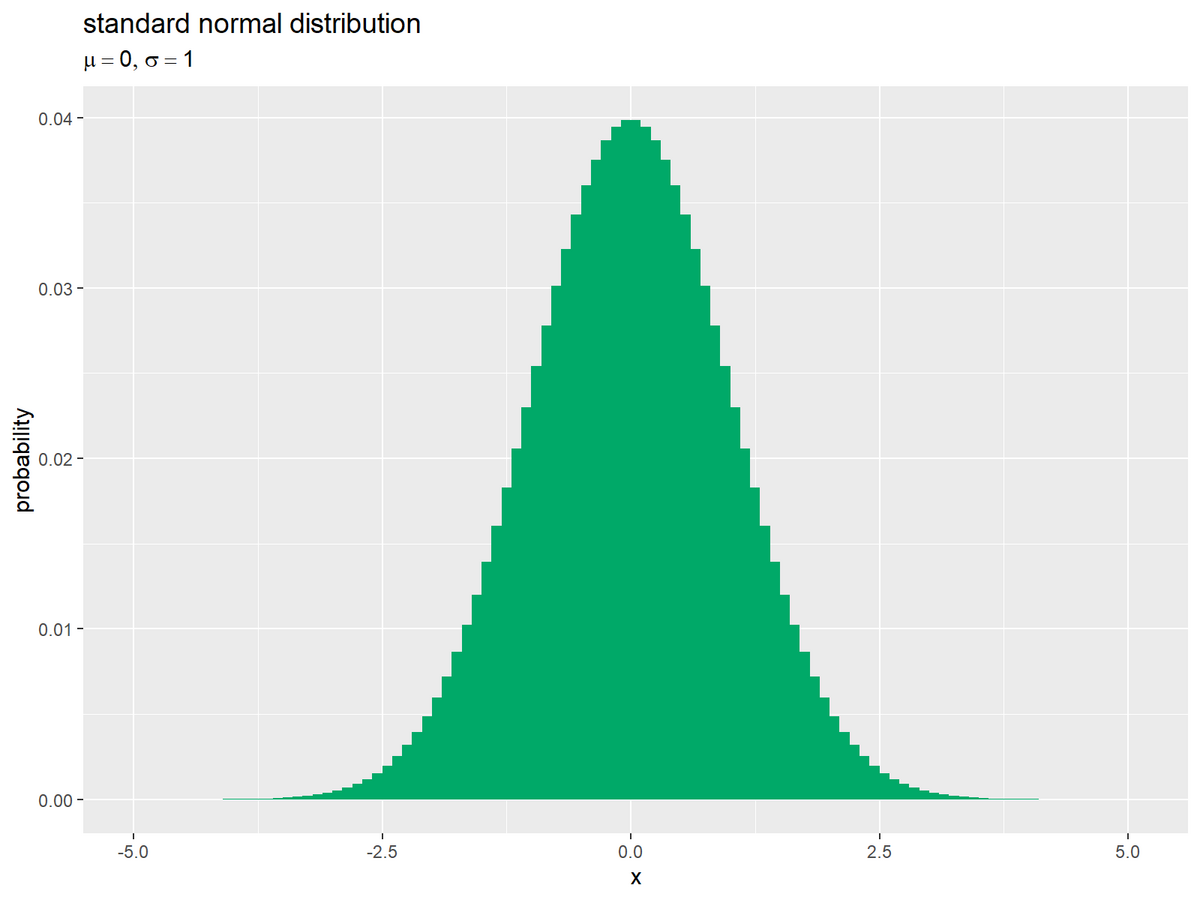
　geom_bar()のwidth引数にx_widthを指定して、各バーの横幅と階級のサイズをあわせます。

折れ線グラフで可視化

　続いて、正規分布の折れ線グラフを作成します。棒グラフの階級の幅を無限に小さくしたグラフに相当します。

　確率密度を計算します。

# (連続値的な)x軸の値を指定
x_vec = seq(from = -5, to = 5, length.out = 501)

# 確率密度を計算
dens_df <- tibble::tibble(
  x = x_vec, 
  density = dnorm(x = x_vec, mean = mu, sd = sigma)
)
dens_df

## # A tibble: 501 × 2
##        x    density
##    <dbl>      <dbl>
##  1 -5    0.00000149
##  2 -4.98 0.00000164
##  3 -4.96 0.00000181
##  4 -4.94 0.00000200
##  5 -4.92 0.00000221
##  6 -4.9  0.00000244
##  7 -4.88 0.00000269
##  8 -4.86 0.00000296
##  9 -4.84 0.00000327
## 10 -4.82 0.00000360
## # … with 491 more rows

　滑らかな曲線になるように、棒グラフのときよりも小さい間隔の確率変数(x軸)の値を作成して、(確率ではなく)確率密度を計算します。

　点の間隔は重要ではないので、要素数の引数length.outに点の数を指定して、数値ベクトルを作成します。
　正規分布の確率密度はdnorm()で計算できます。確率変数の引数xにx_vec、平均の引数meanに0、標準偏差の引数sdに1を指定します。

　折れ線グラフとして、標準正規分布を作図します。

# 正規分布を折れ線グラフで作図
ggplot() + 
  geom_line(data = dens_df, mapping = aes(x = x, y = density), 
            color = "#00A968", size = 1) + # 確率密度
  labs(title = "standard normal distribution", 
       subtitle = parse(text = param_label), 
       x = "x", y = "density")

標準正規分布の折れ線グラフ


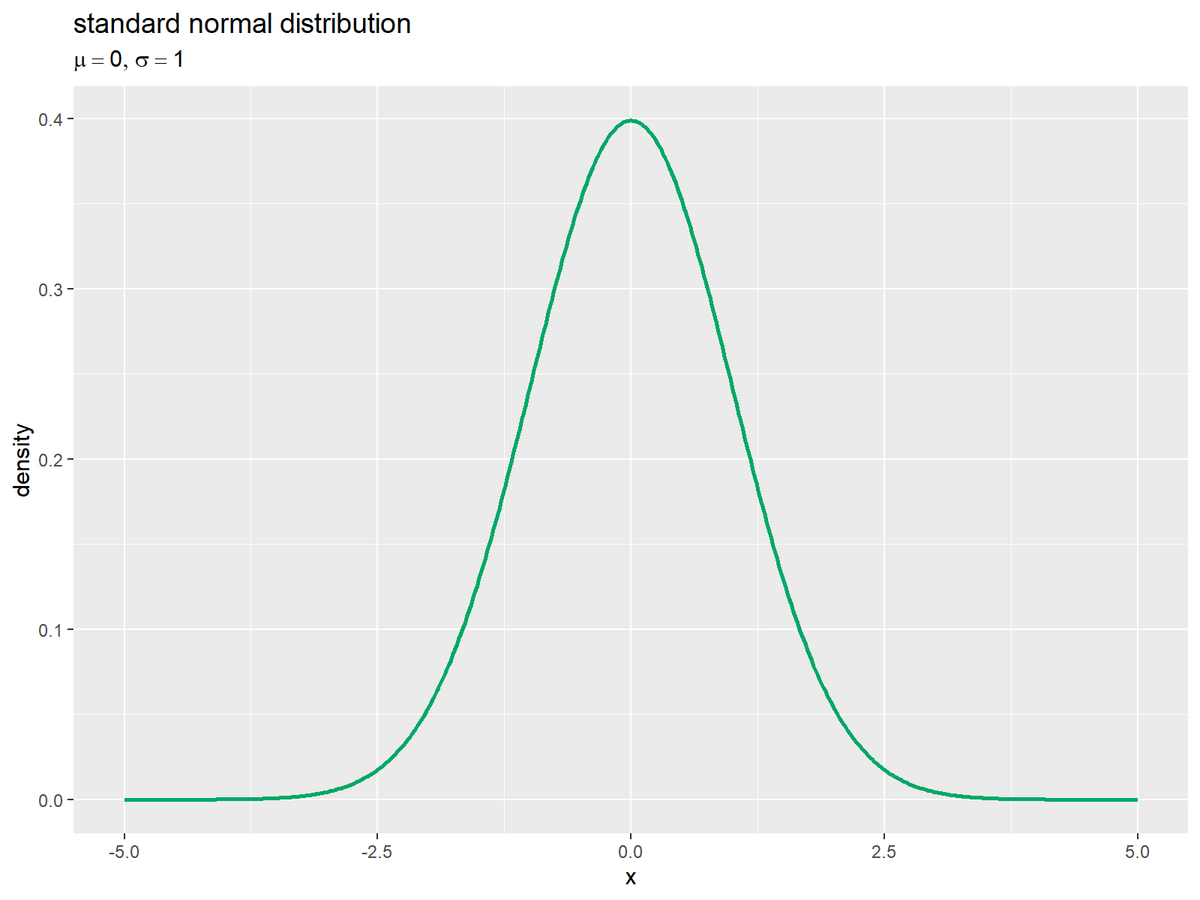
標準偏差の可視化

　ここまでで、(標準)正規分布をグラフ化できました。次に、標準偏差パラメータの影響をグラフで確認します。

　平均を中心に、標準偏差1つ分の範囲の確率密度を計算します。

# 標準偏差1つ分の確率密度を計算
sd_1_df <- tibble::tibble(
  x = seq(from = mu-sigma, to = mu+sigma, length.out = 500), 
  density = dnorm(x = x, mean = mu, sd = sigma)
)
sd_1_df

## # A tibble: 500 × 2
##         x density
##     <dbl>   <dbl>
##  1 -1       0.242
##  2 -0.996   0.243
##  3 -0.992   0.244
##  4 -0.988   0.245
##  5 -0.984   0.246
##  6 -0.980   0.247
##  7 -0.976   0.248
##  8 -0.972   0.249
##  9 -0.968   0.250
## 10 -0.964   0.251
## # … with 490 more rows

　確率変数(x軸)の範囲を \mu - \sigmaから \mu + \sigmaとして、確率密度を計算します。

　同様に、標準偏差2つ分の範囲の確率密度を計算します。

# 標準偏差2つ分の確率密度を計算
sd_2_df <- tibble::tibble(
  x = seq(from = mu-sigma*2, to = mu+sigma*2, length.out = 500), 
  density = dnorm(x = x, mean = mu, sd = sigma)
)
sd_2_df

## # A tibble: 500 × 2
##        x density
##    <dbl>   <dbl>
##  1 -2     0.0540
##  2 -1.99  0.0549
##  3 -1.98  0.0557
##  4 -1.98  0.0566
##  5 -1.97  0.0575
##  6 -1.96  0.0585
##  7 -1.95  0.0594
##  8 -1.94  0.0603
##  9 -1.94  0.0613
## 10 -1.93  0.0622
## # … with 490 more rows

　 \mu - 2 \sigmaから \mu + 2 \sigmaの範囲で確率密度を計算します。

　境界線(標準偏差の範囲)にラベルを表示する用のデータフレームを作成します。作図自体には不要な処理です。

# ラベル用のデータフレームを作成
sd_label_df <- tibble::tibble(
  x = c(mu-sigma*2, mu-sigma, mu, mu+sigma, mu+sigma*2), 
  y = 0, 
  label = c("mu - 2*sigma", "mu - sigma", "mu", "mu + sigma", "mu + 2*sigma")
)
sd_label_df

## # A tibble: 5 × 3
##       x     y label       
##   <dbl> <dbl> <chr>       
## 1    -2     0 mu - 2*sigma
## 2    -1     0 mu - sigma  
## 3     0     0 mu          
## 4     1     0 mu + sigma  
## 5     2     0 mu + 2*sigma

　平均 \muを含めた5点のx軸の値と、対応するexpression()記法の文字列を格納します。y軸の値は全て0とします。

　標準正規分布の折れ線グラフに、標準偏差の範囲を重ねたグラフを作成します。

# 正規分布を折れ線グラフで作図
ggplot() + 
  geom_area(data = sd_1_df, mapping = aes(x = x, y = density), 
            fill = "navy", alpha = 0.5) + # μ ± σ
  geom_area(data = sd_2_df, mapping = aes(x = x, y = density), 
            fill = "blue", alpha = 0.5) + # μ ± 2σ
  geom_line(data = dens_df, mapping = aes(x = x, y = density), 
            color = "#00A968", size = 1) + # 確率密度
  geom_vline(xintercept = mu, color = "red", linetype = "dashed", size = 1) + # μ
  geom_text(data = sd_label_df, mapping = aes(x = x, y = y, label = label), 
            parse = TRUE, vjust = 1, size = 5) + 
  labs(title = "standard normal distribution", 
       subtitle = parse(text = param_label), 
       x = "x", y = "density")

標準偏差1個分と2個分の範囲

　標準偏差1つ分と2つ分の範囲をそれぞれgeom_area()で塗りつぶします。

　続いて、塗りつぶした範囲が占める割合を確認します。

　標準偏差1つ分の範囲となる確率を計算します。

# 標準偏差1個分の範囲の割合を計算
prob_lower <- pnorm(q = mu-sigma, mean = mu, sd = sigma, lower.tail = TRUE)
prob_upper <- pnorm(q = mu+sigma, mean = mu, sd = sigma, lower.tail = FALSE)
prob       <- 1 - prob_lower - prob_upper
prob; prob_lower; prob_upper

## [1] 0.6826895
## [1] 0.1586553
## [1] 0.1586553

　棒グラフ(の各バー)のときと同様に、 p(\mu - \sigma \lt X \lt \mu + \sigma)を計算します。

　同様に、標準偏差2つ分の範囲の割合を計算します。

# 標準偏差2個分の範囲の割合を計算
prob_lower <- pnorm(q = mu-sigma*2, mean = mu, sd = sigma, lower.tail = TRUE)
prob_upper <- pnorm(q = mu+sigma*2, mean = mu, sd = sigma, lower.tail = FALSE)
prob       <- 1 - prob_lower - prob_upper
prob; prob_lower; prob_upper

## [1] 0.9544997
## [1] 0.02275013
## [1] 0.02275013

　 p(\mu - 2 \sigma \lt X \lt \mu + 2 \sigma)を計算します。

　標準偏差1つ分の範囲は約68%、2つ分の範囲は約95%なのを確認できます。

7-2 一般の正規分布の眺め方

　次は、(標準でない)正規分布のグラフを作成します。

　正規分布のパラメータを指定します。

# パラメータを指定
mu    <- 4
sigma <- 3

　平均パラメータ \muと標準偏差パラメータ \sigma > 0を指定します。 \sigmaは0より大きい必要があります。

折れ線グラフで可視化

　任意のパラメータの正規分布と、標準偏差パラメータの影響をグラフで確認します。

　確率密度を計算します。

# 確率密度を計算
dens_df <- tibble::tibble(
  x = seq(from = mu-sigma*3, to = mu+sigma*3, length.out = 501), 
  density = dnorm(x = x, mean = mu, sd = sigma)
)
dens_df

## # A tibble: 501 × 2
##        x density
##    <dbl>   <dbl>
##  1 -5    0.00148
##  2 -4.96 0.00153
##  3 -4.93 0.00159
##  4 -4.89 0.00164
##  5 -4.86 0.00170
##  6 -4.82 0.00177
##  7 -4.78 0.00183
##  8 -4.75 0.00189
##  9 -4.71 0.00196
## 10 -4.68 0.00203
## # … with 491 more rows

　「折れ線グラフで可視化」のときと同様にして、正規分布に従う確率密度を計算します。この例では、平均を中心に標準偏差3つ分を範囲とします。

　「標準偏差の可視化」のコードで、正規分布のグラフを作成します。(タイトル部分は変更しました。)

正規分布のグラフ

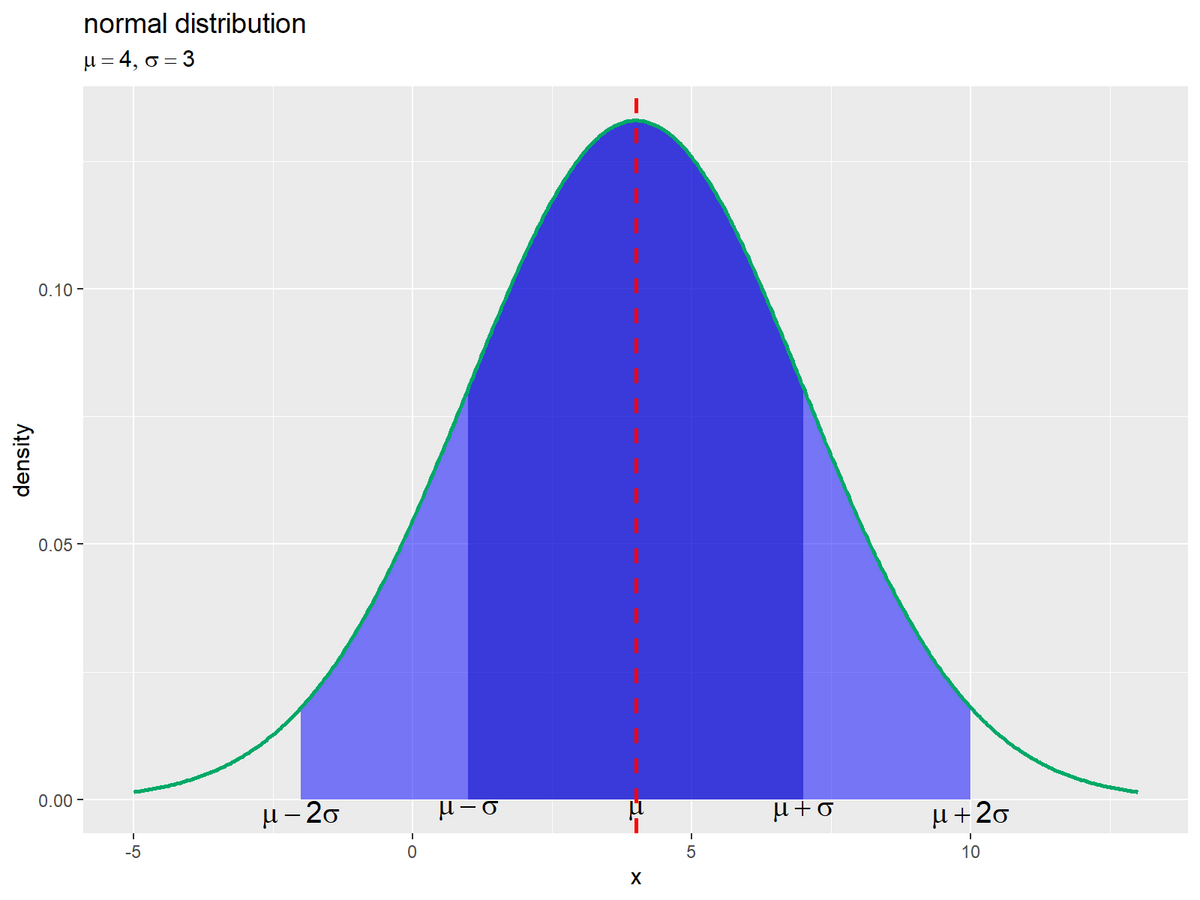
　塗りつぶし範囲の割合が変わらないことを先ほどのコードで確認できます。

データの加工

　標準正規分布から生成したデータの標本平均と標本標準偏差を変更して、正規分布のグラフと比較します。

　データ数を指定して、標準正規分布に従う乱数を生成します。

# データ数を指定
N <- 10000

# 標準正規分布に従うデータを生成
data_z <- rnorm(n = N, mean = 0, sd = 1)

# 標本平均と標本標準偏差を計算
mean_z <- mean(data_z)
sd_z   <- sqrt(sum((data_z - mean_z)^2) / N)
head(data_z); mean_z; sd_z

## [1] -1.2504764  0.8799067 -0.5243010  0.5805865  0.3132378  0.8574646
## [1] 0.001069277
## [1] 1.004217

　正規分布の乱数はrnorm()で生成できます。データ数(サンプルサイズ)の引数nに生成するデータ数、平均の引数meanに0、標準偏差の引数sdに1を指定します。

　平均と標準偏差を用いて、データを加工します。

# データを加工
data_x <- data_z * sigma + mu

# 標本平均と標本標準偏差を計算
mean_x <- mean(data_x)
sd_x   <- sqrt(sum((data_x - mean_x)^2) / N)
head(data_z); mean_x; sd_x

## [1] -1.2504764  0.8799067 -0.5243010  0.5805865  0.3132378  0.8574646
## [1] 4.003208
## [1] 3.012652

　各データから平均を引き標準偏差で割ることで標準化(平均が0で標準偏差が1のデータに加工)しました(第4講)。この計算を式にすると、 z = \frac{x - \mu}{\sigma}です。
　この式を xについて整理すると、 x = \sigma z + \muになります。標準化データに標準偏差を掛けて平均を足すことで、平均が \muで標準偏差が \sigmaのデータに加工できます。

　加工したデータのヒストグラムと、計算した正規分布のグラフを重ねて描画します。

# データを加工して格納
data_df <- tibble::tibble(
  x = data_z * sigma + mu
)

# タイトル用の文字列を作成
data_label <- paste0(
  "list(", 
  "z[n] == sigma * x[n] + mu", 
  ", x[n] %~% N(x ~'|'~ mu == 0, sigma == 1)", 
  ")"
)
param_label <- paste0(
  "list(", 
  "mu==", mu, ", sigma==", sigma, 
  ", bar(x)==", round(mean_x, digits = 2), ", S[x]==", round(sd_x, digits = 2), 
  ")"
)

# 加工データのヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_df, mapping = aes(x = x, y = ..count../N), 
                 binwidth = 1, fill = "green") + 
  geom_line(data = dens_df, mapping = aes(x = x, y = density), 
            color = "#00A968", size = 1) + # 確率密度
  labs(title = parse(text = data_label), 
       subtitle = parse(text = param_label), 
       x = "x", y = "relative frequency")

データの加工と正規分布の関係

　データ数が十分に大きいと、分布が一致しているのが分かります。

7-3 身長のデータは正規分布している

　今度は、身長データとコインの裏表結果が正規分布になっているのをグラフで確認します。

身長データ

　第1講で利用した身長のデータを使います。度数分布表の作成については「【R】第1講：度数分布表とヒストグラムの作成【統計学入門(小島)のノート】 - からっぽのしょこ」を参照してください。

　図表1-1の身長データを読み込みます。

# データを作成:(身長)
data_x <- c(
  151, 154, 158, 162, 
  154, 152, 151, 167, 
  160, 161, 155, 159, 
  160, 160, 155, 153, 
  163, 160, 165, 146, 
  156, 153, 165, 156, 
  158, 155, 154, 160, 
  156, 163, 148, 151, 
  154, 160, 169, 151, 
  160, 159, 158, 157, 
  154, 164, 146, 151, 
  162, 158, 166, 156, 
  156, 150, 161, 166, 
  162, 155, 143, 159, 
  157, 157, 156, 157, 
  162, 161, 156, 156, 
  162, 168, 149, 159, 
  169, 162, 162, 156, 
  150, 153, 159, 156, 
  162, 154, 164, 161
)
length(data_x)

## [1] 80


　階級の上限と下限として用いる値を作成します。

# 階級の幅を指定
x_class_width <- 5

# 階級用の値を作成
x_class_vec <- seq(
  from = floor(min(data_x) / 10) * 10, 
  to = ceiling(max(data_x) / 10) * 10, 
  by = x_class_width
)
x_class_vec

## [1] 140 145 150 155 160 165 170

　階級の幅をclass_widthとして、class_width間隔の数値ベクトルを作成します。
　最小値の1桁をfloor()で切り捨てて、最大値の1桁をceiling()で切り上げて使います(もっといいやり方があれば教えて下さい)。あるいは、from, to(第1・第2)引数に値を直接指定します。

　元データの標本平均と標本標準偏差を計算します。

# 平均値と標準偏差を計算
mean_x <- mean(data_x) 
sd_x   <- sqrt(sum((data_x - mean_x)^2) / length(data_x))
mean_x; sd_x

## [1] 157.575
## [1] 5.370696

　N個のデータ x_nの標本平均を \bar{x}、標本標準偏差を S_xで表します。

　データと階級値を標準化します。

# 平均値と標準偏差を指定
mean_x <- 157.75
sd_x   <- 5.4

# データと階級用の値を標準化
data_z      <- (data_x - mean_x) / sd_x
z_class_vec <- (x_class_vec - mean_x) / sd_x
head(data_z); z_class_vec

## [1] -1.2500000 -0.6944444  0.0462963  0.7870370 -0.6944444 -1.0648148
## [1] -3.2870370 -2.3611111 -1.4351852 -0.5092593  0.4166667  1.3425926  2.2685185

　本では、度数分布表から求めた平均と標準偏差を使っています。計算方法については「第2講」を参照してください。ここでは(面倒なので)、値を直接指定します。
　 z = \frac{x - \bar{x}}{S_x}を計算して、データを標準化します。

　標準化したデータの標本平均と標本標準偏差を計算します。

# 平均値と標本標準偏差を計算
mean_z <- mean(data_z)
sd_z   <- sqrt(sum((data_z - mean_z)^2) / length(data_z))
head(data_z); mean_z; sd_z

## [1] -1.2500000 -0.6944444  0.0462963  0.7870370 -0.6944444 -1.0648148
## [1] -0.03240741
## [1] 0.9945733

　N個のデータ z_nの標本平均を \bar{z}、標本標準偏差を S_zで表します。

　標準化したデータを用いて度数分布表を作成します。

# 度数分布表を作成:(階級が決まっている場合)
freq_df <- tibble::tibble(
  class_lower = z_class_vec[-length(z_class_vec)], # 階級の下限
  class_upper = z_class_vec[-1] # 階級の上限
) |> 
  dplyr::group_by(class_lower, class_upper) |> 
  dplyr::mutate(
    class_value = median(c(class_lower, class_upper)), # 階級値
    freq = sum((data_z >= class_lower) == (data_z < class_upper)) # 度数
  ) |> 
  dplyr::ungroup() |> 
  dplyr::mutate(
    relative_freq = freq / length(data_x), # 相対度数
    cumulative_freq = cumsum(freq) # 累積度数
  )
freq_df

## # A tibble: 6 × 6
##   class_lower class_upper class_value  freq relative_freq cumulative_freq
##         <dbl>       <dbl>       <dbl> <int>         <dbl>           <int>
## 1      -3.29       -2.36      -2.82       1        0.0125               1
## 2      -2.36       -1.44      -1.90       4        0.05                 5
## 3      -1.44       -0.509     -0.972     17        0.212               22
## 4      -0.509       0.417     -0.0463    27        0.338               49
## 5       0.417       1.34       0.880     23        0.288               72
## 6       1.34        2.27       1.81       8        0.1                 80

　「第1講」のときと同様にして、相対度数を計算します。

　標準正規分布を計算します。

# 正規分布のパラメータを指定
mu    <- 0
sigma <- 1

# 確率密度を計算
dens_df <- tibble::tibble(
  x =  seq(from = mu-sigma*3, to = mu+sigma*3, length.out = 501), 
  density = dnorm(x = x, mean = mu, sd = sigma)
)

　これまでと同様にして、処理します。

　標準化したデータのヒストグラムと標準正規分布の折れ線グラフを重ねて描画します。

# 階級の幅を計算
class_width <- freq_df[["class_upper"]][1] - freq_df[["class_lower"]][1]

# タイトル用の文字列を作成
param_label <- paste0(
  "list(", 
  "mu==", mu, ", sigma==", sigma, 
  ", bar(z)==", round(mean_z, digits = 2), ", S[z]==", round(sd_z, digits = 2), 
  ")"
)

# 標準化データの相対度数と標準正規分布の比較
ggplot() + 
  geom_bar(data = freq_df, mapping = aes(x = class_value, y = relative_freq), 
           stat = "identity", width = class_width, fill = "green") + # 標準化データの相対度数
  geom_point(data = freq_df, mapping = aes(x = class_value, y = relative_freq), 
             color = "black", size = 4) + # 標準化データの相対度数
  geom_line(data = dens_df, mapping = aes(x = x, y = density), 
            color = "#00A968", size = 1) + # 標準正規分布の確率密度
  labs(title = "standard normal distribution", 
       subtitle = parse(text = param_label), 
       x = "x", y = "relative frequency")

身長データと正規分布の関係

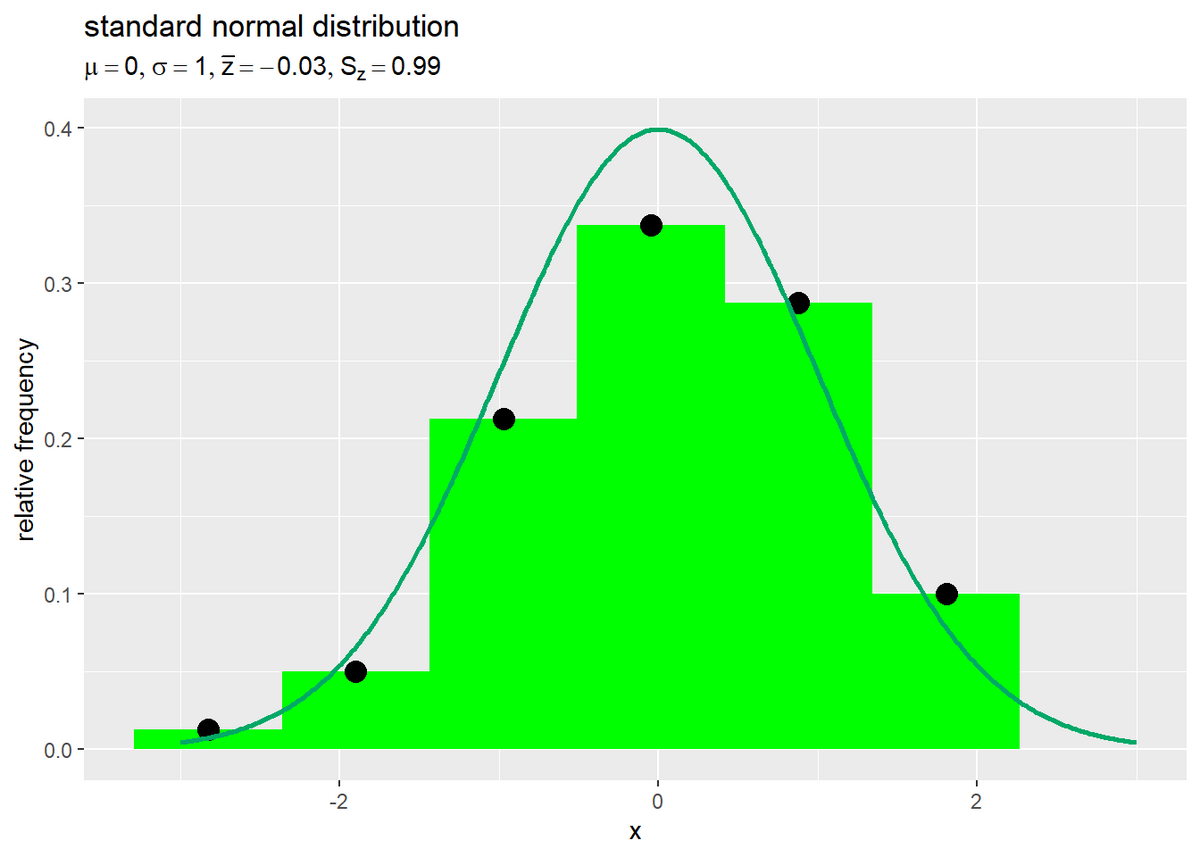
　標準正規分布と概ね一致しているのが分かります。

コインデータ

　複数枚のコインを同時に投げたときの表の枚数の分布(二項分布)と正規分布を比較します。二項分布については「二項分布の定義式 - からっぽのしょこ」を参照してください。

　二項分布のパラメータを設定します。

# コインの枚数を指定
N <- 18

# 表の確率を指定
phi <- 0.5

　試行回数 Nと成功確率 0 \leq \phi \leq 1を指定します。 \phiは0から1の値である必要があります。

　二項分布の平均と標準偏差を計算します。

# 平均と標準偏差を計算
mu    <- N * phi
sigma <- sqrt(N) * phi
mu; sigma

## [1] 9
## [1] 2.12132

　期待値(平均) \mathbb{E}[x] = N \phiを正規分布の平均パラメータ \mu、 \mathbb{s}[x] = \sqrt{N} \phiを標準偏差パラメータ \sigmaとします。

　正規分布に従う確率密度を計算します。

# 正規分布の確率密度を計算
norm_df <- tibble::tibble(
  x = seq(from = 0, to = N, length.out = 501), 
  density = dnorm(x = x, mean = mu, sd = sigma)
)
norm_df

## # A tibble: 501 × 2
##        x   density
##    <dbl>     <dbl>
##  1 0     0.0000232
##  2 0.036 0.0000249
##  3 0.072 0.0000268
##  4 0.108 0.0000288
##  5 0.144 0.0000309
##  6 0.18  0.0000331
##  7 0.216 0.0000356
##  8 0.252 0.0000381
##  9 0.288 0.0000409
## 10 0.324 0.0000439
## # … with 491 more rows

　二項分布の確率変数(N枚のコインを投げたときの表の枚数)は0以上N以下の値なので、0からNの範囲で確率密度を計算します。

　二項分布に従う確率を計算します。

# 二項分布の確率を計算
binom_df <- tibble::tibble(
  x = 0:N, 
  probability = dbinom(x = x, size = N, prob = phi)
)
binom_df

## # A tibble: 19 × 2
##        x probability
##    <int>       <dbl>
##  1     0  0.00000381
##  2     1  0.0000687 
##  3     2  0.000584  
##  4     3  0.00311   
##  5     4  0.0117    
##  6     5  0.0327    
##  7     6  0.0708    
##  8     7  0.121     
##  9     8  0.167     
## 10     9  0.185     
## 11    10  0.167     
## 12    11  0.121     
## 13    12  0.0708    
## 14    13  0.0327    
## 15    14  0.0117    
## 16    15  0.00311   
## 17    16  0.000584  
## 18    17  0.0000687 
## 19    18  0.00000381

　二項分布の確率はdbinom()で計算できます。確率変数の引数xに0からNの整数、試行回数の引数sizeにコインの枚数N、出現確率の引数probに表の確率phiを指定します。

　二項分布と正規分布のグラフを重ねて描画します。

# ラベル用の文字列を作成
dist_label <- paste0(
  "list(", 
  "Bin(x ~'|'~ N, phi), ", 
  "N(x ~'|'~ mu==frac(N, 2), sigma==frac(sqrt(N), 2))", 
  ")"
)
param_label <- paste0(
  "list(", 
  "N==", N, ", phi==", phi, 
  ", mu==", mu, ", sigma==", round(sigma, digits = 2), 
  ")"
)

# 二項分布と正規分布を作図
ggplot() + 
  geom_bar(data = binom_df, mapping = aes(x = x, y = probability), 
           stat = "identity", fill = "green") + # 二項分布
  geom_point(data = binom_df, mapping = aes(x = x, y = probability), 
             size = 4) + # 二項分布
  geom_line(data = norm_df, mapping = aes(x = x, y = density), 
            color = "#00A968", size = 1) + # 正規分布
  labs(title = "binomial distribution and normal distribution", 
       subtitle = parse(text = param_label), 
       x = "x", y = parse(text = dist_label))

コインの裏表データ(二項分布)と正規分布の関係

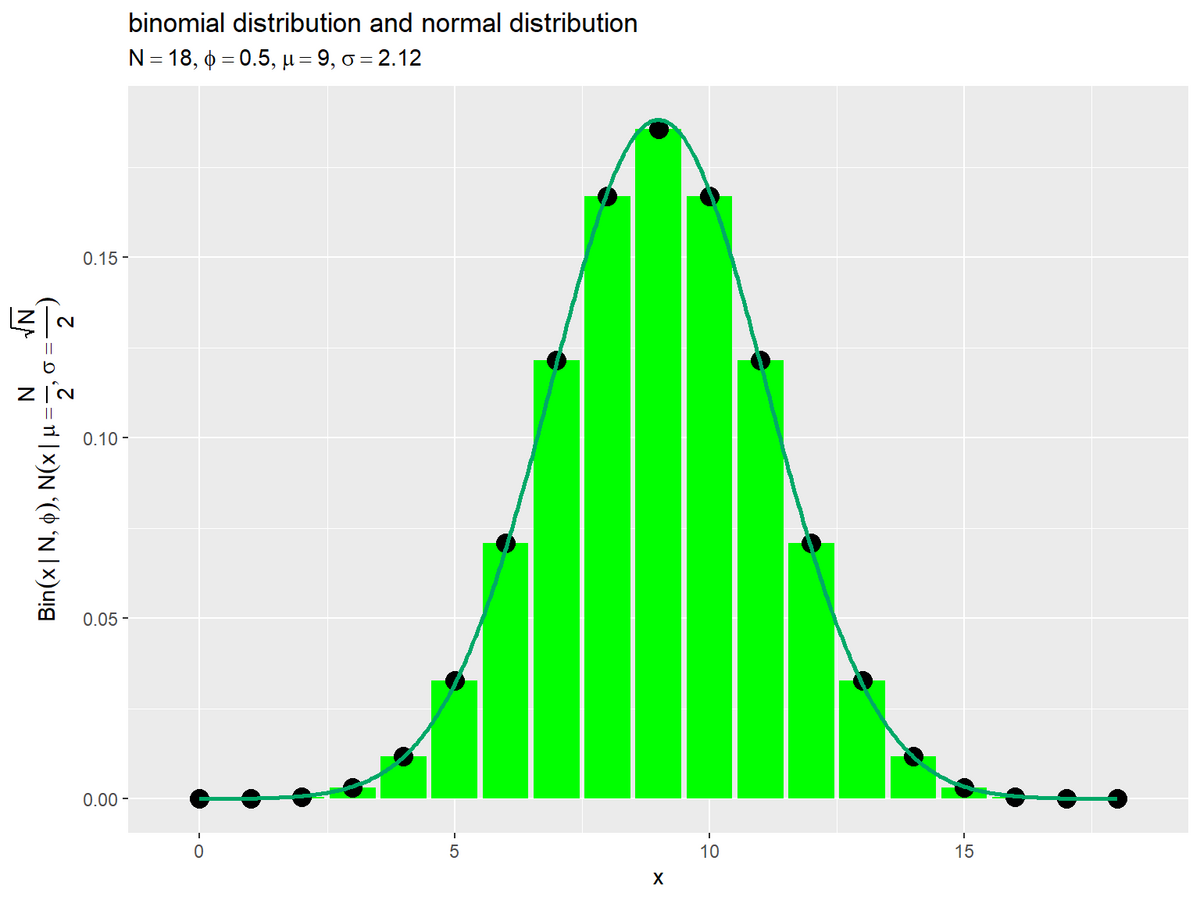
　二項分布は離散値をとり、正規分布は連続値をとりますが、点と曲線が一致しているのが分かります。ただし、二項分布のパラメータを変更すると一致の度合いも変わります。

　この講では、正規分布の性質を確認しました。次講では、○○を確認します。

参考書籍

  • 小島寛之『完全独習 統計学入門』ダイヤモンド社,2006年.

おわりに

　また2か月ほど間が空いてしまい、その間に別シリーズを2つ書いてたこともあり、このシリーズのノリを忘れてしまいました。少し分かっている人向けの解説になってしまったかもしれませんが、頑張って読んでください。
　別のことをしている間に(別のことをしたおかげではないのですが)、棒グラフとして正規分布を描く方法を思いついたのでよしとしましょう。

　2023年3月29日は、元モーニング娘。の佐藤優樹さんのソロデビュー日です！

　おめでとうございます！！！！！！！！！！

【次の節の内容】

つづく