はじめに
『完全独習 統計学入門』の学習ノートです。本に載っている計算や表、グラフをR言語で再現します。本とあわせて読んでください。
この記事では、標準偏差からシャープレシオを計算してグラフで確認します。
【前の節の内容】
【他の節の内容】
【この節の内容】
第6講 標準偏差(S.D.)でハイリスク・ハイリターン(シャープレシオ)も理解できる
前講では、標準偏差をボラティリティとして株の収益率を比較しました。この講では、標準偏差を使ってシャープレシオを計算して金融商品を比較します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(magick)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
6-1 ハイリスク・ハイリターンとローリスク・ローリターン
まずは、データを読み込んで、グラフで確認します。
図表6-1のデータセットをデータフレームとして作成します。
# データを作成:(図表6-1) revenue_df_wide <- tibble::tibble( year = 1988:1995, A = c(13.2, 20.9, -6.9, 35.6, 8.9, 12.5, -1.7, 31.1), B = c(7.7, 9.5, 3.7, 17.2, 7.9, 10.3, -3.7, 15.6), C = c(7.3, 9, 8.1, 5.9, 3.3, 2.6, 3.8, 5.4), D = c(7.4, 8.2, 7.9, 7.1, 4.2, 3.3, 3, 4.9) ) revenue_df_wide
## # A tibble: 8 × 5 ## year A B C D ## <int> <dbl> <dbl> <dbl> <dbl> ## 1 1988 13.2 7.7 7.3 7.4 ## 2 1989 20.9 9.5 9 8.2 ## 3 1990 -6.9 3.7 8.1 7.9 ## 4 1991 35.6 17.2 5.9 7.1 ## 5 1992 8.9 7.9 3.3 4.2 ## 6 1993 12.5 10.3 2.6 3.3 ## 7 1994 -1.7 -3.7 3.8 3 ## 8 1995 31.1 15.6 5.4 4.9
8年分の収益実績です。
作図用に、各商品の収益率のデータ(列)を1列にまとめます。
# 縦型のデータフレームに変換 revenue_df <- revenue_df_wide |> tidyr::pivot_longer( cols = !year, names_to = "name", names_ptypes = list(name = factor()), values_to = "revenue_rate" ) revenue_df
## # A tibble: 32 × 3 ## year name revenue_rate ## <int> <fct> <dbl> ## 1 1988 A 13.2 ## 2 1988 B 7.7 ## 3 1988 C 7.3 ## 4 1988 D 7.4 ## 5 1989 A 20.9 ## 6 1989 B 9.5 ## 7 1989 C 9 ## 8 1989 D 8.2 ## 9 1990 A -6.9 ## 10 1990 B 3.7 ## # … with 22 more rows
pivot_longer()で横型のデータフレームを縦型に変換します。cols引数に変換する列(変換しない列を指定する場合は頭に!を付けます)、names_to引数に「現在の列名」を格納する新たな列の名前、values_to引数に「現在の各列の値」を格納する新たな列の名前を指定します。また、names_ptypes(またはnames_transform)引数で格納後の型を指定できます。
商品ごとに標準偏差と平均値を計算します。
# 標準偏差と平均値を計算 stat_df <- revenue_df |> dplyr::group_by(name) |> # 商品ごとの計算用 dplyr::summarise( sd = sd(revenue_rate), mean = mean(revenue_rate), .groups = "drop" ) stat_df
## # A tibble: 4 × 3 ## name sd mean ## <fct> <dbl> <dbl> ## 1 A 14.7 14.2 ## 2 B 6.58 8.52 ## 3 C 2.34 5.68 ## 4 D 2.13 5.75
商品ごとに(name列で)グループ化して、summarise()を使って標本標準偏差(不偏標準偏差)と標本平均を計算します。summarise()を使って計算すると、計算に利用した行が集約されます(行数が変化します)。
標準偏差を説明変数、平均値を被説明変数として、回帰係数を計算します。
# 回帰係数を計算 res <- lm(stat_df[["mean"]]~stat_df[["sd"]]) # 傾きと切片を取得 a <- res[["coefficients"]][2] # 傾き b <- res[["coefficients"]][1] # 切片 # names属性を削除 names(a) <- NULL names(b) <- NULL a; b
## [1] 0.6790496 ## [1] 4.16055
lm(被説明変数~説明変数)で回帰係数を計算できます。
lm()の出力の"coefficients"から回帰直線の傾き$a$と切片$b$を取り出します。
回帰直線を計算します。
# x軸の最大値を設定 x_max <- ceiling(max(stat_df[["sd"]]))+1 # 回帰直線を計算 regression_df <- tibble::tibble( x = seq(from = 0, to = x_max, by = 0.1), y = a * x + b ) regression_df
## # A tibble: 161 × 2 ## x y ## <dbl> <dbl> ## 1 0 4.16 ## 2 0.1 4.23 ## 3 0.2 4.30 ## 4 0.3 4.36 ## 5 0.4 4.43 ## 6 0.5 4.50 ## 7 0.6 4.57 ## 8 0.7 4.64 ## 9 0.8 4.70 ## 10 0.9 4.77 ## # … with 151 more rows
作図用のx軸の値$x$を作成して、y軸の値$y = a x + b$を計算します。
リスク(標準偏差)とリターン(平均値)の関係に回帰直線を重ねたグラフを作成します。
# y軸の最大値を設定 y_max <- ceiling(max(regression_df[["y"]])) # タイトル用の文字列を作成 regression_label <- paste0("y==", round(a, digits = 2), "*x+", round(b, digits = 2)) # データと回帰直線を作図 ggplot() + geom_point(data = stat_df, mapping = aes(x = sd, y = mean, color = name), size = 4) + # データ geom_line(data = regression_df, mapping = aes(x = x, y = y)) + # 回帰直線 coord_cartesian(ylim = c(0, y_max)) + # 描画範囲 labs(title = "risk and return", subtitle = parse(text = regression_label), x = "S.D.", y = "mean")
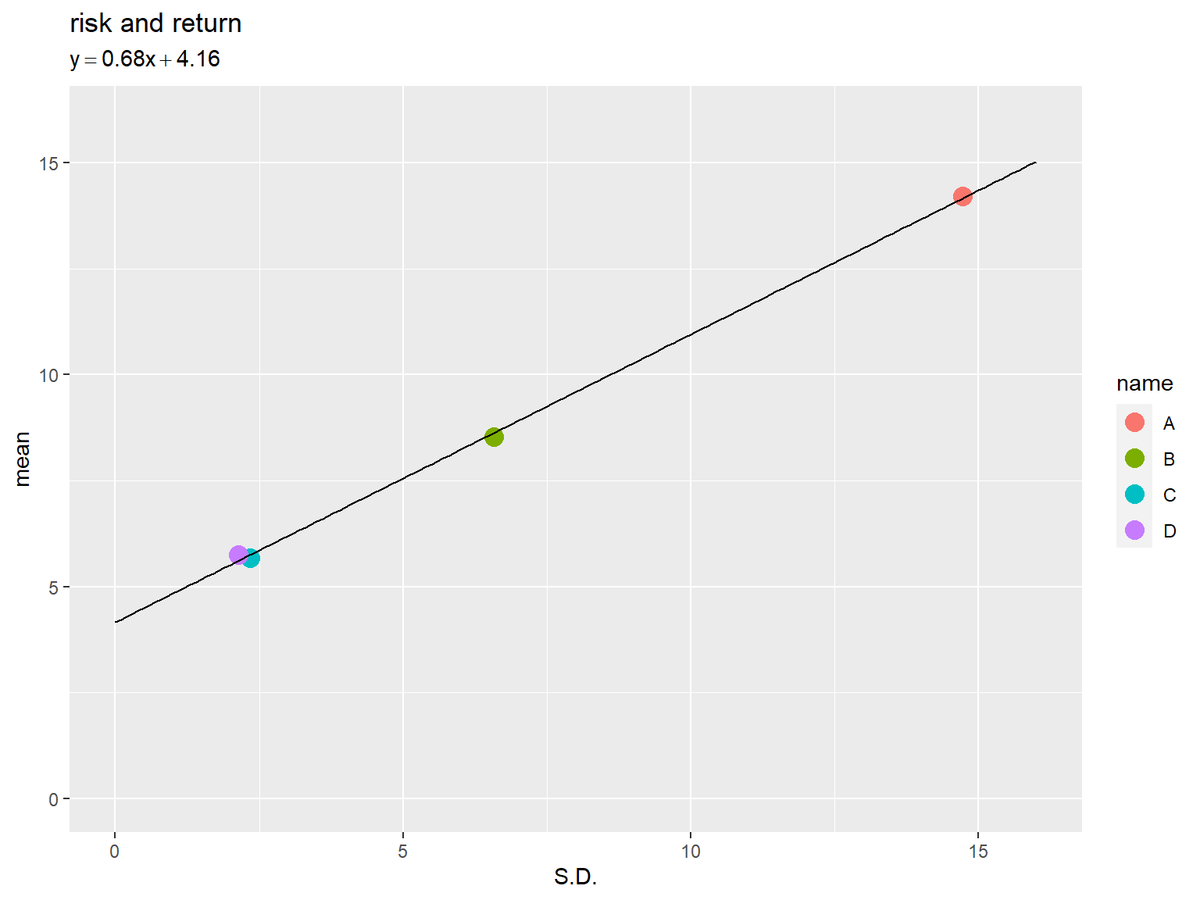
4つの商品(データ)を説明できる直線を引けました。
6-3 金融商品の優劣を測る数値・シャープレシオ
次は、シャープレシオを計算して、グラフを作成します。
図表6-6のデータセットをデータフレームとして作成します。
# 日本国債の利回りを設定:(図表6-6) JGB <- 3.4 # シャープレシオを計算 sharpe_df <- tibble::tibble( id = 1:7, name = c("nissei", "diichi", "sumitomo", "meiji", "asahi", "mitsui", "yasuda"), mean = c(4, 4.69, 4.62, 4.8, 5.41, 6.49, 4.85), sd = c(5.48, 4.47, 5.59, 4.28, 5.64, 4.64, 6.43) ) |> # 値を格納 dplyr::mutate( sharpe_ratio = (mean - JGB) / sd, rank = dplyr::row_number(-sharpe_ratio) ) |> dplyr::arrange(rank) |> dplyr::mutate( name = factor(name, levels = name) # 順位に応じて因子レベルを設定 ) sharpe_df
## # A tibble: 7 × 6 ## id name mean sd sharpe_ratio rank ## <int> <fct> <dbl> <dbl> <dbl> <int> ## 1 6 mitsui 6.49 4.64 0.666 1 ## 2 5 asahi 5.41 5.64 0.356 2 ## 3 4 meiji 4.8 4.28 0.327 3 ## 4 2 diichi 4.69 4.47 0.289 4 ## 5 7 yasuda 4.85 6.43 0.226 5 ## 6 3 sumitomo 4.62 5.59 0.218 6 ## 7 1 nissei 4 5.48 0.109 7
国債の利回りをJGBとして値を指定します。
会社ごとの平均値$\bar{x}$と標準偏差$S$をデータフレームに格納します。
会社ごとにシャープレシオを$\frac{\bar{x} - \mathrm{JGB}}{S}$で計算します。
シャープレシオの値に応じてrow_number()で順位を付けます。row_number()は昇順に行番号を割り当てるので、シャープレシオ列の値に-を付けることで大小関係を反転させて、降順に値を割り当てます。
順位に応じてarrange()で行を並べ替えて、作図時の色付けや凡例の並びを調整するために、会社列を因子型にして因子レベルを設定します。(装飾用の処理なので省略できます。)
シャープレシオ(角度のマーク)を描画するためのデータフレームを作成します。(装飾用の処理です。)
# シャープレシオの angle_df <- sharpe_df |> dplyr::group_by(name) |> # 商品ごとの計算用 dplyr::summarise( theta = seq(from = 0, to = atan(sharpe_ratio), by = 0.01), # 角度(ラジアン)を作成 x = cos(theta) * (id*0.05+0.1), y = sin(theta) * (id*0.05+0.1) + JGB, .groups = "drop" ) angle_df
## # A tibble: 211 × 4 ## name theta x y ## <fct> <dbl> <dbl> <dbl> ## 1 mitsui 0 0.4 3.4 ## 2 mitsui 0.01 0.400 3.40 ## 3 mitsui 0.02 0.400 3.41 ## 4 mitsui 0.03 0.400 3.41 ## 5 mitsui 0.04 0.400 3.42 ## 6 mitsui 0.05 0.400 3.42 ## 7 mitsui 0.06 0.399 3.42 ## 8 mitsui 0.07 0.399 3.43 ## 9 mitsui 0.08 0.399 3.43 ## 10 mitsui 0.09 0.398 3.44 ## # … with 201 more rows
逆タンジェント関数atan()でシャープレシオ(傾き)から弧度法における角度(ラジアン)を作成して、コサイン関数cos()でx軸の値、サイン関数sin()でy軸の値を計算します。さらに、y軸の値に国債の利回りJGBを加えます。(id*0.05+0.1)はサイズ調整用の値です。
リスクとリターンの関係にシャープレシオを重ねたグラフを作成します。
# シャープレシオを作図 ggplot() + geom_point(data = sharpe_df, mapping = aes(x = sd, y = mean, color = name), size = 4) + # データ geom_segment(data = sharpe_df, mapping = aes(x = 0, y = JGB, xend = sd, yend = mean, color = name)) + # データ線 geom_path(data = angle_df, mapping = aes(x = x, y = y, color = name)) + # シャープレシオ geom_hline(yintercept = JGB, linetype = "dotted") + # 国債の利回り labs(title = "sharpe ratio", subtitle = paste0("Japanese Government Bonds : ", JGB), x = "S.D.", y = "mean")

国債の利回りの点と、各商品の点を結ぶ線分をgeom_segment()で描画します。x, y引数に始点の座標(国債の利回り)、xend, yend引数に終点の座標(各会社の実績)を指定します。
国債の利回りを示す水平線をgeom_hline()で描画します。yintercept引数に国債の利回りを指定します。
水平線と線分の角度(傾き)を示す弧(角度のマーク)をgeom_path()で描画します。
平均収益率(y軸の値)の大小ではなく、シャープレシオ(角度)の大きさで商品を評価できます。
この講では、標準偏差を利用してシャープレシオを比較しました。
参考書籍
- 小島寛之『完全独習 統計学入門』ダイヤモンド社,2006年.
おわりに
ここまでが記述統計(的な)の話で一区切りという感じですかね。次からは推測統計の話になるようです。
統計のためにRを始めた人であれば初期に使うであろうlm()をたぶん初めて使いました。ベイズやニューラルネットを使った回帰しかやったことがなかった気がします。1行で回帰分析できるの凄い。
それと、同時並行して始めた三角関数シリーズに関わる内容が出てきたので、不要だと思いつつも書いてしまいました。角度のマークの描き方に興味が湧いたら「Rによる三角関数(円関数)入門:記事一覧 - からっぽのしょこ」を覗いてみてください。
【次の節の内容】