からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

トップ > 攻略ノート > 【R】第3講：標準偏差の計算【統計学入門(小島)のノート】

【R】第3講：標準偏差の計算【統計学入門(小島)のノート】

攻略ノート 攻略ノート-統計学入門(小島) 統計学 R

はじめに

　この記事は「R Advent Calendar 2022」の15日目の記事です。

　『完全独習 統計学入門』の学習ノートです。本に載っている計算や表、グラフをR言語で再現します。本とあわせて読んでください。
　この記事では、度数分布表やヒストグラムと標本標準偏差の関係を確認します。

【前の節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

第3講 データの散らばり具合を見積もる統計量――分散と標準偏差

　前講では、平均値の計算と役割を確認しました。この講では、分散と標準偏差の計算と役割を確認します。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)
library(magick)

　この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
　また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。

3-2 バスの到着時刻の例で、分散を理解する

　まずは、分散と標準偏差の計算を確認します。

　図表3-1のデータセットをベクトルとして作成します。

# データセットを作成
data_x <- c(32, 27, 29, 34, 33)

# データ数を取得
N <- length(data_x)
N

## [1] 5

　データ数を$N$とします。

　標本平均を計算します。

# 平均値を計算
mean_x <- sum(data_x) / N
mean_x

## [1] 31

　標本平均$\bar{x}$は、次の式で定義されます(第2講)。

$$ \begin{aligned} \bar{x} &= \frac{1}{N} \sum_{n=1}^N x_n \\ &= \frac{1}{N} \Bigl( x_1 + x_2 + \cdots + x_N \Bigr) \end{aligned} $$

　偏差を計算します。

# 偏差を計算
deviation_x <- data_x - mean_x
deviation_x

## [1]  1 -4 -2  3  2

　偏差は、各データと平均値の差$x_n - \bar{x}$で定義されます。

　偏差の和を計算してみます。

# 偏差の和を確認
sum(deviation_x)

## [1] 0

　プラスとマイナスが打ち消されて0になります。

　偏差の2乗を計算します。

# 偏差の2乗を確認
deviation_x^2

## [1]  1 16  4  9  4

　偏差の2乗$(x_n - \bar{x})^2$は、2乗の計算により0以上の値になります。

　標本分散を計算します。

# 分散を計算
variance_x <- sum(deviation_x^2) / N
variance_x

## [1] 6.8

　分散$S^2$は、偏差の平均で定義されます。

$$ \begin{aligned} S^2 &= \frac{1}{N} \sum_{n=1}^N (x_n - \bar{x})^2 \\ &= \frac{1}{N} \Bigl\{ (x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_N - \bar{x})^2 \Bigr\} \end{aligned} $$

　標本標準偏差を計算します。

# 標準偏差を計算
sd_x <- sqrt(variance_x)
sd_x

## [1] 2.607681

　標準偏差$S$は、分散の平方根で定義されます。

$$ \begin{aligned} S &= \sqrt{S^2} \\ &= \sqrt{\frac{\sum_{n=1}^N (x_n - \bar{x})}{N}} \end{aligned} $$

　平方根はsqrt()で計算できます。

　以上が、標準偏差の計算です。

　ちなみに、組み込み関数のvar()で分散、sd()で標準偏差を計算できます。

# 不偏分散と不偏標準偏差を計算
variance_x <- var(data_x)
sd_x       <- sd(data_x)
variance_x; sd_x

## [1] 8.5
## [1] 2.915476

　ただしこの関数は、不偏分散と不偏標準偏差を計算します。詳しくは省略しますが、不偏分散$U^2$は、$N$ではなく$N-1$で割った値です。不偏標準偏差$U$は、不偏分散の平方根です。

$$ \begin{aligned} U^2 &= \frac{1}{N - 1} \sum_{n=1}^N (x_n - \bar{x}) \\ U &= \sqrt{U^2} \\ &= \sqrt{ \frac{\sum_{n=1}^N (x_n - \bar{x})}{N - 1} } \end{aligned} $$

　よって、$N-1$を掛けて$N$で割ることで標本分散と標本標準偏差に変換できます。

# 関数を使う場合
variance_x <- var(data_x) * (N - 1) / N
sd_x       <- sd(data_x) * sqrt(N - 1) / sqrt(N)
variance_x; sd_x

## [1] 6.8
## [1] 2.607681

　不偏分散に$\frac{N - 1}{N}$を掛けると標本分散になります。

$$ \begin{aligned} U^2 \frac{N - 1}{N} &= \frac{\sum_{n=1}^N (x_n - \bar{x})}{N - 1} \frac{N - 1}{N} \\ &= \frac{\sum_{n=1}^N (x_n - \bar{x})}{N} = S^2 \end{aligned} $$

　また、不偏標準偏差に$\sqrt{\frac{N - 1}{N}}$を掛けると標本標準偏差になります。

$$ \begin{aligned} U \sqrt{\frac{N - 1}{N}} &= \frac{\sqrt{\sum_{n=1}^N (x_n - \bar{x})}}{\sqrt{N - 1}} \frac{\sqrt{N - 1}}{\sqrt{N}} \\ &= \frac{\sqrt{\sum_{n=1}^N (x_n - \bar{x})}}{\sqrt{N}} \\ &= \sqrt{S^2} = S \end{aligned} $$

　平方根の性質より$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$です。

3-3 標準偏差の意味

　次は、2つのデータを標準偏差を用いて比較します。

　2種類のデータセットを指定します。

# データセットを作成
data_x <- c(4, 4, 5, 6, 6)
data_y <- c(1, 2, 6, 7, 9)

# データ数を取得
N_x <- length(data_x)
N_y <- length(data_y)


　それぞれ標本平均を計算します。

# 平均値を計算
mean_x <- sum(data_x) / N_x
mean_y <- sum(data_y) / N_y
mean_x; mean_y

## [1] 5
## [1] 5

　平均値は一致しています(比較のため、平均値が等しくなるようなデータを用意しています)。

　偏差を計算します。

# 偏差を計算
deviation_x <- data_x - mean_x
deviation_y <- data_y - mean_y
deviation_x; deviation_y

## [1] -1 -1  0  1  1
## [1] -4 -3  1  2  4

　データYの方が平均から離れている(偏差の絶対値が大きい)のが分かります。

　偏差の和を計算してみます。

# 偏差の和を確認
sum(deviation_x); sum(deviation_y)

## [1] 0
## [1] 0

　データに関わらず0になります。

　標本分散を計算します。

# 分散を計算
variance_x <- sum(deviation_x^2) / N_x
variance_y <- sum(deviation_y^2) / N_y
variance_x; variance_y

## [1] 0.8
## [1] 9.2

　データYの方が分散が大きいのが分かります。

　標本標準偏差を計算します。

# 標準偏差を計算
sd_x <- sqrt(variance_x)
sd_y <- sqrt(variance_y)
sd_x; sd_y

## [1] 0.8944272
## [1] 3.03315

　分散が大きいと標準偏差も大きくなります。

　標準偏差を計算できました。続いて、ヒストグラムと標準偏差の関係を確認します。

　データセットをそれぞれデータフレームに格納します。

# 作図用のデータフレームを作成
data_x_df <- tibble::tibble(value = data_x)
data_y_df <- tibble::tibble(value = data_y)
data_x_df; data_y_df

## # A tibble: 5 × 1
##   value
##   <dbl>
## 1     4
## 2     4
## 3     5
## 4     6
## 5     6
## # A tibble: 5 × 1
##   value
##   <dbl>
## 1     1
## 2     2
## 3     6
## 4     7
## 5     9


　平均値と標準偏差を重ねてヒストグラムを作成します。

# データセットxのヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_x_df, mapping = aes(x = value), 
                 breaks = 0:11-0.5, closed ="left", fill = "#00A968") + # 度数
  geom_vline(xintercept = mean_x, 
             color = "red", size = 1, linetype = "dashed") + # 平均値
  geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 平均値 ± 標準偏差
  scale_x_continuous(breaks = 0:10) + # x軸目盛
  coord_cartesian(ylim = c(0, 2)) + # 表示範囲
  labs(title = "dataset x", 
       subtitle = parse(text = paste0("list(bar(x)==", mean_x, ", S[x]==", sd_x, ")")), 
       x = "class value", y = "frequency")

# データセットyのヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_y_df, mapping = aes(x = value), 
                 breaks = 0:11-0.5, closed ="left", fill = "#00A968") + # 度数
  geom_vline(xintercept = mean_y, 
             color = "red", size = 1, linetype = "dashed") + # 平均値
  geom_segment(mapping = aes(x = mean_y-sd_y, y = 0, xend = mean_y+sd_y, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 平均値 ± 標準偏差
  scale_x_continuous(breaks = 0:10) + # x軸目盛
  coord_cartesian(ylim = c(0, 2)) + # 表示範囲
  labs(title = "dataset y", 
       subtitle = parse(text = paste0("list(bar(y)==", mean_y, ", S[y]==", sd_y, ")")), 
       x = "class value", y = "frequency")

ヒストグラムと標準偏差の関係

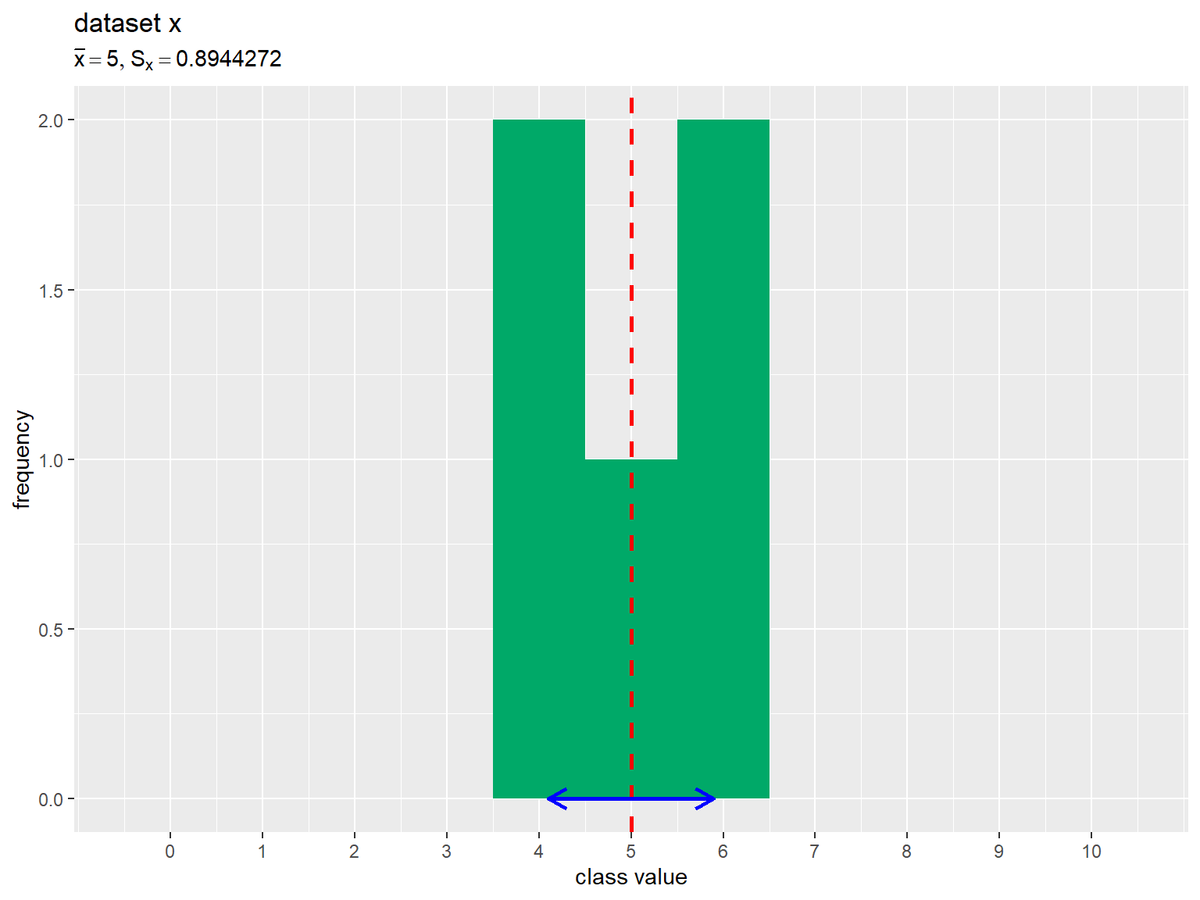
　平均値を赤色の垂線で、平均値を中心に標準偏差1つ分の範囲($\bar{x} - S$から$\bar{x} + S$)を青色の水平線で示します。矢印の範囲が広いほど、標準偏差(データの散らばり具合)が大きいことを表します。
　矢印はgeom_segment()で描画できます。矢印の始点をx, y引数、終点をxend, yend引数に指定します。矢印の形などはarrow引数で指定できます。

　データと平均値・標準偏差の関係を見てみましょう。

作図コード(クリックで展開)

　データを1つずつランダムに生成してヒストグラムのアニメーションを作成します。

# 画像の保存先を指定
dir_path <- "tmp_folder"

# データ数の最大値(フレーム数)を指定
N <- 30

# 階級を変更して作図
data_x <- NULL # 受け皿を作成(初期化)
for(n in 1:N) {
  
  # データを生成
  data_x[n] <- sample(x = 1:10, size = 1)
  
  # データを格納
  data_df <- tibble::tibble(value = data_x)
  
  # 平均値と標準偏差を計算
  mean_x <- sum(data_x) / n
  sd_x   <- sqrt(sum((data_x - mean_x)^2) / n)
  print(sd_x)
  
  # タイトル用の文字列を作成
  title_label <- paste0("list(n==", n, ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), ")")
  
  # ヒストグラムを作成
  g <- ggplot() + 
    geom_histogram(data = data_df, mapping = aes(x = value), 
                   breaks = 0:11-0.5, closed ="left", fill = "#00A968") + # 度数
    geom_vline(xintercept = mean_x, 
               color = "red", size = 1, linetype = "dashed") + # 平均値
    geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
                 color = "blue", size = 1, 
                 arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 平均値 ± 標準偏差
    scale_x_continuous(breaks = 0:10) + # x軸目盛
    coord_cartesian(ylim = c(0, N/5)) + # 表示範囲
    labs(title = "dataset x", 
         subtitle = parse(text = title_label), 
         x = "class value", y = "frequency")
  
  # グラフを書き出し
  file_name <- sprintf(paste0("%0", nchar(N), "d"), n)
  ggplot2::ggsave(
    filename = paste0(dir_path, "/", file_name, ".png"), plot = g, 
    width = 800, height = 600, units = "px", dpi = 100
  )
}

# ファイル名を取得
file_name_vec <- list.files(dir_path)

# gif画像を作成
paste0(dir_path, "/", file_name_vec) |> # ファイルパスを作成
  magick::image_read() |> # 画像ファイルを読み込み
  magick::image_animate(fps = 1, dispose = "previous") |> # gif画像を作成
  magick::image_write_gif(path = "histgram.gif", delay = 1/2) -> tmp_path # gifファイルを書き出し

　データ数の最大値をNとして値を指定します。for()を使って、1データずつ生成します。
　同様に作図してそれぞれグラフを保存します。画像の書き出し先フォルダdir_pathは空である必要があります。また、画像ファイルの読み込み時に、書き出した順番と(文字列基準で)同じ並びになるようなファイル名を付ける必要があります。
　保存した画像ファイルをimage_read()で読み込んで、image_animate()とimage_write_gif()でgif画像に変換します。


データと標準偏差の関係

　(標準偏差ってすぐに収束するんですね。)

3-4 度数分布表から標準偏差を求める

　ここまでは、生データから標準偏差を計算しました。次は、度数分布表を用いて標準偏差を計算します。

　図表3-6のデータを格納して、度数分布表を作成します。

# 度数分布表を作成
freq_df <- tibble::tibble(
  class_value = c(1, 2, 3, 4), # 階級値
  relative_freq = c(0.3, 0.5, 0.1, 0.1) # 相対度数
) |> 
  dplyr::mutate(
    weighted_class_value = class_value * relative_freq, # 階級値 × 相対度数
    deviation = class_value - sum(weighted_class_value), # 偏差
    deviation2 = deviation^2, # 偏差の2乗
    weighted_deviation2 = deviation2 * relative_freq # 偏差の2乗 × 相対度数
  )
freq_df[, c("weighted_class_value", "deviation", "deviation2", "weighted_deviation2")]

## # A tibble: 4 × 4
##   weighted_class_value deviation deviation2 weighted_deviation2
##                  <dbl>     <dbl>      <dbl>               <dbl>
## 1                  0.3        -1          1                 0.3
## 2                  1           0          0                 0  
## 3                  0.3         1          1                 0.1
## 4                  0.4         2          4                 0.4

　第2講と同様に、相対度数を用いて階級値の平均値(加重平均)を計算します。

　標本分散を計算します。

# 分散を計算
variance_x <- sum(freq_df[["weighted_deviation2"]])
variance_x

## [1] 0.8

　偏差の2乗と相対度数の積の総和(相対度数による偏差の2乗の加重平均)を計算します。

　標本標準偏差を計算します。

# 標準偏差を計算
sd_x <- sqrt(variance_x)
sd_x

## [1] 0.8944272

　階級の数を$C$、C個の階級値を$x_i$($i$は1からCの整数)、i番目の階級の度数を$N_i$とすると、相対度数は$\frac{N_i}{N}$で表せ、標本平均(の近似値)を次の式で計算できるのでした(第2講)。

$$ \bar{x} = \sum_{i=1}^C x_i \frac{N_i}{N} $$

　C個の度数の和はデータ数$N = \sum_{i=1}^C N_i$であり、相対度数の総和は$\sum_{i=1}^C \frac{N_i}{N} = 1$です。
　同様に、階級値ごとの偏差の2乗$(x_i - \bar{x})^2$と相対度数の積の和で、標本分散(の近似値)を計算できます。

$$ \begin{aligned} \bar{x} &= (x_1 - \bar{x})^2 \frac{N_1}{N} + (x_2 - \bar{x})^2 \frac{N_2}{N} + \cdots + (x_C - \bar{x})^2 \frac{N_C}{N} \\ &= \sum_{i=1}^C (x_i - \bar{x})^2 \frac{N_i}{N} \\ &= \frac{1}{N} \sum_{i=1}^C (x_i - \bar{x})^2 N_i \end{aligned} $$

　この計算は、相対度数で加重平均を求めています。

練習問題

　データセットを指定します。

# データセットを作成
data_x <- c(6, 4, 6, 6, 6, 3, 7, 2, 2, 8)


　標本平均を計算します。

# 平均値を計算
mean_x <- sum(data_x) / length(data_x)
mean_x

## [1] 5


　偏差を計算します。

# 偏差を計算
deviation_x <- data_x - mean_x
deviation_x

##  [1]  1 -1  1  1  1 -2  2 -3 -3  3


　偏差の2乗を計算します。

# 偏差の2乗を計算
deviation2_x <- deviation_x^2
deviation2_x

##  [1] 1 1 1 1 1 4 4 9 9 9


　標本分散を計算します。

# 分散を計算
variance_x <- sum(deviation2_x) / length(data_x)
variance_x

## [1] 4


　標本標準偏差を計算します。

# 標準偏差を計算
sd_x <- sqrt(variance_x)
sd_x

## [1] 2


　この講では、標準偏差の計算を確認しました。次講では、標準偏差についてさらに確認します。

　Enjoy!

参考書籍

  • 小島寛之『完全独習 統計学入門』ダイヤモンド社,2006年.

おわりに

　正直簡単な内容だしもっとサクサク進められると思ってましたが、1日1つしか進められてません。

【次の節の内容】

www.anarchive-beta.com