はじめに
R言語で三角関数の定義や公式を可視化しようシリーズです。
この記事では、2つの角の差に関する三角関数の加法定理のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
三角関数の加法定の可視化理:その2(2角の差)
三角関数における加法定理(2つの角の差のサインとコサイン)を可視化します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
加法定理の公式
三角関数の加法定理として、次の関係が成り立ちます。
この記事では、$\sin(\alpha - \beta)$と$\cos(\alpha - \beta)$の式に関して可視化して確認します。
加法定理の可視化
三角関数の加法定理($\sin(\alpha - \beta), \cos(\alpha - \beta)$)をグラフで確認します。
グラフの作成
まずは、角度を固定したグラフを作成します。
角度を指定して、ラジアンに変換します。
# 角度を指定 a <- 60 b <- 15 # ラジアンに変換 alpha <- a / 180 * pi beta <- b / 180 * pi alpha; beta
## [1] 1.047198 ## [1] 0.2617994
度数法における角度$0^{\circ} \leq a \leq 90^{\circ}$、$0^{\circ} \leq b \leq a$を指定します。
指定した角度を、弧度法におけるラジアン$\alpha = a \frac{2 \pi}{360}$、$\beta = b \frac{2 \pi}{360}$に変換します。$\pi$は円周率でpiで扱えます。
・コード(クリックで展開)
(第1象限における)単位円を描画するためのデータフレームを作成します。
# 単位円(の4分の1)の描画用 sector_df <- tibble::tibble( c = seq(from = 0, to = 90, by = 1), theta = c / 180 * pi, x = cos(theta), y = sin(theta) ) sector_df
## # A tibble: 91 × 4 ## c theta x y ## <dbl> <dbl> <dbl> <dbl> ## 1 0 0 1 0 ## 2 1 0.0175 1.00 0.0175 ## 3 2 0.0349 0.999 0.0349 ## 4 3 0.0524 0.999 0.0523 ## 5 4 0.0698 0.998 0.0698 ## 6 5 0.0873 0.996 0.0872 ## 7 6 0.105 0.995 0.105 ## 8 7 0.122 0.993 0.122 ## 9 8 0.140 0.990 0.139 ## 10 9 0.157 0.988 0.156 ## # … with 81 more rows
作図用の角度$0^{\circ} \leq c \leq 90^{\circ}$を作成して、ラジアン$\theta = c \frac{2 \pi}{360}$に変換します。
x軸の値は$x = \cos \theta$、y軸の値は$y = \sin \theta$で単位円を描くための点の座標を計算します。
単位正方形を描画するためのデータフレームを作成します。
# 単位正方形の描画用 square_df <- tibble::tibble( x = c(0, 0, 1, 1, 0), y = c(0, 1, 1, 0, 0) ) square_df
## # A tibble: 5 × 2 ## x y ## <dbl> <dbl> ## 1 0 0 ## 2 0 1 ## 3 1 1 ## 4 1 0 ## 5 0 0
単位正方形の頂点の座標を格納します。
加法定理を構成する辺(線分)を描画するためのデータフレームを作成します。
# 因子レベルを指定 fnc_level <- c( "r", "sin(a)", "cos(a)", "sin(a) sin(b)", "cos(a) sin(b)", "sub1", "sub2", "cos(a) cos(b)", "sin(a) cos(b)", "sin(a-b)", "cos(a-b)" ) # 辺の描画用 A_x <- cos(alpha)*cos(beta)^2 A_y <- cos(alpha)*sin(beta)*cos(beta) B_x <- cos(alpha)-sin(alpha)*sin(beta)*cos(beta) B_y <- sin(alpha)-sin(alpha)*sin(beta)^2 C_x <- cos(alpha)+sin(alpha)*sin(beta)*cos(beta) C_y <- sin(alpha)*sin(beta)^2 segment_df <- tibble::tribble( ~fnc, ~type, ~label, ~width, ~x_from, ~y_from, ~x_to, ~y_to, "r", "main", TRUE, "normal", 0, 0, cos(alpha), sin(alpha), "sin(a)", "main", TRUE, "normal", cos(alpha), sin(alpha), cos(alpha), 0, "cos(a)", "main", TRUE, "normal", 0, 0, cos(alpha), 0, "cos(a) cos(b)", "main", TRUE, "normal", 0, 0, A_x, A_y, "sin(a) sin(b)", "main", TRUE, "normal", cos(alpha), sin(alpha), B_x, B_y, "sin(a) sin(b)", "main", FALSE, "normal", A_x, A_y, cos(alpha-beta)*cos(beta), cos(alpha-beta)*sin(beta), "sin(a) sin(b)", "main", FALSE, "normal", cos(alpha), 0, C_x, C_y, "sin(a) cos(b)", "main", TRUE, "normal", cos(alpha), 0, B_x, B_y, "sin(a) cos(b)", "main", FALSE, "normal", cos(alpha), sin(alpha), C_x, C_y, "cos(a) sin(b)", "main", FALSE, "bold", cos(alpha), 0, A_x, A_y, "cos(a) sin(b)", "main", TRUE, "bold", C_x, C_y, cos(alpha-beta)*cos(beta), cos(alpha-beta)*sin(beta), "sin(a-b)", "target", TRUE, "bold", cos(alpha), sin(alpha), cos(alpha-beta)*cos(beta), cos(alpha-beta)*sin(beta), "cos(a-b)", "target", TRUE, "bold", 0, 0, cos(alpha-beta)*cos(beta), cos(alpha-beta)*sin(beta), "r", "sub", FALSE, "normal", cos(beta), sin(beta), cos(alpha-beta)*cos(beta), cos(alpha-beta)*sin(beta), "sub1", "sub", FALSE, "normal", cos(alpha), 0, C_x, 0, "sub1", "sub", FALSE, "normal", cos(alpha), sin(alpha), B_x, sin(alpha), "sub2", "sub", FALSE, "normal", C_x, 0, C_x, C_y, "sub2", "sub", FALSE, "normal", B_x, sin(alpha), B_x, B_y ) |> # 座標を格納 dplyr::mutate( fnc = factor(fnc, levels = fnc_level) # 因子レベルを設定 ) |> dplyr::arrange(fnc) # 並びを統一 segment_df
## # A tibble: 18 × 8 ## fnc type label width x_from y_from x_to y_to ## <fct> <chr> <lgl> <chr> <dbl> <dbl> <dbl> <dbl> ## 1 r main TRUE normal 0 0 0.5 0.866 ## 2 r sub FALSE normal 0.966 0.259 0.683 0.183 ## 3 sin(a) main TRUE normal 0.5 0.866 0.5 0 ## 4 cos(a) main TRUE normal 0 0 0.5 0 ## 5 sin(a) sin(b) main TRUE normal 0.5 0.866 0.283 0.808 ## 6 sin(a) sin(b) main FALSE normal 0.467 0.125 0.683 0.183 ## 7 sin(a) sin(b) main FALSE normal 0.5 0 0.717 0.0580 ## 8 cos(a) sin(b) main FALSE bold 0.5 0 0.467 0.125 ## 9 cos(a) sin(b) main TRUE bold 0.717 0.0580 0.683 0.183 ## 10 sub1 sub FALSE normal 0.5 0 0.717 0 ## 11 sub1 sub FALSE normal 0.5 0.866 0.283 0.866 ## 12 sub2 sub FALSE normal 0.717 0 0.717 0.0580 ## 13 sub2 sub FALSE normal 0.283 0.866 0.283 0.808 ## 14 cos(a) cos(b) main TRUE normal 0 0 0.467 0.125 ## 15 sin(a) cos(b) main TRUE normal 0.5 0 0.283 0.808 ## 16 sin(a) cos(b) main FALSE normal 0.5 0.866 0.717 0.0580 ## 17 sin(a-b) target TRUE bold 0.5 0.866 0.683 0.183 ## 18 cos(a-b) target TRUE bold 0 0 0.683 0.183
各辺の値を格納しやすいように、tribble()を使ってデータフレームを作成します。線分の始点の座標をx_from, y_from列、終点の座標をx_to, y_to列とします。次の「関数名ラベル」の関数の値は線分の長さであり、座標の値とは異なります。
各関数(辺)を区別するためのfnc列、「加法定理を示す線("target)」・「加法定理を求めるための線("main)」・「補助線("sub)」を区別するためのtype列を作成します。fnc列は色分け、type列は線の種類に使います。
平行な同じ長さの辺はfnc列を同じ値とします。ただし、関数名ラベルは1辺のみに描画することにします。ラベルの有無をlabel列で設定します。ラベルを付ける辺はTRUE、付けない辺はFALSEにします。
線が重なる辺があるので、width列で線の太さを設定します。通常を"normal"とし、重なる線(の片方)を"bold"とします。
線の描画順(重なり順)や色付け順は、fnc列の因子レベルに依存するので、fnc_levelとして指定しておきます。
線分ごとに関数名ラベルを描画するためのデータフレームを作成します。
# 関数名ラベルの描画用 segment_label_df <- segment_df |> dplyr::filter(label) |> dplyr::group_by(fnc) |> # 中点の計算用 dplyr::mutate( # 線分の中点に配置 x = median(c(x_from, x_to)), y = median(c(y_from, y_to)) ) |> dplyr::ungroup() |> tibble::add_column( # ラベルが重ならないように調整 h = c(1.0, 0.5, 0.5, 0.5, 0.0, 0.5, 0.5, 0.0, 0.5), v = c(0.5, 0.5, 1.0, 0.0, 0.5, 1.0, 0.5, 0.5, 0.0), # ラベルを作成 fnc_label = c( "r==1", paste0("sin~alpha==", round(sin(alpha), digits = 2)), paste0("cos~alpha==", round(cos(alpha), digits = 2)), paste0("sin~alpha ~ sin~beta==", round(sin(alpha)*sin(beta), digits = 2)), paste0("cos~alpha ~ sin~beta==", round(cos(alpha)*sin(beta), digits = 2)), paste0("cos~alpha ~ cos~beta==", round(cos(alpha)*cos(beta), digits = 2)), paste0("sin~alpha ~ cos~beta==", round(sin(alpha)*cos(beta), digits = 2)), paste0("sin(alpha-beta)==", round(sin(alpha-beta), digits = 2)), paste0("cos(alpha-beta)==", round(cos(alpha-beta), digits = 2)) ) ) |> dplyr::select(fnc, fnc_label, x, y, h, v) segment_label_df
## # A tibble: 9 × 6 ## fnc fnc_label x y h v ## <fct> <chr> <dbl> <dbl> <dbl> <dbl> ## 1 r r==1 0.25 0.433 1 0.5 ## 2 sin(a) sin~alpha==0.87 0.5 0.433 0.5 0.5 ## 3 cos(a) cos~alpha==0.5 0.25 0 0.5 1 ## 4 sin(a) sin(b) sin~alpha ~ sin~beta==0.22 0.392 0.837 0.5 0 ## 5 cos(a) sin(b) cos~alpha ~ sin~beta==0.13 0.700 0.121 0 0.5 ## 6 cos(a) cos(b) cos~alpha ~ cos~beta==0.48 0.233 0.0625 0.5 1 ## 7 sin(a) cos(b) sin~alpha ~ cos~beta==0.84 0.392 0.404 0.5 0.5 ## 8 sin(a-b) sin(alpha-beta)==0.71 0.592 0.525 0 0.5 ## 9 cos(a-b) cos(alpha-beta)==0.71 0.342 0.0915 0.5 0
ラベル付けする辺(label列がTRUEの行)を取り出して、各線分の中点にラベルを配置することにします。
辺ごとに(fnc列でグループ化して)、x軸の値はx_from, x_to列、y軸の値はy_from, y_to列の中央値を計算します。
ラベルとして数式を表示するにはexpression()の記法を使います。
直角を示すためのデータフレームを作成します。
# 直角マークの描画用 d <- 0.03 right_angle_df <- tibble::tibble( x = c( cos(alpha) + c(0, -d, -d), C_x + c(0, -d, -d), C_x + c(cos(beta+0.5*pi)*d, cos(beta+0.5*pi)*d+cos(beta+pi)*d, cos(beta+pi)*d), cos(alpha-beta)*cos(beta) + c(cos(beta+0.5*pi)*d, cos(beta+0.5*pi)*d+cos(beta+pi)*d, cos(beta+pi)*d), B_x + c(d, d, 0), B_x + c(cos(beta)*d, cos(beta)*d+cos(beta+1.5*pi)*d, cos(beta+1.5*pi)*d) ), y = c( 0 + c(d, d, 0), 0 + c(d, d, 0), C_y + c(sin(beta+0.5*pi)*d, sin(beta+0.5*pi)*d+sin(beta+pi)*d, sin(beta+pi)*d), cos(alpha-beta)*sin(beta) + c(sin(beta+0.5*pi)*d, sin(beta+0.5*pi)*d+sin(beta+pi)*d, sin(beta+pi)*d), sin(alpha) + c(0, -d, -d), B_y + c(sin(beta)*d, sin(beta)*d+sin(beta+1.5*pi)*d, sin(beta+1.5*pi)*d) ), id = rep(1:6, each = 3) # 角ラベル ) right_angle_df
## # A tibble: 18 × 3 ## x y id ## <dbl> <dbl> <int> ## 1 0.5 0.03 1 ## 2 0.47 0.03 1 ## 3 0.47 0 1 ## 4 0.717 0.03 2 ## 5 0.687 0.03 2 ## 6 0.687 0 2 ## 7 0.709 0.0870 3 ## 8 0.680 0.0792 3 ## 9 0.688 0.0502 3 ## 10 0.675 0.212 4 ## 11 0.646 0.204 4 ## 12 0.654 0.175 4 ## 13 0.313 0.866 5 ## 14 0.313 0.836 5 ## 15 0.283 0.836 5 ## 16 0.312 0.816 6 ## 17 0.320 0.787 6 ## 18 0.291 0.779 6
直角マークの頂点の座標を計算して格納します。
鋭角を示すためのデータフレームを作成します。
# 因子レベルを指定 ang_level <- c("a", "b", "90-b", "a-b") # 角度マーク(扇形)の描画用 angle_df <- dplyr::bind_rows( # 原点を中心とする角度 tibble::tibble( ang = c( rep("a", times = a+1), rep("b", times = b+1), rep("90-b", times = 90-b+1), rep("a-b", times = a-b+1) ) |> factor(levels = ang_level), # 角ラベル id = dplyr::dense_rank(ang), # 角番号 x0 = 0, y0 = 0, c = c( seq(from = 0, to = a, by = 1), seq(from = 0, to = b, by = 1), seq(from = b, to = 90, by = 1), seq(from = b, to = a, by = 1) ) # 角度 ), # 点(cos α, 0)を中心とする角度 tibble::tibble( ang = c( rep("b", times = b+1), rep("90-b", times = 90-b+1), rep("b", times = b+1), rep("90-b", times = 90-b+1) ) |> factor(levels = ang_level), # 角ラベル id = c( rep(5, times = b+1), rep(6, times = 90-b+1), rep(7, times = b+1), rep(8, times = 90-b+1) ), # 角番号 x0 = cos(alpha), y0 = 0, c = c( seq(from = 0, to = b, by = 1), seq(from = b, to = 90, by = 1), seq(from = 90, to = 90+b, by = 1), seq(from = 90+b, to = 180, by = 1) ) # 角度 ), # 点(cos α, sin β)を中心とする角度 tibble::tibble( ang = c( rep("b", times = b+1), rep("90-b", times = 90-b+1), rep("b", times = b+1) ) |> factor(levels = ang_level), # 角ラベル id = c( rep(9, times = b+1), rep(10, times = 90-b+1), rep(11, times = b+1) ), # 角番号 x0 = cos(alpha), y0 = sin(alpha), c = c( seq(from = 180, to = 180+b, by = 1), seq(from = 180+b, to = 270, by = 1), seq(from = 270, to = 270+b, by = 1) ) # 角度 ) ) |> dplyr::mutate( theta = c / 180 * pi, # ラジアン d = dplyr::case_when( ang == "a" ~ 0.05, ang == "b" ~ 0.06, ang == "90-b" ~ 0.06, ang == "a-b" ~ 0.07 ), # サイズ調整用の値を指定 # 角ごとに配置 x = cos(theta) * d + x0, y = sin(theta) * d + y0 ) angle_df
## # A tibble: 491 × 9 ## ang id x0 y0 c theta d x y ## <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 a 1 0 0 0 0 0.05 0.05 0 ## 2 a 1 0 0 1 0.0175 0.05 0.0500 0.000873 ## 3 a 1 0 0 2 0.0349 0.05 0.0500 0.00174 ## 4 a 1 0 0 3 0.0524 0.05 0.0499 0.00262 ## 5 a 1 0 0 4 0.0698 0.05 0.0499 0.00349 ## 6 a 1 0 0 5 0.0873 0.05 0.0498 0.00436 ## 7 a 1 0 0 6 0.105 0.05 0.0497 0.00523 ## 8 a 1 0 0 7 0.122 0.05 0.0496 0.00609 ## 9 a 1 0 0 8 0.140 0.05 0.0495 0.00696 ## 10 a 1 0 0 9 0.157 0.05 0.0494 0.00782 ## # … with 481 more rows
3つの頂点において複数の角度マークを描画します。
扇形(角度マーク)を描画するための点の角度($0^{\circ} \leq c \leq a$など)を作成して、それぞれラジアン$\theta = c \frac{2 \pi}{360}$に変換して、$x = \cos \theta, y = \sin \theta$で原点を頂点(円の中心)としたときの座標に変換し、角ごとに頂点の座標$x_0, y_0$を加えてプロット位置を変更します。
角を区別するための列(同じ角度の角は同じ文字列)ang、角番号列(角ごとのユニークな通し番号)id、頂点の座標列x0, y0、扇形描画用の点の角度列cを、頂点ごとにデータフレームに格納して、bind_rows()で結合します。全ての頂点のデータを結合した後に、座標を計算します。
扇形のサイズ調整用の値をd列として、角度ごとに値を指定します。
角度ラベルを描画するためのデータフレームを作成します。
# 角度ラベルの描画用 angle_label_df <- angle_df |> dplyr::group_by(id, ang, x0, y0) |> # 中点の計算用 dplyr::summarise( # 角度の中点に配置 c = median(c), .groups = "drop" ) |> dplyr::mutate( theta = c / 180 * pi, # ラジアン angle_label = dplyr::case_when( ang == "a" ~ "alpha", ang == "b" ~ "beta", ang == "90-b" ~ "90*degree-beta", ang == "a-b" ~ "alpha-beta" ), # 角度ラベル d = dplyr::case_when( ang == "a" ~ 0.04, ang == "b" ~ 0.09, ang == "90-b" ~ 0.1, ang == "a-b" ~ 0.1 ), # サイズ調整用の値を指定 # 角ごとに配置 x = cos(theta) * d + x0, y = sin(theta) * d + y0 ) angle_label_df
## # A tibble: 11 × 10 ## id ang x0 y0 c theta angle_label d x y ## <dbl> <fct> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> ## 1 1 a 0 0 30 0.524 alpha 0.04 0.0346 0.02 ## 2 2 b 0 0 7.5 0.131 beta 0.09 0.0892 0.0117 ## 3 3 90-b 0 0 52.5 0.916 90*degree-beta 0.1 0.0609 0.0793 ## 4 4 a-b 0 0 37.5 0.654 alpha-beta 0.1 0.0793 0.0609 ## 5 5 b 0.5 0 7.5 0.131 beta 0.09 0.589 0.0117 ## 6 6 90-b 0.5 0 52.5 0.916 90*degree-beta 0.1 0.561 0.0793 ## 7 7 b 0.5 0 97.5 1.70 beta 0.09 0.488 0.0892 ## 8 8 90-b 0.5 0 142. 2.49 90*degree-beta 0.1 0.421 0.0609 ## 9 9 b 0.5 0.866 188. 3.27 beta 0.09 0.411 0.854 ## 10 10 90-b 0.5 0.866 232. 4.06 90*degree-beta 0.1 0.439 0.787 ## 11 11 b 0.5 0.866 278. 4.84 beta 0.09 0.512 0.777
角ごとに角度の中点に配置することにします。
角ごとに(ang列と中央値の計算後に利用する列でグループ化して)、summarise()を使って角度の中央値を計算して、それぞれ座標を計算します。
加法定理の可視化グラフを作成します。
# タイトル用のラベルを作成 title_label <- paste0( "atop(", "sin~(alpha-beta) == sin~alpha ~ cos~beta - cos~alpha ~ sin~beta", ", cos~(alpha-beta) == cos~alpha ~ cos~beta + sin~alpha ~ sin~beta", ")" ) ver_label <- paste0( "list(", "a==", a, "*degree", ", b==", b, "*degree", ", alpha==", round(a/180, 2), "*pi, beta==", round(b/180, 2), "*pi", ")" ) # 加法定理の可視化 ggplot() + geom_path(data = sector_df, mapping = aes(x = x, y = y), size = 1) + # 単位円 geom_path(data = square_df, mapping = aes(x = x, y = y), linetype = "dotted") + # 単位正方形 geom_segment(data = segment_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = fnc, size = width, linetype = type)) + # 関数の線分 geom_path(data = right_angle_df, mapping = aes(x = x, y = y, group = id)) + # 直角マーク geom_path(data = angle_df, mapping = aes(x = x, y = y, linetype = ang, group = id)) + # 角度マーク geom_text(data = angle_label_df, mapping = aes(x = x, y = y, label = angle_label), parse = TRUE) + # 角度ラベル geom_label(data = segment_label_df, mapping = aes(x = x, y = y, label = fnc_label, hjust = h, vjust = v, color = fnc), parse = TRUE, alpha = 0.5) + # 関数名ラベル scale_size_manual(breaks = c("normal", "bold"), values = c(1, 2)) + # 目的の線を強調 scale_linetype_manual(breaks = c("main", "sub", "target", "a", "b", "90-b", "a-b"), values = c("solid", "dotted", "dashed", "solid", "solid", "dashed", "solid")) + # 目的の線を強調 #scale_color_brewer(palette = "Set1") + theme(legend.position = "none") + # 凡例を非表示 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 labs(title = parse(text = title_label), subtitle = parse(text = ver_label), x = "x", y = "y")
単位円(扇形の線)をgeom_path()、線分をgeom_segment()、ラベル(文字列)をgeom_text()またはgeom_label()で描画します。ラベルとして数式を描画する場合は、parse引数をTRUEにします。
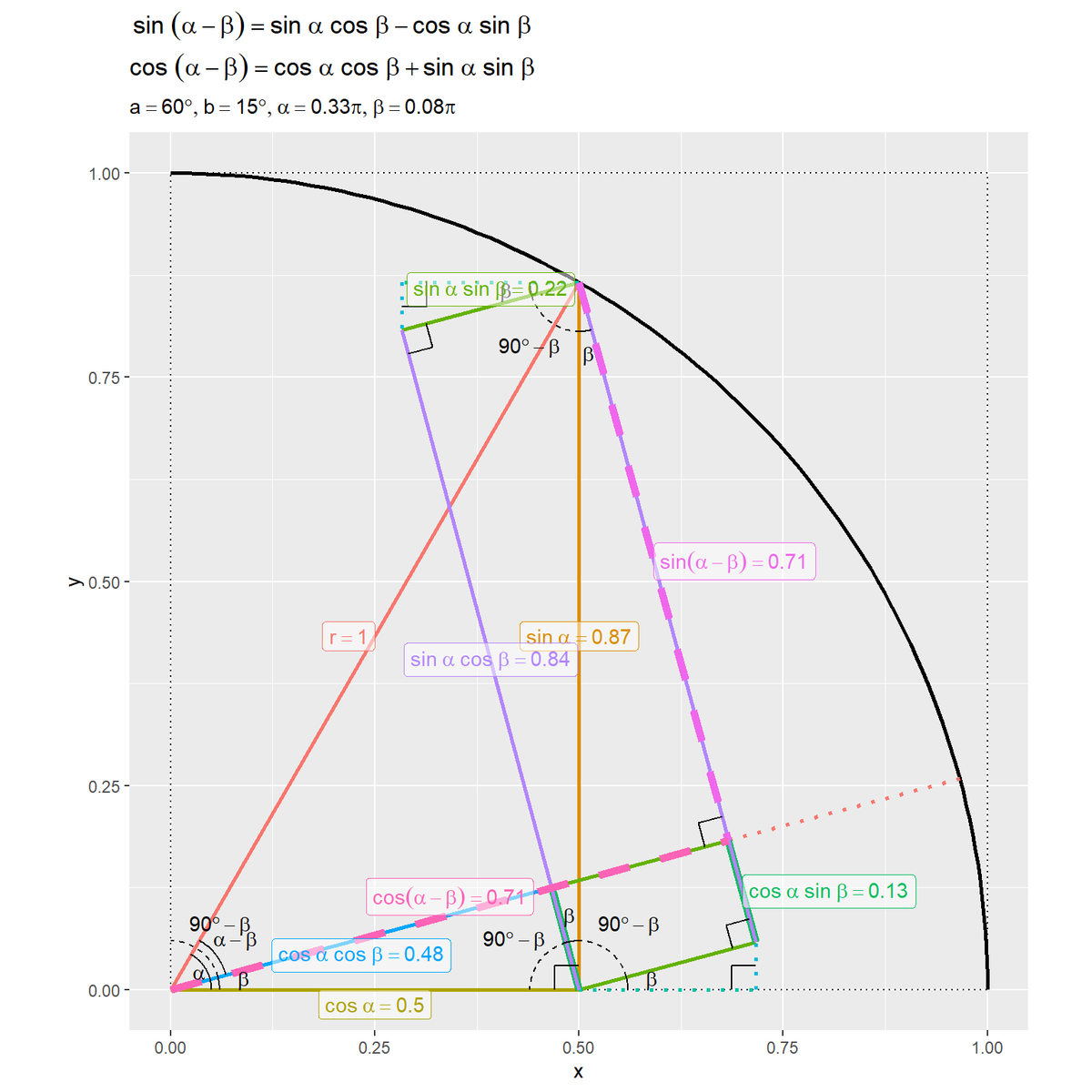
2つの破線とそれぞれ平行な実線を比較すると、次の関係が成り立つのが分かります。
$\sin \alpha \cos \beta$の辺(紫色の線分)は、$\cos \alpha \sin \beta$の辺(青緑色の線分)の全体と重なっています。
アニメーションの作成
次は、角度と加法定理の関係をアニメーションで確認します。
フレームごとに変化させる角度を指定して、ラジアンに変換します。
# フレーム数を指定 frame_num <- 61 # 角度として利用する値を指定:(a,αを変化させる場合) a_vals <- seq(from = 30, to = 90, length.out = frame_num) b_vals <- rep(30, times = frame_num) # 角度として利用する値を指定:(b,βを変化させる場合) #a_vals <- rep(60, times = frame_num) #b_vals <- seq(from = 0, to = 60, length.out = frame_num) # ラジアンに変換 alpha_vals <- a_vals / 180 * pi beta_vals <- b_vals / 180 * pi head(a_vals); head(b_vals); head(alpha_vals); head(beta_vals)
## [1] 30 31 32 33 34 35 ## [1] 30 30 30 30 30 30 ## [1] 0.5235988 0.5410521 0.5585054 0.5759587 0.5934119 0.6108652 ## [1] 0.5235988 0.5235988 0.5235988 0.5235988 0.5235988 0.5235988
フレーム数frame_numを指定してframe_num個の角度$a, b$を作成してa_vals, b_valsとします。$a$を変化させる場合は、a_valsを一定間隔の値にして、b_valsの値を固定します。$b$を変化させる場合は、a_valsの値を固定して、b_valsを一定間隔の値にします。
作成した角度をそれぞれラジアン$\alpha, \beta$に変換してalpha_vals, beta_valsとします。
・コード(クリックで展開)
辺を描画するためのデータフレームを作成します。
# 辺の描画用 A_x <- function(alpha, beta) {cos(alpha)*cos(beta)^2} A_y <- function(alpha, beta) {cos(alpha)*sin(beta)*cos(beta)} B_x <- function(alpha, beta) {cos(alpha)-sin(alpha)*sin(beta)*cos(beta)} B_y <- function(alpha, beta) {sin(alpha)-sin(alpha)*sin(beta)^2} C_x <- function(alpha, beta) {cos(alpha)+sin(alpha)*sin(beta)*cos(beta)} C_y <- function(alpha, beta) {sin(alpha)*sin(beta)^2} anim_segment_df <- tidyr::expand_grid( tibble::tibble( frame_i = 1:frame_num, # フレーム番号 alpha = alpha_vals, beta = beta_vals ), tibble::tibble( fnc = c( "r", "sin(a)", "cos(a)", "cos(a) cos(b)", "sin(a) sin(b)", "sin(a) sin(b)", "sin(a) sin(b)", "sin(a) cos(b)", "sin(a) cos(b)", "cos(a) sin(b)", "cos(a) sin(b)", "sin(a-b)", "cos(a-b)", "r", "sub1", "sub1", "sub2", "sub2" ) |> factor(levels = fnc_level), # 因子レベルを設定, type = c( "main", "main", "main", "main", "main", "main", "main", "main", "main", "main", "main", "target", "target", "sub", "sub", "sub", "sub", "sub" ), label = c( TRUE, TRUE, TRUE, TRUE, TRUE, FALSE, FALSE, TRUE, FALSE, FALSE, TRUE, TRUE, TRUE, FALSE, FALSE, FALSE, FALSE, FALSE ), width = c( "normal", "normal", "normal", "normal", "normal", "normal", "normal", "normal", "normal", "bold", "bold", "bold", "bold", "normal", "normal", "normal", "normal", "normal" ) ) ) |> # フレームごとに受け皿(行)を複製 dplyr::group_by(frame_i) |> dplyr::mutate( # 座標を計算 x_from = c( 0, cos(unique(alpha)), 0, 0, cos(unique(alpha)), A_x(unique(alpha), unique(beta)), cos(unique(alpha)), cos(unique(alpha)), cos(unique(alpha)), cos(unique(alpha)), C_x(unique(alpha), unique(beta)), cos(unique(alpha)), 0, cos(unique(beta)), cos(unique(alpha)), cos(unique(alpha)), C_x(unique(alpha), unique(beta)), B_x(unique(alpha), unique(beta)) ), y_from = c( 0, sin(unique(alpha)), 0, 0, sin(unique(alpha)), A_y(unique(alpha), unique(beta)), 0, 0, sin(unique(alpha)), 0, C_y(unique(alpha), unique(beta)), sin(unique(alpha)), 0, sin(unique(beta)), 0, sin(unique(alpha)), 0, sin(unique(alpha)) ), x_to = c( cos(unique(alpha)), cos(unique(alpha)), cos(unique(alpha)), A_x(unique(alpha), unique(beta)), B_x(unique(alpha), unique(beta)), cos(unique(alpha)-unique(beta))*cos(unique(beta)), C_x(unique(alpha), unique(beta)), B_x(unique(alpha), unique(beta)), C_x(unique(alpha), unique(beta)), A_x(unique(alpha), unique(beta)), cos(unique(alpha)-unique(beta))*cos(unique(beta)), cos(unique(alpha)-unique(beta))*cos(unique(beta)), cos(unique(alpha)-unique(beta))*cos(unique(beta)), cos(unique(alpha)-unique(beta))*cos(unique(beta)), C_x(unique(alpha), unique(beta)), B_x(unique(alpha), unique(beta)), C_x(unique(alpha), unique(beta)), B_x(unique(alpha), unique(beta)) ), y_to = c( sin(unique(alpha)), 0, 0, A_y(unique(alpha), unique(beta)), B_y(unique(alpha), unique(beta)), cos(unique(alpha)-unique(beta))*sin(unique(beta)), C_y(unique(alpha), unique(beta)), B_y(unique(alpha), unique(beta)), C_y(unique(alpha), unique(beta)), A_y(unique(alpha), unique(beta)), cos(unique(alpha)-unique(beta))*sin(unique(beta)), cos(unique(alpha)-unique(beta))*sin(unique(beta)), cos(unique(alpha)-unique(beta))*sin(unique(beta)), cos(unique(alpha)-unique(beta))*sin(unique(beta)), 0, sin(unique(alpha)), C_y(unique(alpha), unique(beta)), B_y(unique(alpha), unique(beta)) ), # 変数ラベルを作成 frame_label = paste0( "a=", a_vals[unique(frame_i)], "°, b=", b_vals[unique(frame_i)], "°", ", α=", round(a_vals[unique(frame_i)]/180, 2), "π, β=", round(b_vals[unique(frame_i)]/180, 2), "π" ) |> factor( levels = paste0( "a=", a_vals, "°, b=", b_vals, "°", ", α=", round(a_vals/180, 2), "π, β=", round(b_vals/180, 2), "π" ) ) # フレーム順序を設定 ) |> dplyr::ungroup() |> dplyr::arrange(frame_i, fnc) # 並びを統一 anim_segment_df
## # A tibble: 1,098 × 12 ## frame_i alpha beta fnc type label width x_from y_from x_to y_to ## <int> <dbl> <dbl> <fct> <chr> <lgl> <chr> <dbl> <dbl> <dbl> <dbl> ## 1 1 0.524 0.524 r main TRUE norm… 0 0 0.866 0.5 ## 2 1 0.524 0.524 r sub FALSE norm… 0.866 0.5 0.866 0.5 ## 3 1 0.524 0.524 sin(a) main TRUE norm… 0.866 0.5 0.866 0 ## 4 1 0.524 0.524 cos(a) main TRUE norm… 0 0 0.866 0 ## 5 1 0.524 0.524 sin(a) sin(b) main TRUE norm… 0.866 0.5 0.650 0.375 ## 6 1 0.524 0.524 sin(a) sin(b) main FALSE norm… 0.650 0.375 0.866 0.5 ## 7 1 0.524 0.524 sin(a) sin(b) main FALSE norm… 0.866 0 1.08 0.125 ## 8 1 0.524 0.524 cos(a) sin(b) main FALSE bold 0.866 0 0.650 0.375 ## 9 1 0.524 0.524 cos(a) sin(b) main TRUE bold 1.08 0.125 0.866 0.5 ## 10 1 0.524 0.524 sub1 sub FALSE norm… 0.866 0 1.08 0 ## # … with 1,088 more rows, and 1 more variable: frame_label <fct>
フレーム番号と対応する角度(ラジアン)を格納したデータフレームと、関数名などの線の装飾用の列を格納したデータフレームの、全ての行の組み合わせをexpand_grid()で作成することで、フレームごとにラベル(値の受け皿となる行)を複製します。
フレームごとに(frame_i列でグループ化して)、線分の始点と終点の座標を計算します。処理の仕方は異なりますが「グラフの作成」のときと同様に計算します。ただし、角度列alpha, betaは行数分の値を持つので、unique()で1つの値にして計算に使います。
また、フレーム切替用のラベル列frame_labelを作成します。因子のレベルがフレームの順番に対応します。
多くの辺の交点となる座標の計算処理を、それぞれ関数として定義して使っています。
関数名ラベルを描画するためのデータフレームを作成します。
# 関数名ラベルの描画用 anim_segment_label_df <- anim_segment_df |> dplyr::filter(label) |> dplyr::group_by(frame_i, fnc) |> # 中点の計算用 dplyr::mutate( # 線分の中点に配置 x = median(c(x_from, x_to)), y = median(c(y_from, y_to)) ) |> dplyr::select(frame_i, frame_label, fnc, alpha, beta, x, y) |> dplyr::group_by(frame_i) |> dplyr::mutate( # ラベルが重ならないように調整 h = c(1.0, 0.5, 0.5, 0.5, 0.0, 0.5, 0.5, 0.0, 0.5), v = c(0.5, 0.5, 1.0, 0.0, 0.5, 1.0, 0.5, 0.5, 0.0), # ラベルを作成 fnc_label = c( "r==1", paste0("sin~alpha==", round(sin(unique(alpha)), digits = 2)), paste0("cos~alpha==", round(cos(unique(alpha)), digits = 2)), paste0("sin~alpha ~ sin~beta==", round(sin(unique(alpha))*sin(unique(beta)), digits = 2)), paste0("cos~alpha ~ sin~beta==", round(cos(unique(alpha))*sin(unique(beta)), digits = 2)), paste0("cos~alpha ~ cos~beta==", round(cos(unique(alpha))*cos(unique(beta)), digits = 2)), paste0("sin~alpha ~ cos~beta==", round(sin(unique(alpha))*cos(unique(beta)), digits = 2)), paste0("sin(alpha-beta)==", round(sin(unique(alpha)-unique(beta)), digits = 2)), paste0("cos(alpha-beta)==", round(cos(unique(alpha)-unique(beta)), digits = 2)) ) ) |> dplyr::ungroup() |> dplyr::arrange(frame_i, fnc) # 並びを統一 anim_segment_label_df
## # A tibble: 549 × 10 ## frame_i frame_label fnc alpha beta x y h v fnc_label ## <int> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> ## 1 1 a=30°, b=30°, … r 0.524 0.524 0.433 0.25 1 0.5 r==1 ## 2 1 a=30°, b=30°, … sin(a) 0.524 0.524 0.866 0.25 0.5 0.5 sin~alph… ## 3 1 a=30°, b=30°, … cos(a) 0.524 0.524 0.433 0 0.5 1 cos~alph… ## 4 1 a=30°, b=30°, … sin(a)… 0.524 0.524 0.758 0.438 0.5 0 sin~alph… ## 5 1 a=30°, b=30°, … cos(a)… 0.524 0.524 0.974 0.312 0 0.5 cos~alph… ## 6 1 a=30°, b=30°, … cos(a)… 0.524 0.524 0.325 0.188 0.5 1 cos~alph… ## 7 1 a=30°, b=30°, … sin(a)… 0.524 0.524 0.758 0.188 0.5 0.5 sin~alph… ## 8 1 a=30°, b=30°, … sin(a-… 0.524 0.524 0.866 0.5 0 0.5 sin(alph… ## 9 1 a=30°, b=30°, … cos(a-… 0.524 0.524 0.433 0.25 0.5 0 cos(alph… ## 10 2 a=31°, b=30°, … r 0.541 0.524 0.429 0.258 1 0.5 r==1 ## # … with 539 more rows
ラベル付けする辺を取り出して、フレームと辺ごとに(frame_i, fnc列でグループ化して)、「グラフの作成」のときと同様に処理します。
直角を示すためのデータフレームを作成します。
# 直角マークの描画用 d <- 0.03 anim_right_angle_df <- tidyr::expand_grid( tibble::tibble( frame_i = 1:frame_num, # フレーム番号 alpha = alpha_vals, beta = beta_vals ), id = rep(1:6, each = 3) # 角ラベル ) |> dplyr::group_by(frame_i) |> # 値の作成用 dplyr::mutate( x = c( cos(unique(alpha)) + c(0, -d, -d), C_x(unique(alpha), unique(beta)) + c(0, -d, -d), C_x(unique(alpha), unique(beta)) + c(cos(unique(beta)+0.5*pi)*d, cos(unique(beta)+0.5*pi)*d+cos(unique(beta)+pi)*d, cos(unique(beta)+pi)*d), cos(unique(alpha)-unique(beta))*cos(unique(beta)) + c(cos(unique(beta)+0.5*pi)*d, cos(unique(beta)+0.5*pi)*d+cos(unique(beta)+pi)*d, cos(unique(beta)+pi)*d), B_x(unique(alpha), unique(beta)) + c(d, d, 0), B_x(unique(alpha), unique(beta)) + c(cos(unique(beta))*d, cos(unique(beta))*d+cos(unique(beta)+1.5*pi)*d, cos(unique(beta)+1.5*pi)*d) ), y = c( 0 + c(d, d, 0), 0 + c(d, d, 0), C_y(unique(alpha), unique(beta)) + c(sin(unique(beta)+0.5*pi)*d, sin(unique(beta)+0.5*pi)*d+sin(unique(beta)+pi)*d, sin(unique(beta)+pi)*d), cos(unique(alpha)-unique(beta))*sin(unique(beta)) + c(sin(unique(beta)+0.5*pi)*d, sin(unique(beta)+0.5*pi)*d+sin(unique(beta)+pi)*d, sin(unique(beta)+pi)*d), sin(unique(alpha)) + c(0, -d, -d), B_y(unique(alpha), unique(beta)) + c(sin(unique(beta))*d, sin(unique(beta))*d+sin(unique(beta)+1.5*pi)*d, sin(unique(beta)+1.5*pi)*d) ), # 変数ラベルを作成 frame_label = paste0( "a=", a_vals[unique(frame_i)], "°, b=", b_vals[unique(frame_i)], "°", ", α=", round(a_vals[unique(frame_i)]/180, 2), "π, β=", round(b_vals[unique(frame_i)]/180, 2), "π" ) |> factor( levels = paste0( "a=", a_vals, "°, b=", b_vals, "°", ", α=", round(a_vals/180, 2), "π, β=", round(b_vals/180, 2), "π" ) ) # フレーム順序を設定 ) |> dplyr::ungroup() anim_right_angle_df
## # A tibble: 1,098 × 7 ## frame_i alpha beta id x y frame_label ## <int> <dbl> <dbl> <int> <dbl> <dbl> <fct> ## 1 1 0.524 0.524 1 0.866 0.03 a=30°, b=30°, α=0.17π, β=0.17π ## 2 1 0.524 0.524 1 0.836 0.03 a=30°, b=30°, α=0.17π, β=0.17π ## 3 1 0.524 0.524 1 0.836 0 a=30°, b=30°, α=0.17π, β=0.17π ## 4 1 0.524 0.524 2 1.08 0.03 a=30°, b=30°, α=0.17π, β=0.17π ## 5 1 0.524 0.524 2 1.05 0.03 a=30°, b=30°, α=0.17π, β=0.17π ## 6 1 0.524 0.524 2 1.05 0 a=30°, b=30°, α=0.17π, β=0.17π ## 7 1 0.524 0.524 3 1.07 0.151 a=30°, b=30°, α=0.17π, β=0.17π ## 8 1 0.524 0.524 3 1.04 0.136 a=30°, b=30°, α=0.17π, β=0.17π ## 9 1 0.524 0.524 3 1.06 0.11 a=30°, b=30°, α=0.17π, β=0.17π ## 10 1 0.524 0.524 4 0.851 0.526 a=30°, b=30°, α=0.17π, β=0.17π ## # … with 1,088 more rows
フレームごとに角度に応じて、直角マークの頂点の座標を計算します。
先に作成したフレーム切り替え用のラベル列と一致するようにラベルを作成します。
鋭角を示すためのデータフレームを作成します。
# 角度マーク(扇形)の描画用 anim_angle_df <- dplyr::bind_rows( # 原点を中心とする角度 tibble::tibble( frame_i = 1:frame_num, # フレーム番号 a = a_vals, b = b_vals ) |> dplyr::group_by(frame_i, a, b) |> dplyr::summarise( c = c( seq(from = 0, to = a, by = 1), seq(from = 0, to = b, by = 1), seq(from = b, to = 90, by = 1), seq(from = b, to = a, by = 1) ), # 角度 .groups = "keep" ) |> dplyr::mutate( ang = c( rep("a", times = unique(a)+1), rep("b", times = unique(b)+1), rep("90-b", times = 90-unique(b)+1), rep("a-b", times = unique(a)-unique(b)+1) ) |> factor(levels = ang_level), # 角ラベル id = c( rep(1, times = unique(a)+1), rep(2, times = unique(b)+1), rep(3, times = 90-unique(b)+1), rep(4, times = unique(a)-unique(b)+1) ), # 角番号 x0 = 0, y0 = 0 ) |> dplyr::ungroup(), # 点(cos α, 0)を中心とする角度 tibble::tibble( frame_i = 1:frame_num, # フレーム番号 a = a_vals, b = b_vals ) |> dplyr::group_by(frame_i, a, b) |> dplyr::summarise( c = c( seq(from = 0, to = b, by = 1), seq(from = b, to = 90, by = 1), seq(from = 90, to = 90+b, by = 1), seq(from = 90+b, to = 180, by = 1) ), # 角度 .groups = "keep" ) |> dplyr::mutate( ang = c( rep("b", times = unique(b)+1), rep("90-b", times = 90-unique(b)+1), rep("b", times = unique(b)+1), rep("90-b", times = 90-unique(b)+1) ) |> factor(levels = ang_level), # 角ラベル id = c( rep(5, times = unique(b)+1), rep(6, times = 90-unique(b)+1), rep(7, times = unique(b)+1), rep(8, times = 90-unique(b)+1) ), # 角番号 x0 = cos(alpha_vals[unique(frame_i)]), y0 = 0, ) |> dplyr::ungroup(), # 点(cos α, sin β)を中心とする角度 tibble::tibble( frame_i = 1:frame_num, # フレーム番号 a = a_vals, b = b_vals ) |> dplyr::group_by(frame_i, a, b) |> dplyr::summarise( c = c( seq(from = 180, to = 180+b, by = 1), seq(from = 180+b, to = 270, by = 1), seq(from = 270, to = 270+b, by = 1) ), # 角度 .groups = "keep" ) |> dplyr::mutate( ang = c( rep("b", times = unique(b)+1), rep("90-b", times = 90-unique(b)+1), rep("b", times = unique(b)+1) ) |> factor(levels = ang_level), # 角ラベル id = c( rep(9, times = unique(b)+1), rep(10, times = 90-unique(b)+1), rep(11, times = unique(b)+1) ), # 角番号 x0 = cos(alpha_vals[unique(frame_i)]), y0 = sin(alpha_vals[unique(frame_i)]), ) |> dplyr::ungroup() ) |> dplyr::mutate( theta = c / 180 * pi, # ラジアン d = dplyr::case_when( ang == "a" ~ 0.05, ang == "b" ~ 0.06, ang == "90-b" ~ 0.06, ang == "a-b" ~ 0.07 ), # サイズ調整用の値を指定 # 角ごとに配置 x = cos(theta) * d + x0, y = sin(theta) * d + y0, # 変数ラベルを作成 frame_label = paste0( "a=", a_vals[frame_i], "°, b=", b_vals[frame_i], "°", ", α=", round(a_vals[frame_i]/180, 2), "π, β=", round(b_vals[frame_i]/180, 2), "π" ) |> factor( levels = paste0( "a=", a_vals, "°, b=", b_vals, "°", ", α=", round(a_vals/180, 2), "π, β=", round(b_vals/180, 2), "π" ) ) # フレーム順序を設定 ) anim_angle_df
## # A tibble: 29,951 × 13 ## frame_i a b c ang id x0 y0 theta d x y ## <int> <dbl> <dbl> <dbl> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 1 30 30 0 a 1 0 0 0 0.05 0.05 0 ## 2 1 30 30 1 a 1 0 0 0.0175 0.05 0.0500 8.73e-4 ## 3 1 30 30 2 a 1 0 0 0.0349 0.05 0.0500 1.74e-3 ## 4 1 30 30 3 a 1 0 0 0.0524 0.05 0.0499 2.62e-3 ## 5 1 30 30 4 a 1 0 0 0.0698 0.05 0.0499 3.49e-3 ## 6 1 30 30 5 a 1 0 0 0.0873 0.05 0.0498 4.36e-3 ## 7 1 30 30 6 a 1 0 0 0.105 0.05 0.0497 5.23e-3 ## 8 1 30 30 7 a 1 0 0 0.122 0.05 0.0496 6.09e-3 ## 9 1 30 30 8 a 1 0 0 0.140 0.05 0.0495 6.96e-3 ## 10 1 30 30 9 a 1 0 0 0.157 0.05 0.0494 7.82e-3 ## # … with 29,941 more rows, and 1 more variable: frame_label <fct>
「グラフの作成」では、頂点ごとに「角ラベル列ang」・「各番号列id」・「頂点の座標列x0, y0」・「扇形描画用の点の角度列c」を格納した3つのデータフレームを結合して、座標を計算しました。
ここでは、頂点ごとにフレーム番号と対応する角度を格納して、フレームごとに(frame_i列と点の作成後に利用する列でグループ化して)、フレームごとの角度(a, b列)に応じて複製した扇形描画用の点の角度をsummarise()で作成します。また、フレームごとの角度に応じて「角ラベル列ang」・「各番号列id」・「頂点の座標列x0, y0」を格納します。
3つの頂点分のデータフレームを結合して、それぞれ座標を計算します。
角度ラベルを描画するためのデータフレームを作成します。
# 角度ラベルの描画用 anim_angle_label_df <- anim_angle_df |> dplyr::group_by(frame_i, frame_label, id, ang, x0, y0) |> # 中点の計算用 dplyr::summarise( # 角度の中点に配置 c = median(c), .groups = "drop" ) |> dplyr::mutate( theta = c / 180 * pi, # ラジアン angle_label = dplyr::case_when( ang == "a" ~ "alpha", ang == "b" ~ "beta", ang == "90-b" ~ "90*degree-beta", ang == "a-b" ~ "alpha-beta" ), # 角度ラベル d = dplyr::case_when( ang == "a" ~ 0.04, ang == "b" ~ 0.09, ang == "90-b" ~ 0.1, ang == "a-b" ~ 0.1 ), # サイズ調整用の値を指定 # 角ごとに配置 x = cos(theta) * d + x0, y = sin(theta) * d + y0 ) anim_angle_label_df
## # A tibble: 671 × 12 ## frame_i frame_label id ang x0 y0 c theta angle_label d ## <int> <fct> <dbl> <fct> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> ## 1 1 a=30°, b=30°… 1 a 0 0 15 0.262 alpha 0.04 ## 2 1 a=30°, b=30°… 2 b 0 0 15 0.262 beta 0.09 ## 3 1 a=30°, b=30°… 3 90-b 0 0 60 1.05 90*degree-be… 0.1 ## 4 1 a=30°, b=30°… 4 a-b 0 0 30 0.524 alpha-beta 0.1 ## 5 1 a=30°, b=30°… 5 b 0.866 0 15 0.262 beta 0.09 ## 6 1 a=30°, b=30°… 6 90-b 0.866 0 60 1.05 90*degree-be… 0.1 ## 7 1 a=30°, b=30°… 7 b 0.866 0 105 1.83 beta 0.09 ## 8 1 a=30°, b=30°… 8 90-b 0.866 0 150 2.62 90*degree-be… 0.1 ## 9 1 a=30°, b=30°… 9 b 0.866 0.5 195 3.40 beta 0.09 ## 10 1 a=30°, b=30°… 10 90-b 0.866 0.5 240 4.19 90*degree-be… 0.1 ## # … with 661 more rows, and 2 more variables: x <dbl>, y <dbl>
フレームと角ごとに、summaraise()で角度の中点を計算して、それぞれ座標を計算します。
加法定理の可視化アニメーションを作成します。
# タイトル用のラベルを作成 title_label <- paste0( "atop(", "sin~(alpha-beta) == sin~alpha ~ cos~beta - cos~alpha ~ sin~beta", ", cos~(alpha-beta) == cos~alpha ~ cos~beta + sin~alpha ~ sin~beta", ")" ) # 加法定理の可視化 anim <- ggplot() + geom_path(data = sector_df, mapping = aes(x = x, y = y), size = 1) + # 単位円 geom_path(data = square_df, mapping = aes(x = x, y = y), linetype = "dotted") + # 単位正方形 geom_segment(data = anim_segment_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = fnc, size = width, linetype = type)) + # 関数の線分 geom_path(data = anim_right_angle_df, mapping = aes(x = x, y = y, group = id)) + # 直角マーク geom_path(data = anim_angle_df, mapping = aes(x = x, y = y, linetype = ang, group = id)) + # 角度マーク geom_text(data = anim_angle_label_df, mapping = aes(x = x, y = y, label = angle_label), parse = TRUE) + # 角度ラベル geom_label(data = anim_segment_label_df, mapping = aes(x = x, y = y, label = fnc_label, hjust = h, vjust = v, color = fnc), parse = TRUE, alpha = 0.5) + # 関数名ラベル gganimate::transition_manual(frames = frame_label) + # フレーム scale_size_manual(breaks = c("normal", "bold"), values = c(1, 2)) + # 目的の線を強調 scale_linetype_manual(breaks = c("main", "sub", "target", "a", "b", "90-b", "a-b"), values = c("solid", "dotted", "dashed", "solid", "solid", "dashed", "solid")) + # 目的の線を強調 theme(legend.position = "none") + # 凡例を非表示 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 labs(title = parse(text = title_label), subtitle = "{current_frame}", x = "x", y = "y") # gif画像を作成 gganimate::animate(plot = anim, nframe = frame_num, fps = 10, width = 1000, height = 800)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のnframes引数にフレーム数、fps引数に1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
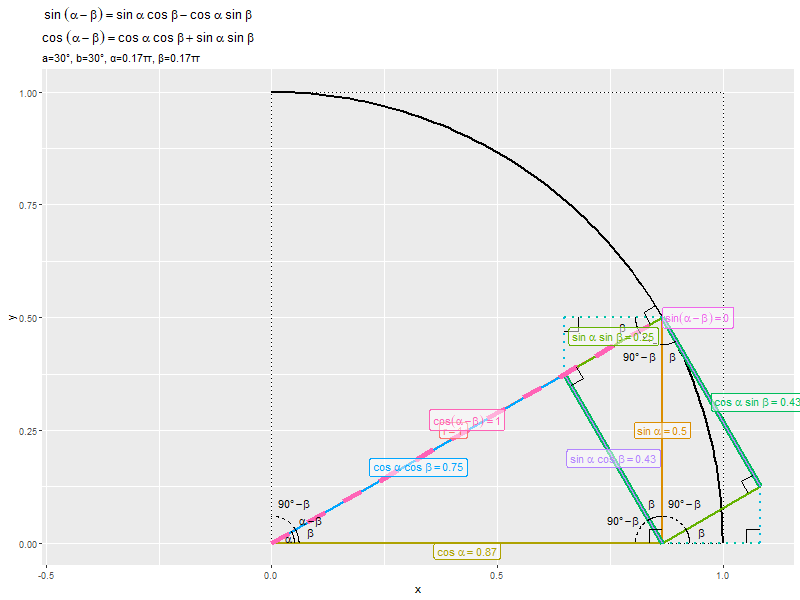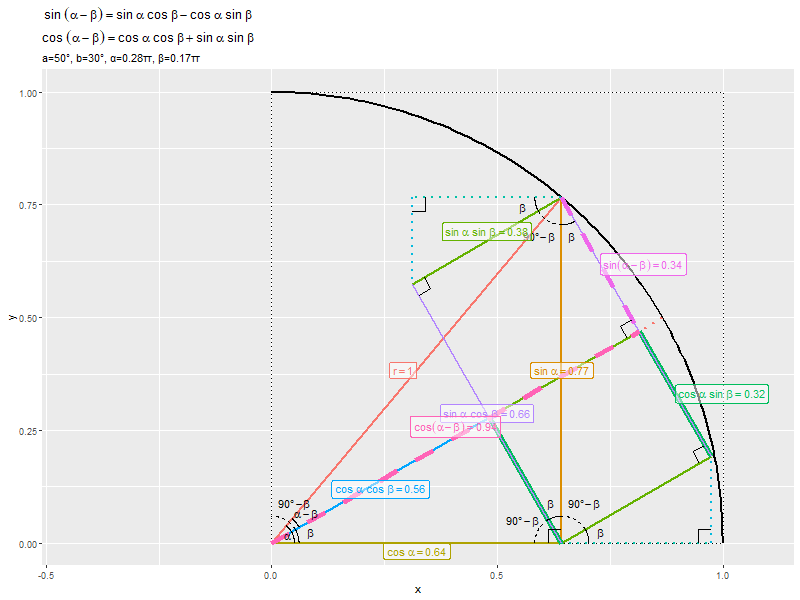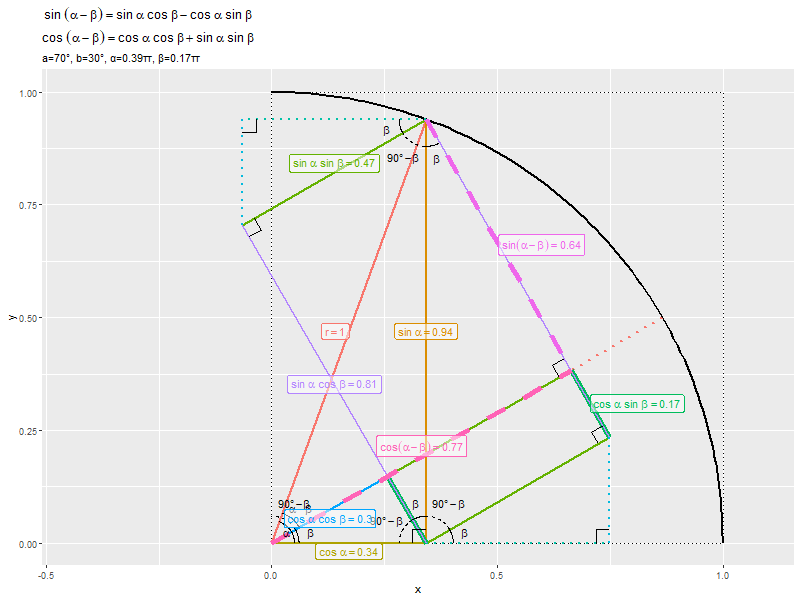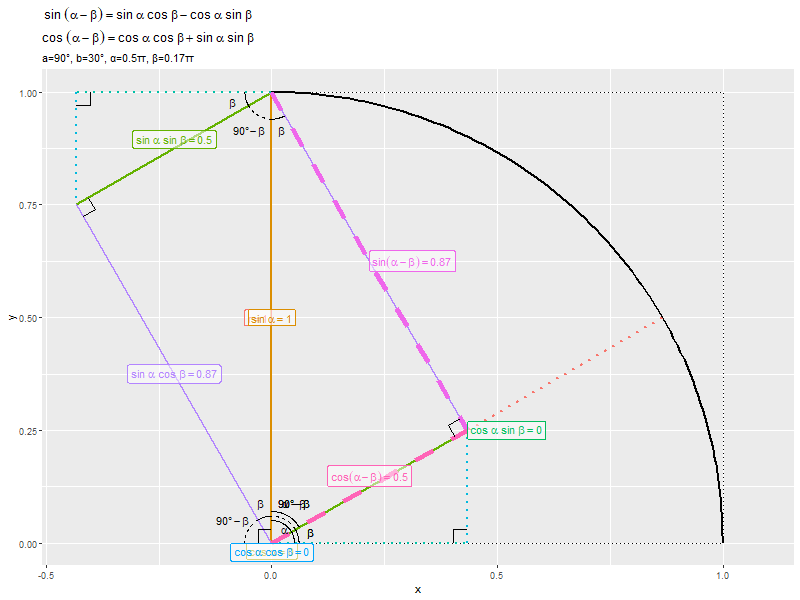
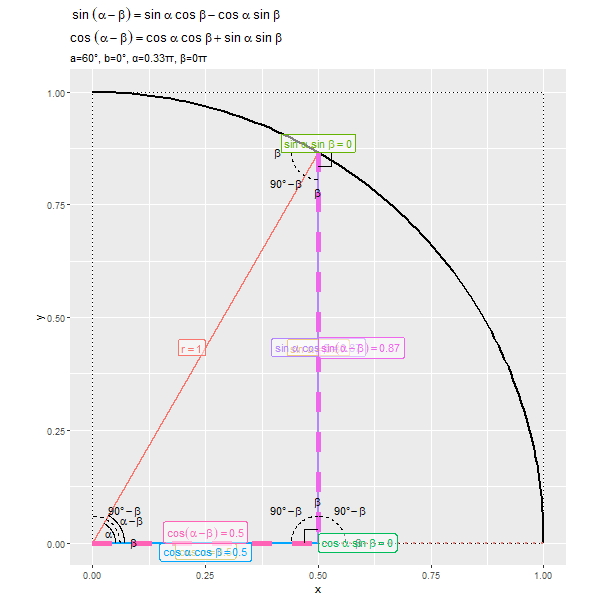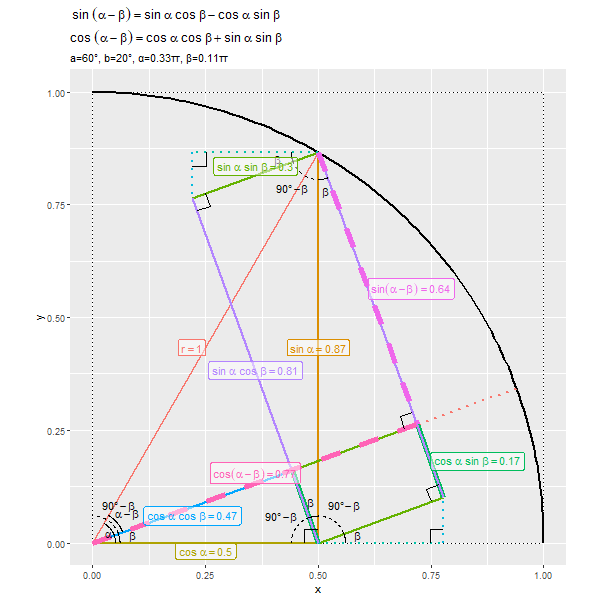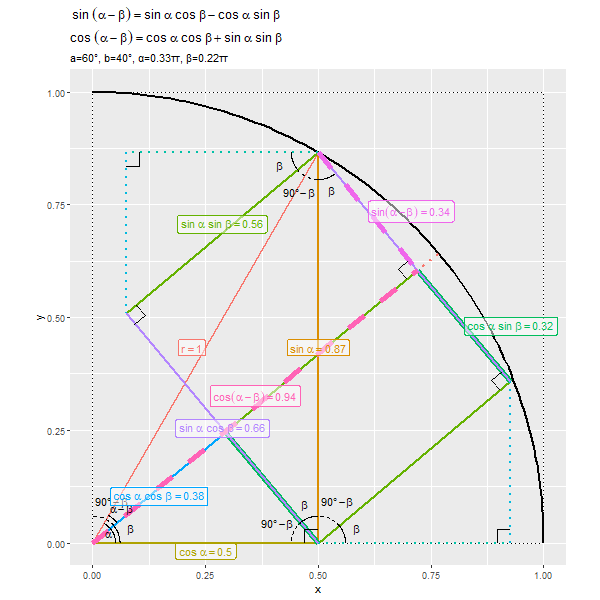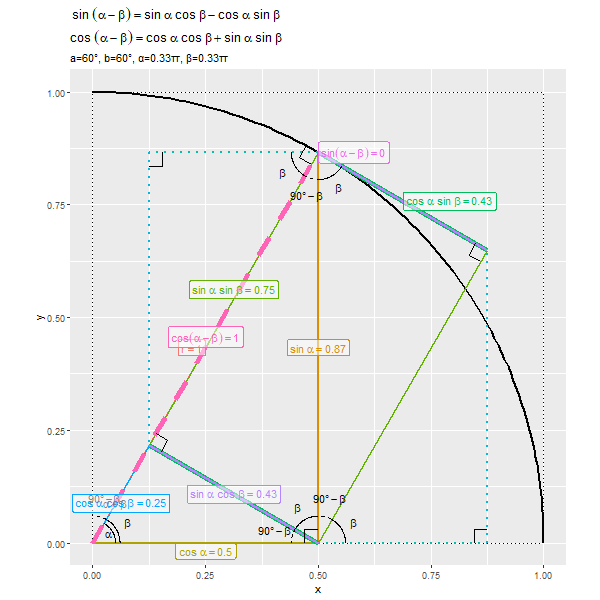
$\alpha - \beta$が$0^{\circ}$から$90^{\circ}$に近付くほど、$\sin(\alpha - \beta)$が0から1に、$\cos(\alpha - \beta)$が1から0に近付くのを確認できます。
この記事では、2角の差のサインとコサインについて可視化しました。次の記事では、2角の和のタンジェントについて可視化できたらいいな。
参考書籍
- 『三角関数(改定第3版)』(Newton別冊)ニュートンプレス,2022年.
おわりに
式が6つあるのに2つ分の図しかないのはなんでだ、ということで自分で考えてみました。+が成立するなら-も成立します、で納得できるのであればそれでいいのだと思います。私はとりあえず面白そうなのでやってみようと思っただけです。そして、1つ目の図よりも線が多くて大変でした。
まだ考え中ですが、残りの2つは別々の図がいりそうです。
最後に書くなって話ですが、他人が読んで理解できる内容ではないですね。1か月後の自分でもムリそうです。コピペすれば動きますので…
【次の内容】
つづくはず