はじめに
『完全独習 統計学入門』の学習ノートです。本に載っている計算や表、グラフをR言語で再現します。本とあわせて読んでください。
この記事では、度数分布表やヒストグラムと平均値の関係を確認します。
【前の節の内容】
【他の節の内容】
【この節の内容】
第2項 平均値とはやじろべえの支点である――平均値の役割と捉え方
平均値の2通りの計算方法と、ヒストグラムとの関係を確認します。度数分布表とヒストグラムの作成については第1講を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(magick)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
2-2 平均値とは
まずは、データの読み込みと、標本平均の計算式を確認します。
図表1-1のデータセットをベクトルとして作成します。
# データを作成:(身長) data_x <- c( 151, 154, 158, 162, 154, 152, 151, 167, 160, 161, 155, 159, 160, 160, 155, 153, 163, 160, 165, 146, 156, 153, 165, 156, 158, 155, 154, 160, 156, 163, 148, 151, 154, 160, 169, 151, 160, 159, 158, 157, 154, 164, 146, 151, 162, 158, 166, 156, 156, 150, 161, 166, 162, 155, 143, 159, 157, 157, 156, 157, 162, 161, 156, 156, 162, 168, 149, 159, 169, 162, 162, 156, 150, 153, 159, 156, 162, 154, 164, 161 ) # データ数を取得 N <- length(data_x) N
## [1] 80
データ数を$N$で表します。
データを用いて標本平均を計算します。
# データセットから平均値を計算 mean_x <- sum(data_x) / N mean_x
## [1] 157.575
N個のデータを$x_n$($n$は1からNの整数)で表すと、標本平均$\bar{x}$は次の式で定義されます。
$x_n$は$n$番目のデータを表し、data_x[n]に対応します。また、$\sum_{n=1}^N x_n$は$N$個のデータの総和を表し、sum(data_x)に対応します。
データ数$N$は、データ番号$n$と無関係な定数なので、総和$\sum_{n=1}^N$の外に出せます。
2-3 度数分布表での平均値
次は、度数分布表を用いて標本平均を計算します。
階級値と相対度数を計算します。詳しい説明や連続値の場合については、第1講を参照してください。
# 階級の幅を指定 class_width <- 5 # 階級用の値を作成 class_vec <- seq( from = floor(min(data_x)/10) * 10, to = ceiling(max(data_x)/10) * 10, by = class_width ) # 度数分布表を作成:(図1-2,2-1) freq_df <- tibble::tibble( class_lower = class_vec[-length(class_vec)] + 1, # 階級の下限 class_upper = class_vec[-1] # 階級の上限 ) |> dplyr::group_by(class_lower, class_upper) |> # 階級ごとの計算用 dplyr::mutate( class_value = median(c(class_lower, class_upper)), # 階級値 freq = sum((data_x >= class_lower) == (data_x <= class_upper)) # 度数 ) |> dplyr::ungroup() |> dplyr::mutate( relative_freq = freq / N, # 相対度数 #cumulative_freq = cumsum(freq), # 累積度数 weighted_class_value = class_value * relative_freq # 階級値 × 相対度数 ) freq_df
## # A tibble: 6 × 6 ## class_lower class_upper class_value freq relative_freq weighted_class_value ## <dbl> <dbl> <dbl> <int> <dbl> <dbl> ## 1 141 145 143 1 0.0125 1.79 ## 2 146 150 148 6 0.075 11.1 ## 3 151 155 153 19 0.238 36.3 ## 4 156 160 158 30 0.375 59.2 ## 5 161 165 163 18 0.225 36.7 ## 6 166 170 168 6 0.075 12.6
第1講で求めた度数分布表の他に、階級値と相対度数の積を計算します。
階級値と相対度数用いて標本平均を計算します。
# 階級値と相対度数から平均値を計算 mean_x <- sum(freq_df[["weighted_class_value"]]) mean_x
## [1] 157.75
階級の数を$C$として、C個の階級値を$x_i$($i$は1からCの整数)、i番目の階級の度数を$N_i$とすると、相対度数は$\frac{N_i}{N}$で表せます。(一般的な表記ではないと思うので、この記号は覚えないでください。また、一般的な表記があるのであれば、教えてください。)
標本平均(の近似値)は、次の式で計算できます。
C個の度数の和はデータ数$N = \sum_{i=1}^C N_i$であり、相対度数の総和は$\sum_{i=1}^C \frac{N_i}{N} = 1$です。これは、$\frac{\sum_{i=1}^C N_i}{N} = \frac{N}{N} = 1$であることから分かります。
2-4 平均値のヒストグラムの中での役割
続いて、平均値とヒストグラムの関係をグラフで確認します。
ヒストグラムに標本平均の位置を重ねて描画します。度数分布表ではなくデータから作図します。詳しくは第1講を参照してください。
# データを格納 data_df <- tibble::tibble(x = data_x) # 階級値を抽出 class_value_vec <- freq_df[["class_value"]] # 集計用に値を追加 class_value_max <- class_value_vec[length(class_value_vec)] # 最後の値を抽出 class_value_vec <- c(class_value_vec, class_value_max+class_width) # 軸目盛ラベルを作成 x_label_vec <- paste0( class_value_vec-0.5*class_width, "~", class_value_vec+0.5*class_width, "\n(", class_value_vec, ")" ) # タイトル用の文字列を作成 title_label <- paste0("list(N==", N, ", bar(x)==", mean_x, ")") # ヒストグラムと平均値の関係を作図 ggplot() + geom_histogram(data = data_df, mapping = aes(x = x, y = ..count..), breaks = class_value_vec-0.5*class_width, fill = "#00A968") + # 度数 geom_vline(xintercept = mean_x, color ="red", size = 1, linetype ="dashed") + # 平均値 scale_x_continuous(breaks = class_value_vec, labels = x_label_vec) + # x軸目盛 labs(title = "Histogram", subtitle = parse(text = title_label), x = "class value", y = "frequency")
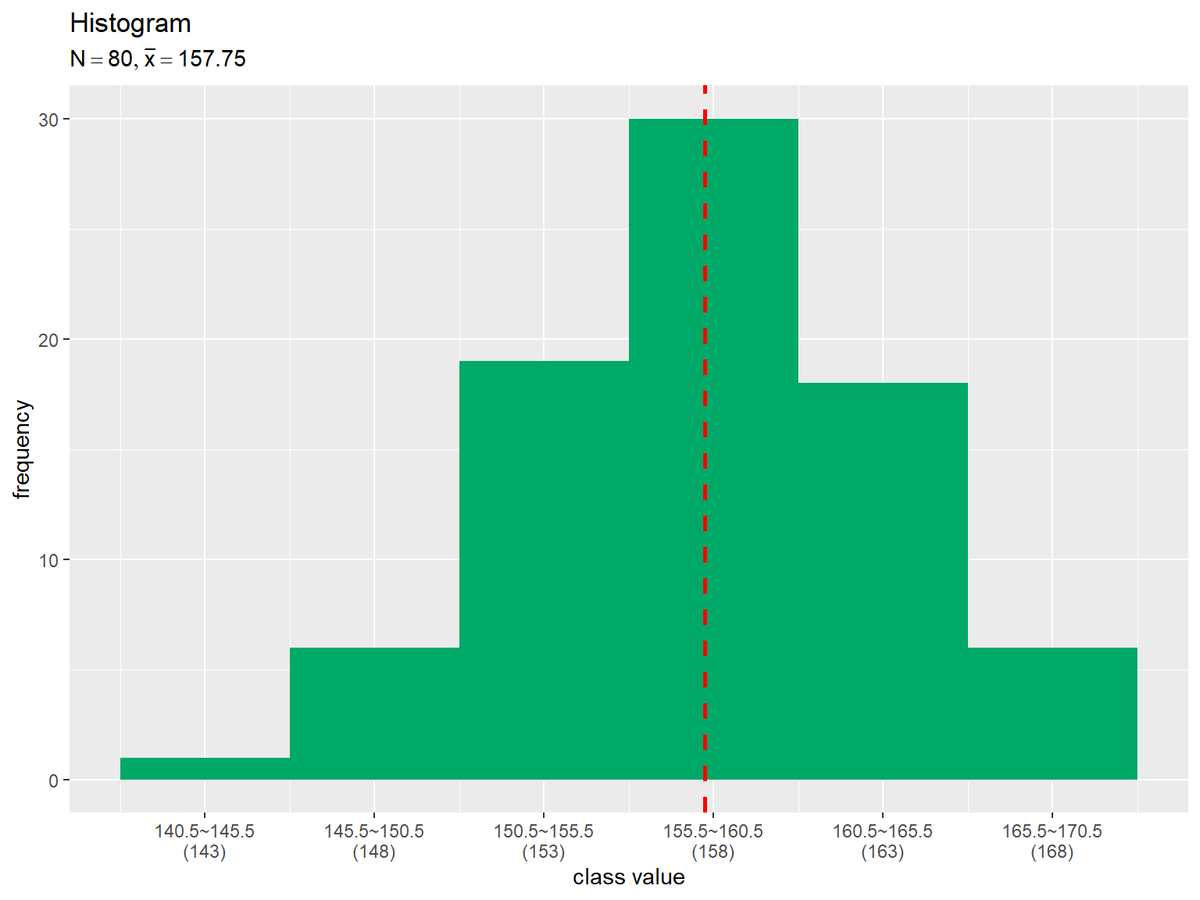
平均値を赤色の破線で示します。垂線はgeom_vline()で描画できます。xintercept引数に平均値を指定します。
(この図は、各バーの中央が階級値となるように、階級が変わらないように階級を変更して、プロットしています。図表2-2は、おそらく離散値の度数分布表と連続値のプロットのギャップを埋めるために、各バーの左側が階級値となるようにプロットされているのだと思います。)
階級(階級値)と平均値の関係を見てみましょう。
作図コード(クリックで展開)
階級の幅を1ずつ大きくするヒストグラムのアニメーションを作成します。
# 画像の保存先を指定 dir_path <- "tmp_folder" # 階級幅の最大値(フレーム数)を指定 class_width_max <- 30 # 階級を変更して作図 for(class_width in 1:class_width_max) { # 階級用の値を作成 class_vec <- seq(from = floor(min(data_x)/10)*10, to = ceiling(max(data_x)/10)*10, by = class_width) class_vec <- c(class_vec, class_vec[length(class_vec)]+class_width) # 集計用に上限以上の値を1つ追加 # 度数分布表を作成:(連続値) freq_df <- tibble::tibble( class_lower = class_vec[-length(class_vec)], # 階級の下限 class_upper = class_vec[-1] # 階級の上限 ) |> dplyr::group_by(class_lower, class_upper) |> dplyr::mutate( class_value = median(c(class_lower, class_upper)), # 階級値 freq = sum((data_x >= class_lower) == (data_x < class_upper)) # 度数 ) |> dplyr::ungroup() |> dplyr::mutate( relative_freq = freq / length(data_x), # 相対度数 weighted_class_value = class_value * relative_freq # 階級値 × 相対度数 ) # 平均値を計算 mean_x <- sum(freq_df[["weighted_class_value"]]) # 装飾用の文字列を作成 title_label <- paste0("list(N==", N, ", bar(x)==", mean_x, ")") x_label_vec <- paste0( freq_df[["class_lower"]], "~", freq_df[["class_upper"]], "\n(", freq_df[["class_value"]], ")" ) # ヒストグラムと平均値の関係を作図 g <- ggplot() + geom_bar(data = freq_df, mapping = aes(x = class_value, y = freq), stat = "identity", width = class_width, fill = "#00A968") + # ヒストグラム geom_vline(xintercept = mean_x, color ="red", size = 1, linetype ="dashed") + # 平均値 scale_x_continuous(breaks = freq_df[["class_value"]], labels = x_label_vec) + # x軸目盛 coord_cartesian(xlim = c(min(data_x), max(data_x)), ylim = c(0, length(data_x))) + # 表示範囲 labs(title = "Histogram", subtitle = parse(text = title_label), x = "class value", y = "frequency") # グラフを書き出し file_name <- sprintf(paste0("%0", nchar(class_width_max), "d"), class_width) ggplot2::ggsave( filename = paste0(dir_path, "/", file_name, ".png"), plot = g, width = 800, height = 600, units = "px", dpi = 100 ) } # ファイル名を取得 file_name_vec <- list.files(dir_path) # gif画像を作成 paste0(dir_path, "/", file_name_vec) |> # ファイルパスを作成 magick::image_read() |> # 画像ファイルを読み込み magick::image_animate(fps = 1, dispose = "previous") |> # gif画像を作成 magick::image_write_gif(path = "histgram.gif", delay = 1/2) -> tmp_path # gifファイルを書き出し
階級の幅の最大値をclass_width_maxとして値を指定します。for()を使って、1からclass_width_maxの整数を順番にclass_vecとします。
同様に作図してそれぞれグラフを保存します。画像の書き出し先フォルダdir_pathは空である必要があります。また、画像ファイルの読み込み時に、書き出した順番と(文字列基準で)同じ並びになるようなファイル名を付ける必要があります。
保存した画像ファイルをimage_read()で読み込んで、image_animate()とimage_write_gif()でgif画像に変換します。
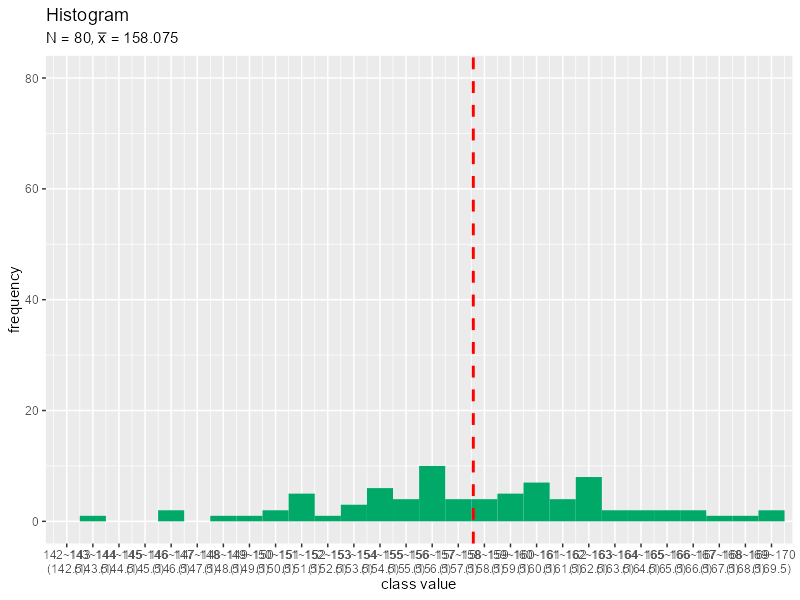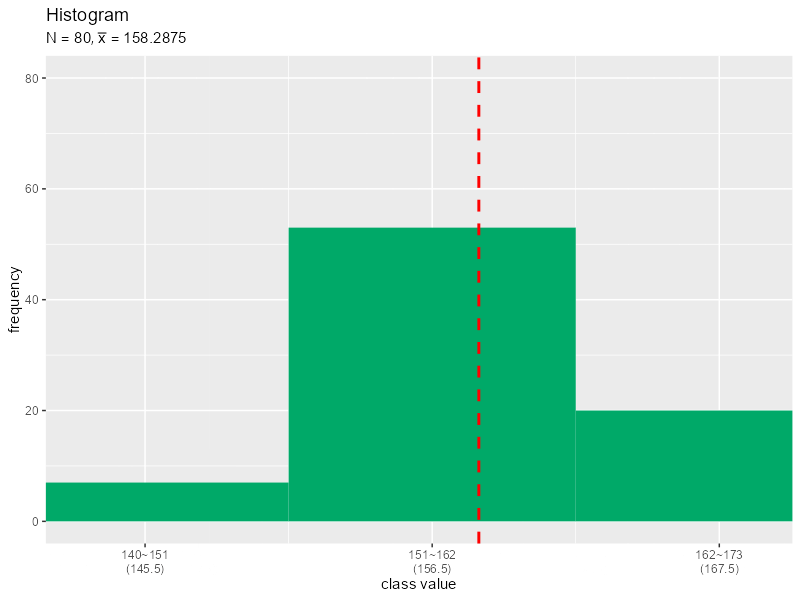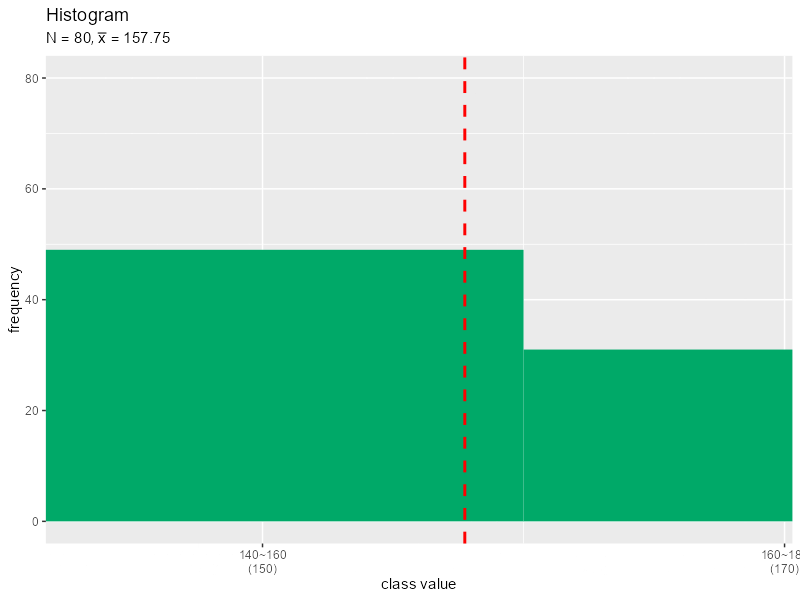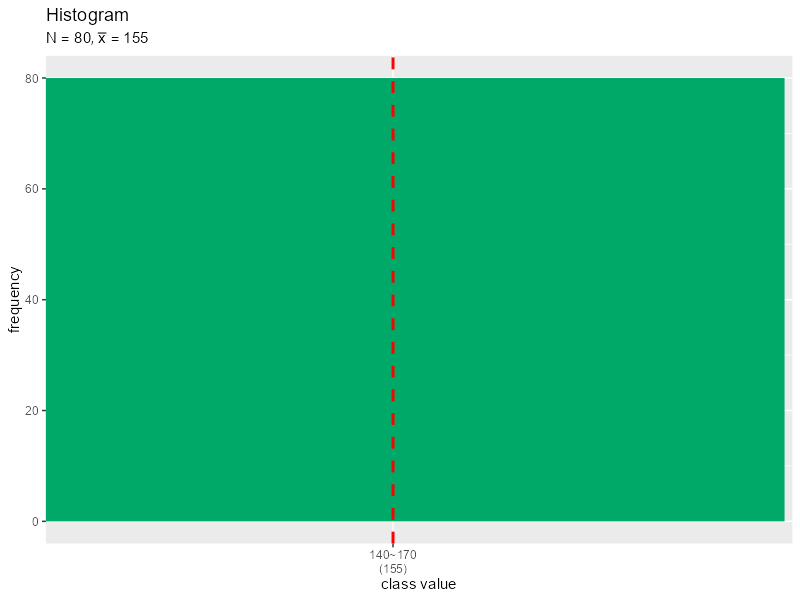
階級の取り方によって平均値が変化しますが、データから求めた平均値と大きく変わらないのが分かります。
2-5 平均値をどう捉えるべきか
最後に、データや階級値と平均値の関係をグラフで確認します。
データとデータ番号をデータフレームに格納します。
# データを格納 data_df <- tibble::tibble( n = 1:N, # データ番号 x = data_x ) data_df
## # A tibble: 80 × 2 ## n x ## <int> <dbl> ## 1 1 151 ## 2 2 154 ## 3 3 158 ## 4 4 162 ## 5 5 154 ## 6 6 152 ## 7 7 151 ## 8 8 167 ## 9 9 160 ## 10 10 161 ## # … with 70 more rows
各データを棒グラフで表します。
# 生データから標本平均を計算 mean_x <- sum(data_df[["x"]]) / N # 生データと平均値の関係を作図 ggplot() + geom_bar(data = data_df, mapping = aes(x = n, y = x), stat = "identity", fill = "#00A968", color = "#00A968") + # データ geom_hline(yintercept = mean_x, color ="red", size = 1, linetype ="dashed") + # 平均値 labs(title = "dataset", subtitle = parse(text = paste0("bar(x)==", mean_x)), x = "n", y = expression(x[n]))
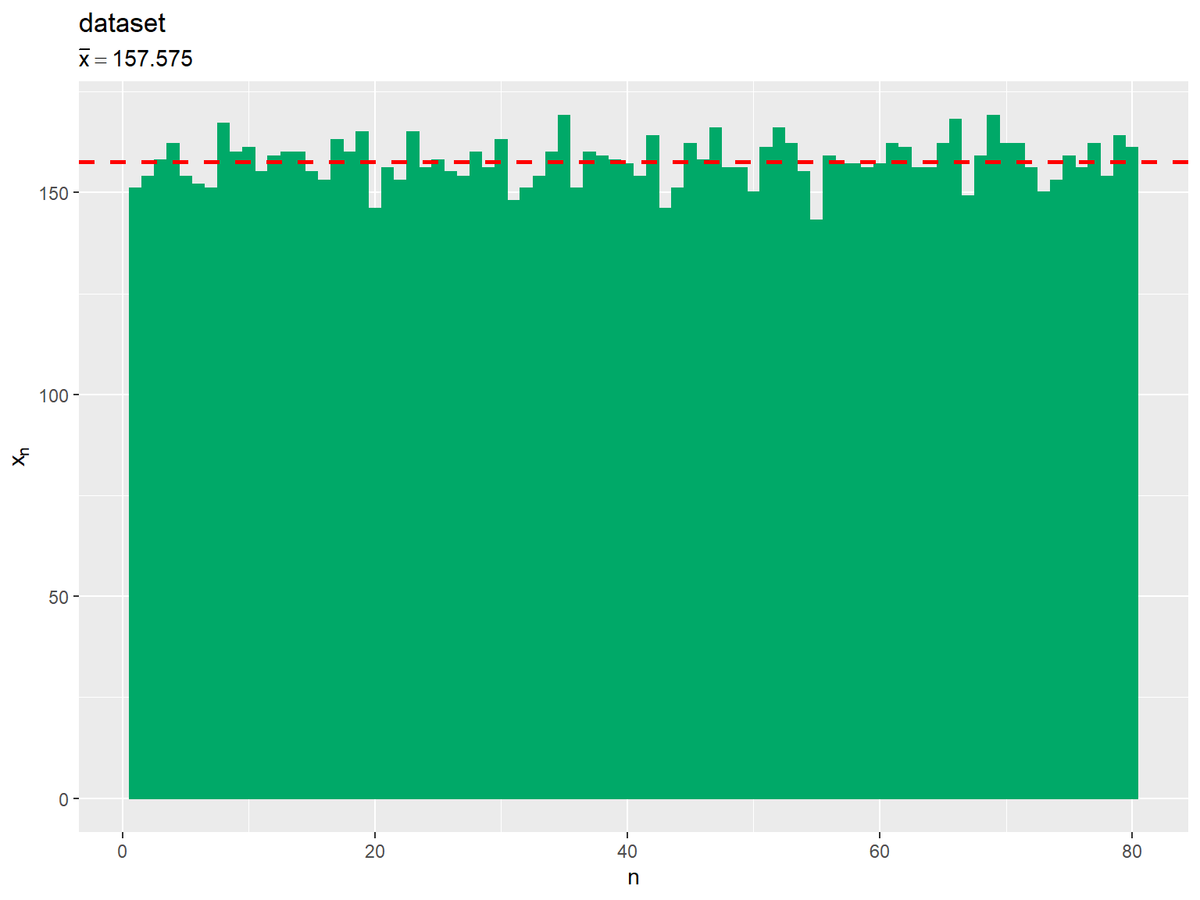
平均値を赤色の破線で示します。水平線はgeom_hline()で描画できます。yintercept引数に平均値を指定します。
データを昇順に並べ替えてみます。
# データを格納 data_df <- tibble::tibble( x = data_x ) |> dplyr::arrange(x) |> # 並べ替え dplyr::mutate(n = dplyr::row_number()) # データ番号を割り当て data_df
## # A tibble: 80 × 2 ## x n ## <dbl> <int> ## 1 143 1 ## 2 146 2 ## 3 146 3 ## 4 148 4 ## 5 149 5 ## 6 150 6 ## 7 150 7 ## 8 151 8 ## 9 151 9 ## 10 151 10 ## # … with 70 more rows
arrange()で昇順に並べ替えて、row_number()で行(データ)番号を追加します。
同じ作図コードで、各データを棒グラフで表します。
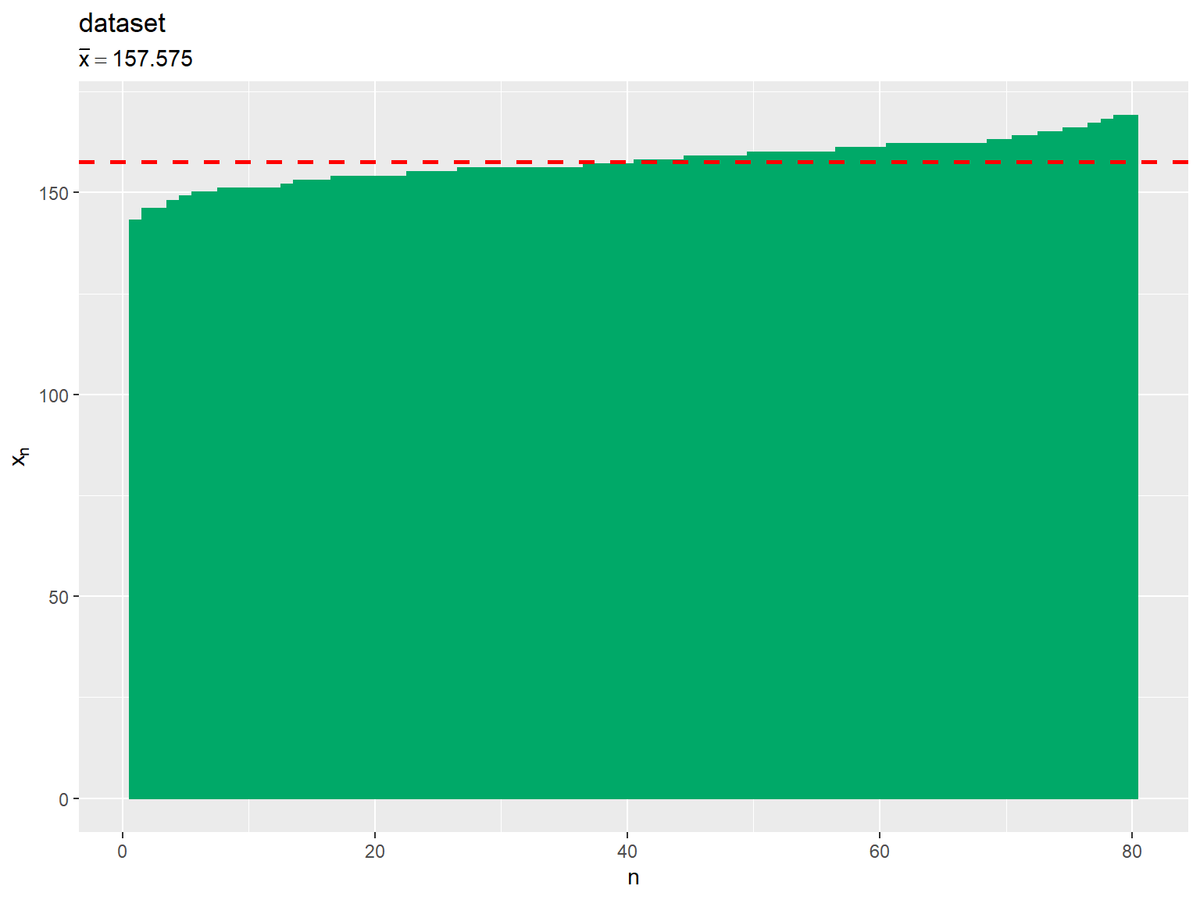
標本平均は、次の式で定義されるのでした。
両辺にデータ数$N$を掛けます。
この式から、標本平均$\bar{x}$を$N$倍すると、データの総和$\sum_{n=1}^N x_n$になるのが分かります。
「緑色のバーの面積」が「データの総和」、「(x軸の同じ範囲における)赤色の水平線からx軸の面積」が「N倍した平均値」に対応します。そして、2つの面積は等しくなります。言い換えると、2つの面積が等しくなるような値が平均値です。
同様に、階級値を用いた場合も確認しましょう。
各階級値を度数に応じて複製します。
# 階級値を複製 class_value_df <- freq_df |> dplyr::select(class_value, freq) |> tidyr::uncount(freq) |> # 度数に応じて複製 dplyr::mutate(n = dplyr::row_number()) # データ番号 class_value_df
## # A tibble: 80 × 2 ## class_value n ## <dbl> <int> ## 1 143 1 ## 2 148 2 ## 3 148 3 ## 4 148 4 ## 5 148 5 ## 6 148 6 ## 7 148 7 ## 8 153 8 ## 9 153 9 ## 10 153 10 ## # … with 70 more rows
freq_dfから、階級値と度数の列を取り出します。
uncount()でfreqに応じて行を複製します。これによりN行のデータフレームになります。
row_number()で行番号を割り当てて、データ番号とします。
複製した階級値を棒グラフで表します。
# 階級値から標本平均を計算 mean_x <- sum(freq_df[["weighted_class_value"]]) # 各階級と平均値の関係を作図 ggplot() + geom_bar(data = class_value_df, mapping = aes(x = n, y = class_value), stat = "identity", fill = "#00A968", color = "#00A968") + # データセット geom_hline(yintercept = mean_x, color ="red", size = 1, linetype ="dashed") + # 平均値 labs(title = "class value", subtitle = parse(text = paste0("bar(x)==", mean_x)), x = "n", y = expression(x[n]))
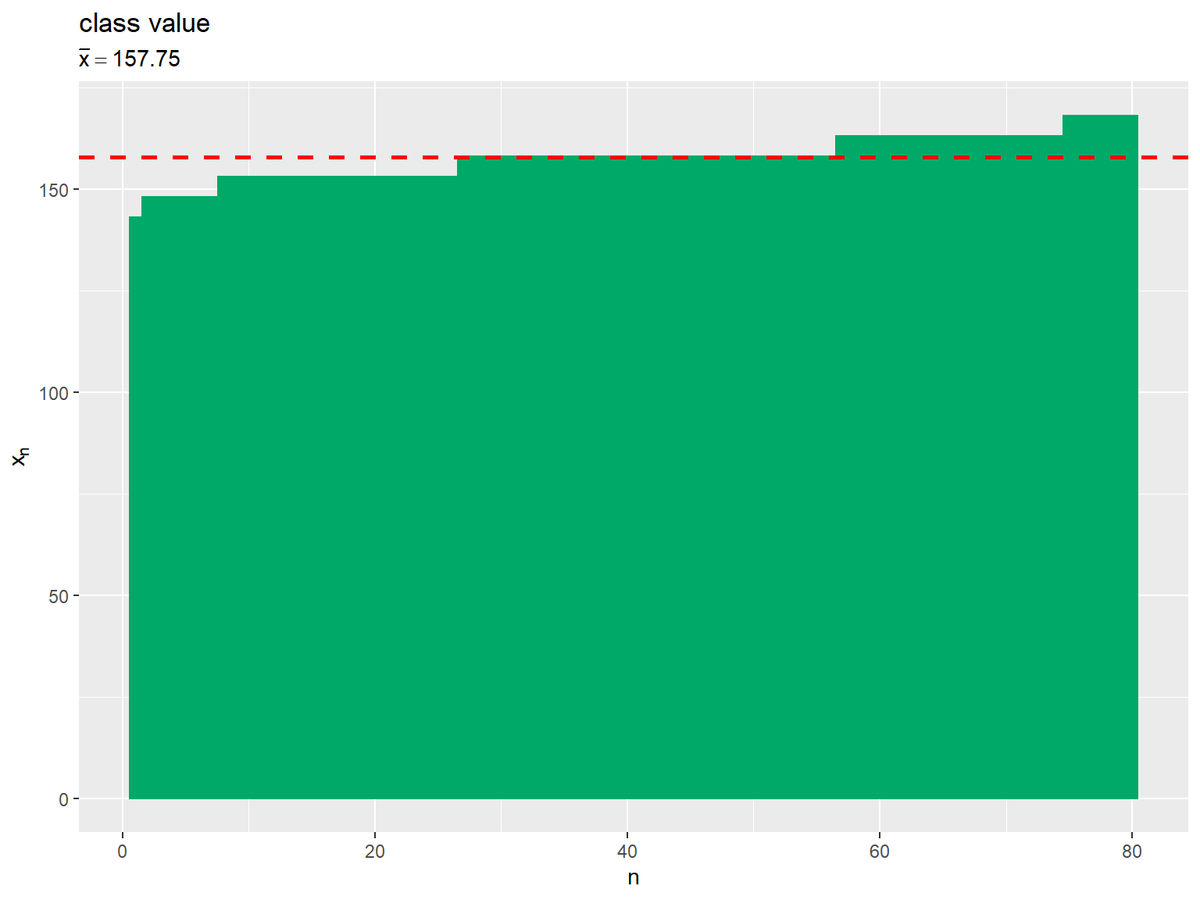
標本平均(の近似値)は、次の式で計算できるのでした。
両辺にデータ数$N$を掛けます。
この式から、$N$倍した標本平均と、階級値と度数の積$x_i N_i$の和が等しいのが分かります。
「同じ高さのバー(度数に応じて複製した階級値のバー)」が「度数$N_i$倍した階級値$x_i$」、「全てのバーの面積」が「各高さのバーのまとまりの和」であり「$x_i N_i$の総和」に対応しています。こちらも、バーの面積と破線からx軸の面積が一致します。
どちらの計算方法(図)においても、平均値(赤色の水平線)を「超える値の合計」と「足りない値の合計」が一致する値が平均値になります。また、超える値と足りない値を偏差と言います。偏差については第3講で説明します。
練習問題
30ページの表を格納して、度数分布表を作成します。
# 度数分布を作成 freq_df <- tibble::tibble( class_value = c(30, 50, 70, 90, 110, 130), # 階級値 freq = c(5, 10, 15, 40, 20, 10) # 度数 ) |> dplyr::mutate( relative_freq = freq / sum(freq), # 相対度数 cumulative_freq = cumsum(freq), # 累積度数 weighted_class_value = class_value * relative_freq # 階級値 × 相対度数 ) freq_df
## # A tibble: 6 × 5 ## class_value freq relative_freq cumulative_freq weighted_class_value ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 30 5 0.05 5 1.5 ## 2 50 10 0.1 15 5 ## 3 70 15 0.15 30 10.5 ## 4 90 40 0.4 70 36 ## 5 110 20 0.2 90 22 ## 6 130 10 0.1 100 13
同様に計算します。
標本平均を計算します。
# 階級値と相対度数から平均値を計算 mean_x <- sum(freq_df[["weighted_class_value"]]) mean_x
## [1] 88
ヒストグラムを作成します。
# 階級の幅を計算 class_width <- freq_df[["class_value"]][2] - freq_df[["class_value"]][1] # タイトル用の文字列を作成 title_label <- paste0("list(N==", sum(freq_df[["freq"]]), ", bar(x)==", mean_x, ")") # ヒストグラムと平均値の関係を作図 ggplot() + geom_bar(data = freq_df, mapping = aes(x = class_value, y = freq), stat = "identity", width = class_width, fill = "#00A968") + # ヒストグラム geom_vline(xintercept = mean_x, color ="red", size = 1, linetype ="dashed") + # 平均値 scale_x_continuous(breaks = freq_df[["class_value"]]) + # x軸 labs(title = "Histogram", subtitle = parse(text = title_label), x = "class value", y = "frequency")
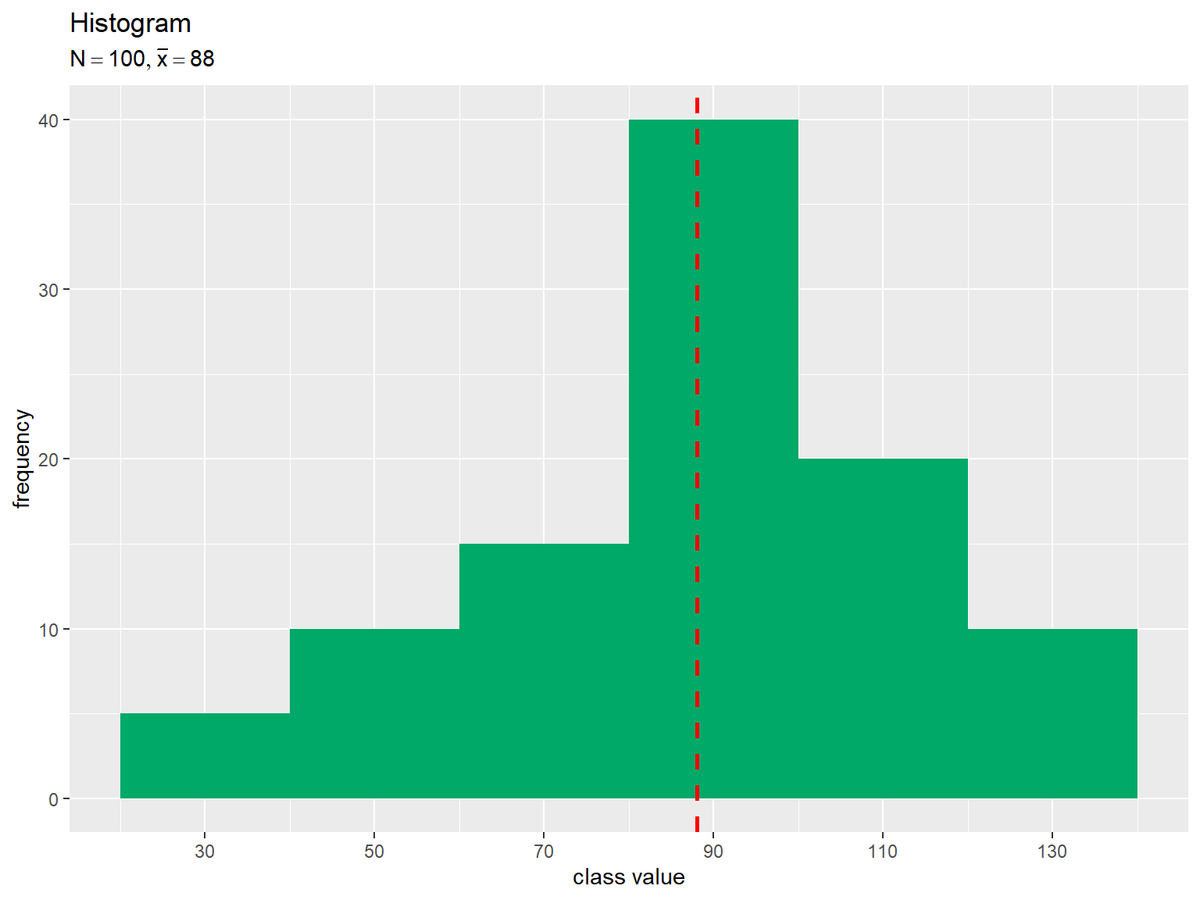
階級値の差から階級の幅を計算して作図します。
この講では、平均値を確認しました。次講では、分散と標準偏差を確認します。
参考書籍
- 小島寛之『完全独習 統計学入門』ダイヤモンド社,2006年.
おわりに
数式を極力使わない方針の本の内容をわざわざ数式に直すのも野暮ですが、統計学の勉強を進めていくには数式による表現を避けられないと思います。数式を使うべきと言いたいのではなく、この本を読んで言葉や図表で理解した状態で数式も読むことで、数式に慣れていけたらいいなと思っています。
このブログではさらにプログラミングも行い、「言葉や図表」・「数式」・「プログラム」の3方向から補完し合いながら理解を目指すのが方針です。ゆくゆくは、数式で説明される方が分かりやすくなるようです(私がそうだとは言ってません)。
このブログでよくする説明なのですが、「N個のデータ($x_n$)の和」を数式で表すと「$\sum_{n=1}^N x_n$」となります。この数式は、(LaTeXコマンドという数式用の言語のようなもの?)で「\sum_{n=1}^N x_n」と書きます。またR言語では、要素数がNのベクトルの変数名をx_nとしておけば「sum(x_n)」で計算できます。ちなみにExcelだと、データが10個のときはsum(X1:X10)ですね。
知らない表現(言語)だと難しく見えますが、同じ計算をそれぞれの言葉で表していて、どれも似たような表現です。なので、1つ分かればそれをきっかけに他も分かりやすくなるでしょうし、3つとも一緒に覚えた方が(最初は大変でしょうが)学習効率がいいと思います(時間効率がいいとは言いません)。
こういうコンセプト(勉強方針)でこのシリーズや他のシリーズの記事を書いていますし、これからも書いていくつもりです。よければお付き合いください。
では次講に続きます。年内にこの本を終えたいけど今のペースではムリそう。
- 2023.01.19
geom_histogram()の使い方をミスってたので書き直しました。
【次の節の内容】