からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

トップ > 攻略ノート > 【R】第4講：データの加工と標準化【統計学入門(小島)のノート】

【R】第4講：データの加工と標準化【統計学入門(小島)のノート】

攻略ノート 攻略ノート-統計学入門(小島) 統計学 R

はじめに

　『完全独習 統計学入門』の学習ノートです。本に載っている計算や表、グラフをR言語で再現します。本とあわせて読んでください。
　この記事では、データを加工した際の統計量の変化を数式とR言語で確認します。

【前の節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

第4講 そのデータは「月並み」か「特殊」か？標準偏差で評価する

　データに一定の値を足したまたは掛けた際のデータと平均値・分散・標準偏差の関係を導出します。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)
library(magick)

　この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
　また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。

4-4 加工されたデータの平均値と標準偏差：数式で確認

　データセットに値を足すや掛ける加工を行ったときの統計量の変化を導出します。

データに一定数を加えて加工する効果

　$N$個のデータ$x_n\ (n = 1, \dots, N)$の全てに$a$を足したときの平均値・分散・標準偏差を考えます。

平均値

　$x_n$の平均値(標本平均)は、次の式で定義されました(第2講)。

$$ \begin{aligned} \bar{x} &= \frac{1}{N} \sum_{n=1}^N x_n \\ &= \frac{1}{N} \Bigl( x_1 + x_2 + \cdots + x_N \Bigr) \end{aligned} $$

　各データに$a$を加えた値を$y_n = x_n + a$で表すことにします。$y_n$の平均値は、次の式になります。

$$ \begin{aligned} \bar{y} &= \frac{1}{N} \sum_{n=1}^N y_n \\ &= \frac{1}{N} \Bigl( y_1 + y_2 + \cdots + y_N \Bigr) \end{aligned} $$

　この式の$y_n$を$x_n + a$に戻して、式を整理します。

$$ \begin{aligned} \bar{y} &= \frac{1}{N} \sum_{n=1}^N (x_n + a) \\ &= \frac{1}{N} \Bigl( (x_1 + a) + (x_2 + a) + \cdots + (x_N + a) \Bigr) \\ &= \frac{1}{N} \Bigl( x_1 + x_2 + \cdots+ x_N + \underbrace{ a + a + \cdots + a }_N \Bigr) \\ &= \frac{1}{N} \Bigl( x_1 + x_2 + \cdots+ x_N + N a \Bigr) \end{aligned} $$

　括弧の$x_n$と$a$に関して、$a (b + c) = a b + a c$のように分割します。

$$ \bar{y} = \frac{1}{N} \Bigl( x_1 + x_2 + \cdots+ x_N \Bigr) + \frac{1}{N} N a $$

　前の項は、$x_n$の平均値の式なので、$\bar{x}$に置き換えられます。

$$ \bar{y} = \bar{x} + a $$

　全てのデータに$a$を加えた平均値$\bar{y}$は、元のデータの平均値$\bar{x}$に$a$を加えた値になるのが分かりました。

偏差

　分散の前に、偏差を考えます。偏差は、各データと平均値の差でした(第3講)。

$$ x_n - \bar{x} $$

　加工後のデータの偏差$y_n - \bar{y}$について、$y_n = x_n + a$と$\bar{y} = \bar{x} + a$で置き換えて、式を整理します。

$$ \begin{aligned} y_n - \bar{y} &= (x_n + a) - (\bar{x} + a) \\ &= x_n + a - \bar{x} - a \\ &= x_n - \bar{x} \end{aligned} $$

　全てのデータに$a$を加えた偏差$y_n - \bar{y}$は、元のデータの偏差$x_n - \bar{x}$と等しくなるのが分かりました。

分散

　続いて、分散(標本分散)は、次の式で定義されました(第3講)。$x_n$の標準偏差を$S_x$、分散を$S_x^2$で表すことにします。

$$ \begin{aligned} S_x^2 &= \frac{1}{N} \sum_{n=1}^N (x_n - \bar{x})^2 \\ &= \frac{1}{N} \Bigl\{ (x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_N - \bar{x})^2 \Bigr\} \end{aligned} $$

　$y_n$の分散は、次の式になります。$y_n$の標準偏差を$S_y$、分散を$S_y^2$で表すことにします。

$$ \begin{aligned} S_y^2 &= \frac{1}{N} \sum_{n=1}^N (y_n - \bar{y})^2 \\ &= \frac{1}{N} \Bigl\{ (y_1 - \bar{y})^2 + (y_2 - \bar{y})^2 + \cdots + (y_N - \bar{y})^2 \Bigr\} \end{aligned} $$

　この式の偏差$y_n - \bar{y}$を$x_n - \bar{x}$に置き換えます。

$$ \begin{aligned} S_y^2 &= \frac{1}{N} \sum_{n=1}^N (x_n - \bar{x})^2 \\ &= S_x^2 \end{aligned} $$

　偏差が等しくなるので、全てのデータに$a$を加えた分散$S_y^2$は、元のデータの分散$S_x^2$になるのが分かりました。

標準偏差

　$x_n$の標準偏差(標本標準偏差)は、次の式で定義されました(第3講)。

$$ S_x = \sqrt{S_x^2} $$

　$y_n$の標準偏差は、次の式になります。

$$ S_y = \sqrt{S_y^2} $$

　$S_y^2 = S_x^2$で置き換えます。

$$ \begin{aligned} S_y &= \sqrt{S_x^2} \\ &= S_x \end{aligned} $$

　分散が等しいので、全てのデータに$a$を加えた標準偏差$S_y$も、元のデータの標準偏差$S_x$と等しくなります。

データに一定数を掛けて加工する効果

　次は、$N$個のデータ$x_n$の全てを$a$倍したときの平均値・分散・標準偏差を考えます。

平均値

　先ほどと同様に、$y_n = a x_n$とおくと、平均値(標本平均)は次の式になります。

$$ \begin{aligned} \bar{y} &= \sum_{n=1}^N y_n \\ &= \frac{1}{N} \Bigl( y_1 + y_2 + \cdots + y_N \Bigr) \end{aligned} $$

　この式の$y_n$を$a x_n$に戻して、式を整理します。

$$ \begin{aligned} \bar{y} &= \frac{1}{N} \Bigl( a x_1 + a x_2 + \cdots + a x_N \Bigr) \\ &= a \frac{1}{N} \Bigl( x_1 + x_2 + \cdots + x_N \Bigr) \end{aligned} $$

　括弧から$a$を括り出すと、$a$以外の項が$x_n$の平均値の式なので、$\bar{x}$に置き換えられます。

$$ \bar{y} = a \bar{x} $$

　全てのデータを$a$倍した平均値$\bar{y}$は、元のデータの平均値$\bar{x}$を$a$倍した値になるのが分かりました。

偏差

　分散の前に、偏差を考えます。加工後のデータの偏差$y_n - \bar{y}$について、$y_n = a x_n$と$\bar{y} = a \bar{x}$で置き換えて、式を整理します。

$$ \begin{aligned} y_n - \bar{y} &= a x_n - a \bar{x} \\ &= a (x_n - \bar{x}) \end{aligned} $$

　全てのデータを$a$倍した偏差$y_n - \bar{y}$は、元のデータの偏差$x_n - \bar{x}$を$a$倍した値になるのが分かりました。

分散

　続いて、$y_n$の分散(標本分散)は、次の式になります。

$$ \begin{aligned} S_y^2 &= \frac{1}{N} \sum_{n=1}^N (y_n - \bar{y})^2 \\ &= \frac{1}{N} \Bigl\{ (y_1 - \bar{y})^2 + (y_2 - \bar{y})^2 + \cdots + (y_N - \bar{y})^2 \Bigr\} \end{aligned} $$

　この式の$y_n$を$a x_n$に戻して、式を整理します。

$$ \begin{aligned} S_y^2 &= \frac{1}{N} \sum_{n=1}^N (a y_n - a \bar{y})^2 \\ &= \frac{1}{N} \Bigl\{ (a x_1 - a \bar{x})^2 + (a x_2 - a \bar{x})^2 + \cdots + (a x_N - a \bar{x})^2 \Bigr\} \\ &= \frac{1}{N} \left\{ \Bigl( a (x_1 - \bar{x}) \Bigr)^2 + \Bigl( a (x_2 - \bar{x}) \Bigr)^2 + \cdots + \Bigl( a (x_N - \bar{x}) \Bigr)^2 \right\} \end{aligned} $$

　偏差の2乗の括弧をそれぞれ$(a b)^2 = a^2 b^2$のように展開します。

$$ \begin{aligned} S_y^2 &= \frac{1}{N} \Bigl\{ a^2 (x_1 - \bar{x})^2 + a^2 (x_2 - \bar{x})^2 + \cdots + a^2 (x_N - \bar{x})^2 \Bigr\} \\ &= a^2 \frac{1}{N} \Bigl\{ (x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_N - \bar{x})^2 \Bigr\} \end{aligned} $$

　括弧から$a$の2乗を括り出すと、$a^2$以外の項が$x_n$の分散の式なので、$S_x$に置き換えられます。

$$ S_y^2 = a^2 S_x^2 $$

　全てのデータを$a$倍した分散$S_y^2$は、元のデータの標準偏差$S_x^2$を$a$の2乗倍した値になるのが分かりました。

標準偏差

　$y_n$の標準偏差は、次の式になります。

$$ S_y = \sqrt{S_y^2} $$

　$S_y^2 = a^2 S_x^2$で置き換えて、平方根の性質$\sqrt{x^2} = |x|$より、式を整理します。

$$ \begin{aligned} S_y &= \sqrt{a^2 S_x^2} \\ &= \sqrt{a^2} \sqrt{S_x^2} \\ &= |a| S_x \end{aligned} $$

　全てのデータを$a$倍した標準偏差$S_y$は、元のデータの標準偏差$S_x$を$|a|$倍した値になるのが分かりました。

S.D.何個分となるようにデータを加工する効果

　ここまでで、データ全体に$a$を加えると平均値が$a$増えて分散と標準偏差は変化しない、$a$を掛けると平均値と標準偏差が$a$倍されて分散は$a$の2乗倍されることが分かりました。
　このことから、平均値が$b$で標準偏差$c$(分散が$c^2$)であるデータに対して、平均値$b$を引いて標準偏差の逆数$\frac{1}{c}$を掛ける(標準偏差$c$で割る)と、平均値が$b - b = 0$で標準偏差が$\frac{c}{c} = 1$のデータになることが分かります。この処理を標準化と呼びます。

4-4 加工されたデータの平均値と標準偏差：グラフで確認

　正規分布によって生成したデータを使って、加工前後のデータのヒストグラムと統計量を比較します。正規分布については第7項を参照してください。

標準正規分布に従うデータ

　まずは、元データとして利用する標準正規分布に従うデータを作成します。

　データ数を指定して、標準正規分布に従う乱数を生成します。

# データ数を指定
N <- 30

# データを生成
data_x <- rnorm(n = N, mean = 0, sd = 1)
head(data_x)

## [1] -0.2381668  0.5984052 -0.8832445  0.8049462  0.4369738 -0.1111931

　正規分布の乱数はrnorm()で生成できます。データ数(サンプルサイズ)の引数nに生成するデータ数、平均の引数meanに0、標準偏差の引数sdに1を指定します。デフォルトは、mean = 0、sd = 1で、標準正規分布に従う乱数を生成します。

　生成したデータの標本平均・標本分散・標本標準偏差を計算します。

# 平均値・分散・標準偏差を計算
mean_x     <- sum(data_x) / length(data_x)
variance_x <- sum((data_x - mean_x)^2) / length(data_x)
sd_x       <- sqrt(variance_x)
mean_x; variance_x; sd_x

## [1] 0.4161358
## [1] 0.9459366
## [1] 0.9725927

　平均値が0、標準偏差が1に近い値になっているのが分かります。

　平均値と標準偏差をサブタイトルに表示する用の文字列を作成します。作図自体には不要な処理です。

# ラベル用の文字列を作成
label_text <- paste0(
  "list(", 
  "N==", N, 
  ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), 
  ")"
)
label_text

## [1] "list(N==30, bar(x)==0.416, S[x]==0.973)"

　expression()の記法に従い指定します。

　ヒストグラムを作成します。

# データを格納
data_x_df <- tibble::tibble(value = data_x)

# ヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_x_df, mapping = aes(x = value), 
                 bins = 30, fill = "#00A968") + # 元データの度数
  geom_vline(xintercept = mean_x, 
             color = "red", size = 1) + # 元データの平均値
  geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 元データの平均値 ± 標準偏差
  scale_x_continuous(breaks = seq(from = floor(min(data_x)), to = ceiling(max(data_x)), by = 1)) + 
  labs(title = expression(x[n] %~% N(x ~ "|" ~ mu==0, sigma==1)), 
       subtitle = parse(text = label_text), 
       x = "class value", y = "frequency")

標準正規分布に従うデータ

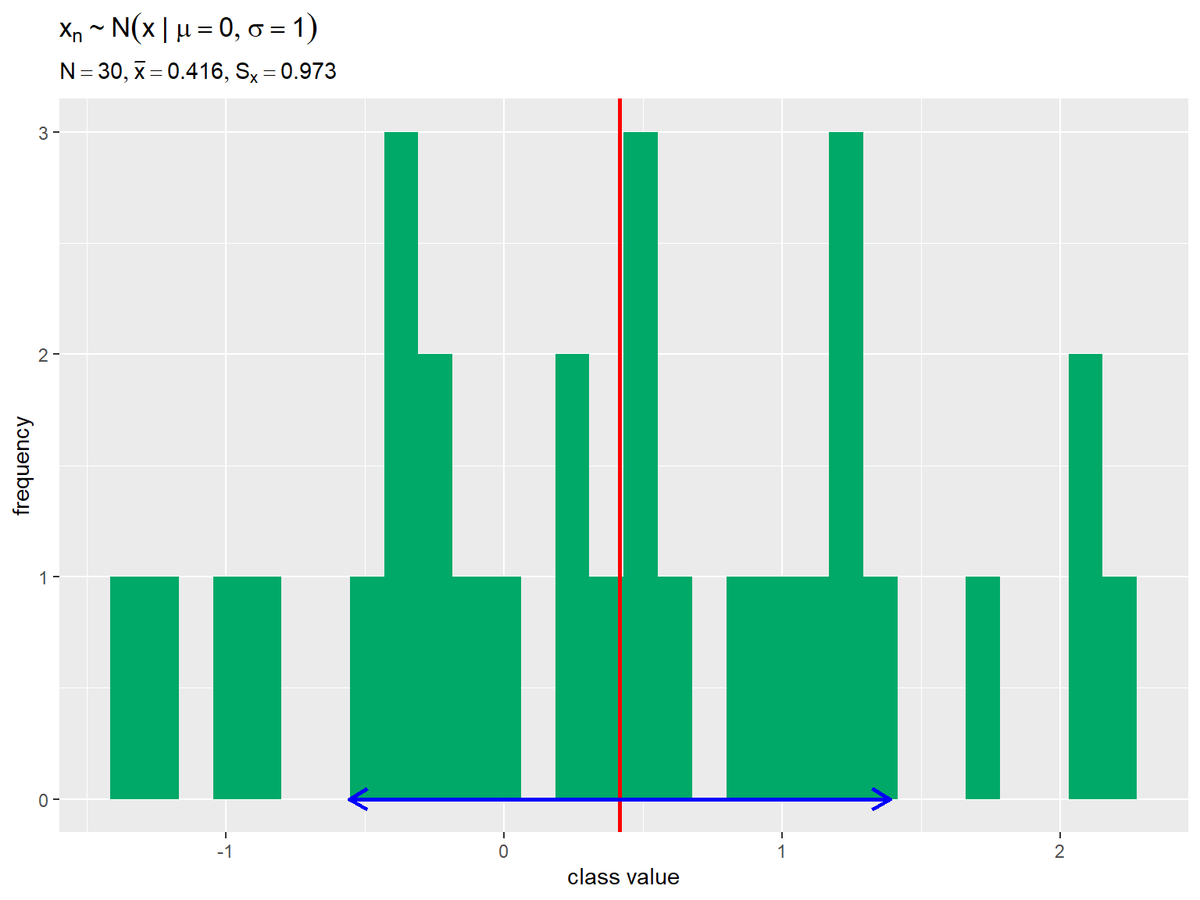
　デフォルトの設定(bins = 30)に従い階級値(バーの区切り)を自動で決めます。階級値の取り方が変わるとヒストグラムの形も変わります。
　平均値を赤色の垂線、平均値を中心に標準偏差1つ分の範囲を青色の水平線(矢印)で示します。平均値(赤色の垂線)が0付近、平均値を中心に標準偏差1つ分の範囲(青色の水平線)が-1から1の範囲付近なのが分かります。


一定数を加算したデータ

　全てのデータに一定の値を加えることでデータを加工します。

　定数を指定して、データに足します。

# 定数を指定
a <- 3

# データを加工
data_y <- data_x + a
head(data_y)

## [1] 2.761833 3.598405 2.116756 3.804946 3.436974 2.888807


　加工後のデータの標本平均・標本分散・標本標準偏差を計算します。

# 平均値・分散・標準偏差を計算
mean_y     <- sum(data_y) / length(data_y)
variance_y <- sum((data_y - mean_y)^2) / length(data_y)
sd_y       <- sqrt(variance_y)
mean_y; variance_y; sd_y

## [1] 3.416136
## [1] 0.9459366
## [1] 0.9725927

　平均値がa変化して、分散と標準偏差に変化がないのが分かります。

　加工前後のデータの最小値から最大値の範囲で階級値を決めます。

# 階級値を作成
class_width <- 0.5
class_value_vec <- seq(
  from = floor(min(data_x, data_y)), 
  to = ceiling(max(data_x, data_y)), 
  by = class_width
)
head(class_value_vec); length(class_value_vec)

## [1] -2.0 -1.5 -1.0 -0.5  0.0  0.5
## [1] 17

　加工前後のデータのヒストグラムにおいて、共通の基準で度数をカウントするのに必要な処理です。

　ラベル表示用の文字列を作成します。

# ラベル用の文字列を作成
label_text <- paste0(
  "list(", 
  "N==", N, 
  ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), 
  ", bar(y)==", round(mean_y, 3), ", S[y]==", round(sd_y, 3), 
  ")"
)
label_text

## [1] "list(N==30, bar(x)==0.416, S[x]==0.973, bar(y)==3.416, S[y]==0.973)"


　加工前後のヒストグラムを並べて描画します。

# データを格納
data_y_df <- tibble::tibble(value = data_y)

# ヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_x_df, mapping = aes(x = value), 
                 breaks = class_value_vec-0.5*class_width, closed = "left", 
                 color = "#00A968", fill = NA, size = 1, linetype = "dashed") + # 元データの度数
  geom_vline(xintercept = mean_x, 
             color = "red", size = 1, linetype = "dashed") + # 元データの平均値
  geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
               color = "blue", size = 1, linetype = "dashed", 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 元データの平均値 ± 標準偏差
  geom_histogram(data = data_y_df, mapping = aes(x = value), 
                 breaks = class_value_vec-0.5*class_width, closed = "left", 
                 fill = "#00A968", alpha = 0.5) + # 加工データの度数
  geom_vline(xintercept = mean_y, 
             color = "red", size = 1) + # 加工データの平均値
  geom_segment(mapping = aes(x = mean_y-sd_y, y = 0, xend = mean_y+sd_y, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 加工データの平均値 ± 標準偏差
  scale_x_continuous(breaks = seq(from = min(class_value_vec), to = max(class_value_vec), by = 1)) + 
  labs(title = expression(y[n] == x[n] + a), 
       subtitle = parse(text = label_text), 
       x = "class value", y = "frequency")

一定数を加算したデータ

　加工前のデータに関するグラフを破線で示します。
　標準偏差が変わらないのでグラフの形も変わらずに、平均値にaが加算されるので山全体が横軸方向にa移動しているのが分かります。aが正の値の場合は右、負の値の場合は左に移動します。

一定数を乗算したデータ

　次は、全てのデータに一定の値を掛けることでデータを加工します。

　定数を指定して、データに掛けます。

# 定数を指定
a <- 3

# データを加工
data_y <- data_x * a
head(data_y)

## [1] -0.7145004  1.7952157 -2.6497334  2.4148385  1.3109213 -0.3335792


　加工後のデータの標本平均・標本分散・標本標準偏差を計算します。

# 平均値・分散・標準偏差を計算
mean_y     <- sum(data_y) / length(data_y)
variance_y <- sum((data_y - mean_y)^2) / length(data_y)
sd_y       <- sqrt(variance_y)
mean_y; variance_y; sd_y

## [1] 1.248408
## [1] 8.513429
## [1] 2.917778

　平均値と標準偏差がa倍され、分散がaの2乗倍されるのが分かります。

　加工前後のデータの最小値から最大値の範囲で階級値を決めます。

# 階級値を作成
class_width <- 0.5
class_value_vec <- seq(
  from = floor(min(data_x, data_y)), 
  to = ceiling(max(data_x, data_y)), 
  by = class_width
)
head(class_value_vec); length(class_value_vec)

## [1] -5.0 -4.5 -4.0 -3.5 -3.0 -2.5
## [1] 25

　加工前後のデータのヒストグラムにおいて、共通の基準で度数をカウントするのに必要な処理です。

　ラベル表示用の文字列を作成します。

# ラベル用の文字列を作成
label_text <- paste0(
  "list(", 
  "N==", N, 
  ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), 
  ", bar(y)==", round(mean_y, 3), ", S[y]==", round(sd_y, 3), 
  ")"
)
label_text

## [1] "list(N==30, bar(x)==0.416, S[x]==0.973, bar(y)==1.248, S[y]==2.918)"


　加工前後のヒストグラムを並べて描画します。

# データを格納
data_y_df <- tibble::tibble(value = data_y)

# ヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_x_df, mapping = aes(x = value), 
                 breaks = class_value_vec-0.5*class_width, closed = "left", 
                 color = "#00A968", fill = NA, size = 1, linetype = "dashed") + # 元データの度数
  geom_vline(xintercept = mean_x, 
             color = "red", size = 1, linetype = "dashed") + # 元データの平均値
  geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
               color = "blue", size = 1, linetype = "dashed", 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 元データの平均値 ± 標準偏差
  geom_histogram(data = data_y_df, mapping = aes(x = value), 
                 breaks = class_value_vec-0.5*class_width, closed = "left", 
                 fill = "#00A968", alpha = 0.5) + # 加工データの度数
  geom_vline(xintercept = mean_y, 
             color = "red", size = 1) + # 加工データの平均値
  geom_segment(mapping = aes(x = mean_y-sd_y, y = 0, xend = mean_y+sd_y, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 加工データの平均値 ± 標準偏差
  scale_x_continuous(breaks = seq(from = min(class_value_vec), to = max(class_value_vec), by = 1)) + 
  labs(title = expression(y[n] == a * x[n]), 
       subtitle = parse(text = label_text), 
       x = "class value", y = "frequency")

一定数を乗算したデータ

　加工前のデータに関するグラフを破線で示します。
　標準偏差がa倍になるのでグラフの散らばり具合が変わって(青色の矢印の長さが変わって)いるのが分かります。aが0より大きく1より小さい値の場合は山が細く高く、1より大きい値の場合は太く低くなります。

正規分布に従うデータ

　続いて、標準化の処理を利用するデータを作成します。(標準正規分布ではない)正規分布に従うデータを元データとします。

　データ数と正規分布のパラメータを指定して、正規分布に従う乱数を生成します。

# データ数を指定
N <- 30

# 平均・標準偏差パラメータを指定
mu    <- 5
sigma <- 2

# データを生成
data_x <- rnorm(n = N, mean = mu, sd = sigma)
head(data_x)

## [1] 7.273988 4.623396 5.114450 9.150246 4.728164 2.474368

　正規分布の平均パラメータをmu、標準偏差パラメータをsigmaとして値を指定します。
　正規分布の乱数生成関数rnorm()の平均の引数meanにmu、標準偏差の引数sdにsigmaを指定して乱数を生成します。

　生成したデータの標本平均・標本分散・標本標準偏差を計算します。

# 平均値・分散・標準偏差を計算
mean_x     <- sum(data_x) / length(data_x)
variance_x <- sum((data_x - mean_x)^2) / length(data_x)
sd_x       <- sqrt(variance_x)
mean_x; variance_x; sd_x

## [1] 5.542696
## [1] 4.234855
## [1] 2.057876

　平均値がmu、標準偏差がsigmaに近い値になっているのが分かります。

　パラメータや統計量をタイトルに表示する用の文字列を作成します。作図自体には不要な処理です。

# ラベル用の文字列を作成
param_text <- paste0(
  'x[n] %~% N(x ~ "|" ~ mu==', mu, ", sigma==", sigma, ")"
)
label_text <- paste0(
  "list(", 
  "N==", N, 
  ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), 
  ")"
)
param_text; label_text

## [1] "x[n] %~% N(x ~ \"|\" ~ mu==5, sigma==2)"
## [1] "list(N==30, bar(x)==5.543, S[x]==2.058)"

　expression()の記法に従い指定します。

　ヒストグラムを作成します。

# データを格納
data_x_df <- tibble::tibble(value = data_x)

# ヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_x_df, mapping = aes(x = value), 
                 bins = 30, fill = "#00A968") + # 元データの度数
  geom_vline(xintercept = mean_x, 
             color = "red", size = 1) + # 元データの平均値
  geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 元データの平均値 ± 標準偏差
  scale_x_continuous(breaks = seq(from = floor(min(data_x)), to = ceiling(max(data_x)), by = 1)) + 
  labs(title = parse(text = param_text), 
       subtitle = parse(text = label_text), 
       x = "class value", y = "frequency")

正規分布に従うデータ

　デフォルトの設定で描画します。

標準化したデータ

　データから平均値を引き、標準偏差の逆数を掛け(標準偏差で割り)ます。

# データを加工
data_y <- (data_x - mean_x) / sd_x
head(data_y)

## [1]  0.8413006 -0.4467226 -0.2081007  1.7530452 -0.3958120 -1.4910167


　加工後のデータの標本平均・標本分散・標本標準偏差を計算します。

# 平均値・分散・標準偏差を計算
mean_y     <- sum(data_y) / length(data_y)
variance_y <- sum((data_y - mean_y)^2) / length(data_y)
sd_y       <- sqrt(variance_y)
mean_y; variance_y; sd_y

## [1] -1.422473e-16
## [1] 1
## [1] 1

　平均値が0になり、分散と標準偏差が1になるのが分かります。ただし、プログラム上の誤差を含みます。

　加工前後のデータの最小値から最大値の範囲で階級値を決めます。

# 階級値を作成
class_width <- 0.5
class_value_vec <- seq(
  from = floor(min(data_x, data_y)), 
  to = ceiling(max(data_x, data_y)), 
  by = class_width
)
head(class_value_vec); length(class_value_vec)

## [1] -2.0 -1.5 -1.0 -0.5  0.0  0.5
## [1] 27

　加工前後のデータのヒストグラムにおいて、共通の基準で度数をカウントするのに必要な処理です。

　ラベル表示用の文字列を作成します。

# ラベル用の文字列を作成
label_text <- paste0(
  "list(", 
  "N==", N, 
  ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), 
  ", bar(y)==", round(mean_y, 3), ", S[y]==", round(sd_y, 3), 
  ")"
)
label_text

## [1] "list(N==30, bar(x)==5.543, S[x]==2.058, bar(y)==0, S[y]==1)"


　加工前後のヒストグラムを並べて描画します。

# データを格納
data_y_df <- tibble::tibble(value = data_y)

# ヒストグラムを作成
ggplot() + 
  geom_histogram(data = data_x_df, mapping = aes(x = value), 
                 breaks = class_value_vec-0.5*class_width, closed = "left", 
                 color = "#00A968", fill = NA, size = 1, linetype = "dashed") + # 元データの度数
  geom_vline(xintercept = mean_x, 
             color = "red", size = 1, linetype = "dashed") + # 元データの平均値
  geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
               color = "blue", size = 1, linetype = "dashed", 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 元データの平均値 ± 標準偏差
  geom_histogram(data = data_y_df, mapping = aes(x = value), 
                 breaks = class_value_vec-0.5*class_width, closed = "left", 
                 fill = "#00A968", alpha = 0.5) + # 加工データの度数
  geom_vline(xintercept = mean_y, 
             color = "red", size = 1) + # 加工データの平均値
  geom_segment(mapping = aes(x = mean_y-sd_y, y = 0, xend = mean_y+sd_y, yend = 0), 
               color = "blue", size = 1, 
               arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 加工データの平均値 ± 標準偏差
  scale_x_continuous(breaks = seq(from = min(class_value_vec), to = max(class_value_vec), by = 1)) + 
  labs(title = expression(y[n] == (x[n] - bar(x)) / S[x]), 
       subtitle = parse(text = label_text), 
       x = "class value", y = "frequency")

標準化したデータ

　平均値(赤色の垂線)が0、平均値を中心に標準偏差1つ分の範囲(青色の水平線)が-1から1の範囲になっているのが分かります。

　データが標準化される様子を見てみましょう。

作図コード(クリックで展開)

　データ加工用の定数を徐々に変化させてヒストグラムのアニメーションを作成します。

# データ数を指定
N <- 30

# 平均・標準偏差パラメータを指定
mu    <- 5
sigma <- 2

# データを生成
data_x <- rnorm(n = N, mean = mu, sd = sigma)

# 平均値・分散・標準偏差を計算
mean_x     <- sum(data_x) / length(data_x)
variance_x <- sum((data_x - mean_x)^2) / length(data_x)
sd_x       <- sqrt(variance_x)

# 画像の保存先を指定
dir_path <- "tmp_folder"

# フレーム数を指定
frame_num <- 30

# 定数として利用する値を作成
a_vals <- seq(from = 0, to = mean_x, length.out = frame_num)
b_vals <- seq(from = 1, to = sd_x, length.out = frame_num)

# データ加工用の値を変更して作図
for(i in 1:frame_num) {
  # i番面の値を取得
  a <- a_vals[i]
  b <- b_vals[i]
  
  # データを加工
  data_y <- (data_x - a) / b
  
  # 平均値・分散・標準偏差を計算
  mean_y     <- sum(data_y) / length(data_y)
  variance_y <- sum((data_y - mean_y)^2) / length(data_y)
  sd_y       <- sqrt(variance_y)
  
  # データを格納
  data_x_df <- tibble::tibble(value = data_x)
  data_y_df <- tibble::tibble(value = data_y)
  
  # 階級値を作成
  class_width <- 0.5
  class_value_vec <- seq(
    from = floor(min(data_x, data_y)), 
    to = ceiling(max(data_x, data_y)), 
    by = class_width
  )
  
  # ラベル用の文字列を作成
  data_text <- paste0(
    "y[n]==(x[n] - ", round(a, 2), ") / ", round(b, 2)
  )
  label_text <- paste0(
    "list(", 
    "N==", N, 
    ", bar(x)==", round(mean_x, 3), ", S[x]==", round(sd_x, 3), 
    ", bar(y)==", round(mean_y, 3), ", S[y]==", round(sd_y, 3), 
    ")"
  )
  
  # ヒストグラムを作成
  g <- ggplot() + 
    geom_histogram(data = data_x_df, mapping = aes(x = value), 
                   breaks = class_value_vec-0.5*class_width, closed = "left", 
                   color = "#00A968", fill = NA, size = 1, linetype = "dashed") + # 元データの度数
    geom_vline(xintercept = mean_x, 
               color = "red", size = 1, linetype = "dashed") + # 元データの平均値
    geom_segment(mapping = aes(x = mean_x-sd_x, y = 0, xend = mean_x+sd_x, yend = 0), 
                 color = "blue", size = 1, linetype = "dashed", 
                 arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 元データの平均値 ± 標準偏差
    geom_histogram(data = data_y_df, mapping = aes(x = value), 
                   breaks = class_value_vec-0.5*class_width, closed = "left", 
                   fill = "#00A968", alpha = 0.5) + # 加工データの度数
    geom_vline(xintercept = mean_y, 
               color = "red", size = 1) + # 加工データの平均値
    geom_segment(mapping = aes(x = mean_y-sd_y, y = 0, xend = mean_y+sd_y, yend = 0), 
                 color = "blue", size = 1, 
                 arrow = arrow(ends = "both", length = unit(10, units = "pt"))) + # 加工データの平均値 ± 標準偏差
    scale_x_continuous(breaks = seq(from = -4, to = 12, by = 1)) + 
    coord_cartesian(xlim = c(-4, 12), ylim = c(0, 8)) + # 表示範囲
    labs(title = parse(text = data_text), 
         subtitle = parse(text = label_text), 
         x = "class value", y = "frequency")
  
  # グラフを書き出し
  file_name <- stringr::str_pad(i, width = 2, side = "left", pad = 0)
  ggplot2::ggsave(
    filename = paste0(dir_path, "/", file_name, ".png"), plot = g, 
    width = 800, height = 600, units = "px", dpi = 100
  )
}

# ファイルパスを作成
file_path_vec <- dir_path |> 
  list.files() |> # ファイル名を取得
  (\(.){paste0(dir_path, "/", .)})()

# gif画像を作成
gif_data <- file_path_vec |> 
  magick::image_read() |> # 画像ファイルを読み込み
  magick::image_animate(fps = 2, dispose = "previous")

# gif画像を書き出し
magick::image_write_gif(image = gif_data, path = "ch04_histgram.gif", delay = 1/2)

　フレーム数frame_numを指定して、0から元データの平均値mean_xまでの値をframe_num個に等間隔に分けてa_vals、1から元データの標準偏差sd_xまでの値をframe_num個に等間隔に分けてb_valsとします。a_vals, b_valsから順番に値を取り出してa, bとして、データからaを引きbで割り元データと重ねてヒストグラムを作成して、グラフを保存します。画像の書き出し先フォルダdir_pathは空である必要があります。\ 　保存した画像ファイルをimage_read()で読み込んで、image_animate()でgif画像に変換します。


標準化の様子

　正規分布に従う形から、徐々に標準正規分布に形に変化するのを確認できます。

　この講では、データの加工と統計量の関係を確認しました。次講では、標準偏差の利用方法を確認します。

参考書籍

  • 小島寛之『完全独習 統計学入門』ダイヤモンド社,2006年.

おわりに

　こんなにも数式が登場することになるとは思っていませんでした。2周目のときにでも改めて読んでもらえればいいと思います。

　そういえば、これまで生データを扱うことがほとんどなかったので記述統計をすることもなく、標準化の計算は知っていましたがデータの加工と統計量の変化を意識することもなかったです。
　なので、式変形してみて面白かったですし勉強になりました。

　2022年12月17日は、つばきファクトリーの小野田紗栞さんの21歳のお誕生日です。

　(サムネの右から2番目の方です。)
　ハロプロは地頭の良いメンバーがぶりっ子キャラを担当しがち(私見)なもんだから、なんだかんだで突っ込み役に回ってキャラどころじゃなくなるのが良いよね？

【次の節の内容】

www.anarchive-beta.com