はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、4.3.2項と4.3.3項の内容です。ニュートン法によるロジスティック回帰の最尤推定をPythonで実装します。
【数式読解編】
【前節の内容】
【他の節一覧】
【この節の内容】
4.3.2 ロジスティック回帰
ニュートン-ラフソン法によるロジスティック回帰の最尤推定を実装します。
利用するライブラリを読み込みます。
# 4.3.2-3項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
推定過程をアニメーション(gif画像)で可視化するのにMatplotlibライブラリのanimationモジュールを利用します。不要であれば省略してください。
・利用する関数の作成
推定に利用する関数を作成します。基底関数については「【Python】3.1.0:基底関数の作図【PRMLのノート】 - からっぽのしょこ」を、計画行列については「[【Python】3.1.1:線形基底関数モデルの実装【PRMLのノート】 - からっぽのしょこ」を参照してください。
ロジスティックシグモイド関数を定義します。
# ロジスティックシグモイド関数を作成 def sigmoid(x): return 1.0 / (1.0 + np.exp(-x))
ロジスティックシグモイド関数は、次の式で定義されます。
この例では、基底関数の数を$M = 2$とし、また$\phi_0(x) = 1$とします。よって、計画行列は
となります。$\phi_1(x)$は非線形変換を行う基底関数で、多項式基底関数かシグモイド基底関数を用います。
多項式基底関数の計画行列を定義します。
# 多項式基底関数を作成 def phi_polynomial(x, j): return x**j # 多項式基底関数の計画行列を作成:(M > 2) def Phi_polynomial(x_n, M, _x_n=None): # 変数を初期化 phi_x_nm = np.ones((len(x_n), M)) # 列ごとに多項式基底関数による変換 for m in range(1, M): phi_x_nm[:, m] = phi_polynomial(x_n, m) return phi_x_nm
シグモイド基底関数の計画行列を定義します。
# シグモイド基底関数を作成 def phi_sigmoid(x, mu, s): a_n = (x - mu) / s return sigmoid(a_n) # シグモイド基底関数の計画行列を作成:(M > 2) def Phi_sigmoid(x_n, M, _x_n=None): # パラメータ設定用の入力値を設定 if _x_n is None: _x_n = x_n.copy() # M-1個のパラメータを作成:(M > 1) s = np.std(_x_n) * 0.5 # 標準偏差で固定(0.5は値の調整) if M == 2: # 入力値の平均 mu_m = np.array([np.mean(_x_n)]) elif M == 3: # 調整幅を指定 sgm = s * 1.0 # 平均を中心に標準偏差のn倍の範囲 mu_m = np.array([np.mean(_x_n) - sgm, np.mean(_x_n) + sgm]) elif M > 3: # 調整幅を指定 sgm = s * 0.25 # 最小値から最大値を等分 mu_m = np.linspace(np.min(_x_n) + sgm, np.max(_x_n) - sgm, num=M-1) # 変数を初期化 phi_x_nm = np.ones((len(x_n), M)) # 列ごとにシグモイド基底関数による変換 for m in range(1, M): phi_x_nm[:, m] = phi_sigmoid(x_n, mu_m[m-1], s) return phi_x_nm
結果の確認時にクラスの境界線を引きます。その際に利用する閾値を計算する関数を作成します。推定自体には使いません。
利用する基底関数や基底関数の数$M$によって閾値の計算が変わるので、それぞれ作成します。
多項式基底関数用の関数を定義します。
# 閾値の計算関数を作成:(多項式基底関数用:M = 2) def threshold_polynomial(w_m, _x_n): # 回帰式の逆関数の計算 return -w_m[0] / w_m[1]
回帰式の逆関数となる計算を行います。
シグモイド基底関数用の関数を定義します。
# 閾値の計算関数を作成:(シグモイド基底関数用:M = 2) def threshold_sigmoid(w_m, _x_n): # 回帰式の逆関数の計算 a = np.log(-w_m[0] / np.sum(w_m)) # 基底関数のパラメータを計算 s = np.std(_x_n) * 0.5 # (0.5は値を調整した場合) mu = np.mean(_x_n) # 標準化の逆関数の計算 x = a * s + mu return x
回帰式の逆関数となる計算を行います。
またシグモイド基底関数の中で標準化を行ったので、その逆関数の計算も行う必要があります。
$y = 0.5$となる$x$の計算式を導出します。
・計算式の導出(クリックで展開)
「出力(クラス1となる確率)$y = 0.5$」を「非線形変換を行った入力の重み付き和$a$」について解きます。
$a = 0$のとき$y = 0.5$となるのが分かりました。
さらに、「$y = 0.5$となる重み付き和$a = 0$」を「入力$x$」について解きます。ただし、$x$は基底関数によって変換しました。よって、利用する基底関数によって計算式が異なります。
まずは、$M = 2$の多項式基底関数の場合を考えます。多項式基底関数の定義より、$\phi_1(x) = x$なので
となります。
つまり、$x > - \frac{w_0}{w_1}$であればクラス1に、$x < - \frac{w_0}{w_1}$であればクラス0に分類します。
続いて、$M = 2$のシグモイド基底関数の場合を考えます。
$y = 0.5$となる$x$の計算式が得られました。最後の行では、$- \log \frac{a}{b} = - (\log a - \log b) = \log b - \log a = \log \frac{b}{a}$の変形を行いました。
つまり、$x > \log (- \frac{w_0}{w_0 + w_1})$であればクラス1に、$x < \log (- \frac{w_0}{w_0 + w_1})$であればクラス0に分類します。
・データの生成
推定に利用するデータを人工的に作成します。
データ生成に関するパラメータを指定します。
# クラス割り当て確率を指定:(クラス1となる確率) p = 0.4 # データ生成の平均・標準偏差を指定:(クラス0, クラス1) mu_k = np.array([-1.0, 9.0]) sigma_k = np.array([3.0, 3.0])
クラス1($t_n = 1$)となる確率pを指定します。
各クラスの平均mu_kと標準偏差sigma_kを指定します。2値分類なのでクラス数$K = 2$です。
指定したパラメータに従って観測データを作成します。
# データ数を指定 N = 100 # 真のクラスを生成 t_n = np.random.binomial(n=1, p=p, size=N) # 真のクラスに従いデータを生成 x_n = np.random.normal(loc=mu_k[t_n], scale=sigma_k[t_n], size=N)
データ数$N$を指定して、観測データ(目標値$\mathbf{t} = \{t_1, \cdots, t_N\}$、入力値$\mathbf{x} = \{x_1, \cdots, x_N\}$)を作成します。
$t_n$は$n$番目のデータのクラスを表し、$t_n = 0$であればクラス0、$t_n = 1$であればクラス1とします。
$x_n$は$n$番目のデータの値です。
$\mathbf{t}$はベルヌーイ分布に従い生成します。ベルヌーイ分布に従う乱数は、二項分布の乱数生成関数np.random.binomial()の試行回数の引数nに1を指定することで生成できます。確率の引数pにp、データ数(サンプルサイズ)の引数sizeにNを指定します。
$\mathbf{x}$はガウス分布に従い生成します。ガウス分布に従う乱数は、np.random.normal()で生成できます。locは平均、scaleは標準偏差の引数です。データごとに割り当てられたクラスに応じてパラメータを指定する必要があります。
クラスに対応したパラメータの値は、次のようにして取り出しています。
# パラメータの取得 print(t_n[:5]) print(mu_k[t_n[:5]])
[0 1 0 0 0]
[-1. 9. -1. -1. -1.]
t_nには各データのクラスが保存されています。
クラス0のパラメータはmu_k[0], sigma_k[0]、クラス1のパラメータはmu_k[1], sigma_k[1]なので、t_nの値がインデックスに対応します。
観測データをヒストグラムで確認します。
# 観測データのヒストグラムを作成 plt.figure(figsize=(12, 9)) plt.hist([x_n[t_n==0], x_n[t_n==1]], histtype='barstacked', color=['blue', 'chocolate'], label=['class 0', 'class 1']) # クラス1の観測データ plt.xlabel('x') plt.ylabel('count') plt.suptitle('Observation Data', fontsize=20) plt.title('$p=' + str(p) + ', N_0=' + str(np.sum(t_n==0)) + ', N_1=' + str(np.sum(t_n==1)) + '$', loc='left') plt.legend() plt.grid() plt.show()
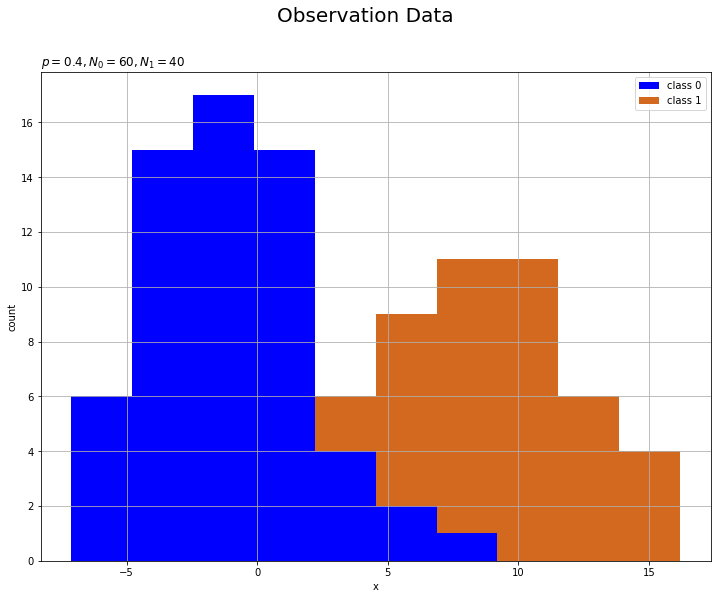
(ロジスティック回帰用のデータがこんな感じでいいのかはよく分かっていません。何か変なら教えてください。)
・ニュートン-ラフソン法による最尤推定
ニュートン-ラフソン法によりロジスティック回帰のパラメータの最尤解を求めます。
・処理の解説
まずは、繰り返し行う個々の処理を解説します。次に、それらをまとめて推定を行います。
基底関数を設定して、計画行列の計算を行い入力値を変換します。
# 基底関数の数を指定 M = 2 # 基底関数を指定 phi = Phi_polynomial #phi = Phi_sigmoid # 基底関数により入力値を変換 phi_x_nm = phi(x_n, M) # 確認 print(phi_x_nm[:5])
[[ 1. 0.11662828]
[ 1. 10.10501145]
[ 1. 8.81649967]
[ 1. 7.42515107]
[ 1. 14.55833771]]
利用する基底関数の計画行列Phi_***()を関数phi()として複製します。
phi()を使って計算します。
変換した入力値の重み付き和を計算します。
# 重みパラメータを初期化 w_m = np.random.uniform(-10.0, 10.0, size=M) # 重み付き和を計算 a_n = np.dot(phi_x_nm, w_m.reshape(-1, 1)).flatten() # 確認 print(w_m) print(a_n[:5])
[-1.89591752 -6.83587416]
[ -2.69317373 -70.97250416 -62.16439976 -52.65331586 -101.41488208]
変換した入力値とロジスティック回帰のパラメータ$\mathbf{w} = (w_0, w_1)^{\top}$の内積を計算します。
この例では、重みパラメータw_mの初期値を一様乱数で設定します。
重み付き和をロジスティックシグモイド関数で変換します。
# ロジスティックシグモイド関数による変換 y_n = sigmoid(a_n) # 確認 print(y_n[:5])
[6.33773623e-02 1.50325645e-31 1.00541235e-27 1.35817417e-23
9.03808311e-45]
始めに作成したsigmoid()で計算します。
出力$\mathbf{y} = \{y_1, \cdots, y_N\}$の各項は、$0 < y_n < 1$の値をとり、対応する入力$x_n$のクラスが1である確率の推定値を表します。
重みパラメータを更新します。
# 中間変数を計算 r_nn = np.diag(y_n) z_n = np.dot(phi_x_nm, w_m.reshape(-1, 1)).flatten() z_n -= np.dot(np.linalg.inv(r_nn), (y_n - t_n).reshape(-1, 1)).flatten() w_term_mm = phi_x_nm.T.dot(r_nn).dot(phi_x_nm) w_term_m1 = phi_x_nm.T.dot(r_nn).dot(z_n.reshape(-1, 1)) # パラメータを更新 w_m = np.dot(np.linalg.inv(w_term_mm), w_term_m1).flatten() # 確認 print(w_m)
[ 9.07711304 -3.29485906]
次の式でパラメータ$\mathbf{w}$を更新します。
以上が1回の試行で行う処理(計算)です。
・全体のコード
ニュートン-ラフソン法によりパラメータの最尤解を計算します。
多項式基底関数Phi_polynomial()またはシグモイド基底関数Phi_sigmoid()を関数phi()として複製して利用します。
また設定した基底関数に応じて、閾値用の関数もthreshold()として複製します。
# 試行回数を指定 max_iter = 100 # 基底関数の数を指定:(固定) M = 2 # 基底関数を指定 #phi = Phi_polynomial phi = Phi_sigmoid # 閾値計算関数を指定 #threshold = threshold_polynomial threshold = threshold_sigmoid # 基底関数により入力値を変換 phi_x_nm = phi(x_n, M) # 重みパラメータを初期化 w_m = np.random.uniform(-10.0, 10.0, size=M) # 推移の記録用の配列を作成 trace_w_arr = np.zeros((max_iter, M)) # 重みパラメータ trace_E_list = np.zeros(max_iter) # 負の対数尤度 # ニュートン-ラフソン法による推定 for i in range(max_iter): # 重み付き和を計算 a_n = np.dot(phi_x_nm, w_m.reshape(-1, 1)).flatten() # ロジスティックシグモイド関数による変換 y_n = sigmoid(a_n) # 中間変数を計算 r_nn = np.diag(y_n) z_n = np.dot(phi_x_nm, w_m.reshape(-1, 1)).flatten() z_n -= np.dot(np.linalg.inv(r_nn), (y_n - t_n).reshape(-1, 1)).flatten() w_term_mm = phi_x_nm.T.dot(r_nn).dot(phi_x_nm) w_term_m1 = phi_x_nm.T.dot(r_nn).dot(z_n.reshape(-1, 1)) # パラメータを更新 w_m = np.dot(np.linalg.inv(w_term_mm), w_term_m1).flatten() # 負の対数尤度関数を計算 y_n = sigmoid(np.dot(phi_x_nm, w_m.reshape(-1, 1)).flatten()) E_val = -np.sum(t_n * np.log(y_n) + (1.0 - t_n) * np.log(1.0 - y_n)) # 値を記録 trace_w_arr[i] = w_m.copy() trace_E_list[i] = E_val
試行回数max_iterを指定して、重みパラメータw_mの値を繰り返し更新します。
また、推移の確認用にパラメータをtrace_w_arrに、負の対数尤度(交差エントロピー誤差)をtrace_E_listに格納していきます。
交差エントロピー誤差は、次の式で計算します。
計算に利用するy_nは、更新したパラメータw_mを使って再計算しています(y_nを2回計算しており明らかに非効率ですが、推定の流れの分かりやすさを優先しました)。誤差は、学習の推移を確認するためのもので、推定には必要ありません。
重みパラメータの初期値によっては(?)、z_nにおける逆行列の計算、E_valにおける対数の計算でエラーになることがあります。
・推定結果の可視化
推定結果と収束過程をグラフで確認します。
推定したパラメータを使って回帰曲線を計算します。
# 作図用のxの点を作成 x_vals = np.linspace(np.min(x_n) - 1.0, np.max(x_n) + 1.0, num=200) # 推定した回帰曲線を計算 phi_x_vals = phi(x_vals, M, x_n) # シグモイド基底関数の場合 a_vals = np.dot(phi_x_vals, w_m.reshape(-1, 1)).flatten() y_vals = sigmoid(a_vals)
x軸の値を作成してx_valsとします。
x_valsの各要素に対して次の計算を行い、x軸の値ごとにクラス1となる確率(y軸の値)を求めます。
ただし、x_valsの全ての要素を一度に処理するために$\boldsymbol{\Phi} \mathbf{w}_{\mathrm{Logistic}}$で計算します。
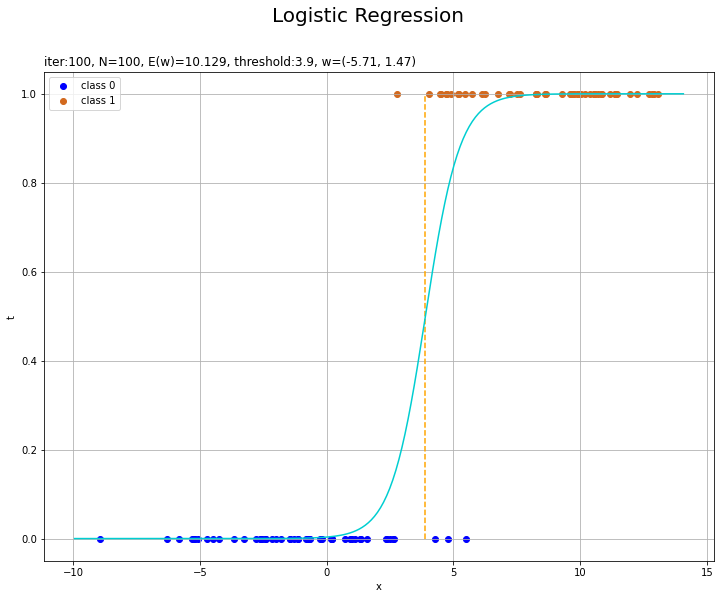
回帰曲線を作図します。
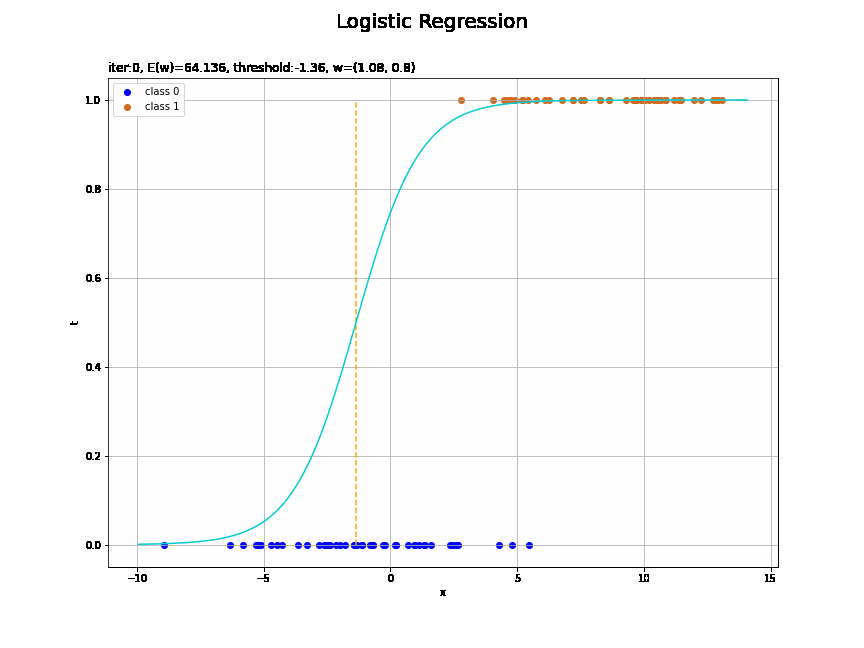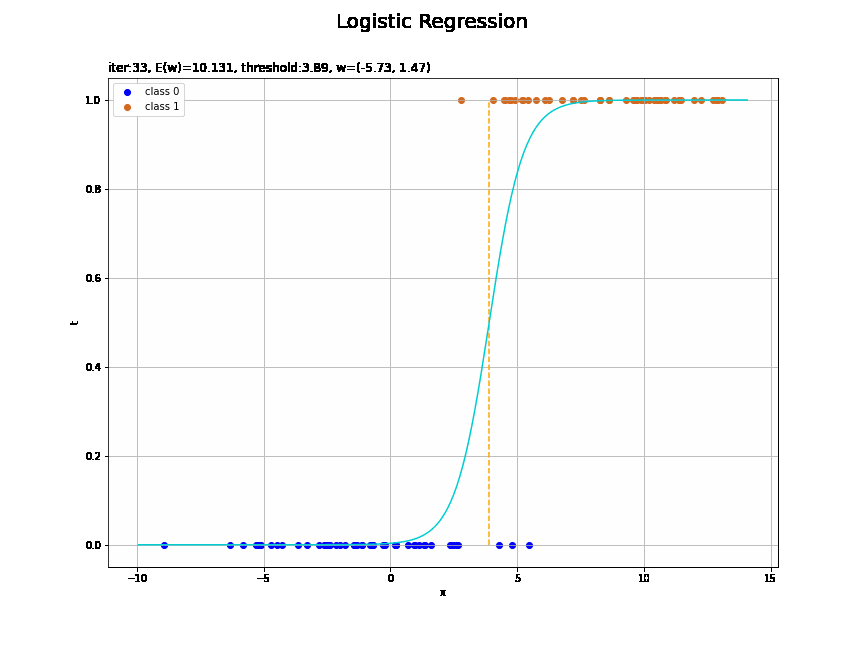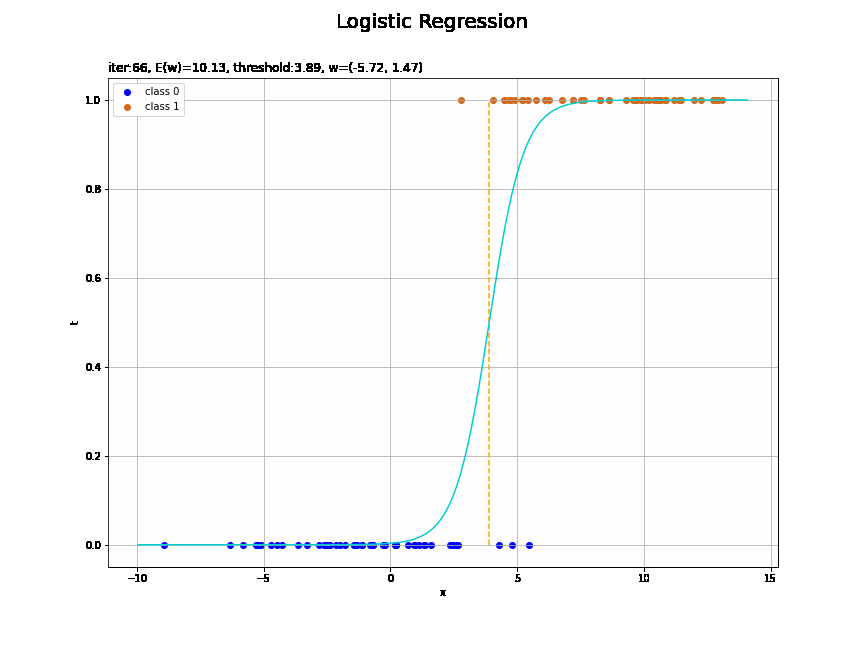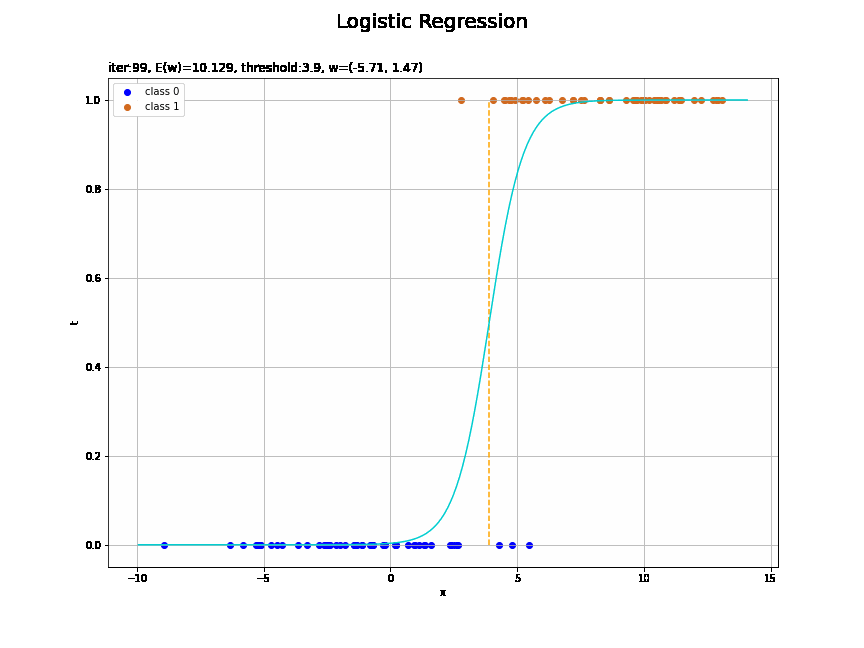
# ロジスティック回帰による回帰曲線を作図 plt.figure(figsize=(12, 9)) plt.scatter(x=x_n[t_n==0], y=np.repeat(0.0, np.sum(t_n==0)), color='blue', label='class 0') # クラス0の観測データ plt.scatter(x=x_n[t_n==1], y=np.repeat(1.0, np.sum(t_n==1)), color='chocolate', label='class 1') # クラス1の観測データ plt.plot(x_vals, y_vals, color='darkturquoise') # 回帰曲線 plt.vlines(x=threshold(w_m, x_n), ymin=0.0, ymax=1.0, color='orange', linestyle='--') # 閾値 plt.xlabel('x') plt.ylabel('t') plt.suptitle('Logistic Regression', fontsize=20) plt.title('iter:' + str(max_iter) + ', N=' + str(N) + ', E(w)=' + str(np.round(E_val, 3)) + ', threshold:' + str(np.round(threshold(w_m, x_n), 2)) + ', w=(' + ', '.join([str(w) for w in np.round(w_m, 2)]) + ')', loc='left') plt.legend() plt.grid() plt.show()
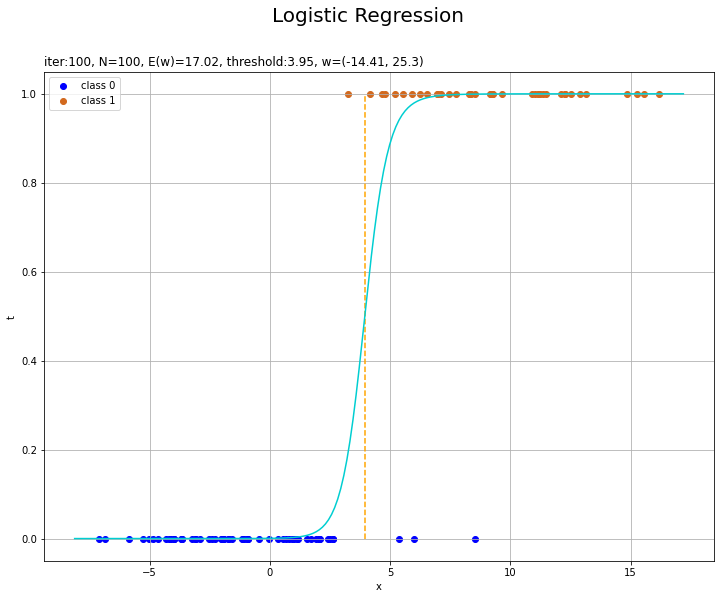
未知の入力$x_{*}$に対して、$y_{*} > 0.5$であればクラス1($t_{*} = 1$)、$y_{*} < 0.5$であればクラス0($t_{*} = 0$)に分類します。そこで、クラスの境界線(オレンジの破線)を引きます。
閾値となるx軸の値は、始めに作成したthreshold()で計算します。
収束する過程をアニメーションで確認します。
・作図コード(クリックで展開)
# 図を初期化 fig = plt.figure(figsize=(12, 9)) fig.suptitle('Logistic Regression', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目のパラメータを取得 w_m = trace_w_arr[i] E_val = trace_E_list[i] # i回目の回帰曲線を計算 a_vals = np.dot(phi_x_vals, w_m.reshape(-1, 1)).flatten() y_vals = sigmoid(a_vals) # ロジスティック回帰による回帰曲線を作図 plt.scatter(x=x_n[t_n==0], y=np.repeat(0.0, np.sum(t_n==0)), color='blue', label='class 0') # クラス0の観測データ plt.scatter(x=x_n[t_n==1], y=np.repeat(1.0, np.sum(t_n==1)), color='chocolate', label='class 1') # クラス1の観測データ plt.plot(x_vals, y_vals, color='darkturquoise') # 回帰曲線 plt.vlines(x=threshold(w_m, x_n), ymin=0.0, ymax=1.0, color='orange', linestyle='--') # 閾値 plt.xlabel('x') plt.ylabel('t') plt.title('iter:' + str(i) + ', E(w)=' + str(np.round(E_val, 3)) + ', threshold:' + str(np.round(threshold(w_m, x_n), 2)) + ', w=(' + ', '.join([str(w) for w in np.round(w_m, 2)]) + ')', loc='left') plt.legend() plt.grid() # gif画像を作成 anime_logistic = FuncAnimation(fig, update, frames=max_iter, interval=100) # gif画像を保存 anime_logistic.save('ch4_3_2_LogisticRegression1D.gif')
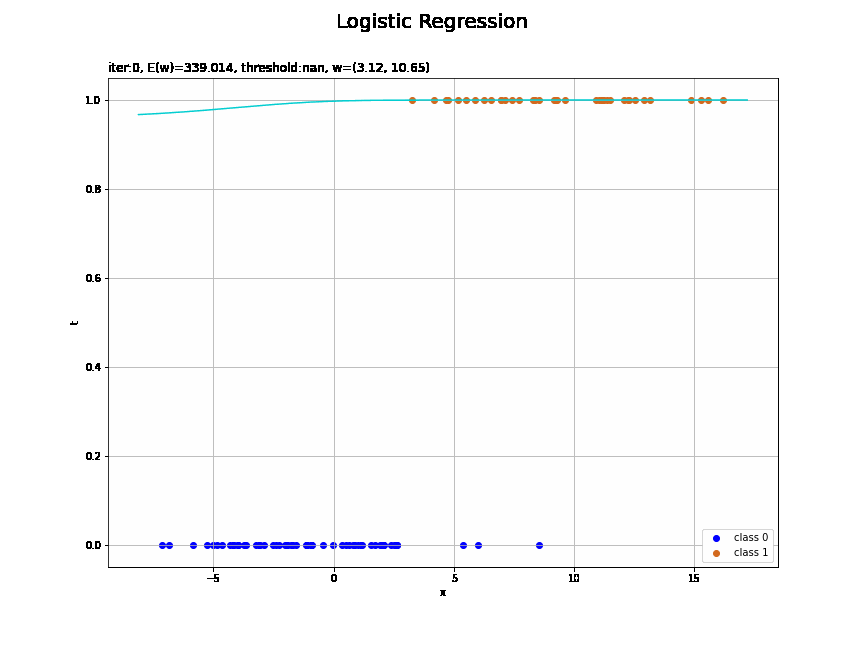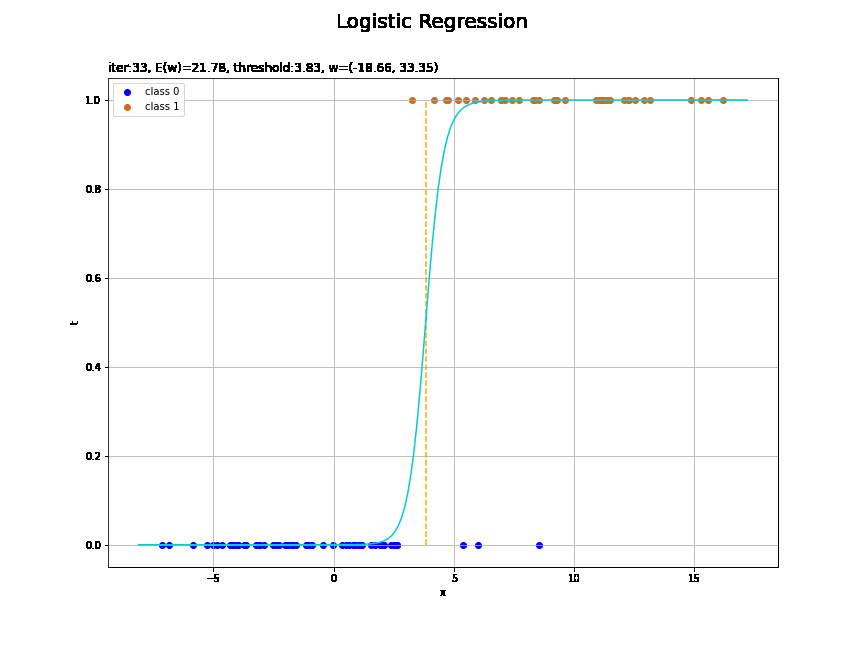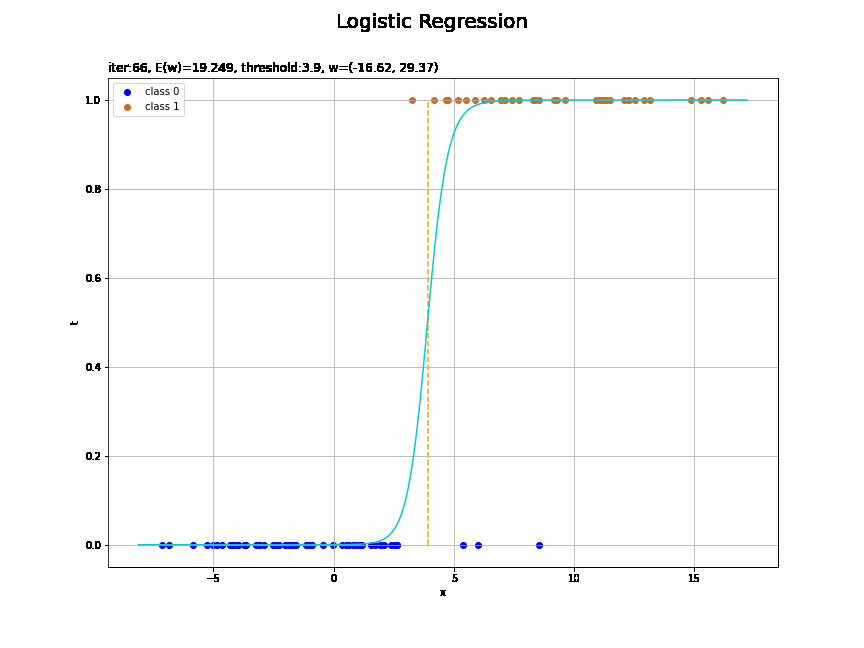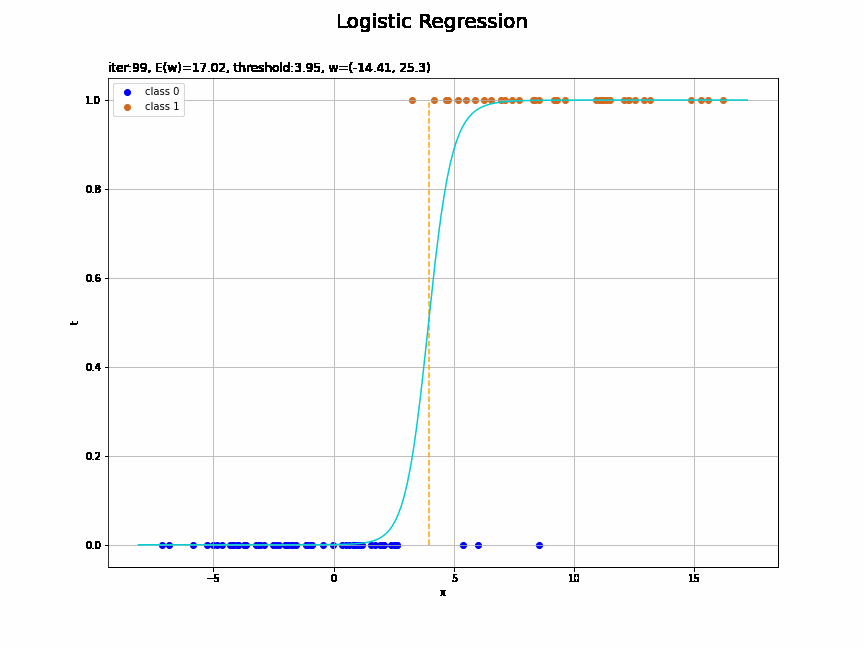
徐々にデータに適合していくのを確認できます。
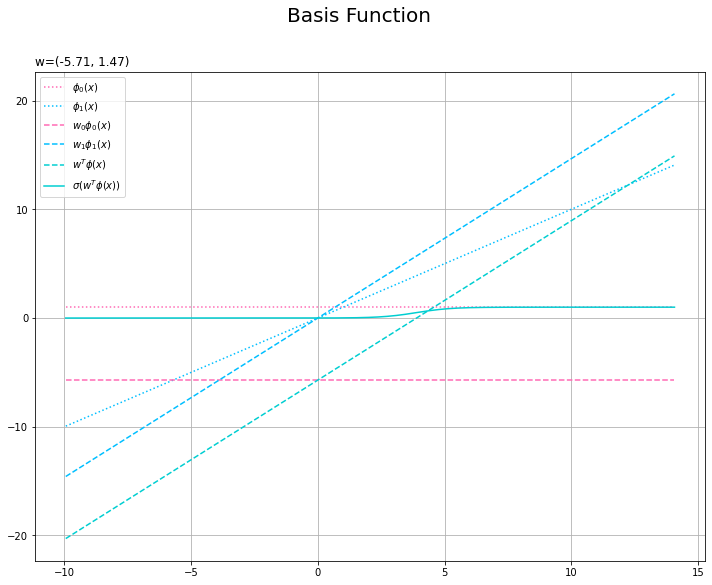
基底関数と重みパラメータの関係を確認します。基底関数ごとに対応するパラメータで重み付けしてグラフを描画します。
# 基底関数ごとに重み付け weight_phi_x_vals = w_m * phi_x_vals # 重み付き基底関数を作図 plt.figure(figsize=(12, 9)) plt.plot(x_vals, phi_x_vals[:, 0], color='hotpink', linestyle=':', label='$\phi_0(x)$') # 0番目の基底関数 plt.plot(x_vals, phi_x_vals[:, 1], color='deepskyblue', linestyle=':', label='$\phi_1(x)$') # 1番目の基底関数 plt.plot(x_vals, weight_phi_x_vals[:, 0], color='hotpink', linestyle='--', label='$w_0 \phi_0(x)$') # 0番目の重み付き基底関数 plt.plot(x_vals, weight_phi_x_vals[:, 1], color='deepskyblue', linestyle='--', label='$w_1 \phi_1(x)$') # 1番目の重み付き基底関数 plt.plot(x_vals, a_vals, color='darkturquoise', linestyle='--', label='$w^T \phi(x)$') # 重み付き和 plt.plot(x_vals, y_vals, color='darkturquoise', label='$\sigma(w^T \phi(x))$') # 回帰曲線 plt.suptitle('Basis Function', fontsize=20) plt.title('w=(' + ', '.join([str(w) for w in np.round(w_m, 2)]) + ')', loc='left') plt.legend() plt.grid() plt.show()
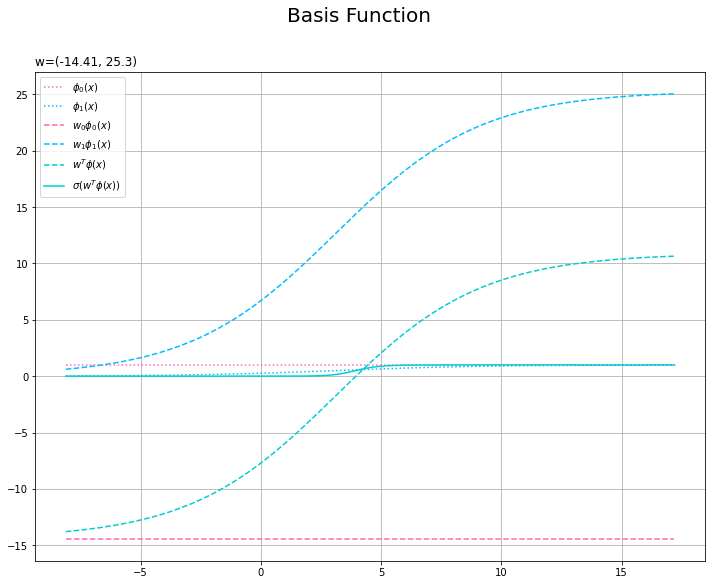
2つの基底関数が点線で、それぞれ重み付けしたのが破線です。$m = 0$の項はバイアスパラメータなので、$\phi_0(x) = 1$、$w_0 \phi_0(x) = w_0$であり、直線になります。
重み付けした基底関数(破線)をy軸方向に和をとったものが重み付き和(青緑色の破線)です。さらに、シグモイド関数によって0から1の値に変換しものが回帰曲線(青緑色の実線)です。
バイアスは一定で、シグモイド関数は単調増加するので、重み付き和も単調増加となります。よって$M = 2$の場合は、回帰曲線もシグモイド関数の形(単調増加するS字型)になります。$M > 2$の場合は、単調増加しない(y軸の値が上がったり下がったりする)曲線になります。
誤差の推移のグラフを作成します。
# 誤差の推移を作図 plt.figure(figsize=(12, 9)) plt.plot(np.arange(1, max_iter+1), trace_E_list) plt.xlabel('iteration') plt.ylabel('E(w)') plt.suptitle('Cross-Entropy Error', fontsize=20) plt.title('$E(w^{(' + str(max_iter) + ')})=' + str(np.round(trace_E_list[max_iter-1], 3)) + '$', loc='left') plt.grid() plt.show()
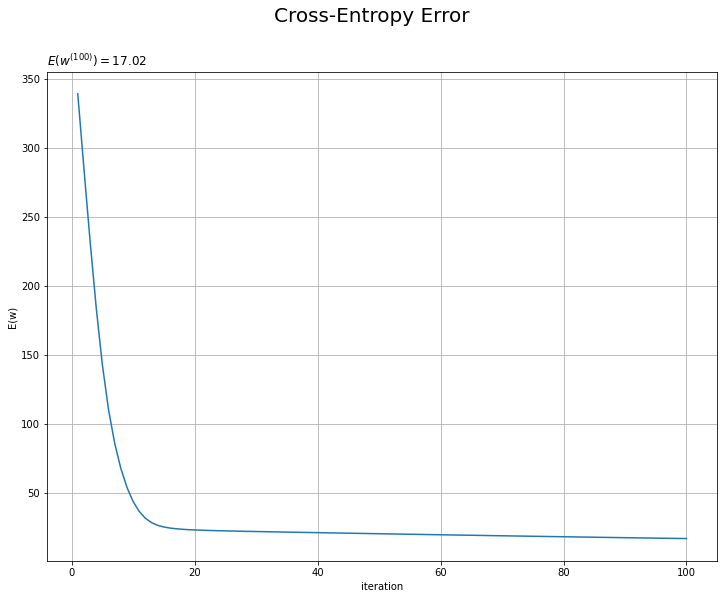
試行回数が増えるにしたがって誤差が小さくなっているのを確認できます。交差エントロピー誤差(負の対数尤度関数)の値が下がるのは、尤度関数の値が上がるのを意味します。
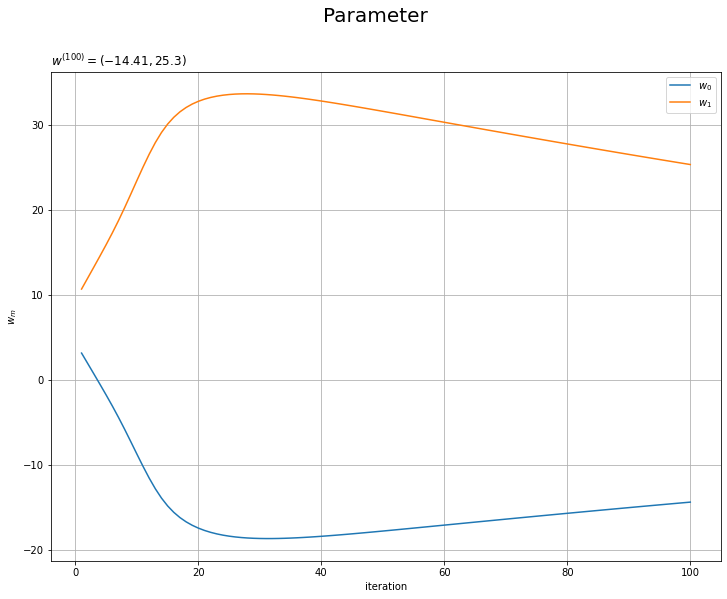
重みパラメータの推移のグラフを作成します。
# 重みの推移を作図 plt.figure(figsize=(12, 9)) for m in range(M): plt.plot(np.arange(1, max_iter+1), trace_w_arr[:, m], label='$w_' + str(m) + '$') plt.xlabel('iteration') plt.ylabel('$w_m$') plt.suptitle('Parameter', fontsize=20) plt.title('$w^{(' + str(max_iter) + ')}=(' + ', '.join([str(w) for w in np.round(trace_w_arr[max_iter-1], 2)]) + ')$', loc='left') plt.legend() plt.grid() plt.show()
最後に、誤差関数のグラフにパラメータの更新値の推移を重ねて確認します。
作図用の重みパラメータの点を作成します。
# 作図用のwの値を指定 w_vals = np.linspace(-100.0, 100.0, num=250) # 作図用のwの点を作成 W0, W1 = np.meshgrid(w_vals, w_vals) # 計算用のwの点を作成 w_im = np.stack([W0.flatten(), W1.flatten()], axis=1) # 確認 print(w_im[:5]) print(len(w_im))
[[-100. -100. ]
[ -99.19678715 -100. ]
[ -98.3935743 -100. ]
[ -97.59036145 -100. ]
[ -96.78714859 -100. ]]
62500
パラメータの各要素$w_k$の値を作成してw_valsとします。
w_valsの全ての組み合わせを持つように点$(w_0, w_1)$を作成しw_imとします。w_imの各行は$\mathbf{w}$がとり得る点に対応します。
w_imの行数はw_valsの2乗になります。処理が重い場合やグラフが粗い場合はw_valsを調整してください。
誤差関数を計算します。
# 誤差関数を計算 y_ni = sigmoid(np.dot(phi_x_nm, w_im.T)) E_i = - np.sum(np.log(y_ni.T**t_n) + np.log((1.0 - y_ni.T)**(1.0 - t_n)), axis=1) # 確認 print(E_i[:5])
[7394.75456674 7362.62605268 7330.49753863 7298.36902457 7266.24051051]
w_imの行ごとに$\mathbf{y} = \sigma(\boldsymbol{\Phi} \mathbf{w})$を計算し、さらに交差エントロピー誤差を計算します。ただし、全ての点$\mathbf{w}$に対して一度の処理で計算するため、推定時とは少し計算コードが変わっています。
回帰式のグラフでは、推定したパラメータ$\mathbf{w}_{\mathrm{Logistic}}$を固定し入力$x$の値を変更して計算しました。損失関数のグラフでは、入力値$\mathbf{x}$を固定しパラメータ$\mathbf{w}$の値を変更して計算します。
手元にある観測データでの誤差関数の等高線図に、パラメータの推移を重ねて描画します。
# 誤差関数を作図 plt.figure(figsize=(12, 9)) plt.scatter(trace_w_arr[:, 0], trace_w_arr[:, 1], label='$w^{(t)}$') # パラメータの推移 plt.contour(W0, W1, E_i.reshape(W0.shape)) # 誤差関数 #plt.contour(W0, W1, E_i.reshape(W0.shape), levels=np.linspace(0.0, 100.0, num=10)) # 誤差関数:(等高線を引く値を指定) plt.xlabel('$w_0$') plt.ylabel('$w_1$') plt.suptitle('Cross-Entropy Error', fontsize=20) plt.title('$E(w^{(' + str(max_iter) + ')})=' + str(np.round(trace_E_list[max_iter-1], 3)) + ', w^{(' + str(max_iter) + ')}=(' + ', '.join([str(w) for w in np.round(trace_w_arr[max_iter-1], 2)]) + ')$', loc='left') plt.colorbar(label='E(w)') plt.legend() plt.grid() plt.show()
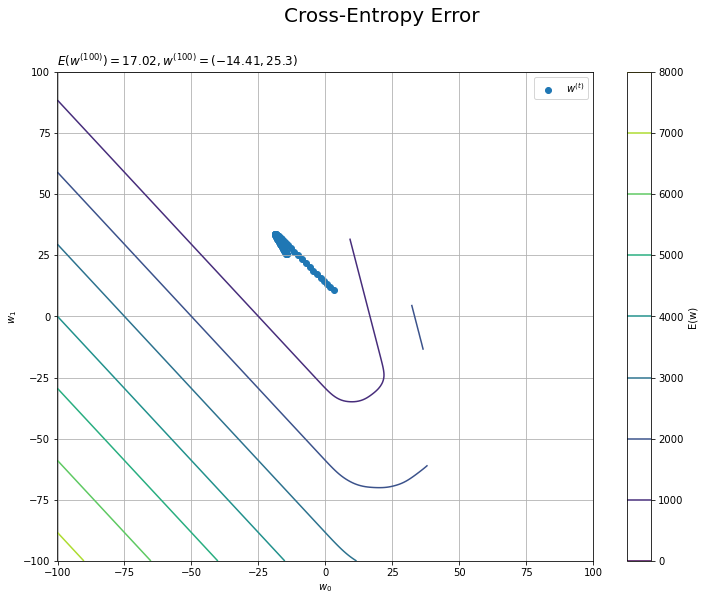
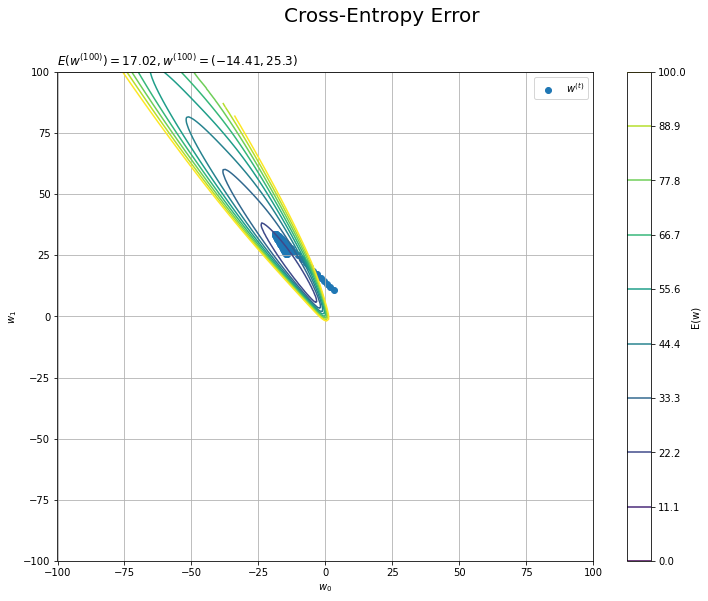
勾配を下るように値が更新されているのを確認できます。
重み付き基底関数のグラフを見ると、$w_1$が大きくなると水色の曲線が上方向に変化します(並行移動ではないです)。このとき、$w_0$が小さくなればピンク色の直線が下方向に変化するので、その和である青緑の曲線への影響は相殺されます。つまり、誤差関数への影響も緩和されます。
逆に、$w_0, w_1$の増減が同じだとモデルと誤差関数への影響は強くなります。このことが誤差関数の等高線の形(左上から右下に伸びる谷の形)からも分かります。
(なんで等高線が途中で切れるんだ?)
以上で、ロジスティック回帰の最尤推定を実装と結果の可視化ができました。
多項式基底関数を使った場合は次のようになります。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
いくつか実装は済んでいるのですが解説を付けて記事化するのに飽きてきて、別のシリーズを並行して始めてしまいました。なのでちょっと更新が滞り気味になっています。
【次節の内容】