はじめに
この記事は、「Rのカレンダー | Advent Calendar 2021 - Qiita」の13日目の記事です。
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、4.3.2項と4.3.3項の内容です。ニュートン法によるロジスティック回帰の最尤推定をR言語で実装します。
【数式読解編】
【前節の内容】
【他の節一覧】
【この節の内容】
4.3.2 ロジスティック回帰の実装
ニュートン-ラフソン法によるロジスティック回帰を実装します。
利用するパッケージを読み込みます。
# 4.3.2項で利用するパッケージ library(tidyverse)
・基底関数の準備
パラメータ推定に利用するロジスティックシグモイド関数とシグモイド基底関数を作成します。基底関数については3.1.0項を、基底関数と計画行列の実装については3.1.1項を参照してください。
ロジスティックシグモイド関数を作成します。
# ロジスティックシグモイド関数を作成 sigmoid <- function(x) { # ロジスティックシグモイド関数の計算 y <- 1 / (1 + exp(-x)) return(y) }
ロジスティックシグモイド関数は、次の式で定義されます。
シグモイド基底関数の計画行列を作成します。
# シグモイド基底関数の計画行列を作成 phi <- function(x_n) { # データを標準化 x_tilde_n <- (x_n - mean(x_n)) / sd(x_n) # マトリクスを初期化 y_n <- matrix(1, nrow = length(x_n), ncol = 2) # ロジスティックシグモイド関数による変換 y_n[, 2] <- sigmoid(x_tilde_n) return(y_n) }
計画行列は次の行列です。
$\phi_j(x)$は非線形変換を行う基底関数です。この例では、$M = 2$として、シグモイド基底関数を用います。ただし、$\phi_0(x) = 1$です。
またこの例では、シグモイド基底関数の計算を行う前に入力値を標準化しておきます(3.1.1項のように任意の値を指定した方がいいのかも?)。
3.1.1項で実装した関数を利用することもできます。その場合は、値が2のオブジェクトMを作成した上で、phi(x_n)をPhi(x_n, M)に置き換える必要があります。
クラスの境界線を引くのに利用する関数を作成します。この関数は推定自体には不要です。
# 閾値の計算関数を作成:(シグモイド基底関数用) threshold <- function(w_m, x_vals) { # 回帰式の逆関数 x_tilde <- log(- w_m[1] / sum(w_m)) # 標準化の逆関数 x <- x_tilde * sd(x_vals) + mean(x_vals) return(x) }
回帰式の逆関数となる計算を行います。
またこの例では標準化を行ったので、その逆関数の計算も行う必要があります。
詳しくは、推定結果の可視化で解説します。
・データの生成
人工的に観測データを作成します。
データ生成に関するパラメータを指定します。
# クラス割り当てのパラメータを指定:(クラス1となる確率) pi <- 0.4 # データ生成のパラメータを指定:(クラス0, クラス1) mu_k <- c(-1, 9) sigma_k <- c(3, 3)
クラス1($t_n = 1$)となる確率piを指定します。
各クラスの平均mu_kと標準偏差sigma_kを指定します。2値分類なのでクラス数$K = 2$です。
指定したパラメータに従って観測データを作成します。
# データ数を指定 N <- 100 # 真のクラスを生成 t_n <- rbinom(n = N, size = 1, prob = pi) # データを生成 x_n <- rnorm(n = N, mean = mu_k[t_n+1], sd = sigma_k[t_n+1])
データ数$N$を指定して、観測データ$\mathbf{t} = {t_1, \cdots, t_N}$、$\mathbf{x} = {x_1, \cdots, x_N}$を作成します。
$t_n$は$n$番目のデータのクラスを表し、$t_n = 0$であればクラス0、$t_n = 1$であればクラス1とします。
$x_n$は$n$番目のデータの値(入力値)です。
$\mathbf{t}$はベルヌーイ分布に従い生成します。ベルヌーイ分布に従う乱数は、二項分布に従う乱数生成関数rbinom()にsize = 1を指定することで生成できます。
$\mathbf{x}$はガウス分布に従い生成します。ガウス分布に従う乱数は、rnorm()で生成できます。meanは平均、sdは標準偏差の引数です。データごとに割り当てられたクラスに応じてパラメータを指定する必要があります。
クラスに対応したパラメータの値は、次のようにして取り出しています。
# パラメータの取得 t_n[1:5] mu_k[t_n+1][1:5]
## [1] 1 0 0 1 0 ## [1] 9 -1 -1 9 -1
t_nには各データのクラスが保存されています。
クラス0のパラメータはmu_k[1], sigma_k[1]、クラス1のパラメータはmu_k[2], sigma_k[2]なので、t_nに1を足すことでクラスとインデックスを対応させます。
作成した観測データを作図用にデータフレームに格納します。
# 観測データをデータフレームに格納 data_df <- tidyr::tibble( x = x_n, t = t_n, class = as.factor(t_n) ) # 確認 head(data_df)
## # A tibble: 6 x 3 ## x t class ## <dbl> <int> <fct> ## 1 13.6 1 1 ## 2 -0.745 0 0 ## 3 -2.69 0 0 ## 4 7.23 1 1 ## 5 -0.598 0 0 ## 6 -1.44 0 0
観測データをヒストグラムで確認します。
# 観測データのヒストグラムを作成 ggplot(data = data_df, aes(x = x, fill = class)) + geom_histogram() + labs(title = "Observation Data", subtitle = paste0("pi=", pi, ", N0=", sum(t_n == 0), ", N1=", sum(t_n == 1)))
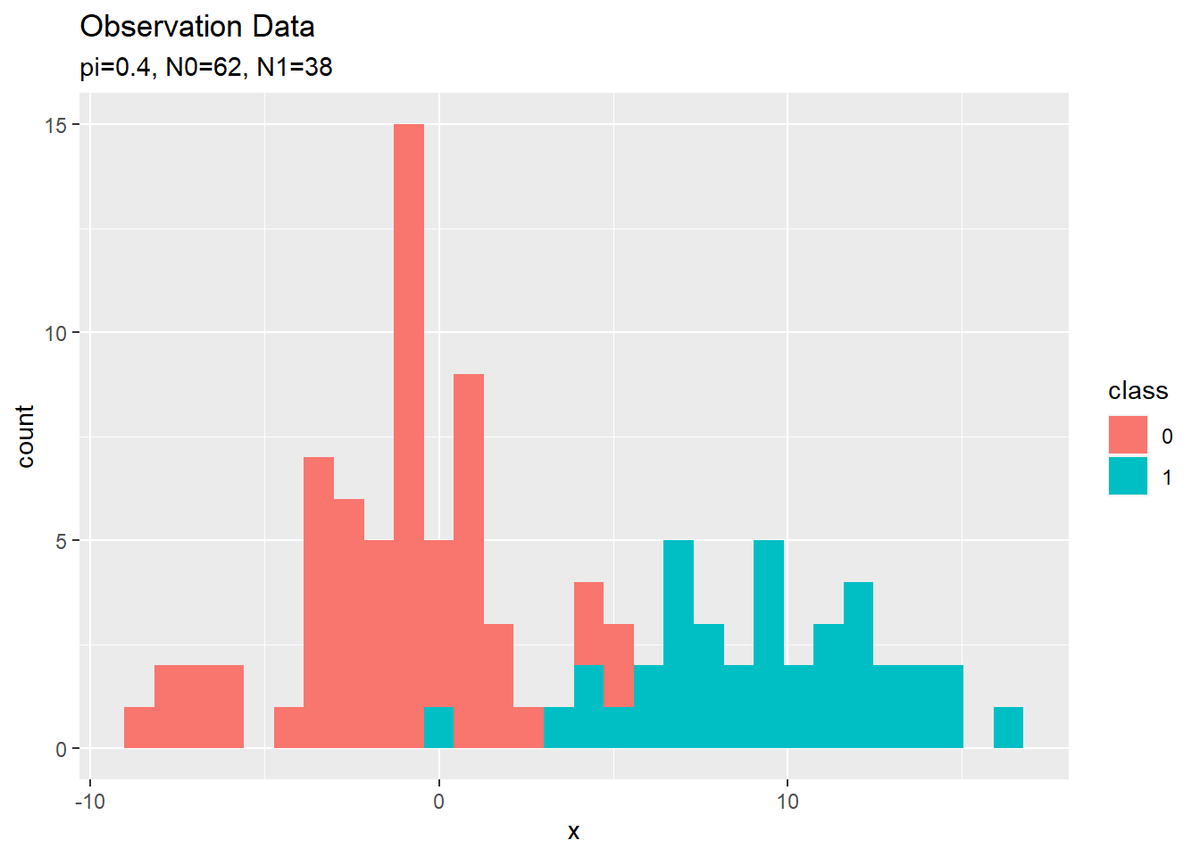
(ロジスティック回帰用のデータがこんな感じでいいのかはよく分かっていません。何か変なら教えてください。)
・ニュートン-ラフソン法による最尤推定
ニュートン-ラフソン法によりロジスティック回帰のパラメータの最尤解を求めます。
・処理の解説
まずは、繰り返し行う個々の処理を解説します。次に、それらをまとめて推定を行います。
計画行列の計算を行い入力値を変換します。
# 基底関数による変換 phi_x_nm <- phi(x_n) # 確認 phi_x_nm[1:5, ]
## [,1] [,2] ## [1,] 1 0.8598586 ## [2,] 1 0.3612318 ## [3,] 1 0.2906225 ## [4,] 1 0.6796877 ## [5,] 1 0.3668483
始めに作成したphi()で計算します。
変換した入力値の重み付き和を計算します。
# パラメータを初期化 w_logistic_m <- runif(n = 2, min = -10, max = 10) # 重み付き和を計算 a_n <- phi_x_nm %*% w_logistic_m %>% as.vector() # 確認 w_logistic_m a_n[1:5]
## [1] 6.659114 -7.965242 ## [1] -0.1898676 3.7818158 4.3442357 1.2452375 3.7370787
変換した入力値とロジスティック回帰のパラメータ$\mathbf{w} = (w_0, w_1)^{\top}$の内積を計算します。
この例では、重みパラメータw_logistic_mの初期値を一様乱数で設定します。
重み付き和をロジスティックシグモイド関数で変換します。
# ロジスティックシグモイド関数による変換 y_n <- sigmoid(a_n) # 確認 y_n[1:5]
## [1] 0.4526752 0.9777261 0.9871849 0.7764744 0.9767308
始めに作成したsigmoid()で計算します。
出力$\mathbf{y} = {y_1, \cdots, y_N}$の各項は、$0 < y_n < 1$の値をとり、対応する入力$x_n$のクラスが1である確率の推定値を表します。
重みパラメータを更新します。
# 中間変数を計算 r_nn <- diag(y_n) z_n <- phi_x_nm %*% w_logistic_m - solve(r_nn) %*% (y_n - t_n) %>% as.vector() # パラメータを更新 w_logistic_m <- solve(t(phi_x_nm) %*% r_nn %*% phi_x_nm) %*% t(phi_x_nm) %*% r_nn %*% z_n %>% as.vector() # 確認 w_logistic_m
## [1] 4.637776 -4.729257
次の式でパラメータ$\mathbf{w}$を更新します。
以上が1回の試行で行う処理(計算)です。
・全体のコード
ニュートン-ラフソン法によりパラメータの最尤解を計算します。
# 繰り返し回数を指定 max_iter <- 100 # 基底関数による変換 phi_x_nm <- phi(x_n) # パラメータを初期化 w_logistic_m <- runif(n = 2, min = -10, max = 10) # ニュートン-ラフソン法による推定 trace_w_mat <- t(w_logistic_m) # パラメータ trace_E_vec <- NULL # 負の対数尤度 for(i in 1:max_iter) { # 重み付き和を計算 a_n <- phi_x_nm %*% w_logistic_m %>% as.vector() # ロジスティックシグモイド関数による変換 y_n <- sigmoid(a_n) # 中間変数を計算 r_nn <- diag(y_n) z_n <- phi_x_nm %*% w_logistic_m - solve(r_nn) %*% (y_n - t_n) %>% as.vector() # パラメータを更新 w_logistic_m <- solve(t(phi_x_nm) %*% r_nn %*% phi_x_nm) %*% t(phi_x_nm) %*% r_nn %*% z_n %>% as.vector() # 推移を記録 trace_w_mat <- rbind(trace_w_mat, w_logistic_m) # パラメータ trace_E_vec <- c(trace_E_vec, - sum(t_n * log(y_n) + (1 - t_n) * log(1 - y_n))) # 負の対数尤度 }
試行回数max_iterを指定して、パラメータw_logistic_mの値を繰り返し更新します。
また、推移の確認用にパラメータをtrace_w_matに、交差エントロピー誤差をtrace_E_vecに格納していきます。ただし誤差については、更新前のパラメータで求めたy_nを使って計算するので、初期値を含み最後(max_iter回目)の値を含みません。
交差エントロピー誤差(負の対数尤度関数)は、次の式で計算します。
・推定結果の可視化
推定結果と収束過程をグラフで確認します。
推定したパラメータを使って回帰曲線を計算します。
# x軸の範囲を指定 x_vals <- seq(min(x_n) - 10, max(x_n) + 10, by = 0.01) # 推定したパラメータによるモデルを計算 logistic_df <- tidyr::tibble( x = x_vals, # 入力値 a = phi(x_vals) %*% w_logistic_m %>% as.vector(), # 変換した入力の重み付き和 y = sigmoid(a) # 推定した確率値 ) # 確認 head(logistic_df)
head(logistic_df) ## # A tibble: 6 x 3 ## x a y ## <dbl> <dbl> <dbl> ## 1 -18.6 -11.6 0.00000876 ## 2 -18.6 -11.6 0.00000879 ## 3 -18.6 -11.6 0.00000881 ## 4 -18.6 -11.6 0.00000884 ## 5 -18.6 -11.6 0.00000886 ## 6 -18.5 -11.6 0.00000889
x軸の値を作成してx_valsとします。
x_valsの各要素に対して次の計算を行い、x軸の値ごとにクラス1となる確率(y軸の値)を求めます。
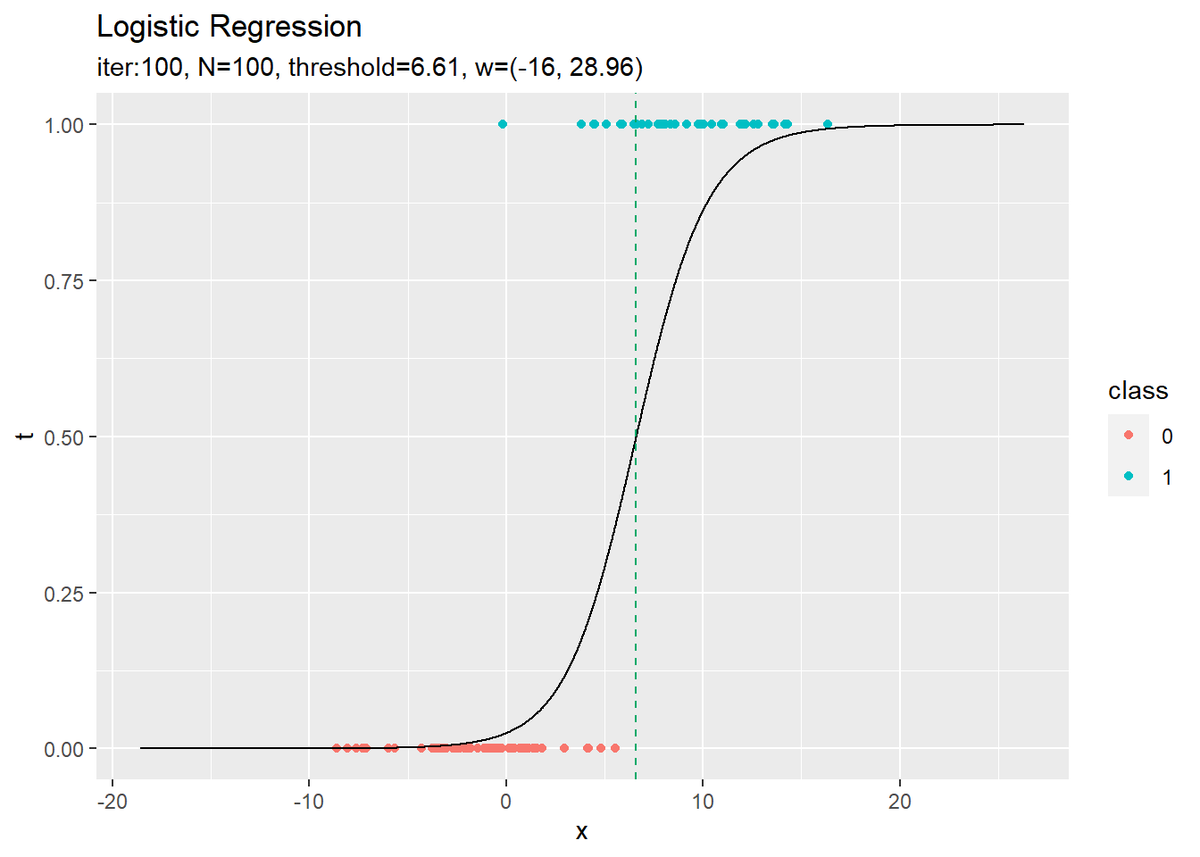
回帰曲線を作図します。
# 推定したパラメータによるモデルを作図 ggplot() + geom_point(data = data_df, aes(x = x, y = t, color = class)) + # 観測データ geom_line(data = logistic_df, aes(x = x, y = y)) + # 推定したモデル geom_vline(xintercept = threshold(w_logistic_m, x_vals), color = "#00A968", linetype = "dashed") + # 閾値 labs(title = "Logistic Regression", subtitle = paste0("iter:", max_iter, ", N=", N, ", threshold=", round(threshold(w_logistic_m, x_vals), 2), ", w=(", paste0(round(w_logistic_m, 2), collapse = ", "), ")"))
未知の入力$x_{*}$に対して、$y_{*} > 0.5$であればクラス1($t_{*} = 1$)、$y_{*} < 0.5$であればクラス0($t_{*} = 0$)に分類します。そこで、クラスの境界線を引きます。
$y = 0.5$となる$x$の値は、始めに作成した関数threshold()で計算します。
・計算式の導出(クリックで展開)
$y = 0.5$となる$x$の計算式を導出します。
「出力(クラス1となる確率)$y = 0.5$」を「非線形変換を行った入力の重み付き和$a$」について解きます。
さらに、「$y = 0.5$となる重み付き和$a = 0$」を「入力$x$」について解きます。ただし、この例で利用している$M = 2$のシグモイド基底関数の場合です。
$y = 0.5$となる$x$の計算式が得られました。つまり、$x_{*} > \log (- \frac{w_0}{w_0 + w_1})$であればクラス1に、$x_{*} < \log (- \frac{w_0}{w_0 + w_1})$であればクラス0に分類します。
誤差の推移のグラフを作成します。
# 誤差の推移をデータフレームに格納 E_df <- tidyr::tibble( iteration = 0:(max_iter - 1), # 試行回数 E = trace_E_vec # 負の対数尤度 ) # 誤差の推移を作図 ggplot(E_df, aes(x = iteration, y = E)) + geom_line() + labs(title = "Cross-Entropy Error", y = expression(E(w)))
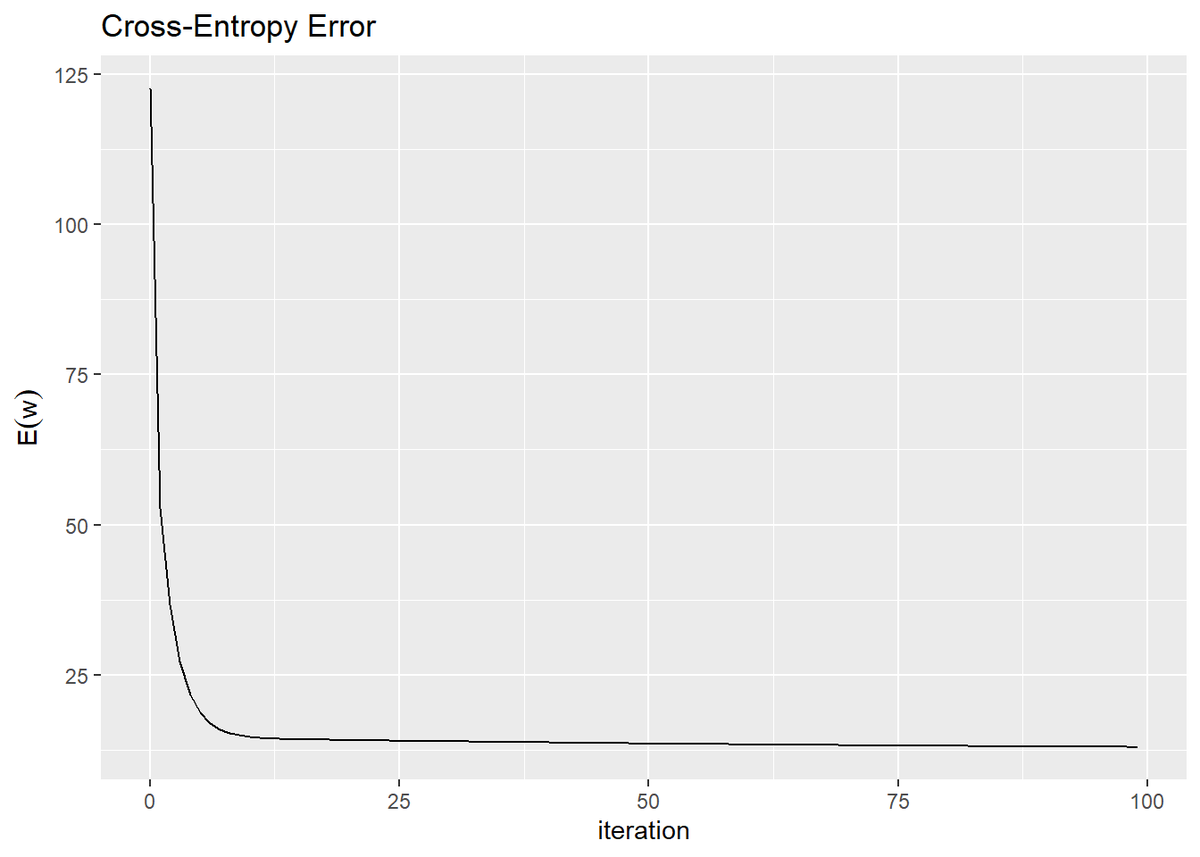
試行回数が増えるにしたがって誤差が小さくなっているのを確認できます。交差エントロピー誤差(負の対数尤度関数)の値が下がるのは、尤度関数の値が上がるのを意味します。
基底関数と重みパラメータの関係をグラフで確認します。
・作図コード(クリックで展開)
基底関数ごとに対応するパラメータで重み付けして、データフレームに格納します。
# M個の基底関数を重み付け phi_w_df <- t(w_logistic_m * t(phi(x_vals))) %>% # 基底関数ごとに重み付け dplyr::as_tibble(.name_repair = "unique") %>% # データフレームに変換 dplyr::rename_with(.fn = ~paste0("m=", 0:1), .cols = 1:2) %>% # 列名を付与 cbind(x = x_vals) %>% # x軸の値を結合 tidyr::pivot_longer( cols = -x, names_to = "phi", names_transform = list(phi = as.factor), values_to = "phi_x" ) # long型に変換 # 確認 head(phi_w_df)
## # A tibble: 6 x 3 ## x phi phi_x ## <dbl> <fct> <dbl> ## 1 -18.6 m=0 -16.0 ## 2 -18.6 m=1 4.36 ## 3 -18.6 m=0 -16.0 ## 4 -18.6 m=1 4.36 ## 5 -18.6 m=0 -16.0 ## 6 -18.6 m=1 4.36
重み付けした基底関数と、重み付き和、回帰曲線を描画します。
# 重み付けしたM個の基底関数を作図 ggplot() + geom_line(data = logistic_df, aes(x = x, y = y), color = "red") + # 推定したモデル geom_line(data = logistic_df, aes(x = x, y = a), color = "orange", size = 1) + # 重み付き和 geom_line(data = phi_w_df, aes(x = x, y = phi_x, color = phi), linetype = "dashed", size = 1) + # 基底関数 geom_point(data = data_df, aes(x = x, y = t)) + # 観測データ #ylim(c(-10, 10)) + # y軸の表示範囲 labs(title = expression(a == w[0] + w[1] * phi[1](x)), subtitle = paste0("w=(", paste0(round(w_logistic_m, 2), collapse = ", "), ")"), x = "x", y = "a", color = expression(phi[m](x)))
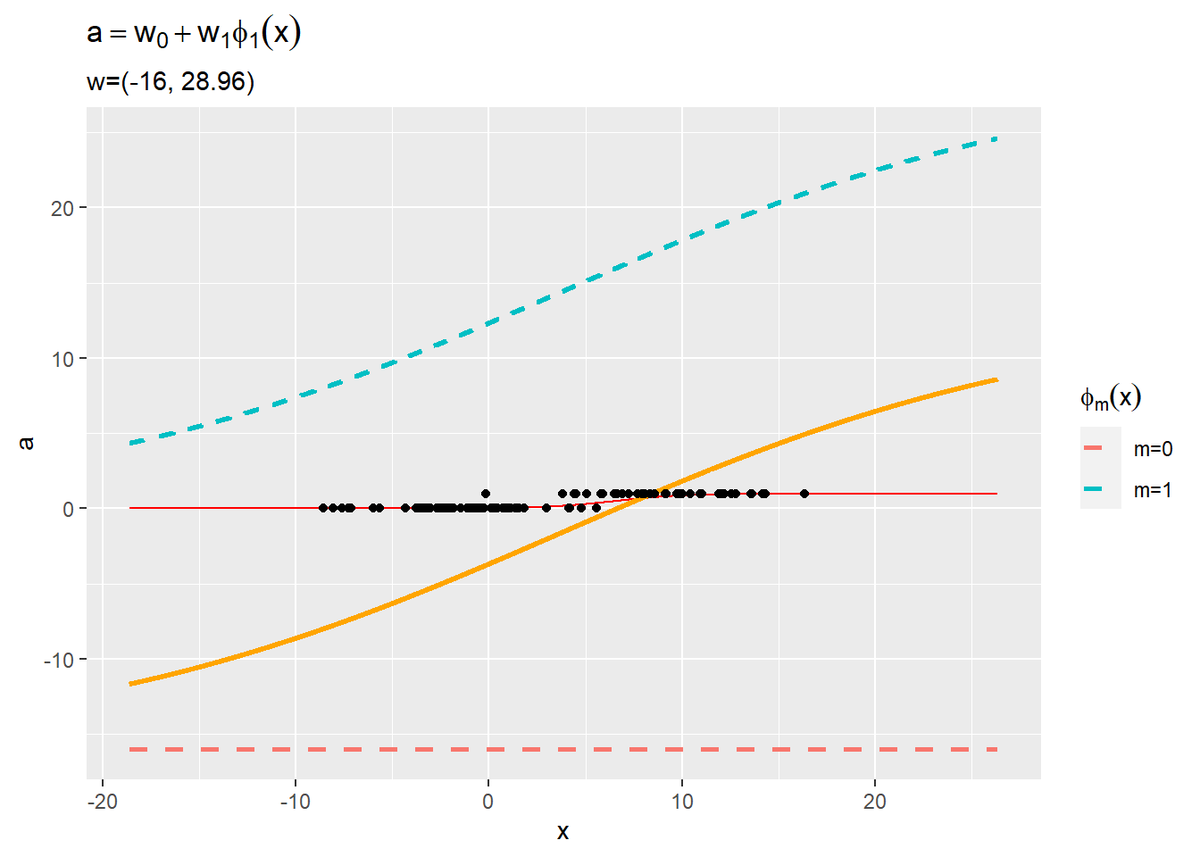
2つの基底関数(破線)をy軸方向に和をとったものが重み付き和(オレンジ色の実線)です。さらに、シグモイド関数によって0から1の値に変換しものが回帰曲線(赤色の実線)です。
誤差関数のグラフにパラメータの更新値の推移を重ねて確認します。
・作図コード(クリックで展開)
誤差関数を計算します。
# 作図用のwの範囲を指定 w_vals <- seq(-100, 100, by = 1) # 作図用のwの点を作成 w_im <- expand.grid(w_vals, w_vals) %>% as.matrix() # 確認 head(w_im) tail(w_im)
## Var1 Var2 ## [1,] -100 -100 ## [2,] -99 -100 ## [3,] -98 -100 ## [4,] -97 -100 ## [5,] -96 -100 ## [6,] -95 -100 ## Var1 Var2 ## [40396,] 95 100 ## [40397,] 96 100 ## [40398,] 97 100 ## [40399,] 98 100 ## [40400,] 99 100 ## [40401,] 100 100
length(w_vals) nrow(w_im)
## [1] 201 ## [1] 40401
パラメータの各要素$w_k$の値を作成してw_valsとします。
w_valsの全ての組み合わせを持つように点$(w_0, w_1)$を作成しw_imとします。w_imの各行は$\mathbf{w}$がとり得る点に対応します。
w_imの行数はw_valsの2乗になります。処理が重い場合はw_valsを調整してください。
誤差関数を計算します。
# 出力を計算 y_ni <- sigmoid(phi_x_nm %*% t(w_im)) # 交差エントロピー誤差を計算 E_i <- - colSums(log(y_ni^t_n) + log((1 - y_ni)^(1 - t_n))) # 誤差関数をデータフレームに格納 w_df <- tidyr::tibble( w_0 = w_im[, 1], # x軸の値 w_1 = w_im[, 2], # y軸の値 E = E_i ) # 確認 head(w_df)
## # A tibble: 6 x 3 ## w_0 w_1 E ## <dbl> <dbl> <dbl> ## 1 -100 -100 6588. ## 2 -99 -100 6550. ## 3 -98 -100 6512. ## 4 -97 -100 6474. ## 5 -96 -100 6436. ## 6 -95 -100 6398.
w_imの行ごとに$\mathbf{y} = \sigma(\boldsymbol{\Phi}^{\top} \mathbf{w})$を計算し、さらに交差エントロピー誤差を計算します。ただし、nrow(w_im)個の点$\mathbf{w}$に対して一度の処理で計算するため、推定時とは少し計算コードが変わっています。
回帰式のグラフでは、推定したパラメータ$\mathbf{w}_{\mathrm{Logistic}}$を固定し入力$x$の値を変更して計算しました。損失関数のグラフでは、入力値${x_1, \cdots, x_N}$を固定しパラメータ$\mathbf{w}$の値を変更して計算します。
パラメータの更新値の推移をデータフレームに格納します。
# パラメータの推移をデータフレームに格納 trace_w_df <- trace_w_mat %>% dplyr::as_tibble() %>% # データフレームに変換 dplyr::rename_with(.fn = ~paste0("w_", 0:1), .cols = 1:2) %>% # 列名を付与 dplyr::mutate(iteration = 0:max_iter) # 試行回数を結合 # 確認 head(trace_w_df)
## # A tibble: 6 x 3 ## w_0 w_1 iteration ## <dbl> <dbl> <int> ## 1 9.85 5.34 0 ## 2 8.27 7.40 1 ## 3 6.70 9.45 2 ## 4 5.13 11.5 3 ## 5 3.56 13.6 4 ## 6 1.99 15.6 5
(これの記録を取り忘れたので後で追記しました…なので前後とは繋がりのない値です。)
今手元にある観測データでの誤差関数の等高線図に、パラメータの推移を重ねて描画します。
# パラメータの推移を作図 ggplot() + geom_contour(data = w_df, aes(x = w_0, y = w_1, z = E, color = ..level..)) + # 誤差関数 #geom_contour(data = w_df, aes(x = w_0, y = w_1, z = E, color = ..level..), breaks = seq(0, 100, length.out = 10)) + # 誤差関数:(等高線を引く値を指定) geom_point(data = trace_w_df, aes(x = w_0, y = w_1), color = "#00A968") + # パラメータの推移:(点) geom_line(data = trace_w_df, aes(x = w_0, y = w_1), color = "#00A968") + # パラメータの推移:(線) labs(title = "Cross-Entropy Error", subtitle = paste0("iter:", max_iter, ", N=", N), x = expression(w[0]), y = expression(w[1]), color = expression(E(w)))
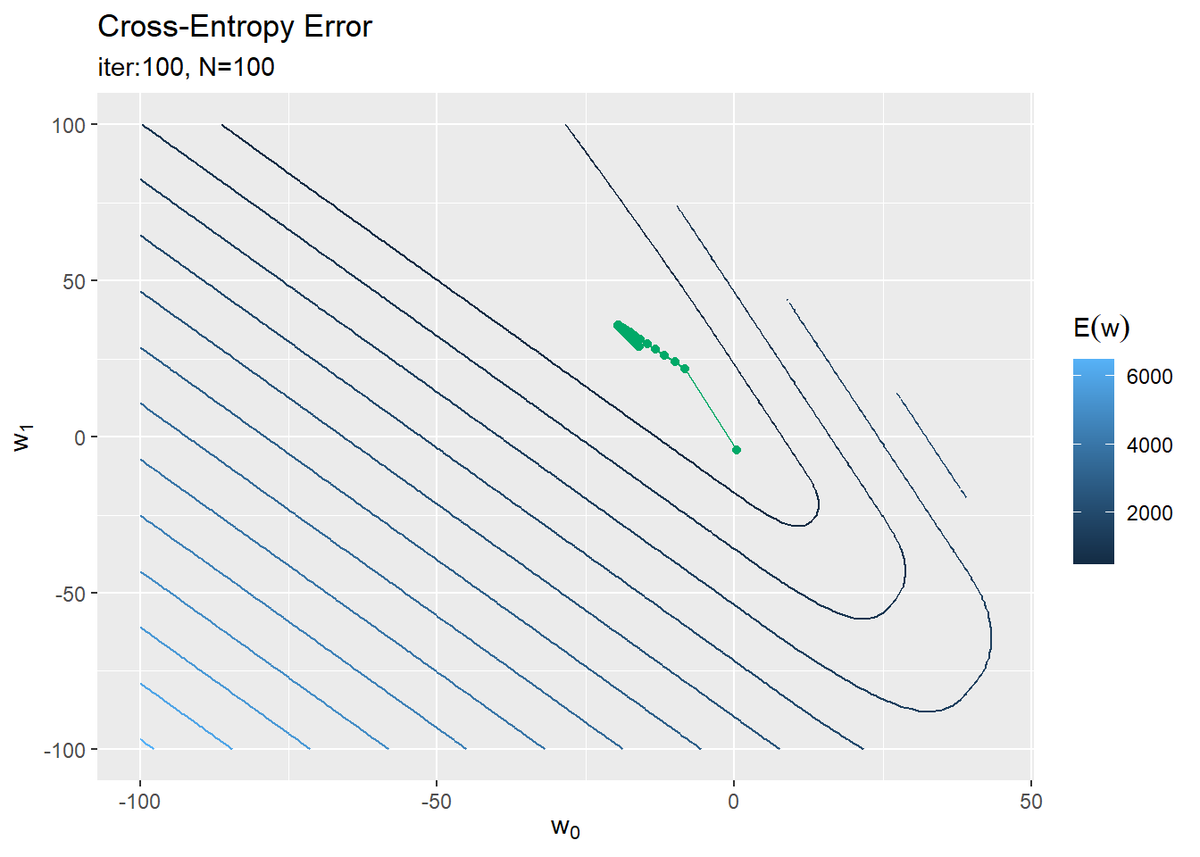
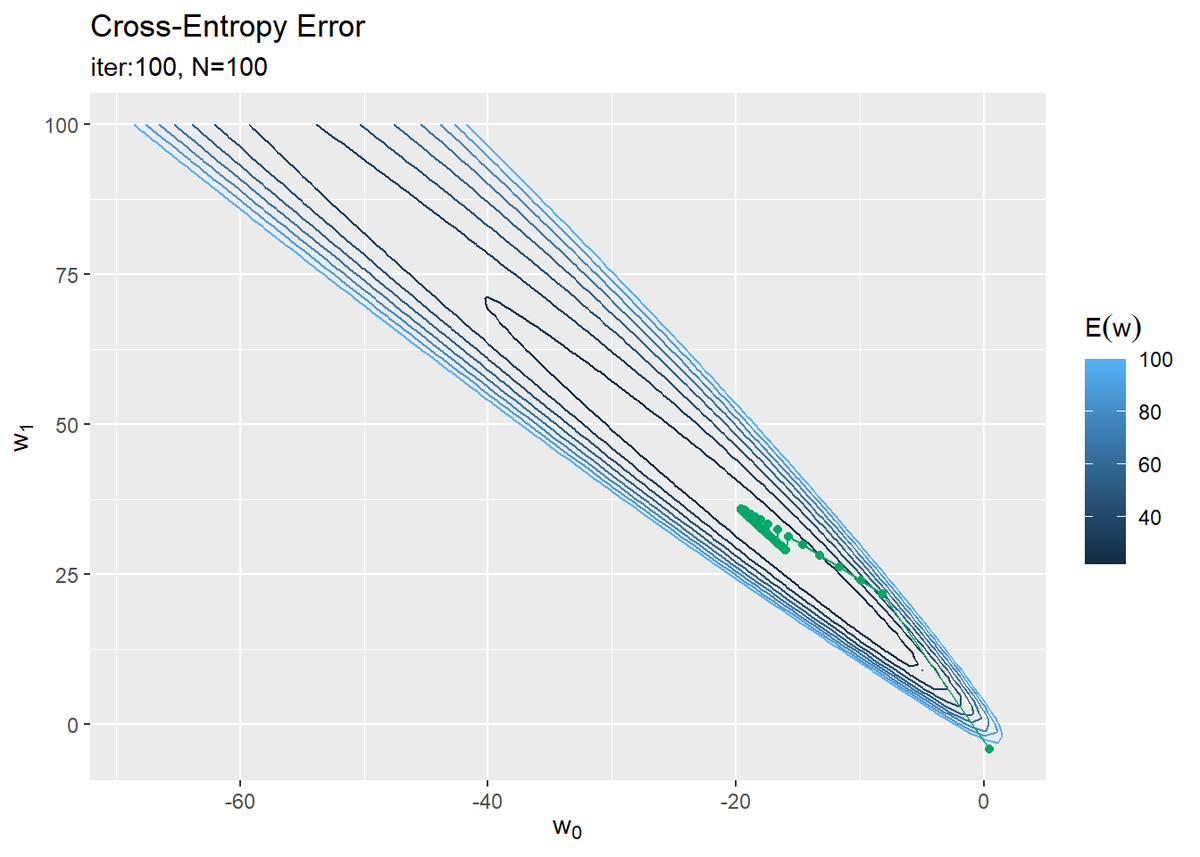
勾配を下るように値が更新されているのが分かります。
重み付け基底関数のグラフを見ると、$w_1$が大きくなると青色の曲線が上方向に変化します(並行移動ではないです)。このとき、$w_0$が小さくなれば赤色の直線が下方向に変化するので、その和であるオレンジと赤の曲線への影響は相殺されます。つまり、誤差関数への影響も緩和されます。
逆に、$w_0, w_1$の増減が同じだとモデルと誤差関数への影響は強くなります。このことが誤差関数の等高線の形からも分かります。
・おまけ:モデルの推移
最後に、パラメータ$\mathbf{w}$が更新されることで変化する回帰曲線をアニメーションで確認します。
・作図コード(クリックで展開)
アニメーション(gif画像)の作成にgganimateパッケージを利用します。
# 追加パッケージ library(gganimate)
各試行におけるモデルを計算します。
# 最終的な誤差を計算 y_n <- sigmoid(as.vector(phi_x_nm %*% w_logistic_m)) trace_E_vec <- c(trace_E_vec, - sum(t_n * log(y_n) + (1 - t_n) * log(1 - y_n))) # 試行ごとのモデルを計算 trace_logistic_df <- tidyr::tibble() for(i in 0:max_iter) { # i回目の値を取得 tmp_w_m <- trace_w_mat[i+1, ] tmp_E <- trace_E_vec[i+1] # i回目のパラメータによるモデルを計算 tmp_logistic_df <- tidyr::tibble( x = x_vals, y = sigmoid(as.vector(phi(x_vals) %*% tmp_w_m)), threshold_x = threshold(tmp_w_m, x_vals), # y=0.5となるxの値 label = paste0( "iter:", i, ", E=", round(tmp_E, 2), ", threshold=", round(threshold(tmp_w_m, x_vals), 2), ", w=(", paste0(round(tmp_w_m, 2), collapse = ", "), ")" ) %>% as.factor() # フレーム切替用のラベル ) # 結果を結合 trace_logistic_df <- rbind(trace_logistic_df, tmp_logistic_df) } # 確認 head(trace_logistic_df)
## # A tibble: 6 x 4 ## x y threshold_x label ## <dbl> <dbl> <dbl> <fct> ## 1 -18.6 0.452 -24.0 iter:0, E=122.62, threshold=-23.99, w=(0.43, -4.16) ## 2 -18.6 0.452 -24.0 iter:0, E=122.62, threshold=-23.99, w=(0.43, -4.16) ## 3 -18.6 0.452 -24.0 iter:0, E=122.62, threshold=-23.99, w=(0.43, -4.16) ## 4 -18.6 0.452 -24.0 iter:0, E=122.62, threshold=-23.99, w=(0.43, -4.16) ## 5 -18.6 0.452 -24.0 iter:0, E=122.62, threshold=-23.99, w=(0.43, -4.16) ## 6 -18.5 0.452 -24.0 iter:0, E=122.62, threshold=-23.99, w=(0.43, -4.16)
各試行で求めたパラメータの値をtrace_w_matから取り出して回帰曲線を計算し、計算結果をデータフレームに追加していきます。
データへの当てはまり具合を確認するため、交差エントロピー誤差の値もtrace_E_vecから取り出します。ただし、最後の試行における誤差は保存されていないので、ここで計算しておきます。
作図してgif画像として出力ます。
# 推定したパラメータによるモデルを作図 anime_graph <- ggplot() + geom_point(data = data_df, aes(x = x, y = t, color = class)) + # 観測データ geom_line(data = trace_logistic_df, aes(x = x, y = y)) + # 推定したモデル geom_vline(data = trace_logistic_df, aes(xintercept = threshold_x), color = "#00A968", linetype = "dashed") + # 閾値 gganimate::transition_manual(label) + # フレーム xlim(c(min(x_vals), max(x_vals))) + # x軸の表示範囲 labs(title = "Logistic Regression", subtitle = "{current_frame}") # gif画像に変換 gganimate::animate(anime_graph, nframe = max_iter + 1, fps = 10)
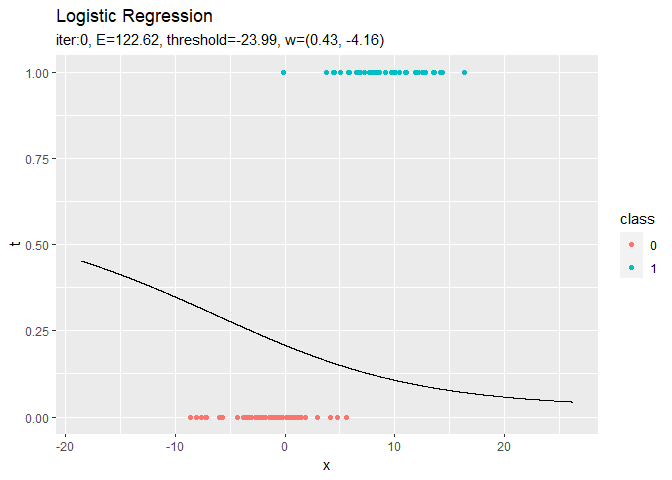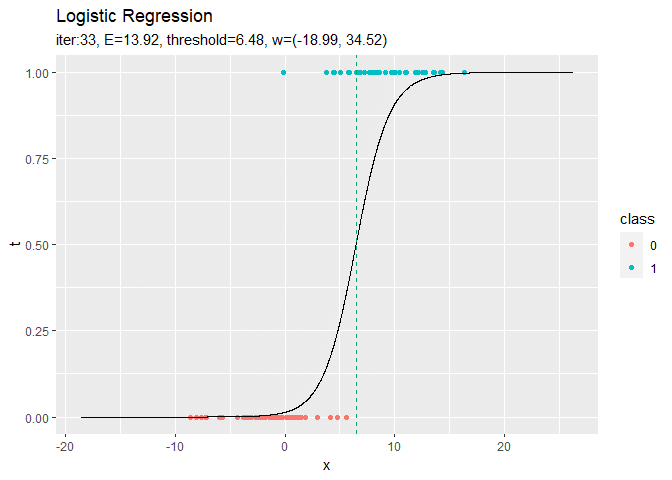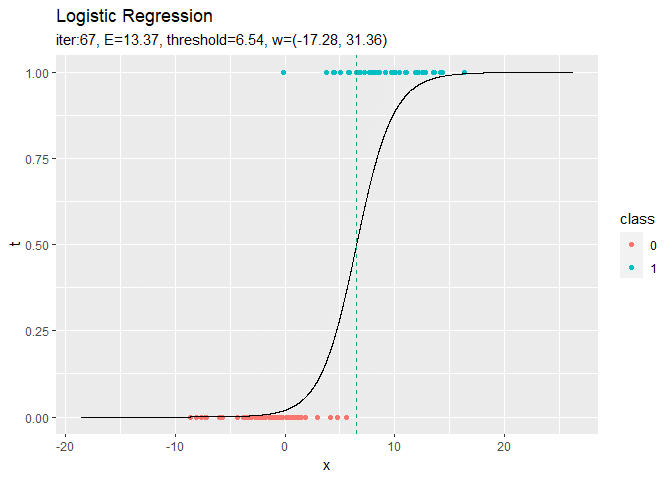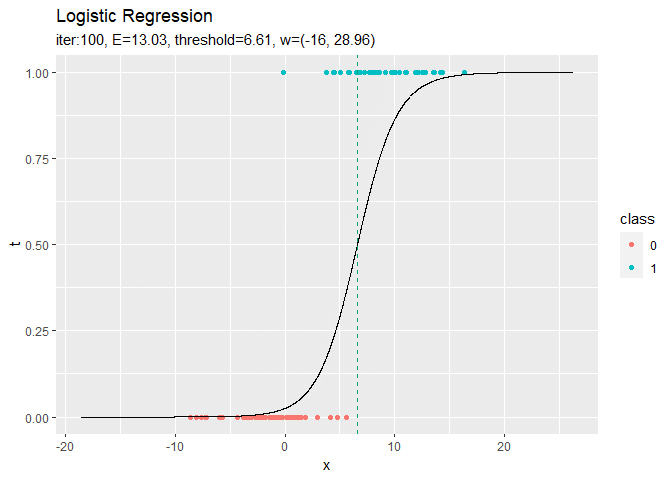
徐々にデータに適合していくのを確認できます。
Enjoy!
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
とりあえずロジスティック回帰の1つ目を攻略できた。今年中にベイズのと変分のまでいきたい。
2021年12月13日は、、、モーニング娘。'21の10期メンバーの佐藤優樹さんの卒業の日です。。
デビューシングル曲
と、私が嵌ったきっかけの曲
と、私が一番(なんて選べないけど)好きな曲
と、ラストシングルから1曲
をどーぞ!!!!
ついにこの日が、、、私がハロプロに嵌ったきっかけの方なのでとても寂しいけど、ソロでも楽し気にパフォーマンスしている姿も待ち遠しい。
最後にもう1曲追加♪
music.apple.com 卒業おめでとうございます!笑顔の君は太陽さ
【次節の内容】

