はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語で二項分布のグラフを作成します。
【前の内容】
【他の記事一覧】
【目次】
二項分布の作図
二項分布(Binomial Distribution)のグラフを作成します。二項分布については「二項分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用するパッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。また、基本的にベースパイプ(ネイティブパイプ)演算子|>を使いますが、パイプ演算子%>%ででないと処理できない部分があるため、magrittrも読み込む必要があります。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、二項分布の定義式を確認します。
二項分布は、次の式で定義されます。
ここで、$x$は成功回数、$M$は試行回数、$\phi$は成功確率($x$が1増える確率)です。
確率変数の値$x$は、$x \in \{0, 1, \ldots, M\}$となります。パラメータ$\phi$は、$\phi \in (0, 1)$を満たす必要があります。また、失敗回数は$M - x$、失敗確率($x$が1増えない確率)は$1 - \phi$で表せます。
二項分布の平均と分散は、次の式で計算できます。
最頻値は、次の式で計算できます。
二項分布の歪度と尖度は、次の式で計算できます。
これらの計算を行いグラフを作成します。
グラフの作成
ggplot2パッケージを利用して、二項分布のグラフを作成します。二項分布の確率や統計量の計算については「【R】二項分布の計算 - からっぽのしょこ」を参照してください。
二項分布のパラメータ$\phi, M$を設定します。
# パラメータを指定 phi <- 0.35 # 試行回数を指定 M <- 10
成功確率$0 < \phi < 1$、試行回数$M$を指定します。
二項分布の確率変数がとり得る値を作成します。
# xがとり得る値を作成 x_vals <- 0:M head(x_vals)
## [1] 0 1 2 3 4 5
$x$がとり得る値$x \in \{0, 1, \ldots, M\}$を作成して、x_valsとします。
$x$の値ごとに確率を計算します。
# 二項分布を計算 prob_df <- tidyr::tibble( x = x_vals, # 確率変数 probability = dbinom(x = x_vals, size = M, prob = phi) # 確率 ) prob_df
## # A tibble: 11 × 2 ## x probability ## <int> <dbl> ## 1 0 0.0135 ## 2 1 0.0725 ## 3 2 0.176 ## 4 3 0.252 ## 5 4 0.238 ## 6 5 0.154 ## 7 6 0.0689 ## 8 7 0.0212 ## 9 8 0.00428 ## 10 9 0.000512 ## 11 10 0.0000276
二項分布の確率は、dbinom()で計算できます。成功回数の引数xにx_vals、試行回数の引数sizeにM、成功確率の引数probにphiを指定します。
x_valsと、x_valsの各要素に対応する確率をデータフレームに格納します。
二項分布のグラフを作成します。
# 二項分布のグラフを作成 ggplot(data = prob_df, mapping = aes(x = x, y = probability)) + # データ geom_bar(stat = "identity", position = "dodge", fill = "#00A968") + # 棒グラフ scale_x_continuous(breaks = x_vals, labels = x_vals) + # x軸目盛 labs(title = "Binomial Distribution", subtitle = paste0("phi=", phi, ", M=", M), # (文字列表記用) #subtitle = parse(text = paste0("list(phi==", phi, ", M==", M, ")")), # (数式表記用) x = "x", y = "probability") # ラベル
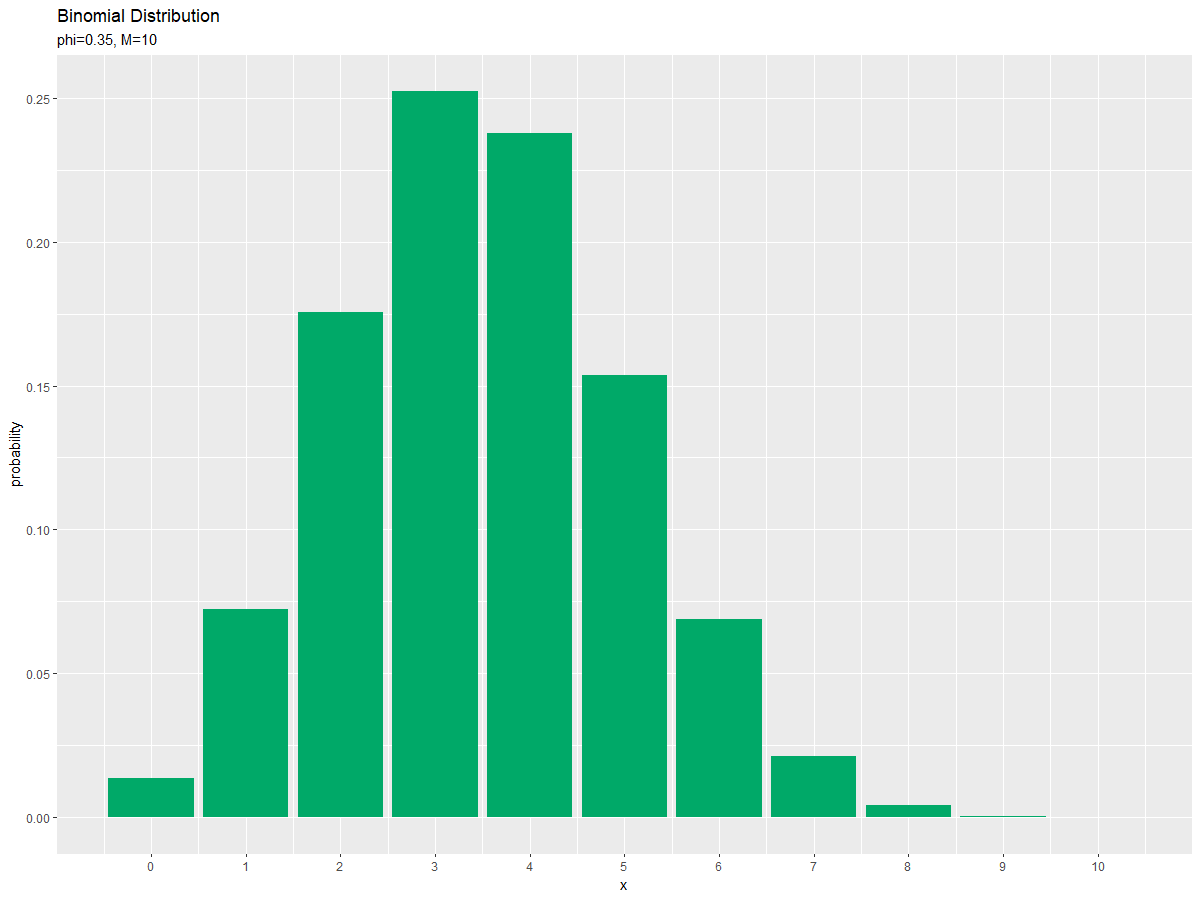
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
この分布に統計量の情報を重ねて表示します。
# 補助線用の統計量を計算 E_x <- M * phi s_x <- sqrt(M * phi * (1 - phi)) mode_x <- floor(phi * (M + 1)) # 統計量を重ねた二項分布のグラフを作成:線のみ ggplot(data = prob_df, mapping = aes(x = x, y = probability)) + # データ geom_bar(stat = "identity", position = "dodge", fill = "#00A968") + # 分布 geom_vline(xintercept = E_x, color = "blue", size = 1, linetype = "dashed") + # 期待値 geom_vline(xintercept = c(E_x-s_x, E_x+s_x), color = "orange", size = 1, linetype = "dotted") + # 期待値 ± 標準偏差 geom_vline(xintercept = mode_x, color = "chocolate", size = 1, linetype = "dashed") + # 最頻値 scale_x_continuous(breaks = x_vals, labels = x_vals) + # x軸目盛 labs(title = "Binomial Distribution", subtitle = parse(text = paste0("list(phi==", phi, ", M==", M, ")")), x = "x", y = "probability") # ラベル

期待値・標準偏差(分散の平方根)・最頻値を計算して、それぞれgeom_vline()で垂直線を引きます。標準偏差については期待値から足し引きした値を使います。
期待値(青色の破線)に近い整数$x$となる確率が最大であり、最頻値(茶色の破線)と一致するのを確認できます。また、各線の位置関係から分布の非対称性が分かります。
凡例を表示する場合は、垂線を引く値をデータフレームにまとめます。
# 統計量を格納 stat_df <- tibble::tibble( statistic = c(E_x, E_x-s_x, E_x+s_x, mode_x), # 統計量 type = c("mean", "sd", "sd", "mode") # 色分け用ラベル ) stat_df
## # A tibble: 4 × 2 ## statistic type ## <dbl> <chr> ## 1 3.5 mean ## 2 1.99 sd ## 3 5.01 sd ## 4 3 mode
各統計量をそれぞれを区別するための文字列と共にデータフレームに格納します。期待値と標準偏差の差・和は同じタイプとします。
折れ線の色や種類、凡例テキストを指定する場合は、設定用の名前付きベクトルを作成します。
# 凡例用の設定を作成:(数式表示用) color_vec <- c(mean = "blue", sd = "orange", mode = "chocolate") linetype_vec <- c(mean = "dashed", sd = "dotted", mode = "dashed") label_vec <- c(mean = expression(E(x)), sd = expression(E(x) %+-% sqrt(V(x))), mode = expression(mode(x))) color_vec; linetype_vec; label_vec
## mean sd mode ## "blue" "orange" "chocolate" ## mean sd mode ## "dashed" "dotted" "dashed" ## expression(mean = E(x), sd = E(x) %+-% sqrt(V(x)), mode = mode(x))
各要素(設定)の名前をtype列の文字列と対応させて、設定を指定します。
凡例付きの二項分布のグラフを作成します。
# 統計量を重ねた二項分布のグラフを作成:凡例付き ggplot() + # データ geom_bar(data = prob_df, mapping = aes(x = x, y = probability), stat = "identity", position = "dodge", fill = "#00A968") + # 分布 geom_vline(data = stat_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1) + # 統計量 scale_x_continuous(breaks = x_vals, labels = x_vals) + # x軸目盛 scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(色指定と数式表示用) scale_linetype_manual(values = linetype_vec, labels = label_vec, name = "statistic") + # 線の種類:(線指定と数式表示用) theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Binomial Distribution", subtitle = parse(text = paste0("list(phi==", phi, ", M==", M, ")")), x = "x", y = "probability") # ラベル

scale_color_manual()のvalues引数に線の色、scale_linetype_manual()のvalues引数に線の種類を指定します。凡例テキストを指定する場合は、それぞれのlabels引数に指定します。names引数は凡例ラベルです。
凡例テキストは、theme()のlegend.text.align引数に0を指定すると左寄せ、デフォルト(1)だと右寄せになります。
二項分布のグラフを描画できました。
パラメータと分布の関係を並べて比較
次は、複数のパラメータのグラフを比較することで、パラメータの値と分布の形状の関係を確認します。
パラメータの影響
複数個のパラメータ$\phi$を指定し、試行回数$M$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータとして利用する値を指定 phi_vals <- c(0.1, 0.33, 0.5, 0.8, 0.9) # 試行回数を指定 M <- 100 # xがとり得る値を作成 x_vals <- 0:M # パラメータごとに二項分布を計算 res_prob_df <- tidyr::expand_grid( x = x_vals, phi = phi_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(phi, x) |> # パラメータごとに並べ替え dplyr::mutate( probability = dbinom(x = x, size = M, prob = phi), parameter = paste0("phi=", phi, ", M=", M) |> factor(levels = paste0("phi=", sort(phi_vals), ", M=", M)) # 色分け用ラベル ) # 確率を計算 res_prob_df
## # A tibble: 505 × 4 ## x phi probability parameter ## <int> <dbl> <dbl> <fct> ## 1 0 0.1 0.0000266 phi=0.1, M=100 ## 2 1 0.1 0.000295 phi=0.1, M=100 ## 3 2 0.1 0.00162 phi=0.1, M=100 ## 4 3 0.1 0.00589 phi=0.1, M=100 ## 5 4 0.1 0.0159 phi=0.1, M=100 ## 6 5 0.1 0.0339 phi=0.1, M=100 ## 7 6 0.1 0.0596 phi=0.1, M=100 ## 8 7 0.1 0.0889 phi=0.1, M=100 ## 9 8 0.1 0.115 phi=0.1, M=100 ## 10 9 0.1 0.130 phi=0.1, M=100 ## # … with 495 more rows
$x$の値x_valsとパラメータphi_valsの各要素の全ての組み合わせをexpand_grid()で作成します。
組み合わせごとに確率を計算して、パラメータごとにラベルを作成します。ラベルは、グラフの設定や凡例テキストとして使います。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
数式を表示する場合は、expression()に対応した記法に変換します。
# 凡例用のラベルを作成:(数式表示用) label_vec <- res_prob_df[["parameter"]] |> unique() |> # 重複を除去 stringr::str_replace_all(pattern = "=", replacement = "==") %>% # 等号表示用の記法に変換 paste0("list(", ., ")") |> # カンマ表示用の記法に変換 parse(text = _) # expression関数化 names(label_vec) <- unique(res_prob_df[["parameter"]]) # ggplotに指定する文字列に対応する名前付きベクトルに変換 label_vec[1]
## expression(`phi=0.1, M=100` = list(phi == 0.1, M == 100))
変換後の文字列のベクトルに対してnames()を使って、元の文字列を各要素の名前として設定します。
res_prob_dfのparameter列の要素phi=0.1, M=100と、変換後の文字列list(phi == 0.1, M == 100)が対応しています。
各パラメータの二項分布を作図します。
# パラメータごとに二項分布のグラフを作成 ggplot(data = res_prob_df, mapping = aes(x = x, y = probability, fill = parameter, color = parameter)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ #scale_x_continuous(breaks = x_vals, labels = x_vals) + # x軸目盛 scale_color_hue(labels = label_vec) + # 線の色:(数式表示用) scale_fill_hue(labels = label_vec) + # 塗りつぶしの色:(数式表示用) theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Binomial Distribution", fill = "parameter", color = "parameter", x = "x", y = "probability") # タイトル

成功確率$\phi$が大きいと、成功回数$x$が大きいほど確率が高くなる(山が右に位置する)のが分かります。このことは、平均の計算式からも分かります。
また分散の計算式からも分かるように、$\phi = 0.5$のとき分散が最大になり、分布の裾が広く確率の最大値が小さく(なだらかな山に)なります。$\phi$と$1 - \phi$の差が大きいほど分散が小さくなり、裾が狭く確率の最大値が大きく(高い山に)なります。
試行回数の影響
続いて、パラメータ$\phi$を固定し、複数個の試行回数$M$を指定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータを指定 phi <- 0.5 # 試行回数として利用する値を指定 M_vals <- c(5, 10, 20, 40) # xがとり得る値を作成 x_vals <- 0:max(M_vals) # パラメータごとに二項分布を計算 res_prob_df <- tidyr::expand_grid( x = x_vals, M = M_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(M, x) |> # 試行回数ごとに並べ替え dplyr::mutate( probability = dbinom(x = x, size = M, prob = phi), parameter = paste0("phi=", phi, ", M=", M) |> factor(levels = paste0("phi=", phi, ", M=", sort(M_vals))) # 色分け用ラベル ) |> # 確率を計算 dplyr::filter(x <= M) # 実現可能な値を抽出 res_prob_df
## # A tibble: 79 × 4 ## x M probability parameter ## <int> <dbl> <dbl> <fct> ## 1 0 5 0.0312 phi=0.5, M=5 ## 2 1 5 0.156 phi=0.5, M=5 ## 3 2 5 0.312 phi=0.5, M=5 ## 4 3 5 0.312 phi=0.5, M=5 ## 5 4 5 0.156 phi=0.5, M=5 ## 6 5 5 0.0312 phi=0.5, M=5 ## 7 0 10 0.000977 phi=0.5, M=10 ## 8 1 10 0.00977 phi=0.5, M=10 ## 9 2 10 0.0439 phi=0.5, M=10 ## 10 3 10 0.117 phi=0.5, M=10 ## # … with 69 more rows
$x$の値x_valsと試行回数M_valsの全ての組み合わせを作成して、「パラメータの影響」と同様に、確率を計算します。
二項分布は$x \leq M$の値しかとらないので、filter()で取り出します。この処理がなくても、$x < M$の確率は0になるので作図に影響しません。
折れ線の設定と作図については、「パラメータの影響」のコードで処理できます。
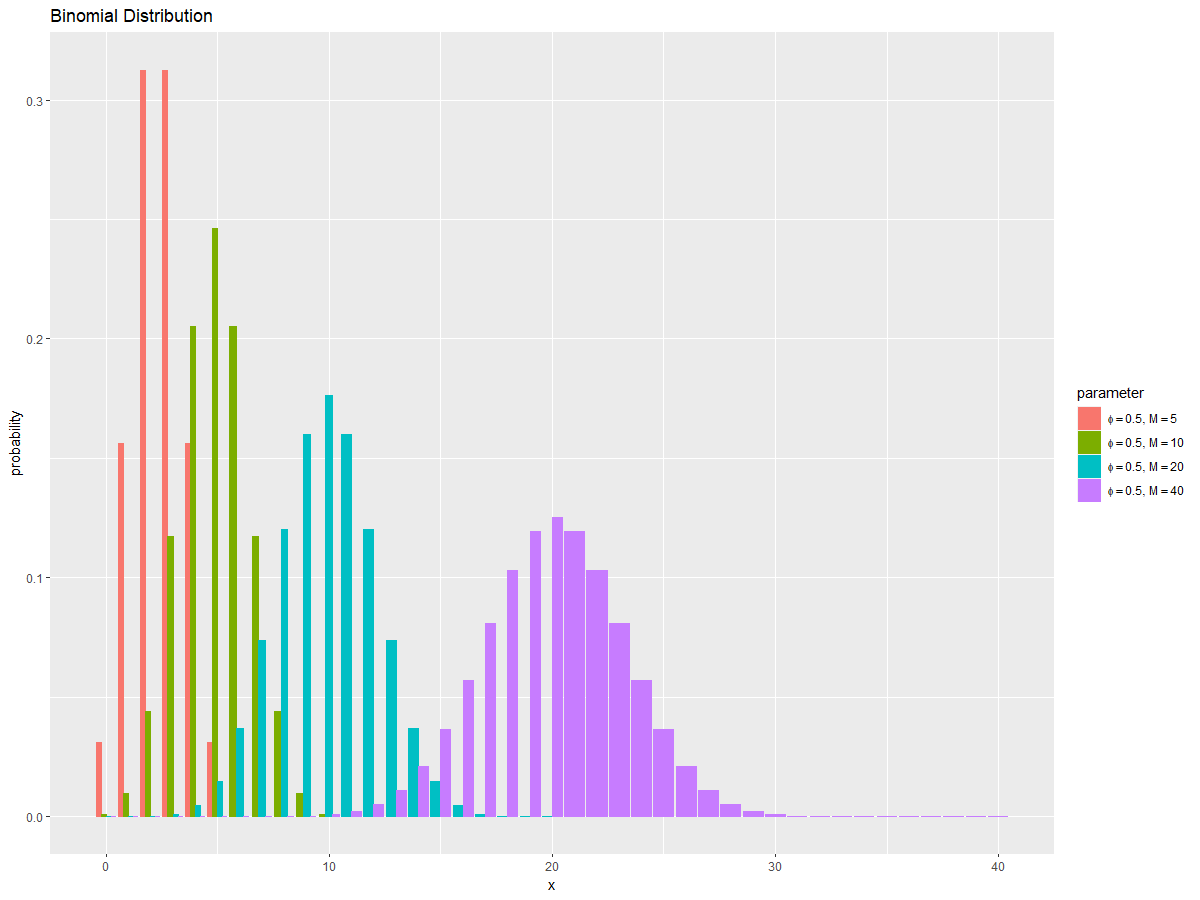
試行回数$M$が大きいほど、成功回数$x$が大きいほど確率が高くなり(山が右に位置し)、分散が大きくなるのが分かります。
パラメータと分布の関係をアニメーションで可視化
前節では、複数のパラメータのグラフを並べて比較しました。次は、パラメータの値を少しずつ変化させて、分布の形状の変化をアニメーションで確認します。
パラメータの影響
パラメータ$\phi$の値を作成し、試行回数$M$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータとして利用する値を指定 phi_vals <- seq(from = 0, to = 1, by = 0.01) #length(phi_vals) # フレーム数 # 試行回数を指定 M <- 10 # xがとり得る値を作成 x_vals <- 0:M # パラメータごとに二項分布を計算 anime_prob_df <- tidyr::expand_grid( x = x_vals, phi = phi_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(phi, x) |> # パラメータごとに並べ替え dplyr::mutate( probability = dbinom(x = x, size = M, prob = phi), parameter = paste0("phi=", phi, ", M=", M) |> factor(levels = paste0("phi=", sort(phi_vals), ", M=", M)) # フレーム切替用ラベル ) # 確率を計算 anime_prob_df
## # A tibble: 1,111 × 4 ## x phi probability parameter ## <int> <dbl> <dbl> <fct> ## 1 0 0 1 phi=0, M=10 ## 2 1 0 0 phi=0, M=10 ## 3 2 0 0 phi=0, M=10 ## 4 3 0 0 phi=0, M=10 ## 5 4 0 0 phi=0, M=10 ## 6 5 0 0 phi=0, M=10 ## 7 6 0 0 phi=0, M=10 ## 8 7 0 0 phi=0, M=10 ## 9 8 0 0 phi=0, M=10 ## 10 9 0 0 phi=0, M=10 ## # … with 1,101 more rows
値の間隔が一定になるようにphi_valsを作成します。パラメータごとにフレームを切り替えるので、phi_valsの要素数がアニメーションのフレーム数になります。
データフレームの変数名以外は「並べて比較」のときと同じ処理です。アニメーションの作図では、parameter列をフレーム切替用のラベルとして使います。
二項分布のアニメーション(gif画像)を作成します。
# 二項分布のアニメーションを作図 anime_prob_graph <- ggplot(data = anime_prob_df, mapping = aes(x = x, y = probability)) + # データ geom_bar(stat = "identity", position = "dodge", fill = "#00A968", color = "#00A968") + # 分布 gganimate::transition_manual(parameter) + # フレーム #gganimate::view_follow(fixed_x = FALSE, fixed_y = TRUE) + # 表示範囲の調整 scale_x_continuous(breaks = x_vals, labels = x_vals) + # x軸目盛 labs(title = "Binomial Distribution", subtitle = "{current_frame}", x = "x", y = "probability") # ラベル # gif画像を作成 gganimate::animate(anime_prob_graph, nframes = length(phi_vals), fps = 100, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。
animate()のフレーム数の引数にnframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。
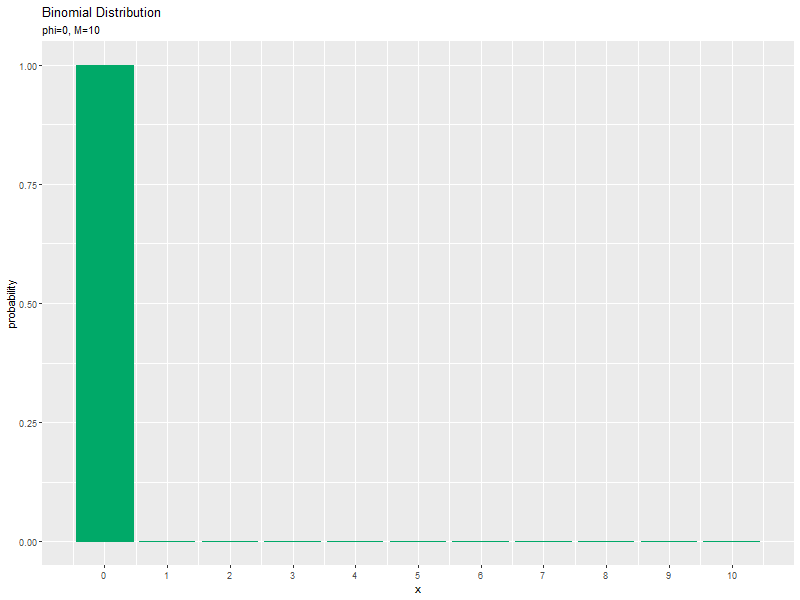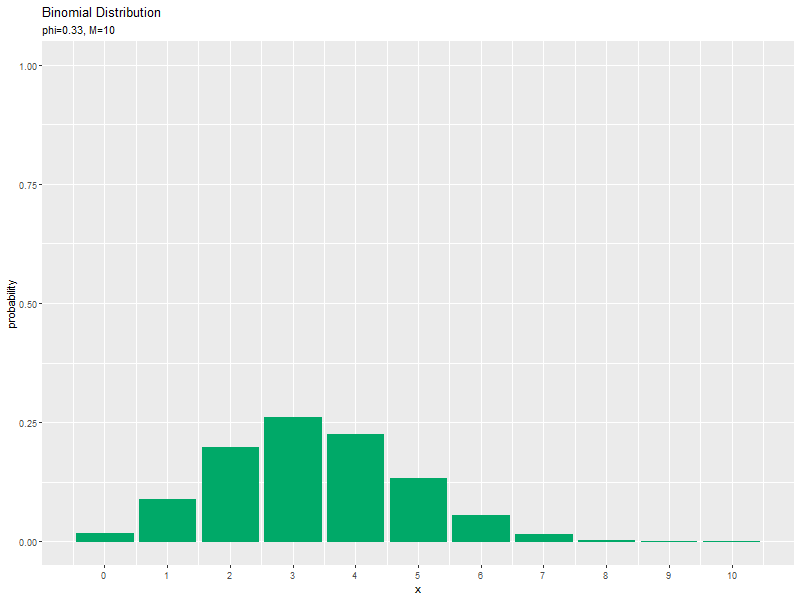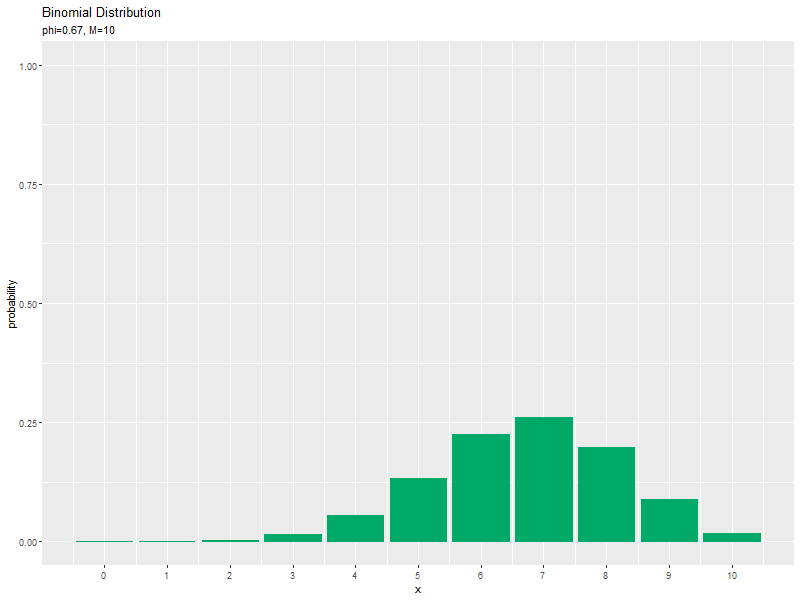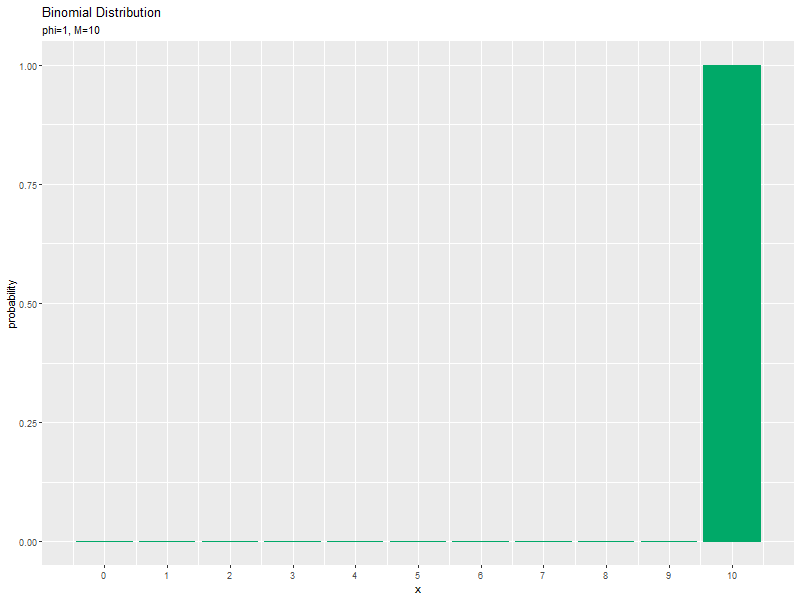
パラメータ$\phi$の値が大きくなるに従って、成功回数$x$が大きいほど確率が高くなる(山が右に移動する)のを確認できます。
試行回数の影響
続いて、$\phi$を固定し、$M$の最大値を指定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータを指定 phi <- 0.3 # 試行回数の最大値を指定 M_max <- 100 # xがとり得る値を作成 x_vals <- 0:M_max # 試行回数ごとに二項分布を計算 anime_prob_df <- tidyr::expand_grid( x = x_vals, M = 1:M_max ) |> # 全ての組み合わせを作成 dplyr::arrange(M, x) |> # 試行回数ごとに並べ替え dplyr::mutate( probability = dbinom(x = x_vals, size = M, prob = phi), parameter = paste0("phi=", phi, ", M=", M) |> factor(levels = paste0("phi=", phi, ", M=", 1:M_max)) # フレーム切替用ラベル ) |> # 確率を計算 dplyr::filter(x <= M) # 実現可能な値を抽出 anime_prob_df
## # A tibble: 5,150 × 4 ## x M probability parameter ## <int> <int> <dbl> <fct> ## 1 0 1 0.7 phi=0.3, M=1 ## 2 1 1 0.3 phi=0.3, M=1 ## 3 0 2 0.49 phi=0.3, M=2 ## 4 1 2 0.42 phi=0.3, M=2 ## 5 2 2 0.09 phi=0.3, M=2 ## 6 0 3 0.343 phi=0.3, M=3 ## 7 1 3 0.441 phi=0.3, M=3 ## 8 2 3 0.189 phi=0.3, M=3 ## 9 3 3 0.0270 phi=0.3, M=3 ## 10 0 4 0.240 phi=0.3, M=4 ## # … with 5,140 more rows
$M$の最大値をM_maxとして、0からM_maxまでの整数を試行回数として使います。「並べて比較」のときのM_valsを1:M_maxに置き換えて処理します。
作図については、「パラメータの影響」のコードで処理できます。ただし、view_follow()を使って(コメントアウトを外して)、$x$の値に応じてx軸の範囲を調整します。フレーム数はM_maxです。
# gif画像を作成 gganimate::animate(anime_prob_graph, nframes = M_max, fps = 100, width = 800, height = 600)
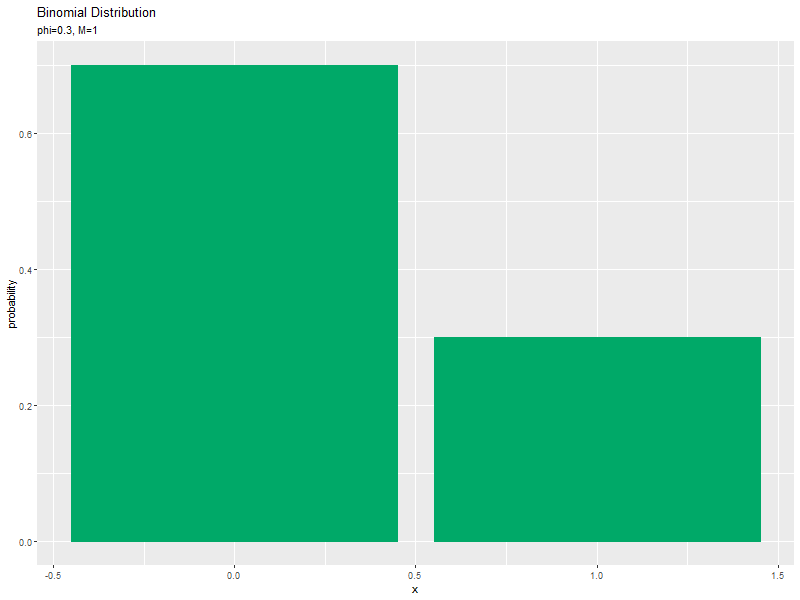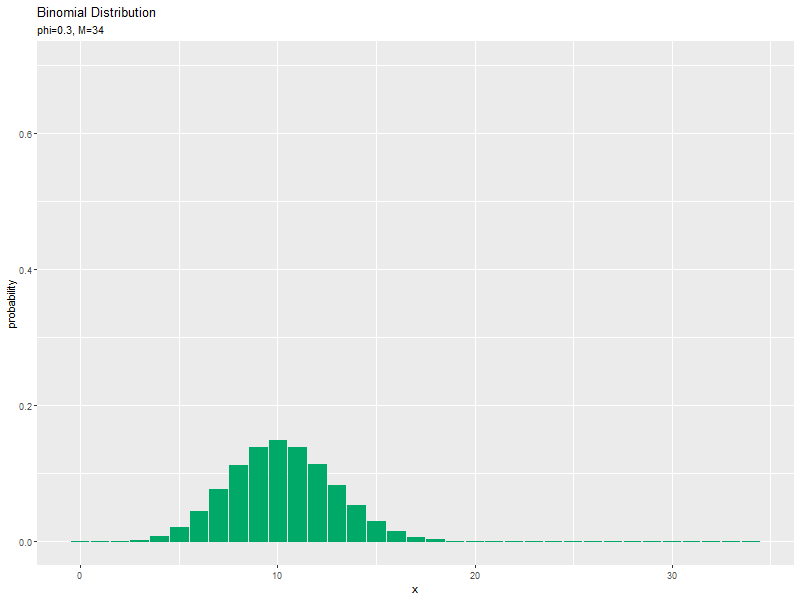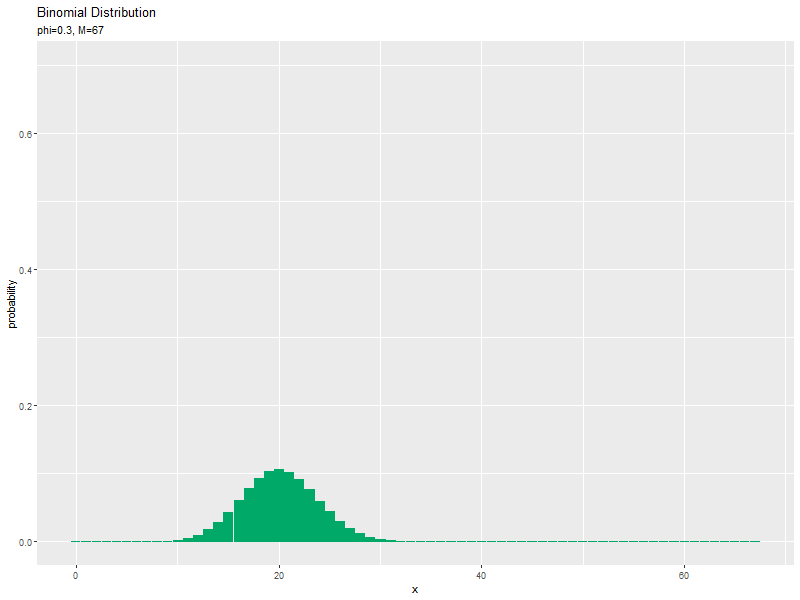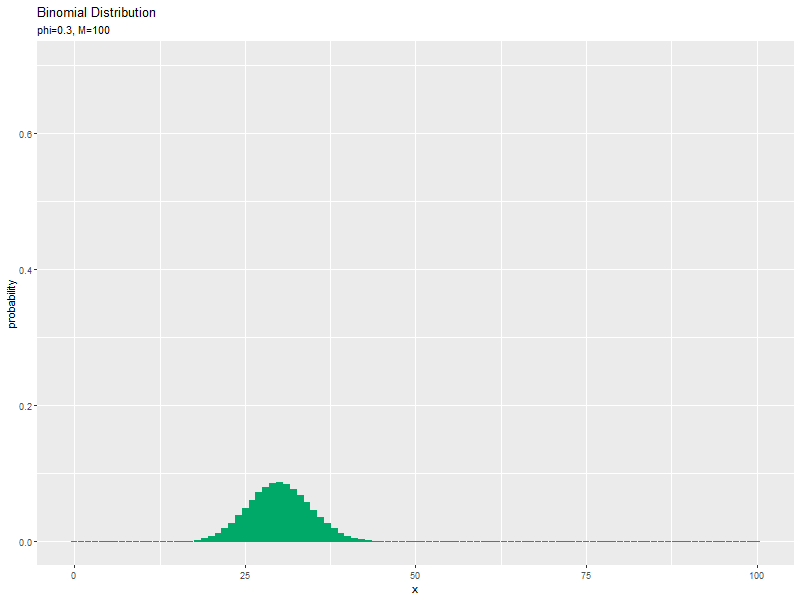
試行回数$M$が増えるに従って、成功回数$x$が大きいほど確率が高くなる(山が右に移動する)のを確認できます。ただし、$x$がとり得る値の範囲x_valsも広がっていくため、x_vals全体における相対的な山の位置は変わりません。
パラメータと統計量の関係をアニメーションで可視化
ここまでは、パラメータと分布の関係を確認しました。次は、パラメータと統計量と歪度・尖度の関係をアニメーションで確認します。
パラメータの影響
パラメータ$\phi$の値を作成し、試行回数$M$を固定して、それぞれ歪度と尖度を計算し、フレーム切替用のラベルを作成します。
・作図コード(クリックで展開)
# パラメータとして利用する値を作成 phi_vals <- seq(from = 0.01, to = 0.99, by = 0.01) #length(phi_vals) # フレーム数 # 試行回数を指定 M <- 10 # xがとり得る値を作成 x_vals <- 0:M # 歪度を計算 skewness_vec <- (1 - 2 * phi_vals) / sqrt(M * phi_vals * (1 - phi_vals)) # 尖度を計算 kurtosis_vec <- (1 - 6 * phi_vals * (1 - phi_vals)) / (M * phi_vals * (1 - phi_vals)) # ラベル用のテキストを作成 label_vec <- paste0( "phi=", phi_vals, ", M=", M, ", skewness=", round(skewness_vec, 3), ", kurtosis=", round(kurtosis_vec, 3) ) head(label_vec)
## [1] "phi=0.01, M=10, skewness=3.115, kurtosis=9.501" ## [2] "phi=0.02, M=10, skewness=2.168, kurtosis=4.502" ## [3] "phi=0.03, M=10, skewness=1.743, kurtosis=2.836" ## [4] "phi=0.04, M=10, skewness=1.485, kurtosis=2.004" ## [5] "phi=0.05, M=10, skewness=1.306, kurtosis=1.505" ## [6] "phi=0.06, M=10, skewness=1.172, kurtosis=1.173"
パラメータごとに歪度と尖度を計算して、フレーム切替用のラベルとして利用します。
パラメータごとに分布を計算します。
# パラメータごとに二項分布を計算 anime_prob_df <- tidyr::expand_grid( x = x_vals, phi = phi_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(phi, x) |> # パラメータごとに並べ替え dplyr::mutate( probability = dbinom(x = x, size = M, prob = phi), parameter = rep(label_vec, each = length(x_vals)) |> factor(levels = label_vec) # フレーム切替用ラベル ) # 確率を計算 anime_prob_df
## # A tibble: 1,089 × 4 ## x phi probability parameter ## <int> <dbl> <dbl> <fct> ## 1 0 0.01 9.04e- 1 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 2 1 0.01 9.14e- 2 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 3 2 0.01 4.15e- 3 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 4 3 0.01 1.12e- 4 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 5 4 0.01 1.98e- 6 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 6 5 0.01 2.40e- 8 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 7 6 0.01 2.02e-10 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 8 7 0.01 1.16e-12 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 9 8 0.01 4.41e-15 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## 10 9 0.01 9.90e-18 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 ## # … with 1,079 more rows
これまでと同様に処理します。フレーム切替用のラベル(parameter列)の値にはlabel_vecを使います。
パラメータごとに統計量を計算します。
# パラメータごとに統計量を計算 anime_stat_df <- tibble::tibble( mean = M * phi_vals, # 期待値 sd = sqrt(M * phi_vals * (1 - phi_vals)), # 標準偏差 mode = floor(phi_vals * (M + 1)), # 最頻値 parameter = factor(label_vec, levels = label_vec) # フレーム切替用のラベル ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !parameter, names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd")) # 期待値±標準偏差のカテゴリを統一 anime_stat_df
## # A tibble: 396 × 3 ## parameter type statistic ## <fct> <chr> <dbl> ## 1 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 mean 0.1 ## 2 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 mode 0 ## 3 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 sd -0.215 ## 4 phi=0.01, M=10, skewness=3.115, kurtosis=9.501 sd 0.415 ## 5 phi=0.02, M=10, skewness=2.168, kurtosis=4.502 mean 0.2 ## 6 phi=0.02, M=10, skewness=2.168, kurtosis=4.502 mode 0 ## 7 phi=0.02, M=10, skewness=2.168, kurtosis=4.502 sd -0.243 ## 8 phi=0.02, M=10, skewness=2.168, kurtosis=4.502 sd 0.643 ## 9 phi=0.03, M=10, skewness=1.743, kurtosis=2.836 mean 0.3 ## 10 phi=0.03, M=10, skewness=1.743, kurtosis=2.836 mode 0 ## # … with 386 more rows
期待値・標準偏差・最頻値を計算して、さらに期待値から標準偏差を引いた値と足した値を求めます。
期待値・標準偏差の和と差・最頻値の4つの列をpivot_longer()でまとめます。列名がラベルになるので、標準偏差の和と差のラベルを統一します。
折れ線と凡例テキストの設定用の名前付きベクトルを作成します。
# 凡例用の設定を作成:(数式表示用) color_vec <- c(mean = "blue", sd = "orange", mode = "chocolate") linetype_vec <- c(mean = "dashed", sd = "dotted", mode = "dashed") label_vec <- c(mean = expression(E(x)), sd = expression(E(x) %+-% sqrt(V(x))), mode = expression(mode(x)))
「グラフの作成」のときと同じ処理です。
統計量の情報を重ねた二項分布のアニメーション(gif画像)を作成します。
# 統計量を重ねた二項分布のアニメーションを作図 anime_prob_graph <- ggplot() + # データ geom_bar(data = anime_prob_df, mapping = aes(x = x, y = probability), stat = "identity", position = "dodge", fill = "#00A968") + # 分布 geom_vline(data = anime_stat_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1) + # 統計量 gganimate::transition_manual(parameter) + # フレーム #gganimate::view_follow(fixed_x = FALSE, fixed_y = TRUE) + # 表示範囲の調整 scale_x_continuous(breaks = x_vals, labels = x_vals) + # x軸目盛 scale_linetype_manual(values = linetype_vec, labels = label_vec, name = "statistic") + # 線の種類:(線指定と数式表示用) scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(色指定と数式表示用) theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Binomial Distribution", subtitle = "{current_frame}", x = "x", y = "probability") # ラベル # gif画像を作成 gganimate::animate(anime_prob_graph, nframes = length(phi_vals), fps = 100, width = 800, height = 600)
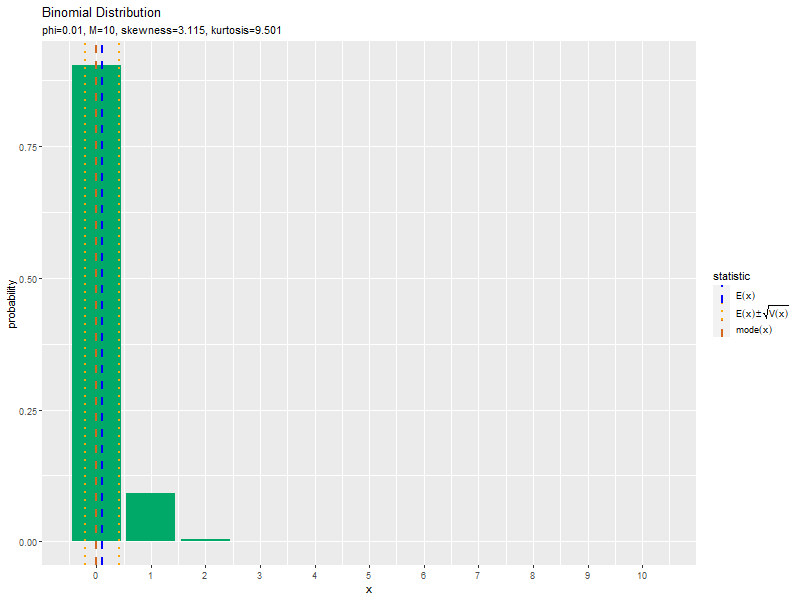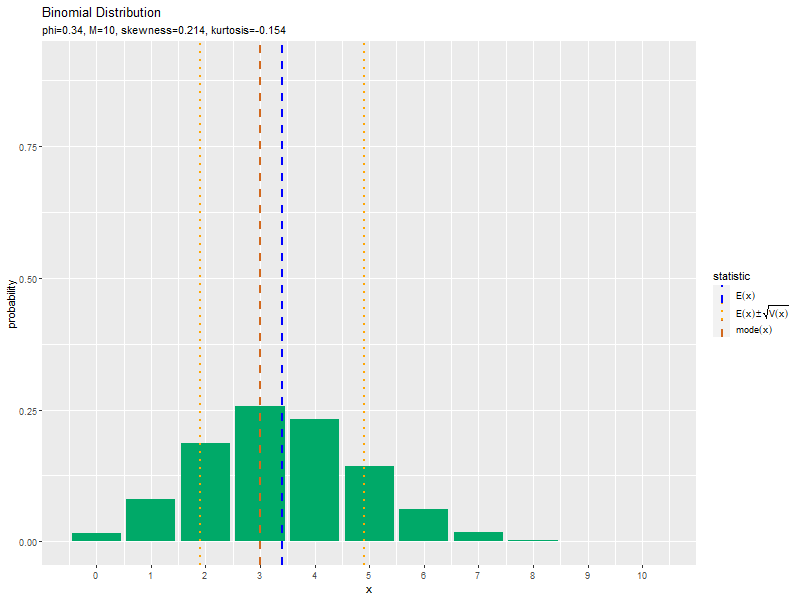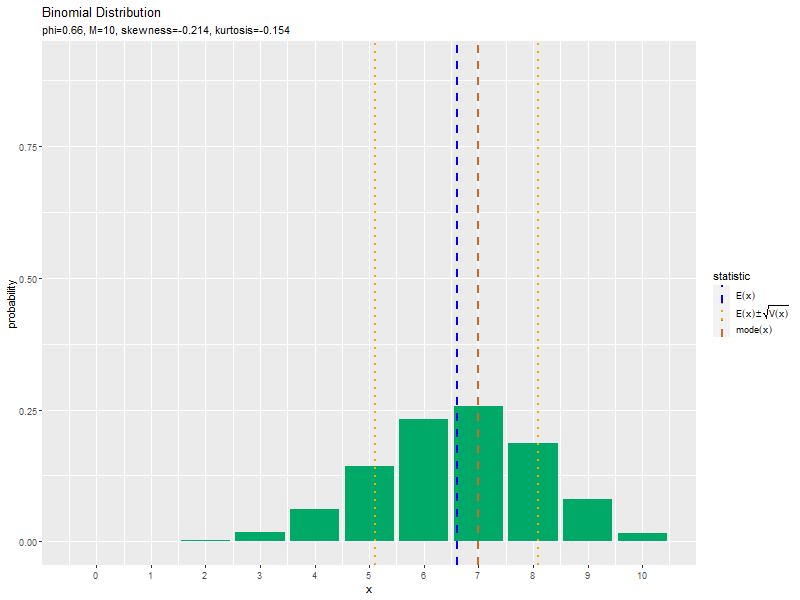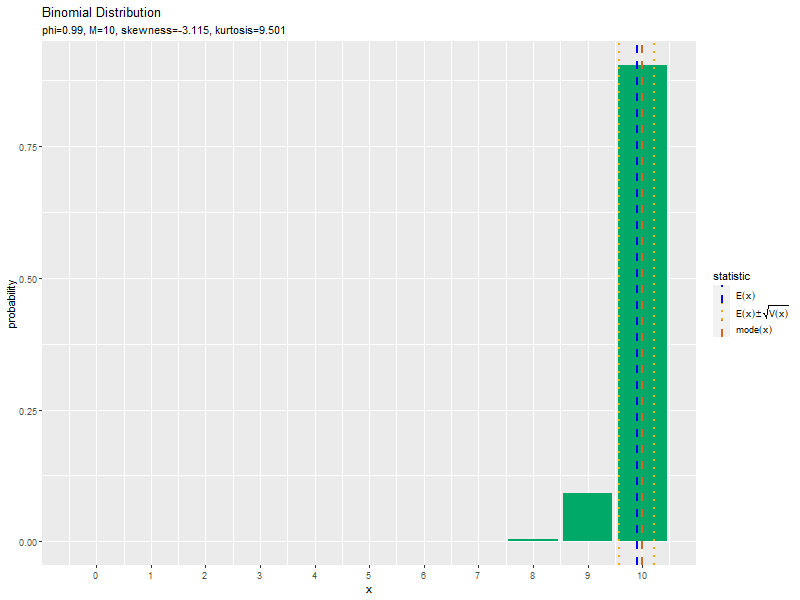
$\phi = 0.5$のとき、歪度が0になり左右対称な分布で、尖度が最小値になるのを確認できます。
試行回数の影響
続いて、パラメータ$\phi$を固定して、試行回数$M$を1ずつ大きくしていき、それぞれ歪度と尖度を計算し、フレーム切替用のラベルを作成します。
・作図コード(クリックで展開)
# パラメータを指定 phi <- 0.35 # 試行回数の最大値を指定 M_vals <- 1:100 # xがとり得る値を作成 x_vals <- 0:max(M_vals) # 歪度を計算 skewness_vec <- (1 - 2 * phi) / sqrt(M_vals * phi * (1 - phi)) # 尖度を計算 kurtosis_vec <- (1 - 6 * phi * (1 - phi)) / (M_vals * phi * (1 - phi)) # ラベル用のテキストを作成 label_vec <- paste0( "phi=", phi, ", M=", M_vals, ", skewness=", round(skewness_vec, 3), ", kurtosis=", round(kurtosis_vec, 3) ) head(label_vec)
## [1] "phi=0.35, M=1, skewness=0.629, kurtosis=-1.604" ## [2] "phi=0.35, M=2, skewness=0.445, kurtosis=-0.802" ## [3] "phi=0.35, M=3, skewness=0.363, kurtosis=-0.535" ## [4] "phi=0.35, M=4, skewness=0.314, kurtosis=-0.401" ## [5] "phi=0.35, M=5, skewness=0.281, kurtosis=-0.321" ## [6] "phi=0.35, M=6, skewness=0.257, kurtosis=-0.267"
「パラメータの影響」のphi_valsをphi、MをM_valsに置き換えると処理できます。
試行回数ごとに分布を計算します。
# 試行回数ごとに二項分布を計算 anime_prob_df <- tidyr::expand_grid( x = x_vals, M = M_vals ) |> # 全ての組み合わせを作成 dplyr::arrange(M, x) |> # 試行回数ごとに並べ替え dplyr::mutate( probability = dbinom(x = x_vals, size = M, prob = phi), parameter = rep(label_vec, each = length(x_vals)) |> factor(levels = label_vec) # フレーム切替用ラベル ) |> # 確率を計算 dplyr::filter(x <= M) # 実現可能な値を抽出 anime_prob_df
## # A tibble: 5,150 × 4 ## x M probability parameter ## <int> <int> <dbl> <fct> ## 1 0 1 0.65 phi=0.35, M=1, skewness=0.629, kurtosis=-1.604 ## 2 1 1 0.35 phi=0.35, M=1, skewness=0.629, kurtosis=-1.604 ## 3 0 2 0.423 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 ## 4 1 2 0.455 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 ## 5 2 2 0.122 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 ## 6 0 3 0.275 phi=0.35, M=3, skewness=0.363, kurtosis=-0.535 ## 7 1 3 0.444 phi=0.35, M=3, skewness=0.363, kurtosis=-0.535 ## 8 2 3 0.239 phi=0.35, M=3, skewness=0.363, kurtosis=-0.535 ## 9 3 3 0.0429 phi=0.35, M=3, skewness=0.363, kurtosis=-0.535 ## 10 0 4 0.179 phi=0.35, M=4, skewness=0.314, kurtosis=-0.401 ## # … with 5,140 more rows
label_vecを使って、これまでと同様に処理します。
試行回数ごとに統計量を計算します。
# 試行回数ごとに統計量を計算 anime_stat_df <- tibble::tibble( mean = M_vals * phi, # 期待値 sd = sqrt(M_vals * phi * (1 - phi)), # 標準偏差 mode = floor(phi * (M_vals + 1)), # 最頻値 parameter = factor(label_vec, levels = label_vec) # フレーム切替用のラベル ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !parameter, names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd")) # 期待値±標準偏差のカテゴリを統一 anime_stat_df
## # A tibble: 400 × 3 ## parameter type statistic ## <fct> <chr> <dbl> ## 1 phi=0.35, M=1, skewness=0.629, kurtosis=-1.604 mean 0.35 ## 2 phi=0.35, M=1, skewness=0.629, kurtosis=-1.604 mode 0 ## 3 phi=0.35, M=1, skewness=0.629, kurtosis=-1.604 sd -0.127 ## 4 phi=0.35, M=1, skewness=0.629, kurtosis=-1.604 sd 0.827 ## 5 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 mean 0.7 ## 6 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 mode 1 ## 7 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 sd 0.0255 ## 8 phi=0.35, M=2, skewness=0.445, kurtosis=-0.802 sd 1.37 ## 9 phi=0.35, M=3, skewness=0.363, kurtosis=-0.535 mean 1.05 ## 10 phi=0.35, M=3, skewness=0.363, kurtosis=-0.535 mode 1 ## # … with 390 more rows
「パラメータの影響」のphi_valsをphi、MをM_valsに置き換えると処理できます。
「パラメータの影響」の作図コードのview_follow()のコメントアウトを外して作図して、フレーム数にM_valsの要素数を指定してgif画像を作成します。
# gif画像を作成 gganimate::animate(anime_prob_graph, nframes = length(M_vals), fps = 100, width = 800, height = 600)
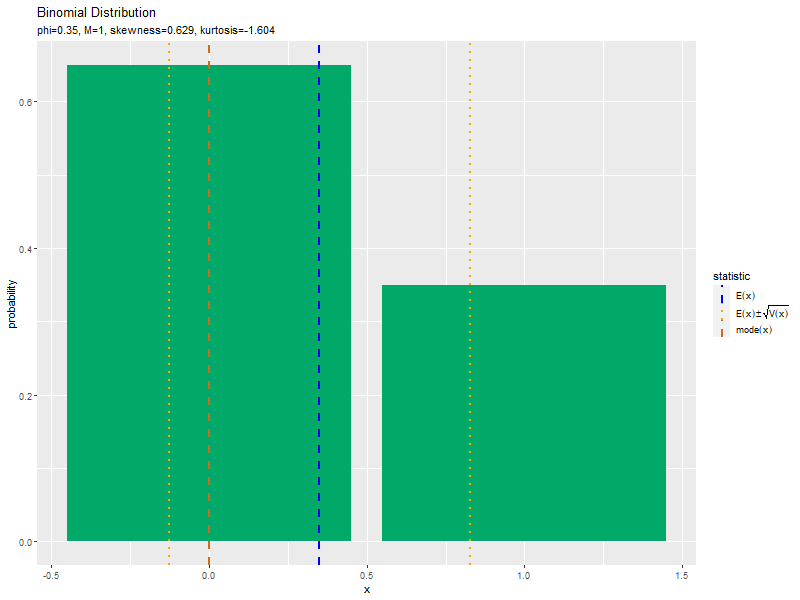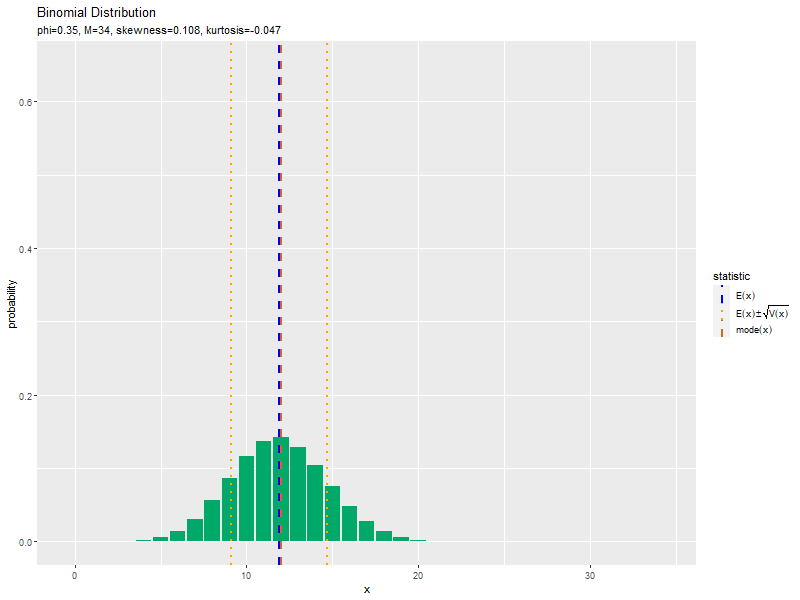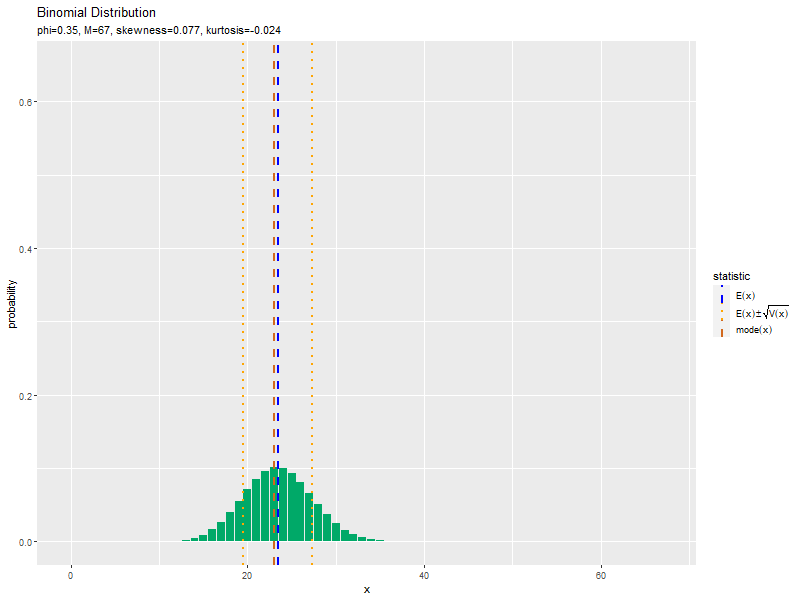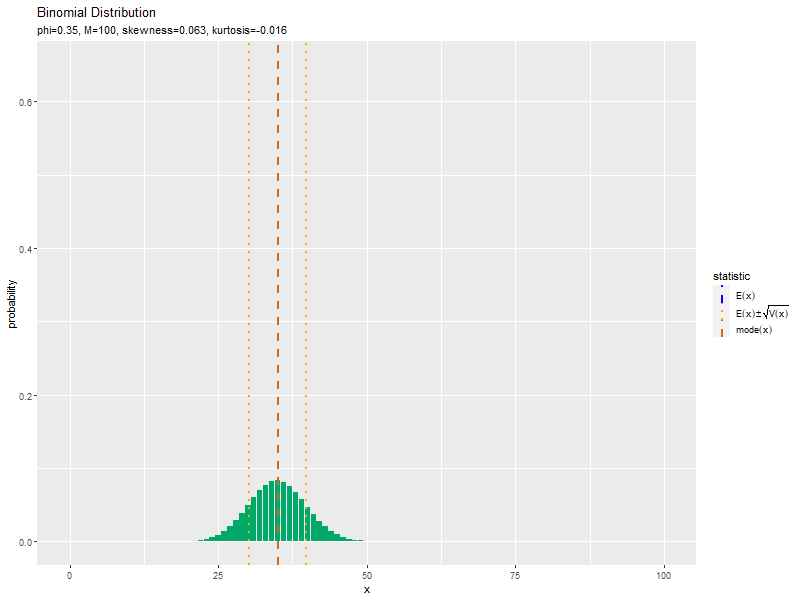
この記事では、二項分布の作図を確認しました。次は、乱数を生成します。
参考文献
- 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.
おわりに
加筆修正の際に青トピシリーズから独立させました。
もっとサクサク進むと思ってましたが、意外と大変でした。
2022.02.19:記事を分割しました。相変わらずグダグダしてます。
2022.06.23:加筆修正しました。
tidyverse力が上がってfor()を全部消せました。
【次の内容】