はじめに
『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本の内容を1つずつ確認しながらゆっくりと組んでいきます。
この記事は、8.3.2項「Attention付きseq2seqの学習」と8.3.3項「Attentionの可視化」の内容です。Attention付きseq2seqの学習処理を解説して、Pythonで実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
8.2.3 seq2seqの実装
この節で実装したEncoderとDecoderを用いてAttention付きseq2seqを実装します。
# 8.2.3項で利用するライブラリ import numpy as np
seq2seqの実装には、8.3節で実装したEncoder・Decoderと5.4.2.3項で実装したTime Softmax with Lossレイヤを利用します。そのため、クラス定義を再実行するか、次の方法で実装済みのクラスを読み込む必要があります。AttentionEncoderとAttentionDecoderは、「ch08」フォルダ内の「attention_seq2seq.py」ファイルに実装されています。RNNで用いるレイヤのクラスは、「common」フォルダ内の「time_layers.py」ファイルに実装されています。
# 実装済みクラスの読み込み用の設定 import sys sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master') # 実装済みのレイヤを読み込み from ch08.attention_seq2seq import AttentionEncoder # 8.3.1項 from ch08.attention_seq2seq import AttentionDecoder # 8.3.2項 from common.time_layers import TimeSoftmaxWithLoss # 5.4.2.3項
「deep-learning-from-scratch-2-master」フォルダにパスを設定しておく必要があります。
または、7.3.3項で実装したSeq2seqクラスを継承します。
・実装
Attention付きseq2seqをクラスとして実装します。7.3.3項で実装したseq2seqのEncoderとDecoderを置き換えるだけです。処理についての詳細は7.3.3項も参照してください。
# Attention付きseq2seqの実装 class AttentionSeq2seq: # 初期化メソッド def __init__(self, vocab_size, wordvec_size, hidden_size): # 変数の形状に関する値を取得 V, D, H = vocab_size, wordvec_size, hidden_size # 各レイヤのインスタンスを作成 self.encoder = AttentionEncoder(V, D, H) self.decoder = AttentionDecoder(V, D, H) self.softmax = TimeSoftmaxWithLoss() # パラメータと勾配をリストに格納 self.params = self.encoder.params + self.decoder.params # パラメータ self.grads = self.encoder.grads + self.decoder.grads # 勾配 # 順伝播メソッド def forward(self, xs, ts): # Decoder用の入植データを作成 decoder_xs = ts[:, :-1] # 入力データ:(最後を除く) decoder_ts = ts[:, 1:] # 教師データ:(最初を除く) # 各レイヤの順伝播を計算 hs = self.encoder.forward(xs) score = self.decoder.forward(decoder_xs, hs) loss = self.softmax.forward(score, decoder_ts) return loss # 逆伝播メソッド def backward(self, dout=1): # 各レイヤの逆伝播を逆順に計算 dout = self.softmax.backward(dout) # スコアの勾配 dhs = self.decoder.backward(dout) # Encoderの隠れ状態の勾配 dout = self.encoder.backward(dhs) # 出力はNone return dout # 文章生成メソッド def generate(self, xs, start_id, sample_size): # 問題文をエンコード hs = self.encoder.forward(xs) # 解答を生成 sampled = self.decoder.generate(hs, start_id, sample_size) return sampled
処理上は問題はありませんが、これまでの数式上の表記と変数名を合わせるために、Encoderの順伝播の出力をhs、Decoderの逆伝播の出力をdhsに変更しました。(本当はdoutも変更したいんですけど、やっぱり本のコードと同じままの方が分かりやすいですよね?)
実装したクラスを試してみましょう。
データとパラメータの形状に関する値を設定して、seq2seqのインスタンスを作成します。
# データとパラメータの形状に関する値を指定 N = 3 # バッチサイズ(入力する文章数) V = 10 # 単語の種類数 D = 5 # 単語ベクトルの次元数(Embedレイヤの中間層のニューロン数) T_enc = 6 # Encoderの時系列サイズ(入力する単語数) T_dec = 4 # Decoderの時系列サイズ(入力・予測する単語数) H = 7 # 隠れ状態のサイズ(LSTMレイヤの中間層のニューロン数) # seq2seqのインスタンスを作成 model = AttentionSeq2seq(V, D, H)
入力データと教師データを簡易的に作成します。
# (簡易的に)入力データを作成 xs = np.random.randint(low=0, high=V, size=(N, T_enc)) print(xs) print(xs.shape) # (簡易的に)教師データを作成 ts = np.random.randint(low=0, high=V, size=(N, T_dec + 1)) print(ts) print(ts.shape)
[[4 7 5 0 2 7]
[3 7 9 3 1 7]
[8 3 5 1 0 2]]
(3, 6)
[[6 6 2 2 8]
[5 6 5 5 4]
[4 8 6 6 3]]
(3, 5)
順伝播と逆伝播を計算します。
# 順伝播を計算 loss = model.forward(xs, ts) print(loss) # 逆伝播を計算 dout = model.backward(dout=1) print(dout)
2.3023338317871094
None
順伝播メソッドを実行すると損失を返します。逆伝播メソッドを実行すると何も返さず、インスタンス内で各レイヤのパラメータの勾配が保存されます。
以上でAttention付きseq2seqを実装できました。次節では、Attention付きseq2seqを使って学習を行います。
8.3.2 Attention付きseq2seqの学習
日付データセットを用いて、Attention付きseq2seqの学習を行います。学習処理は、7.3.4項と同様に行えます。
学習に用いる実装済みのクラスを読み込みます。
# 8.3.2項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt # 実装済みクラスの読み込み用の設定 import sys sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master') # 実装済みのクラスを読み込み from common.optimizer import Adam # 最適化手法 from common.trainer import Trainer # 学習処理:1.4.4項
・データセットの読み込み
日付データセットを読み込みます。
# データセット読み込み用のモジュール from dataset import sequence # データセットの読み込み (x_train, t_train), (x_test, t_test) = sequence.load_data('date.txt') print(x_train.shape) print(t_train.shape) print(x_test.shape) print(t_test.shape) # 文字と文字IDの変換用ディクショナリ変数の読み込み char_to_id, id_to_char = sequence.get_vocab() print(len(char_to_id))
(45000, 29)
(45000, 11)
(5000, 29)
(5000, 11)
59
訓練データが4万5千個、テストデータが5千個です。59種類の文字で構成されています。
文字と文字IDは次のように対応しています。
# 文字と文字IDの変換用ディクショナリ変数を確認 print(char_to_id) print(id_to_char)
{'s': 0, 'e': 1, 'p': 2, 't': 3, 'm': 4, 'b': 5, 'r': 6, ' ': 7, '2': 8, '7': 9, ',': 10, '1': 11, '9': 12, '4': 13, '_': 14, '-': 15, '0': 16, 'A': 17, 'u': 18, 'g': 19, '3': 20, '8': 21, '/': 22, 'T': 23, 'U': 24, 'E': 25, 'S': 26, 'D': 27, 'Y': 28, 'P': 29, 'M': 30, 'B': 31, 'R': 32, '5': 33, 'J': 34, 'N': 35, '6': 36, 'a': 37, 'i': 38, 'l': 39, 'O': 40, 'c': 41, 'o': 42, 'G': 43, 'F': 44, 'y': 45, 'n': 46, 'C': 47, 'W': 48, 'd': 49, 'I': 50, 'L': 51, 'j': 52, 'H': 53, 'v': 54, 'h': 55, 'V': 56, 'f': 57, 'w': 58}
{0: 's', 1: 'e', 2: 'p', 3: 't', 4: 'm', 5: 'b', 6: 'r', 7: ' ', 8: '2', 9: '7', 10: ',', 11: '1', 12: '9', 13: '4', 14: '_', 15: '-', 16: '0', 17: 'A', 18: 'u', 19: 'g', 20: '3', 21: '8', 22: '/', 23: 'T', 24: 'U', 25: 'E', 26: 'S', 27: 'D', 28: 'Y', 29: 'P', 30: 'M', 31: 'B', 32: 'R', 33: '5', 34: 'J', 35: 'N', 36: '6', 37: 'a', 38: 'i', 39: 'l', 40: 'O', 41: 'c', 42: 'o', 43: 'G', 44: 'F', 45: 'y', 46: 'n', 47: 'C', 48: 'W', 49: 'd', 50: 'I', 51: 'L', 52: 'j', 53: 'H', 54: 'v', 55: 'h', 56: 'V', 57: 'f', 58: 'w'}
データを確認しましょう。
# 表示するデータ番号を指定 n = 0 # 文字IDのリストを表示 print(x_train[n]) print(t_train[n]) # テキストに変換して表示 print(''.join([id_to_char[c_id] for c_id in x_train[n]])) print(''.join([id_to_char[c_id] for c_id in t_train[n]]))
[ 8 22 9 22 9 8 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7
7 7 7 7 7]
[14 11 12 9 8 15 16 8 15 16 9]
2/7/72
_1972-02-07
入力する日付データは、データによって形式が異なります。
# 表示するデータ番号を指定 n = 5 # 文字IDのリストを表示 print(x_train[n]) print(t_train[n]) # テキストに変換して表示 print(''.join([id_to_char[c_id] for c_id in x_train[n]])) print(''.join([id_to_char[c_id] for c_id in t_train[n]]))
[30 37 45 7 11 10 7 11 12 9 8 7 7 7 7 7 7 7 7 7 7 7 7 7
7 7 7 7 7]
[14 11 12 9 8 15 16 33 15 16 11]
May 1, 1972
_1972-05-01
どの形式のデータを入力してもyyyy-mm-dd形式に変換します。
7.4.1項で行ったように、入力データを反転させて入力します。
# 入力文を反転 reverse_x_train = x_train[:, ::-1] reverse_x_test = x_test[:, ::-1]
・学習処理
ハイパーパラメータを指定します。
# 文字の種類数(EmbedレイヤとAffineレイヤのニューロン数)を取得 vocab_size = len(char_to_id) # 単語ベクトルのサイズ(Embedレイヤのニューロン数)を指定 wordvec_size = 16 # 隠れ状態のサイズ(LSTMレイヤのニューロン数)を指定 hidden_size = 256 # バッチサイズを指定 batch_size = 128 # エポック当たりの試行回数を指定 max_epoch = 10 # 勾配の閾値を指定 max_grad = 5.0
max_gradは、勾配クリッピングを行う際の閾値です。詳しくは6.1.4項を参照してください。
この例では、通常のseq2seq・Peeky版seq2seq・Attention付きseq2seqの学習を一度に行いましょう。モデルの学習用の用のインスタンスをそれぞれ作成します。
# Attention seq2seqのインスタンスを作成 attention_model = AttentionSeq2seq(vocab_size, wordvec_size, hidden_size) attention_optimizer = Adam() attention_trainer = Trainer(attention_model, attention_optimizer) # Peeky seq2seqのインスタンスを作成 peeky_model = PeekySeq2seq(vocab_size, wordvec_size, hidden_size) peeky_optimizer = Adam() peeky_trainer = Trainer(peeky_model, peeky_optimizer) # Attention seq2seqのインスタンスを作成 base_model = Seq2seq(vocab_size, wordvec_size, hidden_size) base_optimizer = Adam() base_trainer = Trainer(base_model, base_optimizer)
学習処理はTrainerクラスの学習メソッドfit()で行います。バッチデータの切り分けやパラメータの更新も行われます。詳しくは1.4.4項を参照してください。
1エポックごとにテストデータに対する正解率を測ります。結果をacc_listに記録します。
# 正解率の記録用のリストを初期化 attention_acc_list = [] peeky_acc_list = [] base_acc_list = [] # 繰り返し試行 for epoch in range(max_epoch): # 学習 print('----- Attention seq2seq -----') attention_trainer.fit(reverse_x_train, t_train, max_epoch=1, batch_size=batch_size, max_grad=max_grad) print('----- Peeky seq2seq -----') peeky_trainer.fit(reverse_x_train, t_train, max_epoch=1, batch_size=batch_size, max_grad=max_grad) print('----- seq2seq -----') base_trainer.fit(reverse_x_train, t_train, max_epoch=1, batch_size=batch_size, max_grad=max_grad) # 正解数を初期化 attention_correct_num = 0 peeky_correct_num = 0 base_correct_num = 0 # 精度を測定 for n in range(len(reverse_x_test)): # データを取得 question = reverse_x_test[[n]] # Encoderの入力データ(足し算の式) start_id = t_test[n, 0] # Decoderの入力データの最初の文字(区切り文字) correct = t_test[n, 1:] # 教師データ(足し算の答) # 解答を生成 attention_guess = attention_model.generate(question, start_id, len(correct)) peeky_guess = peeky_model.generate(question, start_id, len(correct)) base_guess = base_model.generate(question, start_id, len(correct)) # 正解数をカウント if attention_guess == list(correct): # 解答と正答が一致したら attention_correct_num += 1 if peeky_guess == list(correct): # 解答と正答が一致したら peeky_correct_num += 1 if base_guess == list(correct): # 解答と正答が一致したら base_correct_num += 1 # 正解率を計算 attention_acc = float(attention_correct_num) / len(reverse_x_test) attention_acc_list.append(attention_acc) peeky_acc = float(peeky_correct_num) / len(reverse_x_test) peeky_acc_list.append(peeky_acc) base_acc = float(base_correct_num) / len(reverse_x_test) base_acc_list.append(base_acc) # 途中経過を表示 print('----- results -----') print('val attention acc:' + str(attention_acc * 100)) print('val peeky acc:' + str(peeky_acc * 100)) print('val base acc:' + str(base_acc * 100))
・出力(クリックで展開)
----- Attention seq2seq -----
| epoch 1 | iter 1 / 351 | time 0[s] | loss 4.08
| epoch 1 | iter 21 / 351 | time 11[s] | loss 3.09
| epoch 1 | iter 41 / 351 | time 23[s] | loss 1.91
| epoch 1 | iter 61 / 351 | time 35[s] | loss 1.73
| epoch 1 | iter 81 / 351 | time 47[s] | loss 1.48
| epoch 1 | iter 101 / 351 | time 59[s] | loss 1.20
| epoch 1 | iter 121 / 351 | time 71[s] | loss 1.15
| epoch 1 | iter 141 / 351 | time 85[s] | loss 1.10
| epoch 1 | iter 161 / 351 | time 97[s] | loss 1.06
| epoch 1 | iter 181 / 351 | time 109[s] | loss 1.05
| epoch 1 | iter 201 / 351 | time 121[s] | loss 1.03
| epoch 1 | iter 221 / 351 | time 132[s] | loss 1.03
| epoch 1 | iter 241 / 351 | time 143[s] | loss 1.02
| epoch 1 | iter 261 / 351 | time 155[s] | loss 1.01
| epoch 1 | iter 281 / 351 | time 167[s] | loss 1.01
| epoch 1 | iter 301 / 351 | time 178[s] | loss 1.00
| epoch 1 | iter 321 / 351 | time 190[s] | loss 1.00
| epoch 1 | iter 341 / 351 | time 202[s] | loss 0.99
----- Peeky seq2seq -----
| epoch 1 | iter 1 / 351 | time 0[s] | loss 4.08
| epoch 1 | iter 21 / 351 | time 6[s] | loss 2.91
| epoch 1 | iter 41 / 351 | time 14[s] | loss 1.89
| epoch 1 | iter 61 / 351 | time 20[s] | loss 1.78
| epoch 1 | iter 81 / 351 | time 27[s] | loss 1.70
| epoch 1 | iter 101 / 351 | time 34[s] | loss 1.56
| epoch 1 | iter 121 / 351 | time 40[s] | loss 1.29
| epoch 1 | iter 141 / 351 | time 47[s] | loss 1.15
| epoch 1 | iter 161 / 351 | time 53[s] | loss 1.09
| epoch 1 | iter 181 / 351 | time 60[s] | loss 1.06
| epoch 1 | iter 201 / 351 | time 67[s] | loss 1.05
| epoch 1 | iter 221 / 351 | time 73[s] | loss 1.04
| epoch 1 | iter 241 / 351 | time 80[s] | loss 1.03
| epoch 1 | iter 261 / 351 | time 86[s] | loss 1.02
| epoch 1 | iter 281 / 351 | time 92[s] | loss 1.02
| epoch 1 | iter 301 / 351 | time 98[s] | loss 1.01
| epoch 1 | iter 321 / 351 | time 104[s] | loss 1.00
| epoch 1 | iter 341 / 351 | time 110[s] | loss 0.98
----- seq2seq -----
| epoch 1 | iter 1 / 351 | time 0[s] | loss 4.08
| epoch 1 | iter 21 / 351 | time 5[s] | loss 3.25
| epoch 1 | iter 41 / 351 | time 11[s] | loss 1.93
| epoch 1 | iter 61 / 351 | time 17[s] | loss 1.78
| epoch 1 | iter 81 / 351 | time 23[s] | loss 1.68
| epoch 1 | iter 101 / 351 | time 28[s] | loss 1.49
| epoch 1 | iter 121 / 351 | time 33[s] | loss 1.25
| epoch 1 | iter 141 / 351 | time 39[s] | loss 1.17
| epoch 1 | iter 161 / 351 | time 44[s] | loss 1.12
| epoch 1 | iter 181 / 351 | time 50[s] | loss 1.08
| epoch 1 | iter 201 / 351 | time 55[s] | loss 1.06
| epoch 1 | iter 221 / 351 | time 60[s] | loss 1.05
| epoch 1 | iter 241 / 351 | time 66[s] | loss 1.04
| epoch 1 | iter 261 / 351 | time 72[s] | loss 1.04
| epoch 1 | iter 281 / 351 | time 77[s] | loss 1.03
| epoch 1 | iter 301 / 351 | time 83[s] | loss 1.02
| epoch 1 | iter 321 / 351 | time 89[s] | loss 1.02
| epoch 1 | iter 341 / 351 | time 96[s] | loss 1.01
----- results -----
val attention acc:0.02
val peeky acc:0.0
val base acc:0.0
(省略)
----- Attention seq2seq -----
| epoch 10 | iter 1 / 351 | time 0[s] | loss 0.00
| epoch 10 | iter 21 / 351 | time 9[s] | loss 0.00
| epoch 10 | iter 41 / 351 | time 19[s] | loss 0.00
| epoch 10 | iter 61 / 351 | time 28[s] | loss 0.00
| epoch 10 | iter 81 / 351 | time 38[s] | loss 0.00
| epoch 10 | iter 101 / 351 | time 47[s] | loss 0.00
| epoch 10 | iter 121 / 351 | time 56[s] | loss 0.00
| epoch 10 | iter 141 / 351 | time 65[s] | loss 0.00
| epoch 10 | iter 161 / 351 | time 75[s] | loss 0.00
| epoch 10 | iter 181 / 351 | time 84[s] | loss 0.00
| epoch 10 | iter 201 / 351 | time 93[s] | loss 0.00
| epoch 10 | iter 221 / 351 | time 103[s] | loss 0.00
| epoch 10 | iter 241 / 351 | time 112[s] | loss 0.00
| epoch 10 | iter 261 / 351 | time 121[s] | loss 0.00
| epoch 10 | iter 281 / 351 | time 130[s] | loss 0.00
| epoch 10 | iter 301 / 351 | time 140[s] | loss 0.00
| epoch 10 | iter 321 / 351 | time 149[s] | loss 0.00
| epoch 10 | iter 341 / 351 | time 158[s] | loss 0.00
----- Peeky seq2seq -----
| epoch 10 | iter 1 / 351 | time 0[s] | loss 0.00
| epoch 10 | iter 21 / 351 | time 5[s] | loss 0.00
| epoch 10 | iter 41 / 351 | time 10[s] | loss 0.00
| epoch 10 | iter 61 / 351 | time 16[s] | loss 0.00
| epoch 10 | iter 81 / 351 | time 21[s] | loss 0.00
| epoch 10 | iter 101 / 351 | time 26[s] | loss 0.00
| epoch 10 | iter 121 / 351 | time 32[s] | loss 0.00
| epoch 10 | iter 141 / 351 | time 37[s] | loss 0.00
| epoch 10 | iter 161 / 351 | time 42[s] | loss 0.00
| epoch 10 | iter 181 / 351 | time 48[s] | loss 0.00
| epoch 10 | iter 201 / 351 | time 53[s] | loss 0.00
| epoch 10 | iter 221 / 351 | time 58[s] | loss 0.00
| epoch 10 | iter 241 / 351 | time 64[s] | loss 0.00
| epoch 10 | iter 261 / 351 | time 69[s] | loss 0.00
| epoch 10 | iter 281 / 351 | time 74[s] | loss 0.00
| epoch 10 | iter 301 / 351 | time 80[s] | loss 0.00
| epoch 10 | iter 321 / 351 | time 85[s] | loss 0.00
| epoch 10 | iter 341 / 351 | time 90[s] | loss 0.00
----- seq2seq -----
| epoch 10 | iter 1 / 351 | time 0[s] | loss 0.81
| epoch 10 | iter 21 / 351 | time 5[s] | loss 0.80
| epoch 10 | iter 41 / 351 | time 10[s] | loss 0.80
| epoch 10 | iter 61 / 351 | time 15[s] | loss 0.80
| epoch 10 | iter 81 / 351 | time 20[s] | loss 0.79
| epoch 10 | iter 101 / 351 | time 25[s] | loss 0.80
| epoch 10 | iter 121 / 351 | time 30[s] | loss 0.80
| epoch 10 | iter 141 / 351 | time 35[s] | loss 0.80
| epoch 10 | iter 161 / 351 | time 40[s] | loss 0.79
| epoch 10 | iter 181 / 351 | time 45[s] | loss 0.80
| epoch 10 | iter 201 / 351 | time 50[s] | loss 0.81
| epoch 10 | iter 221 / 351 | time 55[s] | loss 0.80
| epoch 10 | iter 241 / 351 | time 60[s] | loss 0.80
| epoch 10 | iter 261 / 351 | time 65[s] | loss 0.80
| epoch 10 | iter 281 / 351 | time 70[s] | loss 0.80
| epoch 10 | iter 301 / 351 | time 75[s] | loss 0.80
| epoch 10 | iter 321 / 351 | time 80[s] | loss 0.79
| epoch 10 | iter 341 / 351 | time 86[s] | loss 0.79
----- results -----
val attention acc:100.0
val peeky acc:100.0
val base acc:0.06
3つのパターンの認識精度の推移を重ねてプロットしましょう。
# 作図 plt.figure(figsize=(9, 6)) plt.plot(1 + np.arange(len(base_acc_list)), base_acc_list, marker='v', label='baseline') # seq2seqの結果 plt.plot(1 + np.arange(len(peeky_acc_list)), peeky_acc_list, marker='D', label='peeky') # Peeky seq2seqの結果 plt.plot(1 + np.arange(len(attention_acc_list)), attention_acc_list, marker='o', label='attention') # Attention seq2seqの結果 plt.xlabel('epoch') plt.ylabel('accuracy') plt.title('seq2seq', fontsize=20) #plt.ylim(0, 1) # y軸の表示範囲 plt.grid() # グリッド線 plt.legend() plt.show()
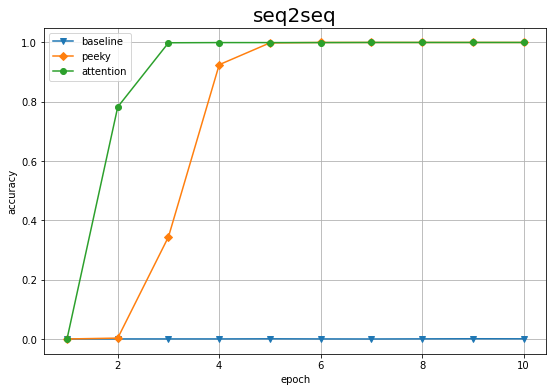
Attention付きseq2seqを利用した結果が一番早く学習できているのを確認できます。
以上でAttention付きseq2seqの実装と学習を行えました。次項では、Attentionについて確認します。
8.3.3 Attentionの可視化
学習済みのAttention付きseq2seqのAttentionの重みをヒートマップにより可視化することで、注意機構がどのように機能しているのかを確認しましょう。
データを1入力して順伝播メソッドを実行します。AttentionSeq2seqのインスタンス変数としてAttentionの重みが保存されます。
# データ番号を設定 idx = [0] # 値を指定 idx = [np.random.randint(0, len(reverse_x_test))] #ランダムに設定 print(idx) # データを取得 x = reverse_x_test[idx] t = t_test[idx] print(x.shape) print(t.shape) # Attentionの重みを生成 attention_model.forward(x, t) # Attentionの重みを取得 weights = attention_model.decoder.attention.attention_weights # リストからNumPy配列に変換 weights = np.array(weights) print(weights.shape)
[4681]
(1, 29)
(1, 11)
(10, 1, 29)
attention_weightsは、Decoderの時系列サイズ$T$(この例ではt_testの要素数-1)、バッチサイズ$N$(この例では1)、Encoderの時系列サイズ$T$(この例ではx_testの要素数)の3次元配列です。
attention_weightsを2次元のヒートマップで可視化するため、2次元配列に変換します。また軸ラベルとして表示するために、EncoderとDecoderに入力した文字IDを文字に変換します。
# 2次元配列に変換 attention_map = weights.reshape((weights.shape[0], weights.shape[2])) print(attention_map.shape) # 反転をされている列を戻す attention_map = attention_map[:, ::-1] # 軸ラベルを作成 row_labels = [id_to_char[c_id] for c_id in x[0, ::-1]] # 再反転 col_labels = [id_to_char[c_id] for c_id in t[0, 1:]] # 区切り文字を除去 print(row_labels) print(col_labels)
(10, 29)
['n', 'o', 'v', ' ', '1', '3', ',', ' ', '1', '9', '8', '7', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ']
['1', '9', '8', '7', '-', '1', '1', '-', '1', '3']
Attentionの重みをヒートマップにより可視化します。
# 作図 plt.figure(figsize=(12, 6)) plt.pcolor(attention_map, cmap='Greys_r', vmin=0.0, vmax=1.0) # ヒートマップ plt.xticks(ticks=np.arange(len(row_labels)) + 0.5, labels=row_labels) # x軸目盛 plt.yticks(ticks=np.arange(len(col_labels)) + 0.5, labels=col_labels) # y軸目盛 plt.gca().invert_yaxis() # y軸を反転 plt.xlabel('input') plt.ylabel('output') plt.title('Attention Weight', fontsize=20) plt.colorbar() plt.show()
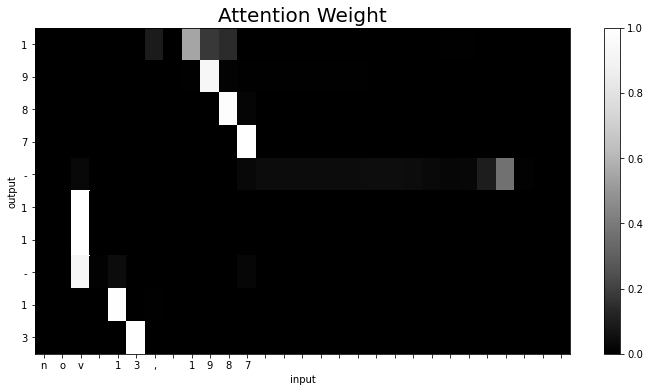
以上で2巻の内容は完了です!
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 2――自然言語処理編』オライリー・ジャパン,2018年.
おわりに
2巻かんりょーーーーーうっ!え?双方向RNN??えっと改良版RNNLMとGRUも飛ばしたんですよねぇ。3巻が終わっ(てあとPythonのことももう少し分かっ)たら1巻の記事から加筆修正していくのでその時にやります。
お疲れ様でした!