はじめに
『ゼロから作るDeep Learning 3』の初学者向け攻略ノートです。『ゼロつく3』の学習の補助となるように適宜解説を加えていきます。本と一緒に読んでください。
本で省略されているクラスや関数の内部の処理を1つずつ解説していきます。
この記事は、主にステップ59「RNNによる時系列データ処理」を補足する内容です。
リカレントニューラルネットワーク(RNN)を用いてサイン波の学習を行います。
【前ステップの内容】
【他の記事一覧】
【この記事の内容】
・ RNNによる時系列データの学習
再帰型ニューラルネットワーク(RNN)を利用して時系列データの学習と推論を行います。RNNレイヤでは、過去の情報を隠れ状態として保存します。 詳しくは、ゼロつく2巻の5章「5.3.1:RNNレイヤの実装【ゼロつく2のノート(実装)】 - からっぽのしょこ」を参照してください 。
次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
予測の推移をアニメーション(gif画像)で確認するのにanimationモジュールのFuncAnimation()を使います。
また、これまでに実装済したクラスを利用します。dezeroフォルダの親フォルダまでのパスをsys.path.append()に指定します。
# 実装済みモジュールの読み込み用設定 import sys sys.path.append('..') #sys.path.append('../deep-learning-from-scratch-3-master') # 実装済みモジュールを読み込み import dezero from dezero.datasets import SinCurve from dezero.models import SimpleRNN import dezero.functions as F
・データセットの確認
まずは、利用する時系列データを確認します。
・訓練データ
この例では、ノイズを加えたサイン波を訓練データとして用います。
SinCurveのtrain引数にTrueを指定して、訓練用のデータセットを持つインスタンスを作成します。
# データセットを作成 train_set = SinCurve(train=True) # データ番号を指定 t = 0 # t番目のデータを取得 print(train_set[t])
(array([0.02675732]), array([-0.01764807]))
スライス機能を使って1つのデータを取り出せます。取り出したデータは、入力データと教師データを1つずつ格納したタプルです。どちらのデータも要素数が1の1次元配列です。
SinCurveは、ランダムな処理を含むため、実行する度に出力が変わります。
作成したインスタンスから、入力データと教師データを作成します。
# 入力データを抽出 xs_train = [example[0] for example in train_set] print(xs_train[:3]) print(len(xs_train)) print(xs_train[0].shape) # 教師データを抽出 ts_train = [example[1] for example in train_set] print(ts_train[:3]) print(len(ts_train)) print(ts_train[0].shape)
[array([0.02675732]), array([-0.01764807]), array([0.02315703])]
999
(1,)
[array([-0.01764807]), array([0.02315703]), array([0.0368507])]
999
(1,)
リスト内包表記を使って順番にデータを取り出します。入力データをxs、教師データをtsとします。どちらも999個の値(要素数が1の1次元配列)を格納したリストです。
データセットをグラフで確認しましょう。
# x軸の値を作成 t_line = np.arange(len(xs_train)) # データセットをプロット plt.figure(figsize=(8, 6)) plt.plot(t_line, xs_train, label='xs') # 入力データ plt.plot(t_line, ts_train, label='ts') # 教師データ plt.plot(np.arange(1000), np.sin(np.linspace(0, 2 * np.pi, 1000)), color='red', linestyle='--', label='y=sin(x)') # ノイズなし plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Sine Curve', fontsize=20) # データの種類 plt.title('T=' + str(len(ts_train)), loc='left') # モデルの設定 plt.legend() plt.grid() #plt.xlim(0, 5) #plt.ylim(-0.1, 0.1) plt.show()
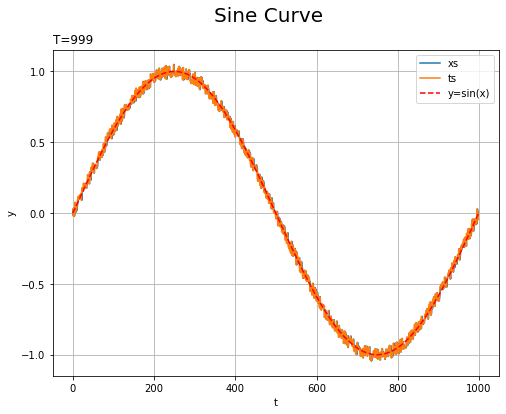
各データの時刻をx軸として表示しています。また、ノイズを含まないサイン波$\sin(\cdot)$を赤色の破線で表示しています。
表示範囲を狭めて確認してみます。
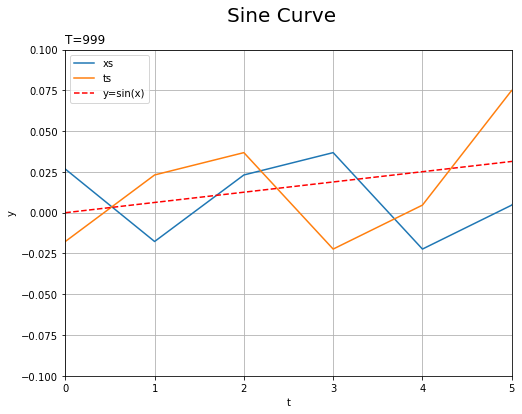
入力データ(青線)と教師データ(オレンジ線)が1時刻ズレて一致しているのが分かります。
時系列データを表すために(?)折れ線グラフにしていますが、散布図にしてみます。
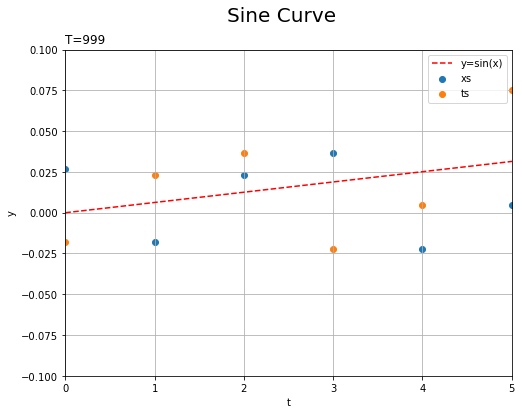
plt.plot()をplt.scatter()に置き換えて実行しました。
$T$個の入力データを$\mathbf{xs} = \{x_0, x_1, x_2, \cdots, x_{T-1}\}$、教師データを$\mathbf{ts} = \{t_0, t_1, t_2, \cdots, t_{T-1}\}$で表します。この例では、$T = 999$です。
グラフのx軸の値は時系列のインデックス$t = 0, 1, 2, \cdots, T-1$、y軸の値は各データ$x_t,\ t_t$の値です。入力データ$x_t$が青色の点、教師データ$t_t$がオレンジの点であり、$x_t = t_{t-1}$です。
(教師データを表すtと時系列を表すtなわけですが、分かりにくくてすみません。以降は登場しません。また、np.cos(x)のxは、入力データxsではなく、0から2 * np.piまでを1000個に等分割した値です。np.cos(x)にノイズを加えた値がyであり、yの最後の要素を除いたものがxsで、最初の要素を除いたものがtsです。)
・テストデータ
また、テストデータにはノイズを含まないコサイン波を用います。
SinCurve()にtrain=Falseを指定することでテストデータも同様に作成できます。
# データセットを作成 test_set = SinCurve(train=False) # 入力データと教師データを抽出 xs_test = [example[0] for example in test_set] ts_test = [example[1] for example in test_set] # x軸の値を作成 t_line = np.arange(len(xs_test)) # データセットをプロット plt.figure(figsize=(8, 6)) plt.plot(t_line, xs_test, label='xs') # 入力データ plt.plot(t_line, ts_test, label='ts') # 教師データ plt.plot(np.arange(1000), np.cos(np.linspace(0, 2 * np.pi, 1000)), color='red', linestyle='--', label='y=cos(x)') # ノイズなし plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Cosine Curve', fontsize=20) # データの種類 plt.title('T=' + str(len(ts_test)), loc='left') # モデルの設定 plt.legend() plt.grid() #plt.xlim(250, 255) #plt.ylim(-0.1, 0.1) plt.show()
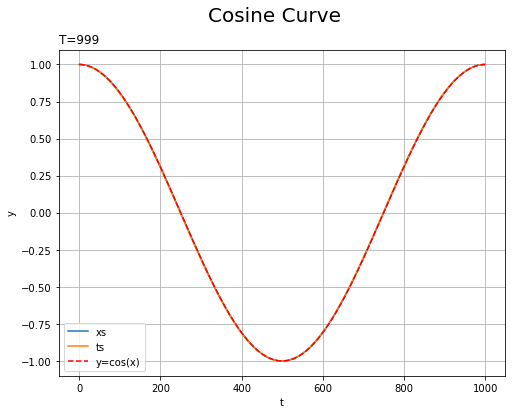
ノイズを含まないため、滑らかな曲線になります。
ただしこの例では、より幅を持たせるため次のように作成することにします。
# (簡易的に)テスト用のデータセットを作成 test_set = np.cos(np.linspace(0, 4 * np.pi, num=1000)) # 入力データと教師データを作成 xs_test = test_set[:-1] ts_test = test_set[1:] # x軸の値を作成 t_line = np.arange(len(xs_test)) # データセットをプロット plt.figure(figsize=(12, 6)) plt.plot(t_line, xs_test, label='xs') # 入力データ plt.plot(t_line, ts_test, label='ts') # 教師データ plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Cosine Curve', fontsize=20) # データの種類 plt.title('T=' + str(len(ts_test)), loc='left') # モデルの設定 plt.legend() plt.grid() #plt.xlim(250, 255) #plt.ylim(-0.1, 0.1) plt.show()
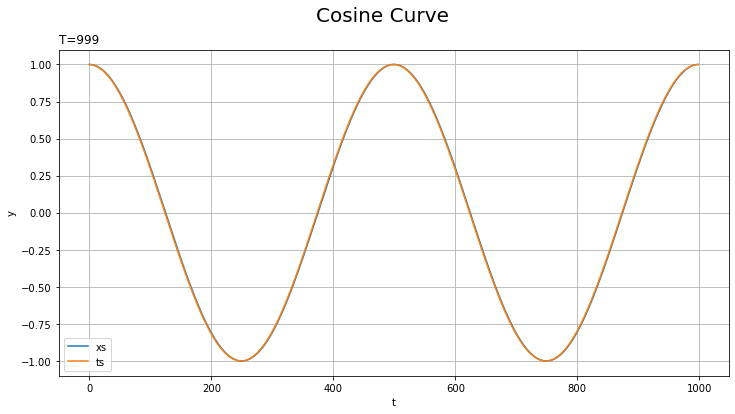
SinCurve内で実行される基本的な処理とほとんど同じです。np.cos()に入力する値を「0から2 * np.pi」から「0から4 * np.pi」にしました。範囲が2倍になりましたが、要素数は同じなので、グラフ上のx軸の値は変わっていません。
範囲を広げたことで、予測が難しくなります(?)。
・時系列データの学習
続いて、RNNを用いて時系列データに対する学習を行います。ノイズ入りサイン波によって学習を行い、コサイン波に対する予測を行います。
基本的な処理はこれまでと同様です。学習(パラメータの更新)を行った後に、テストデータに対する推論を行います。
# 試行回数を指定 max_epoch = 100 # ネッテワークの切断を行うデータ数を指定 bptt_length = 30 # 訓練用のデータセットを初期化 train_set = SinCurve(train=True) # データ数を取得 seqlen = len(train_set) # (簡易的に)テスト用のデータセットを作成 test_set = np.cos(np.linspace(0, 4 * np.pi, num=1000)) xs_test = test_set[:-1] ts_test = test_set[1:] # 中間層の次元数を指定 hidden_size = 100 # RNNモデルのインスタンスを作成 model = SimpleRNN(hidden_size, 1) #model = dezero.models.MLP((hidden_size, hidden_size, 1)) # 最適化手法のインスタンスを作成 optimizer = dezero.optimizers.Adam().setup(model) #optimizer = dezero.optimizers.SGD(0.00005).setup(model) # 推移の確認用のリストを初期化 loss_train_list, loss_test_list = [], [] pred_list = [] # エポックごとの処理 for epoch in range(max_epoch): # 隠れ状態を初期化 model.reset_state() loss, count = 0, 0 # 中間変数を初期化 # 訓練データに対する処理:(学習) for x, t in train_set: # 推論 x = x.reshape(1, 1) # 2次元配列に変形 y = model(x) # 合計損失を計算 loss += F.mean_squared_error(y, t) count += 1 # 指定した回数または1エポックごとの処理 if count % bptt_length == 0 or count == seqlen: # 勾配を計算 model.cleargrads() loss.backward() # ネットワークを切断 loss.unchain_backward() # パラメータを更新 optimizer.update() # 平均損失を計算 avg_loss = float(loss.data) / count loss_train_list.append(avg_loss) # 値を記録 # 途中経過を表示 print('epoch:' + str(epoch + 1)) print('train loss:' + str(avg_loss)) # 隠れ状態を初期化 model.reset_state() tmp_pred, loss = [], 0 # 中間変数を初期化 # テストデータに対する処理:(推論) with dezero.no_grad(): for x, t in zip(xs_test, ts_test): # 推論 x = np.array(x).reshape((1, 1)) # 2次元配列に変形 y = model(x) tmp_pred.append(float(y.data)) # 値を記録 # 合計損失を計算 t = np.array(t).reshape((1, 1)) # 2次元配列に変形 loss += F.mean_squared_error(y, t) # 平均損失を計算 avg_loss = float(loss.data) / len(xs_set) loss_test_list.append(avg_loss) # 値を記録 # i回目の推論結果を記録 pred_list.append(np.array(tmp_pred)) # 途中経過を表示 print('test loss:' + str(avg_loss))
epoch:1
train loss:0.2087385446193373
test loss:0.07712756698456487
epoch:2
train loss:0.05303980453313019
test loss:0.012963443802524916
(省略)
epoch:99
train loss:0.002375721666559195
test loss:0.0022748981968314587
epoch:100
train loss:0.002619202388018717
test loss:0.00304836831082298
損失の推移をグラフ化するために、各試行の平均損失avg_lossをloss_***_listに保存します。
また、テストデータに対する予測の推移をアニメーション化するために、各試行の推論結果tmp_predをpred_listに保存します。アニメーションを作成せずに、最後の結果のみをグラフ化する場合は、本のように処理してください。
MLPを使う場合は、model.reset_state()の処理をコメントアウトする必要があります。
(多層)ニューラルネットワークNN(MLP)とリカレントニューラルネットワークRNNの違いを少しだけ確認します。
これまで扱ったNNでは、各データごとに独立して推論(予測)を行い、パラメータを更新しました。
RNNでは、時刻0の入力データ$x_0$から順番に入力していきます。(NNでも順番に入力しますが、その順番はシャッフルして(生成された順番でなくて)も問題ありません。)
初回の試行では、$x_0$を入力して隠れ状態$h_0$を計算し、さらに$h_0$を用いて0番目の出力データ(予測値)$y_0$を計算します。そして、$y_0$と教師データ(正解ラベル) $t_0$から損失を計算し、勾配を求めてパラメータを更新します。
次の試行では、$x_1$を入力して、$x_1$と$h_0$から$h_1$を計算し、$h_1$から$y_1$を計算します。その後の$y_1$と$t_1$から損失を求めてパラメータを更新する過程は同じです。ただし、1番目の出力データ$y_1$は、$x_0$と$x_1$の情報を用いて求めた予測と言えます。
つまり、時刻$t$の出力データ$y_k$は、これまでの入力データ$\{x_0, \cdots, x_t\}$の情報を考慮した予測であると言えます。このとき、過去の情報$\{x_0, \cdots, x_{t-1}\}$は、隠れ状態$h_{t-1}$として保存されています。(式(59.1)、図59-4)
このように、過去の情報を用いて予測することから、過去のデータの影響を受けて生成される時系列データに適しています。
・学習結果の確認
最後に、学習結果を確認していきます。
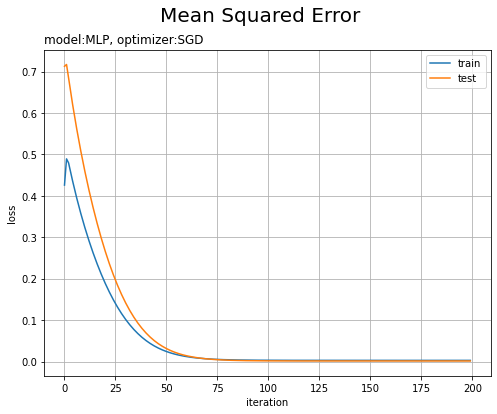
平均2乗誤差の推移をグラフ化します。
# 損失の推移 plt.figure(figsize=(8, 6)) plt.plot(np.arange(max_epoch), loss_train_list, label='train') # 訓練データ plt.plot(np.arange(max_epoch), loss_test_list, label='test') # テストデータ plt.xlabel('iteration') plt.ylabel('loss') plt.suptitle('Mean Squared Error', fontsize=20) plt.title('model:' + str(model.__class__.__name__) + ', optimizer:' + str(optimizer.__class__.__name__), loc='left') # モデルの設定 plt.legend() plt.grid() plt.show()
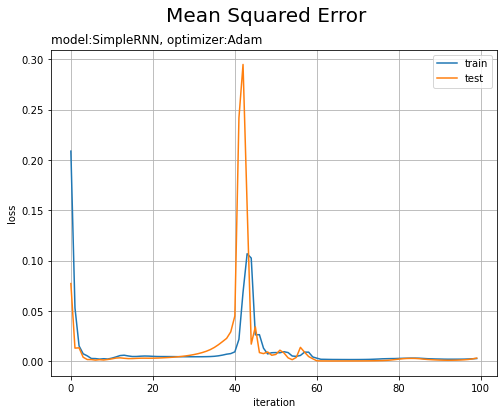
途中で波打っていますが、試行回数が増えるに従って損失が下がっています。
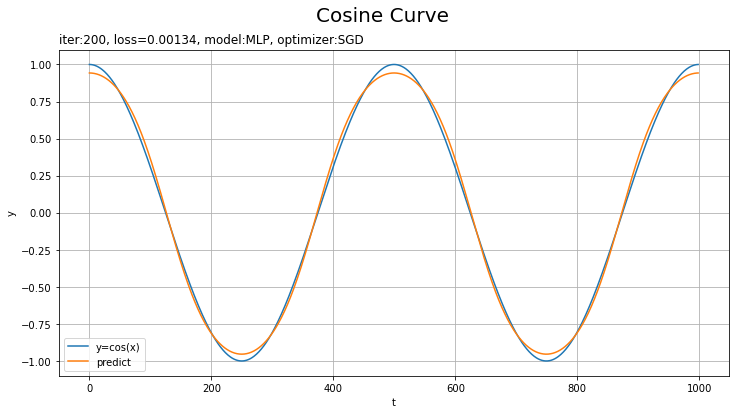
テストデータに対する予測を作図します。
# x軸の値を作成 t_line = np.arange(len(xs_test)) # テストデータに対する予測を作図 plt.figure(figsize=(12, 6)) plt.plot(t_line, xs_test, label='y=cos(x)') # テストデータ plt.plot(t_line, pred_list[max_epoch - 1], label='predict') # 予測 plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Cosine Curve', fontsize=20) # データの種類 plt.title('iter:' + str(max_epoch) + ', loss=' + str(np.round(loss_test_list[max_epoch - 1], 5)) + ', model:' + str(model.__class__.__name__) + ', optimizer:' + str(optimizer.__class__.__name__), loc='left') # モデルの設定 plt.legend() plt.grid() plt.show()

上手く予測(真の曲線を近似)できています。
予測の推移をアニメーションで確認してみましょう。
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(12, 6)) # フレームの間隔を指定:フレームを間引く場合 #n = 2 # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # フレームを間引く場合 #i *= n # i回目の試行の予測を作図 plt.plot(t_line, xs_test, label='y=cos(x)') # テストデータ plt.plot(t_line, pred_list[i], label='predict') # 予測 plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Cosine Curve', fontsize=20) # データの種類 plt.title('iter:' + str(i + 1) + ', loss=' + str(np.round(loss_test_list[i], 5)), loc='left') # 試行回数 plt.legend() plt.grid() plt.ylim(-1.1, 1.1) # gif画像を作成 trace_anime = FuncAnimation(fig, update, frames=max_epoch, interval=100) #trace_anime = FuncAnimation(fig, update, frames=max_epoch // n, interval=100) # フレームを間引く場合 # gif画像を保存 trace_anime.save('step59_rnn.gif')
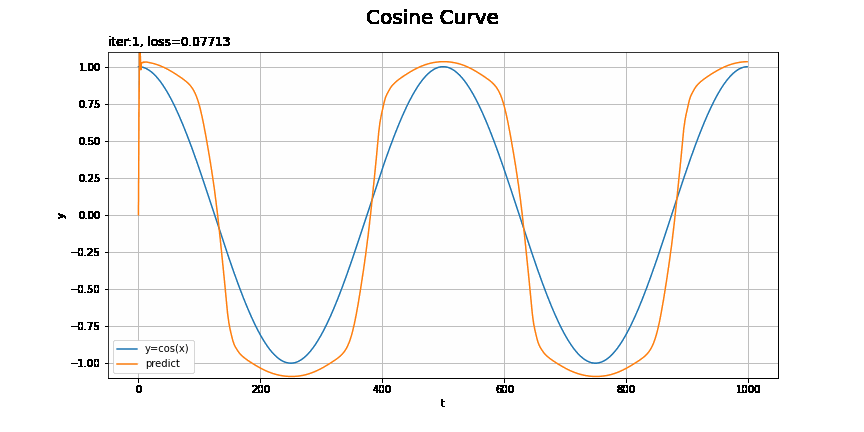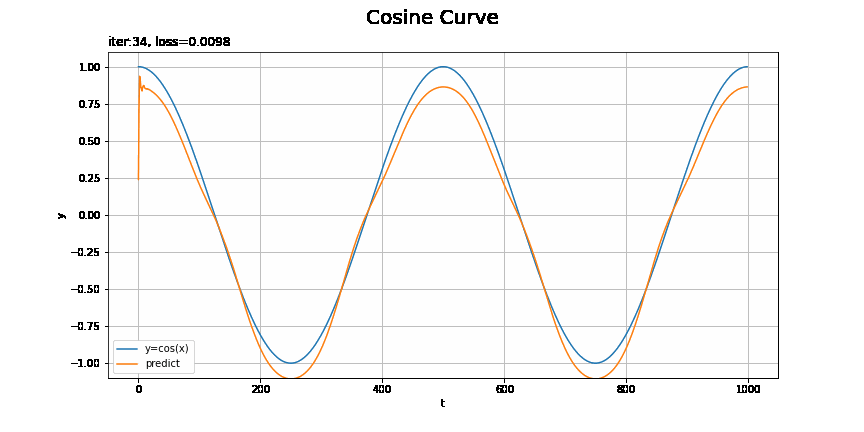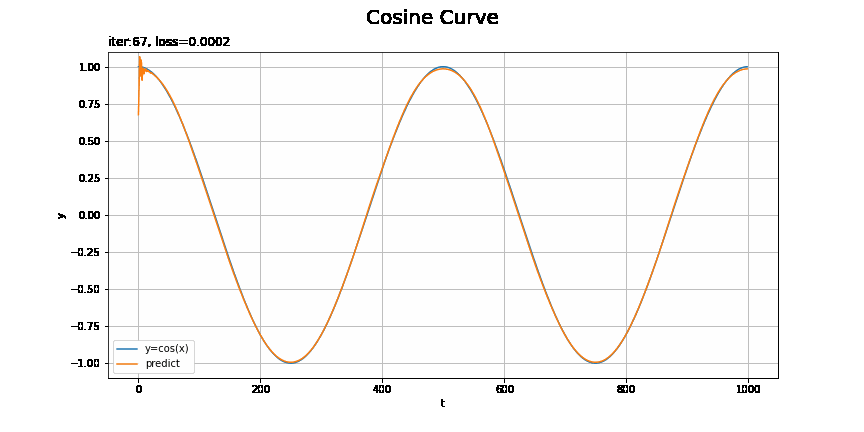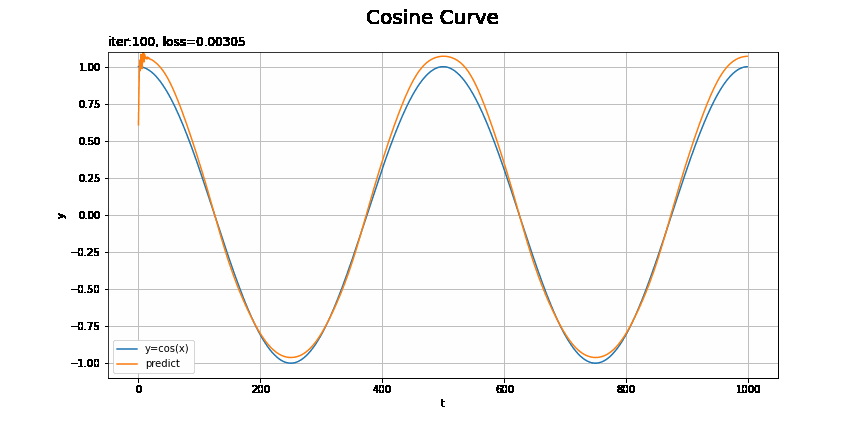
損失のグラフが波打っているタイミングで、当てはまりが悪くなっているのを確認できます。
・他の設定での結果
これまでのニューラルネットワークを用いて試した結果を確認します。
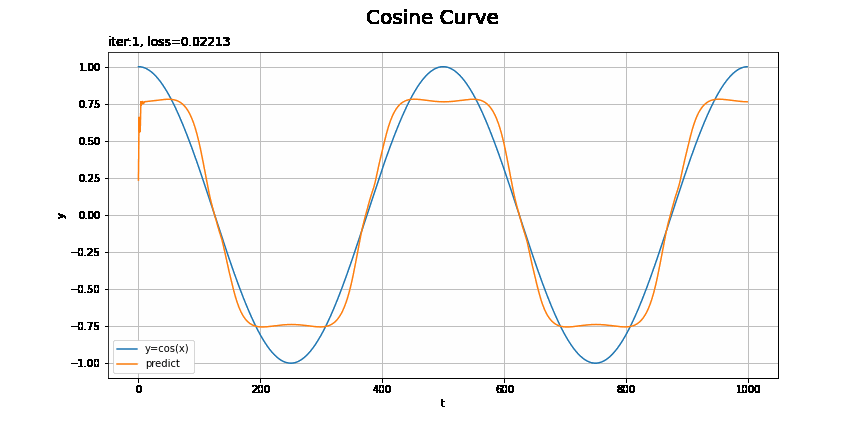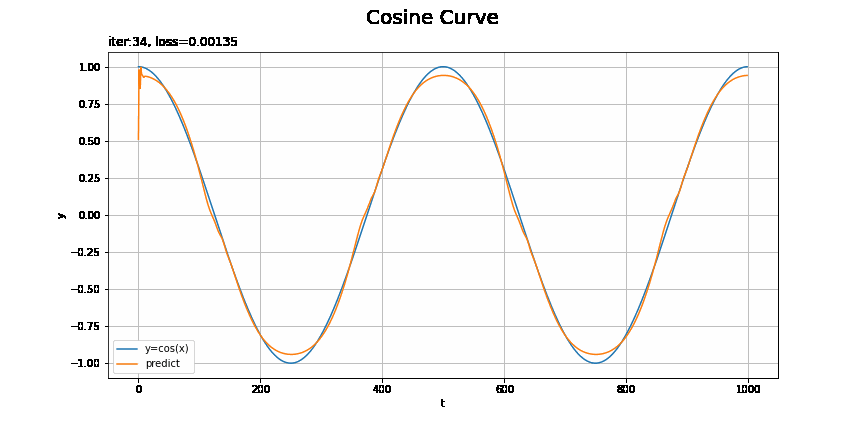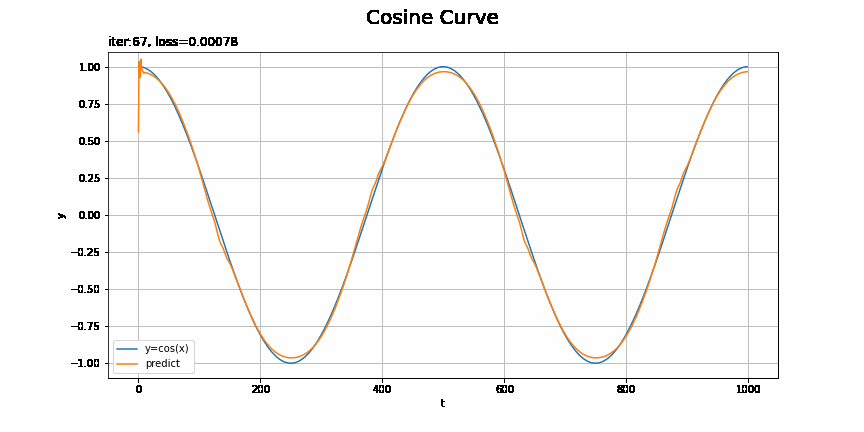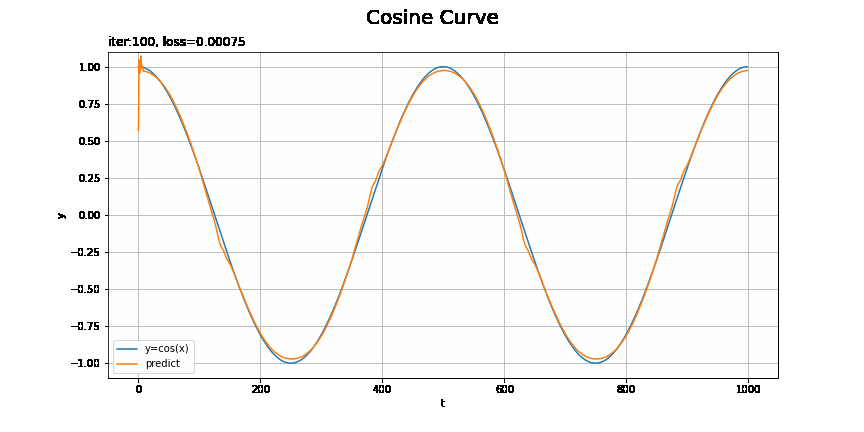
・モデル:RNN、オプティマイザ:SGD、学習率:0.00005
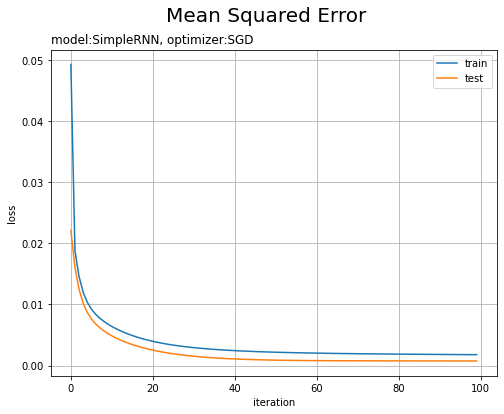
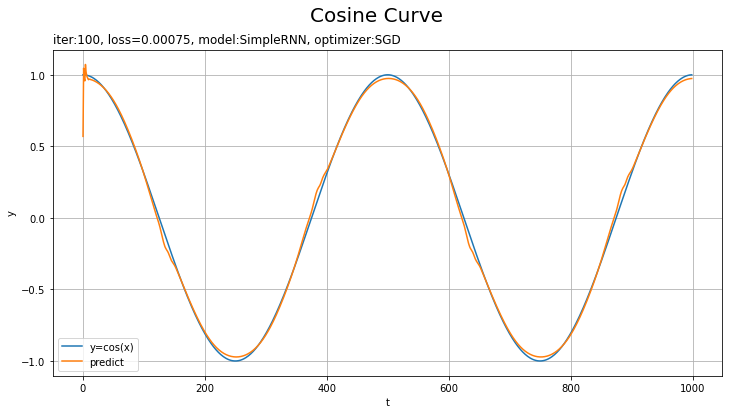
テストデータの方が損失が小さいのは、ノイズを含まないのでデータへの当てはまりが良くなるのだと思います。
・モデル:MLP、オプティマイザ:Adam、学習率:0.001
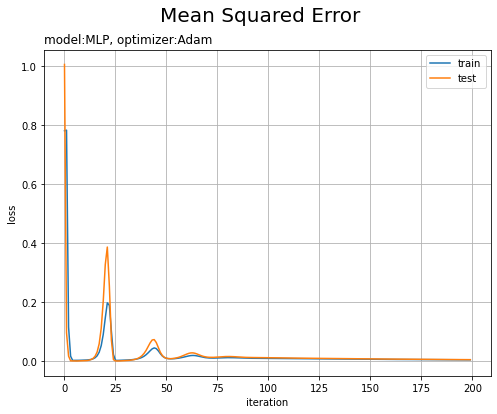
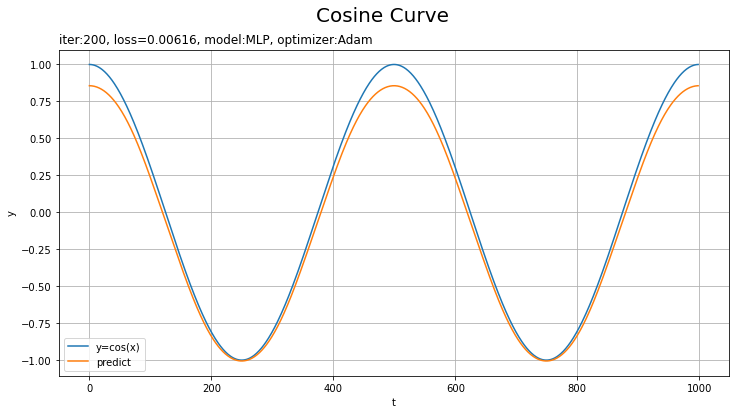
損失が波打つのは、最小値を飛び越えたときなのかな?
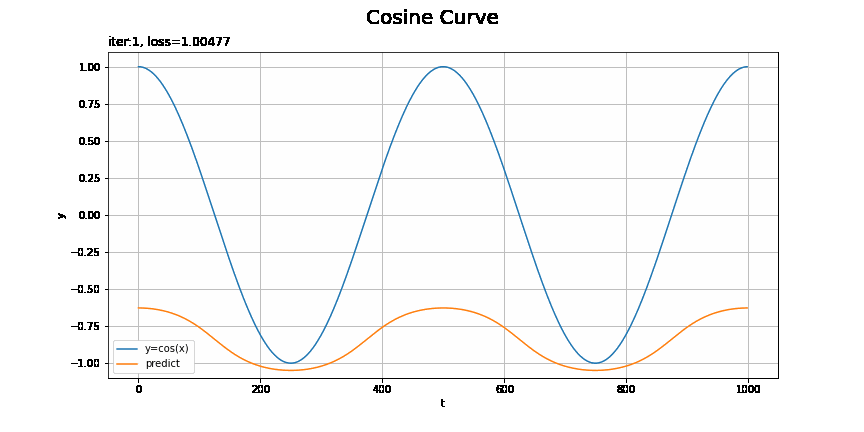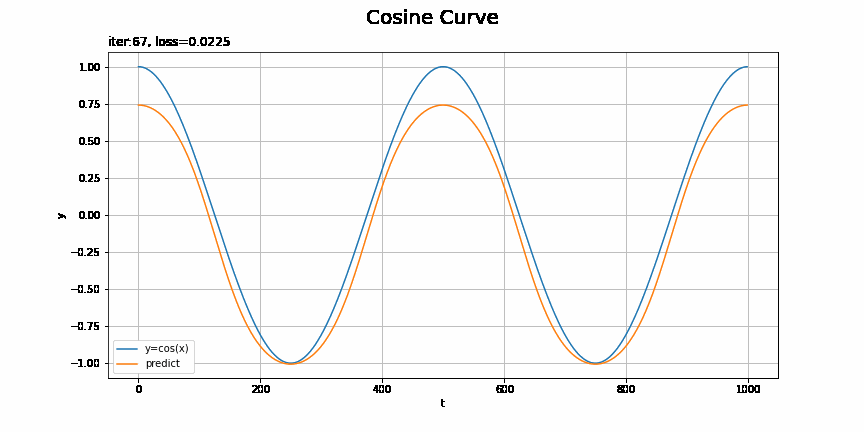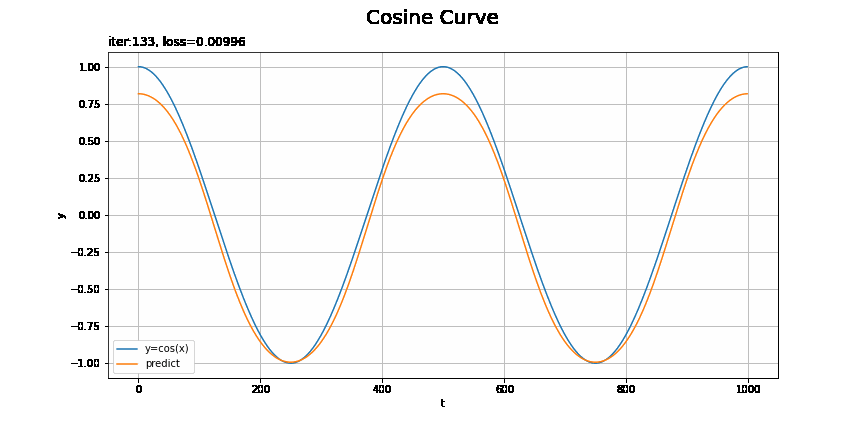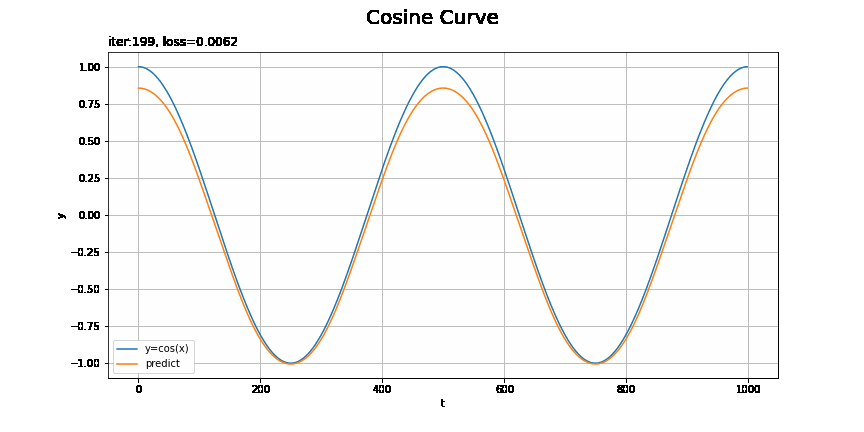
画像ファイルが重くなるため、表示するフレームを間引いています。FuncAnimation()のフレーム数の引数framesにmax_epoch // nを指定して、またupdata()に定義する作図処理の前にインデックスをi *= nとします。この例はnを2としています。
・モデル:MLP、オプティマイザ:SGD、学習率:0.00005
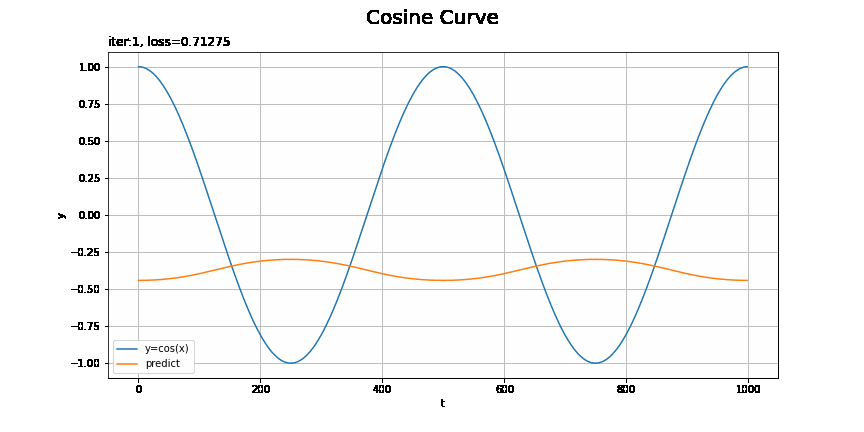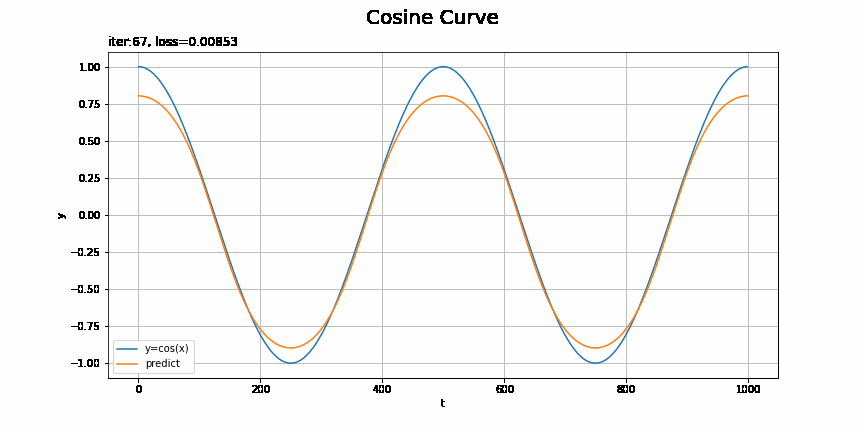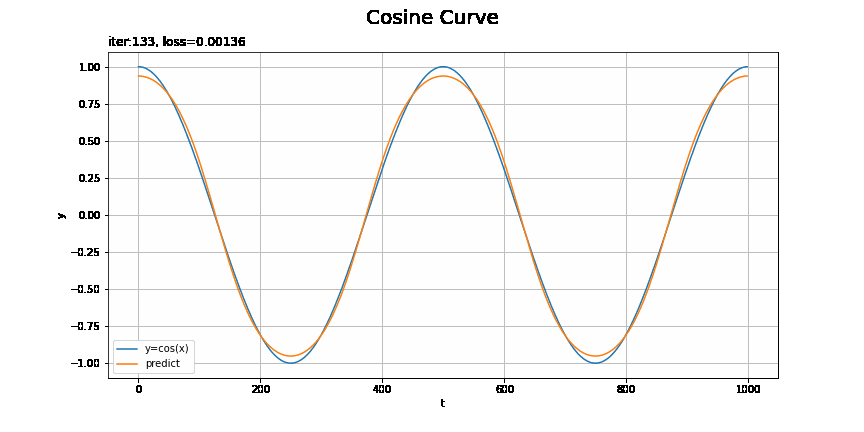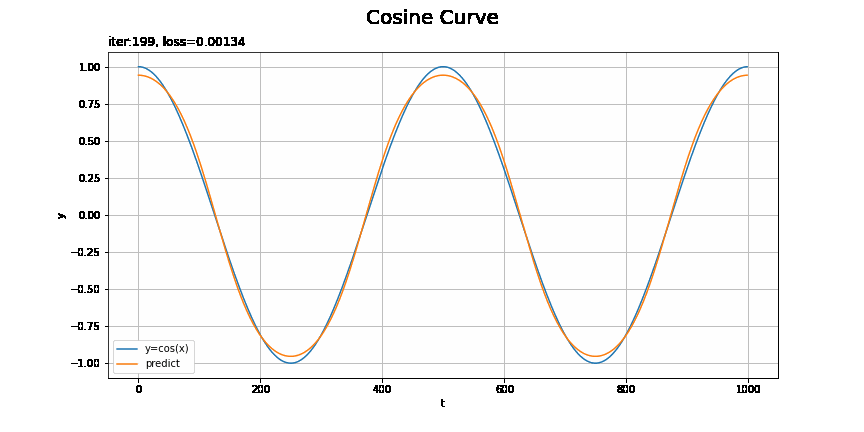
こちらも1試行おきに表示しています。
この問題だと設定によってそこまで差があるようにはみえないような?むしろRNNの$t=0$付近が気になる。時刻が小さい頃は、過去の入力の情報が少ないために予測が悪くなったりするのでしょうか?
以上で、RNNによる時系列データの学習を行えました。次のステップでは、隠れ状態に加えて記憶セルを導入するLSTMを考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 3 ――フレームワーク編』オライリー・ジャパン,2020年.
おわりに
まぁ詳しい話は2巻をやりましょう。あと1ステップ!
この記事の投稿日の前日(この記事を書いている間)に公開されたカバー動画どうぞ。
昨年巷でよく流れていたのとは別の曲です。ハロプロで香水と言ったらこの曲!
【次ステップの内容】