はじめに
『ゼロから作るDeep Learning 3』の初学者向け攻略ノートです。『ゼロつく3』の学習の補助となるように適宜解説を加えていきます。本と一緒に読んでください。
本で省略されているクラスや関数の内部の処理を1つずつ解説していきます。
この記事は、主にステップ60「LSTMとデータローダ」を補足する内容です。
LSTMを用いてサイン波の学習を行います。
【前ステップの内容】
【他の記事一覧】
【この記事の内容】
・LSTMによる時系列データの学習
RNNの発展形であるLSTMを利用して時系列データの学習と推論を行います。LSTMレイヤでは、隠れ状態の他に記憶セルとして過去の情報を保存します。詳しくは、ゼロつく2巻の6章「6.2.3-6:勾配消失とLSTM【ゼロつく2のノート(実装)】 - からっぽのしょこ」を参照してください。
次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
予測の推移をアニメーション(gif画像)で確認するのにanimationモジュールのFuncAnimation()を使います。
また、これまでに実装済したクラスを利用します。dezeroフォルダの親フォルダまでのパスをsys.path.append()に指定します。
# 実装済みモジュールの読み込み用設定 import sys sys.path.append('..') #sys.path.append('../deep-learning-from-scratch-3-master') # 実装済みモジュールを読み込み import dezero from dezero.datasets import SinCurve from dezero import SeqDataLoader from dezero.models import BetterRNN import dezero.functions as F
・時系列データの学習
LSTMを用いて時系列データに対する学習を行います。ノイズ入りサイン波によって学習を行い、コサイン波に対する予測を行います。利用するデータセットについては、前ステップの記事を参照してください。
基本的な処理は前ステップと同様です。学習(パラメータの更新)を行った後に、テストデータに対する推論を行います。
# 試行回数を指定 max_epoch = 100 # ネットワークの切断を行うデータ数を指定 bptt_length = 30 # バッチサイズを指定 batch_size = 30 # 訓練用のデータセットを初期化 train_set = SinCurve(train=True) dataloader = SeqDataLoader(train_set, batch_size=batch_size) # データ数を取得 seqlen = len(train_set) # (簡易的に)テスト用のデータセットを作成 test_set = np.cos(np.linspace(0, 4 * np.pi, num=1000)) xs_test = test_set[:-1] ts_test = test_set[1:] # 中間層の次元数を指定 hidden_size = 100 # LSTMモデルのインスタンスを作成 model = BetterRNN(hidden_size, 1) # 最適化手法のインスタンスを作成 optimizer = dezero.optimizers.Adam().setup(model) #optimizer = dezero.optimizers.SGD(0.00005).setup(model) # 推移の確認用のリストを初期化 loss_train_list, loss_test_list = [], [] pred_list = [] # エポックごとの処理 for epoch in range(max_epoch): # 隠れ状態を初期化 model.reset_state() loss, count = 0, 0 # 中間変数を初期化 # 訓練データに対する処理:(学習) for x, t in dataloader: # 推論 y = model(x) # 合計損失を計算 loss += F.mean_squared_error(y, t) count += 1 # 指定した回数または1エポックごとの処理 if count % bptt_length == 0 or count == seqlen: # 勾配を計算 model.cleargrads() # 勾配を初期化 loss.backward() # ネットワークを切断 loss.unchain_backward() # パラメータを更新 optimizer.update() # 平均損失を計算 avg_loss = float(loss.data) / count loss_train_list.append(avg_loss) # 途中経過を表示 print('epoch:' + str(epoch + 1)) print('train loss:' + str(avg_loss)) # 隠れ状態を初期化 model.reset_state() tmp_pred, loss = [], 0 # 中間変数を初期化 # テストデータに対する処理:(推論) with dezero.no_grad(): for x, t in zip(xs_test, ts_test): # 推論 x = np.array(x).reshape((1, 1)) # 2次元配列に変換 y = model(x) tmp_pred.append(float(y.data)) # 値を記録 # 合計損失を計算 t = np.array(t).reshape((1, 1)) # 2次元配列に変換 loss += F.mean_squared_error(y, t) # 平均損失を計算 avg_loss = float(loss.data) / len(xs_test) loss_test_list.append(avg_loss) # 値を記録 # i回目の推論結果を記録 pred_list.append(np.array(tmp_pred)) # 途中経過を表示 print('test loss:' + str(avg_loss))
epoch:1
train loss:0.6101652676440917
test loss:0.48883494777101516
epoch:2
train loss:0.5052666077373874
test loss:0.38851875594549407
(省略)
epoch:99
train loss:0.012038154213439086
test loss:0.0011738729942530701
epoch:100
train loss:0.011955961290980022
test loss:0.0011573817540585624
損失の推移をグラフ化するために、各試行の平均損失avg_lossをloss_***_listに保存します。
また、テストデータに対する予測の推移をアニメーション化するために、各試行の推論結果tmp_predをpred_listに保存します。アニメーションを作成せずに、最後の結果のみをグラフ化する場合は、本のように処理してください。
バッチデータを入力するため、処理にかかる時間が短くなりました。
テストデータもSeqDataLoaderで扱おうと思ったのですが、ちょっと分かりにくくなったので諦めました。そのため、前ステップと同じく1データずつ処理しています。
・学習結果の確認
最後に、学習結果を確認していきます。
平均2乗誤差の推移をグラフ化します。
# 損失の推移 plt.figure(figsize=(8, 6)) plt.plot(np.arange(max_epoch), loss_train_list, label='train') # 訓練データ plt.plot(np.arange(max_epoch), loss_test_list, label='test') # テストデータ plt.xlabel('iteration') plt.ylabel('loss') plt.suptitle('Mean Squared Error', fontsize=20) plt.title('model:' + str(model.__class__.__name__) + ', optimizer:' + str(optimizer.__class__.__name__), loc='left') # モデルの設定 plt.legend() plt.grid() plt.show()
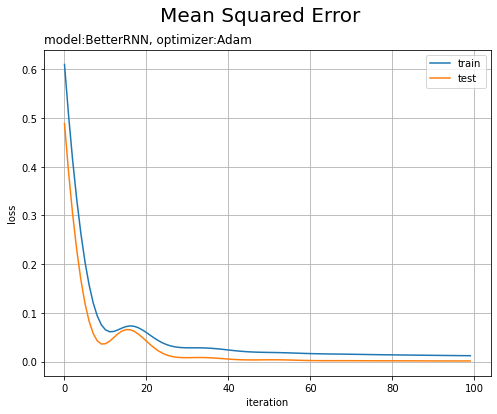
試行回数が増えるに従って損失が下がっています。テストデータはノイズを含まないので、予測の当てはまりが良くなり損失が小さくなっているのだと思います。
テストデータに対する予測を作図します。
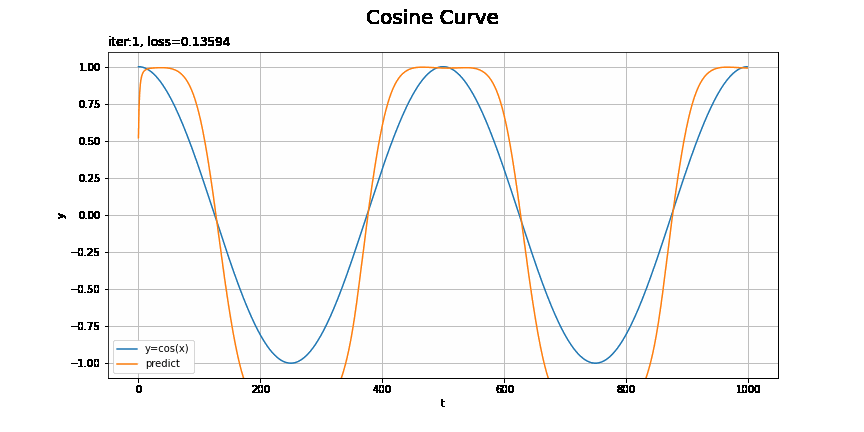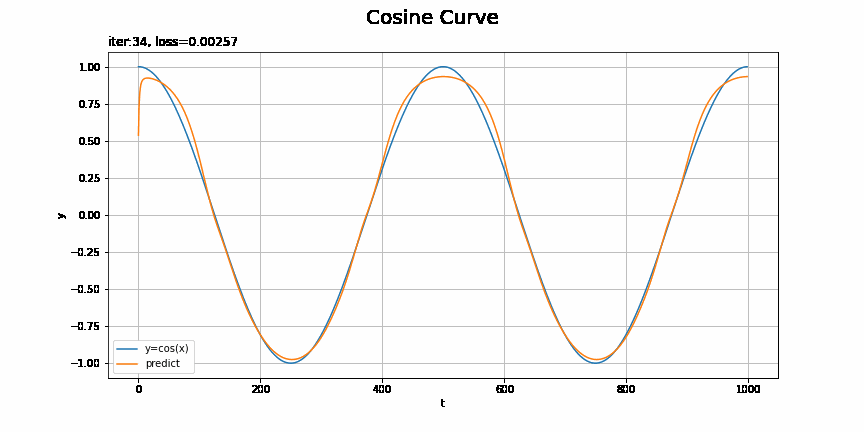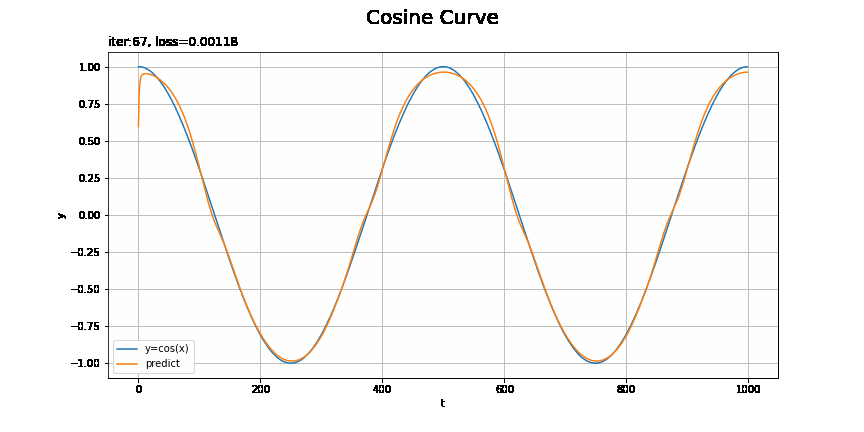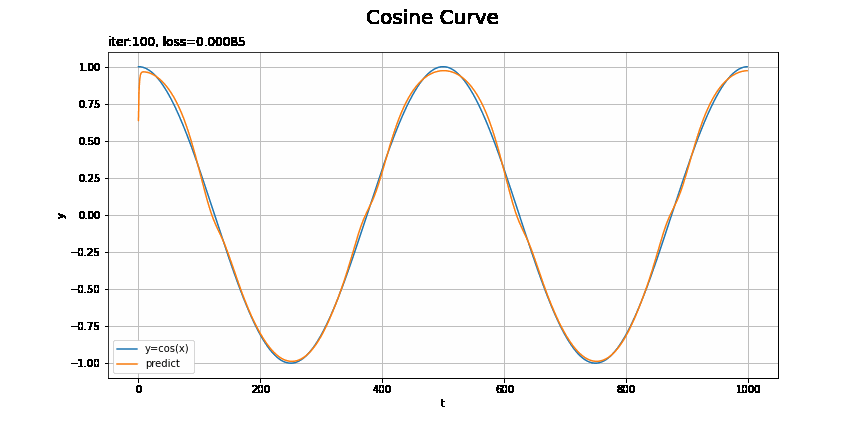
# x軸の値を作成 t_line = np.arange(len(ts_test)) # テストデータに対する予測を作図 plt.figure(figsize=(12, 6)) plt.plot(t_line, xs_test, label='y=cos(x)') # テストデータ plt.plot(t_line, pred_list[max_epoch - 1], label='predict') # 予測 plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Cosine Curve', fontsize=20) # データの種類 plt.title('iter:' + str(max_epoch) + ', loss=' + str(np.round(loss_test_list[max_epoch - 1], 5)) + ', model:' + str(model.__class__.__name__) + ', optimizer:' + str(optimizer.__class__.__name__), loc='left') # モデルの設定 plt.legend() plt.grid() plt.show()
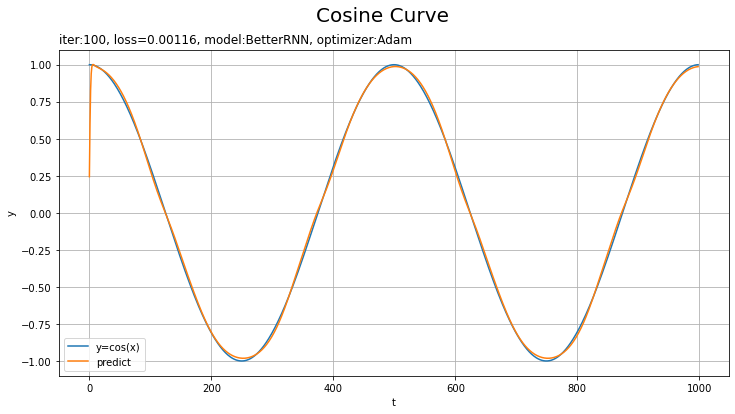
上手く予測(真の曲線を近似)できています。
予測の推移をアニメーションで確認してみましょう。
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(12, 6)) # フレームの間隔を指定:フレームを間引く場合 #n = 2 # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # フレームを間引く場合 #i *= n # i回目の試行の予測を作図 plt.plot(t_line, xs_test, label='y=cos(x)') # テストデータ plt.plot(t_line, pred_list[i], label='predict') # 予測 plt.xlabel('t') # 時系列 plt.ylabel('y') # データの値 plt.suptitle('Cosine Curve', fontsize=20) # データの種類 plt.title('iter:' + str(i + 1) + ', loss=' + str(np.round(loss_test_list[i], 5)), loc='left') # 試行回数 plt.legend() plt.grid() plt.ylim(-1.1, 1.1) # gif画像を作成 trace_anime = FuncAnimation(fig, update, frames=max_epoch, interval=100) # max_epoch // n # フレームを間引く場合 # gif画像を保存 trace_anime.save('step60_lstm.gif')
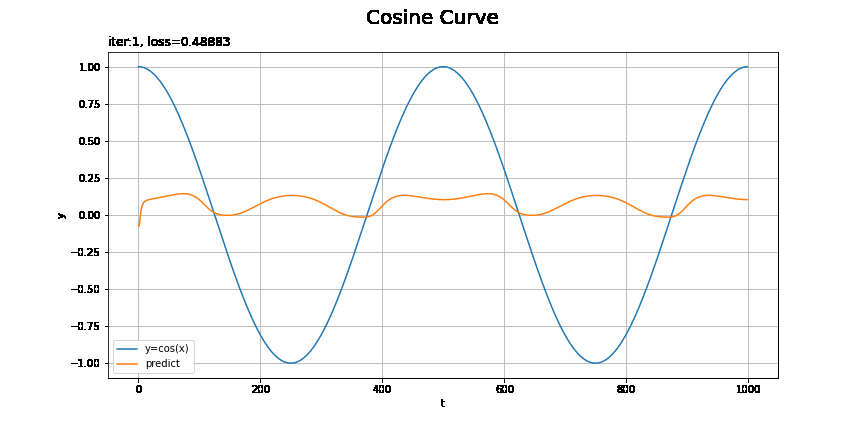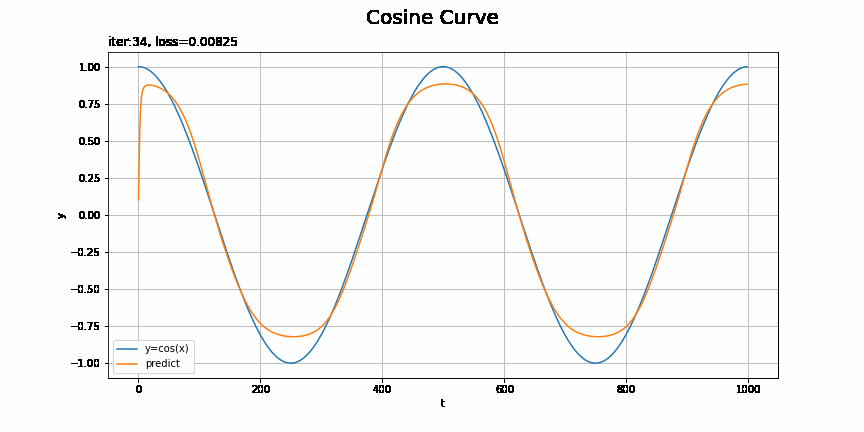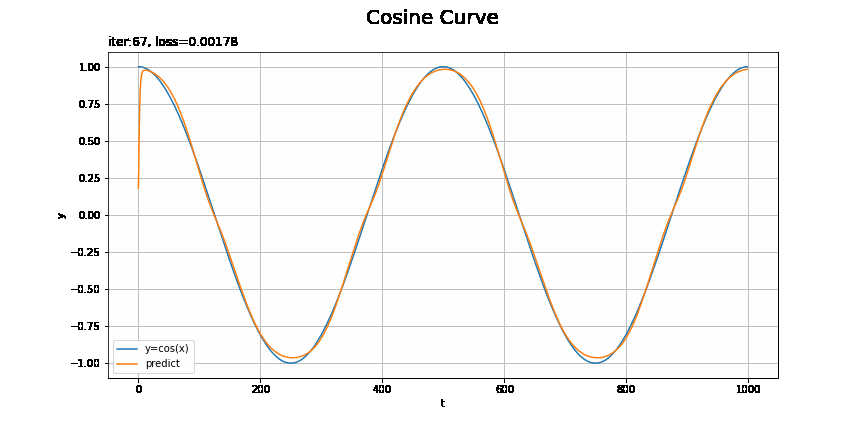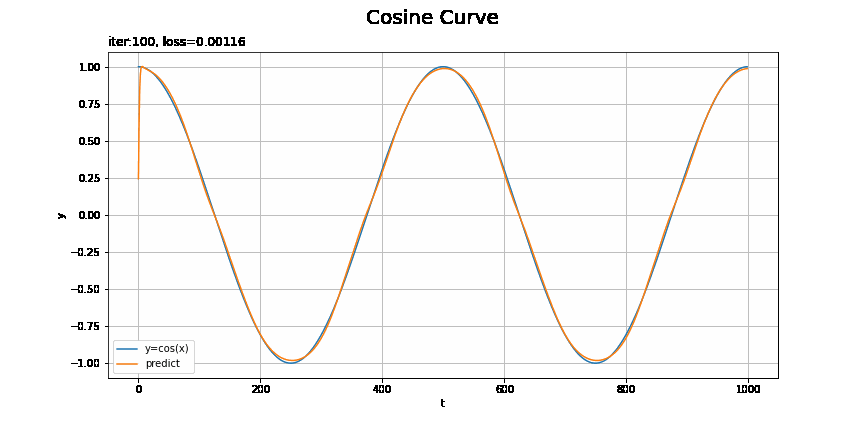
損失のグラフが波打っているタイミングで、最小値を飛び越えて戻ってきたようなことが起きているんですかね(ステップ46)。
・他の設定での結果
・モデル:LSTM、オプティマイザ:SGD、学習率:0.005
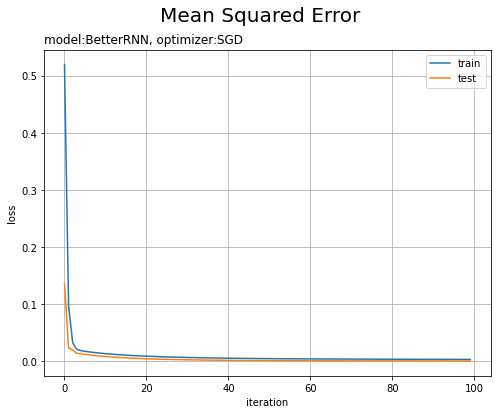
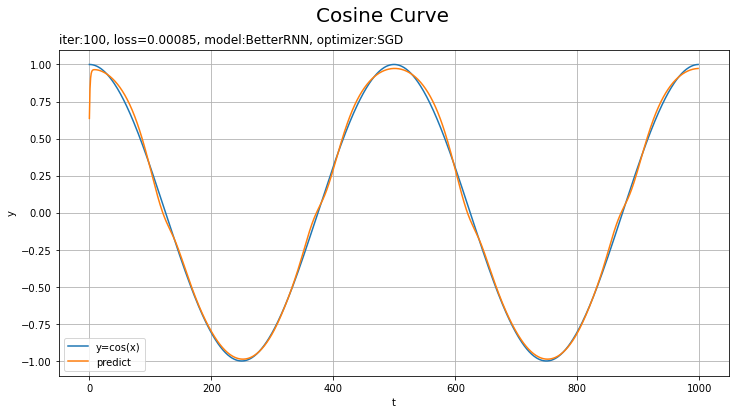
RNNやMLPを使った場合の結果は前ステップの記事を参照してください。
以上で、3巻の内容は完了しました。次は、2巻でやった文章生成まで(自力で)(いつか)実装したいです。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 3 ――フレームワーク編』オライリー・ジャパン,2020年.
おわりに
3巻完了~~~。お疲れ様でした!
いやぁ最初にパラパラ全体の雰囲気を見たときには、2ステップでRNNとLSTMをやるなんてハードだなと思ったものですが、ここまで来てみれば1ステップで実装できてしまうという感動が凄い。
ゼロからDLシリーズは約束された良書です。4巻が待ち遠しい。
エンディングとして先日公開されたカバー動画を観ましょう♪
このYouTube番組は選曲がとても良い。
【次ステップの内容】
完!