はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、6.1.8項「MNISTデータセットによる更新手法の比較」の内容になります。MNISTデータセットに対して、6.1節で実装した5つの最適化手法を用いて学習を行い、学習の精度を比較します。
【前節の内容】
【他の節の内容】
【この節の内容】
6.1.8 MNISTデータセットによる更新手法の比較
6.1節で実装した確率的勾配降下法に関する5つの最適化手法の性能を比較するために、この項ではMNISTデータセットに対する学習を行います。交差エントロピー誤差がどれだけ小さくなるのか、どれだけ早く学習が進むのかを比較します。
この項では、5層のニューラルネットワークを用います。そのための多層ニューラルネットワークのクラスは、6章の最後に実装します。そのためここではマスターデータから同じものを読み込みましょう。またMNISTデータセットも読み込みます。マスターデータからの読み込みに関する詳しい解説は「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を確認してください。
# この項で利用するライブラリを読み込む import numpy as np import matplotlib.pyplot as plt # データ読み込み用ライブラリを読み込む import sys, os # ファイルパスを指定 sys.path.append('C:\\Users\\「ユーザー名」\\Documents\\・・・\\deep-learning-from-scratch-master') # MNISTデータセット読み込み関数を読み込む from dataset.mnist import load_mnist # 多層ニューラルネットワーククラスを読み込む from common.multi_layer_net import MultiLayerNet # 画像データを読み込む (x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_label=True) print(x_train.shape) print(t_train.shape)
(60000, 784)
(60000, 10)
バッチサイズと試行回数を指定します。
# 訓練データ数 train_size = x_train.shape[0] # バッチサイズ指定 batch_size = 128 # 試行回数を指定 max_iterations = 2001
6.1節で実装した5つの最適化手法のインスタンスを作成します。それぞれの手法名をキーとして各クラスのインスタンスをディクショナリ変数optimizersに格納します。
# 各手法のインスタンスをディクショナリ変数に格納 optimizers = {} optimizers['SGD'] = SGD() optimizers['Momentum'] = Momentum() optimizers['AdaGrad'] = AdaGrad() optimizers['RMSProp'] = RMSProp() optimizers['Adam'] = Adam() print(optimizers.keys())
dict_keys(['SGD', 'Momentum', 'AdaGrad', 'RMSProp', 'Adam'])
学習率などのハイパーパラメータはデフォルト値を用います。全ての手法のクラスで更新メソッドをupdate()に統一して実装しているため、キーを変更するだけで手法を切り替えることができます。
手法ごとに多層ニューラルネットワークのインスタンスを作成します。こちらも手法名をキーとしてディクショナリ変数networksに格納します。ここでは5層のニューラルネットワークとするため、中間層のニューロン数の引数hidden_size_listに4つの値をリスト型変数で指定します(詳しくはこの章の最後の実装時に説明します)。任意の値を指定できますが、ここでは全て100とします。
また手法ごとの交差エントロピー誤差を記録するためのリスト型変数も作成し、ディクショナリ変数train_lossに格納しておきます。
# 手法ごとにディクショナリ変数に格納 networks = {} train_loss = {} for key in optimizers.keys(): # 多層ニューラルネットワーク networks[key] = MultiLayerNet( input_size=784, hidden_size_list=[100, 100, 100, 100], output_size=10 ) # 交差エントロピー誤差の受け皿 train_loss[key] = []
ちなみに入出力層の2つと中間層の4つの「間の数」で5層ニューラルネットワークとなります。
5層のニューラルネットワークによる手書き文字認識を行います。処理の流れは「5.7.4:誤差逆伝播法を使った学習【ゼロつく1のノート(実装)】 - からっぽのしょこ」と同様です。
主な違いは、5つの手法を切り替えるためのforループが組み込まれている点です。ただしランダムに取り出すバッチデータが手法ごとに変わってしまうと正しい比較ができないため、バッチデータの抽出後にループ処理を組み込みます。必要な変数等をディクショナリ変数に格納しておき、forでキーを順番に入れ替えて必要な変数やメソッドにアクセスする点はこれまでと同じです。
もう一点、パラメータの更新に関する処理も5章と異なりますが、これも6.1節でこれまで行ってきた方法に変更するだけです。
# 手書き文字認識 for i in range(max_iterations): # ランダムにバッチデータ抽出 batch_mask = np.random.choice(train_size, batch_size, replace=False) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 手法ごとに学習 for key in optimizers.keys(): # 勾配を計算 grads = networks[key].gradient(x_batch, t_batch) # パラメータを更新 optimizers[key].update(networks[key].params, grads) # 損失関数の計算 loss = networks[key].loss(x_batch, t_batch) train_loss[key].append(loss) # 交差エントロピー誤差を記録 # (動作確認も兼ねて)100回ごとに損失関数の値を表示 if i % 100 == 0: print("===========" + "iteration:" + str(i) + "===========") for key in optimizers.keys(): print( key + " " * (8 - len(key)) + ":" + # (`8`は`key`の最大文字数) str(np.round(train_loss[key][i], 5)) )
===========iteration:0===========
SGD :2.34442
Momentum:2.44387
AdaGrad :2.10122
RMSProp :13.97741
Adam :2.15128
===========iteration:100===========
SGD :1.57598
Momentum:0.3157
AdaGrad :0.14139
RMSProp :0.29279
Adam :0.28299
===========iteration:200===========
(省略)
===========iteration:1900===========
SGD :0.13902
Momentum:0.02652
AdaGrad :0.01789
RMSProp :0.07395
Adam :0.02868
===========iteration:2000===========
SGD :0.16854
Momentum:0.02802
AdaGrad :0.01683
RMSProp :0.02769
Adam :0.01085
動作確認については本質的な内容ではないので、コピペでもいいですよ。(文字列に対して*数値とすると、同じ文字列をその数値回繰り返します。ここでは半角スペースを複製して調節しています。)
交差エントロピー誤差の推移をグラフ化します。forを使っているのは5つ分書くのが面倒なだけです(正確には、後に特定の手法だけを比較したくなったようなときに、ここを書き換えなければいけないのはトラブルの種になるためです。このように実装しておけば、最初に手法を設定した1か所だけ変更すればそのまま同じ処理を行えます)。
# 作図用のx軸の点 iterations = np.arange(max_iterations) # 作図 for key in optimizers.keys(): plt.plot(iterations, train_loss[key], label=key, linewidth=0.5, alpha=0.9) plt.xlabel("iterations") # x軸ラベル plt.ylabel("loss") # y軸ラベル plt.ylim(0, 1) # y軸の範囲 plt.legend() # 凡例 plt.show()
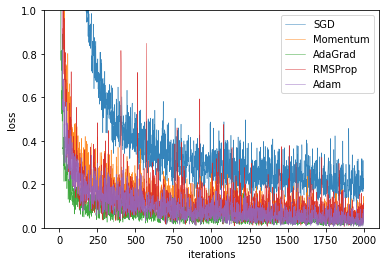
この結果からは、(見にくいですが)AdaGradとAdamの性能がよく見えます。またAdaGradの方が早く収束しています。図6-9は推移を滑らかにする数値計算を行っています。
ただし、一度の結果で判断するのではなく、ハイパーパラメータを調整して比較する必要があります。
実装はしませんが、図6-9を再現できるコードを載せておきます(と言っても用意されている関数を用いるために1つ処理を加えるだけです)。
# 推移を滑らかに変換するための関数を読み込む from common.util import smooth_curve # 作図用のx軸の点 iterations = np.arange(max_iterations) # 作図 for key in optimizers.keys(): plt.plot(iterations, smooth_curve(train_loss[key]), label=key) plt.xlabel("iterations") # x軸ラベル plt.ylabel("loss") # y軸ラベル plt.ylim(0, 1) # y軸の範囲 plt.legend() # 凡例 plt.show()
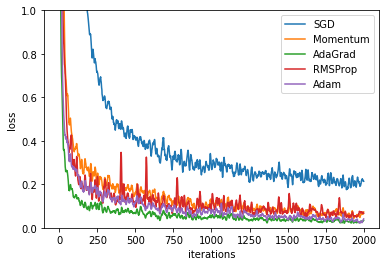
以上でニューラルネットワークの全ての機能を実装できました!!!次は重みの初期値について考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
あなたの推しアルゴリズムは何ですか?私はトピックモデルです!
【次節の内容】
こっちも面白いよ!