はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、6.1.6項「Adam」を繋ぐための内容になります。Adamを説明し、Pythonで実装します。またその学習過程を確認します。
【前節の内容】
【他の節の内容】
【この節の内容】
6.1.6 Adam
Adamは、Momentum SGDとRSMPropのアイデアを融合した手法です。重複する内容は省略しているので、それぞれの項も参考にしてください。
・更新式の確認
重みパラメータを$\mathbf{W}$、損失関数を$L$、$\mathbf{W}$に関する損失関数の勾配を$\frac{\partial L}{\partial \mathbf{W}}$とすると、Adamは以下の式になります。
$\mathbf{m}$は「速度」に対応する概念です。Momentum SGDにおける$\mathbf{v}$(え?文字が違う!ややこしい…)と同じものです。式(6.3)について$\alpha$を$\beta_1$、$\eta$を$1 - \beta_1$となるように設定すると同じ値になります。また$\beta_1$は減衰率で、過去の勾配の情報$\mathbf{m}$と現在の勾配$\frac{\partial L}{\partial \mathbf{W}}$の影響力を調整する項です。この式については「6.1.4:Momentum【ゼロつく1のノート(実装)】 - からっぽのしょこ」で詳しく説明しています。
$\mathbf{v}$は「過去の勾配の2乗和」に関する項です。また$\beta_2$は減衰率で、過去の勾配の情報$\mathbf{v}$と現在の勾配$\frac{\partial L}{\partial \mathbf{W}} \odot \frac{\partial L}{\partial \mathbf{W}}$の影響力を調整する項です。この式については「6.1.x:RMSProp【ゼロつく1のノート(実装)】 - からっぽのしょこ」で詳しく説明しています。
$\mathbf{m},\ \mathbf{v}$は減衰率$\beta_1,\ \beta_2$によって割り引かれた勾配の(2乗の)和であるため、始めの頃は値が小さくなってしまいます。例えば値を0.9に設定すると、勾配の1割しか学習に使わないことになります。これでは効率的に学習が進められないため、次の計算を行い調整します。
ここで$t$は更新回数を表します。$\beta_1^t,\ \beta_2^t$は指数的に0に漸近するため、下のグラフの通り$\frac{1}{1 - \beta_1^t},\ \frac{1}{1 - \beta_2^t}$は次第に1に近づきます。つまり$\mathbf{m},\ \mathbf{v}$に過去の情報が蓄積されるまでは、それぞれ値を拡大して利用しようということです。そして更新が進むにつれてこの計算の影響が薄れていきます。
この$\hat{\mathbf{m}},\ \hat{\mathbf{v}}$を用いて、パラメータ$\mathbf{W}$を更新します。
ここで、$\eta$は学習率、$\epsilon$は0除算を防ぐための微小な値です。
また式(3),(4),(5)を1つの式にまとめると
となります。
# 調整項のイメージ beta = 0.9 t = np.arange(1, 50) plt.plot(t, 1 / (1 - beta ** t)) plt.title("$y = \\frac{1}{1 - \\beta^t},\\ \\beta=$" + str(beta), fontsize=20) plt.xlabel("t") plt.ylabel("y") plt.show()

分かりにくいかもしれませんが0ではなく1に近づいています。
・実装
更新式の確認ができたので、Adamを実装します。
# この項で利用するライブラリを読み込む import numpy as np import matplotlib.pyplot as plt
学習率$\eta$と減衰率$\beta_1,\ \beta_2$は、インスタンスの作成時にそれぞれ引数lr、beta1、beta2として指定し、インスタンス変数として値を保持します。デフォルト値として、よく用いられる値を設定しておきます。
$\mathbf{m},\ \mathbf{v}$はパラメータ$\mathbf{W}$と同じ形状にする必要があるため、インスタンス作成時はNoneを定義してインスタンス変数だけ作成しておきます。更新メソッドの使用時に渡されるパラメータ(とパラメータごとの勾配)と同じ形状で全ての要素が0の変数を作成し、ディクショナリ型のインスタンス変数mとvにそれぞれ格納します。
更新回数$t$も初期値が0のインスタンス変数iterとして作成します。更新の度に1を加算していきます。
# Adamの実装 class Adam: # インスタンス変数を定義 def __init__(self, lr=0.001, beta1=0.9, beta2=0.999): self.lr = lr # 学習率 self.beta1 = beta1 # mの減衰率 self.beta2 = beta2 # vの減衰率 self.iter = 0 # 試行回数を初期化 self.m = None # モーメンタム self.v = None # 適合的な学習係数 # パラメータの更新メソッドを定義 def update(self, params, grads): # mとvを初期化 if self.m is None: # 初回のみ self.m = {} self.v = {} for key, val in params.items(): self.m[key] = np.zeros_like(val) # 全ての要素が0 self.v[key] = np.zeros_like(val) # 全ての要素が0 # パラメータごとに値を更新 self.iter += 1 # 更新回数をカウント lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter) # 式(6)の学習率の項 for key in params.keys(): self.m[key] = self.beta1 * self.m[key] + (1 - self.beta1) * grads[key] # 式(1) self.v[key] = self.beta2 * self.v[key] + (1 - self.beta2) * (grads[key] ** 2) # 式(2) params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7) # 式(6)
更新式(1),(2),(6)に従いパラメータごとに値を更新します。ただし式(6)については、パラメータに依存しない学習率に関する計算を先にしておきます。また0除算にならないように、分母に1e-7を加算しておきます。パラメータと勾配はどちらもディクショナリ変数として更新メソッド.update()の使用時に引数に指定します。
・アルゴリズムの確認
Adamを用いて関数
の最小値となる$x,\ y$を探索します。またこの関数の勾配(偏微分)は
になります。
まずは関数(6.2)とその勾配をそれぞれ関数として定義しておきます。
# 式(6.2) def f(x, y): return x ** 2 / 20.0 + y ** 2 # 式(6.2)の勾配(偏微分) def df(x, y): # 偏微分 dx = x / 10.0 # df / dx dy = 2.0 * y # df / dy return dx, dy # (値を2つ出力!)
元の関数は作図に、勾配はもちろんパラメータの更新に利用します。
ちなみにこの関数を等高線図にすると次のようになります。
# 等高線用の値 x = np.arange(-10, 10, 0.01) # x軸の値 y = np.arange(-5, 5, 0.01) # y軸の値 X, Y = np.meshgrid(x, y) # 格子状の点に変換 Z = f(X, Y) # 作図 plt.contour(X, Y, Z) # 等高線 plt.plot(0, 0, '+') # 最小値の点 plt.xlim(-10, 10) # x軸の範囲 plt.ylim(-10, 10) # y軸の範囲 plt.xlabel("x") # x軸ラベル plt.ylabel("y") # y軸ラベル plt.title("$f(x, y) = \\frac{1}{20} x^2 + y^2$", fontsize=20) # タイトル plt.show()

原点がこの関数の最小値になります。また原点付近が横に広くなだらかに(勾配が小さく)なっていることが確認できます。
初期値は点$(-7, 2)$とします。これまでと同様に、パラメータ(変数)params、パラメータごとの勾配gradsのディクショナリ変数を作成して、パラメータ名をキーとして値を格納します。
学習率と減衰率を指定して、Adamクラスのインスタンスを作成します。
# パラメータの初期値を指定 params = {} params['x'] = -7.0 params['y'] = 2.0 # 勾配の初期値を指定 grads = {} grads['x'] = 0 grads['y'] = 0 # 学習率を指定 lr = 0.3 # 減衰率を指定 beta1 = 0.9 beta2 = 0.999 # インスタンスを作成 optimizer = Adam(lr=lr, beta1=beta1, beta2=beta2)
試行回数を指定して、学習を行います。また、パラメータの更新値を記録するためのリスト型の変数を用意しておきます。値の追加は.append()を使います。
# 試行回数を指定 iter_num = 30 # 更新値の記録用リストを初期化 x_history = [] y_history = [] # 初期値を保存 x_history.append(params['x']) y_history.append(params['y']) # 関数の最小値を探索 for _ in range(iter_num): # 勾配を計算 grads['x'], grads['y'] = df(params['x'], params['y']) # パラメータを更新 optimizer.update(params, grads) # パラメータを記録 x_history.append(params['x']) y_history.append(params['y'])
勾配を計算し、gradsに格納している値をそれぞれ上書きします。そしてAdamクラスの更新メソッド.update()にparamsとgradsを指定して、パラメータを更新します。
更新値の推移を先ほどの等高線グラフに重ねて確認しましょう。
# 作図 plt.plot(x_history, y_history, 'o-') # パラメータの推移 plt.contour(X, Y, Z) # 等高線 plt.plot(0, 0, '+') # 最小値の点 plt.xlim(-10, 10) # x軸の範囲 plt.ylim(-10, 10) # y軸の範囲 plt.xlabel("x") # x軸ラベル plt.ylabel("y") # y軸ラベル plt.title("Adam", fontsize=20) # タイトル plt.text(6, 5, "$\\eta=$" + str(lr) + "\n$\\beta_1=$" + str(beta1) + "\n$\\beta_2=$" + str(beta2) + "\niteration:" + str(iter_num)) # メモ plt.show()
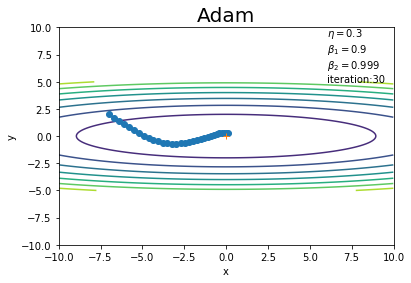
MomentumとAdaGradを平均したような経路を辿っていますね(?)(図6-7)。
学習率や試行回数を変更して試してみましょう!

(水の呼吸…)
確率的勾配降下法を発展した手法をいくつか確認しました。複雑なアルゴリズムが優れたアルゴリズムという訳ではなく、問題により各アルゴリズムの得手不得手があります。なのでいくつかの手法を試してみる必要があります。
そこで次項では、MNISTデータセットを用いてこれまでに実装した5つの手法を比較します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
- Neural Network Console「Deep Learning精度向上テクニック:様々な最適化手法 #1"」Youtube.https://www.youtube.com/watch?v=q933reMpvX8
おわりに
これで全て実装できました!
【次節の内容】