はじめに
「プログラミング」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ実行結果を見ながら処理の意図を確認していきます。
この記事は、5.7.4項「誤差逆伝播法を使った学習」の内容です。前項で実装した2層のニューラルネットワークを用いて学習を行います。
【前節の内容】
【他の節の内容】
【この節の内容】
5.7.4 誤差逆伝播法を使った学習
前項で実装した2層のニューラルネットワークのクラスを用いて、手書き数字認識の学習を行います。
処理の流れは4.5節と同様です。詳しくは「4.5.2-3:ミニバッチ学習【ゼロつく1のノート(実装)】 - からっぽのしょこ」も参照してください。
利用するライブラリを読み込みます。
# 5.7.4項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
また、MNISTデータセットの読み込みに利用する関数load_mnist()を読み込みます。詳しくは「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
# 読み込み用の設定 import sys sys.path.append('../deep-learning-from-scratch-master') # MNISTデータセット読み込み関数を読み込み from dataset.mnist import load_mnist #from ch05.two_layer_net import TwoLayerNet # 2層のニューラルネットワーク:5.7.4項
「4.5.1:2層ニューラルネットワークのクラス【ゼロつく1のノート(実装)】 - からっぽのしょこ」で実装した2層のニューラルネットワークのクラスTwoLayerNetの定義を再度実行する必要があります。または、上の方法で読み込みます。
・データセットの用意
load_mnist()を使って、手書き数字の画像データとラベルデータを読み込みます。この例では、正規化normalize、1次元化flatten、one-hot表現化one_hot_labelの全ての引数をTrueとします。
# MNISTデータセットを取得 (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=True) print(x_train.shape) # 訓練画像 print(t_train.shape) # 訓練ラベル
(60000, 784)
(60000, 10)
6万枚の画像データから、繰り返しバッチサイズ分のデータをランダムに取り出して学習を行います。
・ミニバッチ学習
ミニバッチデータに対する試行回数をiters_num、1回の学習に利用するデータ数をbatch_size、学習率(パラメータを更新する際の調整項)をlearning_rateとして値を指定します。
また、総データ数をtrain_size、総データ数に対するバッチサイズの割合をiter_per_epochとします。
# バッチデータ当たりの試行回数を指定 iters_num = 10000 # バッチサイズ(1試行当たりのデータ数)を指定 batch_size = 100 # データサイズ(総データ数)を取得 train_size = x_train.shape[0] print(train_size) # 全データに対するバッチデータの割合を計算 iter_per_epoch = max(train_size / batch_size, 1) print(iter_per_epoch) # 学習率を指定 learning_rate = 0.1
60000
600.0
iter_per_epochは、バッチデータを何回処理したら1エポック(総データ数)に達するかを表します。ただし、総データ数よりもバッチサイズの方が大きい場合は1未満の値になってしまうので、その場合はmax()によって1になるようにします。
ミニバッチ学習を行います。
データセットx_train, t_trainからランダムにbatch_size個取り出したミニバッチデータx_batch, t_batchを使って学習します。ランダムにデータを取り出すため、1エポック分の処理を行っても全てのデータを1回ずつ利用したわけではありません。
# 2層のニューラルネットワークのインスタンスを作成 network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10) # 推移の記録用のリストを作成 train_loss_list = [network.loss(x_train, t_train)] # 訓練データに対する損失 train_acc_list = [network.accuracy(x_train, t_train)] # 訓練データに対する認識精度 test_acc_list = [network.accuracy(x_test, t_test)] # テストデータに対する認識精度 # ミニバッチ学習 for i in range(iters_num): # ミニバッチデータを取得 batch_mask = np.random.choice(train_size, size=batch_size, replace=False) # データ番号を生成 x_batch = x_train[batch_mask] # 入力データ t_batch = t_train[batch_mask] # 教師データ # 勾配を計算 grad = network.gradient(x_batch, t_batch) # パラメータを更新 for key in ('W1', 'b1', 'W2', 'b2'): # 勾配降下法により値を更新 network.params[key] -= learning_rate * grad[key] # 損失を計算 loss = network.loss(x_batch, t_batch) # 損失を記録 train_loss_list.append(loss) # 途中経過を表示 print( 'iter ' + str(i + 1) + ' (' + str(np.round((i + 1) / iters_num * 100, 1)) + '%) : ' + # 繰り返し 'loss ' + str(loss) # 損失の値 ) # 1エポックごとの処理 if (i + 1) % iter_per_epoch == 0: # 認識精度を計算 train_acc = network.accuracy(x_train, t_train) # 訓練データ test_acc = network.accuracy(x_test, t_test) # テストデータ # 認識精度を記録 train_acc_list.append(train_acc) test_acc_list.append(test_acc) # 途中経過を表示 print('train acc : ' + str(train_acc)) print('test acc : ' + str(test_acc))
iter 1 (0.0%) : loss 2.2994295840222816
iter 2 (0.0%) : loss 2.299959559298681
iter 3 (0.0%) : loss 2.298691017287938
iter 4 (0.0%) : loss 2.3001547523834778
iter 5 (0.0%) : loss 2.2994708719631887
(省略)
iter 9596 (96.0%) : loss 0.0686016490327027
iter 9597 (96.0%) : loss 0.07875868009026829
iter 9598 (96.0%) : loss 0.04808251958687135
iter 9599 (96.0%) : loss 0.08193327076831708
iter 9600 (96.0%) : loss 0.10683527553951039
train acc : 0.9786666666666667
test acc : 0.9704
iter 9601 (96.0%) : loss 0.030370329983089528
iter 9602 (96.0%) : loss 0.04670775103326306
iter 9603 (96.0%) : loss 0.09666796535379164
iter 9604 (96.0%) : loss 0.024727115258999
iter 9605 (96.0%) : loss 0.07192302615885236
(省略)
iter 9996 (100.0%) : loss 0.061240663859318534
iter 9997 (100.0%) : loss 0.0564884736927513
iter 9998 (100.0%) : loss 0.06648179539802367
iter 9999 (100.0%) : loss 0.07731545542379
iter 10000 (100.0%) : loss 0.09496853381056161
5.7.1項で実装した2層のニューラルネットワークのクラスTwoLayerNetのインスタンスを作成します。
入力データの要素数input_sizeはピクセル数の784、クラス数output_sizeは数字の種類数の10にするのでした。中間層のニューロン数hidden_sizeは自由に決められます。ここでは50とします。この値が大きいほどニューラルネットワーク全体のパラメータの要素数が多くなります。パラメータの数が多いほどモデルの表現力が広がりますが、その分過学習の可能性も高まってしまいます。
各パラメータの更新では、for文を使ってキー名'W1', 'b1', 'W2', 'b2'を順番にkeyとして、ディクショナリ型のインスタンス変数paramsとgradから各パラメータの値(配列)を取り出して勾配降下法により値を更新しています。
ミニバッチデータの抽出については4.2.3項を、勾配降下法については4.4.1項を、TwoLayerNetクラスのメソッドやインスタンス変数については5.7.1項を参照してください。
学習状況を確認するために、損失と認識精度の値をリストに記録していきます。append()メソッドでリストに値を追加できます。
損失はバッチごとに、精度はエポックごとに訓練データと評価データに対して計算します。また、リストの作成時に学習前の初期値も計算しておきます。
・結果の確認
学習の推移を確認します。
まずは、損失(交差エントロピー誤差)の推移をプロットします。
# 損失の推移を作図 plt.figure(figsize=(8, 6)) # 図の設定 plt.plot(np.arange(iters_num + 1), train_loss_list) # 折れ線グラフ plt.xlabel('iteration') # x軸ラベル plt.ylabel('loss') # y軸ラベル plt.title('Cross Entropy Error', fontsize=20) # タイトル plt.grid() # グリッド線 plt.show()
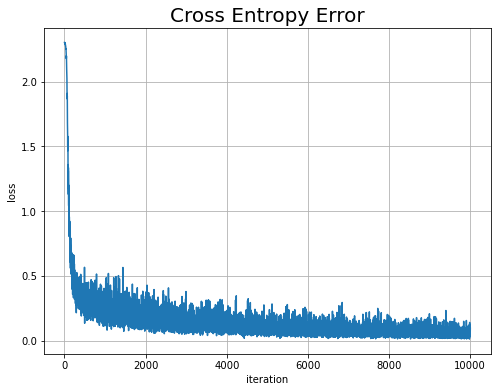
試行回数が増えるに従って、値が下がっている(学習が進んでいる)のが分かります。
続いて、訓練データとテストデータに対する認識精度の推移もプロットします。
# 認識精度の推移を作図 plt.figure(figsize=(8, 6)) # 図の設定 plt.plot(np.arange(len(train_acc_list)), train_acc_list, label='train acc') # 訓練データ plt.plot(np.arange(len(test_acc_list)), test_acc_list, label='test acc') # テストデータ plt.xlabel('epochs') # x軸ラベル plt.ylabel('acc') # y軸ラベル plt.title('Accuracy', fontsize=20) # グラフタイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
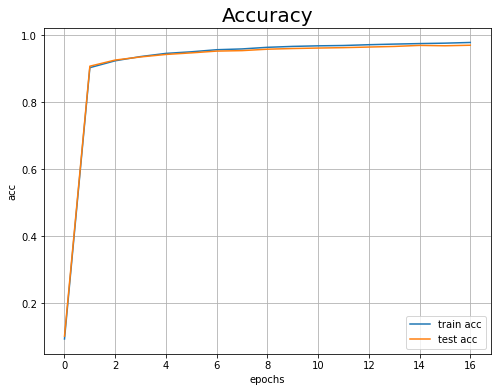
こちらも試行回数が増えるに従って、値が良くなっているのが分かります。また、訓練データだけでなくテストデータに対しても精度が高いため、過学習が起きていないことも確認できます。
以上で5章の内容は完了です。5章では、誤差逆伝播法を用いたニューラルネットワークを実装しました。次章では、学習をよくするための手法を学びます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
5章完了です!!!この章は数学メイン回で大変でしたね。お疲れ様でしたー。
- 2021.10.24:加筆修正しました。
思ったより時間がかかって修正作業に飽きてきてしまった。。。
【次節の内容】