はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、6.5節「ハイパーパラメータの検証」の内容になります。ハイパーパラメータの最適化をPythonで試します。
【前節の内容】
【他の節の内容】
【この節の内容】
6.5 ハイパーパラメータの検証
これまでは、重みやバイアスといったパラメータを最適化してきました。この節では、学習率などのハイパーパラメータを最適化します。
6.5.1 検証データ
ハイパーパラメータの最適化にあたって、訓練データとテストデータとは別に、ハイパーパラメータの性能を評価するための検証データを用意します。
これまでの通り、MNISTデータセットを読み込みます。またこれまでに実装したレイヤなどを再実行が面倒な場合は、「common」フォルダ内の「layers.py」ファイルから読み込みます。あと次節で実装する多層ニューラルネットワーククラスも読み込んでおきます。
# データ読み込み用ライブラリを読み込む import sys, os # ファイルパスを指定 sys.path.append('C:\\Users\\「ユーザー名」\\Documents\\・・・\\deep-learning-from-scratch-master') # MNISTデータセット読み込み関数 from dataset.mnist import load_mnist # 各種レイヤのクラス from common.layers import * # 多層ニューラルネットワーククラス from common.multi_layer_net import MultiLayerNet
まずは、検証データを用意するのに必要な処理を確認します。
np.random.permutation()を使って、データをランダムに並び替えます。np.random.permutation()は、引数に指定した値未満の整数を重複せずにランダムに生成します。これをインデックスとして利用することで、データをシャッフルします。
# 順番に並んだデータを生成 x = np.arange(10) * 10 print(x) # ランダムに並び替えた要素のインデックスを生成 idx = np.random.permutation(x.shape[0]) print(idx) # データを並び替え x = x[idx] print(x)
[ 0 10 20 30 40 50 60 70 80 90]
[3 5 2 0 8 4 7 6 1 9]
[30 50 20 0 80 40 70 60 10 90]
10倍したのは単にデータそのものとインデックスを見分けるためです。
np.random.permutation()に配列を渡すと直接データをシャッフルできますが、訓練データとテストデータを同じ順番にシャッフルする必要があるため、上方法で行います。
# 順番に並んだデータを生成 x = np.arange(10) * 10 print(x) # ランダムに並び替え x = np.random.permutation(x) print(x)
[ 0 10 20 30 40 50 60 70 80 90]
[60 20 0 10 80 30 70 90 40 50]
ではMNISTデータセットを読み込んで、並び替えます。
# 画像データを読み込む (x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_label=True) # ランダムにインデックスを生成 idx = np.random.permutation(x_train.shape[0]) # データを並べ替え x_train = x_train[idx] t_train = t_train[idx] print(x_train.shape) print(t_train.shape)
(60000, 784)
(60000, 10)
当然データ数に変更はありません。
シャッフルしたデータから検証データとして扱うデータを取り出します。
訓練データの内、何割を検証データとするのかを指定します。また訓練データ数との積が検証データ数になります。
# 検証データの割合を指定 validation_rate = 0.2 # 検証データ数を計算 validation_num = int(x_train.shape[0] * validation_rate) print(validation_num) # 検証データを抽出 x_val = x_train[:validation_num] t_val = t_train[:validation_num] print(x_val.shape) print(t_val.shape) # 訓練データを抽出 x_train = x_train[validation_num:] t_train = t_train[validation_num:] print(x_train.shape) print(t_train.shape)
12000
(12000, 784)
(12000, 10)
(48000, 784)
(48000, 10)
これで検証データを用意できました。
6.5.2 ハイパーパラメータの最適化
本を読んで。
6.5.3 ハイパーパラメータ最適化の実装
MNISTデータセットを使ってハイパーパラメータの最適化を行います。この例では、確率的勾配降下法に用いる学習率と、Weight decay(荷重減衰)で用いる係数の最適な値を探索します。
何エポック分試行するのかと、1度に処理するデータ数を指定します。
# エポックあたりの試行回数を指定 max_epoch = 50 # ミニバッチサイズを指定 batch_size = 100 # 高速化のため訓練データの削減 x_train = x_train[:500] t_train = t_train[:500] # 訓練データ数 train_size = x_train.shape[0] # 全データ数に対するバッチデータ数の割合 iter_per_epoch = max(train_size / batch_size, 1) print(iter_per_epoch) # 試行回数を計算 max_iter = int(max_epoch * iter_per_epoch) print(max_iter)
5.0
250
max_iter回試行することで、指定したエポック数の学習を行えます。
とりあえずハイパーパラメータ最適化で行う処理の1回分だけをやってみましょう。
Weight decay(荷重減衰)の係数$\lambda$と学習率$\eta$がとる値の範囲を指定して、ランダムに値を生成します。np.random.uniform()は、第1引数以上第2引数未満の値を一様な確率に従って生成します。生成された値をそれぞれ10の指数とします。
# ハイパーパラメータの範囲を指定してランダムに値を生成 weight_decay_lambda = 10 ** np.random.uniform(-8, -4) # 荷重減衰の係数 lr = 10 ** np.random.uniform(-6, -2) # 学習率 print(weight_decay_lambda) print(lr)
4.258343682964451e-08
1.2480393373210386e-05
多層ニューラルネットワークMultiLayerNetのインスタンスを作成します。
この例では7層のニューラルネットワークとするため、中間層のニューロン数の引数hidden_size_listに6つの値をリスト型変数で指定します(詳しくは実装時に説明します)。任意の値を指定できますが、この例では全て100とします。MNISTデータセットを用いる場合は、入力サイズinput_sizeがピクセル数の784、出力サイズoutput_sizeが数字の数10になります。(ちなみに、入出力層を含めた8つの層の間の数が7になります。)
活性化レイヤにReLU関数を用いるためactivation引数にrelu、重みの初期値をHeの初期値とするためweight_init_std引数に'he'を指定します。
また最適化手法を確率的勾配降下法(SGD)とします。6.1節で実装した他の手法も使えます。
# 7層のニューラルネットワークのインスタンスを作成 network = MultiLayerNet( input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, activation='relu', # 活性化関数 weight_init_std='he', # 重みの初期値の標準偏差 weight_decay_lambda=weight_decay_lambda # 荷重減衰の係数 ) # 最適化手法を指定 optimizer = SGD(lr=0.01)
では実行します。処理の内容についての解説は、6.2節以降のどの内容でも同じような処理をしているので、「『ゼロから作るDeep Learning』の学習ノート:記事一覧 - からっぽのしょこ」こちらの一覧から参考にしてください。
# 認識精度の受け皿を初期化 val_acc_list = [] train_acc_list = [] # ミニバッチデータごとに処理 for i in range(max_iter): # ランダムにバッチデータを抽出 batch_mask = np.random.choice(train_size, batch_size, replace=False) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 勾配を計算 grads = network.gradient(x_batch, t_batch) # パラメータを更新 optimizer.update(network.params, grads) # エポックごとに認識精度を測定 if i % iter_per_epoch == 0: # 認識精度を測定 val_acc = network.accuracy(x_val, t_val) train_acc = network.accuracy(x_train, t_train) # 値を記録 val_acc_list.append(val_acc) train_acc_list.append(train_acc) # (動作確認も兼ねて)認識精度を表示 print( "=============== Result ===============" + "\nlr:" + str(lr) + ", lambda:" + str(weight_decay_lambda) + "\nval acc " + ":" + str(np.round(val_acc, 5)) + "\ntrain acc" + ":" + str(np.round(train_acc, 5)) )
=============== Result ===============
lr:1.2480393373210386e-05, lambda:4.258343682964451e-08
val acc :0.78625
train acc:0.926
認識精度の推移をプロットします。
# 作図用のx軸の値 epochs = np.arange(max_epoch) # 作図 plt.plot(epochs, val_acc_list, label='val') # 訓練データ plt.plot(epochs, train_acc_list, label='train', linestyle='--') # テストデータ plt.ylim(0, 1) # y軸の範囲 plt.xlabel("epochs") # x軸ラベル plt.ylabel("accuracy") # y軸ラベル plt.title("Accuracy", fontsize=20) # タイトル plt.text(-1, 0.7, "lr:" + str(np.round(lr, 5)) + "\nlambda:" + str(np.round(weight_decay_lambda, 5))) # メモ plt.legend() # 凡例 plt.show()
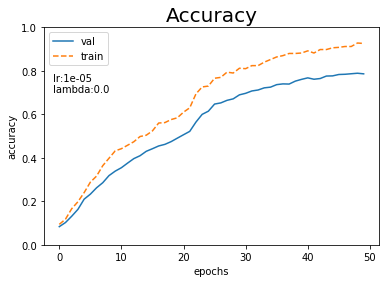
ここまでがハイパーパラメータ検証における1回の処理になります。
これを何度も繰り返すことで、最適な値を探索します。
ではそれを実装してみましょう!といきたいところですが私はもう疲れました。また理論というよりもプログラミングの側面が強いため、解説は省略します。
以下はマスターデータの「ch06」フォルダ内の「hyperparameter_optimization.py」ファイルのソースコードの出力です。頑張ってコードを解読してください、、
val acc:0.15725 | lr:0.0012901986579313943, weight decay:1.3723595902610677e-05
val acc:0.28775 | lr:0.00100868175988271, weight decay:4.681586497784612e-07
val acc:0.10225 | lr:2.7387944926667495e-05, weight decay:1.041203511412172e-06
(省略)
val acc:0.12708333333333333 | lr:0.00021500460257806528, weight decay:2.1064861855606342e-08
val acc:0.20025 | lr:0.001373695455226091, weight decay:2.870256687133167e-07
=========== Hyper-Parameter Optimization Result ===========
Best-1(val acc:0.7995) | lr:0.00990963982031193, weight decay:3.305822212360609e-05
Best-2(val acc:0.7785) | lr:0.009084590500825319, weight decay:2.8149160480947467e-07
Best-3(val acc:0.76825) | lr:0.007994348155964953, weight decay:3.318529096669812e-08
(省略)
Best-19(val acc:0.3740833333333333) | lr:0.0016386671234562005, weight decay:1.766499712495318e-05
Best-20(val acc:0.3640833333333333) | lr:0.0021128915332461464, weight decay:8.584796667654845e-08
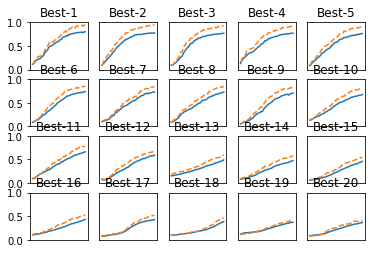
認識精度のベスト20が描画されます(図6-24)。
以上で6章の内容は終了です。が!この章で何度も利用したアレをまだ実装していませんね。というわけで、次は多層ニューラルネットワークのクラスを実装しましょう!
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
もう、ゴールしていいよね。
ダメです。まだあと2つ本に載ってない内容を追加しました。
【次節の内容】