はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、6.2節「重みの初期値」の内容になります。使用する活性化関数と重みの初期値の設定の出力データへの影響をPythonを使って確認します。
【前節の内容】
【他の節の内容】
【この節の内容】
6.2 重みの初期値
この節では、重みパラメータの初期値について考えます。
# この節で用いるライブラリを読み込む import numpy as np import matplotlib.pyplot as plt
この節で利用する活性化関数を簡単に作成しておきます。勿論これまでに実装したものを用いてもいいです。
# シグモイド関数の定義 def sigmoid(x): return 1 / (1 + np.exp(-x)) # ReLU関数の定義 def relu(x): return np.maximum(0, x) # tanh関数の定義 def tanh(x): return np.tanh(x)
・tanh関数
tanh関数とは、シグモイド関数とよく似たS字カーブの関数です。シグモイド関数との主な違いは、出力が-1から1までの値をとるところです。またそれに伴って原点で対称なS字カーブになります。
グラフで確認してみましょう。
# 作図用のx軸の点 x_vec = np.arange(-10.0, 10.0, 0.1) # 作図 plt.plot(x_vec, tanh(x_vec)) plt.title("tanh Function", fontsize=20) plt.show()
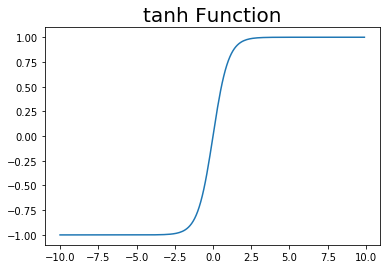
3つの関数のグラフと重ねて比較します。
# 作図 plt.plot(x_vec, tanh(x_vec), label="tanh function") # tanh関数 plt.plot(x_vec, sigmoid(x_vec), label="sigmoid function") # シグモイド関数 plt.plot(x_vec, relu(x_vec), label="relu function") # ReLU関数 plt.hlines(y=0, xmin=-10.0, xmax=10.0, linestyle="--", linewidth=1) # 水平線 plt.vlines(x=0, ymin=-1.5, ymax=1.5, linestyle="--", linewidth=1) # 垂直線 plt.ylim(-1.5, 1.5) # y軸の範囲 plt.xlabel("x") # x軸ラベル plt.ylabel("y") # y軸ラベル plt.legend() # 凡例 plt.show()
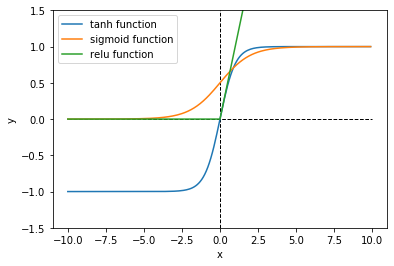
・ガウス分布の標準偏差の設定
正規分布のことを深層学習・機械学習の分野ではガウス分布と呼ばれます。6.3節でもう少し詳しく扱いますが、平均が0で標準偏差が1のガウス分布(標準正規分布)に従う要素に対して、任意の数を掛けることで標準偏差をその掛けた数に変更することができます。
標準正規分布に従う乱数生成関数np.random.randn()を使って確認します。
# 標準偏差を指定 std = 100 # 標準正規分布に従う乱数を生成 W = np.random.randn(10, 100) print(np.round(np.std(W, axis=1), 4)) # (行ごとの)標準偏差 print(np.round(np.std(W * std, axis=1), 2)) # (行ごとの)標準偏差
[0.9406 1.0249 0.9208 1.0605 0.9983 1.0036 1.0262 1.0387 1.0637 1.0632]
[ 94.06 102.49 92.08 106.05 99.83 100.36 102.62 103.87 106.37 106.32]
各行の標準偏差が100倍になっていることを確認できます(全体の標準偏差を計算しても同じことを確認できます)。これまでは、np.random.randn()の出力に0.01を掛けた値(つまり標準偏差0.01のガウス分布に従う乱数)を重みの初期値として用いてきました。
次は標準正規分布に従う乱数のヒストグラムを作図して見ます。
# 標準正規分布に従う乱数を生成 W = np.random.randn(10000) # 作図 plt.hist(W, bins=50) # ヒストグラム plt.title('Standard Gaussian Distribution', fontsize=20) # タイトル plt.show()
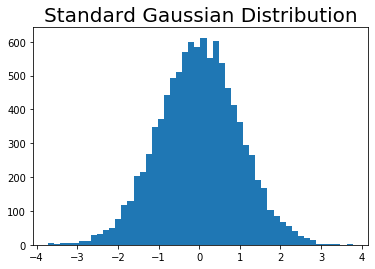
データ数が増えると釣鐘型の分布になっていきます。
前層のノード(ニューロン)数を$n$として、標準偏差を$\frac{1}{\sqrt{n}}$とした初期値をXavierの初期値、$\sqrt{\frac{2}{n}}$とした初期値をHeの初期値と呼びます。これについては、次の項で確認します。
ここではあくまでイメージですが、nに値を指定して各初期値の分布を確認しましょう。
# 前層のノード数を指定 n = 100 # スケール(標準偏差の値)を計算 xavier_scale = np.sqrt(1 / n) he_scale = np.sqrt(2 / n) print(xavier_scale) print(he_scale) # 作図 plt.hist(W * he_scale, bins=50, alpha=0.5, label="He") # Heの初期値 plt.hist(W * xavier_scale, bins=50, alpha=0.5, label="Xavier") # Xavierの初期値 plt.hist(W * 0.01, bins=50, alpha=0.5, label="std=0.01") # 0.01 plt.title('Gaussian Distribution', fontsize=20) # タイトル plt.legend() # 凡例 plt.show()
0.1
0.1414213562373095
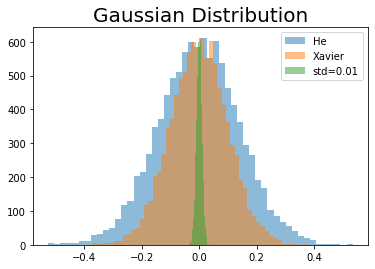
標準偏差は分布の散らばり具合を表す統計量なので、値が小さいほど分布の形状が細くなります。これは平均値付近の値に集中していることを表します。
では活性化関数と標準偏差について確認できたので、次からはこの組み合わせによるアクティベーションへの影響を見ていきます。
6.2.2 隠れ層のアクティベーション分布
重みの初期値の影響を見るために、アクティベーションに注目します。アクティベーションとは、活性化関数の出力データのことです。活性化関数と重みの初期値の標準偏差の組み合わせ方によって、各層のアクティベーションの分布がどのように変化するのかを見ていきます。
3つの活性化関数を、ディクショナリ変数activation_layerに格納しておきます。キーはそれぞれ関数名とします。
# 活性化層のディクショナリ変数を作成 activation_layer = {'sigmoid': sigmoid, 'relu': relu, 'tanh': tanh} print(activation_layer.keys())
dict_keys(['sigmoid', 'relu', 'tanh'])
キーを指定することで、指定した活性化関数による計算を行えます。
# 仮のデータを指定 x = [-5, 0, 10] # 使用する活性化関数のキーを指定 key = "relu" # 活性化 z = activation_layer[key](x) print(z)
[ 0 0 10]
少々手間ですが、これはこの節の最後に実装する多層ニューラルネットワークのための練習でもあります。
ニューラルネットワークの層の数とニューロン数を指定します。この例では、層の数を5、全ての層のニューロン(ノード)の数を等しく設定します。
# 層の数を指定 layer_size = 5 # ニューロン数を指定 node_num = 100
(このレジュメ(本)では、5層のニューラルネットワークとは「層の間の数」が5ということを意味し、つまりAffineレイヤと活性化レイヤの組み合わせが6つで構成されます。この例では簡易的な実験のため単に5つの層と表現しています。)
入力データ数を指定して、ランダムに値を生成します。この入力データは手書き文字画像に対応するデータです。
# 入力データ数を指定 data_size = 1000 # ランダムにデータを生成 input_data = np.random.randn(data_size, node_num) print(input_data.shape)
(1000, 100)
データ数行、ノード(ニューロン)数列のデータが生成されました。
ランダムにデータを生成しているため、この処理を再度実行すると当然データが変わります。活性化関数や標準偏差の影響を比較するために、このデータinput_dataをxに移してから使用することで同じデータを用いて実験します。
この節では他の節のように5層のニューラルネットワークを構築するのではなく、単にfor文で5回処理を繰り返すことでニューラルネットワークを再現します。
活性化関数と標準偏差を指定します。まずは、活性化関数としてシグモイド関数を用い、標準偏差を1として実験します。
活性化後のデータは、ディクショナリ変数activationsに、何層目の処理(試行回数)を示すiの値をキーとして格納します。また前層の出力が現在の層の入力になるため、2層目以降の処理を始める際にactivationsから値を取り出してxに代入して同じ処理を繰り返します。
指定した標準偏差は一旦weight_init_stdに代入します。数値であればそのまま重みの値を生成します。'xavier'か'he'を指定している場合は、if文により対応する値に変更(再代入)します。
# 活性化関数を選択(キーを指定) activation_key = 'sigmoid' #activation_key = 'relu' #activation_key = 'tanh' # 重みの初期値の標準偏差を選択 weight_init_std = 1.0 #weight_init_std = 0.01 #weight_init_std = 'xavier' #weight_init_std = 'he' # 入力データを複製 x = input_data # 活性化後のデータの受け皿を初期化 activations = {} # 1層ずつ処理 for i in range(layer_size): # 前の層(i-1回目)の出力データを現在の層の入力データとして代入 if i != 0: # 初回は飛ばす x = activations[i-1] # 指定した標準偏差に対応する値(スケール)を取得 scale = weight_init_std if weight_init_std == 'xavier': # xavierのとき scale = np.sqrt(1.0 / node_num) # Xavierの初期値 elif weight_init_std == 'he': # heのとき scale = np.sqrt(2.0 / node_num) # Heの初期値 # 指定した標準偏差に従い重みをランダムに生成 w = scale * np.random.randn(node_num, node_num) # Affineレイヤの計算 a = np.dot(x, w) # 活性化 z = activation_layer[activation_key](a) # 活性化関数の出力データ(アクティベーション)を記録 activations[i] = z
各層のアクティベーション(出力データ)の値の分布をヒストグラムで確認します。
# 作図 for i, z in activations.items(): plt.subplot(1, len(activations), i + 1) # グラフの表示位置 plt.hist(z.flatten(), 30, range=(0, 1)) # ヒストグラム plt.xticks([0.0, 0.5, 1.0]) # x軸目盛 if i != 0: # 一番左以外 plt.yticks([], []) # y軸目盛(を非表示) plt.title(str(i + 1) + "-layer") # グラフごとのタイトル plt.suptitle("function:" + activation_key + ", W:std=" + str(weight_init_std)) # グラフ全体のタイトル plt.show()

全ての層で値が0か1に偏っていることが分かります(図6-10)。0と1に偏ったデータ分布だと勾配消失の問題が生じます。
次は標準偏差を0.01として試してみます。
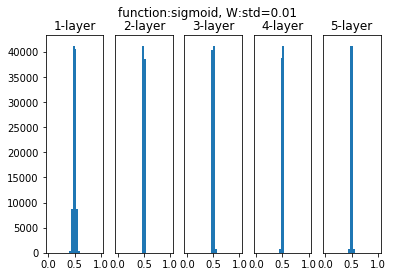
どの層のアクティベーションも0.5に近い値になってしまっています(6-11)。アクティベーションが偏ると表現力に問題が生じます。
続いて「Xavierの初期値」を設定します。Xavierの初期値とは、前層のノード数を$n$とすると$\frac{1}{\sqrt{n}}$の標準偏差を持つ分布に従う初期値のことです。
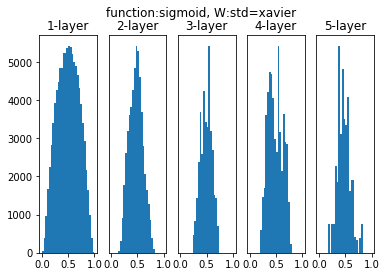
ある程度の広がりを保っています(図6-13)。Xavierの初期値を用いることで、先ほどの問題を回避することができました。
tanh関数とXavierの初期値の組み合わせを見ます。
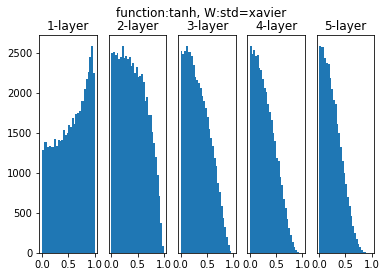
(tanh関数についてはこの後登場しません…)
6.2.3 ReLUの場合の重みの初期化
次は、活性化関数にReLU関数を用いる場合を確認していきます。先ほどと同じコードを使います。
まずは標準偏差を0.01とする場合を見ましょう。(コードは再掲)
# 活性化関数を選択(キーを指定) #activation_key = 'sigmoid' activation_key = 'relu' #activation_key = 'tanh' # 重みの初期値の標準偏差を選択 #weight_init_std = 1.0 weight_init_std = 0.01 #weight_init_std = 'xavier' #weight_init_std = 'he' # 入力データを複製 x = input_data # 活性化後のデータの受け皿を初期化 activations = {} # 1層ずつ処理 for i in range(layer_size): # 前の層(i-1回目)の出力データを現在の層の入力データとして代入 if i != 0: # 初回は飛ばす x = activations[i-1] # 指定した標準偏差に対応する値を取得 scale = weight_init_std if weight_init_std == 'xavier': # xavierのとき scale = np.sqrt(1.0 / node_num) # Xavierの初期値 elif weight_init_std == 'he': # heのとき scale = np.sqrt(2.0 / node_num) # Heの初期値 # 指定した標準偏差に従い重みをランダムに生成 w = scale * np.random.randn(node_num, node_num) # Affineレイヤの計算 a = np.dot(x, w) # 活性化 z = activation_layer[activation_key](a) # 活性化関数の出力データを記録 activations[i] = z # 作図 for i, z in activations.items(): plt.subplot(1, len(activations), i + 1) # グラフの表示位置 plt.hist(z.flatten(), 30, range=(0, 1)) # ヒストグラム plt.xticks([0.0, 0.5, 1.0]) # x軸目盛 if i != 0: # 一番左以外 plt.yticks([], []) # y軸目盛(を非表示) plt.title(str(i + 1) + "-layer") # グラフごとのタイトル plt.suptitle("function:" + activation_key + ", W:std=" + str(weight_init_std)) # グラフ全体のタイトル plt.show()

どの層のアクティベーションも0に近い値になってしまっています(図6-14の1枚目)。
続いて「Xavierの初期値」を設定します。

ReLU関数は負の値が全て0になるので0以外の要素に注目すると、第1層の出力時は値が均一に分布していますが、層が進むごとに小さい値に分布が偏っていきます(図6-14の2枚目)。
続いて「Heの初期値」を設定します。Heの初期値とは、前層のノード数を$n$とすると$\sqrt{\frac{2}{n}}$の標準偏差を持つ分布に従う初期値のことです。

どの層のアクティベーションも分布が均一に保たれています(図6-14の3枚目)。
簡易的な実験ですが活性化関数と初期値の分布によるアクティベーションへの影響を確認できました。次項では、MNISTデータセットを用いて、初期値の標準偏差と交差エントロピー誤差への影響を考えます。
・重みの初期化メソッドの実装
とその前におまけとして、重みの初期化(メソッド)を実装しておきます。これ自体は今後使いません。あくまでこの節の最後に実装する(前に何度も利用する)多層ニューラルネットワーククラスの1メソッドとして実装するときのイメージ(簡易版)です。なのでおまけです。
# 重みの初期化メソッドの定義 class init_weight: # インスタンス変数の定義 def __init__(self, input_size, output_size, weight_init_std): self.input_size = input_size self.output_size = output_size # 変数のみ作成 self.W = None # 初期値を設定 self.__init_weight(weight_init_std) # 重みの初期化メソッドの定義 def __init_weight(self, weight_init_std): # 重みの初期値の標準偏差の設定:引数に数値を指定した場合はこのまま scale = weight_init_std # 特定の初期値を指定した場合の処理 if weight_init_std == 'he': # 'he'を指定した場合 scale = np.sqrt(2.0 / self.input_size) # Heの初期値を使用 elif weight_init_std == 'xavier': # `xavier`を指定した場合 scale = np.sqrt(1.0 / self.input_size) # Xavierの初期値を使用 # 重みの初期値をランダムに設定 self.W = scale * np.random.randn(self.input_size, self.output_size)
インスタンス作成時に__init__()が実行されますね。その時に__init_weight()で重みの初期化メソッドも実行され、重みのインスタンス変数self.Wに値が代入(初期値が設定)されます。(このように内部だけで実行されるメソッド名の頭には__を付けて明示しておきます。)
実際には、インスタンス変数Wではなくバイアスも含めてディクショナリ型の変数paramsに値を格納する、'relu'や'sigmoid'でも指定できるようにするなどの違いはあります。
次項で多層ニューラルネットワークを利用するための予行として使ってみます。
# 標準偏差を指定 weight_init_std = 0.01 # インスタンスを作成 param = init_weight(input_size=100, output_size=100, weight_init_std=weight_init_std) # 作図 plt.hist(param.W.flatten(), bins=50, label="std:" + str(weight_init_std)) # ヒストグラム plt.title('Gaussian Distribution', fontsize=20) # タイトル plt.legend() # 凡例 plt.show()
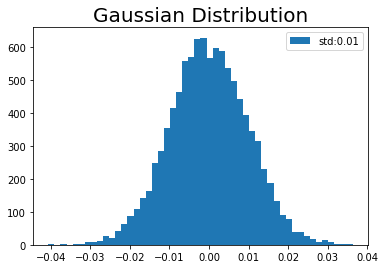
# 標準偏差を指定 weight_init_std = 'he' # インスタンスを作成 param = init_weight(input_size=100, output_size=100, weight_init_std=weight_init_std) # 作図 plt.hist(param.W.flatten(), bins=50, label="std:" + str(weight_init_std)) # ヒストグラム plt.title('Gaussian Distribution', fontsize=20) # タイトル plt.legend() # 凡例 plt.show()
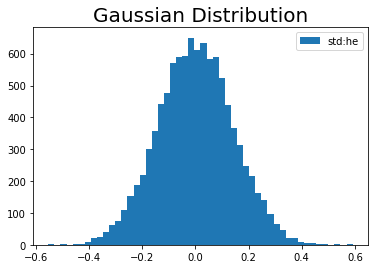
# 標準偏差を指定 weight_init_std = 'xavier' # インスタンスを作成 param = init_weight(input_size=100, output_size=100, weight_init_std=weight_init_std) # 作図 plt.hist(param.W.flatten(), bins=50, label="std:" + str(weight_init_std)) # ヒストグラム plt.title('Gaussian Distribution', fontsize=20) # タイトル plt.legend() # 凡例 plt.show()
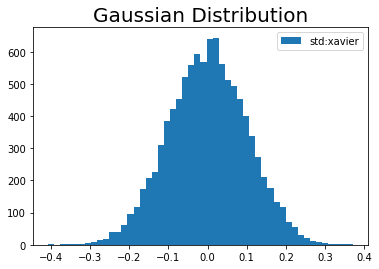
では話戻って、今確認した機能をメソッドとして持つクラスを使います。
6.2.4 MNISTデータセットによる重みの初期値の比較
前項では、活性化関数と初期値の標準偏差の組み合わせによって、アクティベーションの分布がどうなるのかを確認しました。この項では、ReLU関数と3種類の標準偏差の組み合わせによって、学習(交差エントロピー誤差推移)にどのように影響するのかを確認します。
この項では5層のニューラルネットワークを用います。そのための多層ニューラルネットワークのクラスは、6章の最後に実装します。そのためここでは、マスターデータから(将来の自分が実装した)クラスを読み込みましょう。このクラスを用いた基本的な処理の流れは「6.1.8:MNISTデータセットによる更新手法の比較【ゼロつく1のノート(実装)】 - からっぽのしょこ」と同じです。そちらも参考にしてください。
またMNISTデータセットも読み込みます。マスターデータからの読み込みに関する詳しい解説は「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を確認してください。
# データ読み込み用ライブラリを読み込む import sys, os # ファイルパスを指定 sys.path.append('C:\\Users\\「ユーザー名」\\Documents\\・・・\\deep-learning-from-scratch-master') # MNISTデータセット読み込み関数を読み込む from dataset.mnist import load_mnist # 多層ニューラルネットワーククラスを読み込む from common.multi_layer_net import MultiLayerNet # 各種レイヤのクラス from common.layers import * # 画像データを読み込む (x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_label=True) print(x_train.shape) print(t_train.shape)
(60000, 784)
(60000, 10)
バッチサイズと試行回数を指定します。
# 訓練データ数 train_size = x_train.shape[0] # バッチサイズ指定 batch_size = 128 # 試行回数を指定 max_iterations = 2001
前項で確認した3種類の初期値の設定方法について、次のようなディクショナリ変数を作成しておきます。この変数のキーは、他のディクショナリ変数のキーとしても利用します。
# ディクショナリ変数を作成 weight_init_types = {'std=0.01': 0.01, 'xavier': 'xavier', 'he': 'he'}
これは極力自動化してタイプミスなどを防ぎたいのと、数値と文字列をうまいこと扱うためです。
この例では確率的勾配降下法(SGD)で最適化を行います。勿論他の手法を用いてもいいです。
# 各手法のインスタンスをディクショナリ変数に格納 optimizer = SGD(lr=0.01)
初期値の設定方法ごとに多層ニューラルネットワークのインスタンスを作成します。作成したインスタンスは、weight_init_typesのキーをそのままキーとしてディクショナリ変数networksに格納します。
この例では5層のニューラルネットワークとするため、中間層のニューロン数の引数hidden_size_listに4つの値をリスト型変数で指定します(詳しくは実装時に説明します)。任意の値を指定できますが、この例では全て100とします。MNISTデータセットを用いる場合は、入力サイズinput_sizeがピクセル数の784、出力サイズoutput_sizeが数字の数10になります。(ちなみに入出力層を含めた6つの層の間の数で5になります。)
利用する活性化関数を指定する引数activationには、'relu'を指定します。
引数weight_init_stdが、重みの初期値を指定するための引数です。ここにweight_init_typesの値を順番に指定します。
また標準偏差の設定ごとの交差エントロピー誤差を記録するための空のリスト型変数も作成し、ディクショナリ変数train_lossに格納しておきます。
# 初期値の設定方法ごとにディクショナリ変数に格納 networks = {} train_loss = {} for key, weight_type in weight_init_types.items(): # 多層ニューラルネットワーク networks[key] = MultiLayerNet( input_size=784, hidden_size_list=[100, 100, 100, 100], output_size=10, activation='relu', # 利用する活性化関数 weight_init_std=weight_type # 利用する初期値の標準偏差 ) # 交差エントロピー誤差の受け皿 train_loss[key] = [] print(networks.keys()) print(train_loss.keys())
dict_keys(['std=0.01', 'xavier', 'he'])
dict_keys(['std=0.01', 'xavier', 'he'])
他の初期値の設定を試したくなった場合は、weight_init_typesの設定を変更・追加するだけで行えます。
では5層のニューラルネットワークによる手書き文字認識を行います。
それぞれの初期値に対して同じバッチデータを用いるため、バッチデータの抽出後にfor文によってインスタンスを切り替えます。必要な変数等をディクショナリ変数に格納しておき、forでキーを順番に入れ替えて必要な変数やメソッドにアクセスする点はこれまでと同じです。
# 手書き文字認識 for i in range(max_iterations): # ランダムにバッチデータ抽出 batch_mask = np.random.choice(train_size, batch_size, replace=False) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 初期値の設定方法ごとに学習 for key in weight_init_types.keys(): # 勾配を計算 grads = networks[key].gradient(x_batch, t_batch) # パラメータを更新 optimizer.update(networks[key].params, grads) # 損失関数の計算 loss = networks[key].loss(x_batch, t_batch) train_loss[key].append(loss) # 交差エントロピー誤差を記録 # (動作確認も兼ねて)100回ごとに損失関数の値を表示 if i % 100 == 0: print("===========" + "iteration:" + str(i) + "===========") for key in weight_init_types.keys(): print( key + " " * (8 - len(key)) + ":" + # (`8`は`key`の最大文字数) str(np.round(train_loss[key][i], 5)) )
===========iteration:0===========
std=0.01:2.30251
xavier :2.32469
he :2.3232
===========iteration:100===========
std=0.01:2.30292
xavier :2.24603
he :1.62498
===========iteration:200===========
(省略)
===========iteration:1900===========
std=0.01:2.30754
xavier :0.31051
he :0.21244
===========iteration:2000===========
std=0.01:2.29798
xavier :0.27087
he :0.16562
交差エントロピー誤差の推移をグラフ化します。plt.plot()の設定についても、forを使って自動化しておきます。
# 作図用のx軸の点 iterations = np.arange(max_iterations) # 作図 for key in weight_init_types.keys(): plt.plot(iterations, train_loss[key], label=key) plt.xlabel("iterations") # x軸ラベル plt.ylabel("loss") # y軸ラベル #plt.ylim(0, 1) # y軸の範囲 plt.legend() # 凡例 plt.show()
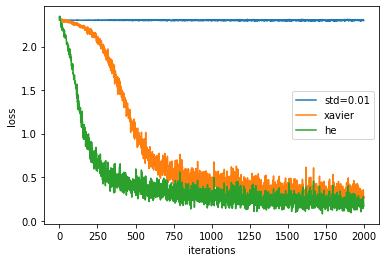
この結果から、ReLU関数に対してはHeの初期値を用いた方が学習が早く進むことが分かります。また標準偏差を0.01に設定した場合は、全く学習できていないことが分かります。
マスターデータの関数smooth_curve()を使って、図6-15を再現できるコードを載せておきます(モノクロになる訳ではないのでマーカーは入れてません)。
# 推移を滑らかに変換するための関数を読み込む from common.util import smooth_curve # 作図用のx軸の点 iterations = np.arange(max_iterations) # 作図 for key in weight_init_types.keys(): plt.plot(iterations, smooth_curve(train_loss[key]), label=key) plt.xlabel("iterations") # x軸ラベル plt.ylabel("loss") # y軸ラベル #plt.ylim(0, 1) # y軸の範囲 plt.legend() # 凡例 plt.show()
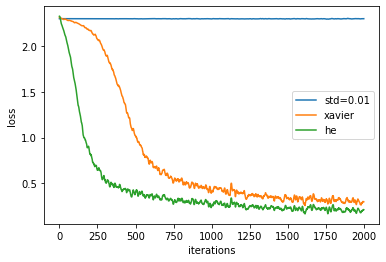
以上で、重みの初期値の設定によってアクティベーションの分布を調整する方法を確認できました!次は、アクティベーション自体を正規化することよって調整する方法を考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
前回だかにこれでパーツは全て揃った的なことを言った気がするのですが、まだまだ実装が続くようです。まぁこれまでは必要不可欠なパーツで、この後のは精度を高めるための装備品的な理解でお願いします。
【次節の内容】