はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、6.4.2項「Weight decay」の内容になります。大きな重みを持つことにペナルティを課すWeight decay(荷重減衰)を説明します。
【前節の内容】
【他の節の内容】
【この節の内容】
6.4.1 過学習
過学習は、データに対してパラメータが多すぎる場合や、訓練データが少ない場合に起こります。この項では、MNISTデータセットの300枚分のデータだけを用いることで、過学習を起こしてみます。
この項では7層のニューラルネットワークを用います。そのための多層ニューラルネットワークのクラスは、6章の最後に実装します。そのためここでは、マスターデータから(将来の自分が実装した)クラスを読み込みましょう。このクラスを用いた基本的な処理の流れは6.1.8項や6.2.4項、6.3.2項と同じです。そちらも参考にしてください。
またMNISTデータセットも読み込みます。マスターデータからの読み込みに関する詳しい解説は「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を確認してください。
# データ読み込み用ライブラリを読み込む import sys, os # ファイルパスを指定 sys.path.append('C:\\Users\\「ユーザー名」\\Documents\\・・・\\deep-learning-from-scratch-master') # MNISTデータセット読み込み関数 from dataset.mnist import load_mnist # 各種レイヤのクラス from common.layers import * # 多層ニューラルネットワーククラス from common.multi_layer_net import MultiLayerNet # 画像データを読み込む (x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_label=True) print(x_train.shape) print(t_train.shape)
(60000, 784)
(60000, 10)
ここから300データだけを取り出します。また更に1回の試行に使用するデータ数を指定し、batch_sizeとします。
# 学習データを削減 x_train = x_train[:300] t_train = t_train[:300] # 訓練データ数 train_size = x_train.shape[0] # バッチサイズを指定 batch_size = 100
まだ何のことだか知らない荷重減衰の係数weight_decay_lambdaを0とします。
多層ニューラルネットワークMultiLayerNetのインスタンスを作成します。
この例では7層のニューラルネットワークとするため、中間層のニューロン数の引数hidden_size_listに6つの値をリスト型変数で指定します(詳しくは実装時に説明します)。任意の値を指定できますが、この例では全て100とします。MNISTデータセットを用いる場合は、入力サイズinput_sizeがピクセル数の784、出力サイズoutput_sizeが数字の数10になります。(ちなみに、入出力層を含めた8つの層の間の数が7になります。)
活性化レイヤにReLU関数を用いるためactivation引数にrelu、重みの初期値をHeの初期値とするためweight_init_std引数に'he'を指定します。
また最適化手法を確率的勾配降下法(SGD)とします。6.1節で実装した他の手法も使えます。
# 荷重減衰の係数を指定 weight_decay_lambda = 0 # 7層のニューラルネットワークのインスタンスを作成 network = MultiLayerNet( input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, activation='relu', # 活性化関数 weight_init_std='he', # 重みの初期値の標準偏差 weight_decay_lambda=weight_decay_lambda # 荷重減衰の係数 ) # 最適化手法を指定 optimizer = SGD(lr=0.01)
試行回数を指定して実行します。
これまではfor文のrange()等に試行回数を指定していましたが、この例では次のようにして操作します。ミニバッチデータごとに(試行する度に)epoch_cntに1を加えることで試行回数を記録します。このカウントが指定した回数max_epochsに達すると、breakによってループ処理を終了します。この操作の前にforループが終わらないようにするため、range()には大きな値を与えています。値自体に特別な意味はありません。
# エポック当たりの試行回数を指定 max_epochs = 201 # 全データ数に対するバッチデータ数の割合(エポック数判定用) iter_per_epoch = max(train_size / batch_size, 1) # 試行回数のカウントを初期化 epoch_cnt = 0 # 認識精度の受け皿を初期化 train_loss_list = [] train_acc_list = [] test_acc_list = [] for i in range(1000000000): # ランダムにバッチデータ抽出 batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 勾配を計算 grads = network.gradient(x_batch, t_batch) # パラメータを更新 optimizer.update(network.params, grads) # 1エポックごとに認識精度を測定 if i % iter_per_epoch == 0: # 認識精度を測定 train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) # 値を記録 train_acc_list.append(train_acc) test_acc_list.append(test_acc) # 損失関数を計算 train_loss = network.loss(x_train, t_train) # 値を記録 train_loss_list.append(train_loss) # (動作確認も兼ねて)10エポックごとに認識精度を表示 if epoch_cnt % 10 == 0: print( "===========" + "epoch:" + str(epoch_cnt) + "===========" + "\ntrain acc:" + str(np.round(train_acc, 3)) + "\ntest acc :" + str(np.round(test_acc, 3)) ) # エポック数をカウント epoch_cnt += 1 # 最大エポック数に達すると終了 if epoch_cnt >= max_epochs: break
===========epoch:0===========
train acc:0.12
test acc :0.091
===========epoch:10===========
train acc:0.447
test acc :0.321
===========epoch:20===========
(省略)
===========epoch:190===========
train acc:1.0
test acc :0.747
===========epoch:200===========
train acc:1.0
test acc :0.75
訓練データとテストデータに対する認識精度の推移をグラフ化します。
# 作図用のx軸の値 epoch_vec = np.arange(max_epochs) # 作図 plt.plot(epoch_vec, train_acc_list, label='train') # 訓練データ plt.plot(epoch_vec, test_acc_list, label='test') # テストデータ plt.xlabel("epochs") # x軸ラベル plt.ylabel("accuracy") # y軸ラベル plt.title("Accuracy", fontsize=20) # タイトル plt.legend() # 凡例 plt.show()
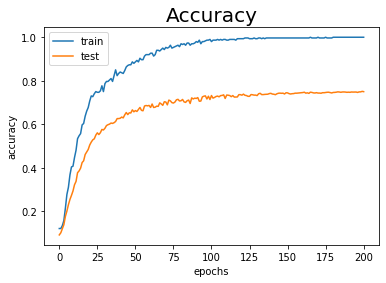
訓練データに対する認識精度が100%になりました。しかしテストデータに対しては75%しか認識できていません。これは訓練データに過剰に適応(過学習)してしまったといえます(図6-20)。
一応損失関数の値の推移も見ておきましょう。
# 作図用のx軸の値 epoch_vec = np.arange(max_epochs) # 作図 plt.plot(epoch_vec, train_loss_list) plt.xlabel("epochs") # x軸ラベル plt.ylabel("loss") # y軸ラベル plt.title("Cross Entropy Error", fontsize=20) # タイトル plt.show()
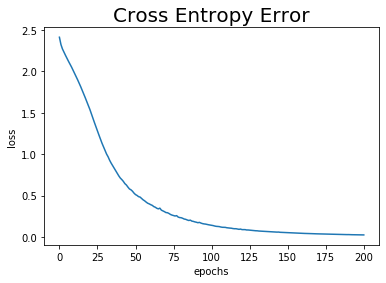
訓練データに対する認識精度が100%なのですから、当然誤差は0になりますね。
6.4.2 Weight decay
ニューラルネットワークの学習では、確率的勾配降下法によって損失関数の値$L$が小さくなるようにパラメータを更新するのでした。そこで損失関数(の計算)に、重みの値が大きいと損失関数の値も大きくなるように$\frac{1}{2} \lambda \mathbf{W}^2$を加えることにします。これによって、交差エントロピー誤差とともに$\frac{1}{2} \lambda \mathbf{W}^2$(つまり重み)を小さくするように学習します。
重み$\mathbf{W}$の要素は負の値にもなるので2乗しているわけですね。$\lambda$は正則化の強さを調整するハイパーパラメータです。$\lambda$が小さいほど$\mathbf{W}^2$が割り引かれるので、重みの影響が弱くなります。誤差逆伝播法では損失関数の勾配、つまり微分を伝播するのでした。$\frac{1}{2}$は、$\frac{1}{2} \lambda \mathbf{W}^2$を$\mathbf{W}$で微分したときに項を扱いやすくする(指数の2を打ち消す)ための定数項です。
従って逆伝播では$\lambda \mathbf{W}$を伝播します。
・実装イメージ
MultiLayerNetの実装おいてどのように正則化処理を行うのか確認しておきます。
簡単なMultiLayerNetのインスタンスを作成します。このクラスには既にWeight decayが実装されていますが、同じ処理を再現してみます。
# 4層のニューラルネットワークのインスタンスを作成 network = MultiLayerNet( input_size=784, hidden_size_list=[10, 10, 10], output_size=10, activation='relu', # 活性化関数 weight_init_std='he', # 重みの初期値の標準偏差 ) # 最適化手法を指定 optimizer = SGD(lr=0.01)
推論メソッド.predict()で、ニューラルネットワークの計算を行います。ただしこの処理では最終層の活性化レイヤは含まれないため、ソフトマックス関数による正規化は行われません。
# ニューラルネットワークの計算 y = network.predict(x_train) # 最終層の重みを確認 print(np.round(network.params['W4'], 2))
[[ 0.1 -0.41 0.38 0.59 0.04 -0.13 -0.2 0.15 1.17 -0.16]
[ 0.27 -0.12 0.4 0. -0.29 0.03 0.09 0.57 0.3 0.44]
[ 0.1 -0.66 0.18 -0.85 0.76 0.1 0.23 0.2 0.47 -0.07]
[ 0.13 -0.55 -0.46 0.65 0.08 -0.56 -0.69 0.19 0.32 -0.56]
[ 0.48 0.33 0.02 0.27 -0.34 0.1 -0.13 0.5 -0.5 -0.2 ]
[-0.27 -0.43 -0.48 -0.34 0.58 -0.5 -0.35 0.37 -0.04 0.09]
[-0.58 0.14 -0.16 0.15 -0.04 0.32 0.46 -0.03 0.68 0.32]
[-0.71 0.07 0.18 0.24 0.35 -0.11 0.51 0.11 0.32 0.37]
[ 0.79 0.73 0.83 -0.18 0. -0.2 0.02 -0.09 -0.51 0.76]
[ 0.53 -0.12 0.64 -0.07 -0.21 0.14 0.1 0.07 -0.01 1.19]]
最終層の重みはこんな感じになります。
荷重減衰の係数を指定して、Wight decayを計算します。
全てのレイヤの重みに対して順番に$\frac{1}{2} \lambda \mathbf{W}^2$の計算をして、weight_decayに加えていきます。
# 荷重減衰の係数を指定 weight_decay_lambda = 0.1 # 荷重減衰を初期化 weight_decay = 0 for i in range(1, network.hidden_layer_num + 2): # 重みを複製 W = network.params['W' + str(i)] # Weight decay(荷重減衰)を計算 weight_decay += 0.5 * weight_decay_lambda * np.sum(W ** 2) print(weight_decay)
3.886345630072221
全ての要素の和をとるので、weight_decayはスカラになります(そんな説明あったっけ?)。
インスタンス変数last_layerは、5.6.3項で実装したソフトマックス関数と交差エントロピー誤差のクラスSoftmaxWithLossのインスタンスです。よってこの順伝播メソッド.update()で交差エントロピー誤差を計算します。この値にweight_decayを加えた値が損失関数の値$L$となります。
# L2正則化版損失関数の計算 loss = network.last_layer.forward(y, t_train) + weight_decay print(loss)
6.245466282883789
重みの値が大きいと損失関数の値も大きくなることをイメージできますね。勾配降下法によりこの損失関数の値lossが小さくなるようにパラメータを更新するということは、weight_decayの影響も小さくなるようにパラメータを更新するということです。つまり重みの値を小さくするように働きます。
またこの処理だと、weight_decay_lambdaの値を0とすることで、weight_decayも0になります。よって正則化をするのかしないかによって条件分岐などの必要もなく実装できます。
以上がWeight decayの処理になります。これらは損失関数メソッド.loss()の中に定義されています。
・過学習の抑制効果を確認
荷重減衰の係数の値を指定して、先ほどと同じ処理を行います。
# 荷重減衰の係数を指定 weight_decay_lambda = 0.1 # 7層のニューラルネットワークのインスタンスを作成 network = MultiLayerNet( input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, activation='relu', # 活性化関数 weight_init_std='he', # 重みの初期値の標準偏差 weight_decay_lambda=weight_decay_lambda# 荷重減衰の係数 ) # 最適化手法を指定 optimizer = SGD(lr=0.01)
# エポック当たりの試行回数を指定 max_epochs = 201 # 全データ数に対するバッチデータ数の割合(エポック数判定用) iter_per_epoch = max(train_size / batch_size, 1) # 試行回数のカウントを初期化 epoch_cnt = 0 # 認識精度の受け皿を初期化 train_loss_list = [] train_acc_list = [] test_acc_list = [] for i in range(1000000000): # ランダムにバッチデータ抽出 batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 勾配を計算 grads = network.gradient(x_batch, t_batch) # パラメータを更新 optimizer.update(network.params, grads) # 1エポックごとに認識精度を測定 if i % iter_per_epoch == 0: # 認識精度を測定 train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) # 値を記録 train_acc_list.append(train_acc) test_acc_list.append(test_acc) # 損失関数を計算 train_loss = network.loss(x_train, t_train) # 値を記録 train_loss_list.append(train_loss) # (動作確認も兼ねて)10エポックごとに認識精度を表示 if epoch_cnt % 10 == 0: print( "===========" + "epoch:" + str(epoch_cnt) + "===========" + "\ntrain acc:" + str(np.round(train_acc, 3)) + "\ntest acc :" + str(np.round(test_acc, 3)) ) # エポック数をカウント epoch_cnt += 1 # 最大エポック数に達すると終了 if epoch_cnt >= max_epochs: break
===========epoch:0===========
train acc:0.11
test acc :0.118
===========epoch:10===========
train acc:0.29
test acc :0.212
===========epoch:20===========
(省略)
===========epoch:190===========
train acc:0.92
test acc :0.708
===========epoch:200===========
train acc:0.903
test acc :0.711
認識精度と交差エントロピー誤差の推移をグラフ化して確認しましょう。
# 作図用のx軸の値 epoch_vec = np.arange(max_epochs) # 作図 plt.plot(epoch_vec, train_acc_list, label='train') # 訓練データ plt.plot(epoch_vec, test_acc_list, label='test') # テストデータ plt.ylim(0, 1) # y軸の範囲 plt.xlabel("epochs") # x軸ラベル plt.ylabel("accuracy") # y軸ラベル plt.title("Accuracy", fontsize=20) # タイトル plt.legend() # 凡例 plt.show()
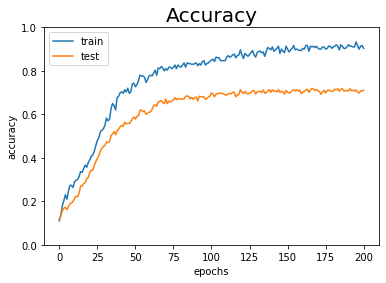
荷重減衰を行わないときよりも、訓練データとテストデータに対しての認識精度の差が小さくなりました(図6-21)。(テストデータに対する認識精度が上がったわけではないけどいいの?)
交差エントロピー誤差の推移もプロットしましょう。
# 作図用のx軸の値 epoch_vec = np.arange(max_epochs) # 作図 plt.plot(epoch_vec, train_loss_list) plt.xlabel("epochs") # x軸ラベル plt.ylabel("loss") # y軸ラベル plt.title("Cross Entropy Error", fontsize=20) # タイトル plt.show()
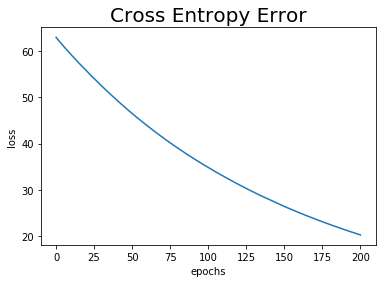
訓練データに対する認識精度が100%ではなくなったので、こちらの値も0ではなくなりました。
以上でWeight decayの確認ができました。Weight decayとは、過学習を抑制するために重みの値が大きくなることに対してペナルティを与える(損失関数の値が大きくなる)ものでした。次項では、ランダムにニューロンを消去することで過学習を抑制する手法について考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
L2ノルムのWeight decayは、$\frac{1}{2} \lambda \mathbf{W}^2$になり
という本の説明がよく分かりませんでした。L2ノルムは2乗和の平方根ですよね。ここから何をどうしたんだ???
【次節の内容】