はじめに
円関数(三角関数)の定義や公式をR言語で可視化して理解しようシリーズの補足シリーズ(黄金比編)です。
この記事では、黄金比の定義を確認します。
【前の内容】
【他の記事一覧】
【この記事の内容】
黄金比の可視化
黄金比(golden ratio)の定義と性質を数式とグラフで確認します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse)
この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要です。ただし、作図コードについてはパッケージ名を省略するので、 ggplot2 を読み込む必要があります。
また、ネイティブパイプ演算子 |> を使います。magrittr パッケージのパイプ演算子 %>% に置き換えられますが、その場合は magrittr を読み込む必要があります。
黄金比の定義
まずは、黄金比の定義を数式とグラフで確認します。
黄金分割
黄金分割のグラフを作成します。
長辺を1とする場合
黄金分割した際の長い方の線分を基準として考えます。
黄金数を作成します。
# 黄金数を計算 phi <- 0.5 * (1 + sqrt(5)) phi
[1] 1.618034
黄金数(黄金比率) を作成します。式については「黄金数の計算式」で確認します。
線分の長さを作成します。
# 長辺の長さを指定 a <- 1 # 短辺の長さを計算 b <- a / phi # 全体の長さを計算 ab <- a * phi ab; a; b
[1] 1.618034 [1] 1 [1] 0.618034
分割した2つの線分の内、長い方の線分 を指定して、短い方の線分
、線分全体(線分の和)
を計算します。
・作図コード(クリックで展開)
線分の描画用のデータフレームを作成します。
# 線分の座標を作成 edge_df <- tibble::tibble( edge_label = c("a + b", "a", "b") |> factor(levels = c("a + b", "a", "b")), # 描画順を指定 x_from = c(0, 0, a), x_to = c(ab, a, a+b), x_med = c(0.5*ab, 0.5*a, a+0.5*b), y = c(1, 0, 0), v = c(-0.5, 1.5, 1.5) ) edge_df
# A tibble: 3 × 6 edge_label x_from x_to x_med y v <fct> <dbl> <dbl> <dbl> <dbl> <dbl> 1 a + b 0 1.62 0.809 1 -0.5 2 a 0 1 0.5 0 1.5 3 b 1 1.62 1.31 0 1.5
線分 を横、線分
を縦に並ぶように始点と終点の座標を格納します。
黄金比により分割した線分のグラフを作成します。
# ラベル用の文字列を作成 def_label <- paste0( "list(", "phi1 == frac(1 + sqrt(5), 2), ", "(a + b) : a : b == phi1 : 1 : frac(1, phi1)", ")" ) len_label_vec <- c( "a + b == a * phi1^1", "a == a * phi1^0", "b == a * phi1^{-1}" ) # 線分を作図 ggplot() + geom_segment(data = edge_df, mapping = aes(x = x_from, y = y, xend = x_to, yend = y, color = edge_label), linewidth = 1) + # 線分 geom_text(data = edge_df, mapping = aes(x = x_med, y = y, label = edge_label, vjust = v), parse = TRUE, size = 6) + # 線分ラベル geom_vline(xintercept = c(0, a, ab), linetype = "dotted") + # 分割位置 scale_color_hue(labels = parse(text = len_label_vec), name = "length") + # 凡例表示用 scale_x_continuous(sec.axis = sec_axis(trans = ~., breaks = c(0, a, ab), labels = round(c(0, a, ab), digits = 2))) + # 分割位置ラベル scale_y_continuous(breaks = c(0, 1), labels = NULL, minor_breaks = FALSE) + coord_cartesian(y = c(-0.5, 1.5)) + labs(title = "golden ratio", subtitle = parse(text = def_label), x = "x", y = "")
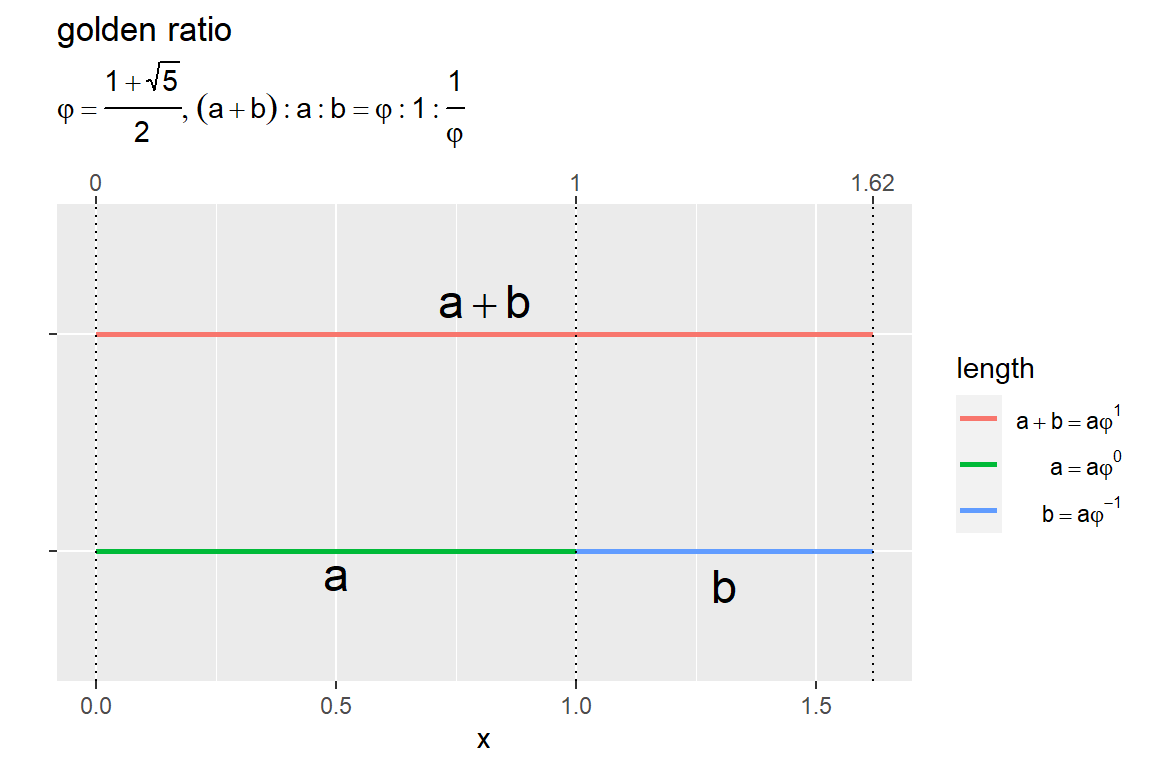
分割した長い方の線分の長さを 、短い方の線分の長さを
として、元の線分を
で表します。
3つの線分の関係が
となるような分割比率(長さ比率)を黄金比と呼びます。また、黄金比率を黄金数、黄金比による分割を黄金分割と呼びます。
黄金比率 により分割したときの3つの線分の長さ比は
になります。
よって、長辺 と短辺とは
、元の線分とは
の関係です。
指数の定義より、0乗は1 、マイナス1乗は逆数
、マイナスn乗は逆数のn乗(n乗の逆数)
です。
短辺を1とする場合
黄金分割した際の短い方の線分を基準として考えます。
線分の長さを作成します。
# 短辺の長さを指定 b <- 1 # 長辺の長さを計算 a <- b * phi # 全体の長さを計算 ab <- b * phi^2 ab; a; b
[1] 2.618034 [1] 1.618034 [1] 1
短い方の線分 を指定して、長い方の線分
、線分全体
を計算します。
先ほどのコードでグラフを作成します。ただし、凡例ラベル用の文字列は変更しています。
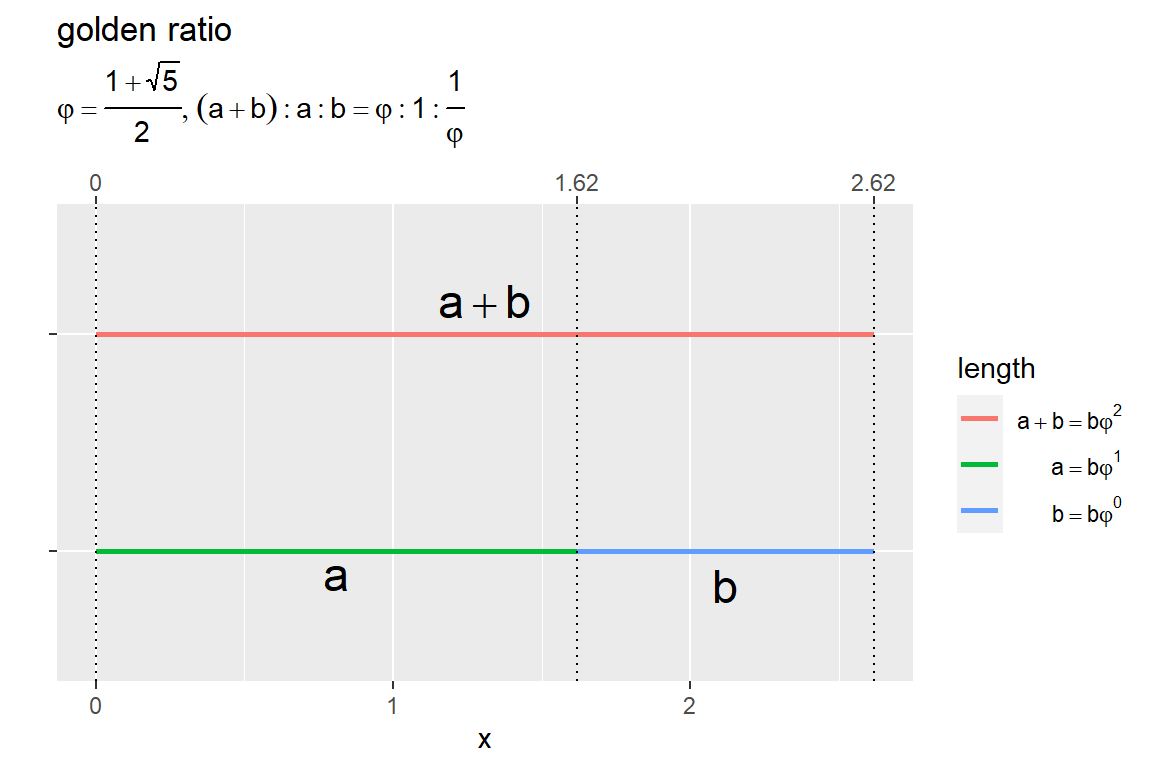
短辺 と長辺とは
、元の線分とは
の関係です。
3つの線分の比例式の右辺の全ての項に を掛けた
に対応します。
全体を1とする場合
黄金分割した際の線分全体を基準として考えます。
線分の長さを作成します。
# 全体の長さを指定 ab <- 1 # 長辺の長さを計算 a <- ab / phi # 短辺の長さを計算 b <- ab / phi^2 ab; a; b
[1] 1 [1] 0.618034 [1] 0.381966
線分全体 を指定して、長い方の線分
、短い方の線分
を計算します。
先ほどのコードでグラフを作成します。
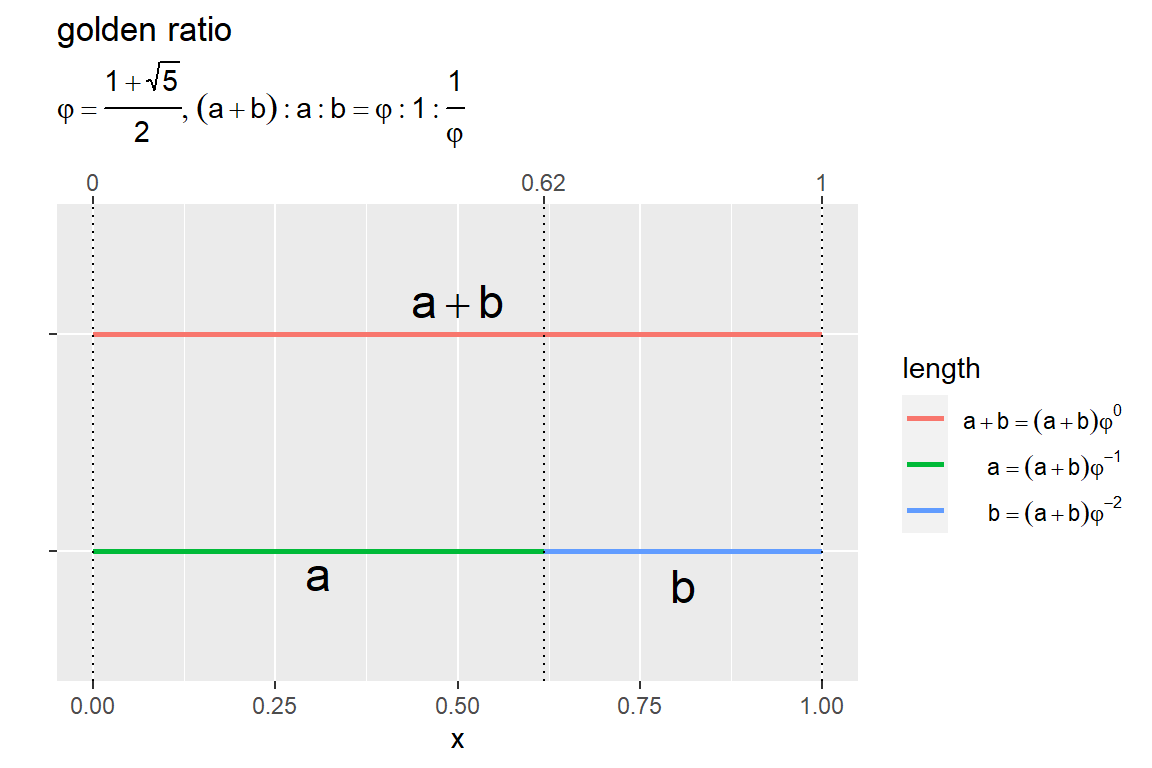
元の線分 と長辺とは
、短辺とは
の関係です。
比例式の右辺に を掛けた
に対応します。
黄金数の計算式
次は、黄金数(黄金比率)の計算式を導出します。
黄金比は、次の比例式で定義されました。
比例式の性質より、内項の積と外項の積が等しいので、次の式が成り立ちます。
両辺を短い方の長さ の2乗で割って、長さ比
について式を整理します。
について解く(
と置いて解の公式に代入する)と
となります。長さ比は正の値をとるので、2次関数の正の解が黄金数に対応します。
黄金数の計算式が得られました。
ちなみに、負の解は黄金数の負の逆数(マイナス1乗)で表わせます。
黄金数の逆数については「黄金数の性質の導出 - からっぽのしょこ」の「マイナス1乗」で確認します。
黄金比の性質
最後は、黄金長方形を用いて黄金比の性質を数式とグラフで確認します。
黄金長方形
黄金長方形のグラフを作成します。
分割する場合
黄金比により各辺を分割していくことを考えます。
黄金数を作成します。
# 黄金数を計算 phi <- 0.5 * (1 + sqrt(5)) # 黄金数の逆数を計算 recip_phi <- 1 / phi phi; recip_phi
[1] 1.618034 [1] 0.618034
黄金数(黄金比率) とその逆数
を作成します。
辺の長さを作成します。
# 辺の長さを指定 a0 <- 1 # 辺の長さを計算 a1 <- a0 * recip_phi a2 <- a1 * recip_phi a3 <- a2 * recip_phi a4 <- a3 * recip_phi a5 <- a4 * recip_phi a6 <- a5 * recip_phi a0; a1; a2; a3; a4; a5; a6
[1] 1 [1] 0.618034 [1] 0.381966 [1] 0.236068 [1] 0.145898 [1] 0.09016994 [1] 0.05572809
基準となる(この例では最長の)辺の長さ を指定して、各辺の長さ(
回分割した際の長い方の線分)
を計算します。
・作図コード(クリックで展開)
黄金長方形の描画用のデータフレームを作成します。
# 辺の座標を作成 edge_line_df <- dplyr::bind_rows( # 長さがa0の正方形の座標 tibble::tibble( i = 0, x_from = c(0, 0, a0, a0), y_from = c(0, a0, a0, 0), x_to = c(0, a0, a0, 0), y_to = c(a0, a0, 0, 0) ), # 長さがa1の正方形の座標 tibble::tibble( i = 1, x_from = c(0, 0, a1, a1) + a0, y_from = c(0, a1, a1, 0), x_to = c(0, a1, a1, 0) + a0, y_to = c(a1, a1, 0, 0) ), # 長さがa2の正方形の座標 tibble::tibble( i = 2, x_from = c(0, 0, a2, a2) + a0, y_from = c(0, a2, a2, 0) + a1, x_to = c(0, a2, a2, 0) + a0, y_to = c(a2, a2, 0, 0) + a1 ), # 長さがa3の正方形の座標 tibble::tibble( i = 3, x_from = c(0, 0, a3, a3) + a0+a2, y_from = c(0, a3, a3, 0) + a1, x_to = c(0, a3, a3, 0) + a0+a2, y_to = c(a3, a3, 0, 0) + a1 ), # 長さがa4の正方形の座標 tibble::tibble( i = 4, x_from = c(0, 0, a4, a4) + a0+a2, y_from = c(0, a4, a4, 0) + a1+a3, x_to = c(0, a4, a4, 0) + a0+a2, y_to = c(a4, a4, 0, 0) + a1+a3 ), # 長さがa5の正方形の座標 tibble::tibble( i = 5, x_from = c(0, 0, a5, a5) + a0+a2+a4, y_from = c(0, a5, a5, 0) + a1+a3, x_to = c(0, a5, a5, 0) + a0+a2+a4, y_to = c(a5, a5, 0, 0) + a1+a3 ), # 長さがa5の辺の座標 tibble::tibble( i = 5, x_from = a0+a2+a4, y_from = a1+a3+a5+a6, x_to = a0+a2+a4+a5, y_to = a1+a3+a5+a6 ), # 長さがa6の辺の座標 tibble::tibble( i = 6, x_from = c(0, a5) + a0+a2+a4, y_from = c(0, a6) + a1+a3+a5, x_to = c(0, a5) + a0+a2+a4, y_to = c(a6, 0) + a1+a3+a5 ) ) edge_line_df
# A tibble: 27 × 5
i x_from y_from x_to y_to
<dbl> <dbl> <dbl> <dbl> <dbl>
1 0 0 0 0 1
2 0 0 1 1 1
3 0 1 1 1 0
4 0 1 0 0 0
5 1 1 0 1 0.618
6 1 1 0.618 1.62 0.618
7 1 1.62 0.618 1.62 0
8 1 1.62 0 1 0
9 2 1 0.618 1 1
10 2 1 1 1.38 1
# ℹ 17 more rows
作成した辺の数に応じて(右・上方向に交互に正方形が積み上がっていくように)、各頂点(各辺の始点と終点)の座標を格納します。
この例では、各正方形の左下の頂点を原点として4つの座標をベクトルに格納しておき、それぞれx軸・y軸方向に平行移動するように(値を加えて)設定しています。
辺(長さ)ラベルの描画用のデータフレームを作成します。
# 辺ラベルの座標を作成 edge_label_df <- tibble::tibble( x = c( 0, 0.5*a0, a0, a0 +0.5*a1, a0, a0 +0.5*a2, a0+a2, a0+a2 +0.5*a3, a0+a2, a0+a2 +0.5*a4, a0+a2+a4, a0+a2+a4+0.5*a5, a0+a2+a4 ), y = c( 0.5*a0, 0, 0.5*a1, 0, a1 + 0.5*a2, a1, a1 + 0.5*a3, a1, a1+a3 + 0.5*a4, a1+a3, a1+a3 + 0.5*a5, a1+a3, a1+a3+a5+0.5*a6 ), len_label = c( "a[0]", "a[0]", "a[1]", "a[1]", "a[2]", "a[2]", "a[3]", "a[3]", "a[4]", "a[4]", "a[5]", "a[5]", "a[6]" ), ratio_label = c( "1", "1", "frac(1, phi1)", "frac(1, phi1)", "frac(1, phi1^2)", "frac(1, phi1^2)", "frac(1, phi1^3)", "frac(1, phi1^3)", "frac(1, phi1^4)", "frac(1, phi1^4)", "frac(1, phi1^5)", "frac(1, phi1^5)", "frac(1, phi1^6)" ), h = c( 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2 ), v = c( 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5, 1.2, 0.5 ), s = c( 6, 6, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3 ) ) edge_label_df
# A tibble: 13 × 7
x y len_label ratio_label h v s
<dbl> <dbl> <chr> <chr> <dbl> <dbl> <dbl>
1 0 0.5 a[0] 1 1.2 0.5 6
2 0.5 0 a[0] 1 0.5 1.2 6
3 1 0.309 a[1] frac(1, phi1) 1.2 0.5 3
4 1.31 0 a[1] frac(1, phi1) 0.5 1.2 3
5 1 0.809 a[2] frac(1, phi1^2) 1.2 0.5 3
6 1.19 0.618 a[2] frac(1, phi1^2) 0.5 1.2 3
7 1.38 0.736 a[3] frac(1, phi1^3) 1.2 0.5 3
8 1.5 0.618 a[3] frac(1, phi1^3) 0.5 1.2 3
9 1.38 0.927 a[4] frac(1, phi1^4) 1.2 0.5 3
10 1.45 0.854 a[4] frac(1, phi1^4) 0.5 1.2 3
11 1.53 0.899 a[5] frac(1, phi1^5) 1.2 0.5 3
12 1.57 0.854 a[5] frac(1, phi1^5) 0.5 1.2 3
13 1.53 0.972 a[6] frac(1, phi1^6) 1.2 0.5 3
各正方形の縦・横の2辺の中点にラベルを表示することにします。
黄金長方形のグラフを作成します。
# 辺の長さを格納 a_vals <- c(a0, a1, a2, a3, a4, a5, a6) # 分割回数を設定 n <- length(a_vals) - 1 # 辺インデックスを作成 i_vals <- 0:n # ラベル用の文字列を作成 def_label <- paste0( "list(", "phi1 == frac(1 + sqrt(5), 2), ", "a[i+1] : a[i] : a[i-1] == phi1 : 1 : frac(1, phi1), ", "a[i] == frac(a[0], phi1^i)", ")" ) len_label_vec <- paste0( "a[", i_vals, "] == ", round(a_vals, digits = 2) ) len_label_vec <- paste0( "a[", i_vals, "] == a[0] * phi1^{", -i_vals, "}" ) # 黄金長方形を作図 ggplot() + geom_segment(data = edge_line_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = factor(i)), linewidth = 1) + # 辺 geom_text(data = edge_label_df, mapping = aes(x = x, y = y, label = len_label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 長さラベル # geom_text(data = edge_label_df, # mapping = aes(x = x, y = y, label = ratio_label, # hjust = h, vjust = v, size = s), # parse = TRUE) + # 長さ比ラベル scale_color_hue(labels = parse(text = len_label_vec), name = "length") + # 凡例の表示用 # scale_size_identity(guide = "none") + # 分数の場合のサイズ分け用 theme(legend.text.align = 0) + coord_fixed(ratio = 1, xlim = c(0, a0+a1), ylim = c(-0.5*a1, a0+0.5*a1)) + # グリッド線の調整用 labs(title = "golden rectangle", subtitle = parse(text = def_label), x = "x", y = "y")
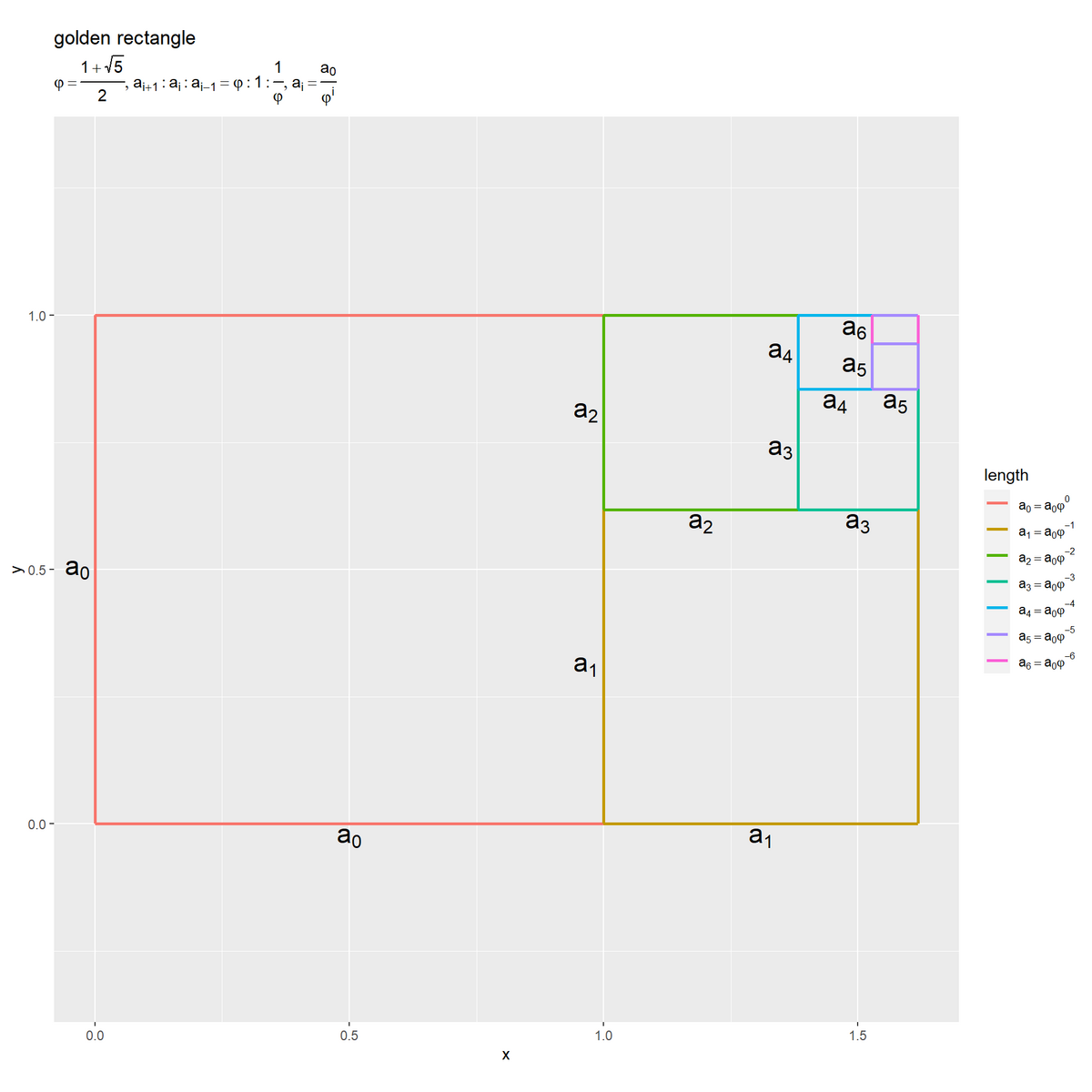
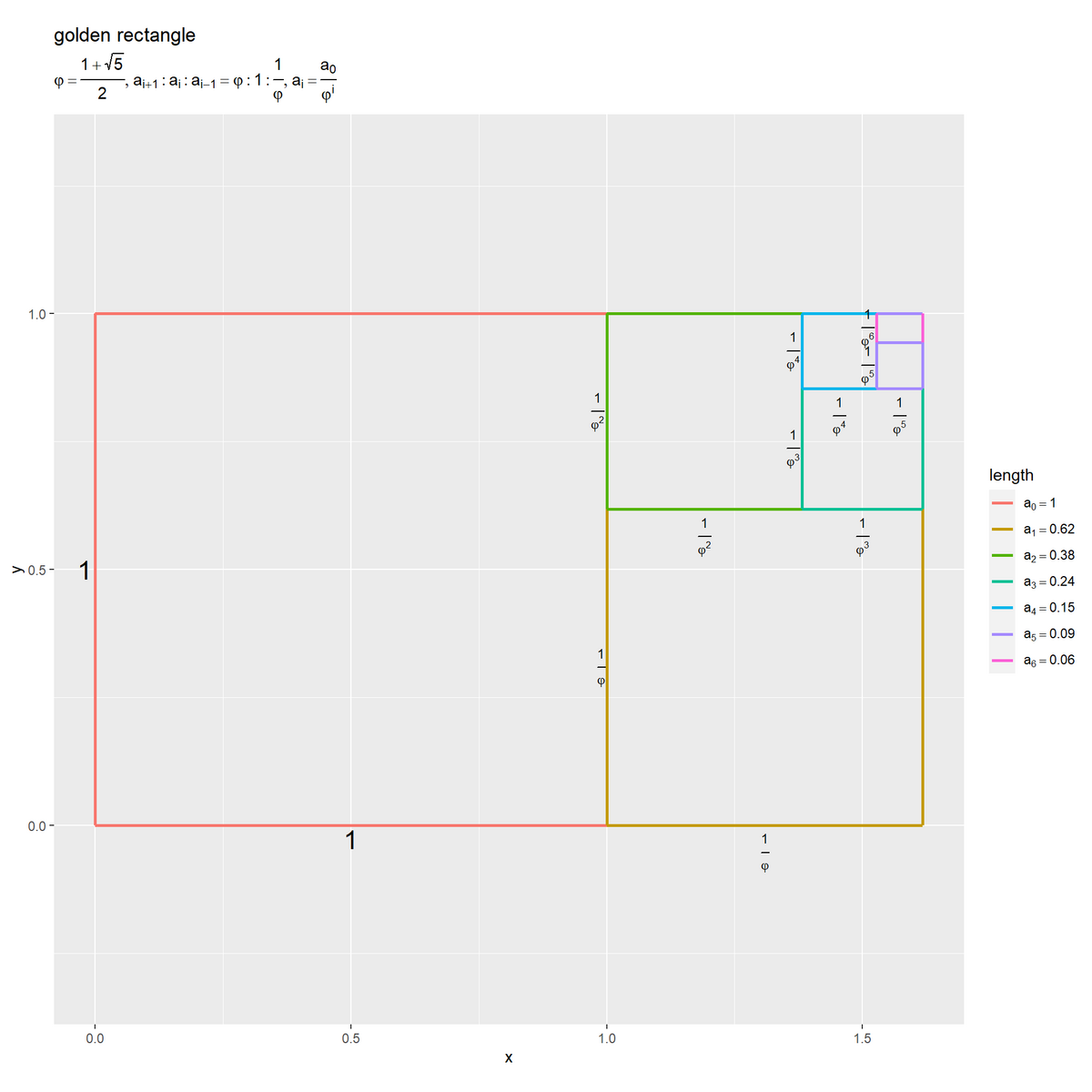
各辺を黄金分割した2つの線分をそれぞれ1辺とする正方形を(無限に)並べてできる長方形を黄金長方形と呼びます。隣り合う辺は、黄金分割した全体と長辺であり、また長辺と短辺の関係です。
基準となる辺を として、
回分割してできる長辺の長さを
で表します。長さが
の辺を3回分割すると(分割した長辺の長さは)
になります。
隣り合う辺の長さは であり、長さ比は
になるのを確認できます。
各辺と基準の辺は の関係です。分割した「全体
と長辺
」または「長辺
と短辺
」は
の関係です。
分割されるごとに辺の長さが 倍されます。
結合する場合
黄金比により各辺を結合していくことを考えます。
辺の長さを作成します。
# 辺の長さを指定 a0 <- 1 # 辺の長さを計算 a1 <- a0 * recip_phi a2 <- a1 * recip_phi a_1 <- a0 * phi a_2 <- a_1 * phi a_3 <- a_2 * phi a_4 <- a_3 * phi a_5 <- a_4 * phi a_6 <- a_5 * phi a2; a1; a0; a_1; a_2; a_3; a_4; a_5; a_6
[1] 0.381966 [1] 0.618034 [1] 1 [1] 1.618034 [1] 2.618034 [1] 4.236068 [1] 6.854102 [1] 11.09017 [1] 17.94427
基準となる(この例では一辺が2番目に短い正方形の)辺の長さ を指定して、各辺の長さ(
回結合(
回分割)した際の線分)
を計算します。
また、 を分割した2つの線分
を作成しておきます。
・作図コード(クリックで展開)
黄金長方形の描画用のデータフレームを作成します。
# 辺の座標を作成 edge_line_df <- dplyr::bind_rows( # 長さがa_2の辺の座標 tibble::tibble( i = 2, x_from = c(0, 0), y_from = c(0, a1), x_to = c(a2, a2), y_to = c(0, a1) ), # 長さがa_1の辺の座標 tibble::tibble( i = 1, x_from = 0, y_from = 0, x_to = 0, y_to = a1 ), # 長さがa_1の正方形の座標 tibble::tibble( i = 1, x_from = c(0, 0, a1, a1) + a2, y_from = c(0, a1, a1, 0), x_to = c(0, a1, a1, 0) + a2, y_to = c(a1, a1, 0, 0) ), # 長さがa_0の正方形の座標 tibble::tibble( i = 0, x_from = c(0, 0, a0, a0), y_from = c(0, a0, a0, 0) + a1, x_to = c(0, a0, a0, 0), y_to = c(a0, a0, 0, 0) + a1 ), # 長さがa_-1の正方形の座標 tibble::tibble( i = -1, x_from = c(0, 0, a_1, a_1) + a0, y_from = c(0, a_1, a_1, 0), x_to = c(0, a_1, a_1, 0) + a0, y_to = c(a_1, a_1, 0, 0) ), # 長さがa_-2の正方形の座標 tibble::tibble( i = -2, x_from = c(0, 0, a_2, a_2), y_from = c(0, a_2, a_2, 0) + a_1, x_to = c(0, a_2, a_2, 0), y_to = c(a_2, a_2, 0, 0) + a_1 ), # 長さがa_-3の正方形の座標 tibble::tibble( i = -3, x_from = c(0, 0, a_3, a_3) + a_2, y_from = c(0, a_3, a_3, 0), x_to = c(0, a_3, a_3, 0) + a_2, y_to = c(a_3, a_3, 0, 0) ), # 長さがa_-4の正方形の座標 tibble::tibble( i = -4, x_from = c(0, 0, a_4, a_4), y_from = c(0, a_4, a_4, 0) + a_3, x_to = c(0, a_4, a_4, 0), y_to = c(a_4, a_4, 0, 0) + a_3 ), # 長さがa_-5の正方形の座標 tibble::tibble( i = -5, x_from = c(0, 0, a_5, a_5) + a_4, y_from = c(0, a_5, a_5, 0), x_to = c(0, a_5, a_5, 0) + a_4, y_to = c(a_5, a_5, 0, 0) ) ) |> dplyr::arrange(i) # 線の重なり順用 edge_line_df
# A tibble: 31 × 5
i x_from y_from x_to y_to
<dbl> <dbl> <dbl> <dbl> <dbl>
1 -5 6.85 0 6.85 11.1
2 -5 6.85 11.1 17.9 11.1
3 -5 17.9 11.1 17.9 0
4 -5 17.9 0 6.85 0
5 -4 0 4.24 0 11.1
6 -4 0 11.1 6.85 11.1
7 -4 6.85 11.1 6.85 4.24
8 -4 6.85 4.24 0 4.24
9 -3 2.62 0 2.62 4.24
10 -3 2.62 4.24 6.85 4.24
# ℹ 21 more rows
結合した辺の数に応じて(上・右方向に交互に正方形が積み上がっていくように)、各頂点(各辺の始点と終点)の座標を格納します。
また、分割した辺を使って、逆方向に正方形または長方形の座標を格納します。
線の描画順(重なり順)を調整するために、arrange() で行を逆順に並べ替えます(逆順に格納することも可能ですが、直感的な順番に格納しています)。
辺(長さ)ラベルの描画用のデータフレームを作成します。
# 辺ラベルの座標を作成 edge_label_df <- tibble::tibble( x = c( 0.5*a2, a0, a2 +0.5*a1, a0, 0.5*a0, a_2, a0 +0.5*a_1, a_2, 0.5*a_2, a_4, a_2+0.5*a_3, a_4, 0.5*a_4, a_6, a_4+0.5*a_5 ), y = c( a1, 0.5*a1, a1, a1 +0.5*a0, a_1, 0.5*a_1, a_1, a_1+0.5*a_2, a_3, 0.5*a_3, a_3, a_3+0.5*a_4, a_5, 0.5*a_5, a_5 ), len_label = c( "a[2]", "a[1]", "a[1]", "a[0]", "a[0]", "a[-1]", "a[-1]", "a[-2]", "a[-2]", "a[-3]", "a[-3]", "a[-4]", "a[-4]", "a[-5]", "a[-5]" ), ratio_label = c( "frac(1, phi1^2)", "frac(1, phi1)", "frac(1, phi1)", "1", "1", "phi1", "phi1", "phi1^2", "phi1^2", "phi1^3", "phi1^3", "phi1^4", "phi1^4", "phi1^5", "phi1^5" ), h = c( 0.5, -0.5, 0.5, -0.5, 0.5, -0.5, 0.5, -0.5, 0.5, -0.5, 0.5, -0.5, 0.5, -0.5, 0.5 ), v = c( -0.1, 0.5, -0.1, 0.5, -0.1, 0.5, -0.1, 0.5, -0.1, 0.5, -0.1, 0.5, -0.1, 0.5, -0.1 ), s = c( 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6 ) ) edge_label_df
# A tibble: 15 × 7
x y len_label ratio_label h v s
<dbl> <dbl> <chr> <chr> <dbl> <dbl> <dbl>
1 0.191 0.618 a[2] frac(1, phi1^2) 0.5 -0.1 3
2 1 0.309 a[1] frac(1, phi1) -0.5 0.5 3
3 0.691 0.618 a[1] frac(1, phi1) 0.5 -0.1 3
4 1 1.12 a[0] 1 -0.5 0.5 6
5 0.5 1.62 a[0] 1 0.5 -0.1 6
6 2.62 0.809 a[-1] phi1 -0.5 0.5 6
7 1.81 1.62 a[-1] phi1 0.5 -0.1 6
8 2.62 2.93 a[-2] phi1^2 -0.5 0.5 6
9 1.31 4.24 a[-2] phi1^2 0.5 -0.1 6
10 6.85 2.12 a[-3] phi1^3 -0.5 0.5 6
11 4.74 4.24 a[-3] phi1^3 0.5 -0.1 6
12 6.85 7.66 a[-4] phi1^4 -0.5 0.5 6
13 3.43 11.1 a[-4] phi1^4 0.5 -0.1 6
14 17.9 5.55 a[-5] phi1^5 -0.5 0.5 6
15 12.4 11.1 a[-5] phi1^5 0.5 -0.1 6
各正方形の縦・横の2辺の中点にラベルを表示することにします。
黄金長方形のグラフを作成します。
# 辺の長さを格納 a_vals <- c(a_5, a_4, a_3, a_2, a_1, a0, a1, a2) # 分割回数・結合回数を設定 split_num <- 2 join_num <- 5 # 辺インデックスを作成 i_vals <- -join_num:split_num # ラベル用の文字列を作成 def_label <- paste0( "list(", "phi1 == frac(1 + sqrt(5), 2), ", "a[i+1] : a[i] : a[i-1] == phi1 : 1 : frac(1, phi1), ", "a[i] == a[0] * phi1^{-i}", ")" ) len_label_vec <- paste0( "a[", i_vals, "] == ", round(a_vals, digits = 2) ) len_label_vec <- paste0( "a[", i_vals, "] == a[0] * phi1^{", -i_vals, "}" ) # 黄金長方形を作図 ggplot() + geom_segment(data = edge_line_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = factor(i)), linewidth = 1) + # 辺 geom_text(data = edge_label_df, mapping = aes(x = x, y = y, label = len_label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 長さラベル # geom_text(data = edge_label_df, # mapping = aes(x = x, y = y, label = ratio_label, # hjust = h, vjust = v, size = s), # parse = TRUE) + # 長さ比ラベル scale_color_hue(labels = parse(text = len_label_vec), name = "length") + # 凡例の表示用 #scale_size_identity(guide = "none") + # 分数の場合のサイズ分け用 theme(legend.text.align = 0) + coord_fixed(ratio = 1, xlim = c(0, a_6), ylim = c(-0.5*a_4, a_5+0.5*a_4)) + # グリッド線の調整用 labs(title = "golden rectangle", subtitle = parse(text = def_label), x = "x", y = "y")
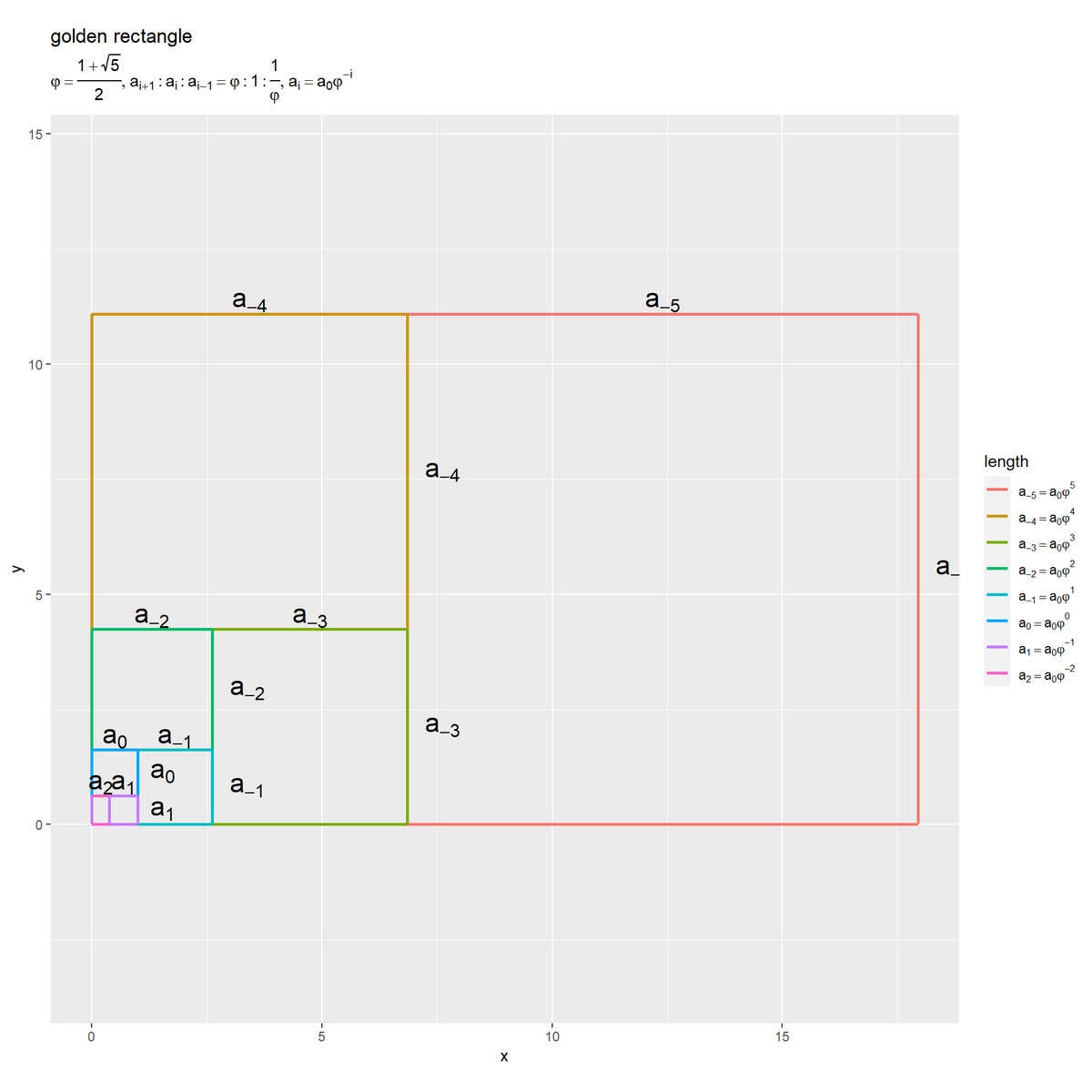
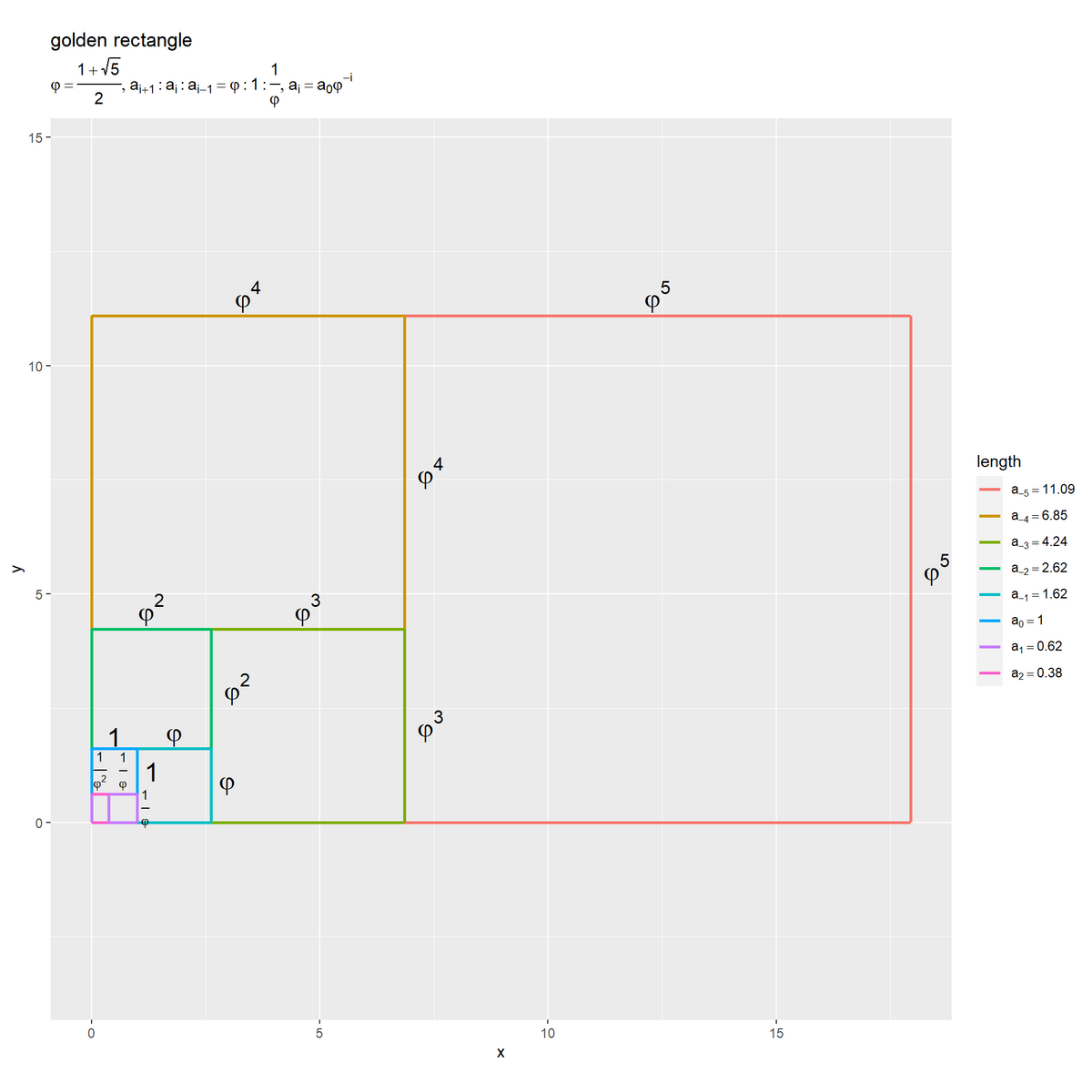
「分割する場合」と同じく、隣り合う辺は、黄金分割した全体と長辺であり、また長辺と短辺の関係です。
基準となる辺を として、
回分割した長辺(長い方の線分)を
としました。
回結合(黄金分割と逆の操作)した線分を
として
で表せます。辺
を基準として
回分割した長辺は
になります。長さが
の辺を3回分割すると(分割した長辺の長さは)
になります。
が負の整数であっても、各辺の長さが
、また
、長さ比が
になるのを確認できます。
分割( 倍する)の逆の操作なので、結合されるごとに辺の長さが
倍されます。
(各正方形の配置が「長辺を1とする場合」の図と回転した構成になっているのは作図の都合(基準となる辺の始点を原点にしている方が簡単なので)です。)
分割回数と長さの関係
分割回数と長さの関係のグラフを作成します。
分割する場合
黄金比により各辺を分割していくことを考えます。
・作図コード(クリックで展開)
分割回数と長さの関係の描画用のデータフレームを作成します。
# 分割回数の最大値を指定 max_num <- 10 # 比率の推移を作成 curve_df <- tibble::tibble( i = -1:max_num, a = a0 * recip_phi^i ) curve_df
# A tibble: 12 × 2
i a
<int> <dbl>
1 -1 1.62
2 0 1
3 1 0.618
4 2 0.382
5 3 0.236
6 4 0.146
7 5 0.0902
8 6 0.0557
9 7 0.0344
10 8 0.0213
11 9 0.0132
12 10 0.00813
分割回数を指定して、線分の長さ を計算します。
黄金長方形の辺の長さとの比較用のデータフレームを作成します。
# 辺の長さを格納 a_vals <- c(a0, a1, a2, a3, a4, a5, a6) # 分割回数を設定 n <- length(a_vals) - 1 # 辺の長さを格納 length_df <- dplyr::bind_rows( # 長辺 tibble::tibble( i = 0:n, x = i, y_from = 0, y = a_vals ), # 短辺 tibble::tibble( i = 1:n, x = i-1, y_from = a_vals[-n], y = y_from + a_vals[-1] ) ) length_df
# A tibble: 13 × 4
i x y_from y
<int> <dbl> <dbl> <dbl>
1 0 0 0 1
2 1 1 0 0.618
3 2 2 0 0.382
4 3 3 0 0.236
5 4 4 0 0.146
6 5 5 0 0.0902
7 6 6 0 0.0557
8 1 0 1 1.62
9 2 1 0.618 1
10 3 2 0.382 0.618
11 4 3 0.236 0.382
12 5 4 0.146 0.236
13 6 5 0.0557 0.111
分割前後の対応関係を示すめに、「黄金長方形」における長辺と短辺の長さを分割回数ごとに格納します。
分割回数と長さの関係のグラフを作成します。
# ラベル用の文字列を作成 def_label <- paste0( "list(", "phi1 == frac(1 + sqrt(5), 2), ", "a[i] == frac(a[0], phi1^i)", ")" ) # 分割回数と長さの関係を作図 ggplot() + geom_line(data = curve_df, mapping = aes(x = i, y = a), linewidth = 1) + # 線分の長さの推移 geom_segment(data = length_df, mapping = aes(x = x, y = y_from, xend = x, yend = y, color = factor(i)), linewidth = 1) + # 辺の長さ geom_hline(mapping = aes(yintercept = a_vals, color = factor(0:n)), linewidth = 0.8, linetype = "dotted") + # 辺の長さ scale_color_hue(labels = parse(text = paste0("a[", -1:n, "]")), name = "length") + # 凡例表示用 scale_x_continuous(breaks = -1:max_num, minor_breaks = FALSE) + # 分割回数軸 scale_y_continuous(sec.axis = sec_axis(trans = ~., breaks = a_vals, labels = round(a_vals, digits = 2))) + # 長さ軸 theme(legend.text.align = 0) + labs(title = "golden ratio", subtitle = parse(text = def_label), x = expression(i), y = expression(a[i]))
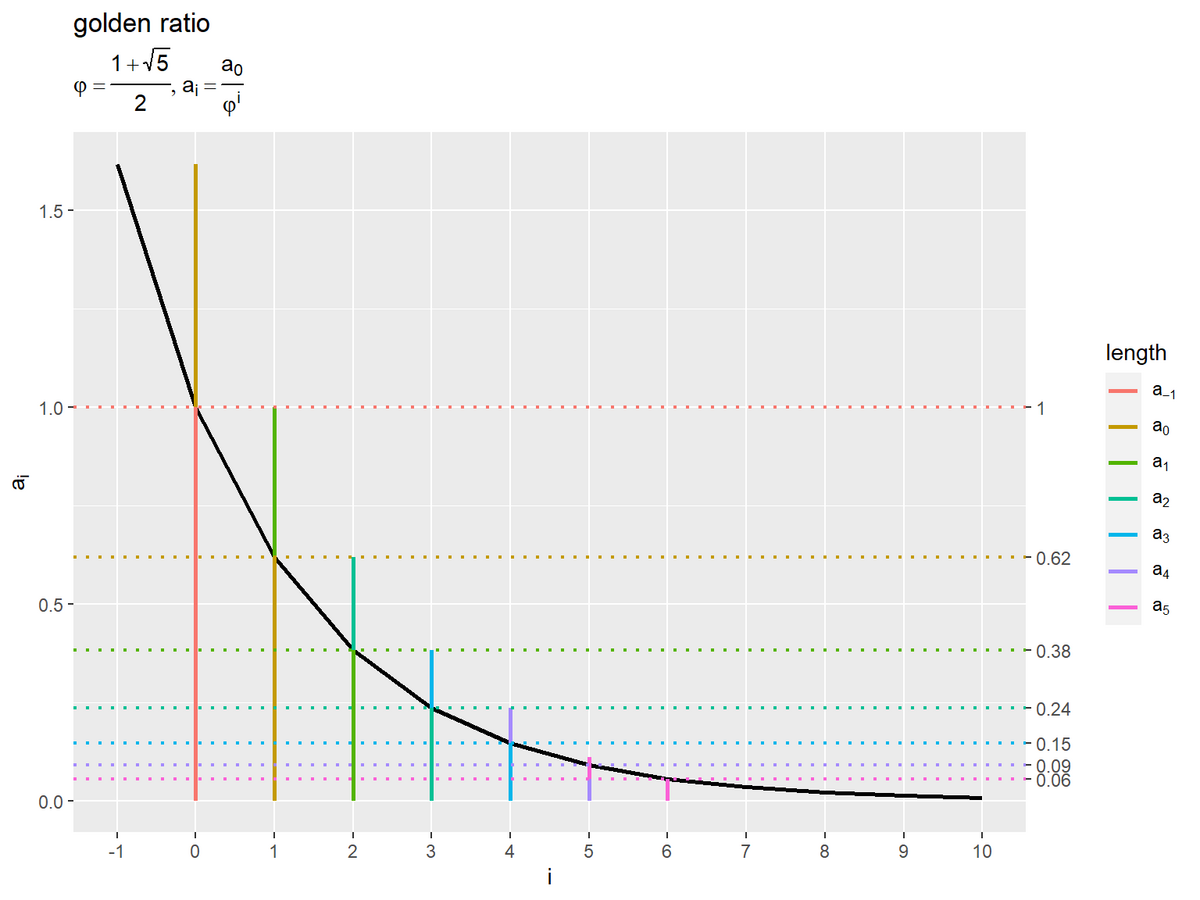
分割するごとに 倍ずつ減少する線分の長さを黒色の折れ線で表します。またイメージしやすいように、黄金長方形のグラフにおける色で直線を描画します(縮尺の関係でグラフ上での長さは一致していません)。
長さ の線分を黄金分割すると長さ
の2つの線分になり、また長い方の線分
を黄金分割した際の長い方の線分が
になるのを確認できます。
結合する場合
黄金比により各辺を結合していくことを考えます。
・作図コード(クリックで展開)
結合回数と長さの関係の描画用のデータフレームを作成します。
# 辺の長さを格納 a_vals <- c(a_5, a_4, a_3, a_2, a_1, a0, a1, a2) # 分割回数・結合回数を設定 split_num <- 2 join_num <- 5 # 辺インデックスを作成 i_vals <- -join_num:split_num # 比率の推移を作成 curve_df <- tibble::tibble( i = (-join_num-1):split_num, a = a0 * recip_phi^i ) curve_df
# A tibble: 9 × 2
i a
<int> <dbl>
1 -6 17.9
2 -5 11.1
3 -4 6.85
4 -3 4.24
5 -2 2.62
6 -1 1.62
7 0 1
8 1 0.618
9 2 0.382
分割回数と結合回数を指定して、線分の長さ を計算します。
黄金長方形の辺の長さとの比較用のデータフレームを作成します。
# 辺の長さを格納 length_df <- dplyr::bind_rows( tibble::tibble( i = i_vals, j = -i, x = i, y_from = 0, y = a_vals ), tibble::tibble( i = i_vals[-1], j = -i, x = i-1, y_from = a_vals[-n], y = y_from + a_vals[-1] ) ) length_df
# A tibble: 15 × 5
i j x y_from y
<int> <int> <dbl> <dbl> <dbl>
1 -5 5 -5 0 11.1
2 -4 4 -4 0 6.85
3 -3 3 -3 0 4.24
4 -2 2 -2 0 2.62
5 -1 1 -1 0 1.62
6 0 0 0 0 1
7 1 -1 1 0 0.618
8 2 -2 2 0 0.382
9 -4 4 -5 11.1 17.9
10 -3 3 -4 6.85 11.1
11 -2 2 -3 4.24 6.85
12 -1 1 -2 2.62 4.24
13 0 0 -1 1.62 2.62
14 1 -1 0 0.618 1.24
15 2 -2 1 0.382 0.764
分割前後の対応関係を示すめに、「黄金長方形」における長辺と短辺の長さを結合(分割)回数ごとに格納します。
結合回数と長さの関係のグラフを作成します。
# 分割回数と長さの関係を作図 ggplot() + geom_line(data = curve_df, mapping = aes(x = i, y = a), linewidth = 1) + # 線分の長さの推移 geom_segment(data = length_df, mapping = aes(x = x, y = y_from, xend = x, yend = y, color = factor(i)), linewidth = 1) + # 辺の長さ geom_hline(mapping = aes(yintercept = a_vals, color = factor(i_vals)), linewidth = 0.8, linetype = "dotted") + # 辺の長さ scale_color_hue(labels = parse(text = paste0("a[", i_vals, "]")), name = "length") + # 凡例表示用 scale_x_continuous(breaks = curve_df[["i"]], minor_breaks = FALSE) + # 分割回数軸 scale_y_continuous(sec.axis = sec_axis(trans = ~., breaks = a_vals, labels = round(a_vals, digits = 2))) + # 長さ軸 theme(legend.text.align = 0) + labs(title = "golden ratio", subtitle = parse(text = def_label), x = expression(i), y = expression(a[i]))
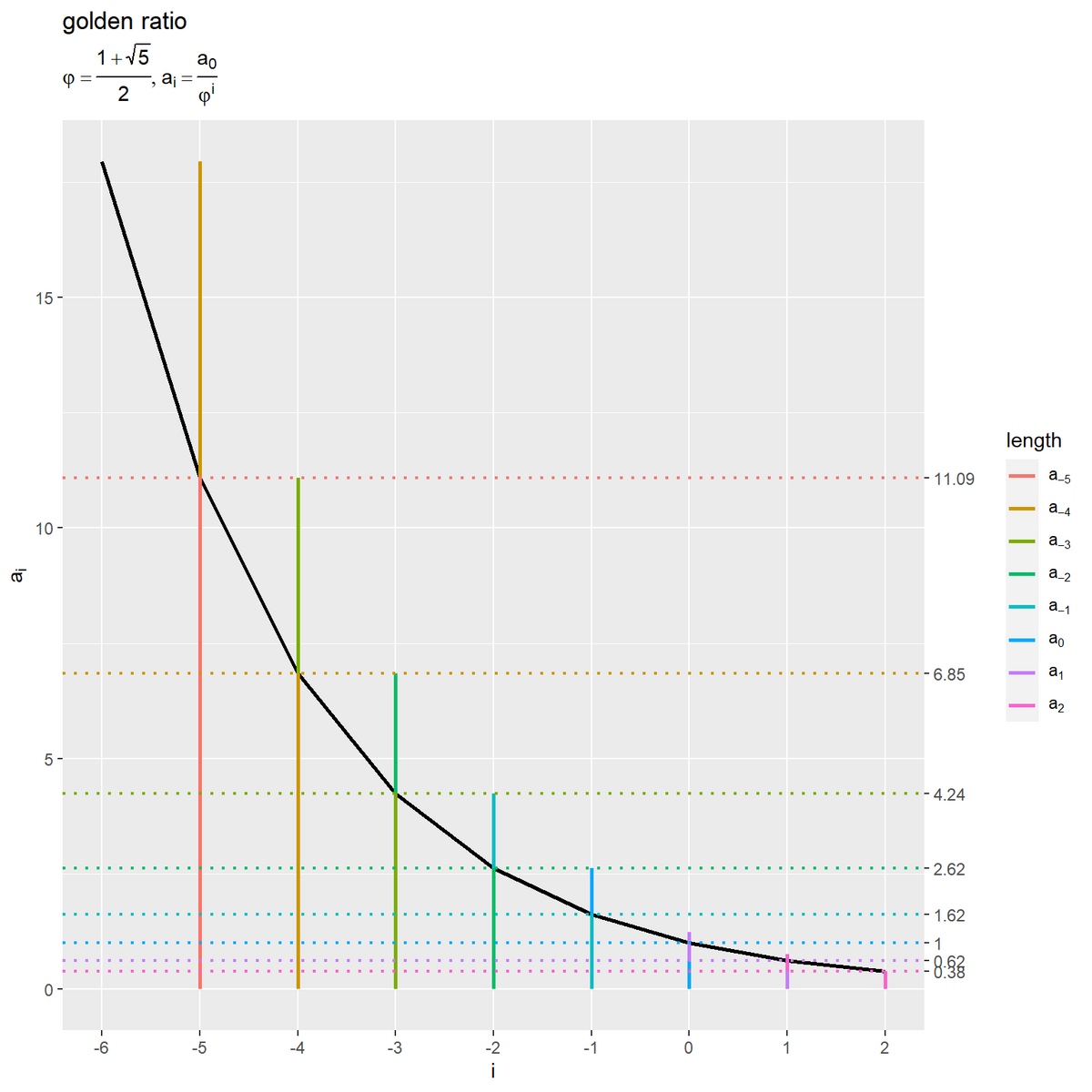
分割回数 が負の整数のとき、基準の線分
に結合した線分であることを表します。
分割する( が小さくなる)ごとに
倍ずつ減少し、結合する(
が大きくなる)ごとに
倍ずつ増加するのを確認できます。
の符号(正負)は基準となる線分から見た大小関係を表し、
の値に関わらず分割(結合)前後の比率は一定です。
この記事では、黄金比の定義と性質を確認しました。次の記事では、黄金長方形と螺旋の関係を確認します。
参考書籍
- 若原龍彦『図と数式で表す黄金比の不思議』プレアデス出版,2010年.
おわりに
あくまで螺旋シリーズの補足として書き始めた当初は、黄金比のネタを思い付けず、フィボナッチ数列の記事でさらっと黄金比に触れて黄金角の話に移るつもりでした。ところが、アドバイスをいただいたこともあって、黄金比関連の本を漁ってみたらネタの宝庫で黄金比シリーズに派生することになりました。めでたしめでたし。
これ以上脱線するわけにはいかないので、今回はフェルマー螺旋に必要な内容だけにしておきます。
いつかアレコレやってみたいですが、随分前からRで表現するような内容じゃないですよね。数学をアニメーションで可視化でき、かつブログに転載しやすいファイルを作成できるツールといえば何なんでしょうか?まぁRが好きだからRを使うために数学の勉強をしてる面もあるので、移行できるかは分かりませんが。
ところで、黄金比で本を探すと結構な数で料理本が引っ掛かったのが面白かったです。その路線で言うと、ファッション関連の本が多そうに思いますが(たぶん)無かったのが意外でした。
2023年11月30日は、元モーニング娘。の加賀楓さんの24歳のお誕生日です。
卒業後すぐにミュージカル「ムーラン・ルージュ」のニニ役をされていました。来年、関西で再演とのことで観に行きたいのですがはたして。
それでは!(・Д・)ノ
【次の内容】
もう少し黄金長方形を深掘りしたければこちらの記事をどうぞ。
もう少し黄金比率を深掘りしたければこちらの記事をどうぞ。
円周(角度)の黄金分割に興味があればこちらの記事をどうぞ。