はじめに
円関数(三角関数)の定義や公式をR言語で可視化して理解しようシリーズの補足シリーズ(黄金比編)です。
この記事では、黄金比を用いた長方形と螺旋の関係を確認します。
【前の内容】
【他の記事一覧】
【この記事の内容】
黄金長方形と黄金螺旋の関係
黄金比(golden ratio)により構成される黄金長方形(golden rectangle)上の螺旋と黄金螺旋(golden spiral)をグラフで確認します。
黄金比と黄金長方形については「【R】黄金比の可視化 - からっぽのしょこ」、黄金螺旋の一般形である対数螺旋(logarithmic spiral)については「【R】対数螺旋の可視化 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse)
この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要です。ただし、作図コードについてはパッケージ名を省略するので、 ggplot2 を読み込む必要があります。
また、ネイティブパイプ演算子 |> を使います。magrittr パッケージのパイプ演算子 %>% に置き換えられますが、その場合は magrittr を読み込む必要があります。
黄金比の性質
黄金長方形を用いて黄金比の性質をグラフで確認します。
黄金長方形
黄金長方形のグラフを作成します。
黄金数を作成します。
# 黄金数を計算 phi <- 0.5 * (1 + sqrt(5)) # 黄金数の逆数を計算 recip_phi <- 1 / phi phi; recip_phi
[1] 1.618034 [1] 0.618034
黄金数(黄金比率) とその逆数
を作成します。
辺の長さを作成します。
# 辺の長さを指定 a0 <- 1 # 辺の長さを計算 a1 <- a0 * recip_phi a2 <- a1 * recip_phi a3 <- a2 * recip_phi a4 <- a3 * recip_phi a5 <- a4 * recip_phi a6 <- a5 * recip_phi a0; a1; a2; a3; a4; a5; a6
[1] 1 [1] 0.618034 [1] 0.381966 [1] 0.236068 [1] 0.145898 [1] 0.09016994 [1] 0.05572809
基準となる(この例では最長の)辺の長さ を指定して、各辺の長さ(
回分割した際の長い方の線分)
を計算します。
・作図コード(クリックで展開)
黄金長方形の描画用のデータフレームを作成します。
# 辺の座標を作成 edge_line_df <- dplyr::bind_rows( # 長さがa0の正方形の座標 tibble::tibble( i = 0, x_from = c(0, 0, a0, a0), y_from = c(0, a0, a0, 0), x_to = c(0, a0, a0, 0), y_to = c(a0, a0, 0, 0) ), # 長さがa1の正方形の座標 tibble::tibble( i = 1, x_from = c(0, 0, a1, a1) + a0, y_from = c(0, a1, a1, 0) + a2, x_to = c(0, a1, a1, 0) + a0, y_to = c(a1, a1, 0, 0) + a2 ), # 長さがa2の正方形の座標 tibble::tibble( i = 2, x_from = c(0, 0, a2, a2) + a0+a3, y_from = c(0, a2, a2, 0), x_to = c(0, a2, a2, 0) + a0+a3, y_to = c(a2, a2, 0, 0) ), # 長さがa3の正方形の座標 tibble::tibble( i = 3, x_from = c(0, 0, a3, a3) + a0, y_from = c(0, a3, a3, 0), x_to = c(0, a3, a3, 0) + a0, y_to = c(a3, a3, 0, 0) ), # 長さがa4の正方形の座標 tibble::tibble( i = 4, x_from = c(0, 0, a4, a4) + a0, y_from = c(0, a4, a4, 0) + a3, x_to = c(0, a4, a4, 0) + a0, y_to = c(a4, a4, 0, 0) + a3 ), # 長さがa5の正方形の座標 tibble::tibble( i = 5, x_from = c(0, 0, a5, a5) + a0+a4, y_from = c(0, a5, a5, 0) + a3+a6, x_to = c(0, a5, a5, 0) + a0+a4, y_to = c(a5, a5, 0, 0) + a3+a6 ), # 長さがa5の辺の座標 tibble::tibble( i = 5, x_from = a0+a4, y_from = a3, x_to = a0+a4+a5, y_to = a3 ), # 長さがa6の辺の座標 tibble::tibble( i = 6, x_from = c(0, a5) + a0+a4, y_from = c(0, a6) + a3, x_to = c(0, a5) + a0+a4, y_to = c(a6, 0) + a3 ) ) edge_line_df
# A tibble: 27 × 5
i x_from y_from x_to y_to
<dbl> <dbl> <dbl> <dbl> <dbl>
1 0 0 0 0 1
2 0 0 1 1 1
3 0 1 1 1 0
4 0 1 0 0 0
5 1 1 0.382 1 1
6 1 1 1 1.62 1
7 1 1.62 1 1.62 0.382
8 1 1.62 0.382 1 0.382
9 2 1.24 0 1.24 0.382
10 2 1.24 0.382 1.62 0.382
# ℹ 17 more rows
「黄金長方形」のときと同様に、作成した辺の数に応じて(時計回りに正方形が敷き詰められていくように)、各頂点(各辺の始点と終点)の座標を格納します。
長さ比ラベルの描画用のデータフレームを作成します。
# 辺ラベルの座標を格納 edge_label_df <- tibble::tibble( x = c( 0, 0.5*a0, a0+0.5*a1, a0+a1, a0+a1, a0+a3+0.5*a2, a0+0.5*a3, a0, a0, a0+0.5*a4, a0+a4+0.5*a5, a0+a4+a5, a0+a4+a5 ), y = c( 0.5*a0, a0, a0, a2+0.5*a1, 0.5*a2, 0, 0, 0.5*a3, a3+0.5*a4, a2, a2, a3+a6+0.5*a5, a3+0.5*a6 ), len_label = c( "a[0]", "a[0]", "a[1]", "a[1]", "a[2]", "a[2]", "a[3]", "a[3]", "a[4]", "a[4]", "a[5]", "a[5]", "a[6]" ), ratio_label = c( "phi1^0", "phi1^0 == 1", "phi1^{-1}", "phi1^{-1}", "phi1^{-2}", "phi1^{-2}", "phi1^{-3}", "phi1^{-3}", "phi1^{-4}", "phi1^{-4}", "phi1^{-5}", "phi1^{-5}", "phi1^{-6}" ), h = c( 1.2, 0.2, 0.2, -0.2, -0.2, 0.2, 0.2, 1.2, 1.2, 0.2, 0.2, -0.2, -0.2 ), v = c( 0.2, -0.2, -0.2, 0.2, 0.2, 1.2, 1.2, 0.2, 0.2, -0.2, -0.2, 0.2, 0.2 ) ) edge_label_df
# A tibble: 13 × 6
x y len_label ratio_label h v
<dbl> <dbl> <chr> <chr> <dbl> <dbl>
1 0 0.5 a[0] phi1^0 1.2 0.2
2 0.5 1 a[0] phi1^0 == 1 0.2 -0.2
3 1.31 1 a[1] phi1^{-1} 0.2 -0.2
4 1.62 0.691 a[1] phi1^{-1} -0.2 0.2
5 1.62 0.191 a[2] phi1^{-2} -0.2 0.2
6 1.43 0 a[2] phi1^{-2} 0.2 1.2
7 1.12 0 a[3] phi1^{-3} 0.2 1.2
8 1 0.118 a[3] phi1^{-3} 1.2 0.2
9 1 0.309 a[4] phi1^{-4} 1.2 0.2
10 1.07 0.382 a[4] phi1^{-4} 0.2 -0.2
11 1.19 0.382 a[5] phi1^{-5} 0.2 -0.2
12 1.24 0.337 a[5] phi1^{-5} -0.2 0.2
13 1.24 0.264 a[6] phi1^{-6} -0.2 0.2
各正方形の縦・横の2辺の中点にラベルを表示することにします。
黄金長方形のグラフを作成します。
# 辺の長さを格納 a_vals <- c(a0, a1, a2, a3, a4, a5, a6) # 分割回数を設定 n <- length(a_vals) - 1 # 辺インデックスを作成 i_vals <- 0:n # ラベル用の文字列を作成 def_label <- paste0( "list(", "phi1 == frac(1 + sqrt(5), 2), ", "a[i+1] : a[i] : a[i-1] == phi1 : 1 : frac(1, phi1), ", "a[i] == frac(a[0], phi1^i)", ")" ) len_label_vec <- paste0( "a[", i_vals, "] == ", round(a_vals, digits = 2) ) # 黄金長方形上の螺旋を作図 ggplot() + geom_segment(data = edge_line_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = factor(i)), linewidth = 1) + # 辺 geom_text(data = edge_label_df, mapping = aes(x = x, y = y, label = ratio_label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 長さラベル scale_color_hue(labels = parse(text = len_label_vec), name = "length") + # 凡例の表示用 theme(legend.text.align = 0) + coord_fixed(ratio = 1, xlim = c(0, a0+a1), ylim = c(-0.5*a1, a0+0.5*a1)) + # グリッド線の調整用 labs(title = "golden rectangle", subtitle = parse(text = def_label), x = "x", y = "y")
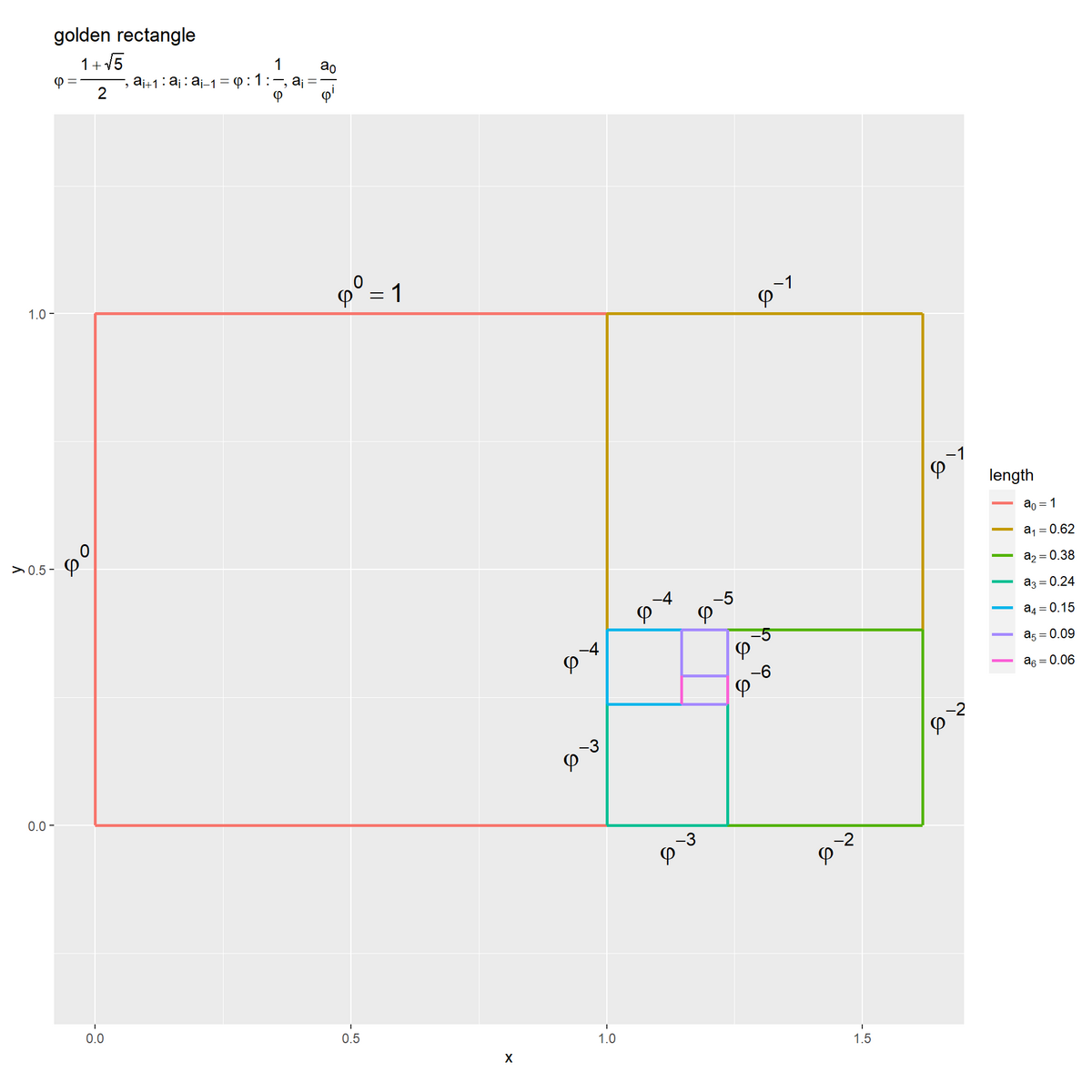
「黄金比の可視化」のときとは正方形の配置が異なりますが、黄金分割の性質は変わりません。
辺(線分)を黄金分割するごとに黄金数の逆数 倍ずつ短くなっていきます。よって、基準とする辺の長さを
として、
回分割した辺の長さは
であり、隣り合う辺の長さは
です。黄金比で結合(分割の逆の操作)する場合は
であり、
回結合すると
になるのでした。
長辺が で短辺が
の長方形の中に、長辺が
で短辺が
の長方形が含まれます。さらに中に、長辺が
で短辺が
の長方形を無数に持ち、そのすべてが黄金長方形です。この例では、7個描画しています。
黄金長方形上の螺旋
黄金長方形を構成する正方形ごとに一辺の長さを半径とする円弧(四分円)を描き、黄金螺旋の近似曲線を作成します。
・作図コード(クリックで展開)
螺旋の描画用のデータフレームを作成します。
# 螺旋の座標を作成 a7 <- a6 * recip_phi arc_df <- dplyr::bind_rows( # 半径がa0の円弧の座標 tibble::tibble( i = 0, t = seq(from = 0.5*pi, to = pi, length.out = 91), x = a0 + a0 * cos(t), y = 0 + a0 * sin(t) ), # 半径がa1の円弧の座標 tibble::tibble( i = 1, t = seq(from = 0, to = 0.5*pi, length.out = 91), x = a0 + a1 * cos(t), y = a2 + a1 * sin(t) ), # 半径がa2の円弧の座標 tibble::tibble( i = 2, t = seq(from = 1.5*pi, to = 2*pi, length.out = 91), x = a0+a3 + a2 * cos(t), y = a2 + a2 * sin(t) ), # 半径がa3の円弧の座標 tibble::tibble( i = 3, t = seq(from = 1*pi, to = 1.5*pi, length.out = 91), x = a0+a3 + a3 * cos(t), y = a3 + a3 * sin(t) ), # 半径がa4の円弧の座標 tibble::tibble( i = 4, t = seq(from = 0.5*pi, to = 1*pi, length.out = 91), x = a0+a4 + a4 * cos(t), y = a3 + a4 * sin(t) ), # 半径がa5の円弧の座標 tibble::tibble( i = 5, t = seq(from = 0, to = 0.5*pi, length.out = 91), x = a0+a4 + a5 * cos(t), y = a3+a6 + a5 * sin(t) ), # 半径がa6の円弧の座標 tibble::tibble( i = 6, t = seq(from = 1.5*pi, to = 2*pi, length.out = 91), x = a0+a4+a7 + a6 * cos(t), y = a3+a6 + a6 * sin(t) ) ) arc_df
# A tibble: 637 × 4
i t x y
<dbl> <dbl> <dbl> <dbl>
1 0 1.57 1 1
2 0 1.59 0.983 1.00
3 0 1.61 0.965 0.999
4 0 1.62 0.948 0.999
5 0 1.64 0.930 0.998
6 0 1.66 0.913 0.996
7 0 1.68 0.895 0.995
8 0 1.69 0.878 0.993
9 0 1.71 0.861 0.990
10 0 1.73 0.844 0.988
# ℹ 627 more rows
円弧が時計回りに繋がるように中心とする頂点の位置を変えて、正方形ごとに辺の長さと同じ半径の四分円の座標を格納します。
対角線の描画用のデータフレームを作成します。
# 対角線の座標を作成 diagonal_df <- tibble::tibble( # 傾き alpha = c( recip_phi^3, -recip_phi, -phi^3, phi ), # 切片 beta = c( 0, a0, a0 * (phi^3 + 1), -a0 * phi ) ) diagonal_df
# A tibble: 4 × 2 alpha beta <dbl> <dbl> 1 0.236 0 2 -0.618 1 3 -4.24 5.24 4 1.62 -1.62
2つの正方形の頂点を結ぶ直線
の傾きと切片を格納します。計算式については「対角線の導出」で確認します。
黄金長方形と近似黄金螺旋のグラフを作成します。
# 黄金長方形上の螺旋を作図 ggplot() + geom_segment(data = edge_line_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = factor(i)), linewidth = 1) + # 辺 geom_text(data = edge_label_df, mapping = aes(x = x, y = y, label = len_label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 長さラベル geom_abline(data = diagonal_df, mapping = aes(slope = alpha, intercept = beta)) + # 対角線 geom_path(data = arc_df, mapping = aes(x = x, y = y, group = factor(i)), linewidth = 1) + # 螺旋 scale_color_hue(labels = parse(text = len_label_vec), name = "length") + # 凡例の表示用 theme(legend.text.align = 0) + coord_fixed(ratio = 1, xlim = c(0, a0+a1), ylim = c(-0.5*a1, a0+0.5*a1)) + # グリッド線の調整用 labs(title = "golden rectangle", subtitle = parse(text = def_label), x = "x", y = "y")
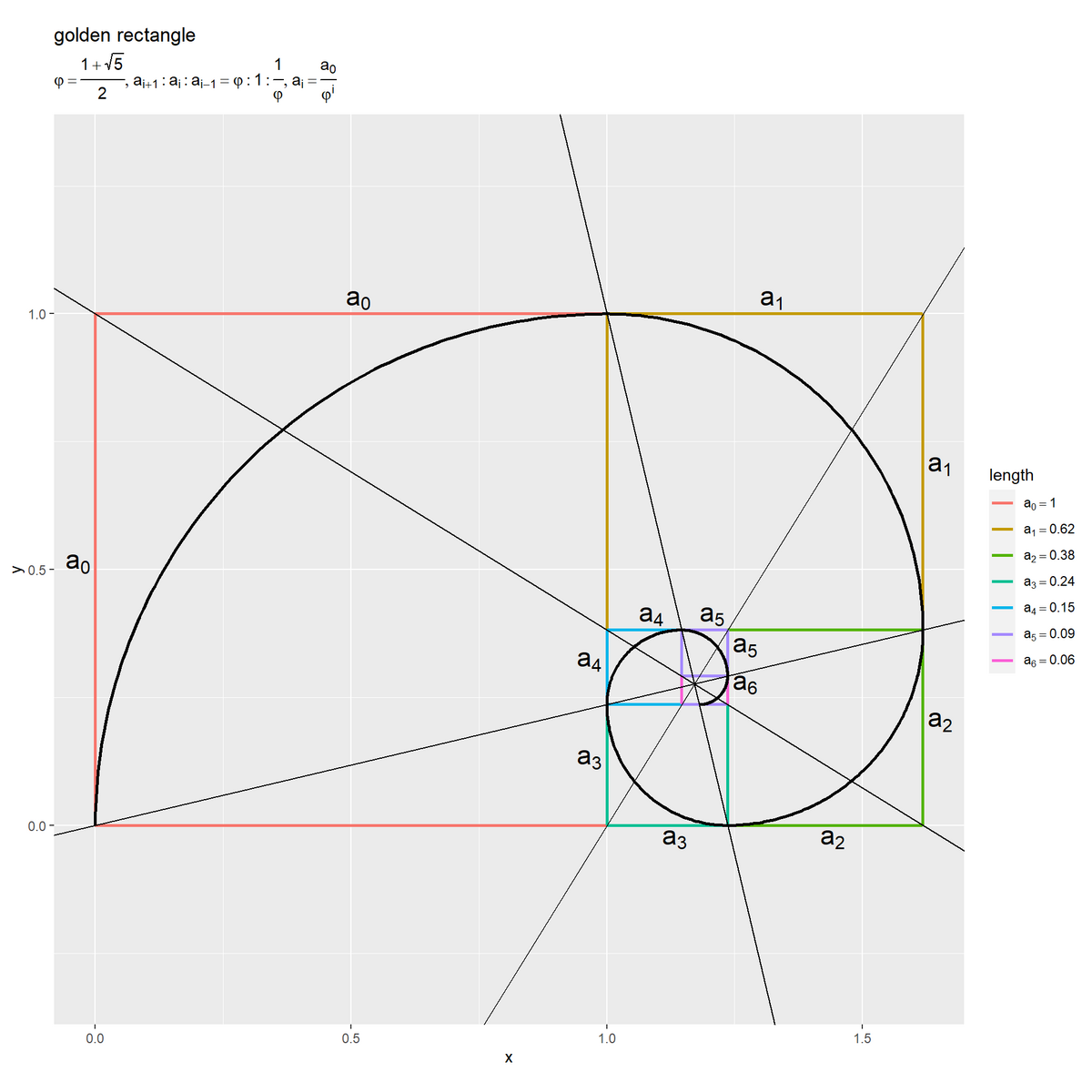
各正方形の一辺の長さ は、黄金数(黄金比率)
ずつ変化するのでした。正方形の対角線を結ぶように引かれた四分円の弧の半径も
であり
ずつ変化します。円弧が螺旋状に繋がるように描画しています。言い換えると、螺旋は黄金長方形の頂点を通っています。
黄金長方形を構成するの外側の長方形(正方形)の内2つの頂点を結ぶ直線は、内側の長方形(正方形)の頂点も通り、交点が一致します。(直交してる気もしますがよく分かりません。)
黄金長方形の対角線の交点が螺旋の中心となり、黄金長方形はこの点に収束します。
黄金螺旋
黄金螺旋を作成します。各種計算式については「補足」で確認します。
・作図コード(クリックで展開)
螺旋の中心の座標を作成します。
# 中心の座標を計算 x0 <- 0.1 * (5 + 3 * sqrt(5)) * a0 y0 <- 0.1 * (5 - sqrt(5)) * a0 x0; y0
[1] 1.17082 [1] 0.2763932
螺旋の中心として、対角線の交点 を計算します。
原点に対応する角度を作成します。
# 中心点から見た原点の角度を計算 t0 <- atan2(-y0, -x0) # 中心点と原点のノルムを計算 r0 <- sqrt(x0^2 + y0^2) r0 <- -x0 / cos(t0) r0 <- -y0 / sin(t0) t0; r0
[1] -2.909769 [1] 1.203002
中心点 から見た原点の角度(中心点と原点を結ぶ半直線の偏角)を
で計算します。引数を2つとる逆タンジェント関数は
atan2() で計算できます。
原点と中心点のノルム(距離)を で計算します。
螺旋のパラメータを作成します。
# パラメータを計算 beta <- log(phi) * 2/pi alpha <- r0 / exp(beta * t0) alpha; beta
[1] 2.933583 [1] 0.306349
黄金螺旋のパラメータ を計算します。
螺旋の描画用のデータフレームを作成します。
# 螺旋用のラジアン(弧度法の角度)を作成 t_vec <- seq(from = -10*pi, to = 0, length.out = 1000) # 螺旋の座標を作成 spiral_df <- tibble::tibble( t = t_vec, # ラジアン r = alpha * exp(beta * t), # ノルム x = x0 + r * cos(t), y = y0 + r * sin(t) ) spiral_df
# A tibble: 1,000 × 4
t r x y
<dbl> <dbl> <dbl> <dbl>
1 -31.4 0.000194 1.17 0.276
2 -31.4 0.000196 1.17 0.276
3 -31.4 0.000198 1.17 0.276
4 -31.3 0.000200 1.17 0.276
5 -31.3 0.000202 1.17 0.276
6 -31.3 0.000204 1.17 0.276
7 -31.2 0.000205 1.17 0.276
8 -31.2 0.000207 1.17 0.276
9 -31.2 0.000209 1.17 0.276
10 -31.1 0.000211 1.17 0.276
# ℹ 990 more rows
対数螺旋の座標は、次の式で計算できます。
黄金長方形と黄金螺旋のグラフを作成します。
# ラベル用の文字列を作成 def_label <- paste0( "list(", "r == alpha ~ exp(beta * theta), ", "alpha == ", round(alpha, digits = 2), ", ", "beta == ", round(beta, digits = 2), ")" ) # 黄金長方形と黄金螺旋を作図 ggplot() + geom_hline(yintercept = y0, linetype = "dotted") + # x軸目盛の補助線 geom_vline(xintercept = x0, linetype = "dotted") + # y軸目盛の補助線 geom_segment(data = edge_line_df, mapping = aes(x = x_from, y = y_from, xend = x_to, yend = y_to, color = factor(i)), linewidth = 1) + # 辺 geom_text(data = edge_label_df, mapping = aes(x = x, y = y, label = len_label, hjust = h, vjust = v), parse = TRUE, size = 6) + # 長さラベル geom_abline(data = diagonal_df, mapping = aes(slope = alpha, intercept = beta)) + # 対角線 geom_path(data = arc_df, mapping = aes(x = x, y = y, group = factor(i)), linewidth = 1) + # 近似螺旋 geom_path(data = spiral_df, mapping = aes(x = x, y = y), color = "red", linewidth = 1) + # 黄金螺旋 scale_color_hue(labels = parse(text = len_label_vec), name = "length") + # 凡例の表示用 scale_x_continuous(sec.axis = sec_axis(trans = ~., breaks = x0, labels = round(x0, digits = 2))) + # 中心のx座標 scale_y_continuous(sec.axis = sec_axis(trans = ~., breaks = y0, labels = round(y0, digits = 2))) + # 中心のy座標 theme(legend.text.align = 0) + coord_fixed(ratio = 1, xlim = c(0, a0+a1), ylim = c(-0.5*a1, a0+0.5*a1)) + # グリッド線の調整用 labs(title = "golden spiral", subtitle = parse(text = def_label), x = expression(x == x[0] + r ~ cos~theta), y = expression(y == y[0] + r ~ sin~theta))
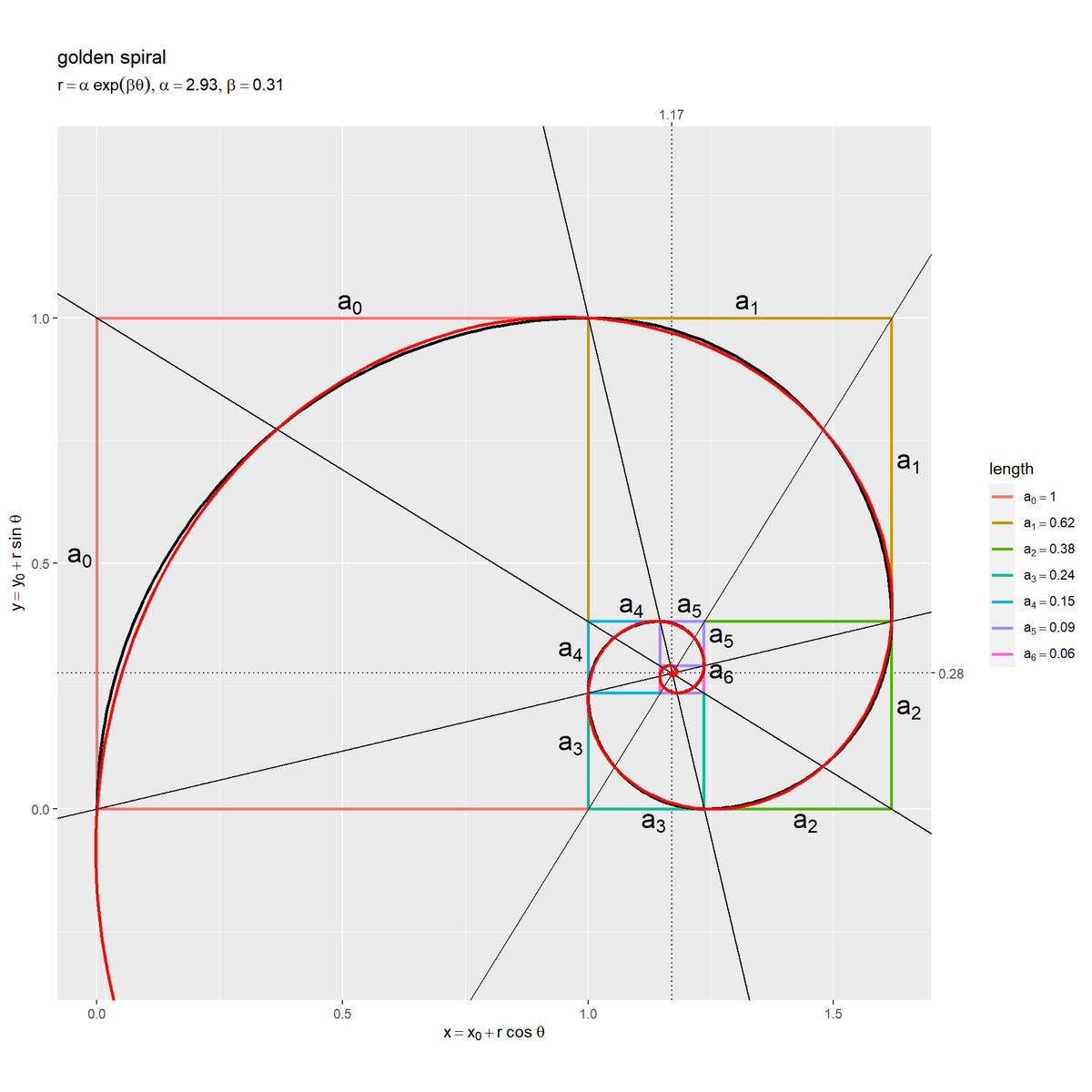
黄金螺旋を赤色の曲線、近似螺旋を黒色の線で示します。
黄金螺旋( 黄金数を用いた対数螺旋・等角螺旋)が黄金長方形の頂点を通るのを確認できます。また、正方形ごとに引いた円弧が黄金螺旋を近似しているのも分かります。
補足
作図に用いる計算式を確認します。
黄金数については「黄金数の性質の導出 - からっぽのしょこ」を参照してください。
黄金長方形の対角線の計算式
黄金長方形の頂点を結ぶ対角線の計算式(傾きと切片)を導出します。
傾きを 、切片を
として、直線の式
を求めます。
のときのx座標
と傾き
が分かっている場合、切片は
で求められます。
対角線を引く頂点を黄金長方形のグラフで確認します。
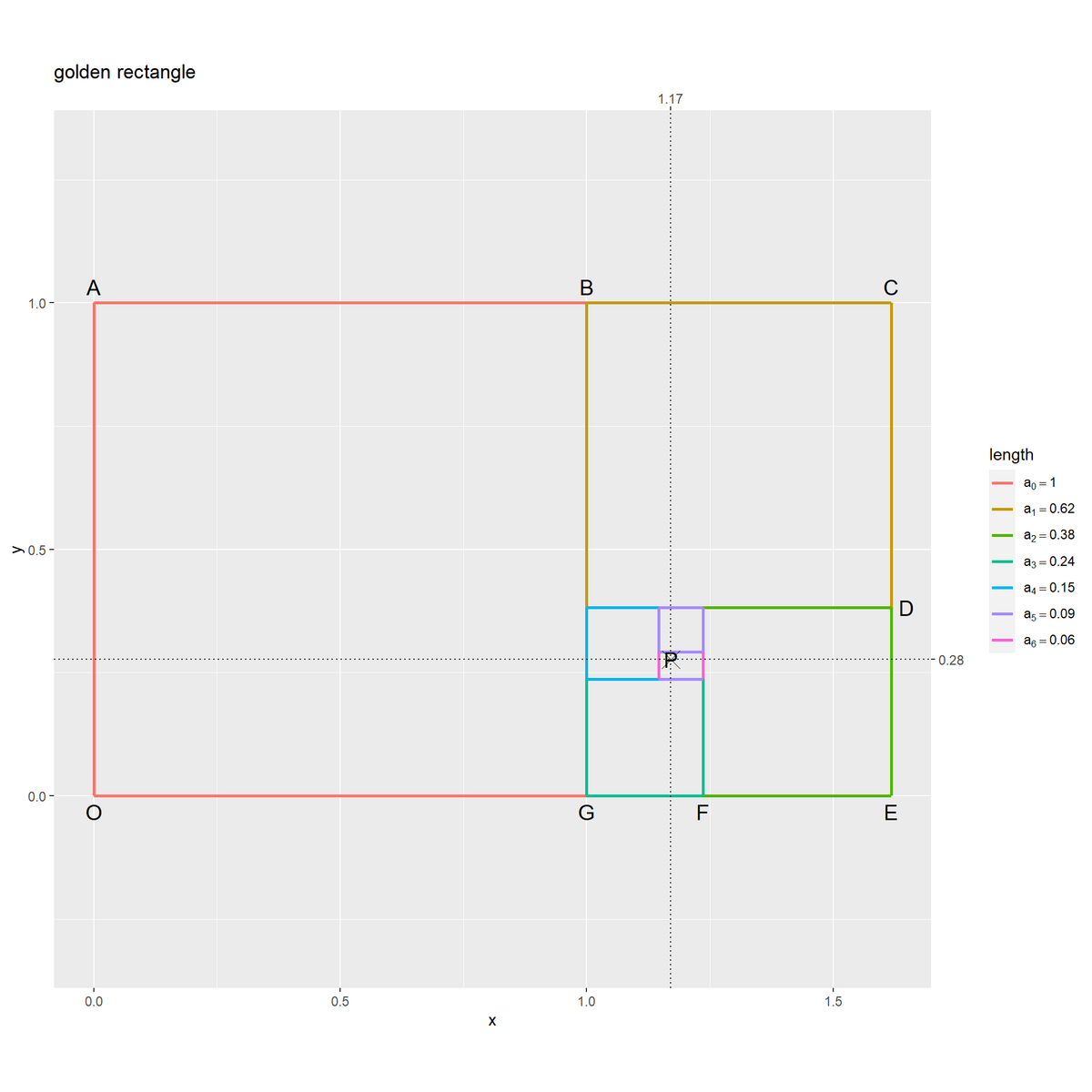
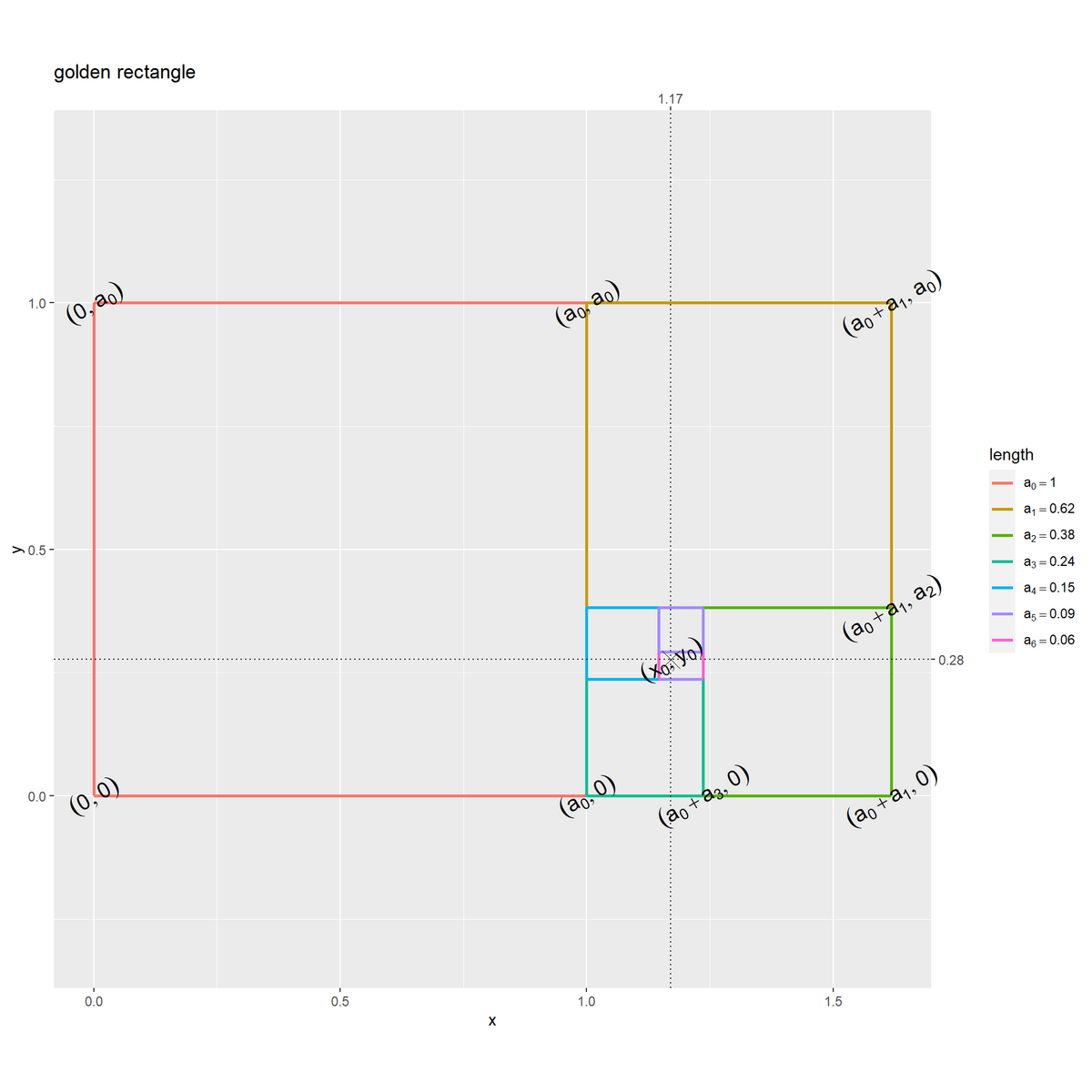
(この図の一番大きな)黄金長方形の辺上の8つの点の内、2つの点を通るの直線の式をそれぞれ求めていきます。
点ODを通る直線
「一辺が の正方形の左下の頂点
」と「一辺が
の正方形の右下の頂点
」を通る直線の式を導出します。
2点間の増加量より、傾きを求めます。
黄金分割の性質より、、
です。
のときの頂点の座標より、切片は
です。
よって、対角線は次の式になります。
点AEを通る直線
「一辺が の正方形の左上の頂点
」と「一辺が
の正方形の右上の頂点
」を通る直線の式を導出します。
2点間の増加量より、傾きを求めます。
黄金分割の性質より、 です。
のときの頂点の座標より、切片は
です。
よって、対角線は次の式になります。
点BFを通る直線
「一辺が の正方形の左上の頂点
」と「一辺が
の正方形の右下の頂点
」を通る直線の式を導出します。
2点間の増加量より、傾きを求めます。
黄金分割の性質より、 です。
のときの頂点の座標より、切片を求めます。
よって、対角線は次の式になります。
点CGを通る直線
「一辺が の正方形の右上の頂点
」と「一辺が
の正方形の左下の頂点
」を通る直線の式を導出します。
2点間の増加量より、傾きを求めます。
黄金分割の性質より、 です。
のときの頂点の座標より、切片を求めます。
よって、対角線は次の式になります。
以上で、4つの対角線の式が得られました。この4つの直線は1点で交わります。
黄金長方形の対角線の交点の計算式
続いて、対角線の交点の座標を導出します。この点は、黄金螺旋の中心の座標になります。
4つの直線の内(どの組み合わせでもよいので)、2つの直線の交点を求めます。この例では、式(3)と式(5)を用います。
式(3)の左辺に式(5)の右辺を代入して、交点のx座標を求めます。
黄金数の性質より
で置き換えます。詳しくは「黄金数の性質の導出」を参照してください。
さらに、この式を式(3)に代入して、交点のy座標を求めます。
直線の交点の座標が得られました。
ただし、原点を起点(左下の頂点)として黄金長方形の座標を決めている場合の座標です。
黄金螺旋のパラメータの計算式
黄金螺旋となる対数螺旋のパラメータを導出します。
ノルムと角度
パラメータの計算に用いるノルムと角度を黄金長方形のグラフで確認します。
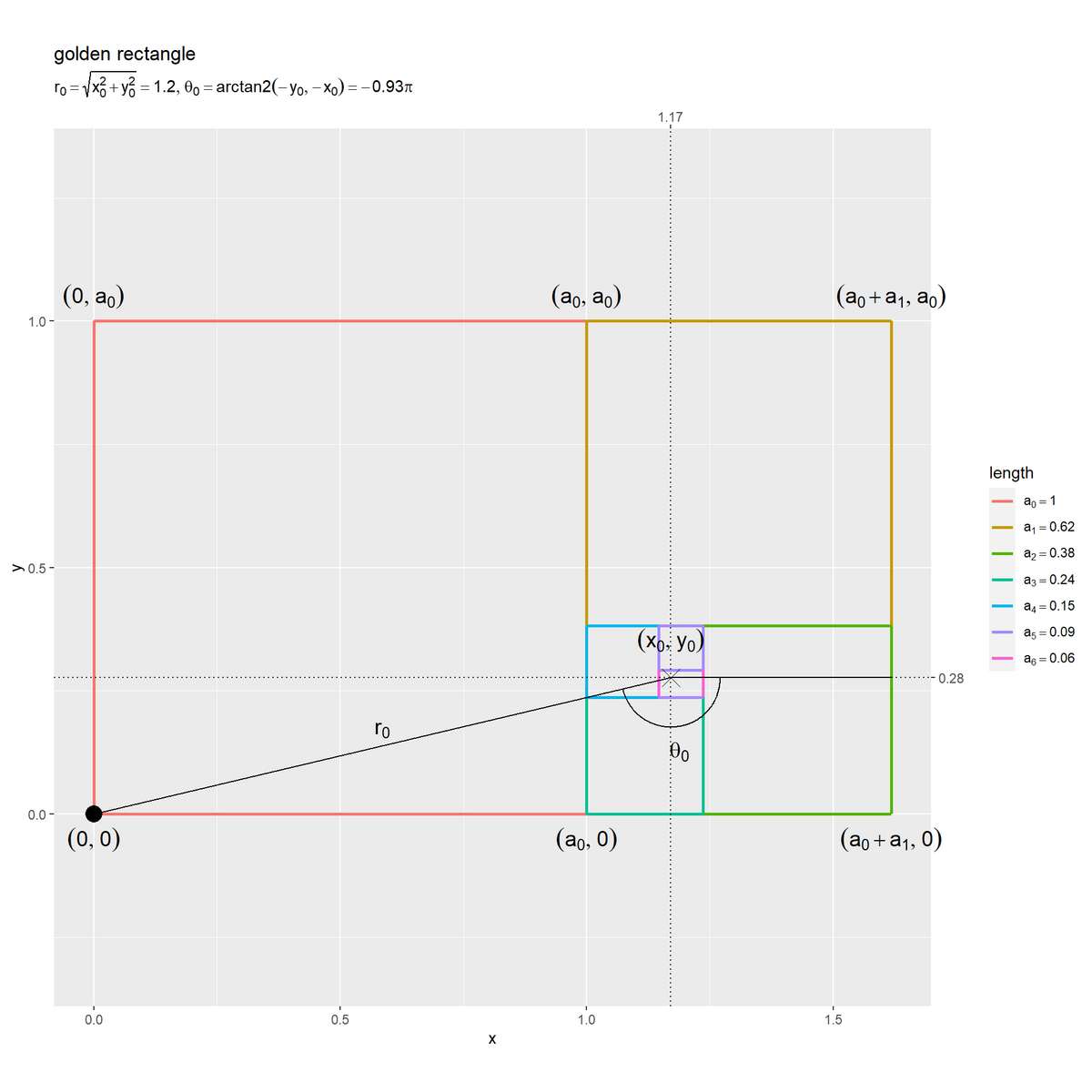
原点 と螺旋の中心
のノルム(距離)
と、中心点から見た原点の角度(中心点と原点を結ぶ半直線の偏角)
を求めます。
対角線の交点より、黄金螺旋の中心の座標は、次の式でした。
中心の座標より、中心点と原点の角度は、次の式で求められます。
中心 を点
として見ると、原点の座標は
と言えます。点
の偏角
は、引数を2つとる逆タンジェント関数
を用いて計算できます。
はラジアン(弧度法の角度)です。
点 を中心とする対数螺旋は、パラメータ
を用いて、次の式で定義されます。
は中心からのノルム、
は自然対数の底(ネイピア数)です。定義式については「対数螺旋の可視化」を参照してください。
点 を中心とする対数螺旋の定義式より、中心と原点(
のとき)のノルムは、次の式でも求められます。
ノルムは、2乗和のルートでも求められます。
以上で、黄金螺旋のパラメータに用いる値が得られました。
パラメータ
続いて、黄金螺旋となる対数螺旋のパラメータ を求めます。
対数螺旋における中心から螺旋上の点のノルム(距離)は
でした。
また、黄金長方形における辺の長さは、反時計回りに四分円( 回転する)ごとに
倍され、
となるのでした。時計回りに考えると
倍され、
です。
は(基準となる辺からの)黄金分割(結合)回数に対応します。
黄金長方形に対応する黄金螺旋は、 が
増えるごとに、
が
倍になる螺旋です。
よって、次の式が成り立ちます。
指数の性質より、、
です。
この式の両辺の対数をとって、 について整理します。
黄金螺旋となるパラメータ の計算式が得られました。
螺旋上の点の内(どの点でもよいので、)、螺旋上の点が原点のときノルムを考えて、 について整理します。
黄金螺旋となるパラメータ の計算式が得られました。
以上で、黄金螺旋となる対数螺旋のパラメータが得られました。
この記事では、黄金長方形と螺旋の関係を確認しました。次の記事では、黄金数の性質を確認します。
参考書籍
- 『曲線と曲面(改訂版)-微分幾何的アプローチ-』梅原 雅顕・山田 光太郎,裳華房,2015年.
おわりに
そもそもはフェルマー螺旋の応用例で登場した黄金角のために黄金比を勉強する必要があって、派生シリーズ黄金比編が誕生しました。この度、黄金比の応用例で対数螺旋が登場し、螺旋編に返ってきました。勉強を進めることで知識がくるっと一周して理解が深まる、まさに螺旋。おあとがよろしいようで。
投稿日に、柏木ひなたさんの2nd EPがリリースされました。
サンタ サンタ サンタ もう年末ですねー。
【次の内容】