はじめに
『問題解決力を鍛える! アルゴリズムとデータ構造』の学習ノートです。
本に掲載されているコードや図をR言語で再現します。本と一緒に読んでください。
この記事は、12.4節「ソート(2):マージソート」の内容です。
マージソートのアルゴリズムを確認します。
【前節の内容】
【他の節の内容】
【この節の内容】
12.4 マージソートの実装と可視化
マージソート(merge sort)を実装します。また、ソートの推移のアニメーションを作成して、アルゴリズムを確認します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的に パッケージ名::関数名() の記法を使っているので、パッケージを読み込む必要はありません。ただし、作図コードについてはパッケージ名を省略しているので、ggplot2 を読み込む必要があります。
また、ネイティブパイプ演算子 |> を使っています。magrittr パッケージのパイプ演算子 %>% に置き換えても処理できますが、その場合は magrittr を読み込む必要があります。
「ソートの可視化」において、gganimate パッケージを利用してアニメーション(gif画像)を作成します。ソートの実装自体には使いません。
ソートの実装
まずは、マージソートのアルゴリズムを関数として実装します。
マージソートを実装します。
# マージソートの実装 merge_sort <- function(vec) { # 入替範囲の要素数を取得 l <- 1 r <- length(vec) # 要素数が1なら再帰処理を終了 if(r == 1) return(vec) # 分割位置mを計算:(l ≤ m ≤ r) m <- l + (r - l) %/% 2 # 分割してそれぞれソート buf <- c( merge_sort(vec[l:m]), merge_sort(vec[(m+1):r]) |> rev() ) # 入替範囲内のインデックスを初期化 idx_l <- 1 idx_r <- 0 # 要素ごとに処理 for(i in 1:r) { # 小さい方の要素を取り出して併合 if(buf[idx_l] <= buf[r-idx_r]) { # 左側が小さい場合 # 左側の要素をj番目に格納 vec[i] <- buf[idx_l] # インデックスを更新 idx_l <- idx_l + 1 } else { # 右側が小さい場合 # 右側の要素をj番目に格納 vec[i] <- buf[r-idx_r] # インデックスを更新 idx_r <- idx_r + 1 } } # 数列を出力 return(vec) }
ソート対象の数列のうち、分割された一部の要素を vec として受け取ります。
vec の要素数を r とします。また、l を 1 としておきます。(数列全体を見た際のlからrの範囲に対応した変数名です。ここでは一部だけを扱っているので1とnの方が分かりやすいかもしれません。)
vec (l から r の範囲)をさらに分割する位置(インデックス)を m とします。
「l 番目から m 番目までの要素」と「m+1 番目から r 番目までの要素」に分割してそれぞれ merge_sort() でソートします。
2つに分割したうち、「前(1から)の方はそのまま」で「後(m+1から)の方は逆順」にして結合したベクトルを一時変数 buf とします。1 から m 番目までは昇順、m+1 から r 番目までは降順に並んだ状態です。
頭と尻の要素の大小を(勝ち抜け戦の要領で)比較して、小さい順に取り出して vec に格納していきます。
merge_sort() を実行すると内部でさらに(全ての分割範囲が1になるまで再帰的に) merge_sort() が実行され、分割と併合(ソート)が繰り返されて、全体がソートされます。
アルゴリズムの詳しい解説は、本のcode 12.2などを参照してください。
実装した関数を試してみます。
要素数を指定して、数列を作成します。
# 要素数を指定 N <- 50 # 数列を生成 a <- sample(x = 1:(2*N), size = N, replace = TRUE) a
## [1] 26 92 77 93 18 74 69 36 75 39 9 75 65 88 3 22 25 81 86 75 74 5 90 58 83 ## [26] 57 7 90 38 66 2 20 42 78 22 48 93 67 60 8 41 88 50 35 63 69 45 91 9 49
乱数生成関数 sample() などで数値ベクトルを生成します。
マージソートにより並べ替えます。
# ソート merge_sort(a)
## [1] 2 3 5 7 8 9 9 18 20 22 22 25 26 35 36 38 39 41 42 45 48 49 50 57 58 ## [26] 60 63 65 66 67 69 69 74 74 75 75 75 77 78 81 83 86 88 88 90 90 91 92 93 93
目で確認するのはアレなので、組み込み関数のソート結果と比較して確認します。
# 確認 sum(!(merge_sort(a) == sort(a)))
## [1] 0
! で TRUE, FALSE を反転させて sum() で合計することで、一致しない要素数を得られます。結果が 0 であれば全ての要素が一致したことが分かります。
ソートの可視化
次は、マージソートのアルゴリズムをグラフで確認します。
数列の初期値を作成して、グラフで確認します。
・作図コード(クリックで展開)
要素数を指定して、数列を作成します。
# 要素数を指定 N <- 35 # 数列を生成 a <- rnorm(n = N, mean = 0, sd = 1) |> round(digits = 1) table(a)
## a ## -2.6 -2.4 -2.3 -2.2 -1.9 -1.7 -1.5 -0.8 -0.7 -0.5 -0.4 -0.3 -0.2 -0.1 0 0.2 ## 1 1 1 1 1 1 1 1 3 1 2 1 2 2 2 2 ## 0.3 0.4 0.6 0.7 1.1 1.3 1.4 1.5 1.6 2.6 ## 1 1 1 1 2 1 1 2 1 1
この例では、(負の値を含めるため)正規乱数生成関数 rnorm() で値を生成して、(重複を含めるため)丸め込み関数 round() で小数第一位にしておきます。
数列をデータフレームに格納します。
# 要素数を取得 N <- length(a) # 数列を格納 tmp_df <- tibble::tibble( iteration = 0, # 試行回数 id = 1:N, # 元のインデックス index = 1:N, # 各試行のインデックス value = a # 要素 ) tmp_df
## # A tibble: 35 × 4 ## iteration id index value ## <dbl> <int> <int> <dbl> ## 1 0 1 1 0.3 ## 2 0 2 2 -0.1 ## 3 0 3 3 -1.7 ## 4 0 4 4 0.6 ## 5 0 5 5 0 ## 6 0 6 6 1.5 ## 7 0 7 7 0.4 ## 8 0 8 8 1.5 ## 9 0 9 9 1.1 ## 10 0 10 10 -0.2 ## # ℹ 25 more rows
作図用に、インデックスなどの値とあわせて数列を格納します。数列のみが与えられている場合は、要素数を N とします。
数列を棒グラフで確認します。
# 数列を作図 ggplot() + geom_bar(data = tmp_df, mapping = aes(x = index, y = value, fill = factor(value)), stat = "identity") + theme(panel.grid.minor.x = element_blank()) + labs(title = "numerical sequence", subtitle = paste0("iteration: ", unique(tmp_df[["iteration"]])), fill = "value", x = "index", y = "value")
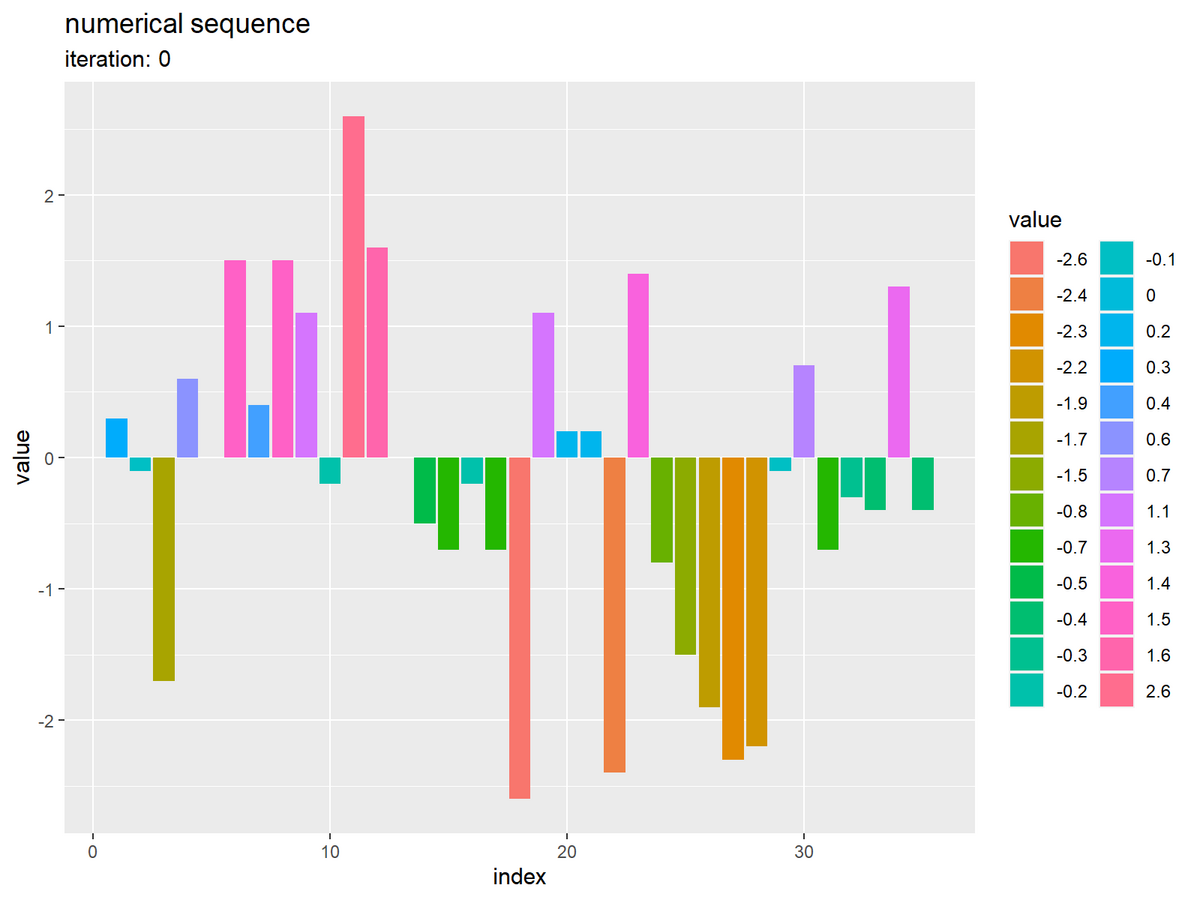
この要素(バー)を昇順に並べ替えます。
アルゴリズムに従いソートを行って、作図用のデータを作成します。
この例では、数列の全ての範囲に対して分割または併合を行う処理を1試行とします。再帰的な処理を行うと次の試行になります。ただし実際(関数内部)の処理では、1試行の処理が全て終わる前に再帰処理が行われることもあります。
・作図コード(クリックで展開)
マージソートでは、1要素ずつになるまで数列を二分割していき、分割した数列の一部を(分割時とは逆方向に)併合しながら昇順に並べ替えていくのでした。つまり、要素の入れ替えを行う前に数列を分割しておく必要があります。
そこで、数列の分割に対応するインデックスを作成する関数を定義しておきます。
# インデックスの分割の実装 trace_idx <- function(mat = NA, iter = 0, left = 1, right = 1) { # 分割範囲を取得 i <- iter l <- left r <- right # 試行回数をカウント if(i == 0) { # 初回ならマトリクスを初期化 mat <- matrix(data = NA, nrow = 1, ncol = r) i <- 1 } else if(l == 1) { # 左端の範囲なら行を追加 mat <- rbind( mat, matrix(data = NA, nrow = 1, ncol = ncol(mat)) ) i <- i + 1 } else { i <- i + 1 } # 分割位置mを計算:(l ≤ m ≤ r) m <- l + (r - l) %/% 2 # 分割範囲のインデックスを格納 mat[i, l:r] <- 1:(r-l+1) # 範囲が1なら再帰処理を終了 if(l == r) return(mat) # インデックスを取得 mat <- trace_idx(mat, iter = i, left = l, right = m) mat <- trace_idx(mat, iter = i, left = (m+1), right = r) # インデックスを出力 return(mat) }
(分割の仕方自体は重要ではないと思いますが、)merge_sort() の内部と同じ挙動になるように(頑張って)処理します。
試行ごとにマトリクスに行を追加します。l が 1 のとき、つまりソート対象の数列の左端の要素を含む範囲のとき、新たな試行とみなします。
分割範囲ごとに通し番号のインデックスを割り当てますが、使うのは 1 の位置(列番号)のみです。
実装した関数を使って、分割した際のインデックスを作成します。
# 分割インデックスを作成 trace_idx_mat <- trace_idx(mat = NA, iter = 0, left = 1, right = N) trace_idx_mat[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 1 2 3 4 5 ## [2,] 1 2 3 4 5 ## [3,] 1 2 3 4 5 ## [4,] 1 2 3 4 5 ## [5,] 1 2 3 1 2 ## [6,] 1 2 1 1 1 ## [7,] 1 1 NA NA NA
分割された範囲の要素数が1になると、その範囲では再帰処理が行われません。そのため、他の範囲で再帰処理が行われると、既に要素数が1の範囲の次の行は欠損値 NA になります。
trace_idx() が出力したマトリクスに対して、is.na() が TRUE になる要素(欠損値)に 1 を代入します。
# 欠損値を補完 trace_idx_mat[is.na(trace_idx_mat)] <- 1 trace_idx_mat[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 1 2 3 4 5 ## [2,] 1 2 3 4 5 ## [3,] 1 2 3 4 5 ## [4,] 1 2 3 4 5 ## [5,] 1 2 3 1 2 ## [6,] 1 2 1 1 1 ## [7,] 1 1 1 1 1
数列の要素数に応じて、分割(入替)の範囲が決まります。
最後の行は、全ての要素が 1 になり、1要素ずつに分割された状態を表し、また併合されていない状態(数列の初期値)を表します。
1試行ずつ入れ替え処理を行い、数列を記録します。
# 試行回数を取得:(初期値は除く) max_iter <- nrow(trace_idx_mat) - 1 # 作図用のオブジェクトを初期化 id_vec <- 1:N trace_df <- tmp_df # マージソート for(i in 1:max_iter) { # 分割範囲のインデックスを作成 l_idx_vec <- which(trace_idx_mat[max_iter-i+1, ] == 1) r_idx_vec <- c(l_idx_vec[-1]-1, N) m_idx_vec <- l_idx_vec + (r_idx_vec - l_idx_vec) %/% 2 # 分割数を取得 max_k <- length(l_idx_vec) # 分割範囲ごとに処理 for(k in 1:max_k) { # 分割範囲を取得 l <- l_idx_vec[k] r <- r_idx_vec[k] m <- m_idx_vec[k] # 前回の要素IDを保存 old_id_vec <- id_vec # 数列を分割 if(l == r) { # 要素数が1の場合 buf <- a[l] } else { buf <- c(a[l:m], rev(a[(m+1):r])) } # 分割範囲内のインデックスを初期化 idx_l <- 1 idx_r <- 0 max_r <- length(buf) # 要素ごとに処理 for(j in l:r) { # 小さい方の要素を取り出して併合 if(buf[idx_l] <= buf[max_r-idx_r]) { # 左側の要素をj番目に格納 a[j] <- buf[idx_l] id_vec[1:N] <- replace(x = id_vec, list = j, values = old_id_vec[l+idx_l-1]) # インデックスを更新 idx_l <- idx_l + 1 } else { # 右側の要素をj番目に格納 a[j] <- buf[max_r-idx_r] id_vec[1:N] <- replace(x = id_vec, list = j, values = old_id_vec[m+idx_r+1]) # インデックスを更新 idx_r <- idx_r + 1 } } } # 数列を格納 tmp_df <- tibble::tibble( iteration = i, id = id_vec, index = 1:N, value = a ) # 数列を記録 trace_df <- dplyr::bind_rows(trace_df, tmp_df) # 途中経過を表示 print(paste0("--- iteration: ", i, " ---")) print(a) }
分割した範囲内のインデックス trace_idx_mat の最後の行(初期値に対応するインデックス)を除き、後の行から順番に取り出して処理します。そのため、trace_idx_mat の行数-1を試行回数の最大値 max_iter とします。
trace_idx_mat の各行について、値が 1 の要素の列インデックスが、分割範囲の左端のインデックス l_idx_vec に対応します。
l_idx_vec の最初の要素(1)を除き、最後に要素数(N)を追加したベクトルが、分割範囲の右端のインデックス r_idx_vec に対応します。
l_idx_vec, r_idx_vec から分割点のインデックス m_idx_vec を作成します。m_idx_vec + 1 と l_idx_vec の値が併合における1試行前(分割だと1試行後)の l_idx_vec の値です。
*_idx_vec の要素数が各試行の分割数に対応します。
分割範囲ごとに分割範囲と分割位置のインデックスと取り出して、「ソートの実装」のときと同様にして、要素を入れ替えていきます。
数列 a の初期値のインデックス(1 から N の整数)を id_vec としておき、a の要素の入れ替えに対応するように id_vec の要素も入れ替えます。
試行ごとに、数列やインデックスをデータフレームに保存します。
初期値のときのコードで、ソートした数列をグラフで確認します。
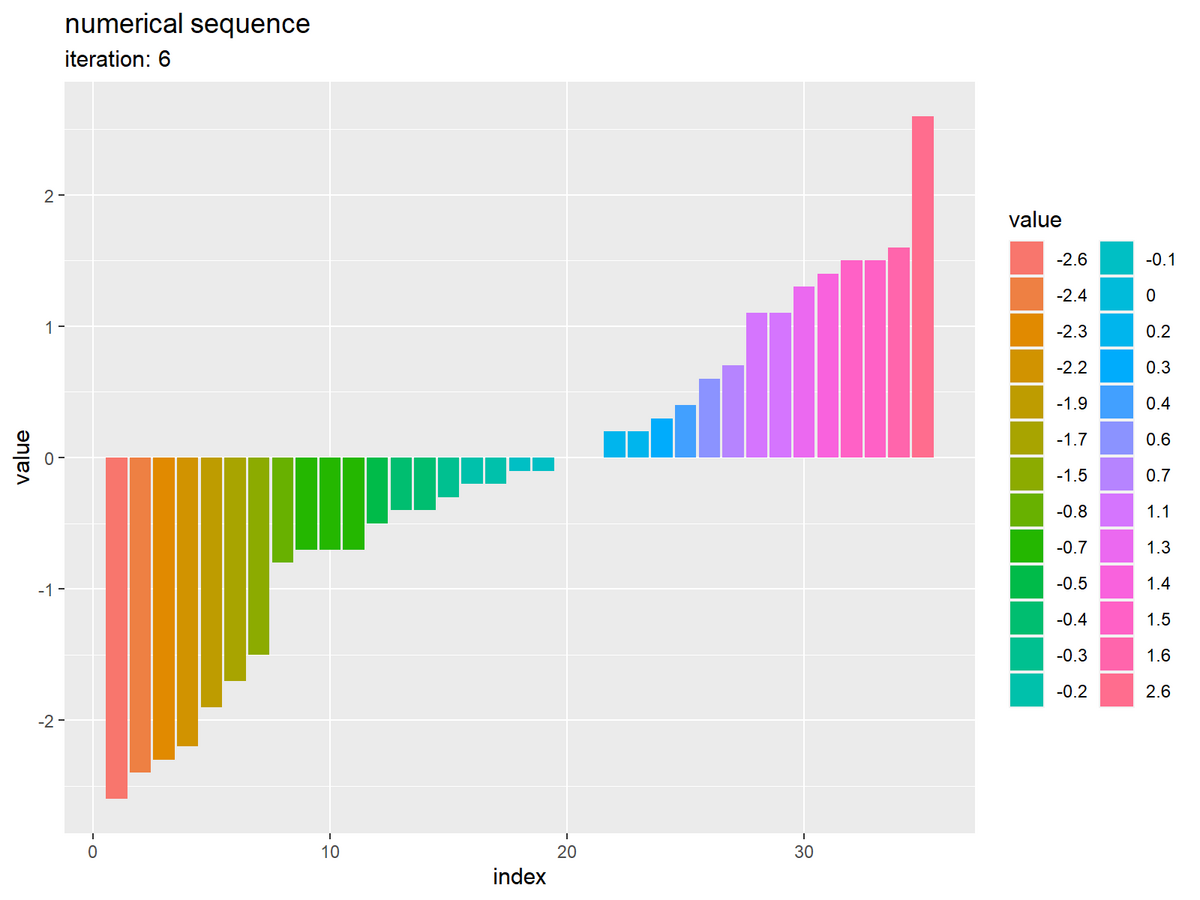
昇順に並んでいるのが分かります。
各試行の数列のグラフを並べて推移を確認します。
・作図コード(クリックで展開)
分割範囲(入替範囲)の描画用のデータフレームを作成します。
# 入替範囲を作成 range_df <- trace_idx_mat[(max_iter+1):1, ] |> # (逆順に並べ替え) tibble::as_tibble(.name_repair = NULL) |> tibble::add_column(iteration = 0:max_iter) |> # 試行回数列を追加 tidyr::pivot_longer( cols = !iteration, names_to = "index", names_prefix = "V", names_transform = list(index = as.numeric), values_to = "split_flag" ) |> # 分割インデックス列をまとめる dplyr::filter(split_flag == 1) |> # 分割位置を抽出 dplyr::arrange(iteration, index) |> # 分割範囲の作成用 dplyr::group_by(iteration) |> # 分割範囲の作成用 dplyr::mutate( # 分割範囲を作成 left = index, right = dplyr::lead(index, n = 1, default = N+1), # タイル用 x = 0.5 * (right + left - 1), y = 0.5 * (max(a) + min(c(0, a))), width = right - left, height = max(a) - min(c(0, a)) + 1 ) |> dplyr::ungroup() range_df
## # A tibble: 98 × 9 ## iteration index split_flag left right x y width height ## <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 0 1 1 1 2 1 0 1 6.2 ## 2 0 2 1 2 3 2 0 1 6.2 ## 3 0 3 1 3 4 3 0 1 6.2 ## 4 0 4 1 4 5 4 0 1 6.2 ## 5 0 5 1 5 6 5 0 1 6.2 ## 6 0 6 1 6 7 6 0 1 6.2 ## 7 0 7 1 7 8 7 0 1 6.2 ## 8 0 8 1 8 9 8 0 1 6.2 ## 9 0 9 1 9 10 9 0 1 6.2 ## 10 0 10 1 10 11 10 0 1 6.2 ## # ℹ 88 more rows
分割した範囲内のインデックス trace_idx_mat をデータフレームに変換して、pivot_longer() で全ての値を1つの列にまとめます。列名(を加工した値)は数列全体のインデックスに対応します。
trace_idx_mat の行番号の逆順に 0 から max_iter までの整数を割り当てて、試行回数列とします。
分割範囲内インデックスが 1 の要素(行)を取り出します。抽出された要素の全体のインデックスが、分割範囲の左端の位置lに対応します。また、1 を除き N+1 を追加したインデックスが右端の位置rに対応します。
そこで、lead() で1行前にズラして、最後に(default 引数で) N+1 を追加した列を作成します。
試行ごとに数列のグラフを作成します。
# 全試行の数列を作図 ggplot() + geom_bar(data = trace_df, mapping = aes(x = index, y = value, fill = factor(value)), stat = "identity") + # 全ての要素 geom_tile(data = range_df, mapping = aes(x = x, y = y, width = width, height = height), color = "red", alpha = 0, linewidth = 0.6, linetype = "dashed") + # 入替範囲 facet_wrap(iteration ~ ., scales = "free_x", labeller = label_both) + # 試行ごとに分割 theme(panel.grid.minor.x = element_blank(), legend.position = "none") + labs(title = "merge sort", fill = "value", x = "index", y = "value")
facet_wrap() で、試行(iteration 列)ごとに分割して棒グラフを描画します。
要素の入れ替えが行われた(分割された)範囲を geom_tile() で描画します。(geom_bar() を使って範囲を描画しようとすると、描画自体はできるのですが、width 引数について警告文が出たので避けました。原因は不明です。)
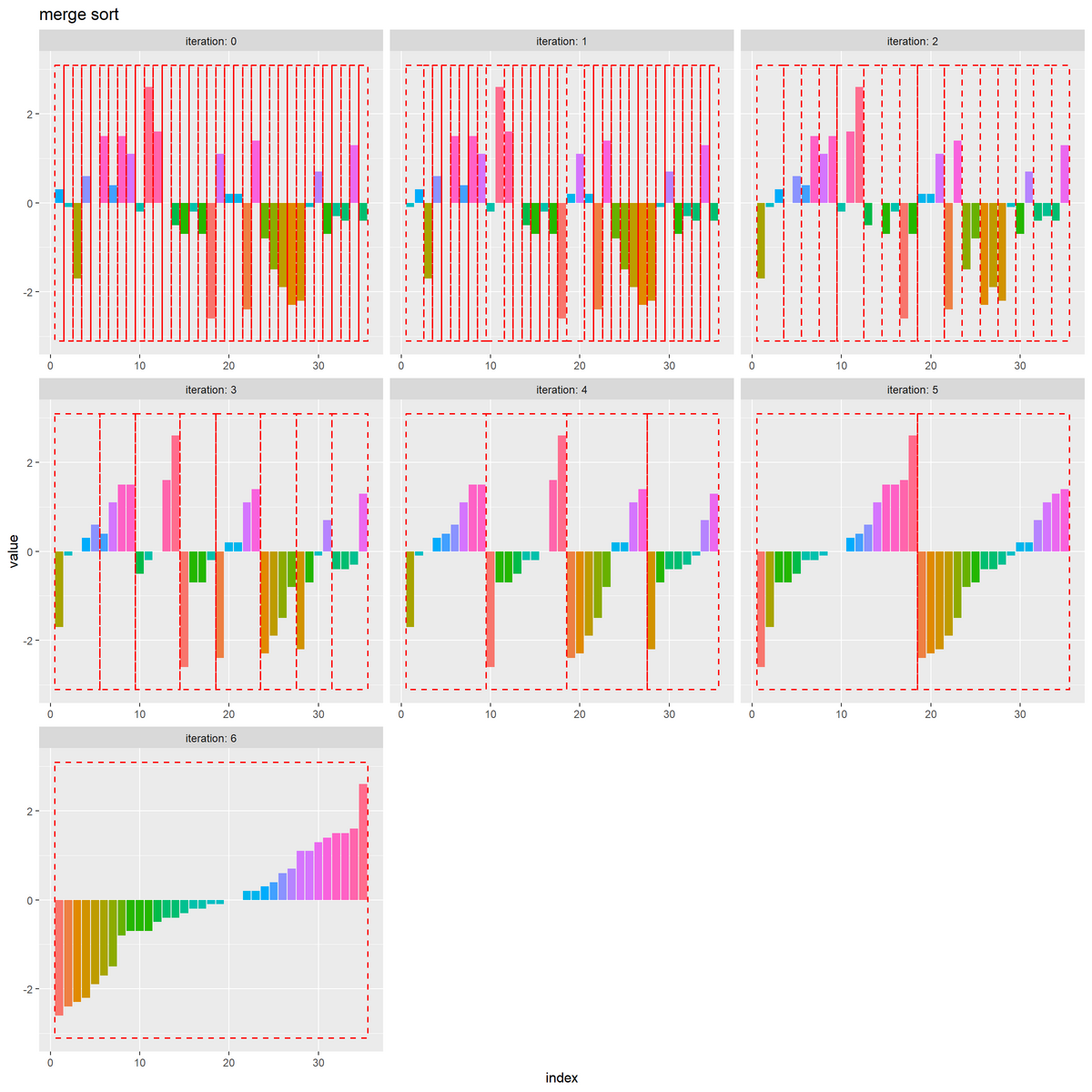
初期値を0回目として、各試行における「入れ替え後の数列」をそれぞれ棒グラフ(バー)で表します。
i回目の試行(i+1枚目のグラフ)において、入れ替えの行われた(分割された)範囲を赤色の破線の枠で示します。
各グラフを見ると、枠内の要素(バー)が昇順に並んでいるのが分かります。また次のグラフを見ると、隣り合う枠(範囲)を併合しながら全体がソートされるのが分かります。
各試行の数列のグラフを切り替えて推移を確認します。
・作図コード(クリックで展開)
同様に、入替範囲の描画用のデータフレームを作成します。
# 入替範囲を作成 range_df <- trace_idx_mat[max_iter:1, ] |> # (最後を除き逆順に並べ替え) tibble::as_tibble(.name_repair = NULL) |> tibble::add_column(iteration = 0:(max_iter-1)) |> # 試行回数列を追加 tidyr::pivot_longer( cols = !iteration, names_to = "index", names_prefix = "V", names_transform = list(index = as.numeric), values_to = "split_flag" ) |> # 分割インデックス列をまとめる dplyr::filter(split_flag == 1) |> # 分割位置を抽出 dplyr::arrange(iteration, index) |> # 分割範囲の作成用 dplyr::group_by(iteration) |> # 分割範囲の作成用 dplyr::mutate( # 分割範囲を作成 left = index, right = dplyr::lead(index, n = 1, default = N+1), # タイル用 x = 0.5 * (right + left - 1), y = 0.5 * (max(a) + min(c(0, a))), width = right - left, height = max(a) - min(c(0, a)) + 1 ) |> dplyr::ungroup() |> dplyr::mutate( id = dplyr::row_number() # 通し番号 ) range_df
## # A tibble: 63 × 10 ## iteration index split_flag left right x y width height id ## <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> ## 1 0 1 1 1 3 1.5 0 2 6.2 1 ## 2 0 3 1 3 4 3 0 1 6.2 2 ## 3 0 4 1 4 5 4 0 1 6.2 3 ## 4 0 5 1 5 6 5 0 1 6.2 4 ## 5 0 6 1 6 7 6 0 1 6.2 5 ## 6 0 7 1 7 8 7 0 1 6.2 6 ## 7 0 8 1 8 9 8 0 1 6.2 7 ## 8 0 9 1 9 10 9 0 1 6.2 8 ## 9 0 10 1 10 12 10.5 0 2 6.2 9 ## 10 0 12 1 12 13 12 0 1 6.2 10 ## # ℹ 53 more rows
こちらは、1試行分タイミングを早めてデータを作成します。
重複ラベルの描画用のデータフレームを作成します。
# 重複ラベルを作成 dup_label_df <- trace_df |> dplyr::arrange(iteration, id) |> # IDの割当用 dplyr::group_by(iteration, value) |> # IDの割当用 dplyr::mutate( dup_id = dplyr::row_number(id), # 重複IDを割り当て dup_num = max(dup_id), # 重複の判定用 dup_label = dplyr::if_else( condition = dup_num > 1, true = paste0("(", dup_id, ")"), false = "" ) # 重複要素のみラベルを作成 ) |> dplyr::ungroup() |> dplyr::arrange(iteration, index) dup_label_df
## # A tibble: 245 × 7 ## iteration id index value dup_id dup_num dup_label ## <dbl> <int> <int> <dbl> <int> <int> <chr> ## 1 0 1 1 0.3 1 1 "" ## 2 0 2 2 -0.1 1 2 "(1)" ## 3 0 3 3 -1.7 1 1 "" ## 4 0 4 4 0.6 1 1 "" ## 5 0 5 5 0 1 2 "(1)" ## 6 0 6 6 1.5 1 2 "(1)" ## 7 0 7 7 0.4 1 1 "" ## 8 0 8 8 1.5 2 2 "(2)" ## 9 0 9 9 1.1 1 2 "(1)" ## 10 0 10 10 -0.2 1 2 "(1)" ## # ℹ 235 more rows
重複している値の要素にのみ、それぞれ通し番号のラベルを作成します。
推移のアニメーションを作成します。
# ソートのアニメーションを作図 graph <- ggplot() + geom_bar(data = trace_df, mapping = aes(x = index, y = value, fill = factor(value)), stat = "identity") + # 全ての要素 geom_tile(data = range_df, mapping = aes(x = x, y = y, width = width, height = height, group = factor(id)), color = "red", alpha = 0, linewidth = 1, linetype = "dashed") + # 入替範囲 geom_text(data = trace_df, mapping = aes(x = index, y = 0, label = as.character(value), group = factor(id)), vjust = -0.5, size = 5) + # 要素ラベル geom_text(data = dup_label_df, mapping = aes(x = index, y = 0, label = dup_label, group = factor(id)), vjust = 1, size = 4) + # 重複ラベル gganimate::transition_states(states = iteration, transition_length = 9, state_length = 1, wrap = FALSE) + # フレーム遷移 gganimate::ease_aes("cubic-in-out") + # 遷移の緩急 theme(panel.grid.minor.x = element_blank(), legend.position = "none") + labs(title = "merge sort", subtitle = "iteration: {next_state}", fill = "value", x = "index", y = "value") # 遷移フレーム数を指定 s <- 20 # gif画像を作成 gganimate::animate( plot = graph, nframes = (max_iter+1 + 2)*s, start_pause = s, end_pause = s, fps = 20, width = 1200, height = 900, renderer = gganimate::gifski_renderer() )
transition_states() のフレーム制御の引数 states に試行回数列 iteration を指定して、これまでと同様に作図します。
animate() の plot 引数にグラフオブジェクト、nframes 引数にフレーム数を指定して、gif画像を作成します。
初期値を含むため試行回数は max_iter+1 (trace_idx_mat の行数)です。transition_states() でアニメーションを作成すると、フレーム間の値を補完して、状態の遷移を描画します。遷移(1試行当たり)のフレーム数を s として、試行回数の s 倍の値を nframes 引数に指定します。
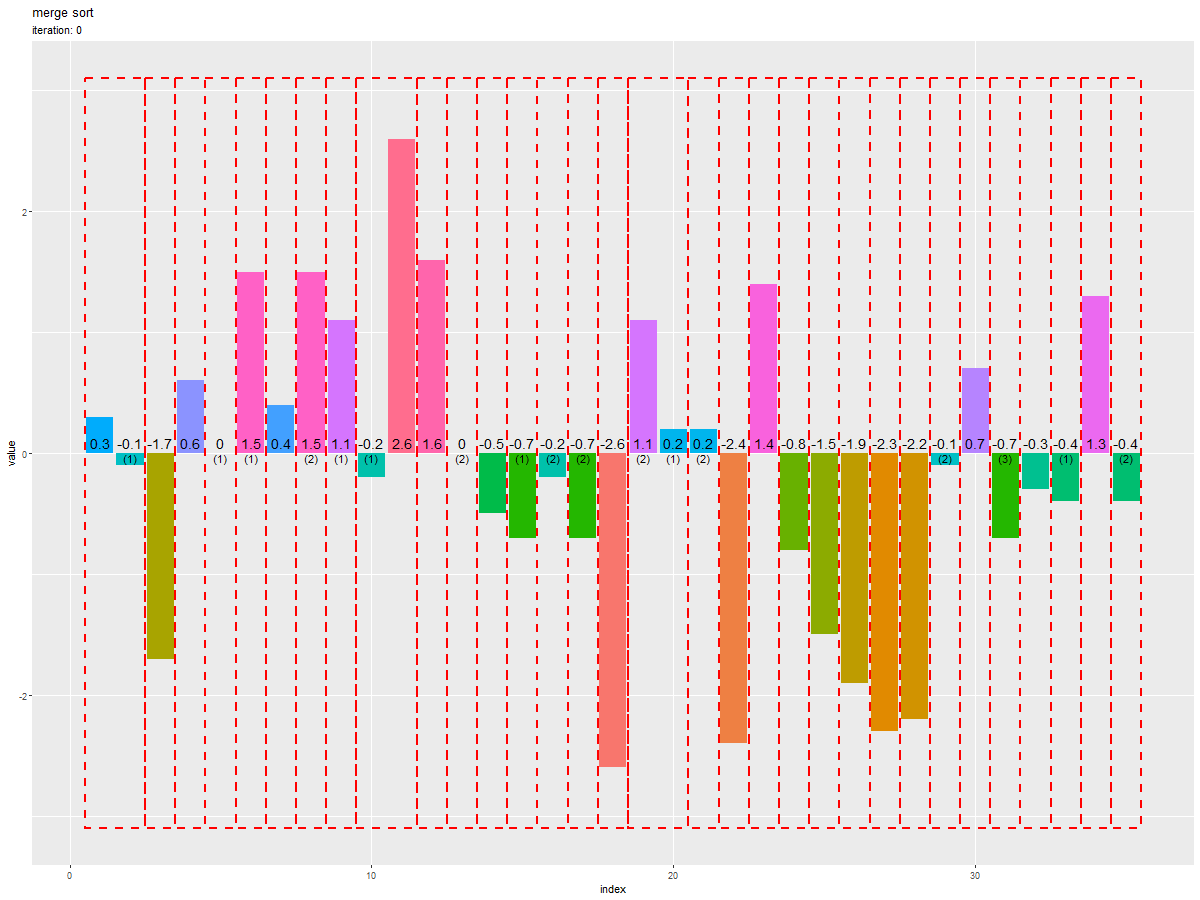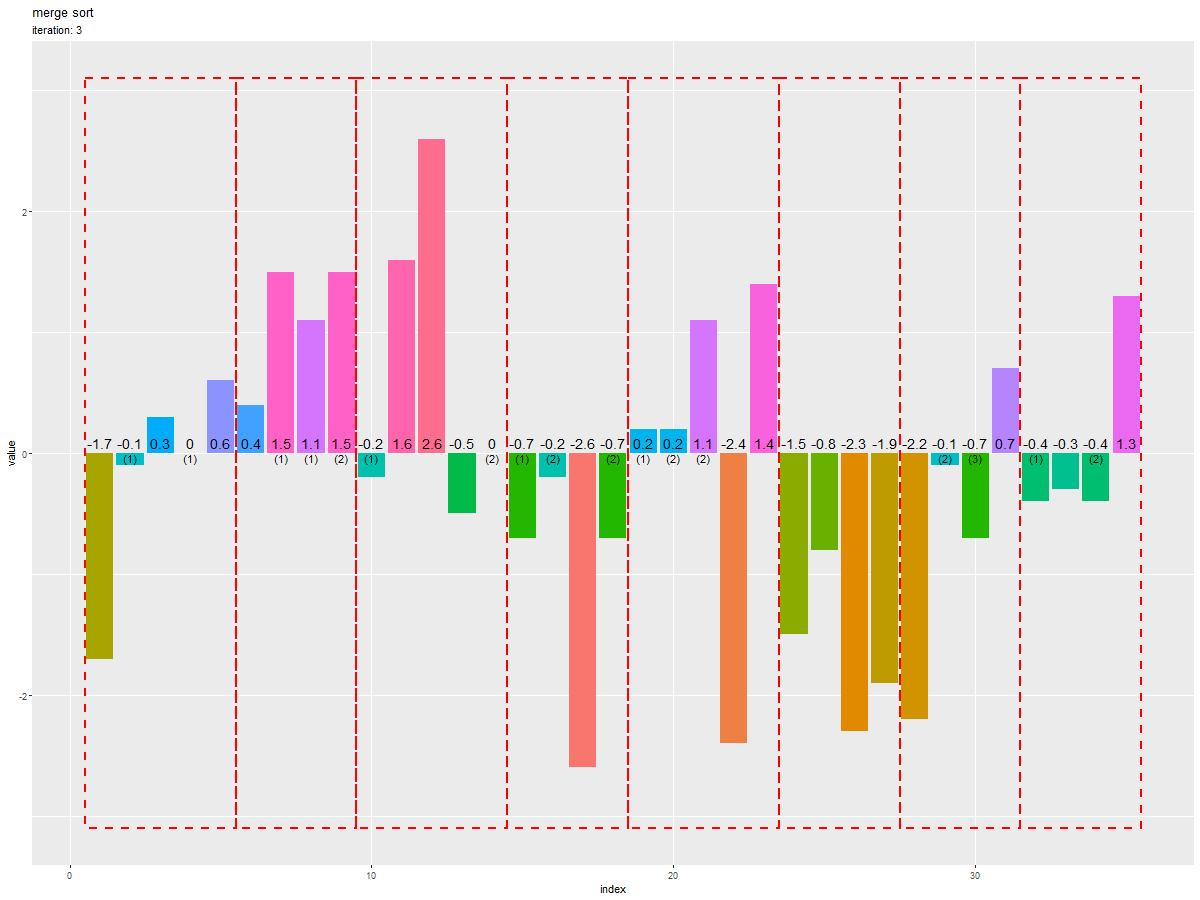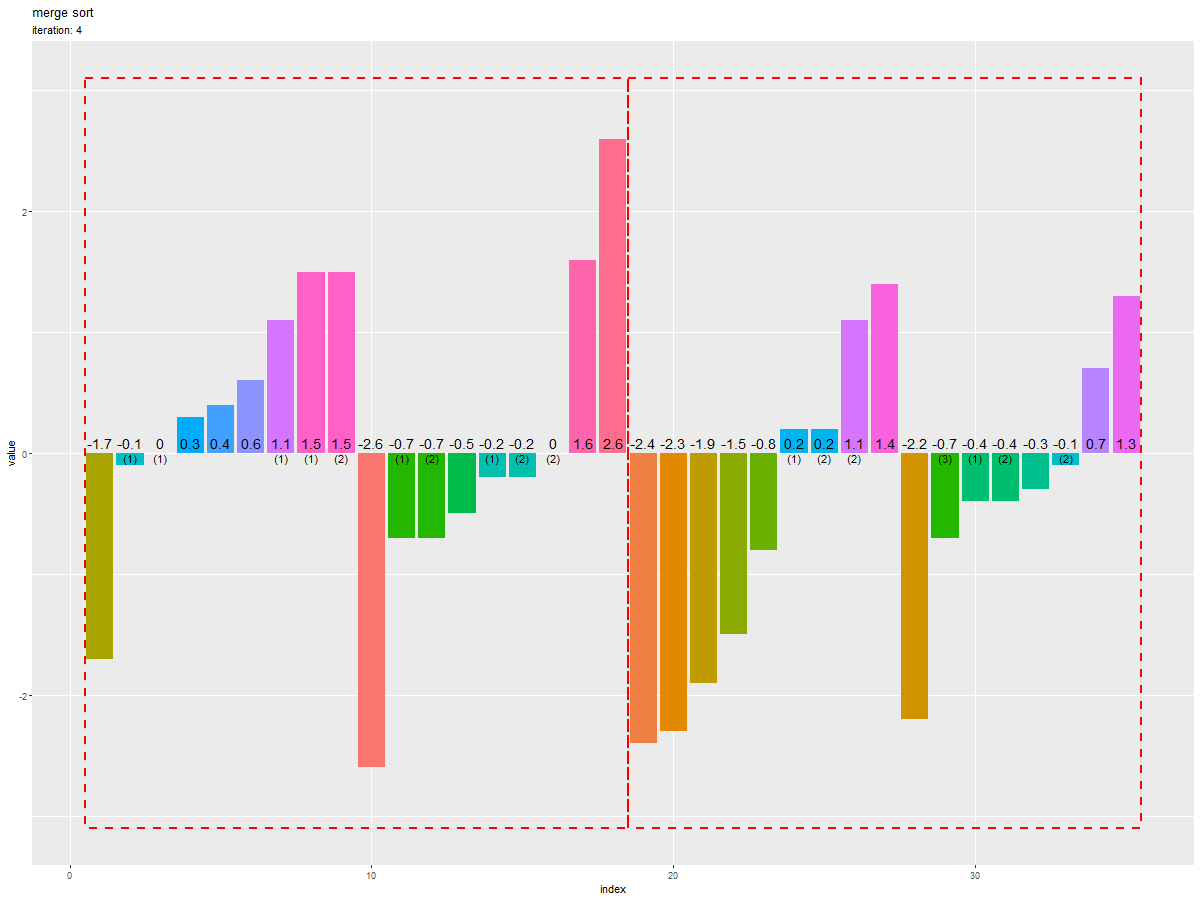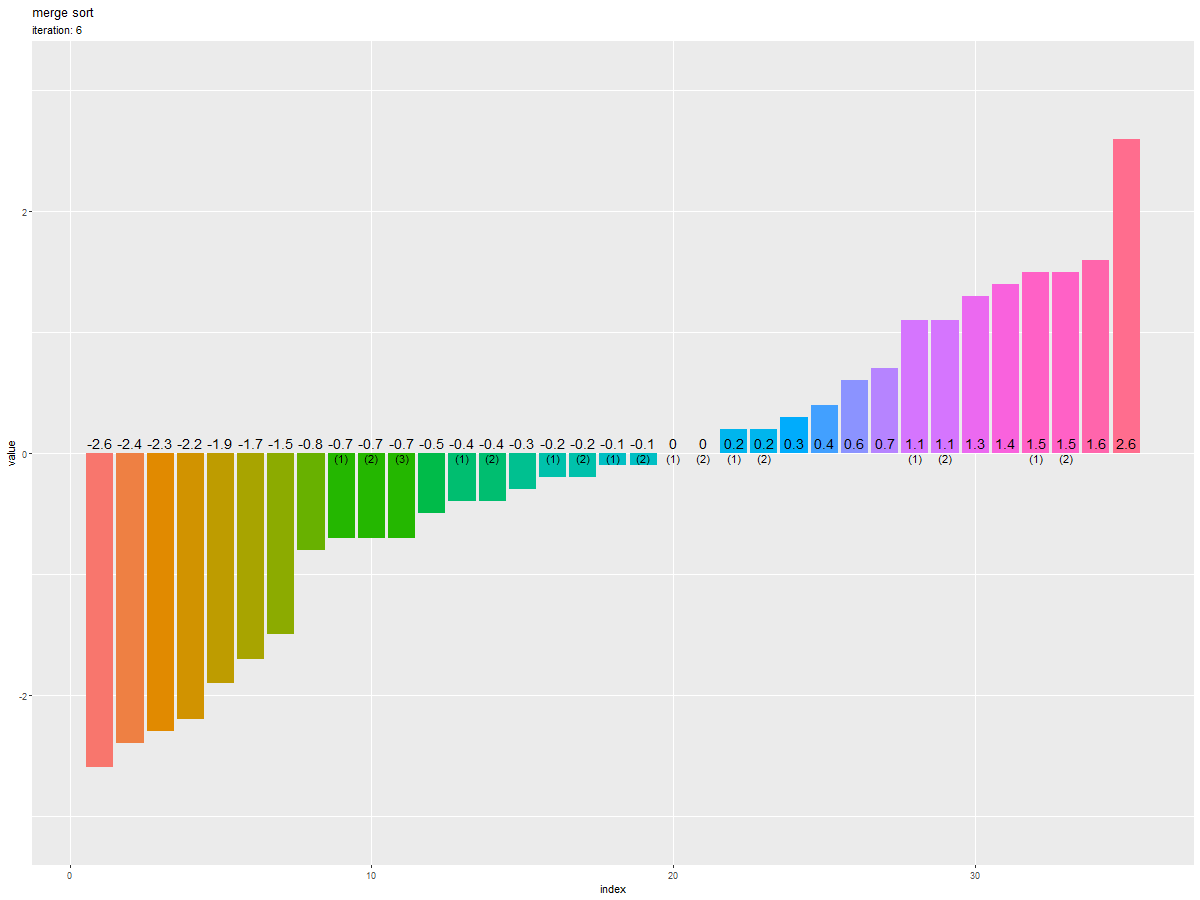
分割された範囲が併合する度にソートされるのを確認できます。
また、重複要素の順序が入れ替わらない(安定性・stable性)のも分かります。
ここでの試行回数(iterationの値)は、この可視化方法における試行番号(作図処理上の値)であり他の手法と対応していません。
この記事では、マージソートを実装しました。次の記事では、クイックソートを実装します。
参考文献
- 大槻兼資(著), 秋葉拓哉(監修)『問題解決力を鍛える! アルゴリズムとデータ構造』講談社サイエンティク, 2021年.
おわりに
この本は(現時点で12章しか読んでいませんが)、文章での説明が分かりやすく、概ね図でも解説されていて、疑似コードではなく実際のコードが載っており(私はC++は使えませんが)、コードの解説も付いていて、さらに数式も行数を使って丁寧に(初心者にとっては数式は多い方が良いんです!)書かれているっぽくて(私は今回は飛ばすことにしましたが)、至れり尽くせりです。
なので今回のシリーズでは、R言語への翻訳と本には載せられずこのブログではお馴染みのアニメーションによるアルゴリズムの図示の2本立ての予定です。作図コードが主目的な人もほぼいないでしょうし、いつもより簡単な解説にしようと思っていたのですが、つい手癖で書き込んでしまいます。
再帰的な処理をアニメーションで表現しようとすると、途中の数列を取り出して保存する必要があり、どうしたものか凄く悩みました。
特にこのアルゴリズムだと、分割と併合のセットの処理の扱いに難儀しました。よくよく考えると分割と併合って別にセットで行っているわけではなかったことに気付いて、最初に分割をやり切っておき、逆向きに併合していくことでなんとかなりました。もう少しスマートにやれそうな気もしますが、現レベルではこれが限界です。
他のアルゴリズムも含めて、思っていた以上に満足に可視化できた気がします。
投稿日の前日に公開されたカバー動画を視聴しましょう。
ももち先輩の曲を愛弟子まなかんが歌うというだけで最高なのですが、そもそもの楽曲自体も最高なBuono!曲なのでまーじで聴いてください。いや冗談じゃなく本当に1回聴いてみてください!
【次節の内容】