はじめに
機械学習でも登場する情報理論におけるエントロピーを1つずつ確認していくシリーズです。
この記事では、相互情報量を扱います。
【前の内容】
【今回の内容】
相互情報量の定義
相互情報量(mutual information)の定義を数式とグラフで確認します。また、各種エントロピーの関係を確認します。エントロピーについては「平均情報量(エントロピー)の定義 - からっぽのしょこ」、結合エントロピーについては「結合エントロピーの定義 - からっぽのしょこ」、条件付きエントロピーについては「条件付きエントロピーの定義 - からっぽのしょこ」を参照してください。
定義
まずは、相互情報量の定義を数式で確認します。
相互情報量の定義式
事象間に依存関係がない(独立の)とき、結合確率は「各事象の確率」の積
で、依存関係があるとき、結合確率は「条件の確率」と「条件付き確率」の積
で定義されるのでした。
相互情報量 は、「各事象の確率の積」と「結合確率」の商(比)の自己情報量(負の対数)の期待値で定義されます。
対数の性質より です。
事象間に依存関係がないとき確率の積と結合確率との比が であり、
なので、最小値の
になります。相互情報量は非負の値
をとります(証明はいつか)。
他のエントロピーとの関係
続いて、式(1)を整理して、平均情報量(エントロピー)・結合エントロピ・条件付きエントロピーまたはKL情報量との関係を導出します。
エントロピー
を条件として結合確率を分割
または
で置き換えます。
対数の性質より です。
さらに、総和についての括弧を展開します。
結合確率を周辺化(ある変数に関する足し合わせ) しています。
は
と無関係なので影響しません。
前の因子は符号を反転させる(-1を掛ける)と条件付きエントロピー、後の因子はエントロピーの定義式なので、次の関係が得られます。
「条件付きエントロピー」は、「エントロピー」と「条件付きエントロピー」の差です。
また、条件付きエントロピーは、「結合エントロピー」と条件の「エントロピー」の差 で置き換えられます。
「条件付きエントロピー」は、各事象の「エントロピー」の和と「結合エントロピー」との差でも表わせます。
条件を入れ替えた場合も同様に求められます。
条件に関わらず式が一致したことから、相互情報量は対称性を持ちます。
各種エントロピーは非負の値なので、式(3)の関係
より、相互情報量はエントロピー以下の値なのが分かります。
また、式(3)を条件付きエントロピーについて整理すると
となるので、条件付きエントロピーはエントロピー以下の値なのが分かります。
KL情報量
式(1)は、KL情報量の定義式です。
相互情報量は、「結合分布 」と各事象系の「分布の積
」のKL情報量です。
また、式(2)の結合確率を分割します。
は
の影響を受けないので
の外に出せます。
の因子について、「
の条件付き確率
」と「
の確率
」のKL情報量なので
で置き換えると、KL情報量の期待値の式になります。
相互情報量は、条件の分布 による「条件付きの確率
と条件なしの確率
のKL情報量」の期待値です。
に依存関係がないとき
なので、KL情報量は最小値の
になり、相互情報量も最小値の
になります。
以上で、各エントロピーとの関係が得られました。
エントロピーの性質
これまでに導出したエントロピー(平均情報量)・条件付きエントロピー・結合エントロピー・相互情報量の関係をまとめます。
各種エントロピーは、次の関係があります。
事象間に依存関係がないとき です。
また、次の大小関係があります。
可視化
次は、2変数(2次元)の結合確率や条件付き確率、自己情報量のヒートマップから相互情報量をグラフで確認します。結合確率や条件付き確率の可視化については「条件付きエントロピーの定義 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
結合確率と条件付き確率のヒートマップ
各種確率をヒートマップで可視化します。
この例では、事象の値をインデックス 、
の関係を倍数
とします。
は整数です。定数倍でない事象の確率を
とします。
・作図コード(クリックで展開)
事象数を指定して、2つの事象系のインデックスと確率を作成します。
# 事象のインデックス(事象数)を指定 x_idx <- 1:5 y_idx <- 1:10 # 事象の確率を一様に作成 #p_x_vec <- rep(1 / length(x_idx), times = length(x_idx)) #r_y_vec <- rep(1 / length(y_idx), times = length(y_idx)) # 事象の確率をランダムに作成 p_x_vec <- MCMCpack::rdirichlet(n = 1, alpha = rep(1, times = length(x_idx))) |> as.vector() r_y_vec <- MCMCpack::rdirichlet(n = 1, alpha = rep(1, times = length(y_idx))) |> as.vector() p_x_vec; r_y_vec
## [1] 0.27976249 0.36154973 0.16394002 0.05245692 0.14229084 ## [1] 0.06088479 0.15525617 0.06075668 0.01663508 0.11831716 0.08625983 ## [7] 0.18500126 0.09202403 0.20007312 0.02479189
1:事象数の形で事象の数を指定して、インデックス を作成します。
各事象の確率を等しく設定する場合は、(事象の数をnとして)n分の1の値をn個作成します。
各事象の確率をランダムに設定する場合は、ディリクレ分布に従う乱数(総和が1になる非負の値)を使います。ディリクレ乱数は、MCMCpackパッケージのrdirichlet()で生成できます。サンプルサイズの引数nに1、パラメータの引数alphaにn個の値を指定します。
の値を
p_x_vec、 を作成するための値を
r_y_vecとします。
2つの事象系の全ての組み合わせを作成して、各種自己情報量を計算します。
# 座標を作成 coord_x_vec <- c(0, cumsum(p_x_vec)[-length(p_x_vec)]) + 0.5*p_x_vec # x・yの自己情報量を計算 entropy_xy_df <- tidyr::expand_grid( i = x_idx, # xのインデックス j = y_idx # yのインデックス ) |> # 全ての組み合わせを作成 dplyr::mutate( x = i, # xの事象 y = j, # yの事象 p_x = p_x_vec[i], # xの確率 r_y = r_y_vec[j], # yの元の確率 p_y.x = dplyr::if_else(condition = y %% x == 0, true = r_y, false = 0), # yを条件付け:(y = nx) #p_y.x = dplyr::if_else(condition = y >= x, true = r_y, false = 0), # yを条件付け:(y ≧ x) #p_y.x = r_y, # yを条件付けない:(y ≠ x) coord_x = coord_x_vec[i] # x軸の値 ) |> dplyr::group_by(i) |> # 確率の正規化と座標計算用 dplyr::mutate( p_y.x = p_y.x / sum(p_y.x), # yの条件付き確率 coord_y.x = c(0, cumsum(p_y.x)[-length(p_y.x)]) + 0.5*p_y.x # y軸の値 ) |> dplyr::group_by(j) |> # xについての周辺化用 dplyr::mutate( p_xy = p_x * p_y.x, # xyの結合確率:(依存あり) p_y = sum(p_xy) # yの周辺確率 ) |> dplyr::group_by(i) |> # 座標計算用 dplyr::mutate( coord_y = c(0, cumsum(p_y)[-length(p_y)]) + 0.5*p_y # y軸の値 ) |> dplyr::ungroup() |> dplyr::mutate( p_x_y = p_x * p_y, # xyの確率の積:(依存なし) I_x = - log2(p_x), # xの自己情報量 I_y = - log2(p_y), # yの自己情報量 I_y.x = - log2(p_y.x), # yの条件付き自己情報量 I_xy = - log2(p_xy), # xyの結合自己情報量:(依存あり) I_x_y = - log2(p_x_y), # xyの確率の積の自己情報量:(依存なし) label_p_x = paste0("p(x[", i, "])"), # xの確率の式 label_p_y = paste0("p(y[", j, "])"), # yの確率の式 label_p_y.x = dplyr::if_else( condition = p_y.x > 0, true = paste0("p(y[", j, "]~'|'~x[", i, "])"), false = "" ), # yの条件付き確率の式 label_p_xy = dplyr::if_else( condition = p_xy > 0, true = paste0("p(x[", i, "], y[", j, "])"), false = "" ), # xyの結合確率の式:(依存あり) label_p_x_y = paste0("p(x[", i, "]) * p(y[", j, "])") # xyの確率の積の式:(依存なし) ) |> dplyr::select( i, j, p_x, p_y, p_y.x, p_xy, p_x_y, I_x, I_y, I_y.x, I_xy, I_x_y, coord_x, coord_y, coord_y.x, label_p_x, label_p_y, label_p_y.x, label_p_xy, label_p_x_y )
インデックス を
i, j列として、expand_grid()で全ての組み合わせを作成します。
i, j列の値を用いて、対応する確率と座標をベクトルから取り出して、p_x, r_y列とcoord_x列として格納します。
各セルの中心の座標は、各セルの縦または横サイズを確率に合わせるため、「累積確率」+「その事象の確率の半分」の値とします。
事象 を
x, y列として作成します。
の依存関係を持つ条件付き確率
を
p_y.x列として作成します。yがxの倍数(y, xの商余が0)の行をy_pの値、倍数でない行を0とする列を作成しておき、条件の事象 ごとに(
i列でグループ化して)、総和で割ることで正規化(確率値に変換)します。
結合確率 を
p_xy列として計算します。
周辺確率 を
p_y列として計算します。事象 ごとに(
j列でグループ化して)、結合確率の和をとることで周辺化します。
2事象の確率の積 を
p_x_y列として計算します。依存関係がない結合確率と言えます。
各種の自己情報量をI_***列として計算します。
各事象の自己情報量 、
、条件付けられた事象の自己情報量
、依存関係がある結合事象の自己情報量
、依存関係がないとみなした2事象の自己情報量
を計算します。
expression()の記法を使って、数式ラベル列label_***を作成します。確率が0のラベルを描画しない場合は、ラベル用の文字列を空白""にしておきます。
作成したデータフレームは次のようになります。
# 確認 entropy_xy_df |> dplyr::select(1:7) # インデックス列と確率列 entropy_xy_df |> dplyr::select(8:15) # 自己情報量列と座標列 entropy_xy_df |> dplyr::select(16:20) # ラベル列
## # A tibble: 50 × 7 ## i j p_x p_y p_y.x p_xy p_x_y ## <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 1 1 0.280 0.0170 0.0609 0.0170 0.00477 ## 2 1 2 0.280 0.193 0.155 0.0434 0.0540 ## 3 1 3 0.280 0.0457 0.0608 0.0170 0.0128 ## 4 1 4 0.280 0.0287 0.0166 0.00465 0.00804 ## 5 1 5 0.280 0.151 0.118 0.0331 0.0422 ## 6 1 6 0.280 0.148 0.0863 0.0241 0.0414 ## 7 1 7 0.280 0.0518 0.185 0.0518 0.0145 ## 8 1 8 0.280 0.159 0.0920 0.0257 0.0445 ## 9 1 9 0.280 0.150 0.200 0.0560 0.0421 ## 10 1 10 0.280 0.0555 0.0248 0.00694 0.0155 ## # … with 40 more rows
## # A tibble: 50 × 8 ## I_x I_y I_y.x I_xy I_x_y coord_x coord_y coord_y.x ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 1.84 5.88 4.04 5.88 7.71 0.140 0.00852 0.0304 ## 2 1.84 2.37 2.69 4.53 4.21 0.140 0.114 0.139 ## 3 1.84 4.45 4.04 5.88 6.29 0.140 0.233 0.247 ## 4 1.84 5.12 5.91 7.75 6.96 0.140 0.270 0.285 ## 5 1.84 2.73 3.08 4.92 4.57 0.140 0.360 0.353 ## 6 1.84 2.76 3.54 5.37 4.59 0.140 0.509 0.455 ## 7 1.84 4.27 2.43 4.27 6.11 0.140 0.609 0.591 ## 8 1.84 2.65 3.44 5.28 4.49 0.140 0.715 0.729 ## 9 1.84 2.73 2.32 4.16 4.57 0.140 0.869 0.875 ## 10 1.84 4.17 5.33 7.17 6.01 0.140 0.972 0.988 ## # … with 40 more rows
## # A tibble: 50 × 5 ## label_p_x label_p_y label_p_y.x label_p_xy label_p_x_y ## <chr> <chr> <chr> <chr> <chr> ## 1 p(x[1]) p(y[1]) p(y[1]~'|'~x[1]) p(x[1], y[1]) p(x[1]) * p(y[1]) ## 2 p(x[1]) p(y[2]) p(y[2]~'|'~x[1]) p(x[1], y[2]) p(x[1]) * p(y[2]) ## 3 p(x[1]) p(y[3]) p(y[3]~'|'~x[1]) p(x[1], y[3]) p(x[1]) * p(y[3]) ## 4 p(x[1]) p(y[4]) p(y[4]~'|'~x[1]) p(x[1], y[4]) p(x[1]) * p(y[4]) ## 5 p(x[1]) p(y[5]) p(y[5]~'|'~x[1]) p(x[1], y[5]) p(x[1]) * p(y[5]) ## 6 p(x[1]) p(y[6]) p(y[6]~'|'~x[1]) p(x[1], y[6]) p(x[1]) * p(y[6]) ## 7 p(x[1]) p(y[7]) p(y[7]~'|'~x[1]) p(x[1], y[7]) p(x[1]) * p(y[7]) ## 8 p(x[1]) p(y[8]) p(y[8]~'|'~x[1]) p(x[1], y[8]) p(x[1]) * p(y[8]) ## 9 p(x[1]) p(y[9]) p(y[9]~'|'~x[1]) p(x[1], y[9]) p(x[1]) * p(y[9]) ## 10 p(x[1]) p(y[10]) p(y[10]~'|'~x[1]) p(x[1], y[10]) p(x[1]) * p(y[10]) ## # … with 40 more rows
各事象系の自己情報量をそれぞれ取り出します。
# xの自己情報量を抽出 entropy_x_df <- entropy_xy_df |> dplyr::select(i, p_x, I_x, coord_x, label_p_x) |> dplyr::distinct() # 重複を除去 # yの自己情報量を抽出 entropy_y_df <- entropy_xy_df |> dplyr::select(j, p_y, I_y, coord_y, label_p_y) |> dplyr::distinct() # 重複を除去 entropy_x_df; entropy_y_df
## # A tibble: 5 × 5 ## i p_x I_x coord_x label_p_x ## <int> <dbl> <dbl> <dbl> <chr> ## 1 1 0.280 1.84 0.140 p(x[1]) ## 2 2 0.362 1.47 0.461 p(x[2]) ## 3 3 0.164 2.61 0.723 p(x[3]) ## 4 4 0.0525 4.25 0.831 p(x[4]) ## 5 5 0.142 2.81 0.929 p(x[5]) ## # A tibble: 10 × 5 ## j p_y I_y coord_y label_p_y ## <int> <dbl> <dbl> <dbl> <chr> ## 1 1 0.0170 5.88 0.00852 p(y[1]) ## 2 2 0.193 2.37 0.114 p(y[2]) ## 3 3 0.0457 4.45 0.233 p(y[3]) ## 4 4 0.0287 5.12 0.270 p(y[4]) ## 5 5 0.151 2.73 0.360 p(y[5]) ## 6 6 0.148 2.76 0.509 p(y[6]) ## 7 7 0.0518 4.27 0.609 p(y[7]) ## 8 8 0.159 2.65 0.715 p(y[8]) ## 9 9 0.150 2.73 0.869 p(y[9]) ## 10 10 0.0555 4.17 0.972 p(y[10])
全ての組み合あわせの(複製された)データentropy_xy_dfから、 に関する列をそれぞれ取り出して、重複する行を削除します。
確率と座標を取り出します。
# yの周辺確率を抽出 p_y_vec <- entropy_y_df |> dplyr::pull(p_y) # 座標を抽出 coord_y_vec <- entropy_y_df |> dplyr::pull(coord_y) p_y_vec; sum(p_y_vec); coord_y_vec
## [1] 0.01703328 0.19313556 0.04569449 0.02872455 0.15074140 0.14804840 ## [7] 0.05175641 0.15890212 0.15047301 0.05549077 ## [1] 1 ## [1] 0.00851664 0.11360106 0.23301609 0.27022561 0.35995858 0.50935349 ## [7] 0.60925589 0.71458516 0.86927273 0.97225462
軸目盛の作図用に、確率と座標をそれぞれベクトルとして取り出します。
確率分布 のヒートマップを作成します。
# 確率(グラデーション)の最大値を設定 p_max <- entropy_xy_df |> dplyr::select(p_x, p_y, p_y.x, p_xy, p_x_y) |> # 確率列 max() |> (\(.){ceiling(. * 10) / 10})() # 小数点第二位で切り上げ # xの確率を作図 prob_x_graph <- ggplot() + geom_tile(data = entropy_x_df, mapping = aes(x = coord_x, y = 0, width = p_x, height = 1, fill = p_x), color = "black", alpha = 0.8) + # 確率 geom_text(data = entropy_x_df, mapping = aes(x = coord_x, y = 0, label = label_p_x), parse = TRUE) + # 確率の式 scale_x_continuous(breaks = coord_x_vec, labels = x_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_x_vec)), digits = 2), name = expression(sum(p(x[i]), i)))) + # xのインデックスと累積確率 scale_y_continuous(breaks = 0, labels = NULL) + # yのインデックス scale_fill_viridis_c(limits = c(0, p_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "probability", subtitle = expression(list(x == (list(x[1], cdots, x[n])), p(x))), fill = "p", x = "i", y = "") prob_x_graph
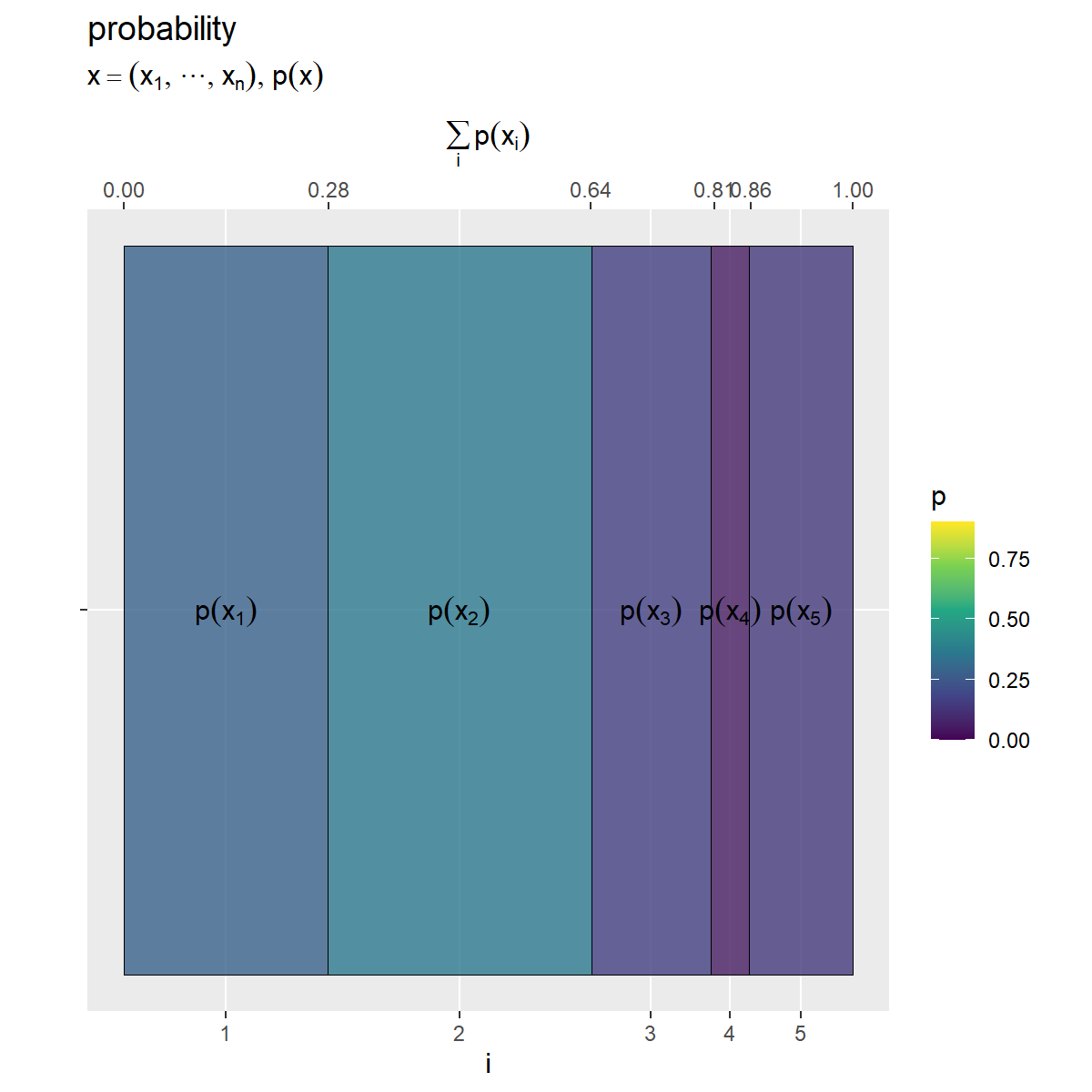
他のヒートマップとグラデーションの基準を統一するために、確率の最大値をp_maxとしておきます。
geom_tile()でヒートマップを描画します。x引数に座標列coord_x、width引数に確率列p_xを指定して、各セルの横サイズを確率に対応付けます。y引数の値は何でもよく、height引数に1を指定して、ヒートマップ全体の面積が1×1になるようにします。また、fill引数に確率列を指定して、各セルの色を確率に対応付けます。
scale_*_continuous()で軸目盛を設定します。breaks引数に確率に応じた座標coord_x_vec、labels引数にインデックスx_idxを指定して、主軸(第1軸)目盛が各セルの中心に対応するようにインデックスを表示します。sec.axis引数にsec_axis()を使って、第2軸が各セルの端に対応するように累積確率を表示します。
同様に、確率分布 のヒートマップを作成します。
# yの確率を作図 prob_y_graph <- ggplot() + geom_tile(data = entropy_y_df, mapping = aes(x = 0, y = coord_y, width = 1, height = p_y, fill = p_y), color = "black", alpha = 0.8) + # 確率 geom_text(data = entropy_y_df, mapping = aes(x = 0, y = coord_y, label = label_p_y), parse = TRUE) + # 確率の式 scale_x_continuous(breaks = 0, labels = NULL) + # xのインデックス scale_y_continuous(breaks = coord_y_vec, labels = y_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_y_vec)), digits = 2), name = expression(sum(p(y[j]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, p_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "probability", subtitle = expression(list(y == (list(y[1], cdots, y[m])), p(y))), fill = "p", x = "", y = "j") prob_y_graph
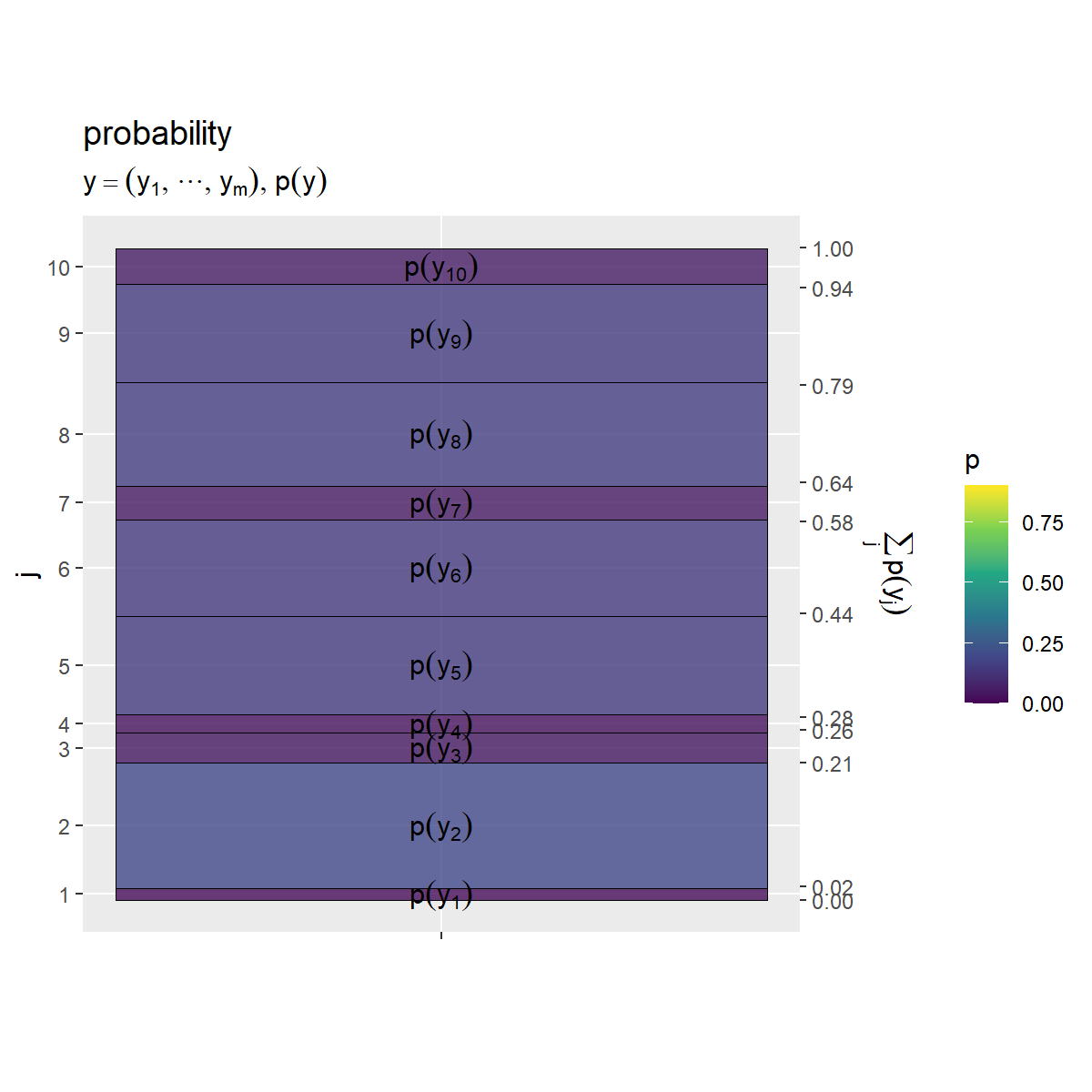
確率の積(依存関係がないとみなした結合確率) のヒートマップを作成します。
# x・yの確率の積を作図 prob_x_y_graph <- ggplot() + geom_tile(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y, width = p_x, height = p_y, fill = p_x_y), color = "black", alpha = 0.8) + # 確率 geom_text(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y, label = label_p_x_y), parse = TRUE, angle = 30, size = 2.5) + # 確率の式 scale_x_continuous(breaks = coord_x_vec, labels = x_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_x_vec)), digits = 2), name = expression(sum(p(x[i]), i)))) + # xのインデックスと累積確率 scale_y_continuous(breaks = coord_y_vec, labels = y_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_y_vec)), digits = 2), name = expression(sum(p(y[j]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, p_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "product of probability", subtitle = expression(p[list(i, j)] == p(x[i]) * p(y[j])), fill = "p", x = "i", y = "j") prob_x_y_graph
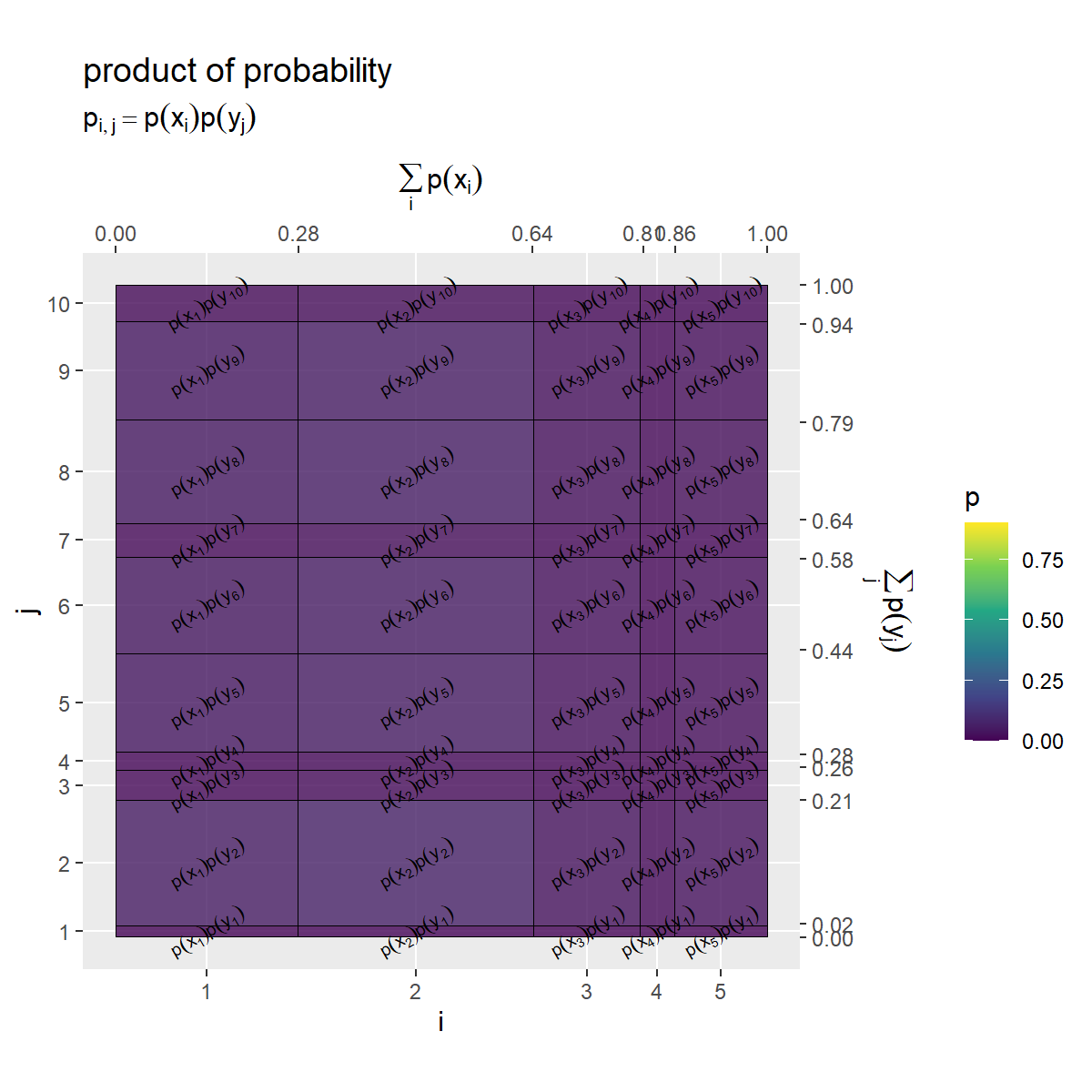
ここまでと同様に、x軸とy軸を確率に対応付けて作図します。
条件付き確率 のヒートマップを作成します。
# ラベル用の文字列を作成 fnc_label <- paste0( "list(", "x[i] == i, y[j] == j", ", ", "y[j] == n * x[i]", ", ", "p(y[j]~'|'~x[i]) == frac(p(x[i], y[j]), p(x[i]))", ")" ) # yの条件付き確率を作図 prob_y.x_graph <- ggplot() + geom_tile(data = entropy_xy_df, mapping = aes(x = 0, y = coord_y.x, width = 1, height = p_y.x, fill = p_y.x), color = "black", alpha = 0.8) + # 確率 geom_text(data = entropy_xy_df, mapping = aes(x = 0, y = coord_y.x, label = label_p_y.x), parse = TRUE, angle = 0) + # 確率の式 scale_x_continuous(breaks = 0, labels = NULL) + # xのインデックス scale_y_continuous(breaks = 0.5, labels = NULL, sec.axis = sec_axis(trans = ~., breaks = seq(from = 0, to = 1, by = 0.25), name = expression(sum(p(y[j]~'|'~x[i]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, p_max)) + # グラデーション facet_grid(. ~ i, labeller = label_bquote(cols = x[.(i)])) + # xの事象(条件)ごとに分割 coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "conditional probability", subtitle = parse(text = fnc_label), fill = "p", x = "i", y = "j") prob_y.x_graph
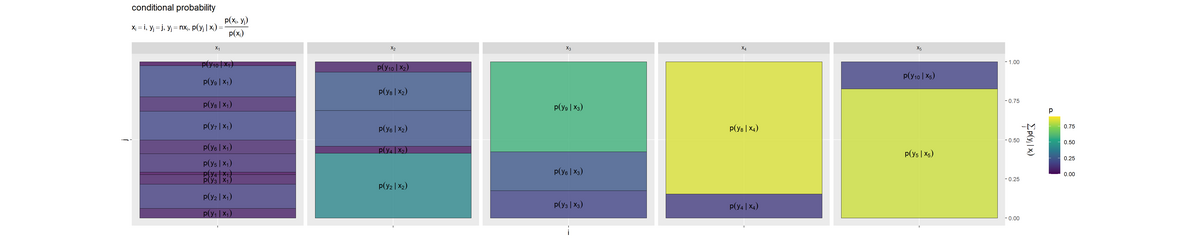
facet_grid()で条件(事象 )ごとにグラフを分割して描画します。
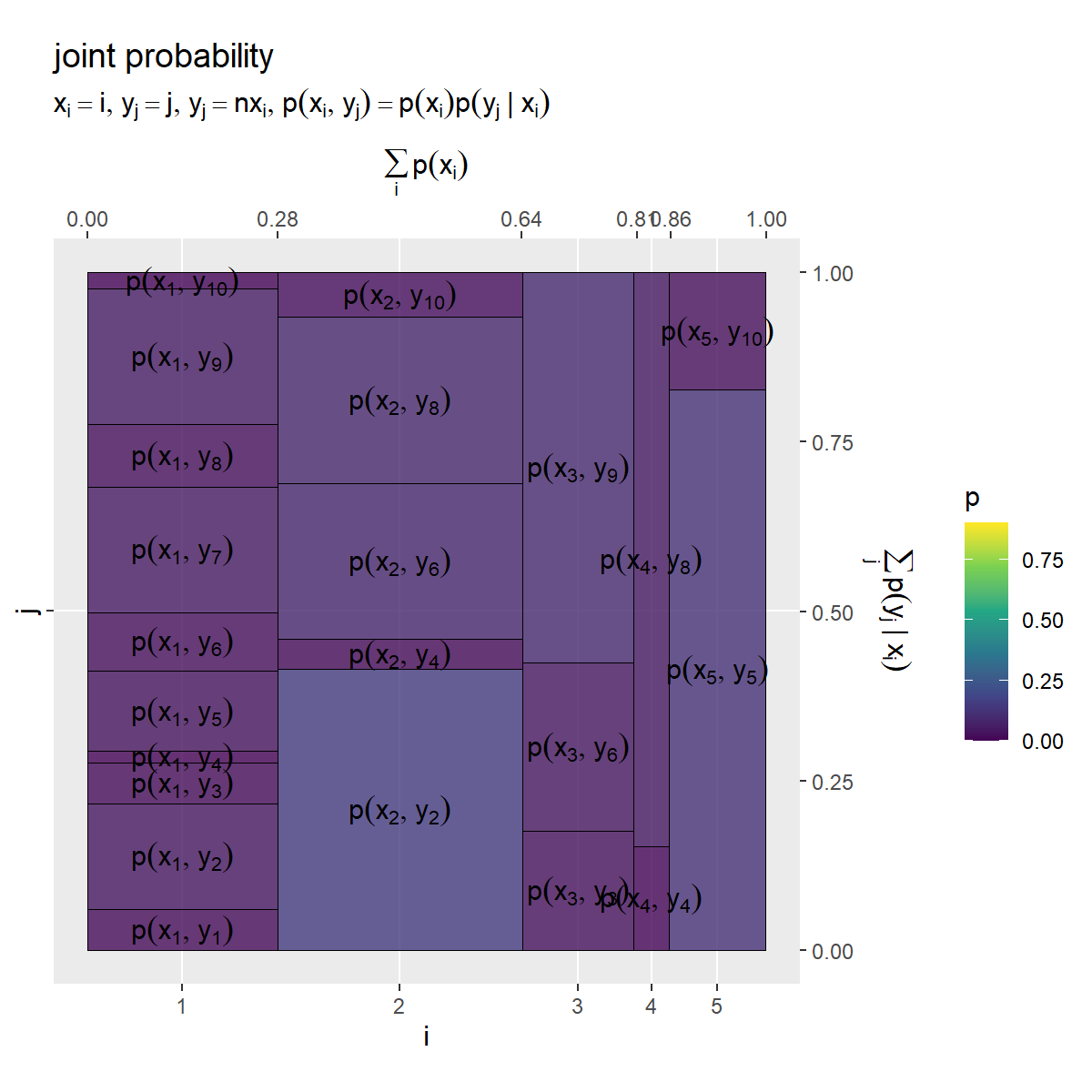
依存関係を持つ結合確率 のヒートマップを作成します。
# ラベル用の文字列を作成 fnc_label <- paste0( "list(", "x[i] == i, y[j] == j", ", ", "y[j] == n * x[i]", ", ", "p(x[i], y[j]) == p(x[i]) * p(y[j]~'|'~x[i])", ")" ) # x・yの結合確率を作図 prob_xy_graph <- ggplot() + geom_tile(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y.x, width = p_x, height = p_y.x, fill = p_xy), color = "black", alpha = 0.8) + # 確率 geom_text(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y.x, label = label_p_xy), parse = TRUE, angle = 0) + # 確率の式 scale_x_continuous(breaks = coord_x_vec, labels = x_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_x_vec)), digits = 2), name = expression(sum(p(x[i]), i)))) + # xのインデックスと累積確率 scale_y_continuous(breaks = 0.5, labels = NULL, sec.axis = sec_axis(trans = ~., breaks = seq(from = 0, to = 1, by = 0.25), name = expression(sum(p(y[j]~'|'~x[i]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, p_max)) + # グラデーション coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "joint probability", subtitle = parse(text = fnc_label), fill = "p", x = "i", y = "j") prob_xy_graph
5つのグラフを並べて描画します。
# 並べて描画 prob_joint_graph <- patchwork::wrap_plots( (prob_y_graph | prob_y.x_graph) / (prob_x_graph | (prob_x_y_graph | prob_xy_graph)), heights = 1, guides = "collect" ) prob_joint_graph
patchworkパッケージのwrap_plots()を使って、複数のグラフを並べて描画します。|演算子で横に、/演算子で縦に並べて描画します。()で囲ったグラフを1つのまとまりとして扱います。
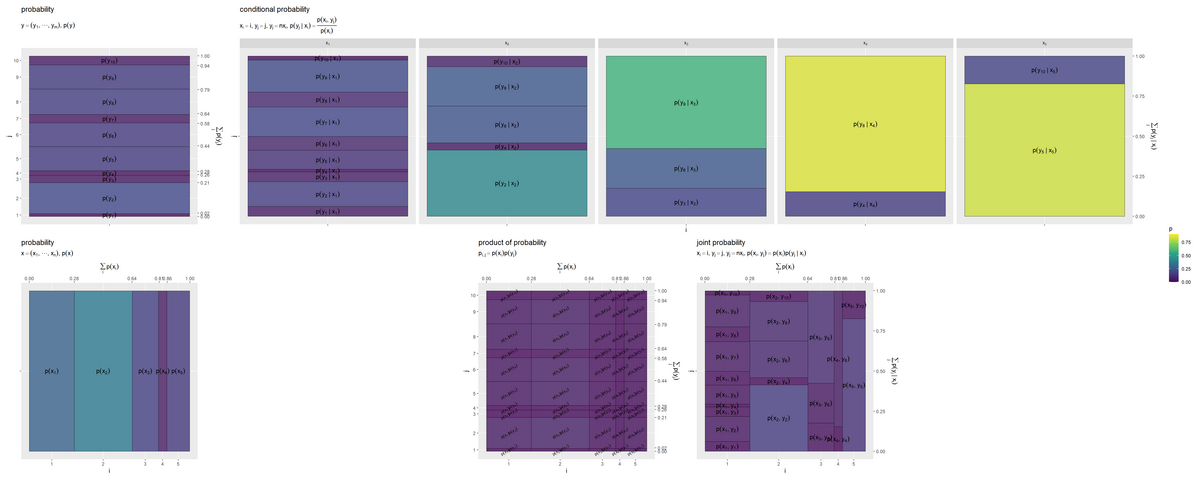
アスペクト比を1にしてセルの縦または横サイズを確率に合わせることで、全体の面積に占めるセル面積の割合が各事象の確率に対応します。セルが大きいほど確率が大きく、セルが小さいほど確率も小さいことを表します。
左上のグラフは、 の確率分布
であり、
個の事象
の確率を表します。
左下のグラフは、 の確率分布
であり、
個の事象
の確率を表します。右下のグラフのインデックス
が同じセルを足し合わせたサイズと一致します。
右上のn個のグラフは、 の条件付き分布
であり、事象(条件)
ごとの
の確率の確率を表すのでした。この図では、確率が0の事象(
の倍数でない
)のセルラベルは表示していません。
下段真ん中のグラフは、 の確率分布の積(依存関係がないとみなした結合分布)
であり、
の値(横方向のサイズ)と
の値(縦方向のサイズ)により
の値(セルサイズ)が決まるのでした。
右下のグラフは、 の(依存関係を持つ)結合分布
であり、
の値(横方向のサイズ)と
の値(縦方向のサイズ)により
の値(セルサイズ)が決まるのでした。
個のグラフの横幅が、条件の確率により加重平均をとるように縮小されています。
結合確率と確率の積の比を棒グラフで可視化します。
・作図コード(クリックで展開)
結合確率(依存あり)と2事象の確率の積(依存なし)の比の自己情報量を計算します。
# x・yの確率の比の自己情報量を計算 entropy_xy.x.y_df <- entropy_xy_df |> dplyr::select(i, j, p_x, p_y, p_y.x, p_xy) |> dplyr::mutate( r_xy.x.y = p_y.x / p_y, # 依存あり・なしの確率の比 I_xy.x.y = log2(r_xy.x.y), # 確率の比の自己情報量 label_p_xy.x.y = paste0("frac(p(x[", i, "], y[", j, "]), p(x[", i, "]) * p(y[", j, "]))") # 確率の式 ) entropy_xy.x.y_df
## # A tibble: 50 × 9 ## i j p_x p_y p_y.x p_xy r_xy.x.y I_xy.x.y label_p_xy.x.y ## <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> ## 1 1 1 0.280 0.0170 0.0609 0.0170 3.57 1.84 frac(p(x[1], y[1])… ## 2 1 2 0.280 0.193 0.155 0.0434 0.804 -0.315 frac(p(x[1], y[2])… ## 3 1 3 0.280 0.0457 0.0608 0.0170 1.33 0.411 frac(p(x[1], y[3])… ## 4 1 4 0.280 0.0287 0.0166 0.00465 0.579 -0.788 frac(p(x[1], y[4])… ## 5 1 5 0.280 0.151 0.118 0.0331 0.785 -0.349 frac(p(x[1], y[5])… ## 6 1 6 0.280 0.148 0.0863 0.0241 0.583 -0.779 frac(p(x[1], y[6])… ## 7 1 7 0.280 0.0518 0.185 0.0518 3.57 1.84 frac(p(x[1], y[7])… ## 8 1 8 0.280 0.159 0.0920 0.0257 0.579 -0.788 frac(p(x[1], y[8])… ## 9 1 9 0.280 0.150 0.200 0.0560 1.33 0.411 frac(p(x[1], y[9])… ## 10 1 10 0.280 0.0555 0.0248 0.00694 0.447 -1.16 frac(p(x[1], y[10]… ## # … with 40 more rows
entropy_xy_dfから関連する列を取り出して、結合確率と各事象の確率の積の比 を
r_xy.x.y列、比の対数をI_xy.x.y列として計算します。
事象の組み合わせごとに、結合確率と確率の積の比の棒グラフを作成します。
# ラベル用の文字列を作成 fnc_label <- "paste(p[list(i, j)] == frac(p(x[i], y[j]), p(x[i])*p(y[j])), {} == frac(p(y[j]~'|'~x[i]), p(y[j])))" # 結合確率と2事象の確率の比を作図 ratio_xy.x.y_graph <- ggplot() + geom_bar(data = entropy_xy.x.y_df, mapping = aes(x = i, y = r_xy.x.y), stat = "identity", width = 1, alpha = 0.8) + # 確率の比 geom_text(data = entropy_xy.x.y_df, mapping = aes(x = i, y = 0, label = label_p_xy.x.y), parse = TRUE, vjust = 0, size = 3) + # 確率の式 scale_x_continuous(breaks = x_idx, minor_breaks = FALSE) + # xのインデックス scale_y_continuous(sec.axis = sec_axis(trans = ~., breaks = 0, labels = NULL, name = "j")) + # 確率の比とyのインデックス facet_grid(j ~ i, labeller = label_bquote(rows = y[.(j)], cols = x[.(i)]), scales = "free_x") + # 事象の組み合わせごとに分割 labs(title = " ratio of probabilities with and without conditions", subtitle = parse(text = fnc_label), x = "i", y = expression(p[list(i, j)])) ratio_xy.x.y_graph
facet_grid()で事象の組み合わせ ごとにグラフを分割して、
geom_bar()で棒グラフを描画します。

結合確率(依存あり)と2事象の確率の積(依存なし)の比は なので、
に依存関係がない
のとき1になります。
自己情報量のヒートマップ
続いて、自己情報量をヒートマップで可視化して、相互情報量を確認します。
・作図コード(クリックで展開)
の各事象の自己情報量のヒートマップを作成します。
# 自己情報量(グラデーション)の最大値を設定 I_max <- entropy_xy_df |> dplyr::select(I_x, I_y, I_y.x, I_xy, I_x_y) |> # 自己情報量列 (\(.){.[. < Inf]})() |> # 確率が0の事象を除く max() |> ceiling() # 小数点以下を切り上げ # 平均情報量を計算 H_x <- sum(entropy_x_df[["p_x"]] * entropy_x_df[["I_x"]], na.rm = TRUE) # ラベル用の文字列を作成 fnc_label <- paste0( "list(", "I(x[i]) == - log[2]*p(x[i])", ", ", "H(x) == sum(p(x[i]) * I(x[i]), i==1, n)", ")" ) H_x_label <- paste0("H(x) == ", round(H_x, digits = 3)) # xの自己情報量を作図 entropy_x_graph <- ggplot() + geom_tile(data = entropy_x_df, mapping = aes(x = coord_x, y = 0, width = p_x, height = 1, fill = I_x), color = "black", alpha = 0.8) + # 自己情報量 geom_text(data = entropy_x_df, mapping = aes(x = coord_x, y = 0, label = label_p_x), parse = TRUE) + # 確率の式 geom_label(mapping = aes(x = -Inf, y = Inf), label = H_x_label, hjust = 0, vjust = 1, parse = TRUE, alpha = 0.5) + # エントロピーの値 scale_x_continuous(breaks = coord_x_vec, labels = x_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_x_vec)), digits = 2), name = expression(sum(p(x[i]), i)))) + # xのインデックスと累積確率 scale_y_continuous(breaks = 0, labels = NULL) + # yのインデックス scale_fill_viridis_c(limits = c(0, I_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "self-information", subtitle = parse(text = fnc_label), fill = "I", x = "i", y = "") entropy_x_graph
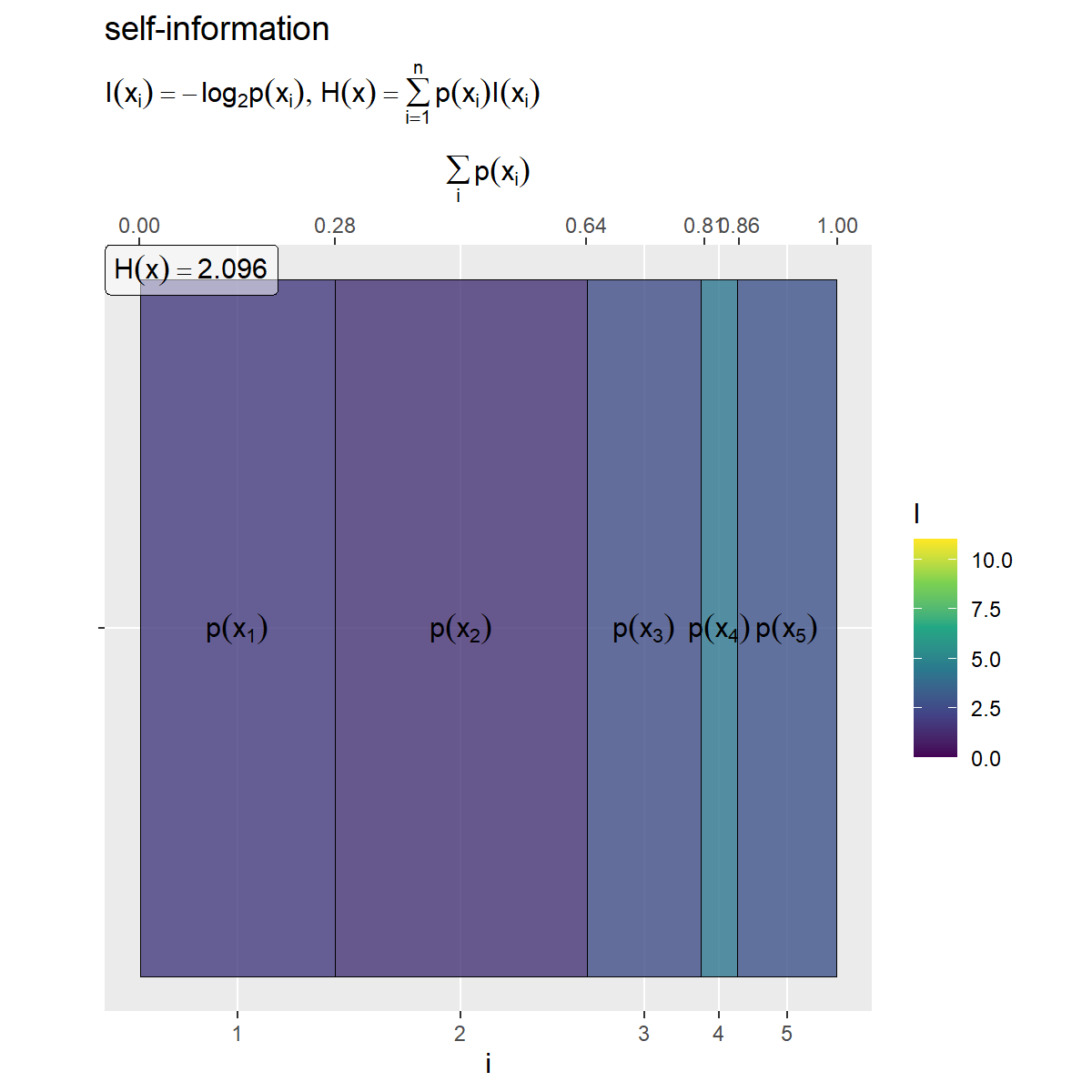
自己情報量の最大値をI_maxとしておき、塗りつぶし色(z軸の値)を自己情報量列として、「条件付き確率のヒートマップ」のときと同様に作図します。
エントロピー を計算して、
geom_label()でラベルとして表示します。
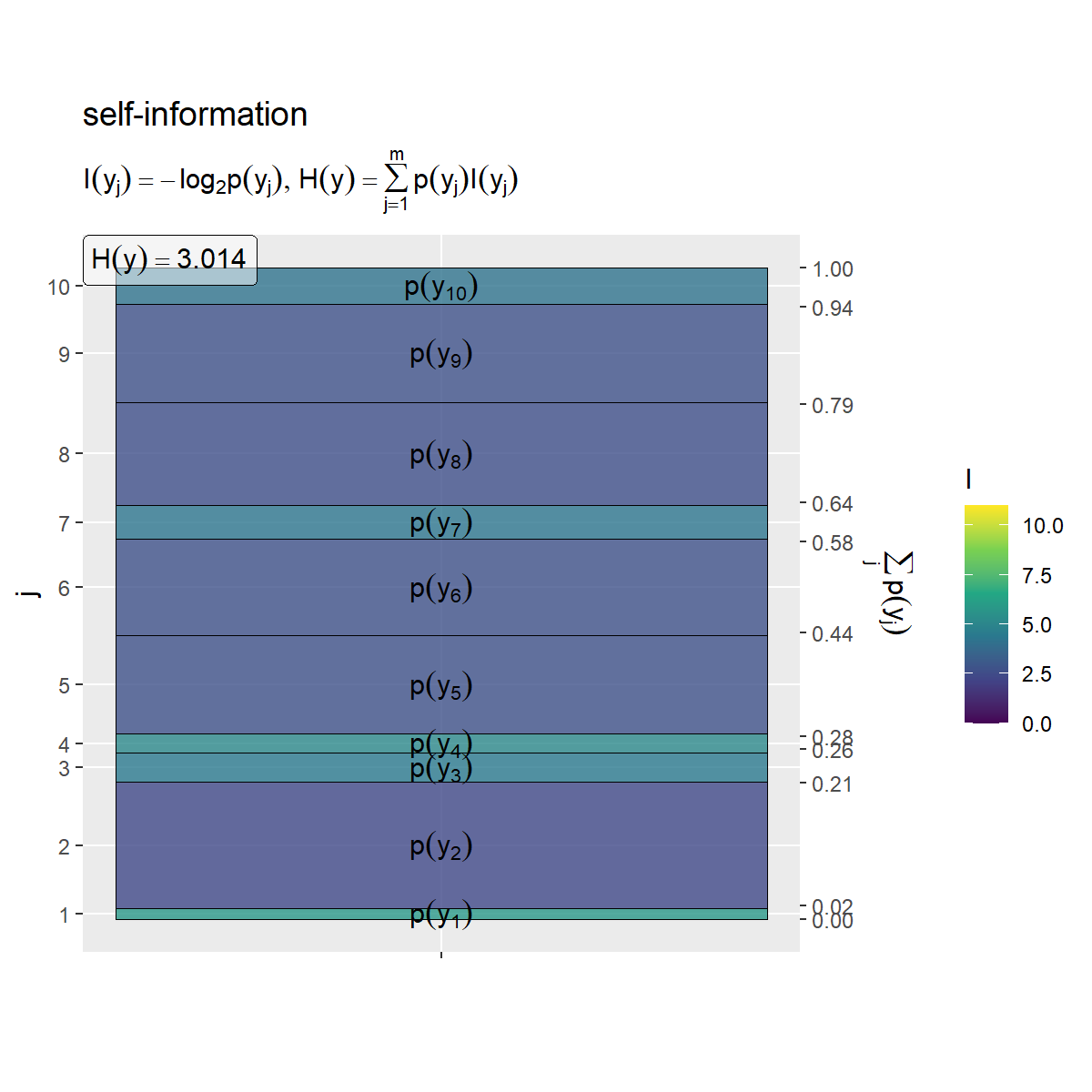
同様に、 の各事象の自己情報量のヒートマップを作成します。
# 平均情報量を計算 H_y <- sum(entropy_y_df[["p_y"]] * entropy_y_df[["I_y"]], na.rm = TRUE) # ラベル用の文字列を作成 fnc_label <- paste0( "list(", "I(y[j]) == - log[2]*p(y[j])", ", ", "H(y) == sum(p(y[j]) * I(y[j]), j==1, m)", ")" ) H_y_label <- paste0("H(y) == ", round(H_y, digits = 3)) # yの自己情報量を作図 entropy_y_graph <- ggplot() + geom_tile(data = entropy_y_df, mapping = aes(x = 0, y = coord_y, width = 1, height = p_y, fill = I_y), color = "black", alpha = 0.8) + # 自己情報量 geom_text(data = entropy_y_df, mapping = aes(x = 0, y = coord_y, label = label_p_y), parse = TRUE) + # 確率の式 geom_label(mapping = aes(x = -Inf, y = Inf), label = H_y_label, hjust = 0, vjust = 1, parse = TRUE, alpha = 0.5) + # エントロピーの値 scale_x_continuous(breaks = 0, labels = NULL) + # xのインデックス scale_y_continuous(breaks = coord_y_vec, labels = y_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_y_vec)), digits = 2), name = expression(sum(p(y[j]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, I_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "self-information", subtitle = parse(text = fnc_label), fill = "I", x = "", y = "j") entropy_y_graph
の事象の組み合わせごとの(依存関係がないとみなした)自己情報量のヒートマップを作成します。
# 平均情報量を計算 H_x_y <- sum(entropy_xy_df[["p_x_y"]] * entropy_xy_df[["I_x_y"]], na.rm = TRUE) # ラベル用の文字列を作成 fnc_label <- paste0( "list(", "p[list(i, j)] == p(x[i]) * p(y[j])", ", ", "I[list(i, j)] == - log[2]*(p(x[i]) * p(y[j]))", ", ", "H[list(x, y)] == sum({}, i==1, n) * sum({}, j==1, m) * p[list(i, j)] * I[list(i, j)]", ")" ) H_x_y_label <- paste0("H[list(x, y)] == ", round(H_x_y, digits = 3)) # x・yの自己情報量を作図 entropy_x_y_graph <- ggplot() + geom_tile(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y, width = p_x, height = p_y, fill = I_x_y), color = "black", alpha = 0.8) + # 確率 geom_text(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y, label = label_p_x_y), parse = TRUE, angle = 30, size = 2.5) + # 確率の式 geom_label(mapping = aes(x = -Inf, y = Inf), label = H_x_y_label, hjust = 0, vjust = 1, parse = TRUE, alpha = 0.5) + # エントロピーの値 scale_x_continuous(breaks = coord_x_vec, labels = x_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_x_vec)), digits = 2), name = expression(sum(p(x[i]), i)))) + # xのインデックスと累積確率 scale_y_continuous(breaks = coord_y_vec, labels = y_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_y_vec)), digits = 2), name = expression(sum(p(y[j]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, I_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "product of probability", subtitle = parse(text = fnc_label), fill = "I", x = "i", y = "j") entropy_x_y_graph
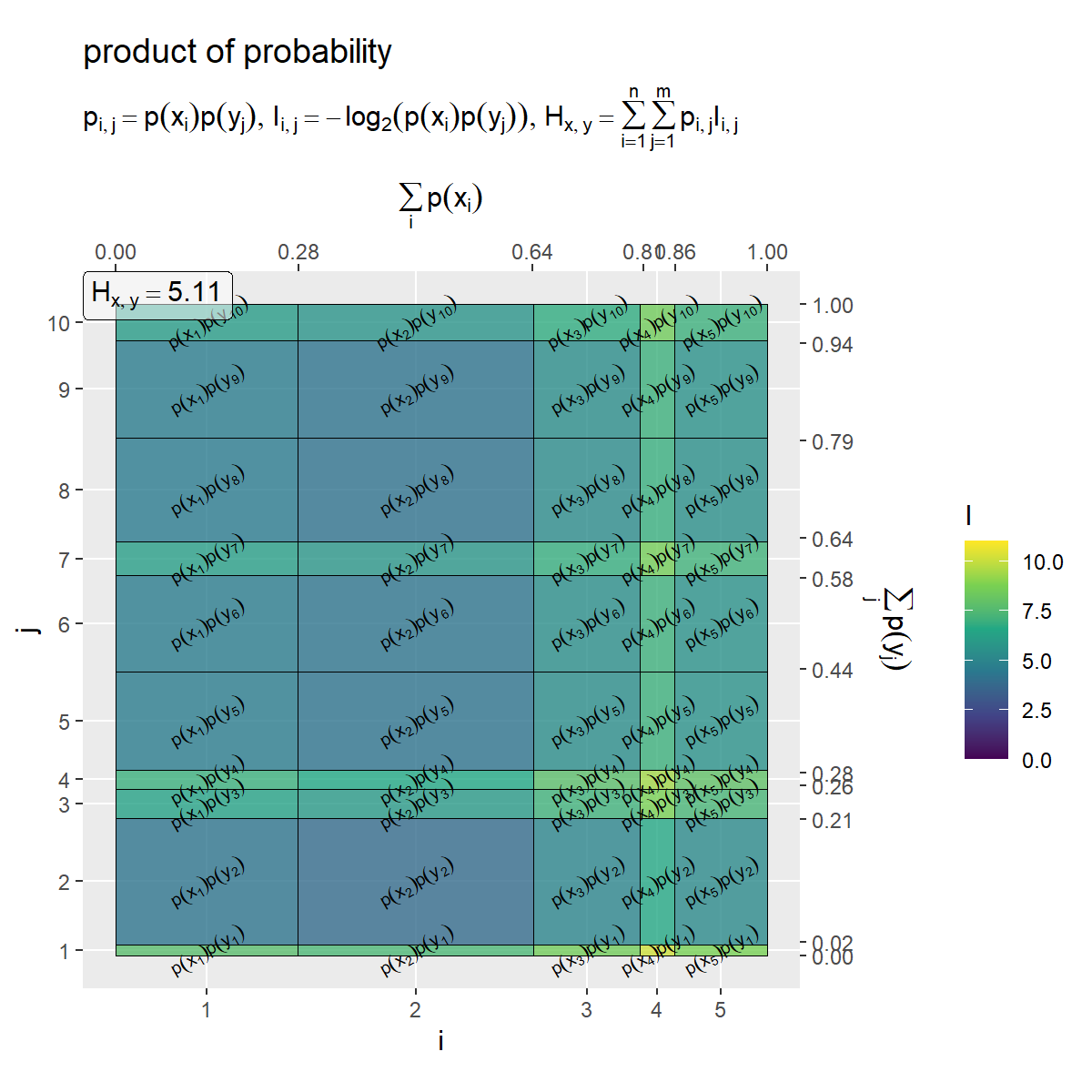
確率の積を用いてエントロピー を計算して、ラベルとして表示します。
条件付けされた の各事象の自己情報量のヒートマップを作成します。
# 平均情報量を計算 H_y.x <- sum(entropy_xy_df[["p_xy"]] * entropy_xy_df[["I_y.x"]], na.rm = TRUE) # ラベル用の文字列を作成 fnc_label <- paste0( "list(", "x[i] == i, y[j] == j", ", ", "y[j] == n * x[i]", ", ", "I(y[j]~'|'~x[i]) == - log[2]*p(y[j]~'|'~x[i])", ", ", "H(x, y) == sum({}, i==1, n) * sum({}, j==1, m) * p(x[i], y[j]) * I(y[j]~'|'~x[i])", ")" ) H_y.x_label_df <- tibble::tibble( i = 1, # xのインデックス(ラベルを配置する条件番号) H_y.x_label = paste0("H(y~'|'~x) == ", round(H_y.x, digits = 3)) ) # 条件付きyの自己情報量を作図 entropy_y.x_graph <- ggplot() + geom_tile(data = entropy_xy_df, mapping = aes(x = 0, y = coord_y.x, width = 1, height = p_y.x, fill = I_y.x), color = "black", alpha = 0.8) + # 自己情報量 geom_text(data = entropy_xy_df, mapping = aes(x = 0, y = coord_y.x, label = label_p_y.x), parse = TRUE, angle = 0) + # 確率の式 geom_label(data = H_y.x_label_df, mapping = aes(x = -Inf, y = Inf, label = H_y.x_label), hjust = 0, vjust = 1, parse = TRUE, alpha = 0.5) + # エントロピーの値 scale_x_continuous(breaks = 0, labels = NULL) + # xのインデックス scale_y_continuous(breaks = 0.5, labels = NULL, sec.axis = sec_axis(trans = ~., breaks = seq(from = 0, to = 1, by = 0.25), name = expression(sum(p(y[j]~'|'~x[i]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, I_max)) + # グラデーション facet_grid(. ~ i, labeller = label_bquote(cols = x[.(i)])) + # xの事象(条件)ごとに分割 coord_fixed(ratio = 1) + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "conditional information", subtitle = parse(text = fnc_label), fill = "I", x = "i", y = "j") entropy_y.x_graph
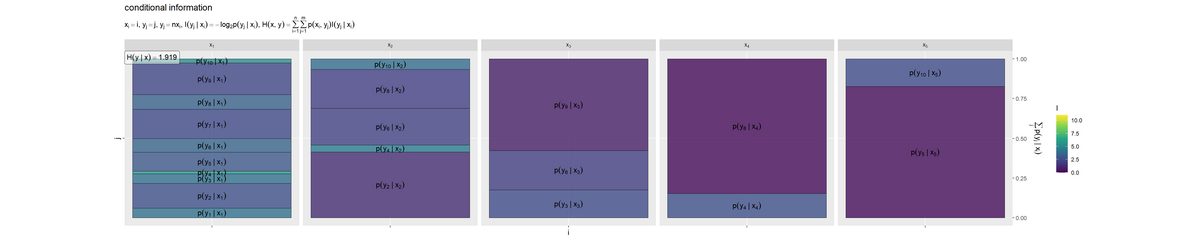
条件付きエントロピー を計算して、ラベルとして表示します。条件付き確率
p_y.xではなく、結合確率p_xyを用いて期待値をとる点に注意してください。
の事象の組み合わせごとの自己情報量のヒートマップを作成します。
# 平均情報量を計算 H_xy <- sum(entropy_xy_df[["p_xy"]] * entropy_xy_df[["I_xy"]], na.rm = TRUE) # ラベル用の文字列を作成 fnc_label <- paste0( "list(", "x[i] == i, y[j] == j", ", ", "y[j] == n * x[i]", ", ", "p(x[i], y[j]) == p(x[i]) * p(y[j]~'|'~x[i])", ", ", "I(x[i], y[j]) == - log[2]*p(x[i], y[j])", ", ", "H(x, y) == sum({}, i==1, n) * sum({}, j==1, m) * p(x[i], y[j]) * I(x[i], y[j])", ")" ) H_xy_label <- paste0("H(x, y) == ", round(H_xy, digits = 3)) # x・yの自己情報量を作図 entropy_xy_graph <- ggplot() + geom_tile(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y.x, width = p_x, height = p_y.x, fill = I_xy), color = "black", alpha = 0.8) + # 自己情報量 geom_text(data = entropy_xy_df, mapping = aes(x = coord_x, y = coord_y.x, label = label_p_xy), parse = TRUE, angle = 0) + # 確率の式 geom_label(mapping = aes(x = -Inf, y = Inf), label = H_xy_label, hjust = 0, vjust = 1, parse = TRUE, alpha = 0.5) + # エントロピーの値 scale_x_continuous(breaks = coord_x_vec, labels = x_idx, sec.axis = sec_axis(trans = ~., breaks = round(cumsum(c(0, p_x_vec)), digits = 2), name = expression(sum(p(x[i]), i)))) + # xのインデックスと累積確率 scale_y_continuous(breaks = 0.5, labels = NULL, sec.axis = sec_axis(trans = ~., breaks = seq(from = 0, to = 1, by = 0.25), name = expression(sum(p(y[j]~'|'~x[i]), j)))) + # yのインデックスと累積確率 scale_fill_viridis_c(limits = c(0, I_max)) + # グラデーション coord_fixed(ratio = 1, clip = "off") + # アスペクト比 theme(panel.grid.minor = element_blank()) + # 図の体裁 labs(title = "joint information", subtitle = parse(text = fnc_label), fill = "I", x = "i", y = "j") entropy_xy_graph
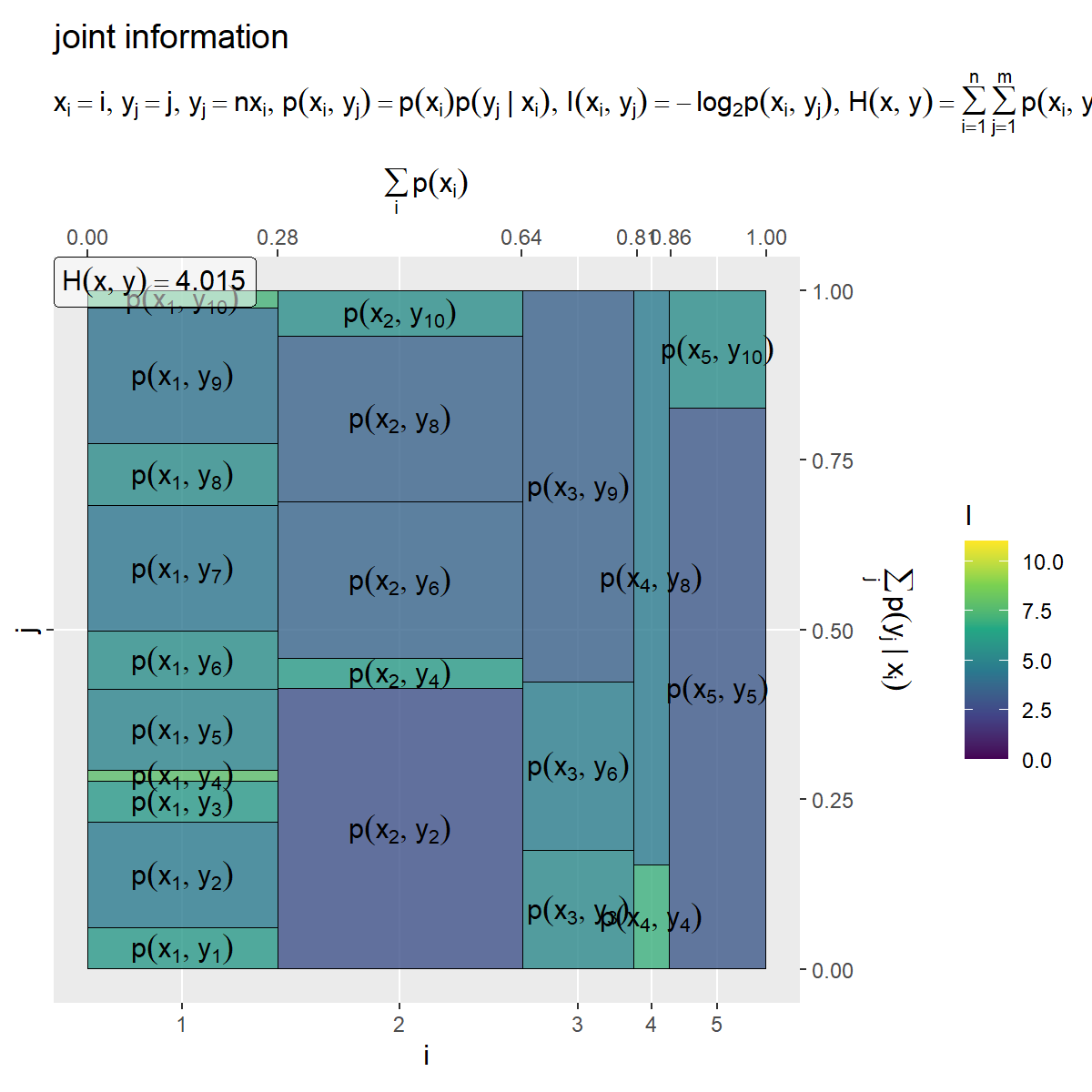
結合エントロピー(多変数の平均情報量) を計算して、ラベルとして表示します。
5つのグラフを並べて描画します。
# 並べて描画 entropy_joint_graph <- patchwork::wrap_plots( (entropy_y_graph | entropy_y.x_graph) / (entropy_x_graph | (entropy_x_y_graph | entropy_xy_graph)), heights = 1, guides = "collect" ) entropy_joint_graph
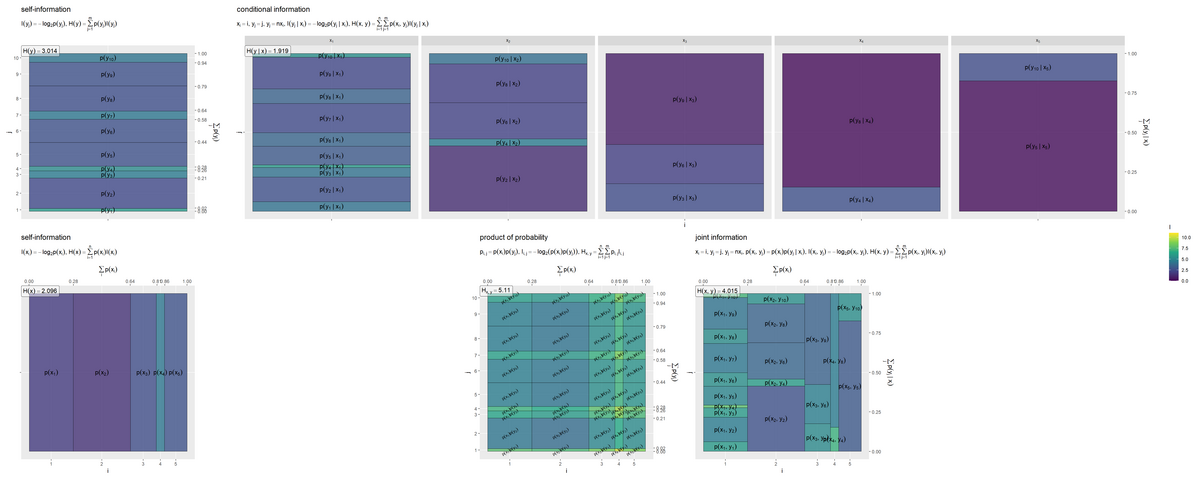
事象(セル)ごとの自己情報量(色を高さとみなして)の期待値(面積の割合と高さの加重平均)がエントロピーや結合エントロピーの値です。
条件付きエントロピーは、条件付き確率(右上のグラフの各セル)の自己情報量を、結合確率(右下のグラフの各セル)により期待値(加重平均)をとった値です。
結合確率と確率の積の比の自己情報量を棒グラフで可視化します。
・作図コード(クリックで展開)
事象の組み合わせごとに、結合確率と確率の積の比の対数の棒グラフを作成します。
# 相互情報を計算 I_mutual <- sum(entropy_xy.x.y_df[["p_xy"]] * entropy_xy.x.y_df[["I_xy.x.y"]], na.rm = TRUE) # ラベル用の文字列を作成 fnc_label <- paste0( "list(", "paste(p[list(i, j)] == frac(p(x[i], y[j]), p(x[i])*p(y[j])), {} == frac(p(y[j]~'|'~x[i]), p(y[j])))", ", ", "I[list(i, j)] == log[2]*p[list(i, j)]", ", ", "I(x~';'~y) == sum({}, i==1, n) * sum({}, j==1, m) * p(x[i], y[j]) * I[list(i, j)]", ")" ) I_mutual_label_df <- tibble::tibble( i = max(x_idx), # xのインデックス(ラベルを配置する事象番号) j = 1, # yのインデックス(ラベルを配置する事象番号) I_mutual_label = paste0("I(x~';'~y) == ", round(I_mutual, digits = 3)) ) # 結合確率と2事象の確率の比の対数を作図 entropy_xy.x.y_graph <- ggplot() + geom_bar(data = entropy_xy.x.y_df, mapping = aes(x = i, y = I_xy.x.y), stat = "identity", width = 1, alpha = 0.8) + # 確率の比の対数 geom_text(data = entropy_xy.x.y_df, mapping = aes(x = i, y = 0, label = label_p_xy.x.y), parse = TRUE, vjust = 0, size = 3) + # 確率の式 geom_label(data = I_mutual_label_df, mapping = aes(x = Inf, y = Inf, label = I_mutual_label), hjust = 1, vjust = 1, parse = TRUE, alpha = 0.5) + # エントロピーの値 scale_x_continuous(breaks = x_idx, minor_breaks = FALSE) + # xのインデックス scale_y_continuous(sec.axis = sec_axis(trans = ~., breaks = 0, labels = NULL, name = "j")) + # 確率の比とyのインデックス facet_grid(j ~ i, labeller = label_bquote(rows = y[.(j)], cols = x[.(i)]), scales = "free_x") + # 事象の組み合わせごとに分割 coord_cartesian(clip = "off") + # 描画範囲 labs(title = " ratio of probabilities with and without conditions", subtitle = parse(text = fnc_label), x = "i", y = expression(I[list(i, j)])) entropy_xy.x.y_graph

対数関数は単調増加するので、比が大きいほど対数も大きくなります。比が0から1の値のとき対数は負の値になります。(負の値もとる比の対数の期待値が常に非負の値になる理由がとても気になりますが今回は飛ばしました。)
エントロピーラベルを比較すると「エントロピーの性質」の関係を確認できます。
・元の確率分布を一様に設定した場合
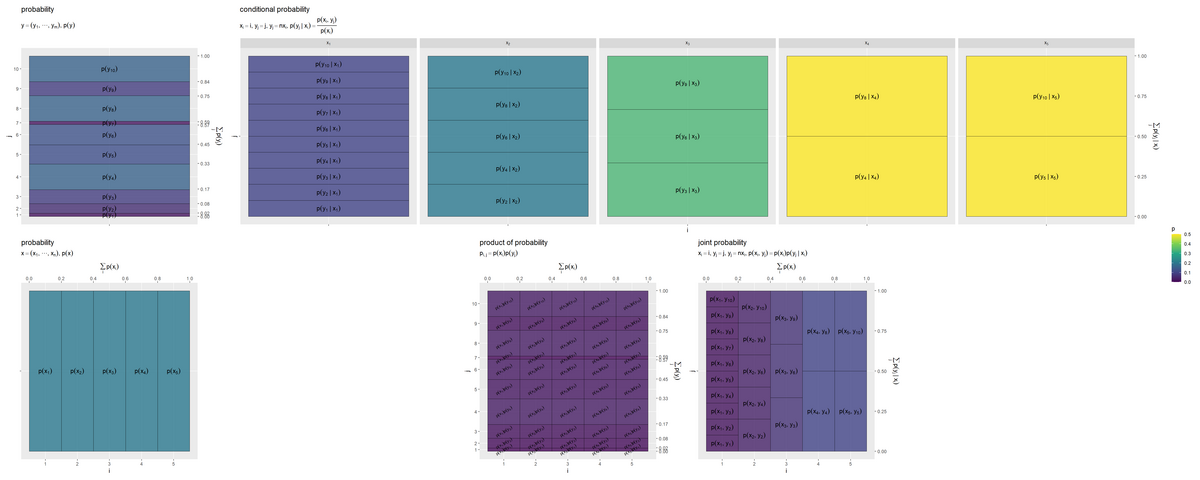
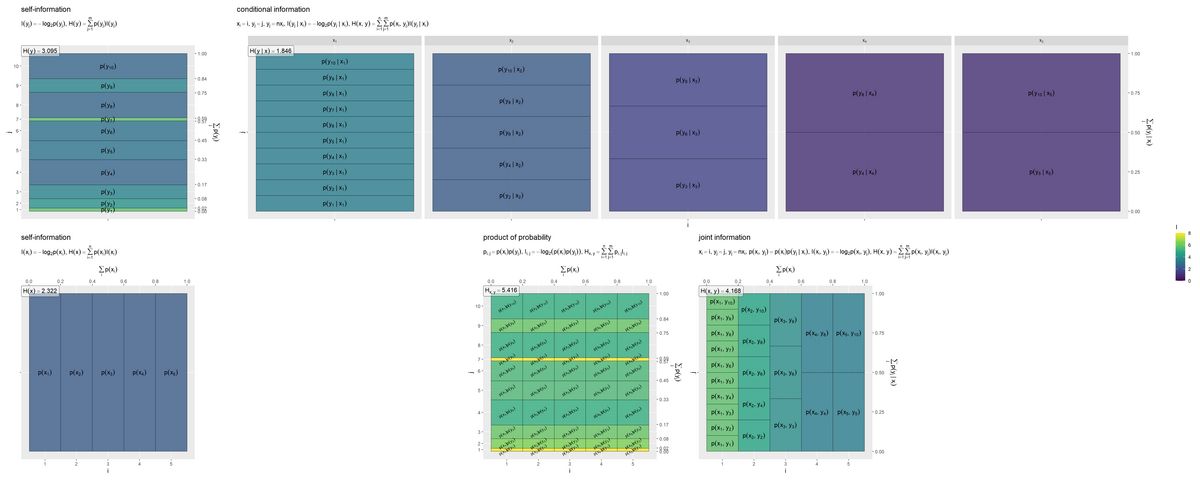


の周辺確率
は、依存関係(によって決まる条件付き確率
)によって変わるので、一様になっていません。
・依存関係を設定しない場合
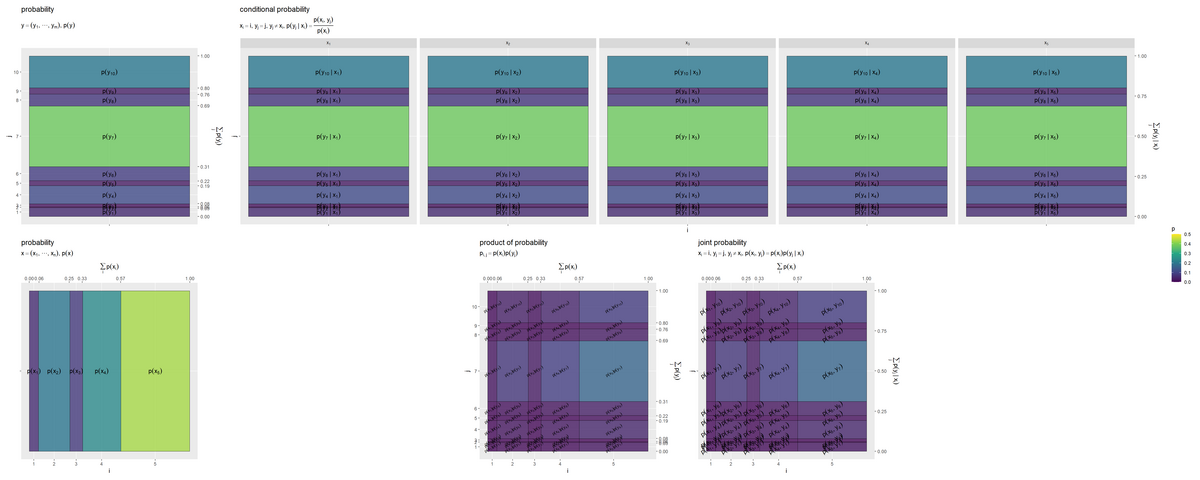
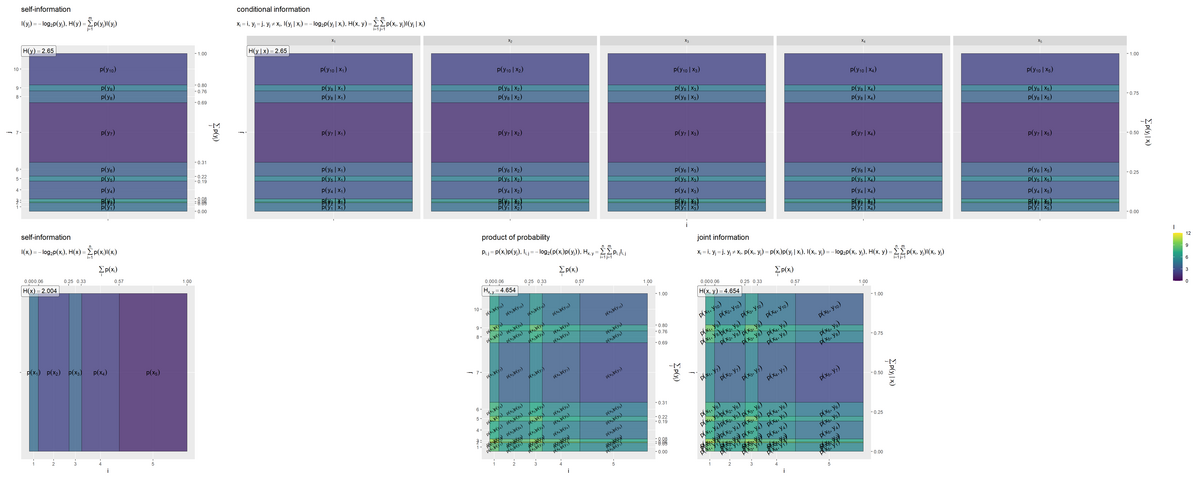

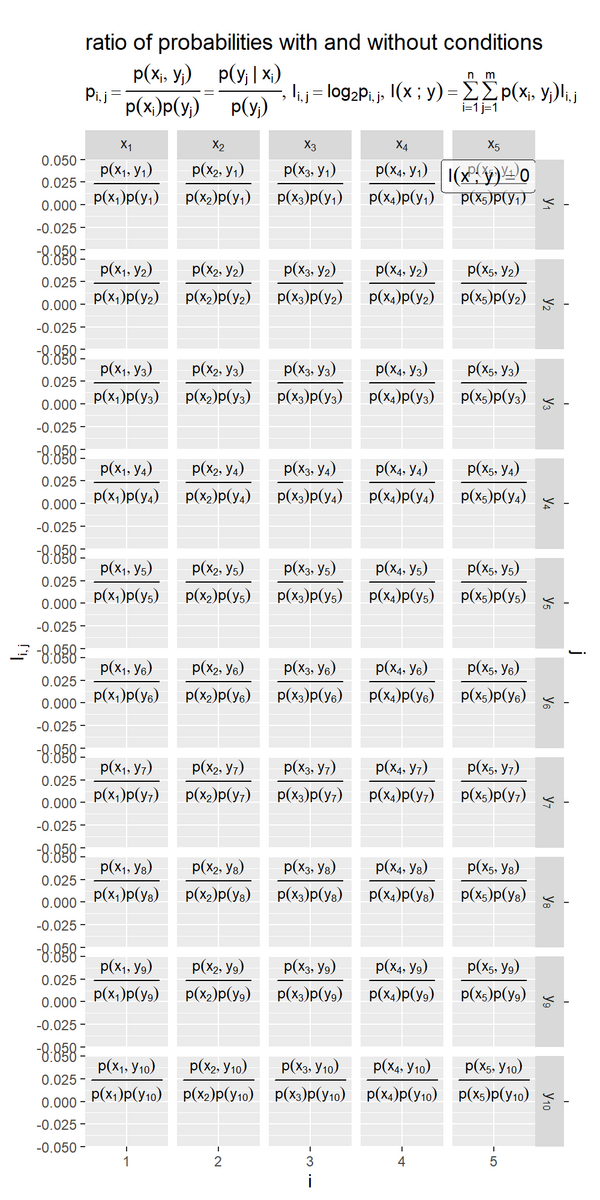
事象 が独立なので、条件付き確率が全て同じ分布になり、確率の積と結合確率のグラフが一致しています。
(プログラム上の誤差の影響でバーが描画されることがありますが、縦軸を見るとほぼ0なのが分かります。)
この記事では、相互情報量の定義を確認しました。次の記事では、KL情報量の定義を確認します。
参考文献
- 『わかりやすい ディジタル情報理論』(改訂2版)塩野 充・蜷川 繁,オーム社,2021年.
おわりに
相互情報量まで辿り着きました。参考にした本だとここで終わりですが、この文脈でKL情報量と交差エントロピーも書こうと思います、近い内に。これ以上グラフがマシマシにならないことを祈る。
【次の内容】
つづく