はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は7.1節「幾何変換」の内容です。
ベクトルのスケーリングの計算を確認して、グラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
ベクトルの拡大・縮小の可視化
行列計算によるベクトルのスケーリング(拡大・縮小)(vector scaling)を数式とグラフで確認します。今回は、全ての次元(軸)で倍率を固定します。次回は、次元(軸)ごとに倍率を変更します。
行列とベクトルの積については「【Python】行列のベクトル積の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」、ベクトルのスケーリングについては「【Python】1.3:ベクトルのスカラー倍の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
ベクトルの拡大・縮小の計算式
まずは、ベクトルのスケーリングを数式で確認します。
スカラー と
の単位行列による
の対角行列
を用いて、2次元ベクトル を変換します。
も2次元ベクトルになります。単位行列との積は
です。
ベクトルの拡大・縮小の作図
次は、ベクトルのスケーリングをグラフで確認します。
倍率を指定して、スケーリング用の行列を作成します。
# スカラを指定 alpha = 2.5 # スケール行列を作成 A = alpha * np.identity(2) print(A) print(A.shape)
[[2.5 0. ]
[0. 2.5]]
(2, 2)
拡大(縮小)する倍率 をスカラ
alpha として値を指定します。
スケール行列 を2次元配列
A として作成します。
ベクトルを指定して、行列との積により変換します。
# ベクトルを指定 x = np.array([3.0, 2.0]) print(x) print(x.shape) # ベクトルを変換 y = np.dot(A, x) print(y) print(y.shape)
[3. 2.]
(2,)
[7.5 5. ]
(2,)
入力ベクトル を1次元配列
x として値を指定します。
拡大(縮小)ベクトル(出力ベクトル) を計算して
y とします。
ベクトル のグラフを作成します。
# グラフサイズ用の値を設定 x1_min = np.floor(np.min([0.0, x[0], y[0]])) - 1 x1_max = np.ceil(np.max([0.0, x[0], y[0]])) + 1 x2_min = np.floor(np.min([0.0, x[1], y[1]])) - 1 x2_max = np.ceil(np.max([0.0, x[1], y[1]])) + 1 # 倍率の符号を取得 sgn_a = 1.0 if alpha >= 0.0 else -1.0 # 繰り返し回数を設定 rep_num = np.ceil(abs(alpha)).astype(np.int16) # 2D拡大ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.quiver(0, 0, *x, color='black', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$x=({}, {})'.format(*x)+'$') # 入力ベクトル ax.quiver(0, 0, *y, color='red', units='dots', width=3, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$y=({:.2f}, {:.2f})'.format(*y)+'$') # 出力ベクトル for i in range(rep_num): ax.quiver(sgn_a*x[0]*i, 0, sgn_a*x[0], 0, fc='white', ec='black', linewidth=1.5, linestyle=':', units='dots', width=1, headwidth=15, headlength=15, headaxislength=2.5, angles='xy', scale_units='xy', scale=1) # 水平方向の倍率 ax.quiver(alpha*x[0], sgn_a*x[1]*i, 0, sgn_a*x[1], fc='white', ec='black', linewidth=1.5, linestyle=':', units='dots', width=1, headwidth=15, headlength=15, headaxislength=2.5, angles='xy', scale_units='xy', scale=1) # 垂直方向の倍率 ax.set_xticks(ticks=np.arange(x1_min, x1_max+1)) ax.set_yticks(ticks=np.arange(x2_min, x2_max+1)) ax.set_xlim(left=x1_min, right=x1_max) ax.set_ylim(bottom=x2_min, top=x2_max) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$y = A x, ' + '\\alpha = '+str(alpha)+', ' + 'A = ('+', '.join(map(str, A.flatten()))+')$', loc='left') fig.suptitle('scaling', fontsize=20) ax.grid() ax.legend(loc='upper left') ax.set_aspect('equal') plt.show()
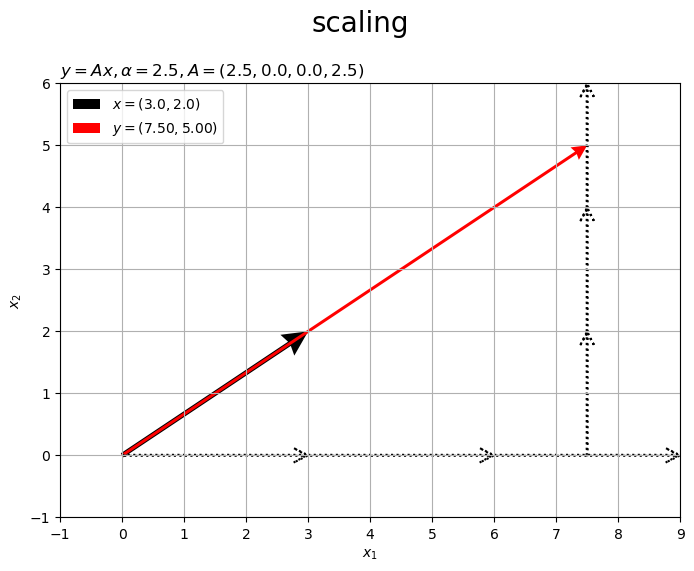
入力ベクトル を黒色の矢印、出力ベクトルを
を赤色の矢印で示します。また、x軸・y軸それぞれの方向への倍率を点線の矢印で表します。
行列 によって変換したベクトル
が、ベクトル
をx軸とy軸方向に
倍したベクトルなのが分かります。
倍率または入力ベクトルを変化させたアニメーションで確認します。
・作図コード(クリックで展開)
フレーム数を指定して、変化する倍率と固定する入力ベクトルを作成します。
# フレーム数を指定 frame_num = 101 # 倍率の範囲を指定 alpha_n = np.linspace(start=-2.0, stop=2.0, num=frame_num) print(alpha_n[:5]) # ベクトルを指定 x = np.array([-3.0, 2.0])
[-2. -1.96 -1.92 -1.88 -1.84]
フレーム数を frame_num として整数を指定します。
倍率の範囲を指定して、frame_num 個の倍率 alpha_n を作成します。入力ベクトル x は先ほどと同様に指定します。
または、固定する倍率と変化する入力ベクトルを作成します。
# フレーム数を指定 #frame_num = 90 # スカラを指定 alpha = -2.5 # ベクトルとして用いる値を指定 r = 2.0 rad_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] x_n = np.array( [r * np.cos(rad_n), r * np.sin(rad_n)] ).T print(x_n[:5])
[[2. 0. ]
[1.9951281 0.13951295]
[1.98053614 0.2783462 ]
[1.9562952 0.41582338]
[1.92252339 0.55127471]]
frame_num 個の入力ベクトル x_nを作成します。倍率 alpha は先ほどと同様に指定します。
この例では、入力ベクトル(の先端)が原点からの半径が r の円周上を移動するように設定しています。
倍率と入力ベクトルの両方を変化させることもできます。
アニメーションを作成します。
# グラフサイズ用の値を設定 axis_size = np.ceil(abs(alpha_n).max() * abs(x).max()) + 1 #axis_size = np.ceil(abs(alpha) * abs(x_n).max()) + 1 #axis_size = np.ceil(abs(alpha_n * x_n.T).max()) + 1 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white') fig.suptitle('scaling', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の値を作成 alpha = alpha_n[i] #x = x_n[i] # スケール行列を作成 A = alpha * np.identity(2) # ベクトルを変換 y = np.dot(A, x) # 倍率の符号を取得 sgn_a = 1.0 if alpha >= 0.0 else -1.0 # 繰り返し回数を設定 rep_num = np.ceil(abs(alpha)).astype(np.int16) # 2D拡大ベクトルを作図 ax.quiver(0, 0, *x, color='black', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$x=({: .2f}, {: .2f})'.format(*x)+'$') # 入力ベクトル ax.quiver(0, 0, *y, color='red', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$y=({: .2f}, {: .2f})'.format(*y)+'$') # 出力ベクトル for i in range(rep_num): ax.quiver(sgn_a*x[0]*i, 0, sgn_a*x[0], 0, fc='white', ec='black', linewidth=1.5, linestyle=':', units='dots', width=1, headwidth=15, headlength=15, headaxislength=2.5, angles='xy', scale_units='xy', scale=1) # 水平方向の倍率 ax.quiver(alpha*x[0], sgn_a*x[1]*i, 0, sgn_a*x[1], fc='white', ec='black', linewidth=1.5, linestyle=':', units='dots', width=1, headwidth=15, headlength=15, headaxislength=2.5, angles='xy', scale_units='xy', scale=1) # 垂直方向の倍率 ax.set_xticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_yticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$y = A x, ' + '\\alpha = {: .2f}'.format(alpha)+', ' + 'A = ('+', '.join(['{: .2f}'.format(a) for a in A.flatten()])+')$', loc='left') ax.grid() ax.legend(loc='upper left') ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('scaling_alpha.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。
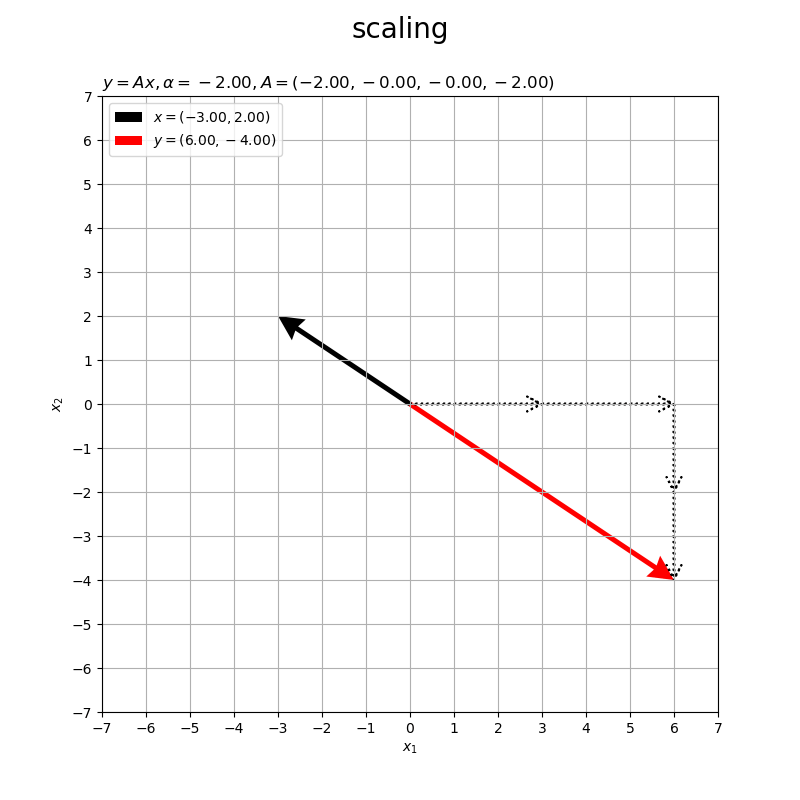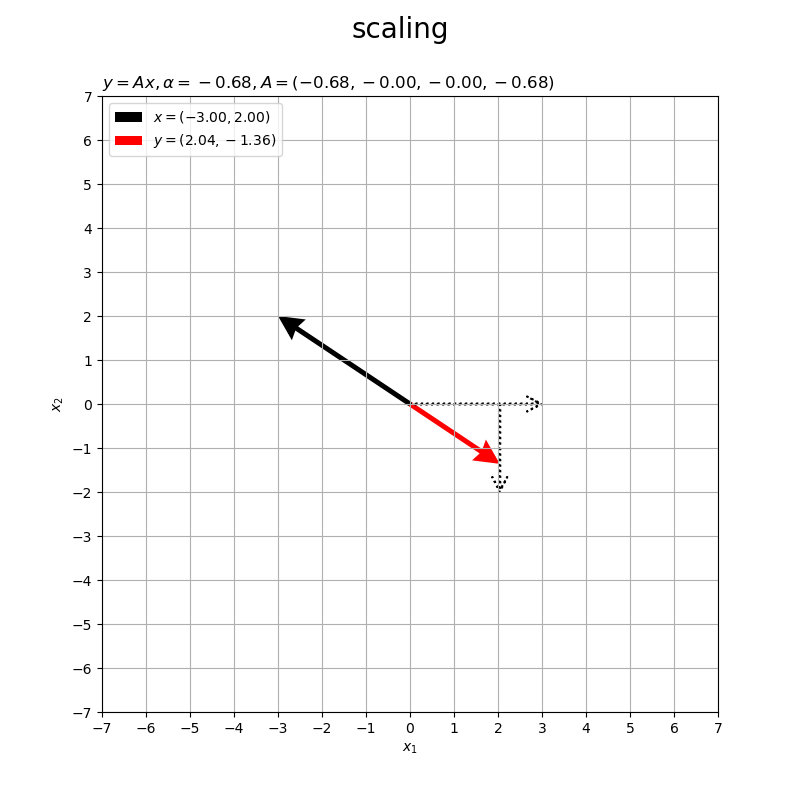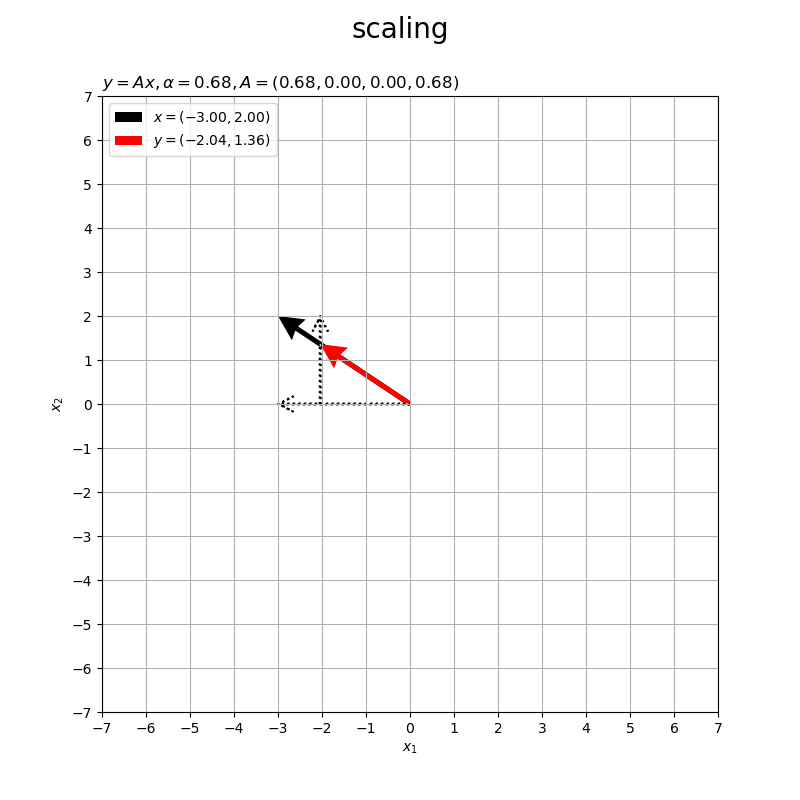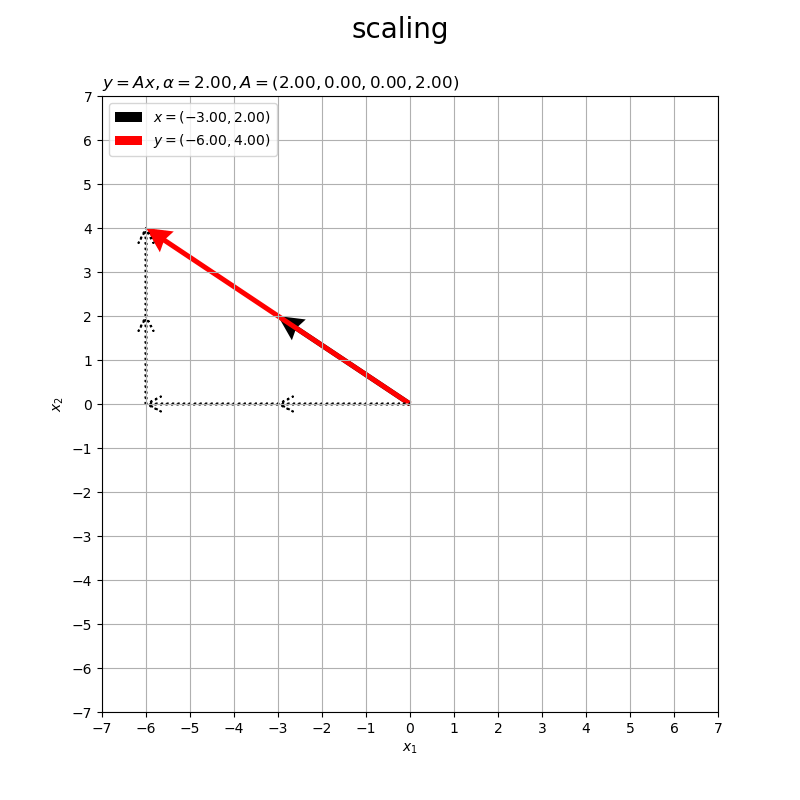

倍率が1より大きい と拡大、
だと等倍(変わらない)、1より小さい正の値
だと縮小、負の値
だと逆向きに
倍にスケーリングされます。
この記事では、行列計算によるベクトルの全ての次元で固定した倍率のスケーリングを確認しました。次の記事では、次元ごとのスケーリングを確認します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
7章に突入です。内容的には1章の始めでもやりましたね。物足りなければ次の記事とセットで読むと面白みがあると思います。
【次の内容】