はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は6.4節「行列ベクトル積」の内容です。
Pythonを使って行列とベクトルの積のグラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
行列のベクトル積の可視化
行列とベクトルの積の計算をグラフで確認します。
行列の作図については「【Python】行列の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt
行列とベクトルの積の作図
まずは、行列とベクトルの積の計算をヒートマップで可視化します。
行列とベクトルを指定して、積を計算します。
# 行列を指定 A = np.array( [[-3.0, -2.5, -2.0, -1.5], [-1.0, -0.5, 0.0, 0.5], [1.0, 1.5, 2.0, 2.5]] ) print(A) print(A.shape) # ベクトルを指定 x = np.array([0.0, 2.0, 4.0, 8.0]) print(x) print(x.shape) # 行列とベクトルの積を計算 y = np.dot(A, x) print(y) print(y.shape)
[[-3. -2.5 -2. -1.5]
[-1. -0.5 0. 0.5]
[ 1. 1.5 2. 2.5]]
(3, 4)
[0. 2. 4. 8.]
(4,)
[-25. 3. 31.]
(3,)
行列の行数とベクトルの次元数(要素数)が一致している必要があります。
グラデーションの配色用の最小値と最大値を設定します。
# 最小・最大値を設定 a_max = max(A.max(), abs(A.min())) a_max = 1.0 if a_max < 1.0 else a_max a_min = -a_max print(a_min) print(a_max) v_max = max( x.max(), (A*x).max(), y.max(), abs(x.min()), abs((A*x).min()), abs(y.min()) ) v_max = 1.0 if v_max < 1.0 else v_max v_min = -v_max print(v_min) print(v_max)
-3.0
3.0
-31.0
31.0
「行列の作図」のときと同様に、グラデーションの最小値と最大値を設定します。
行列とベクトルの積のヒートマップを作成します。
# 行・列数を取得 m, n = A.shape # 行列とベクトルの積のヒートマップを作図 fig, axes = plt.subplots(nrows=2, ncols=3, width_ratios=[1, n, n], height_ratios=[m, 1], figsize=((n+n+1)*1.5, (m+1)*1.5), facecolor='white') fig.suptitle('$y = A x$', fontsize=20) # 行列のヒートマップを作図 axes[0, 2].imshow(A, cmap='bwr', vmin=a_min, vmax=a_max) # ヒートマップ for i in range(m): for j in range(n): axes[0, 2].text(j, i, s=str(A[i, j]), size=15, ha='center', va='center') # 要素ラベル axes[0, 2].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[0, 2].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 2].set_xlabel('j') axes[0, 2].set_ylabel('i') axes[0, 2].set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') # 入力ベクトルのヒートマップを作図 axes[1, 2].imshow(x[np.newaxis, :], cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for j in range(n): axes[1, 2].text(j, 0, s=str(x[j]), size=15, ha='center', va='center') # 要素ラベル axes[1, 2].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[1, 2].set_yticks(ticks=[]) axes[1, 2].set_xlabel('j') axes[1, 2].set_title('$x = (x_1, \cdots, x_n)$', loc='left') # 行列とベクトルのアダマール積のヒートマップを作図 axes[0, 1].imshow(A*x, cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): for j in range(n): axes[0, 1].text(j, i, s=str(A[i, j]*x[j]), size=15, ha='center', va='center') # 要素ラベル axes[0, 1].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[0, 1].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 1].set_xlabel('j') axes[0, 1].set_ylabel('i') axes[0, 1].set_title('$(a_{11} x_1, \cdots, a_{mn} x_n)$', loc='left') # 出力ベクトルのヒートマップを作図 axes[0, 0].imshow(y[:, np.newaxis], cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): axes[0, 0].text(0, i, s=str(y[i]), size=15, ha='center', va='center') # 要素ラベル axes[0, 0].set_xticks(ticks=[]) axes[0, 0].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 0].set_ylabel('i') axes[0, 0].set_title('$y = (y_1, \cdots, y_m)$', loc='left') # 非表示 axes[1, 0].axis('off') axes[1, 1].axis('off') plt.show()
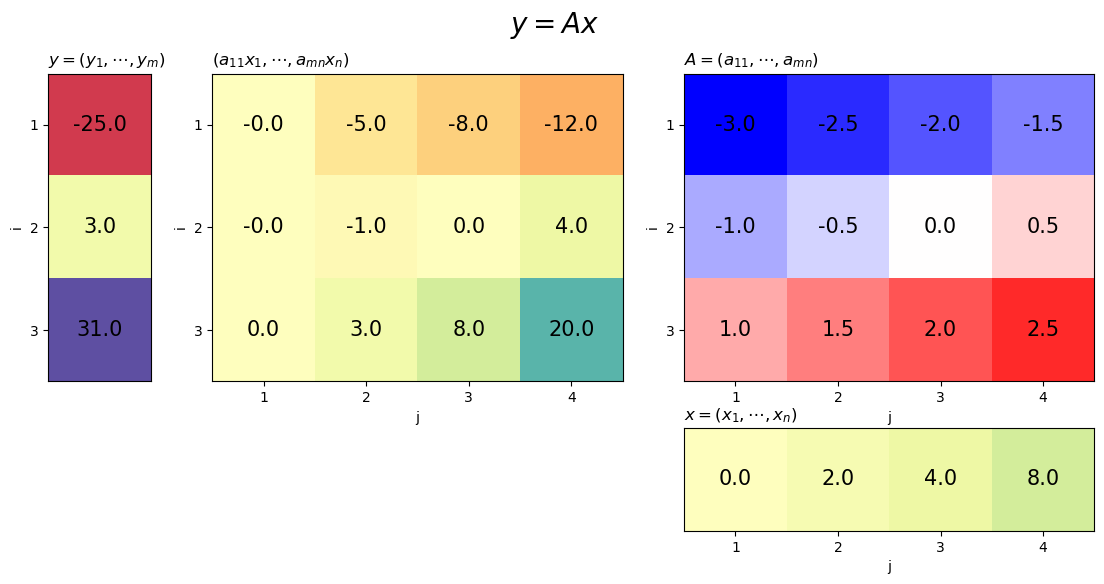
行列とベクトルのグラフを並べて描画します。それぞれ「行列の作図」のときと同様に作図します。
この例では、行列に注目するためカラーマップを変更しています(分かりにくければ普通に統一してください)。
各セルの座標と各要素のインデックスの対応関係を確認します。
・作図コード(クリックで展開)
# 行列とベクトルの積のインデックを作図 fig, axes = plt.subplots(nrows=2, ncols=3, width_ratios=[1, n, n], height_ratios=[m, 1], figsize=((n+n+1)*1.5, (m+1)*1.5), facecolor='white') fig.suptitle('$y = A x$', fontsize=20) # 行列のヒートマップを作図 axes[0, 2].imshow(A, cmap='bwr', vmin=a_min, vmax=a_max) # ヒートマップ for i in range(m): for j in range(n): axes[0, 2].text(j, i, s='$a_{'+str(i+1)+', '+str(j+1)+'}$', size=15, ha='center', va='center') # 要素ラベル axes[0, 2].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[0, 2].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 2].set_xlabel('j') axes[0, 2].set_ylabel('i') axes[0, 2].set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') # 入力ベクトルのヒートマップを作図 axes[1, 2].imshow(x[np.newaxis, :], cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for j in range(n): axes[1, 2].text(j, 0, s='$x_{'+str(j+1)+'}$', size=15, ha='center', va='center') # 要素ラベル axes[1, 2].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[1, 2].set_yticks(ticks=[]) axes[1, 2].set_xlabel('j') axes[1, 2].set_title('$x = (x_1, \cdots, x_n)$', loc='left') # 行列とベクトルのアダマール積のヒートマップを作図 axes[0, 1].imshow(A*x, cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): for j in range(n): axes[0, 1].text(j, i, s='$a_{'+str(i+1)+', '+str(j+1)+'} x_{'+str(j+1)+'}$', size=15, ha='center', va='center') # 要素ラベル axes[0, 1].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[0, 1].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 1].set_xlabel('j') axes[0, 1].set_ylabel('i') axes[0, 1].set_title('$(a_{11} x_1, \cdots, a_{mn} x_n)$', loc='left') # 出力ベクトルのヒートマップを作図 axes[0, 0].imshow(y[:, np.newaxis], cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): axes[0, 0].text(0, i, s='$y_{'+str(i+1)+'} = \sum_{j=1}^{'+str(n)+'} a_{'+str(i+1)+',j} x_j$', size=10, ha='center', va='center') # 要素ラベル axes[0, 0].set_xticks(ticks=[]) axes[0, 0].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 0].set_ylabel('i') axes[0, 0].set_title('$y = (y_1, \cdots, y_m)$', loc='left') # 非表示 axes[1, 0].axis('off') axes[1, 1].axis('off') plt.show()
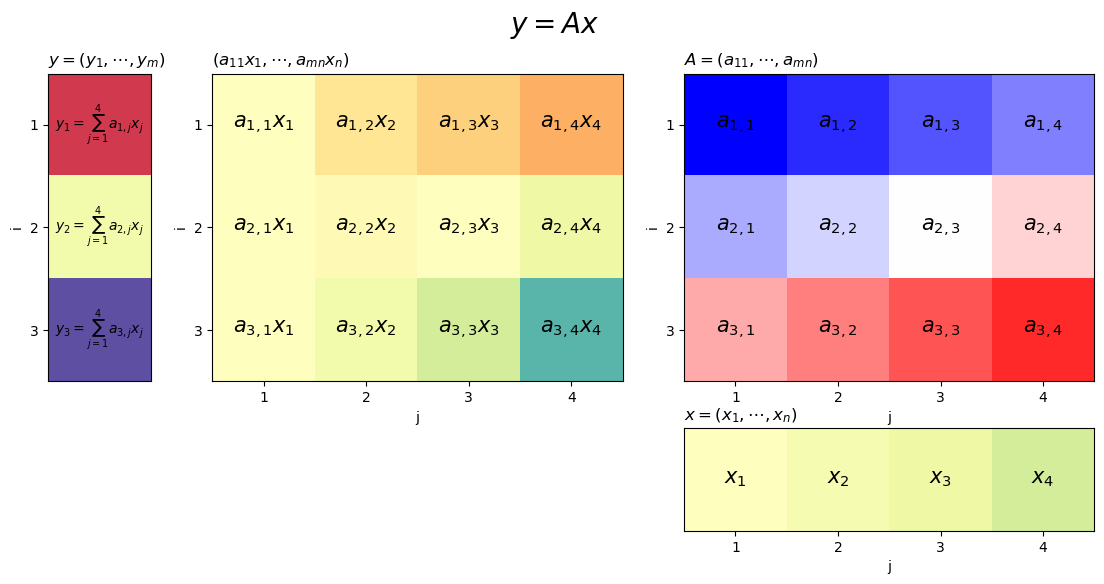
右上の図は 行列のヒートマップ、右下の図は
次元ベクトル(入力ベクトル)のヒートマップです。真ん中の図は、行列の行ごとに入力ベクトルを掛けたヒートマップです。左の図は
次元ベクトル(出力ベクトル)であり、真ん中のグラフを行ごとに和をとったヒートマップです。
行列と
次元ベクトル(
行列)の積は
次元ベクトル(
行列)になります。
行列とベクトルの積の例
次は、行列とベクトルの積を用いた計算例を確認します。
(色々と面倒なので)行列とベクトルの積のヒートマップの作成処理を関数として作成しておきます。
・作図コード(クリックで展開)
# 行列とベクトルの積の作図処理を定義 def plot_matvec_prod(A, x, target=None, scale=1.5, title='matrix-vector product'): # 行列とベクトルの積を計算 y = np.dot(A, x) # 行・列数を取得 m, n = A.shape # カラーマップを設定 if target == 'matrix': cmap_mat, cmap_vec = 'bwr', 'Spectral' a_max = max(A.max(), abs(A.min())) a_max = 1.0 if a_max < 1.0 else a_max a_min = -a_max v_max = max( x.max(), (A*x).max(), y.max(), abs(x.min()), abs((A*x).min()), abs(y.min()) ) v_max = 1.0 if v_max < 1.0 else v_max v_min = -v_max x_min, x_max = v_min, v_max elif target == 'vector': cmap_mat, cmap_vec = 'Spectral', 'bwr' x_max = max(x.max(), abs(x.min())) x_max = 1.0 if x_max < 1.0 else x_max x_min = -x_max v_max = max( A.max(), (A*x).max(), y.max(), abs(A.min()), abs((A*x).min()), abs(y.min()) ) v_max = 1.0 if v_max < 1.0 else v_max v_min = -v_max a_min, a_max = v_min, v_max else: cmap_mat, cmap_vec = 'Spectral', 'Spectral' # 最小・最大値の絶対値を1に再設定 v_max = max( A.max(), x.max(), (A*x).max(), y.max(), abs(A.min()), abs(x.min()), abs((A*x).min()), abs(y.min()) ) v_max = 1.0 if v_max < 1.0 else v_max v_min = -v_max a_min, a_max = v_min, v_max x_min, x_max = v_min, v_max # 行列とベクトルの計算を作図 fig, axes = plt.subplots(nrows=2, ncols=3, width_ratios=[1, n, n], height_ratios=[m, 1], figsize=((n+n+1)*scale, (m+1)*scale), facecolor='white') fig.suptitle(title, fontsize=20) # 行列のヒートマップを作図 axes[0, 2].imshow(A, cmap=cmap_mat, vmin=a_min, vmax=a_max) # ヒートマップ for i in range(m): for j in range(n): axes[0, 2].text(j, i, s=str(A[i, j]), size=15, ha='center', va='center') # 要素ラベル axes[0, 2].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[0, 2].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 2].set_xlabel('j') axes[0, 2].set_ylabel('i') axes[0, 2].set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') # 入力ベクトルのヒートマップを作図 axes[1, 2].imshow(x[np.newaxis, :], cmap=cmap_vec, vmin=x_min, vmax=x_max) # ヒートマップ for j in range(n): axes[1, 2].text(j, 0, s=str(x[j]), size=15, ha='center', va='center') # 要素ラベル axes[1, 2].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[1, 2].set_yticks(ticks=[]) axes[1, 2].set_xlabel('j') axes[1, 2].set_title('$x = (x_1, \cdots, x_n)$', loc='left') # 行列とベクトルのアダマール積のヒートマップを作図 axes[0, 1].imshow(A*x, cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): for j in range(n): axes[0, 1].text(j, i, s=str(A[i, j]*x[j]), size=15, ha='center', va='center') # 要素ラベル axes[0, 1].set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) axes[0, 1].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 1].set_xlabel('j') axes[0, 1].set_ylabel('i') axes[0, 1].set_title('$(a_{11} x_1, \cdots, a_{mn} x_n)$', loc='left') # 出力ベクトルのヒートマップを作図 axes[0, 0].imshow(y[:, np.newaxis], cmap='Spectral', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): axes[0, 0].text(0, i, s=str(y[i]), size=15, ha='center', va='center') # 要素ラベル axes[0, 0].set_xticks(ticks=[]) axes[0, 0].set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) axes[0, 0].set_ylabel('i') axes[0, 0].set_title('$y = (y_1, \cdots, y_m)$', loc='left') # 非表示 axes[1, 0].axis('off') axes[1, 1].axis('off') plt.show()
必要に応じて、引数で設定できるようにします。
ゼロベクトルを作成して、行列とベクトルの積のヒートマップを作成します。
# 行列を指定 A = np.array( [[-3.0, -2.5, -2.0, -1.5], [-1.0, -0.5, 0.0, 0.5], [1.0, 1.5, 2.0, 2.5]] ) # 次元数を取得 n = A.shape[1] # 0ベクトルを作成 o = np.zeros(n) # ヒートマップを作図 plot_matvec_prod(A, o, target='vector', title='matrix-zero vector product')
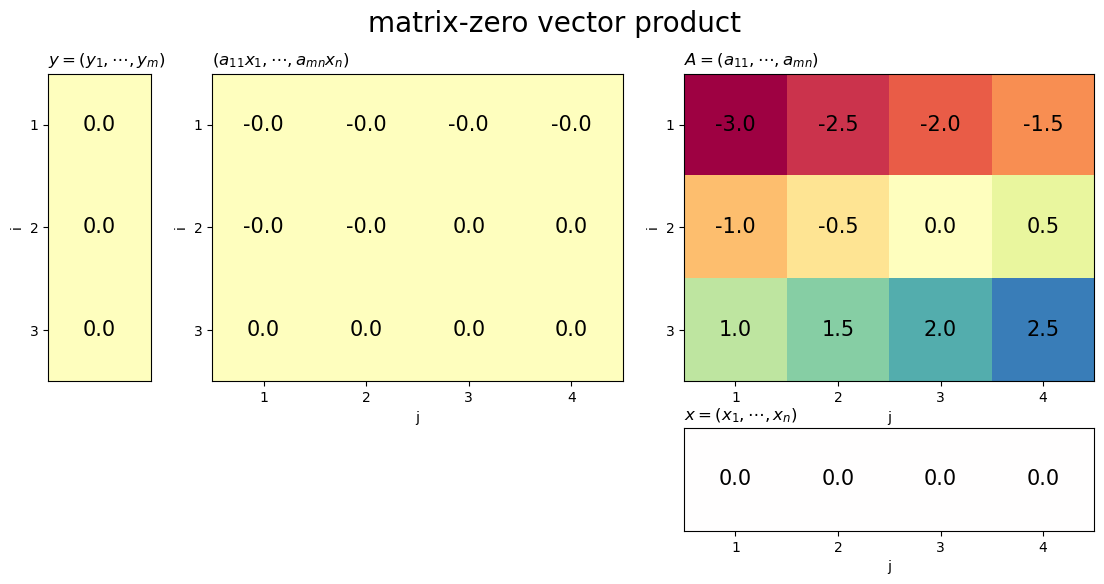
ゼロベクトルとの積は、ゼロベクトルになります。
ゼロ行列を作成して、行列とベクトルの積のヒートマップを作成します。
# ベクトルを指定 x = np.array([-2.0, 0.0, 2.0, 4.0, 8.0]) # 行数を指定 m = 5 # 列数を取得 n = len(x) # 0行列を作成 O = np.zeros((m, n)) # ヒートマップを作図 plot_matvec_prod(O, x, target='matrix', title='zero matrix-vector product')
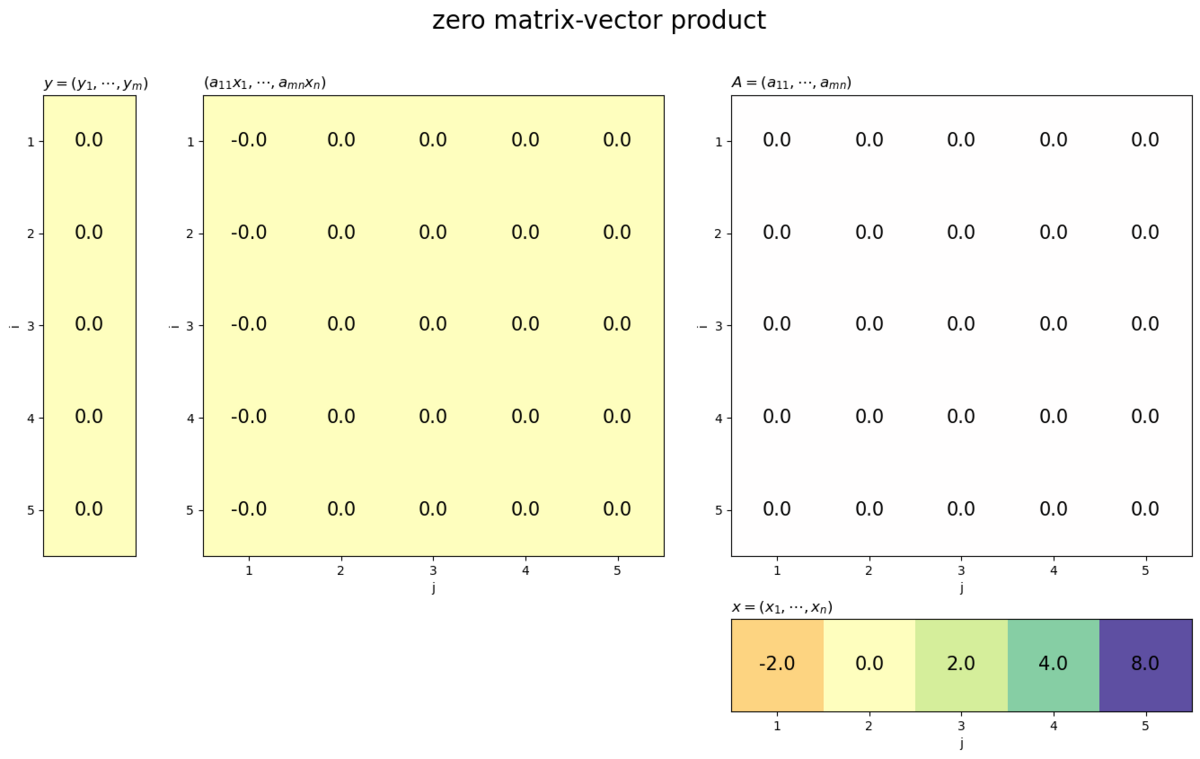
ゼロ行列との積は、ゼロベクトルになります。
列インデックスを指定し、標準単位ベクトルを作成して、行列とベクトルの積のヒートマップを作成します。
# 行列を指定 A = np.array( [[-3.0, -2.5, -2.0, -1.5], [-1.0, -0.5, 0.0, 0.5], [1.0, 1.5, 2.0, 2.5]] ) # 列インデックスを指定 j = 1 # 次元数を取得 n = A.shape[1] # 標準単位ベクトルを作成 e_j = np.zeros(n) e_j[j] = 1.0 # ヒートマップを作図 plot_matvec_prod(A, e_j, target='vector', title='matrix-standard unit vector product')
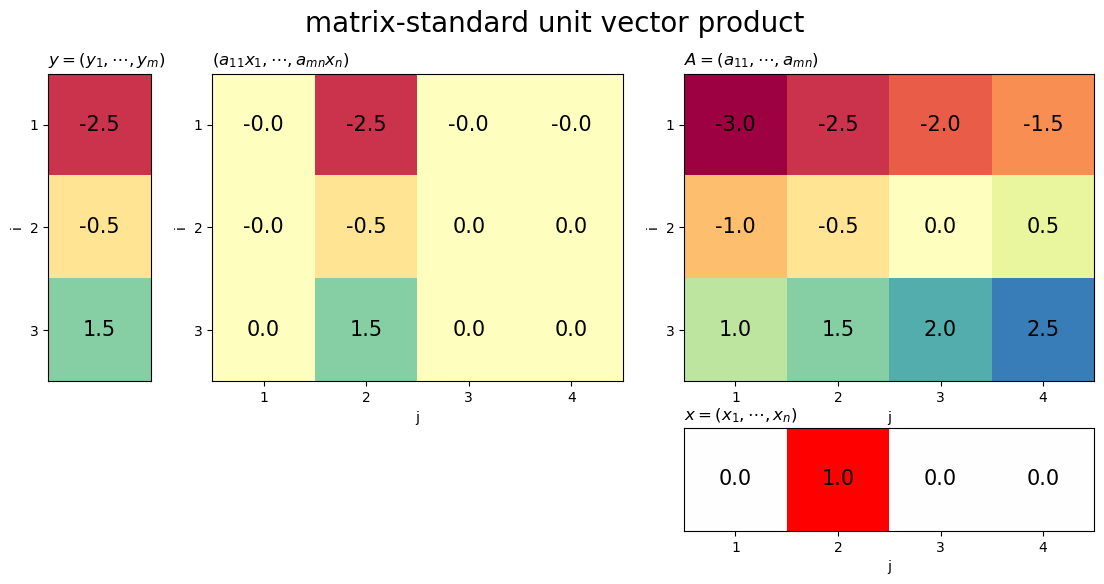
標準単位ベクトルとの積は、行列の対応する列ベクトルが取り出されます。
ベクトルを指定し、単位行列を作成して、行列とベクトルの積のヒートマップを作成します。
# ベクトルを指定 x = np.array([-2.0, 0.0, 2.0, 4.0, 8.0]) # 行(列)数を取得 n = len(x) # 単位行列を作成 I = np.identity(n) # ヒートマップを作図 plot_matvec_prod(I, x, target='matrix', title='unit matrix-vector product')
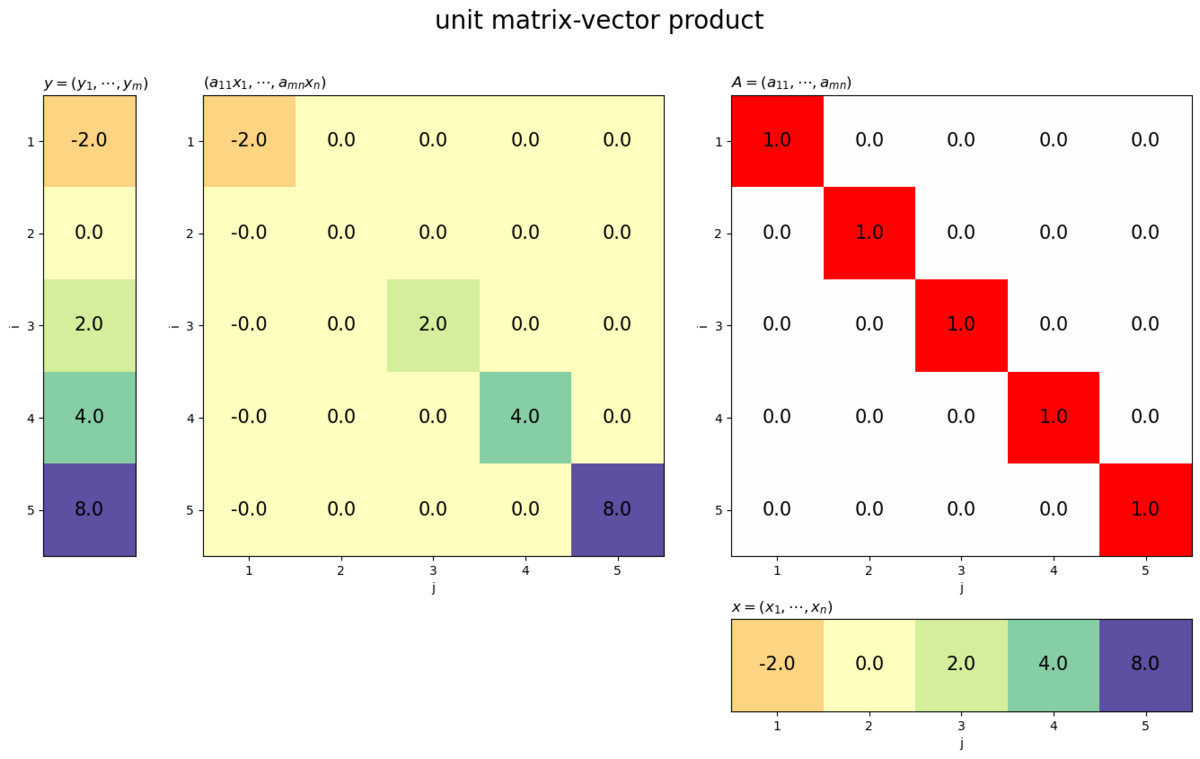
単位行列との積は、ベクトルが変化しません。
対角要素を指定し、対角行列を作成して、行列とベクトルの積のヒートマップを作成します。
# ベクトルを指定 x = np.array([0.0, 1.0, 2.0, 3.0, 4.0]) # 対角要素を指定 a = np.array([-2.0, -1.0, 0.0, 1.0, 2.0]) # 対角行列を作成 A = np.diag(a) # ヒートマップを作図 plot_matvec_prod(A, x, target='matrix', title='diagonal matrix-vector product')
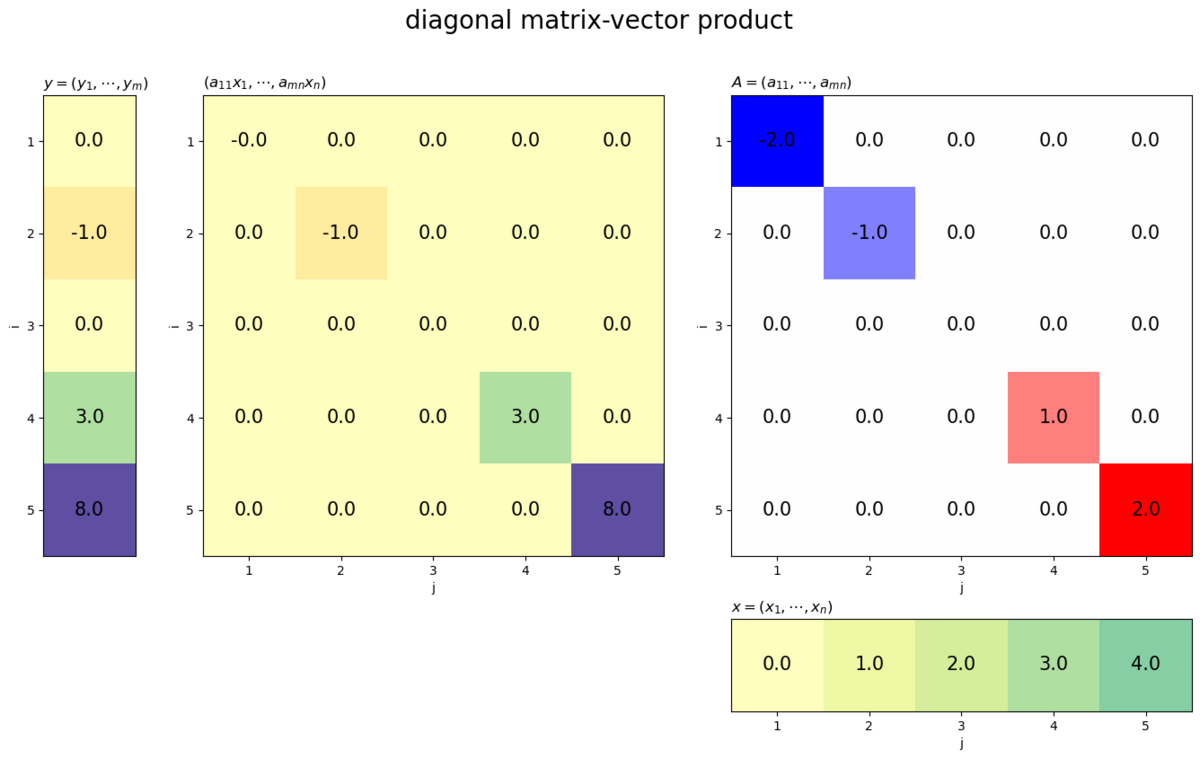
対角行列との積は、ベクトルの各要素が対応する対角要素倍されます。
イチベクトルを作成して、行列とベクトルの積のヒートマップを作成します。
# 行列を指定 A = np.array( [[-3.0, -2.5, -2.0, -1.5], [-1.0, -0.5, 0.0, 0.5], [1.0, 1.5, 2.0, 2.5]] ) # 列数を取得 n = A.shape[1] # 1ベクトルを作成 c = np.ones(n) # ヒートマップを作図 plot_matvec_prod(A, c, target='vector', title='matrix-one vector product')
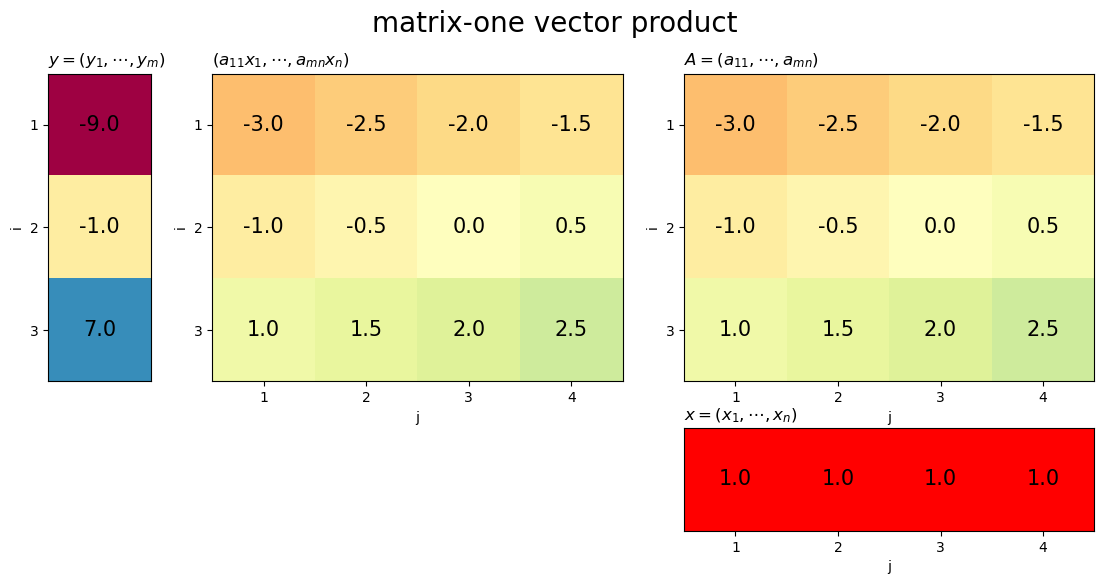
イチベクトルとの積は、行列の行ごとの総和になります。
イチ行列を作成して、行列とベクトルの積のヒートマップを作成します。
# ベクトルを指定 x = np.array([-2.0, 0.0, 2.0, 4.0, 8.0]) # 行数を指定 m = 5 # 列数を取得 n = len(x) # 1行列を作成 C = np.ones((m, n)) # ヒートマップを作図 plot_matvec_prod(C, x, target='matrix', title='one matrix-vector product')
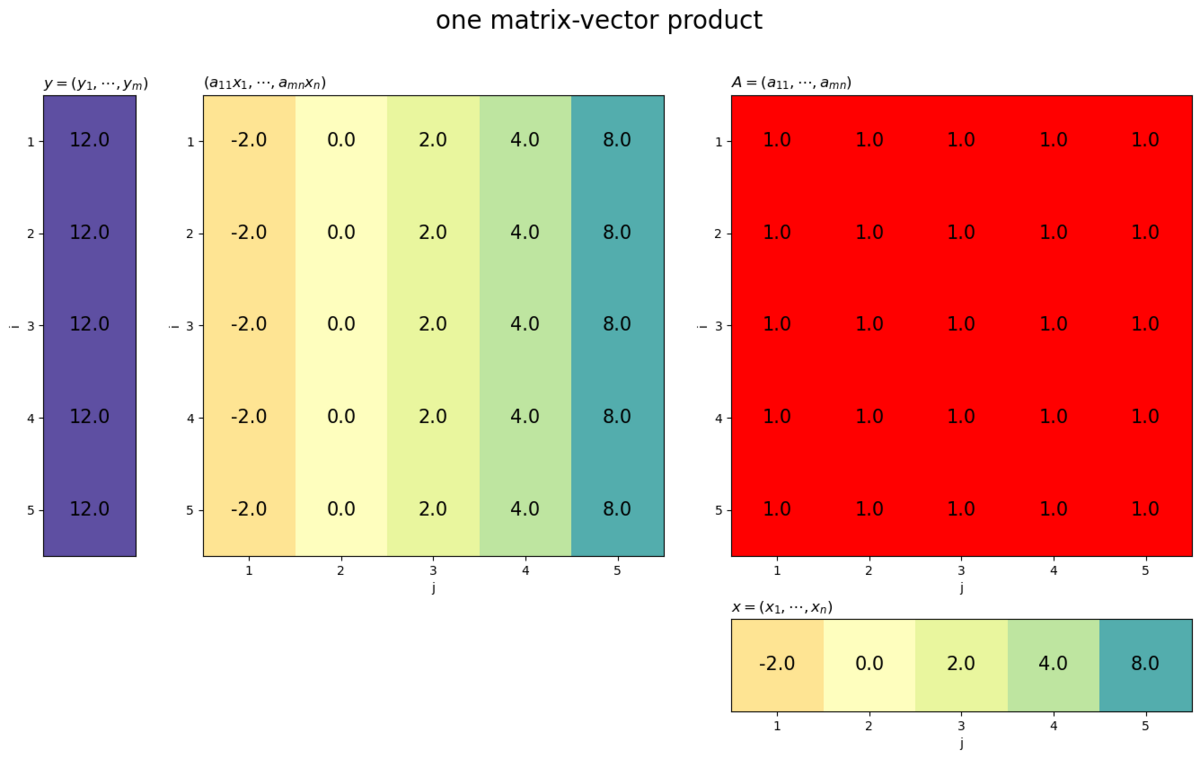
イチ行列との積は、ベクトルの総和が複製されます。
差分行列を作成して、行列とベクトルの積のヒートマップを作成します。
# ベクトルを指定 x = np.array([-2.0, 1.0, 0.5, 4.0, 2.0]) # 列数を取得 n = len(x) # 差分行列を作成 D = np.array( [[-1.0 if i == j else 1.0 if i+1 == j else 0.0 for j in range(n)] for i in range(n-1)] ) # ヒートマップを作図 plot_matvec_prod(D, x, target='matrix', title='difference matrix-vector product')
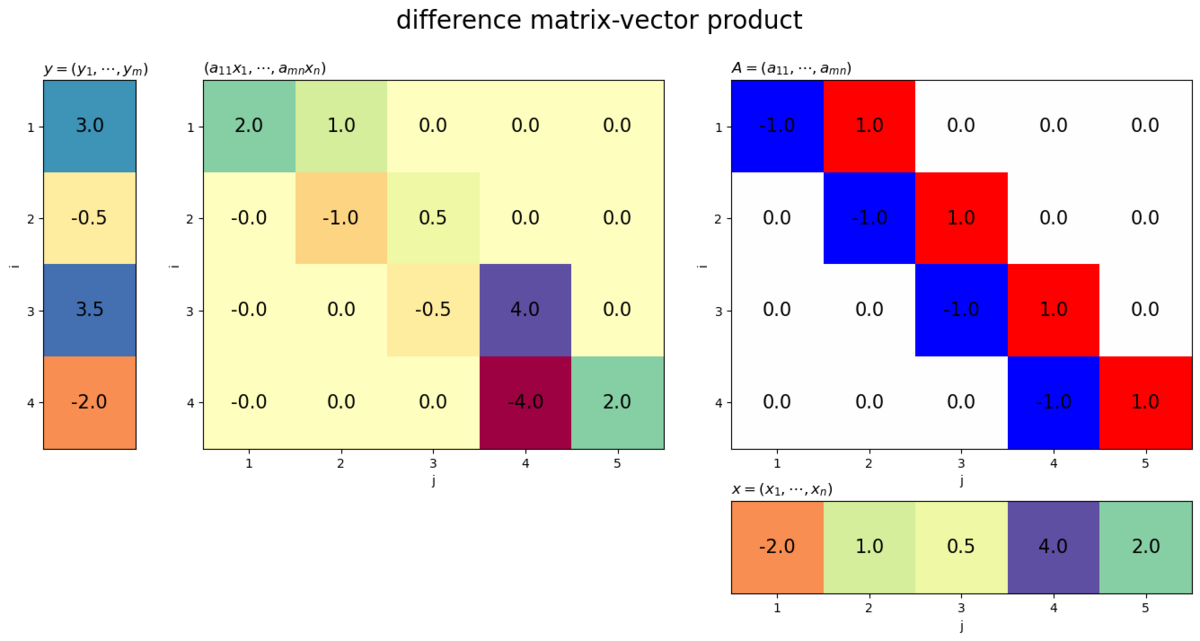
差分行列との積は、ベクトルの隣り合う要素の差になります。
累積和行列を作成して、行列とベクトルの積のヒートマップを作成します。
# ベクトルを指定 x = np.array([-3.0, 1.0, 2.0, 4.0, 8.0]) # 行(列)数を取得 n = len(x) # 累積和行列を作成 S = np.array( [[np.float32(i >= j) for j in range(n)] for i in range(n)] ) # ヒートマップを作図 plot_matvec_prod(S, x, target='matrix', title='running sum matrix-vector product')
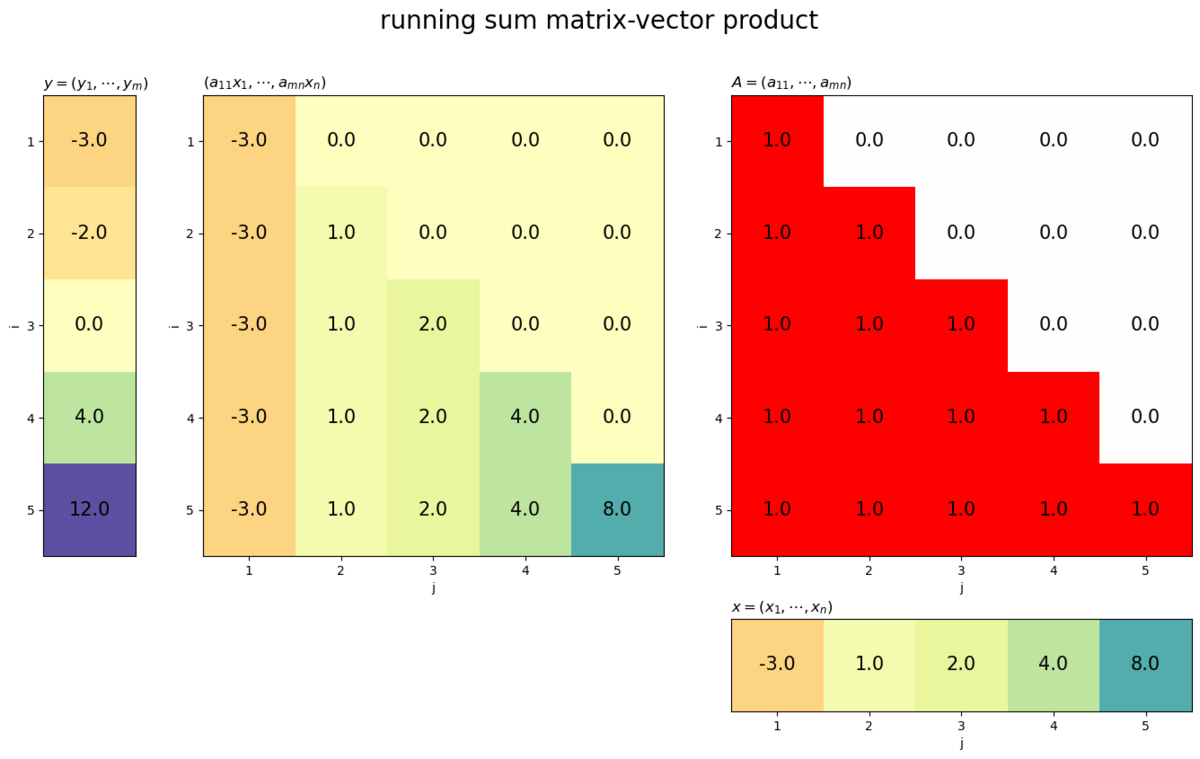
累積和行列との積は、ベクトルの累積和になります。
この記事では、行列とベクトルの積をグラフで確認しました。また、この章では、行列の基本的な計算を確認しました。次章では、より応用的な計算を確認します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
行列計算の可視化にn回目の挑戦です。前回(ゼロつく1巻の3週目のとき)よりも上手くできた気がしますが、分かりやすいって何だろう、とても難しいです。
細かいところで言うと、出力ベクトルを左右のどちらに配置するか悩みました。今回は数式にあわせて左に置きました。あと、真ん中の図の意図を汲み取りづらい気がします。
Djangoで簡単なwebアプリ?にして、数値を自由に弄れるようにしたら分かりやすくなる気がします。やってみたいとはずっと思ってはいるのですが、手が足りない。
【次の内容】