はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は7.1節「幾何変換」の内容です。
ベクトルの回転の計算を確認して、グラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
ベクトルの回転の可視化
行列計算によるベクトルの回転(vector rotation)を数式とグラフで確認します。
行列とベクトルの積については「【Python】行列のベクトル積の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
ベクトルの回転の計算式
まずは、ベクトルの回転を数式で確認します。
行列
を用いて、2次元ベクトル を変換します。
も2次元ベクトルになります。
ベクトルの回転の作図
次は、ベクトルの回転をグラフで確認します。
角度を指定して、回転用の行列を作成します。
# 角度(ラジアン)を指定 theta = 4.0/6.0 * np.pi print(theta) # 弧度法の角度 print(theta * 180.0/np.pi) # 度数法の角度 # 回転行列を作成 A = np.array( [[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]] ) print(A) print(A.shape)
2.0943951023931953
119.99999999999999
[[-0.5 -0.8660254]
[ 0.8660254 -0.5 ]]
(2, 2)
回転する角度(ラジアン) をスカラ
theta として値を指定します。
回転行列 を2次元配列
A として計算します。
ベクトルを指定して、行列との積により変換します。
# ベクトルを指定 x = np.array([3.0, 2.0]) print(x) print(x.shape) # ベクトルを変換 y = np.dot(A, x) print(y) print(y.shape)
[3. 2.]
(2,)
[-3.23205081 1.59807621]
(2,)
入力ベクトル を1次元配列
x として値を指定します。
回転ベクトル(出力ベクトル) を計算して
y とします。
・装飾用の作図コード(クリックで展開)
なす角を示す角度マークと角度ラベルを描画するための座標を作成します。
# 入力ベクトルとx軸のなす角を計算 sgn_x = 1.0 if x[1] >= 0.0 else -1.0 theta_x = sgn_x * np.arccos(x[0] / np.linalg.norm(x)) # 角度マーク用のラジアンを作成 angle_rad_vals = np.linspace(start=theta_x, stop=theta_x+theta, num=100) # 角度マークの座標を計算 r = 0.3 angle_mark_arr = np.array( [r * np.cos(angle_rad_vals), r * np.sin(angle_rad_vals)] ) print(angle_mark_arr[:, :5]) # 角度ラベルの座標を計算 r = 0.45 angle_label_vec = np.array( [r * np.cos(np.median(angle_rad_vals)), r * np.sin(np.median(angle_rad_vals))] ) print(angle_label_vec)
[[0.24961509 0.24603901 0.24235281 0.23855815 0.23465673]
[0.16641006 0.17165316 0.17681944 0.18190659 0.18691233]]
[-0.02896169 0.44906706]
x軸線の正の部分(原点と点 を結ぶ線分)とベクトル
のなす角
theta_x を計算します。
ベクトル から中心角が
の円弧の座標を計算します。円弧の中点にラベルを配置します。
詳しくは「【Python】円周上の点とx軸を結ぶ円弧を作図したい - からっぽのしょこ」を参照してください。
ベクトル のグラフを作成します。
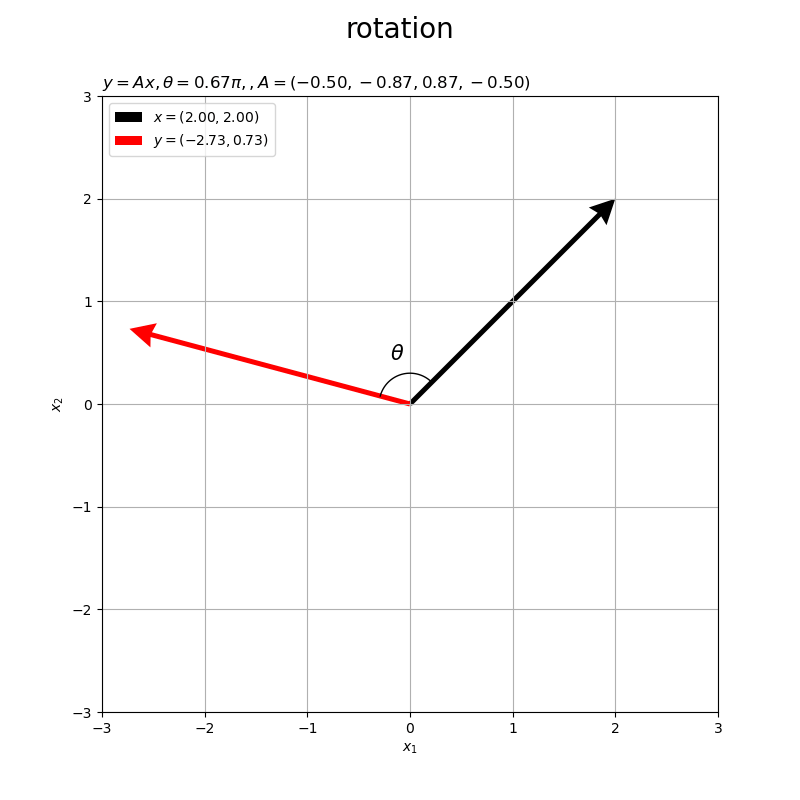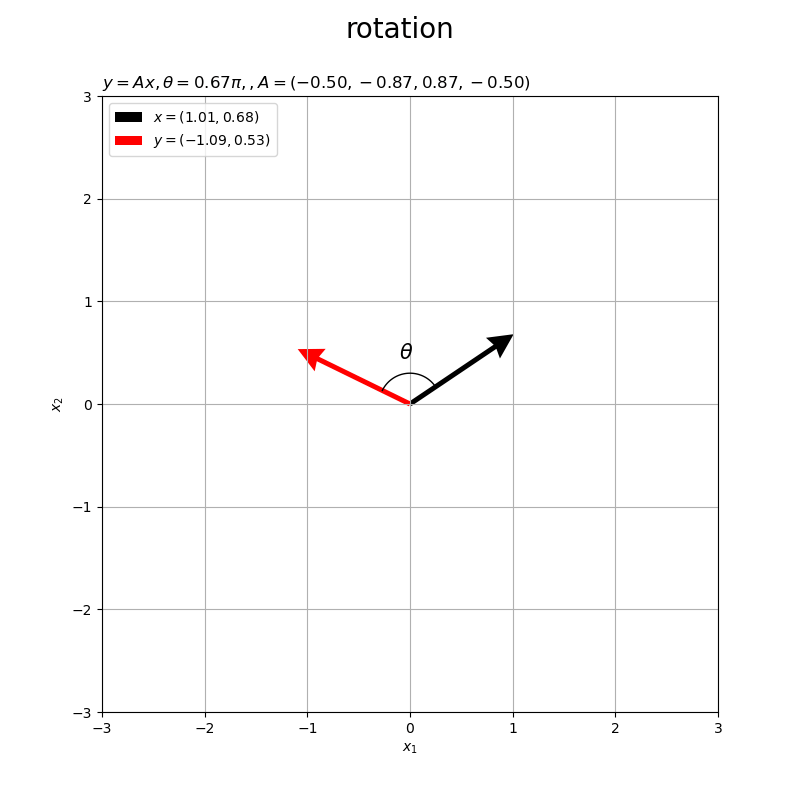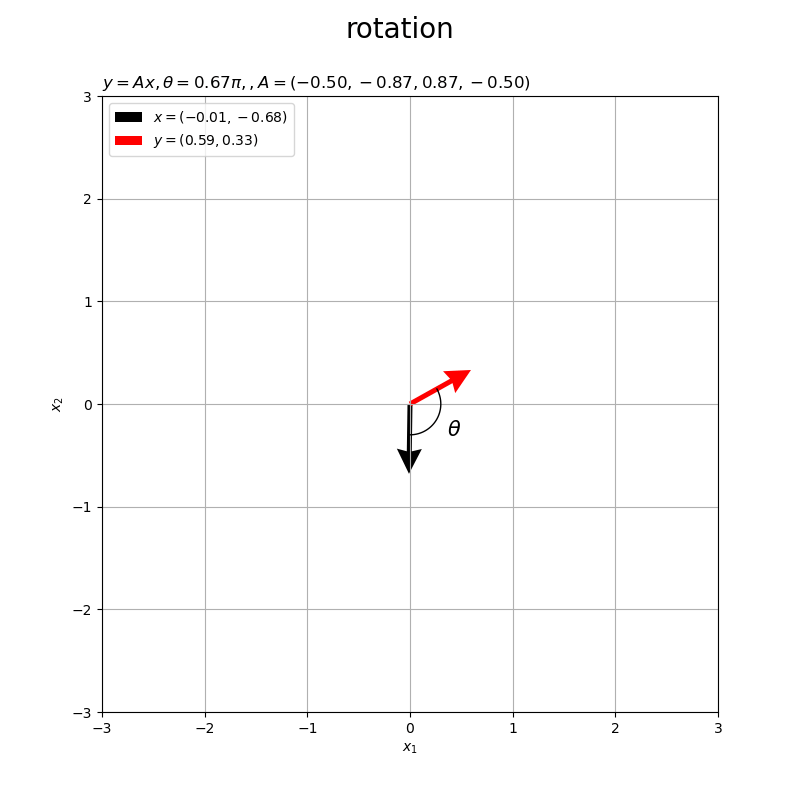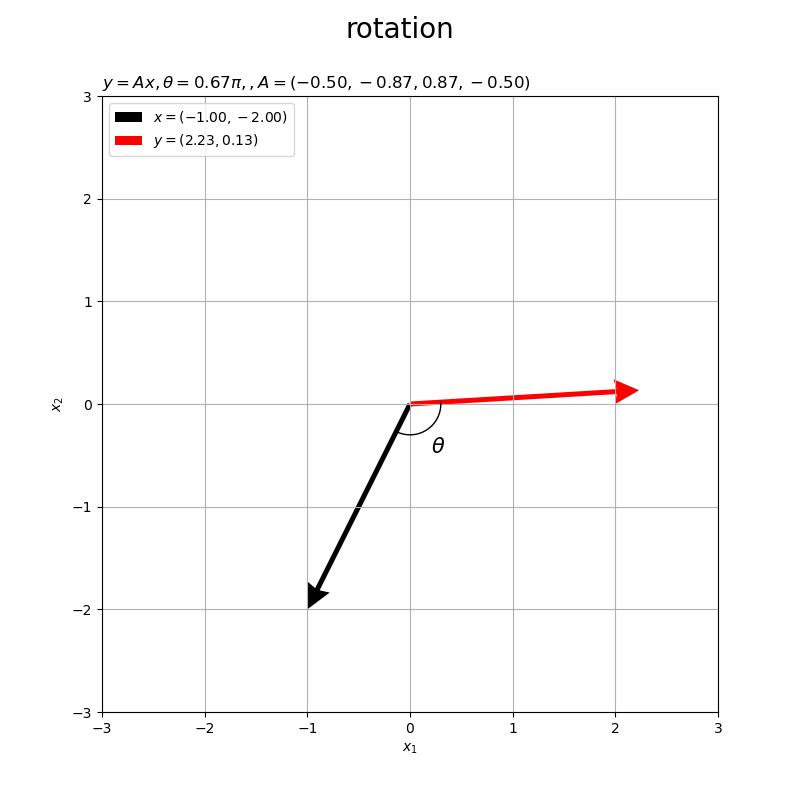
# グラフサイズ用の値を設定 x1_min = np.floor(np.min([0.0, x[0], y[0]])) - 1 x1_max = np.ceil(np.max([0.0, x[0], y[0]])) + 1 x2_min = np.floor(np.min([0.0, x[1], y[1]])) - 1 x2_max = np.ceil(np.max([0.0, x[1], y[1]])) + 1 # 2D回転ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.quiver(0, 0, *x, color='black', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$x=({}, {})'.format(*x)+'$') # 入力ベクトル ax.quiver(0, 0, *y, color='red', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$y=({:.2f}, {:.2f})'.format(*y)+'$') # 出力ベクトル ax.plot(*angle_mark_arr, color='black', linewidth=1) # なす角マーク ax.text(*angle_label_vec, s='$\\theta$', size=15, ha='center', va='center') # なす角ラベル ax.set_xticks(ticks=np.arange(x1_min, x1_max+1)) ax.set_yticks(ticks=np.arange(x2_min, x2_max+1)) ax.set_xlim(left=x1_min, right=x1_max) ax.set_ylim(bottom=x2_min, top=x2_max) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$y = A x, ' + '\\theta = {:.2f} \pi'.format(theta/np.pi)+', ' + 'A = ('+', '.join(['{:.2f}'.format(a) for a in A.flatten()])+')$', loc='left') fig.suptitle('rotation', fontsize=20) ax.grid() ax.legend() ax.set_aspect('equal') plt.show()
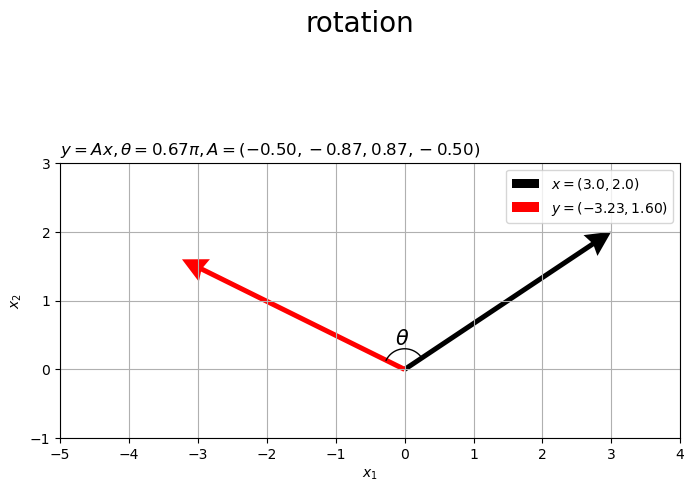
入力ベクトル を黒色の矢印、出力ベクトルを
を赤色の矢印で示します。
行列 によって変換したベクトル
が、ベクトル
を左回りに
回転したベクトルなのが分かります。
回転角度または入力ベクトルを変化させたアニメーションで確認します。
・作図コード(クリックで展開)
フレーム数を指定して、変化する角度と固定する入力ベクトルを作成します。
# フレーム数を指定 frame_num = 180 # 角度(ラジアン)の範囲を指定 theta_n = np.linspace(start=-2.0*np.pi, stop=2.0*np.pi, num=frame_num+1)[:frame_num] print(theta_n[:5]) # ベクトルを指定 x = np.array([3.0, 2.0])
[-6.28318531 -6.21337214 -6.14355897 -6.0737458 -6.00393263]
フレーム数を frame_num として整数を指定します。
ラジアンの範囲を指定して、frame_num 個のラジアン theta_n を作成します。入力ベクトル x は先ほどと同様に指定します。
範囲を にして
frame_num + 1 個の等間隔の値を作成して最後の値を除くと、最後のフレームと最初のフレームがスムーズに繋がります。
または、固定する角度と変化する入力ベクトルを作成します。
# フレーム数を指定 #frame_num = 90 # 角度(ラジアン)を指定 theta = 4.0/6.0 * np.pi # ベクトルとして用いる値を指定 r = 3.0 rad_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] x_n = np.array( [r * np.cos(rad_n), r * np.sin(rad_n)] ).T #x_n = np.array( # [np.linspace(start=2.0, stop=-1.0, num=frame_num), # np.linspace(start=2.0, stop=-2.0, num=frame_num)] #).T print(x_n[:5])
[[3. 0. ]
[2.99269215 0.20926942]
[2.97080421 0.4175193 ]
[2.9344428 0.62373507]
[2.88378509 0.82691207]]
frame_num 個の入力ベクトル x_nを作成します。ラジアン theta は先ほどと同様に指定します。
この例では、入力ベクトル(の先端)が原点からの半径が r の円周上を移動するように設定しています。
角度と入力ベクトルの両方を変化させることもできます。
アニメーションを作成します。
# グラフサイズを設定 axis_size = np.ceil(abs(x).max()) + 1 #axis_size = np.ceil(abs(x_n).max()) + 1 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white') fig.suptitle('rotation', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の値を作成 theta = theta_n[i] #x = x_n[i] # 回転行列を計算 A = np.array( [[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]] ) # ベクトルを変換 y = np.dot(A, x) # 角度マーク用のラジアンを作成 sgn_x = 1.0 if x[1] >= 0.0 else -1.0 theta_x = sgn_x * np.arccos(x[0] / np.linalg.norm(x)) angle_rad_vals = np.linspace(start=theta_x, stop=theta_x+theta, num=100) # 角度マークの座標を計算 r = 0.3 angle_mark_arr = np.array( [r * np.cos(angle_rad_vals), r * np.sin(angle_rad_vals)] ) # 角度ラベルの座標を計算 r = 0.5 angle_label_vec = np.array( [r * np.cos(np.median(angle_rad_vals)), r * np.sin(np.median(angle_rad_vals))] ) # 2D回転ベクトルを作図 ax.quiver(0, 0, *x, color='black', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$x=({: .2f}, {: .2f})'.format(*x)+'$') # 入力ベクトル ax.quiver(0, 0, *y, color='red', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$y=({: .2f}, {: .2f})'.format(*y)+'$') # 出力ベクトル ax.plot(*angle_mark_arr, color='black', linewidth=1) # なす角マーク ax.text(*angle_label_vec, s='$\\theta$', size=15, ha='center', va='center') # なす角ラベル ax.set_xticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_yticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$y = A x, ' + '\\theta = {: .2f} \pi, '.format(theta/np.pi)+', ' + 'A = ('+', '.join(['{: .2f}'.format(a) for a in A.flatten()])+')$', loc='left') ax.grid() ax.legend(loc='upper left') ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('rotation.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。

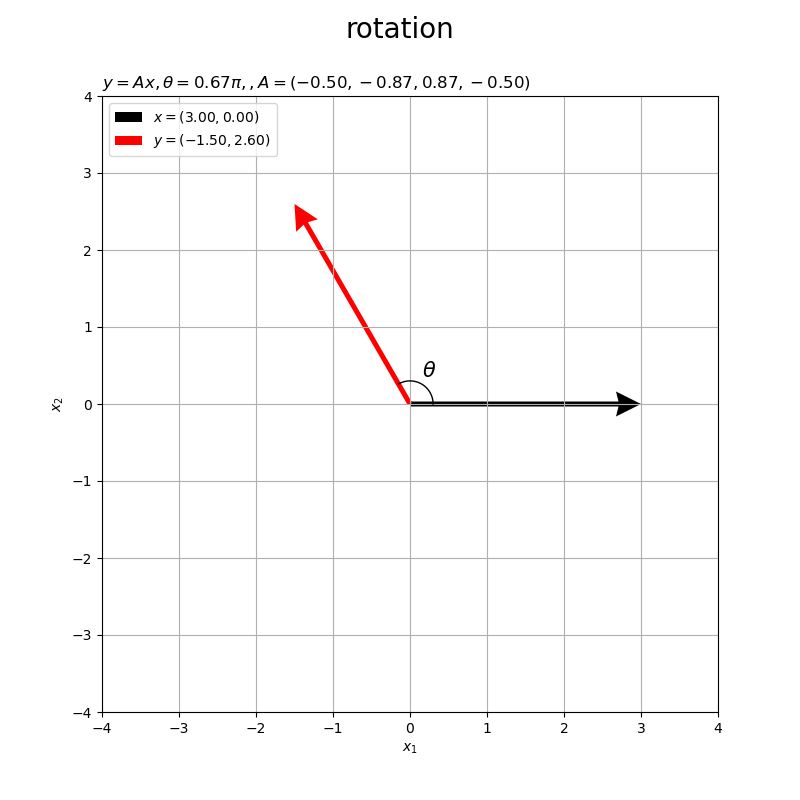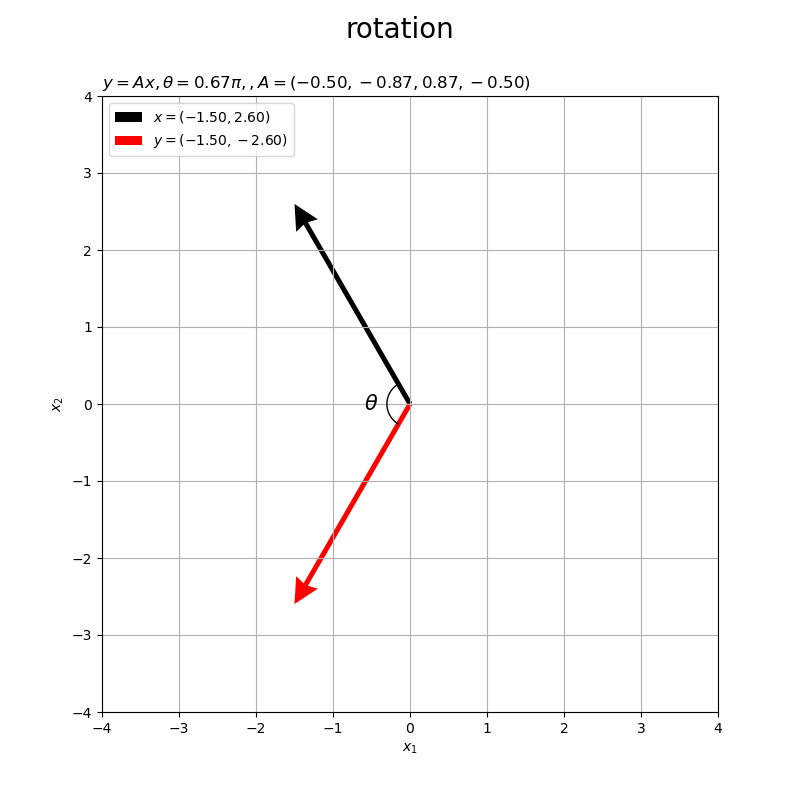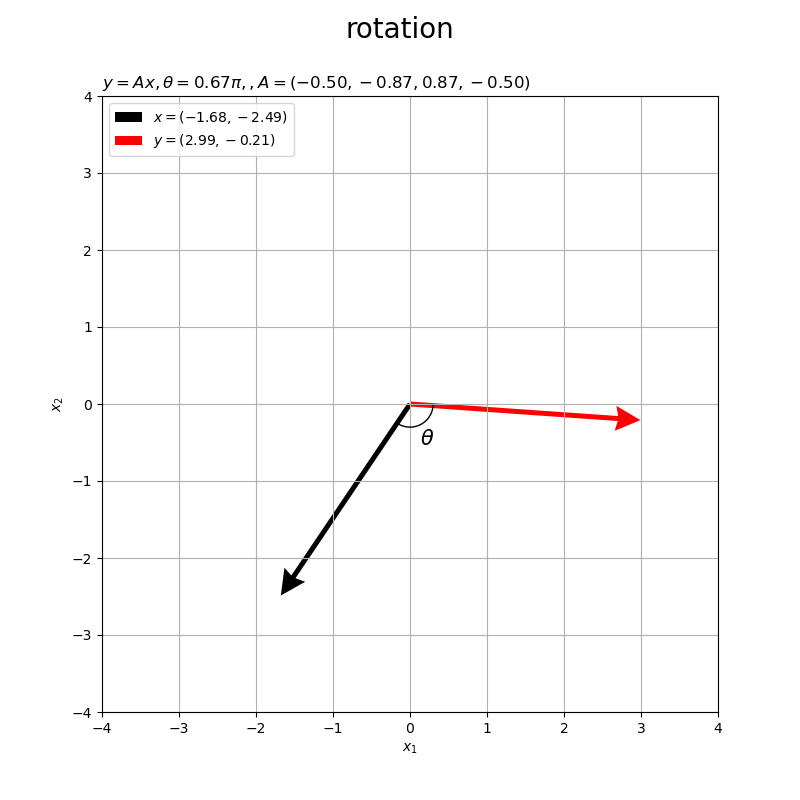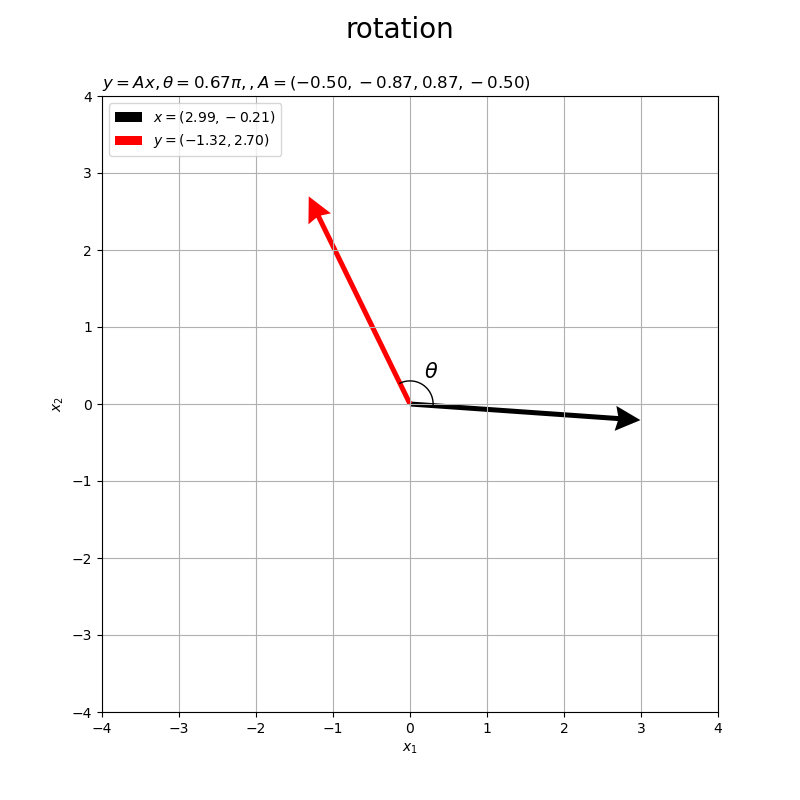
角度が負の値 だと右回りに回転します。
この記事では、ベクトルの回転を確認しました。次の記事では、ベクトルの射影を確認します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
線形代数をやってるはずなのにいつも三角関数になってしまう。
【次の内容】