はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は6.1節「行列」から6.3節「転置, 和, ノルム」の内容です。
Pythonを使って行列の例のグラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
行列の可視化
行列の例をグラフで確認します。
行列の定義については「【Python】6.1-3:行列の定義と性質【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」「6.4:行列のベクトル積の計算例の導出【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt
行列の作図
まずは、行列をヒートマップで可視化します。
行列を指定します。
# 行列を指定 A = np.array( [[-5.0, -4.0, -3.0, -2.0], [-1.0, 0.0, 1.0, 2.0], [3.0, 4.0, 5.0, 6.0]] ) print(A) print(A.shape)
[[-5. -4. -3. -2.]
[-1. 0. 1. 2.]
[ 3. 4. 5. 6.]]
(3, 4)
2次元配列に値を指定します。
行列のヒートマップを作成します。
# 行・列数を取得 m, n = A.shape # 行列のヒートマップを作図 fig, ax = plt.subplots(figsize=(n*1.5, m*1.5), facecolor='white') ax.imshow(A) # ヒートマップ for i in range(m): for j in range(n): ax.text(j, i, s=str(A[i, j]), size=15, ha='center', va='center') # 要素ラベル ax.set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) ax.set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) ax.set_xlabel('j') ax.set_ylabel('i') ax.set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') fig.suptitle('matrix', fontsize=20) plt.show()
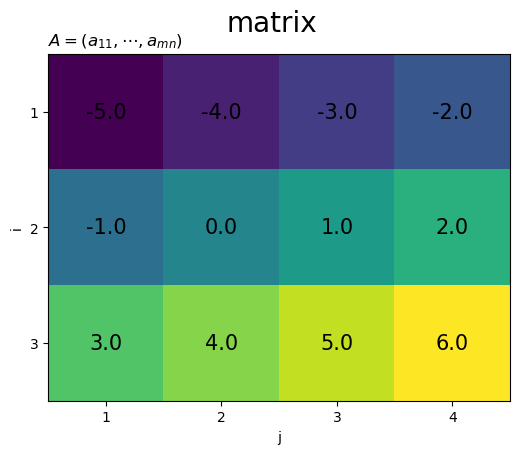
Axes.imshow() でヒートマップ、Axes.text() で各要素の値をラベルとして描画します。
Axes.set_*ticks() で軸目盛ラベルを設定します。各セルの座標は0から割り当てられ、数式上の各要素のインデックスは1からなので、0 から m, n までの整数の位置に 1 から m+1, n+1 の整数を表示して対応します。
各セルの座標と各要素のインデックスの対応関係を確認します。
・作図コード(クリックで展開)
# 行列のインデックスを作図 fig, ax = plt.subplots(figsize=(n*1.5, m*1.5), facecolor='white') ax.imshow(A) # ヒートマップ for i in range(m): for j in range(n): ax.text(j, i, s='$a_{'+str(i+1)+', '+str(j+1)+'}$', size=15, ha='center', va='center') # 要素ラベル ax.set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) ax.set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) ax.set_xlabel('j') ax.set_ylabel('i') ax.set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') fig.suptitle('matrix', fontsize=20) plt.show()
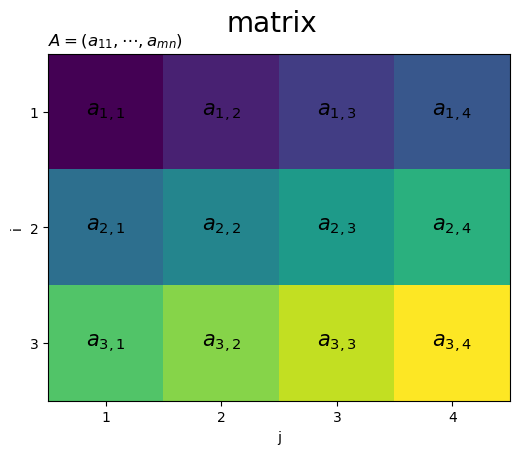
行列のヒートマップを描画できました。
値の正負で色分けすることを考えます。
グラデーションの配色用の最小値と最大値を設定します。
# 最小・最大値を設定 v_max = max(A.max(), abs(A.min())) v_min = -v_max # 最小・最大値の絶対値を1に再設定 v_max = 1.0 if v_max < 1.0 else v_max v_min = -1.0 if v_min > -1.0 else v_min print(v_min) print(v_max)
-6.0
6.0
要素の「最大値」または「最小値の絶対値」の大きい方の値を最大値 v_max とします。v_max の符号を反転させた(-1を掛けた)値を最小値 v_min とします。
この操作により、中央値が0になります。
最大値(最小値)の絶対値が1未満(-1より大きい)の場合は、最小値を -1、最大値を 1 にします。
全ての値が 0 の場合に意図した配色にならないなどの対策です。
カラーマップを指定してヒートマップを作成します。
# 行・列数を取得 m, n = A.shape # 行列のヒートマップを作図 fig, ax = plt.subplots(figsize=(n*1.5, m*1.5), facecolor='white') ax.imshow(A, cmap='bwr', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): for j in range(n): ax.text(j, i, s=str(A[i, j]), size=15, ha='center', va='center') # 要素ラベル ax.set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) ax.set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) ax.set_xlabel('j') ax.set_ylabel('i') ax.set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') fig.suptitle('matrix', fontsize=20) plt.show()
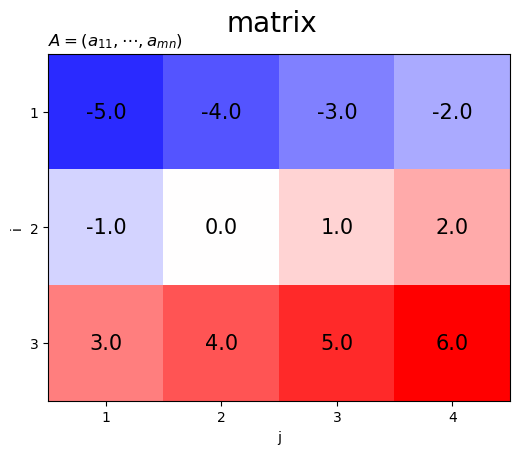
Axes.imshow() の cmap 引数にカラーマップ名、vmin, vmax 引数に最小値・最大値を指定します。
この例( bwr )だと、負の値が青色、0が白色、正の値が赤色のグラデーションになります。
転置行列のヒートマップを作成します。
# 転置行列のヒートマップを作図 fig, ax = plt.subplots(figsize=(m*1.5, n*1.5), facecolor='white') ax.imshow(A.T, cmap='bwr', vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): for j in range(n): ax.text(i, j, s=str(A[i, j]), size=15, ha='center', va='center') # 要素ラベル ax.set_xticks(ticks=np.arange(m), labels=np.arange(1, m+1)) ax.set_yticks(ticks=np.arange(n), labels=np.arange(1, n+1)) ax.set_xlabel('i') ax.set_ylabel('j') ax.set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') fig.suptitle('transposed matrix', fontsize=20) plt.show()
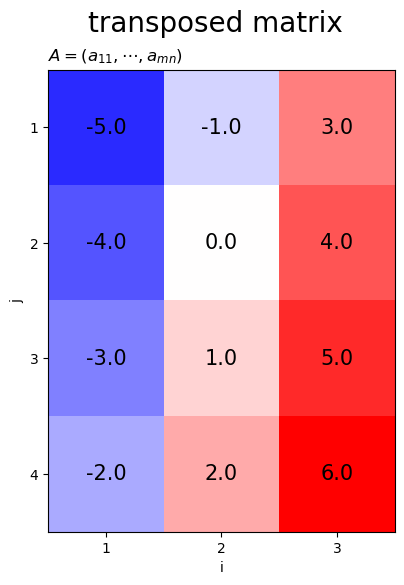
転置行列は、行と列(インデックス )を入れ替えた行列です。
行列の例
次は、個別に名前の付いた(それぞれ特徴を持つ)行列を確認していきます。
(色々と面倒なので)行列のヒートマップの作成処理を関数として作成しておきます。
・作図コード(クリックで展開)
# 行列の作図処理を定義 def plot_matrix(A, cmap='viridis', scale=1.5, title='matrix'): # 行・列数を取得 m, n = A.shape # 最小・最大値を設定 v_max = max(A.max(), abs(A.min())) v_max = 1.0 if v_max < 1.0 else v_max v_min = -v_max # 行列のヒートマップを作図 fig, ax = plt.subplots(figsize=(n*scale, m*scale), facecolor='white') ax.imshow(A, cmap=cmap, vmin=v_min, vmax=v_max) # ヒートマップ for i in range(m): for j in range(n): ax.text(j, i, s=str(A[i, j]), size=15, ha='center', va='center') # 要素ラベル ax.set_xticks(ticks=np.arange(n), labels=np.arange(1, n+1)) ax.set_yticks(ticks=np.arange(m), labels=np.arange(1, m+1)) ax.set_xlabel('j') ax.set_ylabel('i') ax.set_title('$A = (a_{11}, \cdots, a_{mn})$', loc='left') fig.suptitle(title, fontsize=20) plt.show()
必要に応じて、引数で設定できるようにします。
ゼロ行列のヒートマップを作成します。
# 行・列数を指定 m, n = 3, 4 # 0行列を作成 O = np.zeros((m, n)) print(O) print(O.shape) # ヒートマップを作図 plot_matrix(O, cmap='bwr', title='zero matrix')
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
(3, 4)
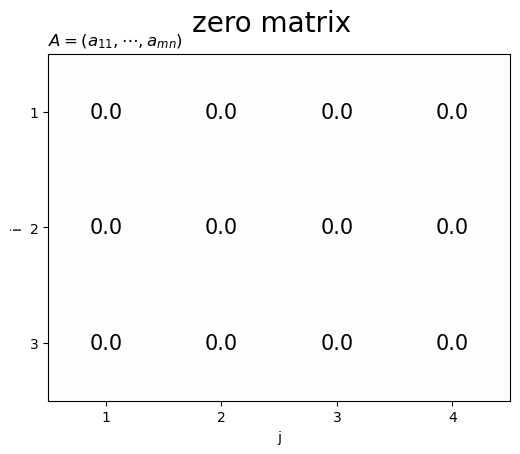
ゼロ行列は、全ての要素が0の行列です。
イチ行列のヒートマップを作成します。
# 行・列数を指定 m, n = 3, 4 # 1行列を作成 C = np.ones((m, n)) print(C) print(C.shape) # ヒートマップを作図 plot_matrix(C, cmap='bwr', title='one matrix')
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
(3, 4)
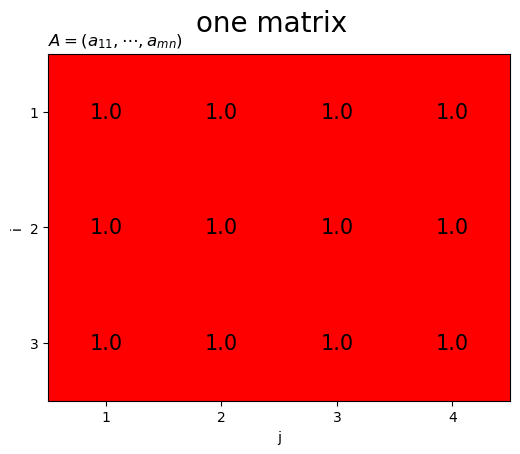
イチ行列は、全ての要素が1の行列です。
単位行列のヒートマップを作成します。
# 行(列)数を指定 n = 4 # 単位行列を作成 I = np.identity(n) print(I) print(I.shape) # ヒートマップを作図 plot_matrix(I, cmap='bwr', title='identity matrix')
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
(4, 4)
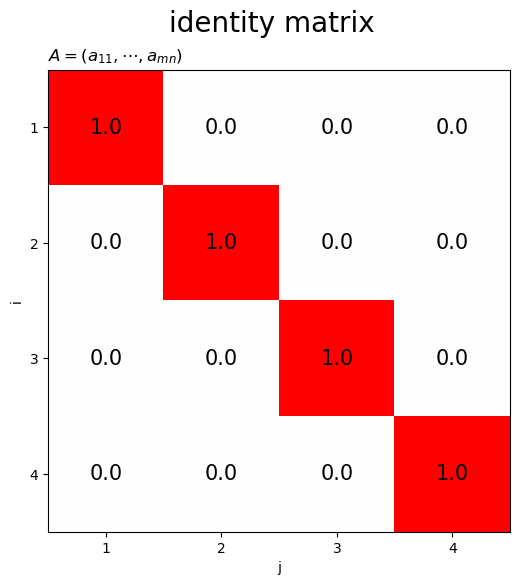
単位行列は、対角要素が1で非対角要素が0の行列です。
対角行列のヒートマップを作成します。
# 対角要素を指定 a = np.array([0.2, -3.0, 0.0, 1.2]) print(a) print(a.shape) # 対角行列を作成 A = np.diag(a) print(A) print(A.shape) # ヒートマップを作図 plot_matrix(A, cmap='bwr', title='diagonal matrix')
[ 0.2 -3. 0. 1.2]
(4,)
[[ 0.2 0. 0. 0. ]
[ 0. -3. 0. 0. ]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 1.2]]
(4, 4)
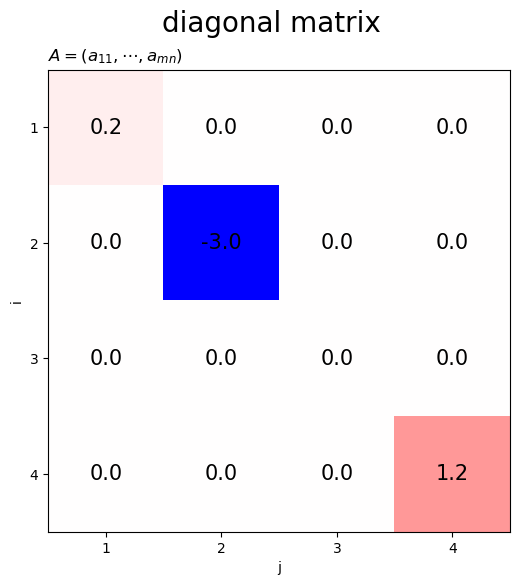
対角行列は、非対角要素が0の行列です。
上三角行列のヒートマップを作成します。
# 行列を指定 A = np.array( [[1.0, -1.0, 0.7], [-0.6, 1.2, -1.1], [-0.3, 3.5, 3.2]] ) # 上三角行列を作成 B = np.triu(A) print(B) print(B.shape) # ヒートマップを作図 plot_matrix(B, cmap='bwr', title='upper triangular matrix')
[[ 1. -1. 0.7]
[ 0. 1.2 -1.1]
[ 0. 0. 3.2]]
(3, 3)
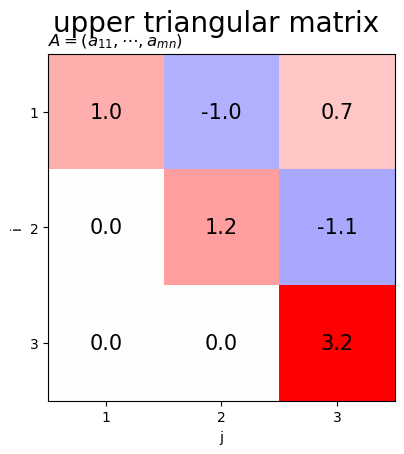
上三角行列は、 の要素が0の行列です。
下三角行列のヒートマップを作成します。
# 下三角行列を作成 B = np.tril(A) print(B) print(B.shape) # ヒートマップを作図 plot_matrix(B, cmap='bwr', title='lower triangular matrix')
[[ 1. 0. 0. ]
[-0.6 1.2 0. ]
[-0.3 3.5 3.2]]
(3, 3)
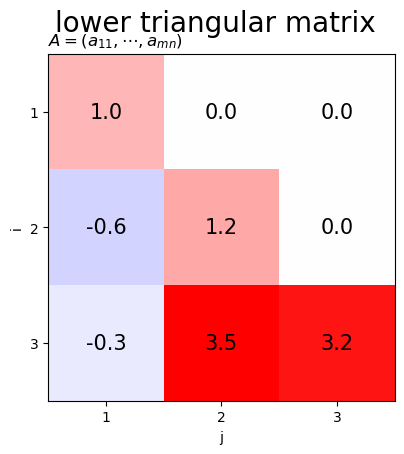
下三角行列は、 の要素が0の行列です。
疎行列のヒートマップを作成します。
# 行・列数を指定 m, n = 3, 4 # 非ゼロの値を指定 a = np.array([-1.0, 3.0, 0.6]) # 非ゼロの行・列インデックスを指定 row_idx = np.array([0, 1, 2]) col_idx = np.array([1, 2, 0]) # 疎行列を作成 A = np.zeros((m, n)) A[row_idx, col_idx] = a print(A) print(A.shape) # ヒートマップを作図 plot_matrix(A, cmap='bwr', title='sparse matrix')
[[ 0. -1. 0. 0. ]
[ 0. 0. 3. 0. ]
[ 0.6 0. 0. 0. ]]
(3, 4)
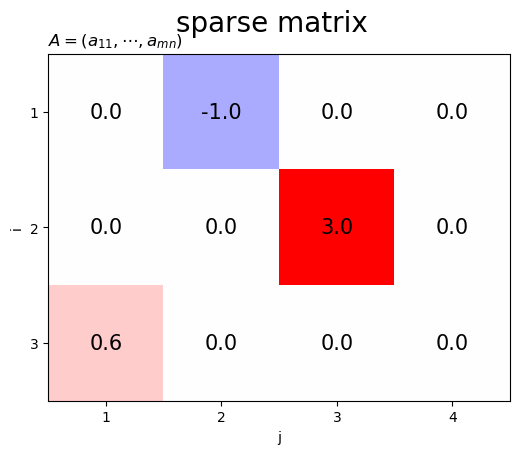
疎行列は、多くの要素が0の行列です。
差分行列のヒートマップを作成します。
# 列数を指定 n = 4 # 差分行列を作成 D = np.array( [[-1.0 if i == j else 1.0 if i+1 == j else 0.0 for j in range(n)] for i in range(n-1)] ) print(D) print(D.shape) # ヒートマップを作図 plot_matrix(D, cmap='bwr', title='difference matrix')
[[-1. 1. 0. 0.]
[ 0. -1. 1. 0.]
[ 0. 0. -1. 1.]]
(3, 4)
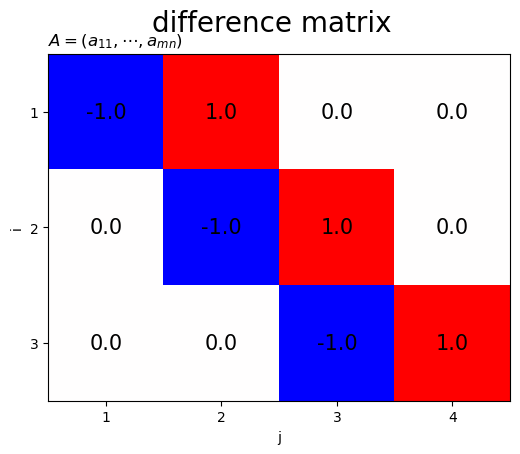
差分行列は、対角要素が-1でその右隣が1でそれ以外の要素が0の行列です。
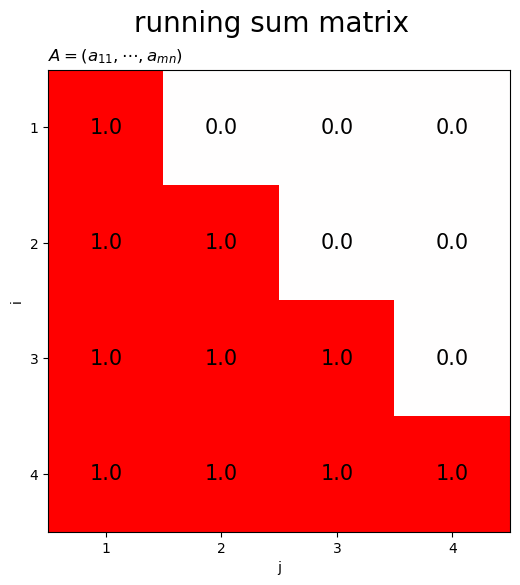
累積和行列のヒートマップを作成します。
# 行(列)数を指定 n = 4 # 累積和行列を作成 S = np.array( [[np.float32(i >= j) for j in range(n)] for i in range(n)] ) print(S) print(S.shape) # ヒートマップを作図 plot_matrix(S, cmap='bwr', title='running sum matrix')
[[1. 0. 0. 0.]
[1. 1. 0. 0.]
[1. 1. 1. 0.]
[1. 1. 1. 1.]]
(4, 4)
差分行列は、対角要素が-1でその右隣が1でそれ以外の要素が0の行列です。
この記事では、行列をグラフで確認しました。次の記事からは、行列の基本的な計算を確認します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
行列計算をなんとか可視化してみたくn回目の挑戦で書いたのですが、文量が増えたので行列の部分だけで1記事としておきます。
数字を羅列するよりはヒートマップにして分かりやすくなった気がしますがどうでしょうか。図で雰囲気を掴んでから数式と見比べると数式でも分かるような気がしますがどうでしょうか。
ゼロ行列と言うならワン行列だろイチ行列ってなんだよと自分でも思うのですが、しかしワン行列もなんとも言えない感じで、零行列と壱行列と呼びたい気もします。
【次の内容】