はじめに
Matplotlibライブラリを利用して、3D矢印プロットを作成します。
【前の内容】
【目次】
quiver関数の矢印サイズの設定:3次元の場合
Matplotlibライブラリのquiver関数で矢印を描画できます。今回は、3次元の場合の矢のサイズ・形状に関する引数を確認します。次回は、矢の色に関する引数を確認します。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
矢印の作図
まずは、3次元の場合の矢印の座標・長さに関する引数を簡単に確認します。
詳しくは「矢印プロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
座標と移動量を指定して、矢印を描画します。
# 座標・移動量を指定 x, y, z = 0.0, 1.0, 2.0 u, v, w = 3.0, 4.0, 5.0 # 矢幅・矢長比・矢頭長比を指定 lw = 1.5 l = 1.0 alr = 0.3 # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(6, 6), facecolor='white', subplot_kw={'projection': '3d'}) ax.scatter(x, y, z, s=100, label='(X, Y, Z)') # 始点 ax.scatter(x+u, y+v, z+w, s=100, label='(X+U, Y+V, Z+W)') # 終点 ax.quiver(x, y, z, u, v, w, linewidth=lw, length=l, arrow_length_ratio=alr, label='({:.2f}, {:.2f}, {:.2f}, {:.2f}, {:.2f}, {:.2f})'.format(x, y, z, u, v, w)) # 矢印 ax.set_xticks(ticks=np.arange(np.floor(x-abs(u))-1, np.ceil(x+abs(u))+2)) ax.set_yticks(ticks=np.arange(np.floor(y-abs(v))-1, np.ceil(y+abs(v))+2)) ax.set_zticks(ticks=np.arange(np.floor(z-abs(w))-1, np.ceil(z+abs(w))+2)) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}, arrow_length_ratio={}'.format(lw, l, alr), loc='left', fontsize=10) fig.suptitle('pyplot.quiver(X, Y, Z, U, V, W)', fontsize=15) ax.legend() ax.set_aspect('equal') plt.show()

3次元ベクトルの場合は、第1・2・3引数に始点の座標 X, Y, Z、第4・5・6引数に移動量 U, V, W を指定します。終点の座標は X+U, Y+V, Z+W になります。
length=1 (デフォルト)を指定すると、指定した座標の通りに描画されます。
形状に関する引数
次からは、矢印の形状(サイズ)に関する引数を確認していきます。2次元の場合とは挙動が異なります。
linewidth引数
linewidth 引数で矢の幅を設定できます。
引数の値を変更した矢印を並べて描画します。
・作図コード(クリックで展開)
# 矢印の数を指定 n = 21 # 矢幅の範囲を指定 lws = np.linspace(start=0, stop=5, num=n) # 矢長比・矢頭長比を指定 l = 1.0 alr = 0.3 # x軸方向の移動量を指定 u = 3.0 # 座標・移動量を作成 os = np.repeat(0, repeats=n) zs = np.arange(n) us = np.repeat(u, repeats=n) # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(os, os, zs, us, os, os, linewidth=lws, length=l, arrow_length_ratio=alr) # 矢印 for i in range(n): ax.text(0, 0, i, s='linewidth={:.2f}'.format(lws[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(u+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=np.arange(n)) ax.set_xlim(-6, np.ceil(u)) ax.set_ylim(-1, 1) ax.set_zlim(-1, n) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('length={}, arrow_length_ratio={}'.format(l, alr), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(linewidth)', fontsize=15) ax.set_aspect('equal') ax.view_init(elev=30, azim=300) # xz面 plt.show()
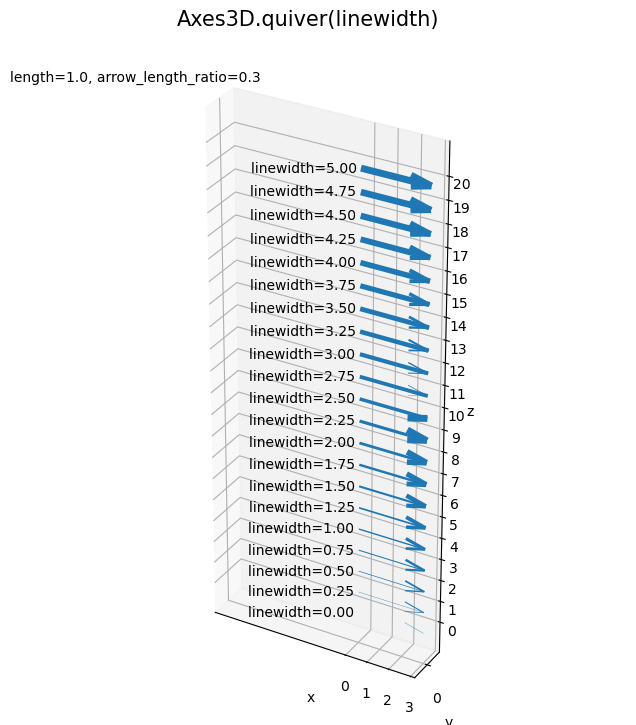
linewidth 引数は、矢全体(を構成する各線)の幅です。値が大きいほど矢が太くなります。デフォルトは 1.5 です。
負の値を指定した場合は絶対値になるようです(?)。( 0 でも微妙に描画されているのも謎です。)
引数の値を変更した矢印のアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を指定 n = 101 # 矢幅の範囲を指定 lws = np.linspace(start=-5, stop=5, num=n) # 矢長比・矢頭長比を指定 l = 1.0 alr = 0.3 # x軸方向の移動量を指定 u = 3.0 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(6, 4), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Axes3D.quiver(linewidth)', fontsize=15) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 3Dベクトルを作図 ax.quiver(0, 0, 0, u, 0, 0, linewidth=lws[i], length=l, arrow_length_ratio=alr) # 矢印 ax.text(0, 0, 0, s='linewidth={: .2f}'.format(lws[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(u+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=[0]) ax.set_xlim(-6, np.ceil(u)) ax.set_ylim(-1, 1) ax.set_zlim(-1, 1) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('length={}, arrow_length_ratio={}'.format(l, alr), loc='left', fontsize=10) ax.set_aspect('equal') ax.view_init(elev=0, azim=270) # xz面 # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=n, interval=100) # gif画像を保存 ani.save(filename='3d_quiver_lw.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。

length引数
length 引数で矢の長さを設定できます。
引数の値を変更した矢印を並べて描画します。引数に複数の値を指定できないので、for 文を使って1つずつ設定を変えて描画します。
・作図コード(クリックで展開)
# 矢印の数を指定 n = 21 # 矢長比の範囲を指定 ls = np.linspace(start=0, stop=2, num=n) # 矢幅・矢頭長比を指定 lw = 1.5 alr = 0.3 # x軸方向の移動量を指定 u = 3.0 # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(n): ax.quiver(0, 0, i, u, 0, 0, linewidth=lw, length=ls[i], arrow_length_ratio=alr) # 矢印 ax.text(0, 0, i, s='length={:.2f}'.format(ls[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(u*ls.max()+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=np.arange(n)) ax.set_xlim(-6, np.ceil(u*ls.max())) ax.set_ylim(-1, 1) ax.set_zlim(-1, n) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('u={:.2f}, linewidth={}, arrow_length_ratio={}'.format(u, lw, alr), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(length)', fontsize=15) ax.set_aspect('equal') ax.view_init(elev=30, azim=300) # xz面 plt.show()
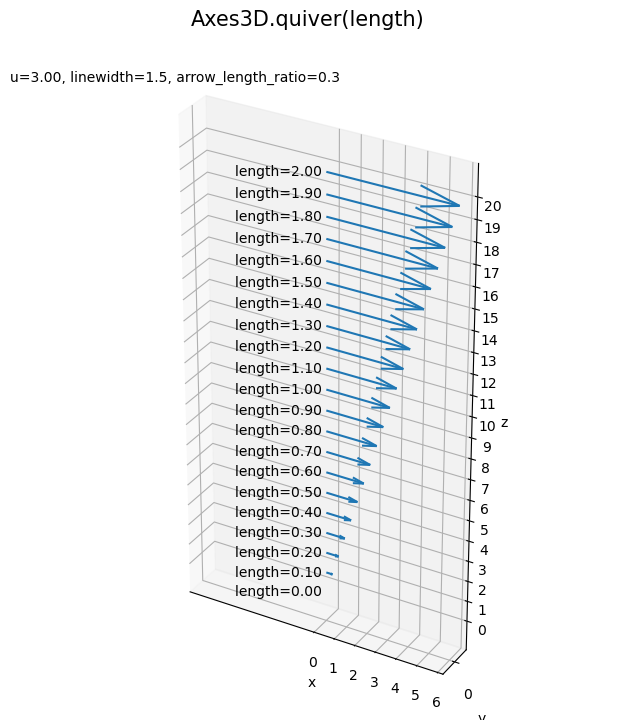
length 引数は、各軸の移動量(ベクトルのノルム)の倍率です。値が大きいほど矢が長くなります。デフォルトは 1 です。
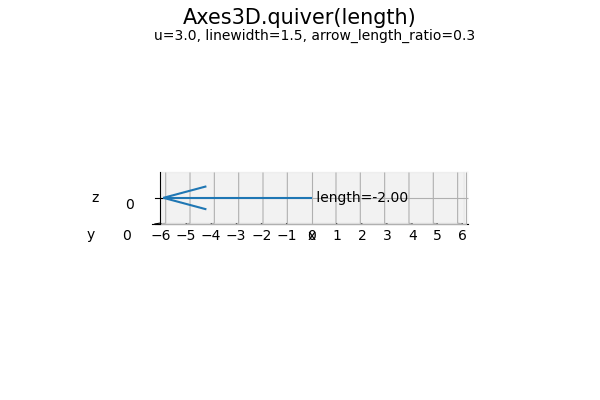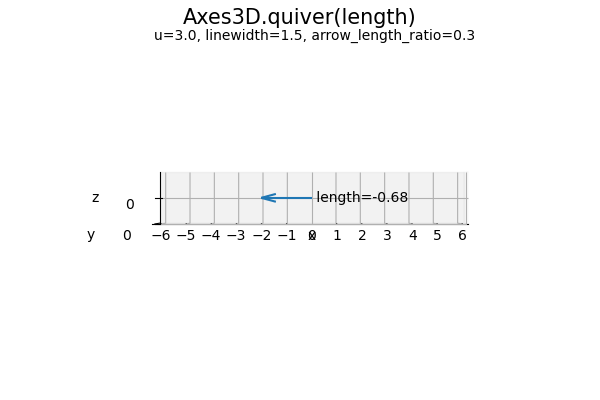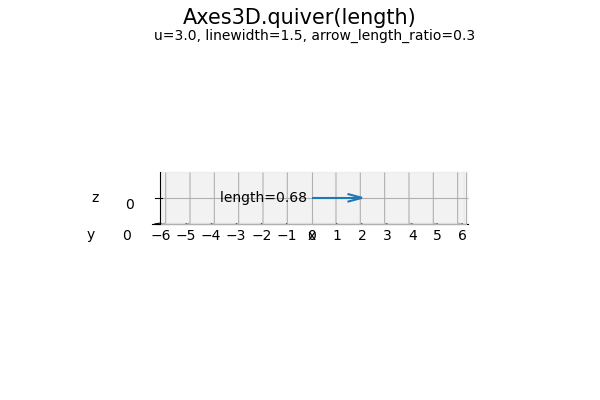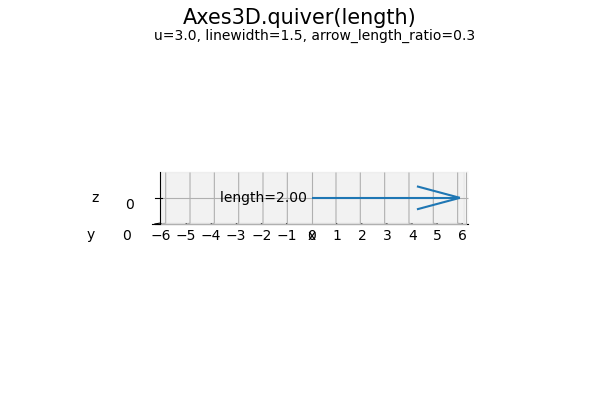
負の値の場合は矢印が逆向きになります。
・作図コード(クリックで展開)
# 矢印の数を指定 n = 21 # 矢長比の範囲を指定 ls = np.linspace(start=-2, stop=2, num=n) # 矢幅・矢頭長比を指定 lw = 1.5 alr = 0.3 # x軸方向の移動量を指定 u = 3.0 # グラフサイズを設定 x_min = np.floor(u * ls.min()) x_max = np.ceil(u * ls.max()) # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(n): ax.quiver(0, 0, i, u, 0, 0, linewidth=lw, length=ls[i], arrow_length_ratio=alr) # 矢印 str_l = 'length={:.2f}'.format(ls[i]) str_l = str_l+' ' if ls[i] >= 0.0 else ' '+str_l offset_l = 'right' if ls[i] >= 0.0 else 'left' ax.text(0, 0, i, s=str_l, size=10, ha=offset_l, va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=np.arange(n)) ax.set_xlim(min(-6, x_min), max(6, x_max)) ax.set_ylim(-1, 1) ax.set_zlim(-1, n) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('u={}, linewidth={}, arrow_length_ratio={}'.format(u, lw, alr), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(length)', fontsize=15) ax.set_aspect('equal') ax.view_init(elev=30, azim=300) # xz面 plt.show()
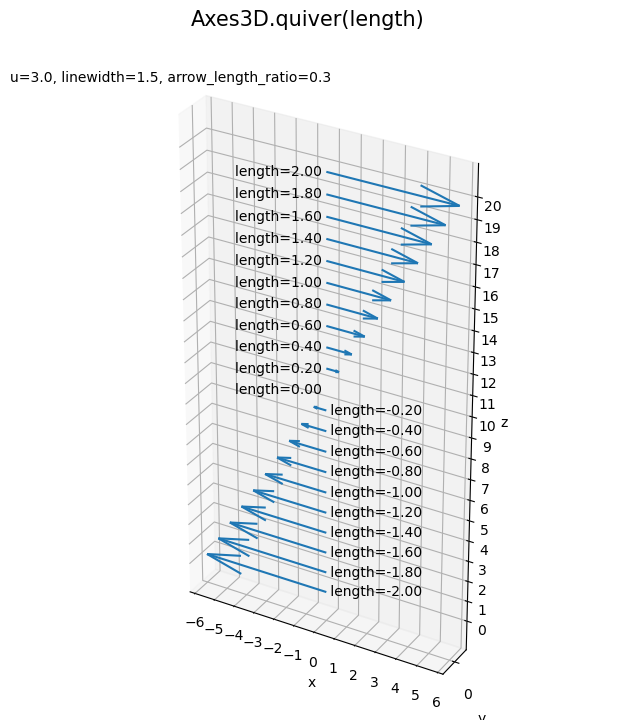
負の値の場合は、絶対値が大きいほど矢が逆方向に長くなります。
引数の値を変更した矢印のアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を指定 n = 101 # 矢長比の範囲を指定 ls = np.linspace(start=-2, stop=2, num=n) # 矢幅・矢頭長比を指定 lw = 1.5 alr = 0.3 # x軸方向の移動量を指定 u = 3.0 # グラフサイズを設定 x_min = np.floor(u * ls.min()) x_max = np.ceil(u * ls.max()) # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(6, 4), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Axes3D.quiver(length)', fontsize=15) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 3Dベクトルを作図 quiv = ax.quiver(0, 0, 0, u, 0, 0, linewidth=lw, length=ls[i], arrow_length_ratio=alr) # 矢印 str_l = 'length={:.2f}'.format(ls[i]) str_l = str_l+' ' if ls[i] >= 0.0 else ' '+str_l offset_l = 'right' if ls[i] >= 0.0 else 'left' ax.text(0, 0, 0, s=str_l, size=10, ha=offset_l, va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=[0]) ax.set_xlim(min(-6, x_min), max(6, x_max)) ax.set_ylim(-1, 1) ax.set_zlim(-1, 1) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('u={}, linewidth={}, arrow_length_ratio={}'.format(u, lw, alr), loc='left', fontsize=10) ax.set_aspect('equal') ax.view_init(elev=0, azim=270) # xz面 # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=n, interval=100) # gif画像を保存 ani.save(filename='3d_quiver_l.gif')
同様に、x・y・z軸の全ての方向に変化させて確認します。
・作図コード(クリックで展開)
# フレーム数を指定 n = 101 # 矢長比の範囲を指定 ls = np.linspace(start=-2, stop=2, num=n) # 座標・移動量を指定 x, y, z = 0.0, 1.0, 2.0 u, v, w = 3.0, 2.0, 1.0 # グラフサイズを設定 x_min = np.floor(x + u * ls.min()) - 1 x_max = np.ceil(x + u * ls.max()) + 1 y_min = np.floor(y + v * ls.min()) - 1 y_max = np.ceil(y + v * ls.max()) + 1 z_min = np.floor(z + w * ls.min()) - 1 z_max = np.ceil(z + w * ls.max()) + 1 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Axes3D.quiver(length)', fontsize=15) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 3Dベクトルを作図 ax.plot(x+u*ls, y+v*ls, z+w*ls, linestyle=':') # 始点と終点を通る直線 ax.scatter(x, y, z, s=100, label='(x, y, z)') # 始点 ax.scatter(x+u, y+v, z+w, s=100, label='(x+u, y+v, z+w)') # 等倍の終点 ax.scatter(x+u*ls[i], y+v*ls[i], z+w*ls[i], s=100, label='(x+lu, y+lv, z+lw)') # length倍の終点 quiv = ax.quiver(x, y, z, u, v, w, length=ls[i]) # 矢印 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('x={}, y={}, z={}'.format(x, y, z)+'\n, '+ 'u={}, v={}, w={}'.format(u, v, w)+'\n, '+ 'l={: .2f}'.format(ls[i]), loc='left', fontsize=10) ax.legend() ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=n, interval=100) # gif画像を保存 ani.save(filename='3d_quiver_l_uvw.gif')

矢印の始点(青色の点)の座標を x, y, z、各軸の移動量を u, v, z、length 引数の値を l とします。
矢印の終点(緑色の点)の座標は、始点とl 倍した移動量の和 x+l*u, y+l*v, z+l*w になります。等倍 length=1 (デフォルト)の場合は、終点(オレンジ色の点)の座標は、始点と移動量の和 x+u, y+v, z+w です。
arrow_length_ratio引数
arrow_length_ratio 引数で矢頭の長さを設定できます。
引数の値を変更した矢印を並べて描画します。
・作図コード(クリックで展開)
# 矢印の数を指定 n = 16 # 矢頭長比の範囲を指定 alrs = np.linspace(start=0, stop=1.5, num=n) # 矢幅・矢長比を指定 lw = 1.5 l = 1.0 # x軸方向の移動量を指定 u = 3.0 # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(n): ax.quiver(0, 0, i, u, 0, 0, linewidth=lw, length=l, arrow_length_ratio=alrs[i]) # 矢印 ax.text(0, 0, i, s='arrow_length_ratio={:.1f}'.format(alrs[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(u+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=np.arange(n)) ax.set_xlim(-6, np.ceil(u)) ax.set_ylim(-1, 1) ax.set_zlim(-1, n) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}'.format(lw, l), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) ax.set_aspect('equal') ax.view_init(elev=30, azim=300) # xz面 plt.show()
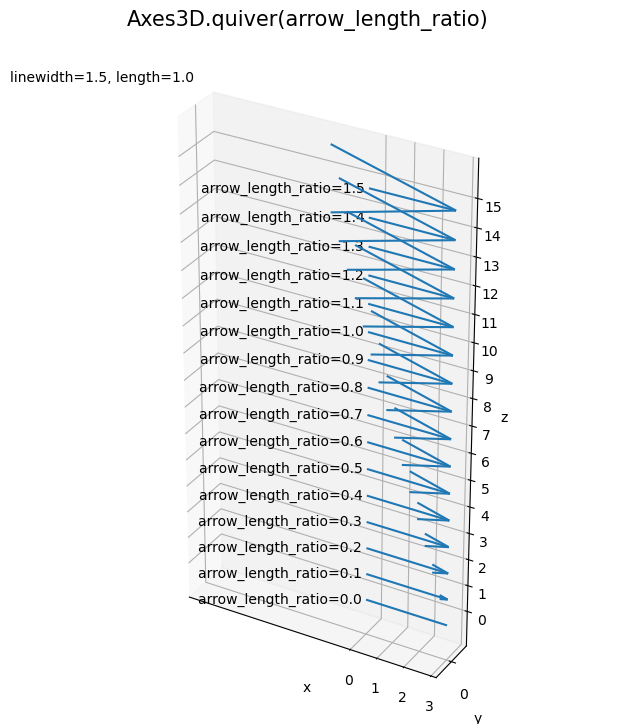
arrow_length_ratio 引数は、「矢頭の長さ」と「矢全体の長さ」の比です。値が大きいほど矢頭が長くなります。矢頭の長さに応じて幅も広くなります。デフォルトは 0.3 です。
1 のとき矢の長さと矢頭の長さが等しくなります。負の値も指定できますが形が崩れます。
引数の値を変更した矢印のアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を指定 n = 101 # 矢頭長比の範囲を指定 alrs = np.linspace(start=-2.0, stop=2.0, num=n) # 矢幅・矢長比を指定 lw = 1.5 l = 1.0 # x軸方向の移動量を指定 u = 3.0 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(6, 4), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 3Dベクトルを作図 ax.quiver(0, 0, 0, u, 0, 0, linewidth=lw, length=l, arrow_length_ratio=alrs[i]) # 矢印 ax.text(0, 0, 0, s='arrow_length_ratio={: .2f}'.format(alrs[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(u+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=[0]) ax.set_xlim(-10, max(np.ceil(u), np.ceil(abs(u*alrs.min())))) ax.set_ylim(-1, 1) ax.set_zlim(-1, 1) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}'.format(lw, l), loc='left', fontsize=10) ax.set_aspect('equal') ax.view_init(elev=0, azim=270) # xz面 # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=n, interval=100) # gif画像を保存 ani.save(filename='3d_quiver_alr.gif')

矢頭の長さの倍率を固定して、移動量を変化させて確認します。
・作図コード(クリックで展開)
# フレーム数を指定 n = 101 # x軸方向の移動量の範囲を指定 us = np.linspace(start=0, stop=5.0, num=n) # 矢幅・矢長比・矢頭長比を指定 lw = 1.5 l = 1.0 alr = 0.3 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(6, 4), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 3Dベクトルを作図 ax.quiver(0, 0, 0, us[i], 0, 0, linewidth=lw, length=l, arrow_length_ratio=alr) # 矢印 ax.text(0, 0, 0, s='U={: .2f}'.format(us[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.set_xticks(ticks=np.arange(us.max()+1)) ax.set_yticks(ticks=[0]) ax.set_zticks(ticks=[0]) ax.set_xlim(-4, np.ceil(us.max())) ax.set_ylim(-1, 1) ax.set_zlim(-1, 1) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}, arrow_length_ratio'.format(lw, l, alr), loc='left', fontsize=10) ax.set_aspect('equal') ax.view_init(elev=0, azim=270) # xz面 # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=n, interval=100) # gif画像を保存 ani.save(filename='3d_quiver_alr_u.gif')

ベクトルの長さ(移動量)が大きいほど矢頭が長くなります。
矢頭の長さの調整
矢頭のサイズは、矢印の長さ(移動量)によって決まりました。最後は、矢印の長さ(ベクトルのノルム)を用いて、矢頭の長さを指定します。
ベクトルをそのベクトルのノルムで割ると、ノルムが1のベクトルになります。ノルムが1のベクトルに定数を掛けると、ノルムが定数のベクトルになります。この性質を用いて、矢頭のサイズを指定します。
ベクトルのノルム(長さ)については「【Python】3.1:ユークリッドノルムの可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
長さの異なる矢印を並べて描画します。
・作図コード(クリックで展開)
# 矢印の数を指定 n = 11 # 座標・移動量の範囲を指定 xs = np.linspace(start=0, stop=0, num=n) ys = np.linspace(start=0, stop=0, num=n) zs = np.arange(n) us = np.linspace(start=0, stop=5.0, num=n) vs = np.linspace(start=0, stop=4.0, num=n) ws = np.linspace(start=0, stop=3.0, num=n) # 矢幅・矢長比・矢頭長比を指定 lw = 1.5 l = 1.0 alr = 0.3 # グラフサイズを設定 x_min = np.floor(min(xs.min(), (xs + us).min())) - 1 x_max = np.ceil(max(xs.max(), (xs + us).max())) + 1 y_min = np.floor(min(ys.min(), (ys + vs).min())) - 1 y_max = np.ceil(max(ys.max(), (ys + vs).max())) + 1 z_min = np.floor(min(zs.min(), (zs + ws).min())) - 1 z_max = np.ceil(max(zs.max(), (zs + ws).max())) + 1 # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(xs, ys, zs, us, vs, ws, linewidth=lw, length=l, arrow_length_ratio=alr) # 矢印 for i in range(n): ax.text(xs[i], ys[i], zs[i], s='arrow_length_ratio={}'.format(alr)+' ', size=10, ha='right', va='center') # 引数ラベル ax.text(xs[i]+us[i], ys[i]+vs[i], zs[i]+ws[i], s=' u={: .2f}, v={: .2f}, w={: .2f}'.format(us[i], vs[i], ws[i]), size=10, ha='left', va='center') # 移動量ラベル ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}'.format(lw, l), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) ax.set_aspect('equal') plt.show()

矢の長さ(ベクトルのノルム)は、始点の座標とは無関係に、移動量によって決まります。
各ベクトルの「ノルムの逆数」を比率として使います。
・作図コード(クリックで展開)
# 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(n): alr = 1.0 / np.linalg.norm([us[i], vs[i], ws[i]]) # ノルムの逆数 ax.quiver(xs[i], ys[i], zs[i], us[i], vs[i], ws[i], linewidth=lw, length=l, arrow_length_ratio=alr) # 矢印 ax.text(xs[i], ys[i], zs[i], s='arrow_length_ratio={: .2f}'.format(alr)+' ', size=10, ha='right', va='center') # 引数ラベル ax.text(xs[i]+us[i], ys[i]+vs[i], zs[i]+ws[i], s=' u={: .2f}, v={: .2f}, w={: .2f}'.format(us[i], vs[i], ws[i]), size=10, ha='left', va='center') # 移動量ラベル ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}'.format(lw, l), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) ax.set_aspect('equal') plt.show()

ベクトルのユークリッドノルムは np.linalg.norm() で計算できます。その逆数(1を割った値)を arrow_length_ratio 引数に指定します。ただし、ノルムが0(移動量が全て0)だと0除算になるため計算できません。
各ベクトルの「ノルムの逆数の定数倍」を比率として使います。
・作図コード(クリックで展開)
# 矢頭長を指定 hl = 0.5 # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(n): alr = hl / np.linalg.norm([us[i], vs[i], ws[i]]) # ノルムの逆数の定数倍 ax.quiver(xs[i], ys[i], zs[i], us[i], vs[i], ws[i], linewidth=lw, length=l, arrow_length_ratio=alr) # 矢印 ax.text(xs[i], ys[i], zs[i], s='arrow_length_ratio={: .2f}'.format(alr)+' ', size=10, ha='right', va='center') # 引数ラベル ax.text(xs[i]+us[i], ys[i]+vs[i], zs[i]+ws[i], s=' u={: .2f}, v={: .2f}, w={: .2f}'.format(us[i], vs[i], ws[i]), size=10, ha='left', va='center') # 移動量ラベル ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}, head length={:.2f}'.format(lw, l, hl), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) ax.set_aspect('equal') plt.show()

矢頭の長さを hl として値を指定します。
ベクトルのノルムの逆数に hl を掛けた値を arrow_length_ratio 引数に指定します。
各矢印の「長さ(ノルム)の逆数の定数倍」を「矢と矢頭の長さの比率」として用いることで、矢印の長さに関わらず、矢頭の長さを指定できます。
続いて、長さが同じで矢頭のサイズが異なる矢印を並べて描画します。
・作図コード(クリックで展開)
# 矢印の数を指定 n = 11 # 座標の範囲を指定 xs = np.linspace(start=0, stop=0, num=n) ys = np.linspace(start=0, stop=0, num=n) zs = np.arange(n) # 移動量を指定 u, v, w = 5.0, 4.0, 3.0 # 矢頭長の範囲を指定 hls = np.linspace(start=0, stop=2, num=n) # 矢頭長比を作成 alrs = hls / np.linalg.norm([u, v, w]) # 矢幅・矢長比を指定 lw = 1.5 l = 1.0 # グラフサイズを設定 x_min = np.floor(min(xs.min(), (xs + u).min())) - 1 x_max = np.ceil(max(xs.max(), (xs + u).max())) + 1 y_min = np.floor(min(ys.min(), (ys + v).min())) - 1 y_max = np.ceil(max(ys.max(), (ys + v).max())) + 1 z_min = np.floor(min(zs.min(), (zs + w).min())) - 1 z_max = np.ceil(max(zs.max(), (zs + w).max())) + 1 # 3Dベクトルを作図 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) for i in range(n): ax.quiver(xs[i], ys[i], zs[i], u, v, w, linewidth=lw, length=l, arrow_length_ratio=alrs[i]) # 矢印 ax.text(xs[i], ys[i], zs[i], s='arrow_length_ratio={: .2f}'.format(alrs[i])+' ', size=10, ha='right', va='center') # 引数ラベル ax.text(xs[i]+u, ys[i]+v, zs[i]+w, s=' u={}, v={}, w={}'.format(u, v, w), size=10, ha='left', va='center') # 移動量ラベル ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('linewidth={}, length={}'.format(lw, l), loc='left', fontsize=10) fig.suptitle('Axes3D.quiver(arrow_length_ratio)', fontsize=15) ax.set_aspect('equal') plt.show()
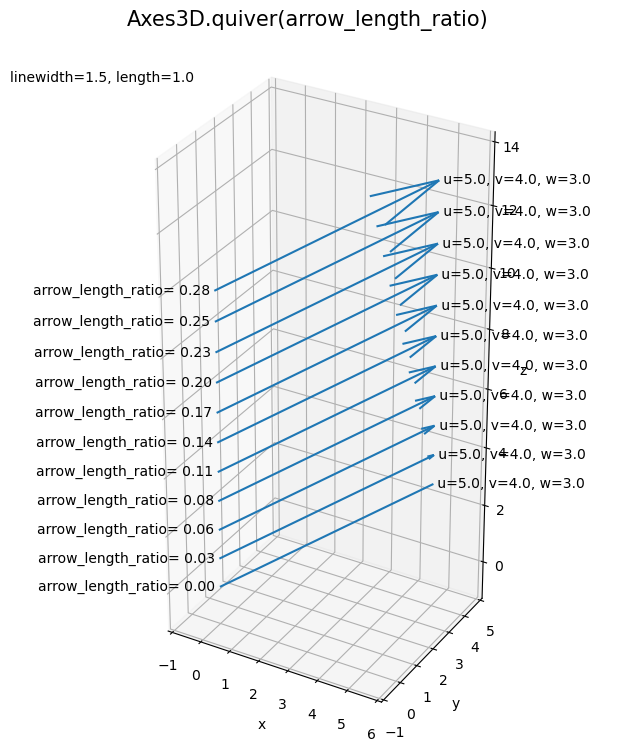
矢頭の長さを hl として値を指定します。
ベクトルのノルムの逆数に hl を掛けた値を arrow_length_ratio 引数に指定します。
矢印の「長さ(ノルム)の逆数の定数倍」の定数を変更することで、矢頭の長さを調整できます。
始点と終点の座標を変更して確認します。
・作図コード(クリックで展開)
# フレーム数を指定 n = 60 # 座標・移動量の計算用の値を指定 r = 1.0 ts = np.linspace(start=0.0, stop=2.0*np.pi, num=n+1)[:n] rs = np.sin(ts)**2 * 2.5 # 座標・移動量を指定 xs = abs(np.linspace(start=-2, stop=2, num=n)) ys = r * np.cos(-ts) zs = r * np.sin(-ts) us = rs * np.sin(2 * ts) vs = rs * np.cos(2 * ts) ws = abs(np.linspace(start=-1, stop=1, num=n)) # 矢頭長を指定 hl = 0.5 # 矢頭長比を作成 alrs = hl / np.linalg.norm(np.vstack([us, vs, ws]).T, axis=1) # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('Axes3D.quiver(X, Y, Z, U, V, W)', fontsize=15) # グラフサイズを設定 x_min = np.floor((xs + us).min()) - 1 x_max = np.ceil((xs + us).max()) + 1 y_min = np.floor((ys + vs).min()) - 1 y_max = np.ceil((ys + vs).max()) + 1 z_min = np.floor((zs + ws).min()) - 1 z_max = np.ceil((zs + ws).max()) + 1 # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 3Dベクトルを作図 ax.scatter(xs[range(i-n+1, i+1)][::-1], ys[range(i-n+1, i+1)][::-1], zs[range(i-n+1, i+1)][::-1], s=np.arange(n)[::-1]/n*50) # 始点の軌道 ax.scatter((xs+us)[range(i-n+1, i+1)][::-1], (ys+vs)[range(i-n+1, i+1)][::-1], (zs+ws)[range(i-n+1, i+1)][::-1], s=np.arange(n)[::-1]/n*50) # 終点の軌道 ax.quiver(xs[i], ys[i], zs[i], us[i], vs[i], ws[i], arrow_length_ratio=alrs[i], label='({: .2f}, {: .2f}, {: .2f}, {: .2f}, {: .2f}, {: .2f})'.format(xs[i], ys[i], zs[i], us[i], vs[i], ws[i])) # 矢印 ax.set_xlim(x_min, x_max) ax.set_ylim(y_min, y_max) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('arrow_length_ratio={:.2f}, head length={}'.format(alrs[i], hl), loc='left', fontsize=10) ax.legend(loc='upper left') ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=n, interval=100) # gif画像を保存 ani.save(filename='3d_quiver_hl.gif')

フレームの最初と最後の座標が同じになるように、上手いこと始点の座標と移動量を指定しています。
各軸の移動量を列として結合して、行(フレーム)ごとにノルムを計算して、矢と矢頭の長さの比を作成します。
矢の長さに関わらず矢頭の長さが変わらないのを確認できます。
この記事では、矢印のサイズ・形状に関する引数を確認しました。次の記事では、色に関する引数を確認します。
参考リンク
おわりに
ノルムによる矢頭のサイズ調整の話はどっかで書き出しておかないとなと思ってました。この機会にまとめられてよかったです。
書くのに手こずってる記事があると他の記事を書くのが捗ります。
2023年8月1日は、アンジュルムとハロー!プロジェクトの元リーダーの和田彩花の29歳のお誕生日です!
才色兼備と言えばいいのか、アイドルとして活動しながら美術を学びあるいは研究しに大学院に進まれた方です。そして現在は歌手として活動しつつフランスに留学中(?)です。
仏像にも造詣が深いというか大好きな方で、もうすぐ仏像巡り番組の第3期が始まるのでぜひ観てください。
【次の内容】