はじめに
機械学習でも登場する情報理論におけるエントロピーを1つずつ確認していくシリーズです。
この記事では、自己情報量を扱います。
【前の内容】
【今回の内容】
自己情報量の定義
事象の起こりやすさ(生起確率)に応じて決まる自己情報量(self-information)を数式とグラフで確認します。自己情報量は情報量(information content)とも呼ばれます。
対数については「対数の定義 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
定義
まずは、自己情報量の定義を数式とグラフで確認します。
確率に応じて変化する量を考えます。
事象 の生起確率を
とします。
自己情報量の前に、確率の逆数をグラフで確認します。
確率の逆数を計算します。
# 確率の逆数を計算 reciprocal_df <- tibble::tibble( p_x = seq(from = 0, to = 1, by = 0.001), # 確率 f_x = 1 / p_x # 逆数 ) reciprocal_df
## # A tibble: 1,001 × 2 ## p_x f_x ## <dbl> <dbl> ## 1 0 Inf ## 2 0.001 1000 ## 3 0.002 500 ## 4 0.003 333. ## 5 0.004 250 ## 6 0.005 200 ## 7 0.006 167. ## 8 0.007 143. ## 9 0.008 125 ## 10 0.009 111. ## # … with 991 more rows
事象 の確率
として
0から1の値を作成し、逆数を計算して、データフレームに格納します。
確率の逆数のグラフを作成します。
# 確率の逆数を作図 ggplot() + geom_line(data = reciprocal_df, mapping = aes(x = p_x, y = f_x)) + coord_cartesian(ylim = c(0, 10)) + # 描画範囲 labs(title = "reciprocal of a probability", subtitle = expression(f(x) == frac(1, p(x))), x = expression(p(x)), y = expression(f(x)))
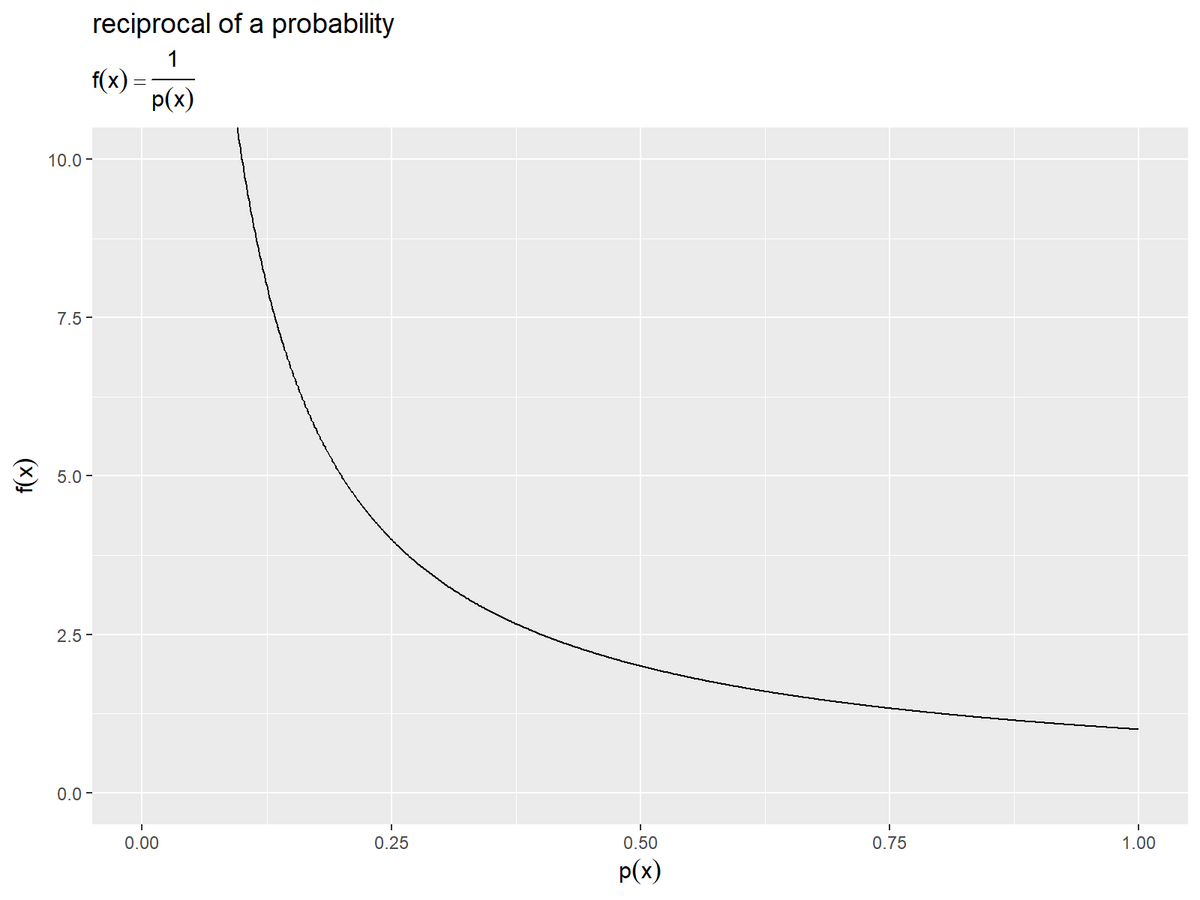
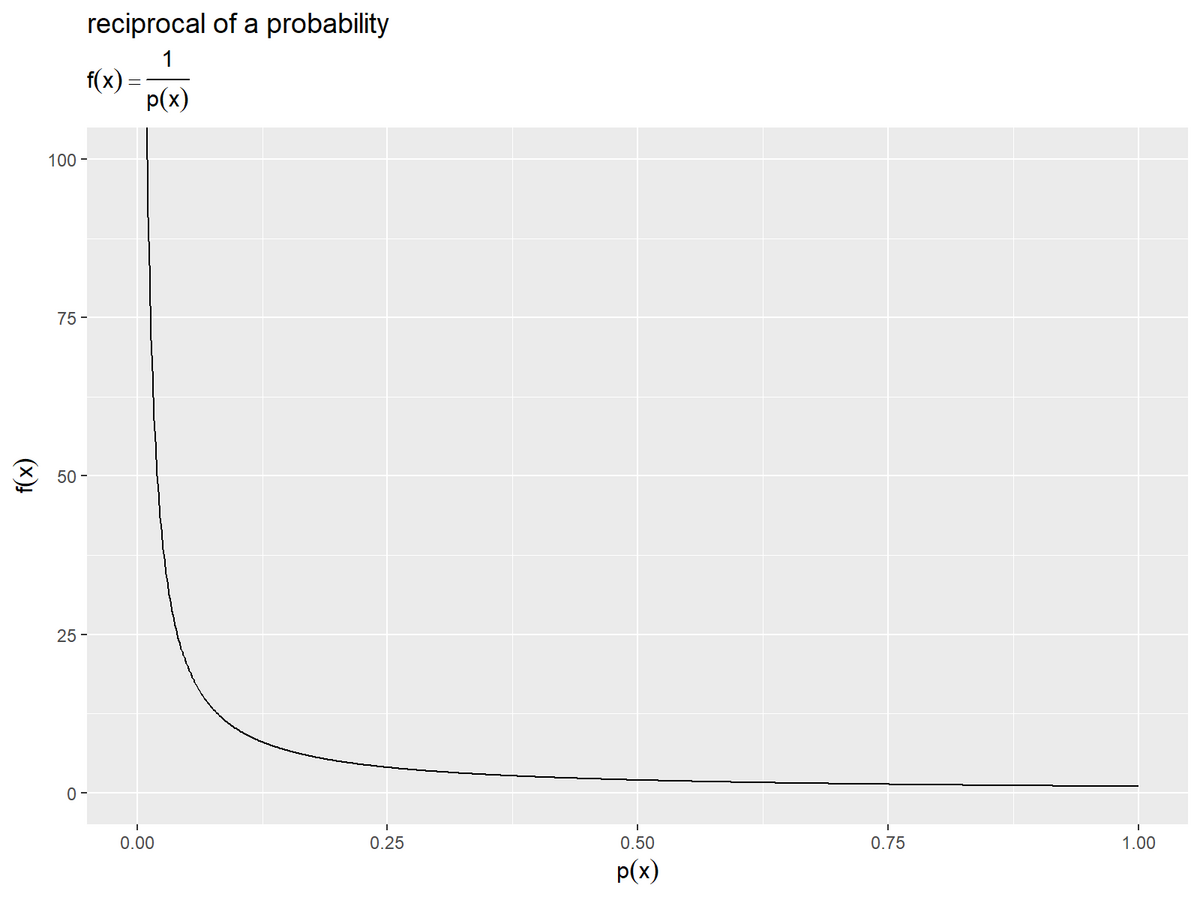
確率に反比例して単調減少するので、確率が小さい(0に近い)ほど値が大きく、大きい(1に近い)ほど値が小さくなります。
生起確率の逆数の対数(負の対数)を自己情報量 とします。定数の底は
(またはネイピア数
)とします。底の値に関わらず基本的な性質は変わりません。詳しくは「対数の性質の導出」を参照してください。
逆数は-1乗 であり、対数の性質より
なので、逆数の対数は負の対数になります。
自己情報量を計算します。
# 自己情報量を計算 information_df <- tibble::tibble( p_x = seq(from = 0, to = 1, by = 0.001), # 確率 I_x = - log2(p_x) # 自己情報量 ) information_df
## # A tibble: 1,001 × 2 ## p_x I_x ## <dbl> <dbl> ## 1 0 Inf ## 2 0.001 9.97 ## 3 0.002 8.97 ## 4 0.003 8.38 ## 5 0.004 7.97 ## 6 0.005 7.64 ## 7 0.006 7.38 ## 8 0.007 7.16 ## 9 0.008 6.97 ## 10 0.009 6.80 ## # … with 991 more rows
確率列を作成し、自己情報量を計算して、データフレームに格納します。二進対数 は
log2()で計算できます。
自己情報量のグラフを作成します。
# 自己情報量を作図 ggplot() + geom_line(data = information_df, mapping = aes(x = p_x, y = I_x)) + coord_cartesian(ylim = c(0, 10)) + # 描画範囲 labs(title = "self-information", subtitle = expression(I(x) == - log[2]*p(x)), x = expression(p(x)), y = expression(I(x)))
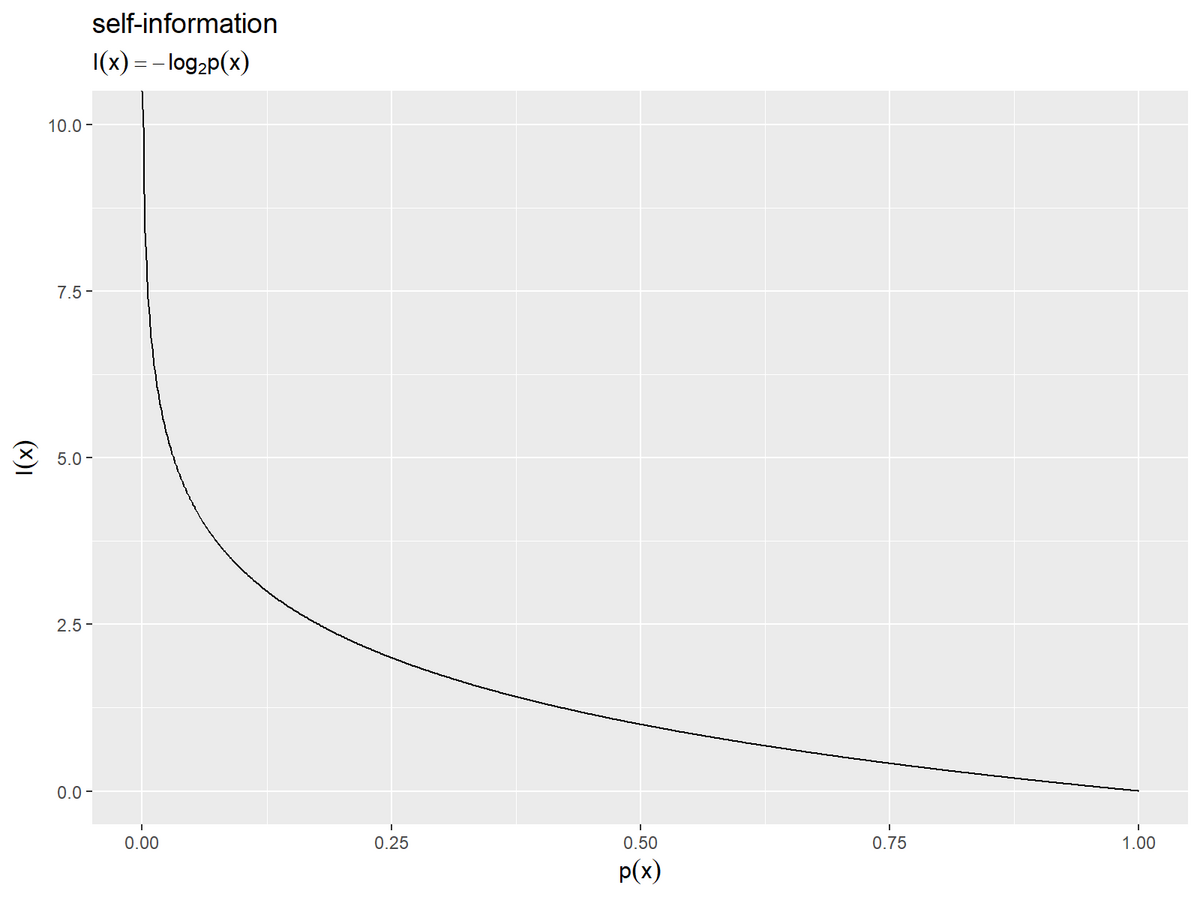
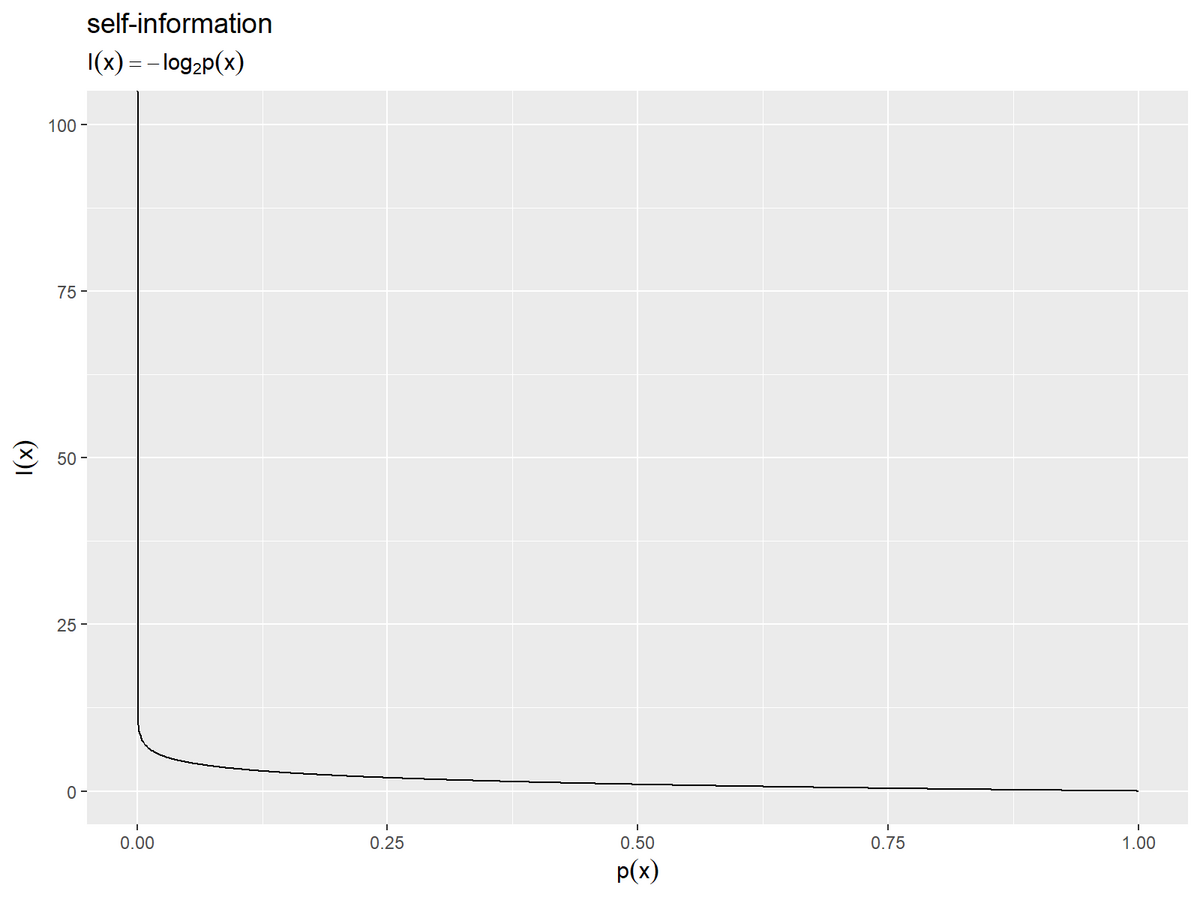
こちらの値も確率の大小に応じて変化しますが、確率が1のとき値が0になります。確率が0のとき無限大 になります。確率は0から1の値なので、確率の対数は負の値になり、自己情報量(確率の負の対数)は正の値になります。
ここまでは、自己情報量の定義を確認しました。
加法性
次は、独立する事象の結合確率(同時確率)の自己情報量を考えます。独立しない事象の情報量については「条件付きエントロピー」で扱います。
独立する事象 の結合確率
は、それぞれの事象の確率の積で表せます。このとき、
の自己情報量
は、それぞれの事象の自己情報量の和で表わせます。
自己情報量は独立した事象に対して加法性を持ちます。
この関係は、結合確率と自己情報量の定義式から導けます。
対数の性質より です。
2つの事象の結合確率と自己情報量を計算します。
# 自己情報量の和を計算 joint_information_df <- tidyr::expand_grid( p_x = seq(from = 0, to = 1, by = 0.01), # xの確率 p_y = seq(from = 0, to = 1, by = 0.01) # yの確率 ) |> # 全ての組み合わせを作成 dplyr::mutate( p_xy = p_x * p_y, # xyの結合確率 I_x = - log2(p_x), # xの自己情報量 I_y = - log2(p_y), # yの自己情報量 #I_xy = I_x + I_y # xyの自己情報量 I_xy = - log2(p_xy) # xyの自己情報量 ) joint_information_df
## # A tibble: 10,201 × 6 ## p_x p_y p_xy I_x I_y I_xy ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 0 0 0 Inf Inf Inf ## 2 0 0.01 0 Inf 6.64 Inf ## 3 0 0.02 0 Inf 5.64 Inf ## 4 0 0.03 0 Inf 5.06 Inf ## 5 0 0.04 0 Inf 4.64 Inf ## 6 0 0.05 0 Inf 4.32 Inf ## 7 0 0.06 0 Inf 4.06 Inf ## 8 0 0.07 0 Inf 3.84 Inf ## 9 0 0.08 0 Inf 3.64 Inf ## 10 0 0.09 0 Inf 3.47 Inf ## # … with 10,191 more rows
2つの確率列を作成し、expand_grid()で全ての組み合わせを作成して、結合確率と自己情報量を計算します。
結合確率のグラフを作成します。
# 結合確率を作図 ggplot() + geom_contour_filled(data = joint_information_df, mapping = aes(x = p_x, y = p_y, z = p_xy)) + # 等高線図 # geom_tile(data = joint_information_df, # mapping = aes(x = p_x, y = p_y, fill = p_xy)) + # ヒートマップ # scale_fill_viridis_c() + # グラデーション:(ヒートマップ用) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "joint probability", subtitle = expression(p(x, y) == p(x) * p(y)), fill = expression(p(x, y)), x = expression(p(x)), y = expression(p(y)))
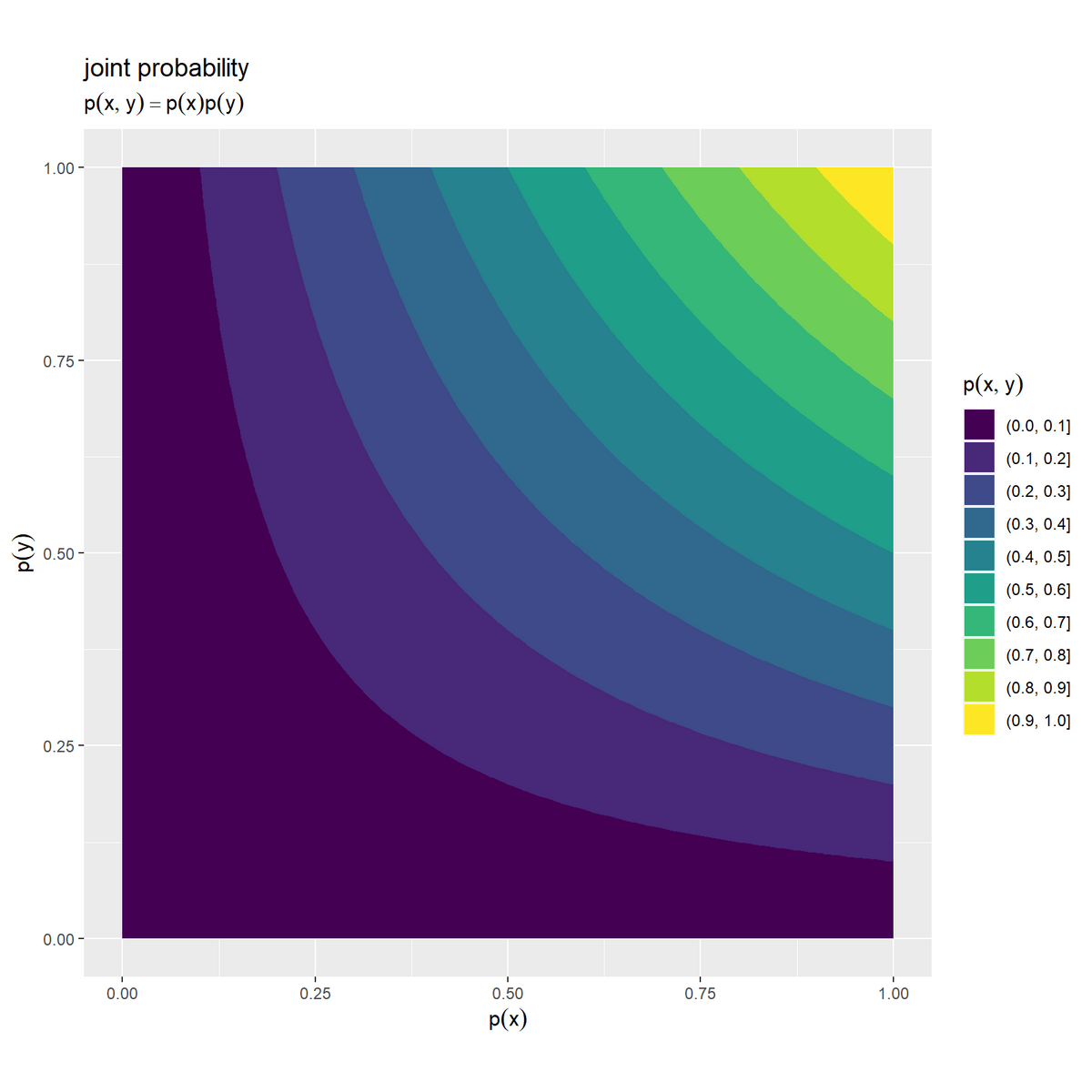
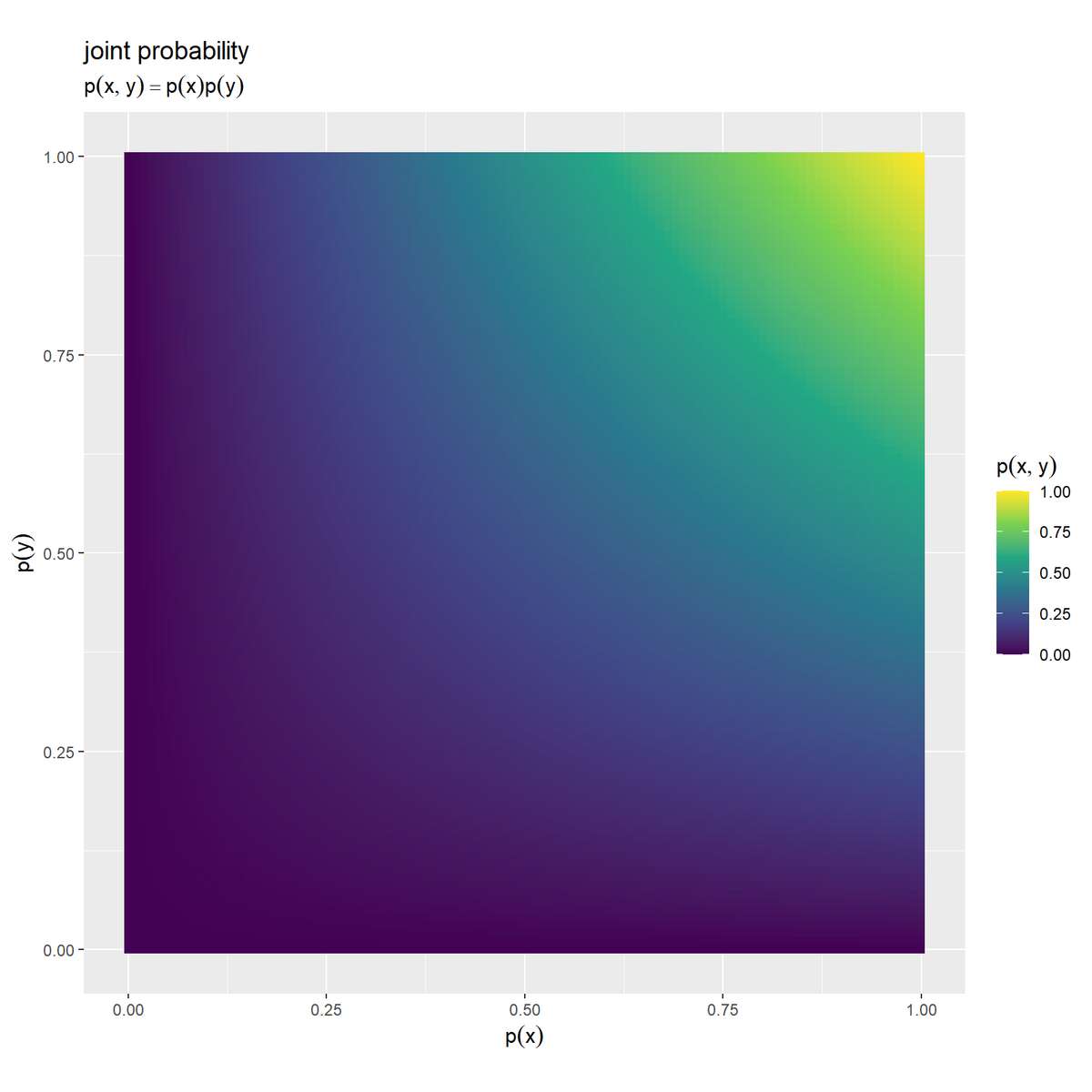
事象 の確率をx軸の値、事象
の確率をy軸の値、事象
の結合確率をz軸の値(グラデーション用の値)として、
geom_contour_filled()で等高線図またはgeom_tile()でヒートマップを描画します。
それぞれの確率が小さいほど結合確率も小さく、それぞれの確率が大きいほど結合確率も大きくなります。各確率は0から1の値なので、結合確率も0から1の値になります。
自己情報量のグラフを作成します。
# 自己情報量の加法性を作図 ggplot() + geom_contour_filled(data = joint_information_df, mapping = aes(x = p_x, y = p_y, z = I_xy)) + # 等高線図 # geom_tile(data = joint_information_df, # mapping = aes(x = p_x, y = p_y, fill = I_xy)) + # ヒートマップ # scale_fill_viridis_c() + # グラデーション:(ヒートマップ用) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "self-information", subtitle = expression(list(I(x, y) == - log[2]*p(x, y), I(x, y) == I(x) + I(y))), fill = expression(I(x, y)), x = expression(p(x)), y = expression(p(y)))
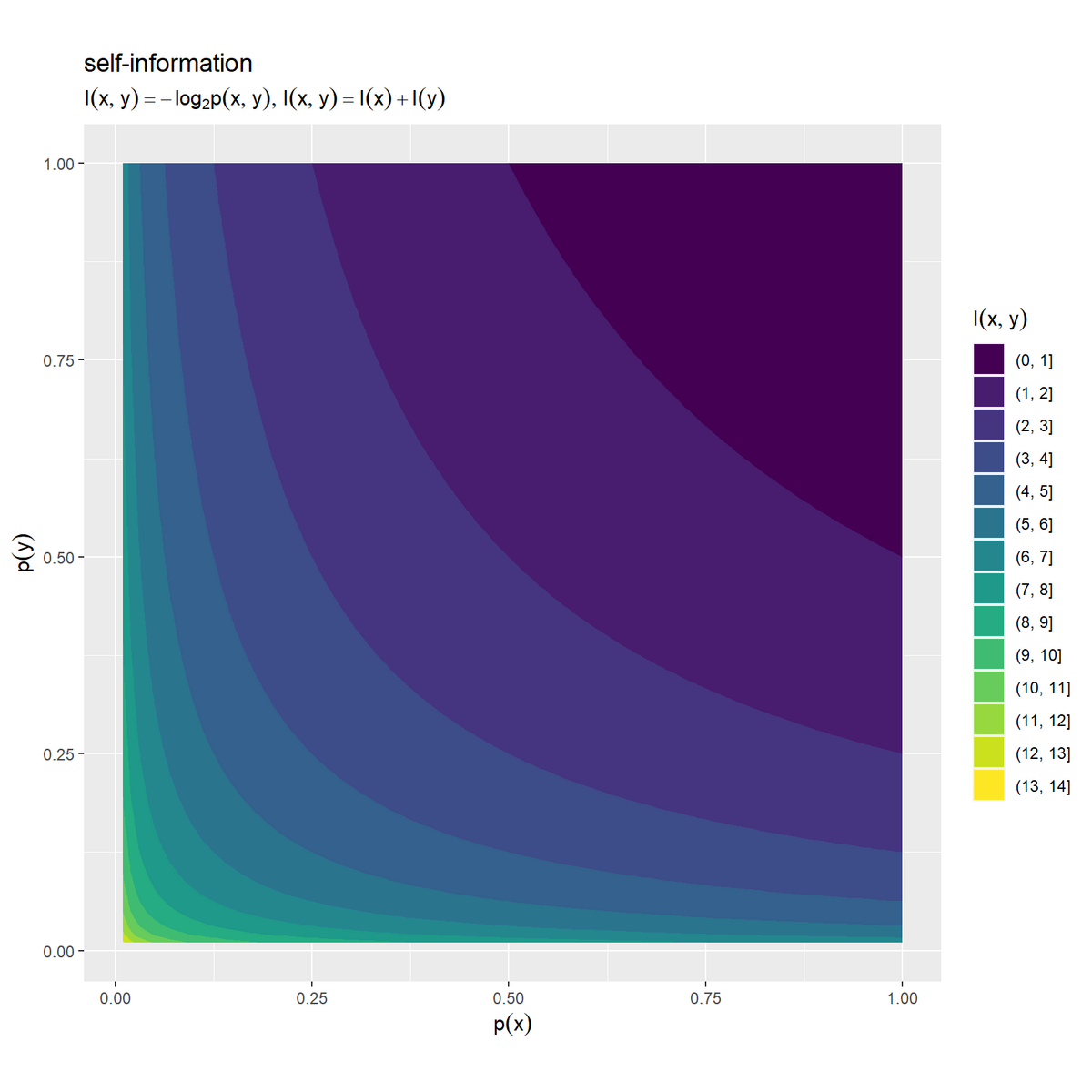
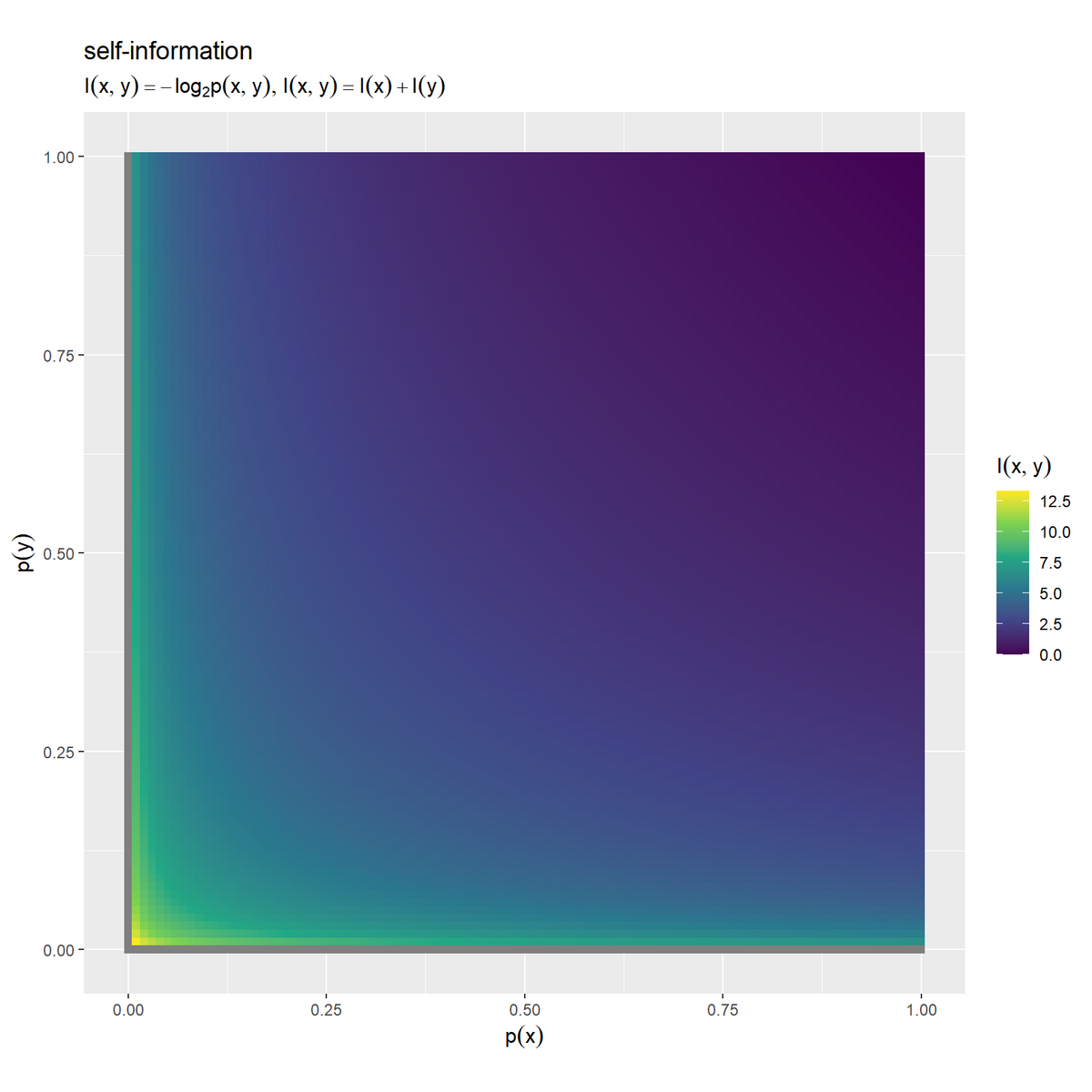
事象 の自己情報量をz軸の値(グラデーション用の値)として、同様に描画します。
1事象における確率と自己情報量の関係と同じく、結合確率が小さいほど自己情報量が大きく、結合確率が大きいほど自己情報量が小さくなります。
この記事では、自己情報量の定義を確認しました。次の記事では、平均情報量の定義を確認します。
参考文献
- 『わかりやすい ディジタル情報理論』(改訂2版)塩野 充・蜷川 繁,オーム社,2021年.
おわりに
かなり前にも情報量について書いた記憶があります。
こっちはもう少し言葉で説明しています。式と図だけじゃなんともなぁという方は覗いてみてください。
先日公開された新MVをどうぞ。
夏は大の苦手なもんで低位で安定的に推移しております…よ?
【次の内容】