はじめに

　機械学習でも登場する情報理論におけるエントロピーを1つずつ確認していくシリーズです。

　この記事では、対数関数を扱います。

【今回の内容】

はじめに
対数の定義
- 定義
- 可視化
  - 対数関数の作図
  - 指数関数との関係
参考文献
おわりに

対数の定義

　対数(logarithm)の定義を数式とグラフで確認します。
　対数の性質については「対数の性質の導出 - からっぽのしょこ」を参照してください。

定義

　まずは、対数の定義を数式で確認します。

　対数は、次の式で定義されます。

$\displaystyle \log_a b = c \Leftrightarrow a^c = b$

　 $a$ を底、 $b$ を真数、 $c$ を指数と呼びます。底は0より大きい1ではない値 $a \gt 0, a \neq 1$ 、真数は0より大きい値 $b \gt 0$ である必要があります。
　底が $2$ のとき二進対数、 $10$ のとき常用対数、ネイピア数 $e = 2.718\dots$ のとき自然対数と呼びます。

　底が $a$ の対数関数 $\log_a x$ は、底が $a$ の指数関数 $a^x$ の逆関数です。

可視化

　次は、対数関数をグラフで確認します。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)

　この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2を読み込む必要があります。
　また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。

対数関数の作図

　対数の底を指定して、対数関数を計算します。

# 底を指定
a <- 2
#a <- 10
#a <- exp(1)

# 対数関数を計算
log_df <- tibble::tibble(
  x = seq(from = -1, to = 10, by = 0.001), # 真数(変数)
  log_a_x  = logb(x, base = a) # 底がaの対数
)
log_df

## # A tibble: 11,001 × 2
##         x log_a_x
##     <dbl>   <dbl>
##  1 -1         NaN
##  2 -0.999     NaN
##  3 -0.998     NaN
##  4 -0.997     NaN
##  5 -0.996     NaN
##  6 -0.995     NaN
##  7 -0.994     NaN
##  8 -0.993     NaN
##  9 -0.992     NaN
## 10 -0.991     NaN
## # … with 10,991 more rows

　任意の底の対数 $\log_a x$ はlogb()で計算できます。base引数に底を指定します。
　 $x \lt 0$ のとき非数NaN、 $x = 0$ のとき負の無限大-Infになります。

　対数関数のグラフを作成します。

# 対数関数を作図
ggplot() + 
  geom_line(data = log_df, 
            mapping = aes(x = x, y = log_a_x), na.rm = TRUE) + 
  labs(title = "logarithmic function", 
       subtitle = parse(text = paste("a==", a)), 
       x = expression(x), 
       y = expression(log[a]*x))

　対数関数は $x \lt 0$ の範囲で単調増加します。

　3つの対数関数を計算します。

# 対数を計算
log_df <- tibble::tibble(
  x = seq(from = 0, to = 5, by = 0.001), # 真数(変数)
  log_2  = log2(x),  # 二進対数
  log_10 = log10(x), # 常用対数
  log_e  = log(x)    # 自然対数
) |> 
  tidyr::pivot_longer(
    cols = !x, # 新列に格納する(しない)現列
    names_to = "a", # 現列名を格納する新列名
    names_prefix = "log_", # 現列名の頭から取り除く文字列
    #names_transform = list(a = factor), # 現列名の格納後の型
    values_to = "log_x" # 現値を格納する新列名
  ) |> 
  dplyr::mutate(
    a = factor(a, levels = c("2", "e", "10")) # 因子レベルを設定
  )
log_df

## # A tibble: 15,003 × 3
##        x a       log_x
##    <dbl> <fct>   <dbl>
##  1 0     2     -Inf   
##  2 0     10    -Inf   
##  3 0     e     -Inf   
##  4 0.001 2       -9.97
##  5 0.001 10      -3   
##  6 0.001 e       -6.91
##  7 0.002 2       -8.97
##  8 0.002 10      -2.70
##  9 0.002 e       -6.21
## 10 0.003 2       -8.38
## # … with 14,993 more rows

　二進対数 $\log_2 x$ はlog2()、常用対数 $\log_{10} x$ はlog10()、自然対数 $\log_e x$ はlog()で計算できます。
　それぞれ別の列として計算して、pivot_longer()で1つの列にまとめます。
　凡例の並び順(色付け順)を指定する場合は因子レベルを設定します。

　3つの対数関数のグラフを作成します。

# 対数関数を作図
ggplot() + 
  geom_line(data = log_df, 
            mapping = aes(x = x, y = log_x, color = a)) + 
  geom_hline(yintercept = 0, linetype = "dotted") + # 水平線
  geom_vline(xintercept = 1, linetype = "dotted") + # 垂直線
  labs(title = "logarithmic functions", 
       x = expression(x), 
       y = expression(log[a]*x))

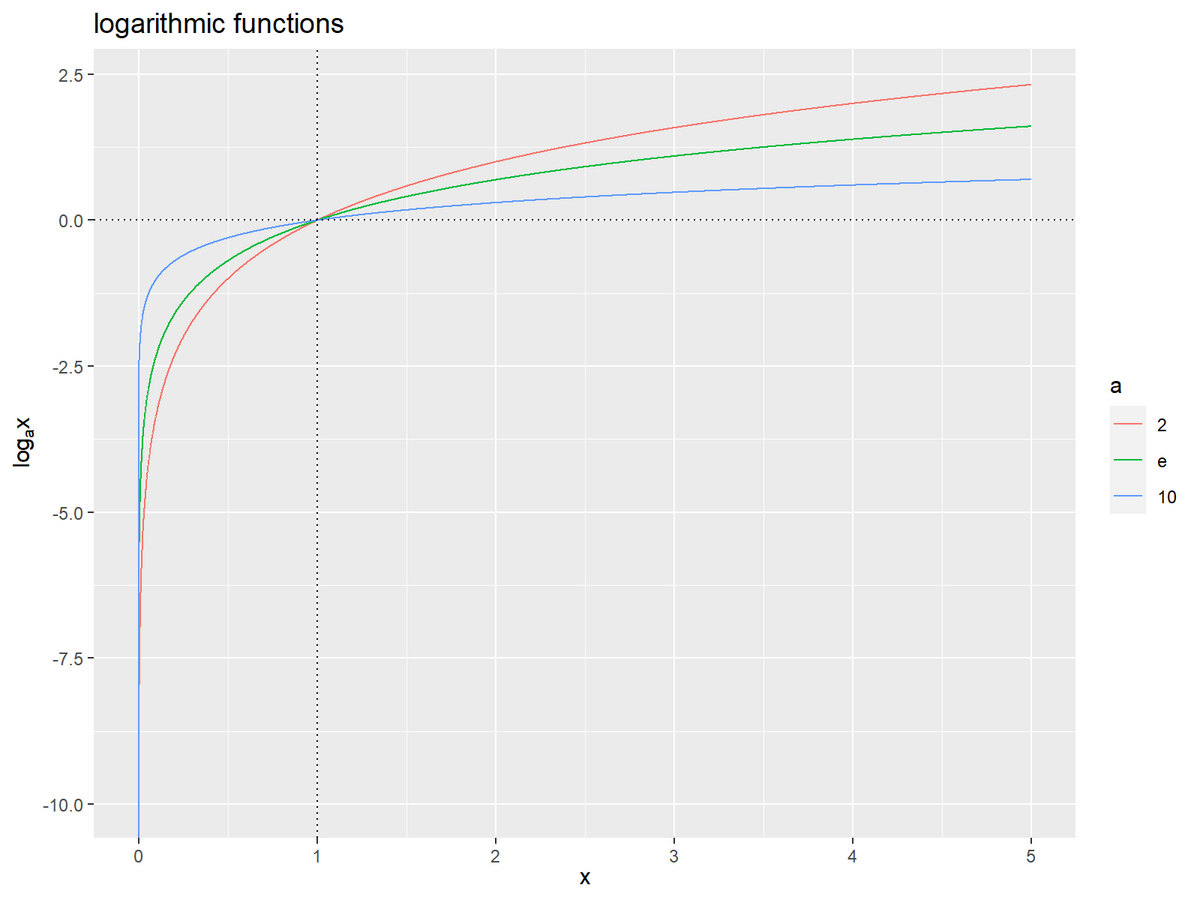
　底に関わらず、 $x \lt 0$ の範囲は定義されず、0のとき負の無限大、0から1のとき負の実数、1のとき0 、1より大きいとき正の実数になります。

$\displaystyle \begin{cases} \log_a 0 = - \infty &\quad (x = 0) \\ - \infty \lt \log_a x \lt 0 &\quad (0 \lt x \lt 1) \\ \log_a 1 = 0 &\quad (x = 1) \\ \log_a x \gt 0 &\quad (x \gt 1) \end{cases}$

　(数式(LaTeXコマンド)では定義されないことをどう表記するのでしょうか?)

指数関数との関係

　続いて、対数関数と指数関数をグラフで比較します。

　3つの指数関数を計算します。

# 対数を計算
exp_df <- tibble::tibble(
  x = seq(from = -5, to = 5, by = 0.001), # 真数(変数)
  exp_2  = 2^x,   # 二進対数の逆関数
  exp_10 = 10^x,  # 常用対数の逆関数
  exp_e  = exp(x) # 自然対数の逆関数
) |> 
  tidyr::pivot_longer(
    cols = !x, # 新列に格納する(しない)現列
    names_to = "a", # 現列名を格納する新列名
    names_prefix = "exp_", # 現列名の頭から取り除く文字列
    #names_transform = list(a = factor), # 現列名の格納後の型
    values_to = "exp_x" # 現値を格納する新列名
  ) |> 
  dplyr::mutate(
    a = factor(a, levels = c("2", "e", "10")) # 因子レベルを設定
  )
exp_df

## # A tibble: 30,003 × 3
##        x a         exp_x
##    <dbl> <fct>     <dbl>
##  1 -5    2     0.0312   
##  2 -5    10    0.00001  
##  3 -5    e     0.00674  
##  4 -5.00 2     0.0313   
##  5 -5.00 10    0.0000100
##  6 -5.00 e     0.00674  
##  7 -5.00 2     0.0313   
##  8 -5.00 10    0.0000100
##  9 -5.00 e     0.00675  
## 10 -5.00 2     0.0313   
## # … with 29,993 more rows

　二進対数(底が2)、常用対数(底が10)、自然対数(底がネイピア数)に対応した指数関数を計算して、1列にまとめます。

　恒等関数を用意します。

# 恒等関数を格納
identity_df <- tibble::tibble(
  x = seq(from = min(exp_df[["x"]]), to = max(exp_df[["x"]]), length.out = 101), 
  f_x = x
)
identity_df

## # A tibble: 101 × 2
##        x   f_x
##    <dbl> <dbl>
##  1  -5    -5  
##  2  -4.9  -4.9
##  3  -4.8  -4.8
##  4  -4.7  -4.7
##  5  -4.6  -4.6
##  6  -4.5  -4.5
##  7  -4.4  -4.4
##  8  -4.3  -4.3
##  9  -4.2  -4.2
## 10  -4.1  -4.1
## # … with 91 more rows

　対数関数と指数関数のグラフは、 $y = x$ の直線で対称になります。
　直線を描画するために、恒等関数 $f(x) = x$ の値をデータフレームに格納します。

　3つの対数関数と指数関数のグラフを作成します。

# 対数関数と指数関数を作図
ggplot() + 
  geom_line(data = log_df, 
            mapping = aes(x = x, y = log_x, color = a, linetype = "log")) + # 対数関数
  geom_line(data = exp_df, 
            mapping = aes(x = x, y = exp_x, color = a, linetype = "exp")) + # 指数関数
  geom_line(data = identity_df, 
            mapping = aes(x = x, y = f_x, linetype = "x")) + # 恒等関数
  geom_vline(xintercept = 0, linetype = "dotted") + # 対数関数の漸近線
  geom_hline(yintercept = 0, linetype = "dotted") + # 指数関数の漸近線
  scale_linetype_manual(breaks = c("log", "exp", "x"), 
                        values = c("solid", "dotdash", "dashed"), 
                        labels = c(expression(log[a]*x), expression(a^x), expression(x)), name = "function") + # 凡例表示用
  coord_fixed(ratio = 1, ylim = c(-5, 5)) + # 描画範囲
  theme(legend.text.align = 0) + # 図の体裁
  labs(title = "Logarithmic functions and Exponential functions", 
       x = expression(x), 
       y = expression(f(x)))

　対数関数は $y = 0$ に漸近し、指数関数は $x = 0$ に漸近し、対数関数と指数関数が $y = x$ の直線で対称なのが分かります。

　複数の底を指定して、それぞれ対数関数を計算します。

# 底を指定
a_vals <- c(0.2, 0.4, 0.6, 0.8)
#a_vals <- c(2, 4, 6, 8)

# 対数関数を計算
log_df <- tidyr::expand_grid(
  a = a_vals, # 底
  x = seq(from = 0, to = 10, length.out = 101) # 変数
) |> # 底の数に応じて変数を複製
  dplyr::mutate(
    log_x = logb(x = x, base = a), # 対数関数
    a = factor(a) # 色分け用に因子化
  )
log_df

## # A tibble: 404 × 3
##    a         x    log_x
##    <fct> <dbl>    <dbl>
##  1 0.2     0   Inf     
##  2 0.2     0.1   1.43  
##  3 0.2     0.2   1     
##  4 0.2     0.3   0.748 
##  5 0.2     0.4   0.569 
##  6 0.2     0.5   0.431 
##  7 0.2     0.6   0.317 
##  8 0.2     0.7   0.222 
##  9 0.2     0.8   0.139 
## 10 0.2     0.9   0.0655
## # … with 394 more rows

　複数個の底をa_valsとして値を指定します。
　底をa列、真数(変数)をx列として、expand_grid()で全ての組み合わせを作成することで、底の個数分に変数の値を複製します。
　底と変数の組み合わせごとに対数を計算します。

　複数の底ごとに指数関数を計算します。

# 指数関数
exp_df <- tidyr::expand_grid(
  a = a_vals, # 底
  x = seq(from = -max(log_df[["x"]]), to = max(log_df[["x"]]), length.out = 101) # 変数
) |> # 底の数に応じて変数を複製
  dplyr::mutate(
    exp_x = a^x, # 指数関数
    a = factor(a) # 色分け用に因子化
  )
exp_df

## # A tibble: 404 × 3
##    a         x    exp_x
##    <fct> <dbl>    <dbl>
##  1 0.2   -10   9765625.
##  2 0.2    -9.8 7077926.
##  3 0.2    -9.6 5129937.
##  4 0.2    -9.4 3718074.
##  5 0.2    -9.2 2694784.
##  6 0.2    -9   1953125 
##  7 0.2    -8.8 1415585.
##  8 0.2    -8.6 1025987.
##  9 0.2    -8.4  743615.
## 10 0.2    -8.2  538957.
## # … with 394 more rows

　対数のときと同様にして、底と変数の組み合わせごとに指数を計算します。

　先ほどのコードで対数関数と指数関数のグラフを作成します。

## 資料作成用:(再掲)

# 恒等関数を格納
identity_df <- tibble::tibble(
  x = seq(from = min(exp_df[["x"]]), to = max(exp_df[["x"]]), length.out = 101), 
  f_x = x
)

# 対数関数を作図
ggplot() + 
  geom_line(data = log_df, 
            mapping = aes(x = x, y = log_x, color = a, linetype = "log")) + # 対数関数
  geom_line(data = exp_df, 
            mapping = aes(x = x, y = exp_x, color = a, linetype = "exp")) + # 指数関数
  geom_line(data = identity_df, 
            mapping = aes(x = x, y = f_x, linetype = "x")) + # 恒等関数
  geom_vline(xintercept = 0, linetype = "dotted") + # 対数関数の漸近線
  geom_hline(yintercept = 0, linetype = "dotted") + # 指数関数の漸近線
  scale_linetype_manual(breaks = c("log", "exp", "x"), 
                        values = c("solid", "dotdash", "dashed"), 
                        labels = c(expression(log[a]*x), expression(a^x), expression(x)), name = "function") + # 凡例表示用
  coord_fixed(ratio = 1, ylim = c(-10, 10)) + # 描画範囲
  theme(legend.text.align = 0) + # 図の体裁
  labs(title = "Logarithmic functions and Exponential functions", 
       x = expression(x), 
       y = expression(f(x)))

　底が $0 \lt a \lt 1$ のときと $a \gt 1$ のときで曲線の形が大きく異なるのを確認できます。

　底と曲線の関係をアニメーションで確認します。

・作図コード(クリックで展開)

　底の範囲と間隔を指定して、それぞれ対数関数と指数関数を計算します。

# 底用の値を作成
a_vals <- seq(from = 0.1, to = 2.5, by = 0.2)

# フレーム数を指定
frame_num <- length(a_vals)

# 底ごとに対数関数と指数関数を計算
anim_df <- tidyr::expand_grid(
  a = a_vals, # 底
  x = seq(from = -10, to = 10, by = 0.01) # 変数
) |> # 底ごとに変数を複製
  dplyr::mutate(
    log_x = dplyr::if_else(
      condition = a != 1, 
      true = logb(x = x, base = a), 
      false = NA_real_
    ), # 対数
    exp_x = a^x # 指数
  )
anim_df

## # A tibble: 26,013 × 4
##        a      x log_x        exp_x
##    <dbl>  <dbl> <dbl>        <dbl>
##  1   0.1 -10      NaN 10000000000.
##  2   0.1  -9.99   NaN  9772372210.
##  3   0.1  -9.98   NaN  9549925860.
##  4   0.1  -9.97   NaN  9332543008.
##  5   0.1  -9.96   NaN  9120108394.
##  6   0.1  -9.95   NaN  8912509381.
##  7   0.1  -9.94   NaN  8709635900.
##  8   0.1  -9.93   NaN  8511380382.
##  9   0.1  -9.92   NaN  8317637711.
## 10   0.1  -9.91   NaN  8128305162.
## # … with 26,003 more rows

　先ほど同様にして計算します。ただし、(変数(真数)が0未満のときのNaNは無視できるが底が1のときのInfは作図に影響するので、)底が1のときの対数を計算しないようにします。

　対数関数と指数関数のアニメーションを作成します。

# 恒等関数を格納
identity_df <- tibble::tibble(
  x = seq(from = min(anim_df[["x"]]), to = max(anim_df[["x"]]), length.out = 101), 
  f_x = x
)

# 対数関数のアニメーションを作図
anim <- ggplot() + 
  geom_line(data = anim_df, 
            mapping = aes(x = x, y = log_x, color = factor(a), linetype = "log"), na.rm = TRUE) + # 対数関数
  geom_line(data = anim_df, 
            mapping = aes(x = x, y = exp_x, color = factor(a), linetype = "exp")) + # 指数関数
  geom_line(data = identity_df, 
            mapping = aes(x = x, y = f_x, linetype = "x")) + # 恒等関数
  geom_vline(xintercept = 0, linetype = "dotted") + # 対数関数の漸近線
  geom_hline(yintercept = 0, linetype = "dotted") + # 指数関数の漸近線
  gganimate::transition_reveal(along = a) + # フレーム:(過去フレームの曲線も描画)
  #gganimate::transition_manual(frames = a) + # フレーム:(フレームごとの曲線を描画)
  scale_color_hue(guide = "none") + # 凡例を非表示
  scale_linetype_manual(breaks = c("log", "exp", "x"), 
                        values = c("solid", "dotdash", "dashed"), 
                        labels = c(expression(log[a]*x), expression(a^x), expression(x)), name = "function") + # 凡例表示用
  coord_fixed(ratio = 1, ylim = c(-10, 10)) + # 描画範囲
  theme(legend.text.align = 0) + # 図の体裁
  labs(title = "Logarithmic functions and Exponential functions", 
       subtitle = "a = {round(frame_along, digits = 2)}", # (transition_reveal関数用)
       #subtitle = "a = {round(as.numeric(current_frame), digits = 2)}", # (transition_manual関数用)
       x = expression(x), 
       y = expression(f(x)))

# 最終フレームの停止フレームを指定
ep <- 10

# gif画像を作成
#gganimate::animate(plot = anim, nframe = frame_num+ep, end_pause = ep, fps = 10, width = 600, height = 600)

　gganimateパッケージを利用して、アニメーション(gif画像)を作成します。
　transition_reveal()またはtransition_manual()のフレーム制御の引数(第1引数)に底の値列aを指定して、底ごとに作図します。transition_reveal()を使うと過去のフレームの曲線も描画します。transition_manual()を使うとフレーム(底の値)ごとに曲線を描画します。
　animate()のplot引数にグラフオブジェクトanim、nframes引数にフレーム数frame_numを指定して、gif画像を作成します。また、fps引数に1秒当たりのフレーム数を指定できます。