はじめに
R言語で三角関数の定義や公式を可視化しようシリーズです。
この記事では、江戸時代の書物に登場する8つの三角関数(八線)を扱います。
【他の記事一覧】
【この記事の内容】
八線表の可視化:三角比
中根元圭の『八線表算法解義』に掲載されている8つの三角関数(正弦・余弦・正接・余接・正割・余割・正矢・余矢)について確認します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているためggplot2を読み込む必要があります。
また、ネイティブパイプ演算子|>を使っています。magrittrパッケージのパイプ演算子%>%に置き換えても処理できますが、その場合はmagrittrも読み込む必要があります。
八線の定義
まずは、八線と狭義の三角関数(サイン・コサイン・タンジェント)の関係を数式で確認します。
| 八線 | 読み | 英名 | 数式表記 | 三角関数による定義 |
|---|---|---|---|---|
| 正弦 | せいげん | sine | $\sin$ | $\sin \theta$ |
| 余弦 | よげん | cosine | $\cos$ | $\cos \theta$ |
| 正接 | せいせつ | tangent | $\tan$ | $\tan \theta = \frac{\sin \theta}{\cos \theta}$ |
| 余接 | よせつ | cotangent | $\cot$ | $\frac{1}{\tan \theta} = \frac{\cos \theta}{\sin \theta}$ |
| 正割 | せいかつ | secant | $\sec$ | $\frac{1}{\cos \theta}$ |
| 余割 | よかつ | cosecant | $\csc, \mathrm{cosec}$ | $\frac{1}{\sin \theta}$ |
| 正矢 | せいし | versed sine | $\mathrm{versin}$ | $1 - \cos \theta$ |
| 余矢 | よし | coversed sine | $\mathrm{coversin}$ | $1 - \sin \theta$ |
八線は、基本的な三角関数として知られているサイン(正弦)・コサイン(余弦)・タンジェント(正接)と、それぞれの逆数(余割・正割・余接)、1とサイン・コサインそれぞれの差(余矢・正矢)の8つの関数です。
八線の計算
次は、八線を計算して、八線表を作成します。
角度を指定して、八線表を作成します。
# 八線表 hassen_df <- tibble::tibble( alpha = seq(from = 0, to = 90, by = 10), # 角度 theta = alpha / 180 * pi, # ラジアン 正弦 = sin(theta), 余弦 = cos(theta), 正接 = tan(theta), 余接 = 1 / tan(theta), 正割 = 1 / cos(theta), 余割 = 1 / sin(theta), 正矢 = 1 - cos(theta), 余矢 = 1 - sin(theta) ) hassen_df
## # A tibble: 10 × 10 ## alpha theta 正弦 余弦 正接 余接 正割 余割 正矢 余矢 ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 0 0 0 1 e+ 0 0 Inf 1 e 0 Inf 0 1 ## 2 10 0.175 0.174 9.85e- 1 1.76e- 1 5.67e+ 0 1.02e 0 5.76 0.0152 0.826 ## 3 20 0.349 0.342 9.40e- 1 3.64e- 1 2.75e+ 0 1.06e 0 2.92 0.0603 0.658 ## 4 30 0.524 0.5 8.66e- 1 5.77e- 1 1.73e+ 0 1.15e 0 2 0.134 0.5 ## 5 40 0.698 0.643 7.66e- 1 8.39e- 1 1.19e+ 0 1.31e 0 1.56 0.234 0.357 ## 6 50 0.873 0.766 6.43e- 1 1.19e+ 0 8.39e- 1 1.56e 0 1.31 0.357 0.234 ## 7 60 1.05 0.866 5 e- 1 1.73e+ 0 5.77e- 1 2 e 0 1.15 0.5 0.134 ## 8 70 1.22 0.940 3.42e- 1 2.75e+ 0 3.64e- 1 2.92e 0 1.06 0.658 0.0603 ## 9 80 1.40 0.985 1.74e- 1 5.67e+ 0 1.76e- 1 5.76e 0 1.02 0.826 0.0152 ## 10 90 1.57 1 6.12e-17 1.63e+16 6.12e-17 1.63e16 1 1 0
度数法における角度$0^{\circ} \leq \alpha \leq 90^{\circ}$を指定して、alpha列とします。
弧度法におけるラジアン$\theta = \alpha \frac{\pi}{180}$に変換して、theta列とします。
角度ごとにそれぞれの関数を計算します。(基本的に、列名に日本語を使うのは避けましょう。)
続いて、八線表をグラフ化します。
・コード(クリックで展開)
作図用に、縦型の八線表を作成します。
# 八線(三角関数)を計算 hassen_df <- tibble::tibble( theta = seq(from = -2*3.1, to = 2*3.1, by = 0.1), # ラジアン 正弦 = sin(theta), 余弦 = cos(theta), 正接 = tan(theta), 余接 = 1 / tan(theta), 正割 = 1 / cos(theta), 余割 = 1 / sin(theta), 正矢 = 1 - cos(theta), 余矢 = 1 - sin(theta) ) |> tidyr::pivot_longer( cols = !theta, names_to = "label", values_to = "value" ) |> dplyr::mutate( label = label |> factor(levels = c("正弦", "余弦", "正接", "余接", "正割", "余割", "正矢", "余矢")) # 色分け用に因子化 ) hassen_df
## # A tibble: 1,000 × 3 ## theta label value ## <dbl> <fct> <dbl> ## 1 -6.2 正弦 0.0831 ## 2 -6.2 余弦 0.997 ## 3 -6.2 正接 0.0834 ## 4 -6.2 余接 12.0 ## 5 -6.2 正割 1.00 ## 6 -6.2 余割 12.0 ## 7 -6.2 正矢 0.00346 ## 8 -6.2 余矢 0.917 ## 9 -6.1 正弦 0.182 ## 10 -6.1 余弦 0.983 ## # … with 990 more rows
こちらは、直接$\theta$を$- 2 \pi$から$2 \pi$の範囲で作成して、それぞれの関数を計算しています。
pivot_longer()で縦型のデータフレームに変換します。
八線のグラフを作成します。
# 八線(三角関数)のグラフを作成 ggplot() + geom_line(data = hassen_df, mapping = aes(x = theta, y = value, color = label)) + # 八線 coord_cartesian(ylim = c(-5, 5)) + # 表示範囲 labs(title = "八線", color = "f", x = expression(theta), y = expression(f(theta)))
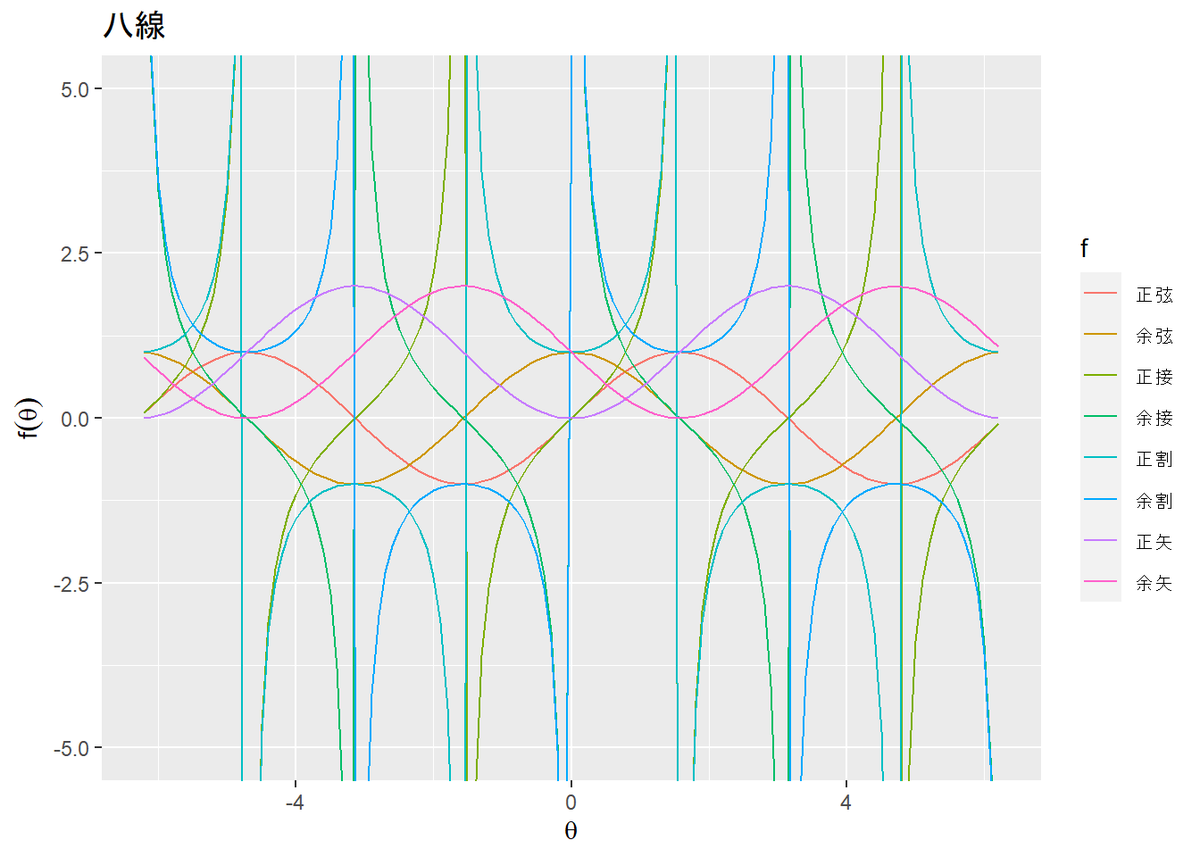
どの関数も周期的に推移しています。
八線の可視化
「八線」と「原点と単位円上の点を斜辺とする直角三角形」の関係をグラフで確認します。
グラフの作成
まずは、角度を固定したグラフを作成します。
角度を指定して、ラジアンに変換します。
# 角度を指定 alpha <- 35 # ラジアンに変換 theta <- alpha / 180 * pi theta
## [1] 0.6108652
度数法における角度$0^{\circ} \leq \alpha \leq 90^{\circ}$を指定して、alphaとします。
弧度法におけるラジアン$\theta = \alpha \frac{2 \pi}{360}$に変換して、thetaとします。
・コード(クリックで展開)
(第1象限における)単位円を描画するためのデータフレームを作成します。
# 単位円(の4分の1)の描画用 sector_df <- tibble::tibble( x = seq(from = 0, to = 1, by = 0.01), y = sqrt(1 - x^2) ) sector_df
## # A tibble: 101 × 2 ## x y ## <dbl> <dbl> ## 1 0 1 ## 2 0.01 1.00 ## 3 0.02 1.00 ## 4 0.03 1.00 ## 5 0.04 0.999 ## 6 0.05 0.999 ## 7 0.06 0.998 ## 8 0.07 0.998 ## 9 0.08 0.997 ## 10 0.09 0.996 ## # … with 91 more rows
単位円の定義が$x^2 + y^2 = 1$なので、$y$について解くと$y = \sqrt{1 - x^2}$で計算できます。
単位正方形を描画するためのデータフレームを作成します。
# 単位正方形の描画用 square_df <- tibble::tibble( x = c(0, 0, 1, 1, 0), y = c(0, 1, 1, 0, 0) ) square_df
## # A tibble: 5 × 2 ## x y ## <dbl> <dbl> ## 1 0 0 ## 2 0 1 ## 3 1 1 ## 4 1 0 ## 5 0 0
単位正方形の頂点の座標を格納します。
八線をそれぞれ線分として描画するためのデータフレームを作成します。
# 八線(線分)の描画用 segment_df <- tibble::tribble( ~label, ~type, ~xstart, ~ystart, ~xend, ~yend, "正弦", "sub", 0, 0, 0, sin(theta), "正弦", "main", cos(theta), 0, cos(theta), sin(theta), "余弦", "main", 0, 0, cos(theta), 0, "余弦", "sub", 0, sin(theta), cos(theta), sin(theta), "正接", "main", 1, 0, 1, tan(theta), "余接", "main", 0, 1, 1/tan(theta), 1, "正割", "main", 0, 0, 1, tan(theta), "余割", "main", 0, 0, 1/tan(theta), 1, "正矢", "main", 1, 0, cos(theta), 0, "余矢", "main", 0, 1, 0, sin(theta) ) |> dplyr::mutate( label = label |> factor(levels = c("正弦", "余弦", "正接", "余接", "正割", "余割", "正矢", "余矢")) # 色分け用に因子化 ) segment_df
## # A tibble: 10 × 6 ## label type xstart ystart xend yend ## <fct> <chr> <dbl> <dbl> <dbl> <dbl> ## 1 正弦 sub 0 0 0 0.574 ## 2 正弦 main 0.819 0 0.819 0.574 ## 3 余弦 main 0 0 0.819 0 ## 4 余弦 sub 0 0.574 0.819 0.574 ## 5 正接 main 1 0 1 0.700 ## 6 余接 main 0 1 1.43 1 ## 7 正割 main 0 0 1 0.700 ## 8 余割 main 0 0 1.43 1 ## 9 正矢 main 1 0 0.819 0 ## 10 余矢 main 0 1 0 0.574
各関数の値を格納しやすいように、tribble()を使ってデータフレームを作成します。線分の始点の座標をxstart, ystart列、終点の座標をxend, yend列とします。「八線の定義」で確認した関数の値は線分の長さであり、座標の値とは異なります。
線分ごとに関数名ラベルを描画するためのデータフレームを作成します。
# ラベルの描画用 segment_label_df <- segment_df |> dplyr::filter(type == "main") |> # 重複を除去 dplyr::group_by(label) |> dplyr::mutate( # 線分の中点に配置 x = median(c(xstart, xend)), y = median(c(ystart, yend)) ) |> dplyr::ungroup() |> dplyr::select(label, x, y) |> tibble::add_column( # ラベルが重ならないように調整 h = c(1, 0.5, 0, 0.5, 0.5, 0.5, 0.5, 0.5), v = c(0.5, 1, 0.5, 0, 0, 1, 1, 0.5), # 別のラベルを作成 tri_label = c( "sin~theta", "cos~theta", "tan~theta", "cot~theta==1/tan~theta", "sec~theta==1/cos~theta", "csc~theta==1/sin~theta", "versin~theta==1-cos~theta", "coversin~theta==1-sin~theta" ), # 関数名と狭義の三角関数による定義 fnc_label = c( paste0("sin~theta==", round(sin(theta), 2)), paste0("cos~theta==", round(cos(theta), 2)), paste0("tan~theta==", round(tan(theta), 2)), paste0("cot~theta==", round(1/tan(theta), 2)), paste0("sec~theta==", round(1/cos(theta), 2)), paste0("csc~theta==", round(1/sin(theta), 2)), paste0("versin~theta==", round(1-cos(theta), 2)), paste0("coversin~theta==", round(1-sin(theta), 2)) ) # 関数名と値 ) segment_label_df
## # A tibble: 8 × 7 ## label x y h v tri_label fnc_label ## <fct> <dbl> <dbl> <dbl> <dbl> <chr> <chr> ## 1 正弦 0.819 0.287 1 0.5 sin~theta sin~theta==0.57 ## 2 余弦 0.410 0 0.5 1 cos~theta cos~theta==0.82 ## 3 正接 1 0.350 0 0.5 tan~theta tan~theta==0.7 ## 4 余接 0.714 1 0.5 0 cot~theta==1/tan~theta cot~theta==1.43 ## 5 正割 0.5 0.350 0.5 0 sec~theta==1/cos~theta sec~theta==1.22 ## 6 余割 0.714 0.5 0.5 1 csc~theta==1/sin~theta csc~theta==1.74 ## 7 正矢 0.910 0 0.5 1 versin~theta==1-cos~theta versin~theta==0.18 ## 8 余矢 0 0.787 0.5 0.5 coversin~theta==1-sin~theta coversin~theta==0.43
各線分の中点にラベルを配置することにします。数式を表示するにはexpression()の記法を使います。
変数となる角度を示すためのデータフレームを作成します。
# 角度記号の描画用 angle_df <- tibble::tibble( alpha = seq(from = 0, to = alpha, by = 0.01), theta = alpha / 180 * pi, x = cos(theta) * 0.1, y = sin(theta) * 0.1 ) angle_df
## # A tibble: 3,501 × 4 ## alpha theta x y ## <dbl> <dbl> <dbl> <dbl> ## 1 0 0 0.1 0 ## 2 0.01 0.000175 0.100 0.0000175 ## 3 0.02 0.000349 0.100 0.0000349 ## 4 0.03 0.000524 0.100 0.0000524 ## 5 0.04 0.000698 0.100 0.0000698 ## 6 0.05 0.000873 0.100 0.0000873 ## 7 0.06 0.00105 0.100 0.000105 ## 8 0.07 0.00122 0.100 0.000122 ## 9 0.08 0.00140 0.100 0.000140 ## 10 0.09 0.00157 0.100 0.000157 ## # … with 3,491 more rows
単位円と同様に、$0^{\circ}$から$\alpha$までの扇状の値を作成します。
変数ラベル(角度ラベル)を描画するためのデータフレームを作成します。
# 角度ラベルの描画用 angle_label_df <- tibble::tibble( alpha = 0.5 * alpha, theta = alpha / 180 * pi, x = cos(theta) * 0.15, y = sin(theta) * 0.15 ) angle_label_df
## # A tibble: 1 × 4 ## alpha theta x y ## <dbl> <dbl> <dbl> <dbl> ## 1 17.5 0.305 0.143 0.0451
角度の中点に配置することにします。
八線のグラフを作成します。
# 変数ラベルを作成 var_label <- paste0("list(alpha==", alpha, "*degree, theta==", round(alpha/180, 3), "*pi)") # 八線の可視化 ggplot() + geom_path(data = sector_df, mapping = aes(x = x, y = y), size = 1) + # 単位円 geom_path(data = square_df, mapping = aes(x = x, y = y), linetype = "dotted") + # 単位正方形 geom_path(data = angle_df, mapping = aes(x = x, y = y)) + # 角度記号 geom_text(data = angle_label_df, mapping = aes(x = x, y = y), label = "theta", parse = TRUE, size = 5) + # 角度ラベル geom_segment(data = segment_df, mapping = aes(x = xstart, y = ystart, xend = xend, yend = yend, color = label, size = label)) + # 八線 geom_label(data = segment_label_df, mapping = aes(x = x, y = y, label = label, color = label, hjust = h, vjust = v), parse = FALSE, alpha = 0.5, size = 4) + # 八線ラベル scale_color_brewer(palette = "Dark2") + # 近い色になるのを避けるため scale_size_manual(breaks = c("正弦", "余弦", "正接", "余接", "正割", "余割", "正矢", "余矢"), values = c(1, 1, 1, 1, 1.5, 1, 1, 1)) + # 正割と余割が重なるため theme(legend.position = "none") + # 凡例を非表示 coord_fixed(ratio = 1, clip = "off") + # アスペクト比 labs(title = "八線", subtitle = parse(text = var_label))
単位円(扇形の線)をgeom_path()、線分をgeom_segment()、ラベル(文字列)をgeom_text()またはgeom_label()で描画します。ラベルとして数式を描画する場合は、parse引数をTRUEにします。
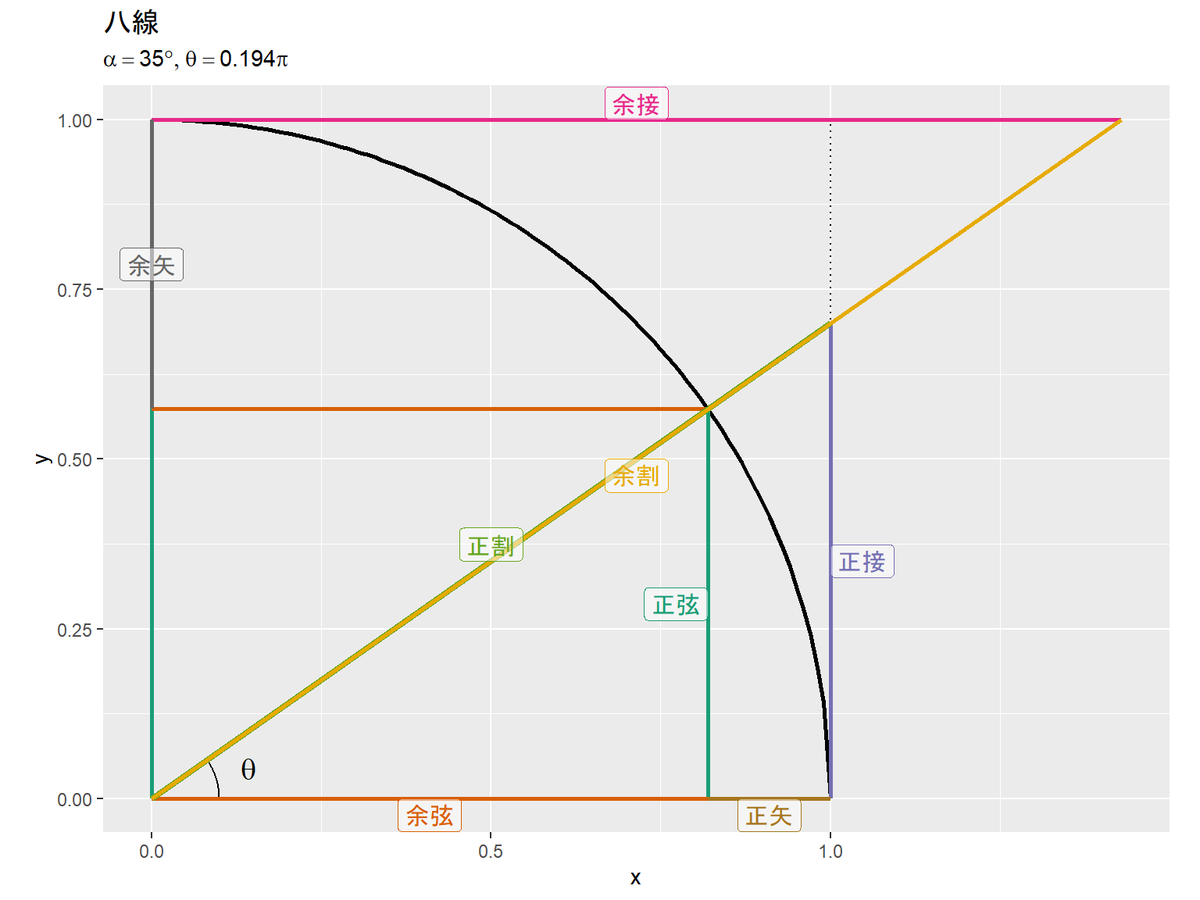
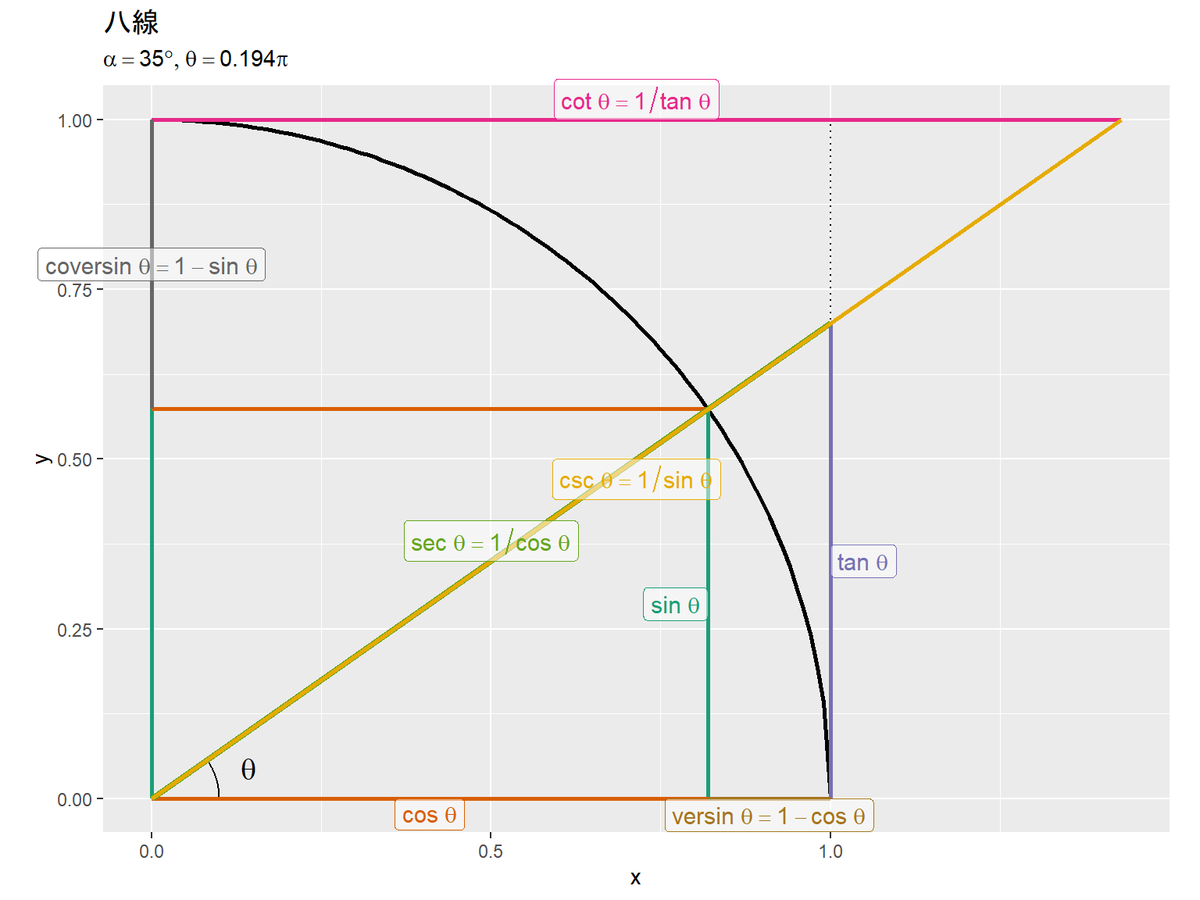
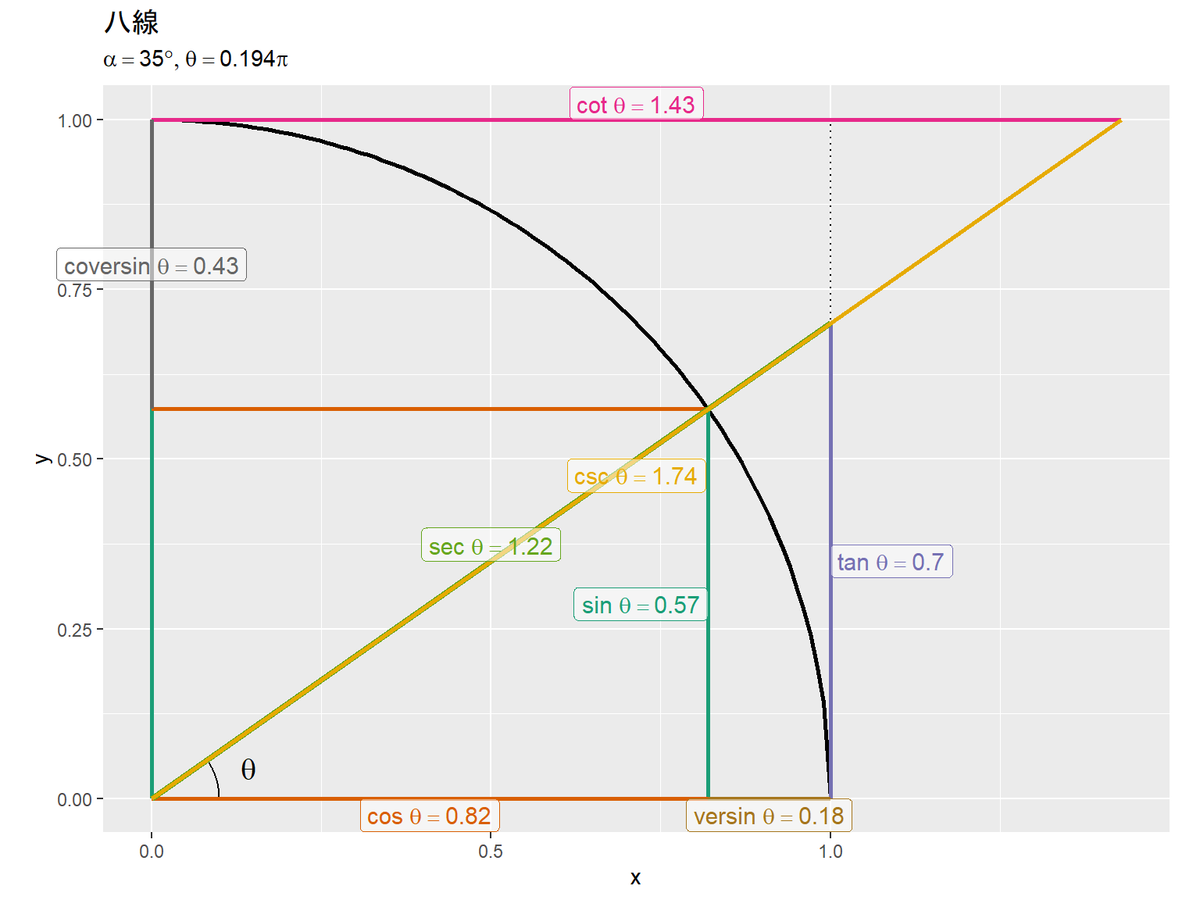
(それぞれの関係を導出してみたかったけどまたの機会に。)
アニメーションの作成
次は、角度と八線の関係をアニメーションで確認します。
・コード(クリックで展開)
フレームごとに八線をそれぞれ線分として描画するためのデータフレームを作成します。
# フレーム数を指定 frame_num <- 101 # 八線(線分)の描画用 anim_segment_df <- tidyr::expand_grid( alpha = seq(from = 0, to = 90, length.out = frame_num), # 角度 label = c("正弦", "正弦", "余弦", "余弦", "正接", "余接", "正割", "余割", "正矢", "余矢") |> factor(levels = c("正弦", "余弦", "正接", "余接", "正割", "余割", "正矢", "余矢")) # 色分け用に因子化 ) |> # 角度ごとに八線(用の行)を複製 dplyr::group_by(alpha) |> dplyr::mutate( theta = unique(alpha) / 180 * pi, # ラジアン type = c("sub", "main", "main", "sub", "main", "main", "main", "main", "main", "main"), xstart = c(0, cos(unique(theta)), 0, 0, 1, 0, 0, 0, 1, 0), ystart = c(0, 0, 0, sin(unique(theta)), 0, 1, 0, 0, 0, 1), xend = c(0, cos(unique(theta)), cos(unique(theta)), cos(unique(theta)), 1, 1/tan(unique(theta)), 1, 1/tan(unique(theta)), cos(unique(theta)), 0), yend = c(sin(unique(theta)), sin(unique(theta)), 0, sin(unique(theta)), tan(unique(theta)), 1, tan(unique(theta)), 1, 0, sin(unique(theta))), frame_label = paste0("α = ", round(unique(alpha), 2), ", Θ = ", round(unique(alpha)/180, 2), "π") |> factor(levels = paste0("α = ", round(seq(0, 90, length.out = frame_num), 2), ", Θ = ", round(seq(0, 90, length.out = frame_num)/180, 2), "π")) # フレーム切替用ラベル ) |> dplyr::ungroup() anim_segment_df
## # A tibble: 1,010 × 9 ## alpha label theta type xstart ystart xend yend frame_label ## <dbl> <fct> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0 正弦 0 sub 0 0 0 0 α = 0, Θ = 0π ## 2 0 正弦 0 main 1 0 1 0 α = 0, Θ = 0π ## 3 0 余弦 0 main 0 0 1 0 α = 0, Θ = 0π ## 4 0 余弦 0 sub 0 0 1 0 α = 0, Θ = 0π ## 5 0 正接 0 main 1 0 1 0 α = 0, Θ = 0π ## 6 0 余接 0 main 0 1 Inf 1 α = 0, Θ = 0π ## 7 0 正割 0 main 0 0 1 0 α = 0, Θ = 0π ## 8 0 余割 0 main 0 0 Inf 1 α = 0, Θ = 0π ## 9 0 正矢 0 main 1 0 1 0 α = 0, Θ = 0π ## 10 0 余矢 0 main 0 1 0 0 α = 0, Θ = 0π ## # … with 1,000 more rows
フレーム数frame_numを指定して、フレームごとに角度を変化させて、それぞれ関数を計算します。
$0^{\circ} \leq \alpha \leq 90^{\circ}$の範囲を等間隔にフレーム数個に分割して、alpha列とします。
expand_grid()で全ての組み合わせを作成することで、alpha列の値ごとにラベル(値の受け皿となる行)を複製します。
フレーム切替用のラベル列を作成します。因子のレベルがフレームの順番に対応します。
フレームごとに関数名ラベルを描画するためのデータフレームを作成します。
# 八線ラベルの描画用 anim_segment_label_df <- anim_segment_df |> dplyr::filter(type == "main") |> # 重複を除去 dplyr::group_by(theta) |> dplyr::mutate( # ラベルが重ならないように調整 h = c(1, 0.5, 0, 0.5, 0.5, 0.5, 0.5, 0.5), v = c(0.5, 1, 0.5, 0, 0, 1, 1, 0.5), # 別のラベルを作成 tri_label = c( "sin~theta", "cos~theta", "tan~theta", "cot~theta==1/tan~theta", "sec~theta==1/cos~theta", "csc~theta==1/sin~theta", "versin~theta==1-cos~theta", "coversin~theta==1-sin~theta" ), # 関数名と狭義の三角関数による定義 fnc_label = c( paste0("sin~theta==", round(sin(unique(theta)), 2)), paste0("cos~theta==", round(cos(unique(theta)), 2)), paste0("tan~theta==", round(tan(unique(theta)), 2)), paste0("cot~theta==", round(1/tan(unique(theta)), 2)), paste0("sec~theta==", round(1/cos(unique(theta)), 2)), paste0("csc~theta==", round(1/sin(unique(theta)), 2)), paste0("versin~theta==", round(1-cos(unique(theta)), 2)), paste0("coversin~theta==", round(1-sin(unique(theta)), 2)) ) # 関数名と値 ) |> dplyr::group_by(alpha, label) |> dplyr::mutate( # 線分の中点に配置 x = median(c(xstart, xend)), y = median(c(ystart, yend)), ) |> dplyr::ungroup() |> dplyr::select(alpha, theta, frame_label, label, fnc_label, tri_label, x, y, h, v) anim_segment_label_df
## # A tibble: 808 × 10 ## alpha theta frame_label label fnc_label tri_label x y h ## <dbl> <dbl> <fct> <fct> <chr> <chr> <dbl> <dbl> <dbl> ## 1 0 0 α = 0, Θ = 0π 正弦 sin~theta… sin~theta 1 0 1 ## 2 0 0 α = 0, Θ = 0π 余弦 cos~theta… cos~theta 0.5 0 0.5 ## 3 0 0 α = 0, Θ = 0π 正接 tan~theta… tan~theta 1 0 0 ## 4 0 0 α = 0, Θ = 0π 余接 cot~theta… cot~thet… Inf 1 0.5 ## 5 0 0 α = 0, Θ = 0π 正割 sec~theta… sec~thet… 0.5 0 0.5 ## 6 0 0 α = 0, Θ = 0π 余割 csc~theta… csc~thet… Inf 0.5 0.5 ## 7 0 0 α = 0, Θ = 0π 正矢 versin~th… versin~t… 1 0 0.5 ## 8 0 0 α = 0, Θ = 0π 余矢 coversin~… coversin… 0 0.5 0.5 ## 9 0.9 0.0157 α = 0.9, Θ = 0π 正弦 sin~theta… sin~theta 1.00 0.00785 1 ## 10 0.9 0.0157 α = 0.9, Θ = 0π 余弦 cos~theta… cos~theta 0.500 0 0.5 ## # … with 798 more rows, and 1 more variable: v <dbl>
フレーム(角度)ごと、同様に処理します。
フレームごとに角度を示すためのデータフレームを作成します。
# 角度記号の描画用 anim_angle_df <- tidyr::expand_grid( frame = 1:frame_num, alpha = seq(from = 0, to = 90, by = 0.1) # 角度 ) |> # フレームごとに全ての値を複製 dplyr::group_by(frame) |> dplyr::filter(alpha <= seq(from = 0, to = 90, length.out = frame_num)[unique(frame)]) |> # フレームごとの角度以下の値を抽出 dplyr::mutate( theta = alpha / 180 * pi, # ラジアン x = cos(theta) * 0.1, y = sin(theta) * 0.1, frame_label = paste0("α = ", round(seq(0, 90, length.out = frame_num)[unique(frame)], 2), ", Θ = ", round(seq(0, 90, length.out = frame_num)[unique(frame)]/180, 2), "π") |> factor(levels = paste0("α = ", round(seq(0, 90, length.out = frame_num), 2), ", Θ = ", round(seq(0, 90, length.out = frame_num)/180, 2), "π")) # フレーム切替用ラベル ) anim_angle_df
## # A tibble: 45,537 × 6 ## # Groups: frame [101] ## frame alpha theta x y frame_label ## <int> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 0 0 0.1 0 α = 0, Θ = 0π ## 2 2 0 0 0.1 0 α = 0.9, Θ = 0π ## 3 2 0.1 0.00175 0.100 0.000175 α = 0.9, Θ = 0π ## 4 2 0.2 0.00349 0.100 0.000349 α = 0.9, Θ = 0π ## 5 2 0.3 0.00524 0.100 0.000524 α = 0.9, Θ = 0π ## 6 2 0.4 0.00698 0.100 0.000698 α = 0.9, Θ = 0π ## 7 2 0.5 0.00873 0.100 0.000873 α = 0.9, Θ = 0π ## 8 2 0.6 0.0105 0.100 0.00105 α = 0.9, Θ = 0π ## 9 2 0.7 0.0122 0.100 0.00122 α = 0.9, Θ = 0π ## 10 2 0.8 0.0140 0.100 0.00140 α = 0.9, Θ = 0π ## # … with 45,527 more rows
フレーム番号列frameと角度列alphaの全ての組み合わせをexpand_grid()で作成します。
alphaが各フレームの角度以下の行のみ取り出して、同様に処理します。
先に作成したフレーム切り替え用のラベル列と一致するようにラベルを作成します。
フレームごとに角度ラベルを描画するためのデータフレームを作成します。
# 角度ラベルの描画用 anim_angle_label_df <- anim_angle_df |> dplyr::group_by(frame_label) |> dplyr::mutate(alpha = median(alpha)) |> dplyr::distinct(frame_label, alpha) |> dplyr::mutate( theta = alpha / 180 * pi, x = cos(theta) * 0.15, y = sin(theta) * 0.15 ) anim_angle_df
## # A tibble: 45,537 × 6 ## # Groups: frame [101] ## frame alpha theta x y frame_label ## <int> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 0 0 0.1 0 α = 0, Θ = 0π ## 2 2 0 0 0.1 0 α = 0.9, Θ = 0π ## 3 2 0.1 0.00175 0.100 0.000175 α = 0.9, Θ = 0π ## 4 2 0.2 0.00349 0.100 0.000349 α = 0.9, Θ = 0π ## 5 2 0.3 0.00524 0.100 0.000524 α = 0.9, Θ = 0π ## 6 2 0.4 0.00698 0.100 0.000698 α = 0.9, Θ = 0π ## 7 2 0.5 0.00873 0.100 0.000873 α = 0.9, Θ = 0π ## 8 2 0.6 0.0105 0.100 0.00105 α = 0.9, Θ = 0π ## 9 2 0.7 0.0122 0.100 0.00122 α = 0.9, Θ = 0π ## 10 2 0.8 0.0140 0.100 0.00140 α = 0.9, Θ = 0π ## # … with 45,527 more rows
フレームごとに、同様に処理します。
八線のアニメーションを作成します。
# 八線のアニメーションを作図 anim <- ggplot() + geom_path(data = sector_df, mapping = aes(x = x, y = y), size = 1) + # 単位円 geom_path(data = square_df, mapping = aes(x = x, y = y), linetype = "dotted") + # 単位正方形 geom_path(data = anim_angle_df, mapping = aes(x = x, y = y)) + # 角度記号 geom_text(data = anim_angle_label_df, mapping = aes(x = x, y = y), label = "theta", parse = TRUE, size = 5) + # 角度ラベル geom_segment(data = anim_segment_df, mapping = aes(x = xstart, y = ystart, xend = xend, yend = yend, color = label, size = label)) + # 八線 geom_label(data = anim_segment_label_df, mapping = aes(x = x, y = y, label = fnc_label, color = label, hjust = h, vjust = v), parse = TRUE, alpha = 0.5, size = 6) + # 八線ラベル gganimate::transition_manual(frames = frame_label) + # フレーム切替 scale_color_brewer(palette = "Dark2") + # 近い色になるのを避けるため scale_size_manual(breaks = c("正弦", "余弦", "正接", "余接", "正割", "余割", "正矢", "余矢"), values = c(1, 1, 1, 1, 1.5, 1, 1, 1)) + # 正割と余割が重なるため theme(legend.position = "none") + # 凡例を非表示 coord_fixed(ratio = 1, xlim = c(0, 2), ylim = c(0, 2), clip = "off") + # アスペクト比 labs(title = "八線", subtitle = "{current_frame}") # gif画像を作成 gganimate::animate(plot = anim, nframe = frame_num, fps = 10, width = 800, height = 800)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のnframes引数にフレーム数、fps引数に1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
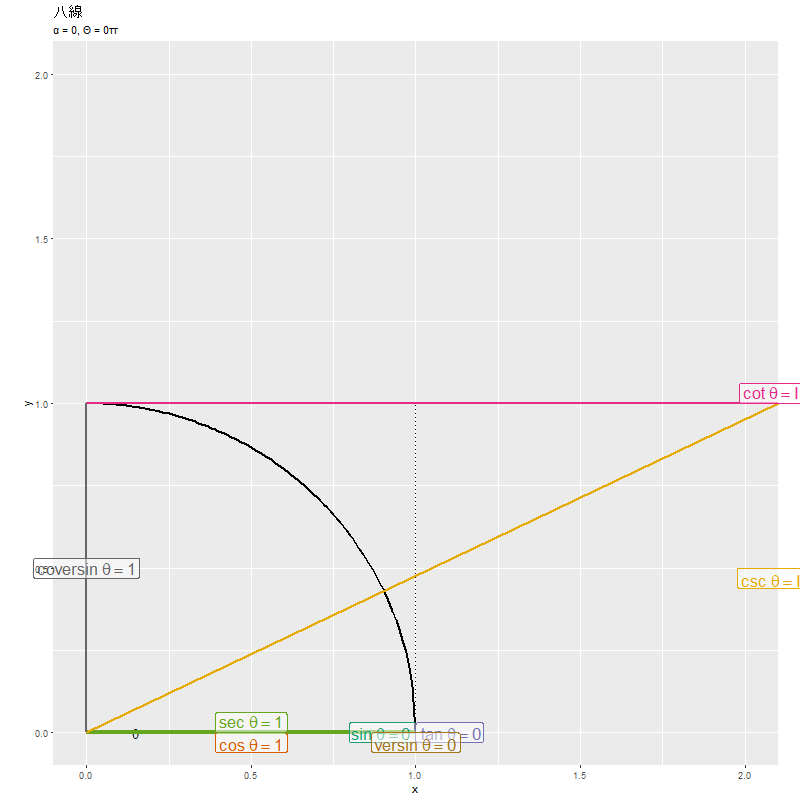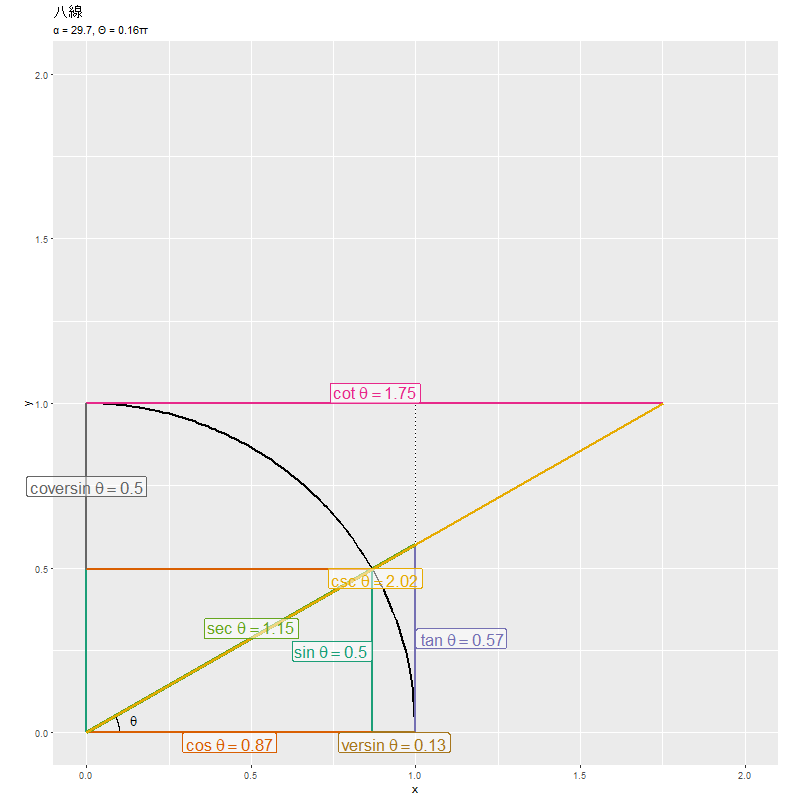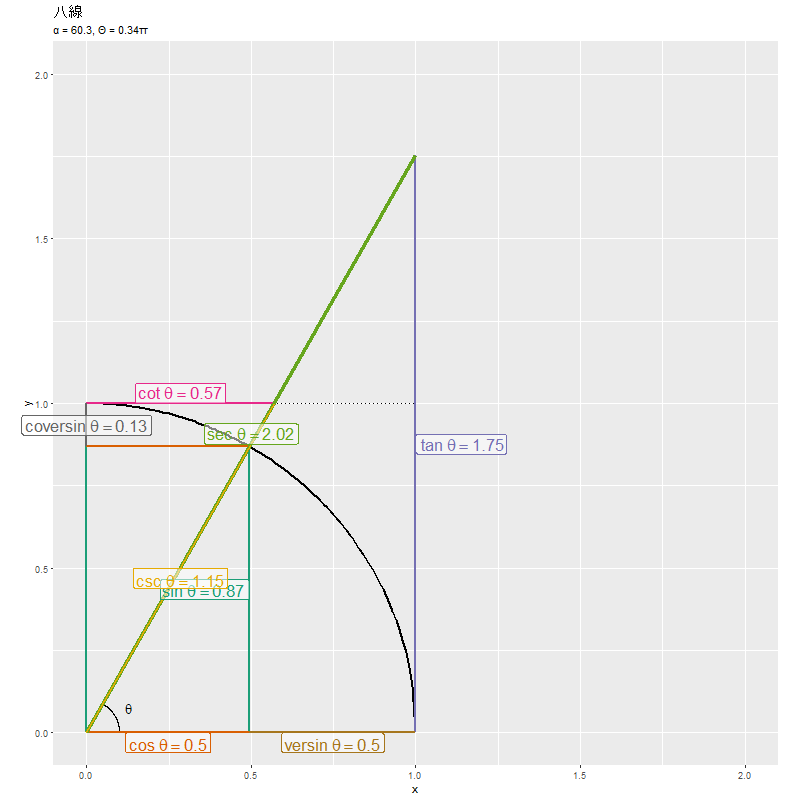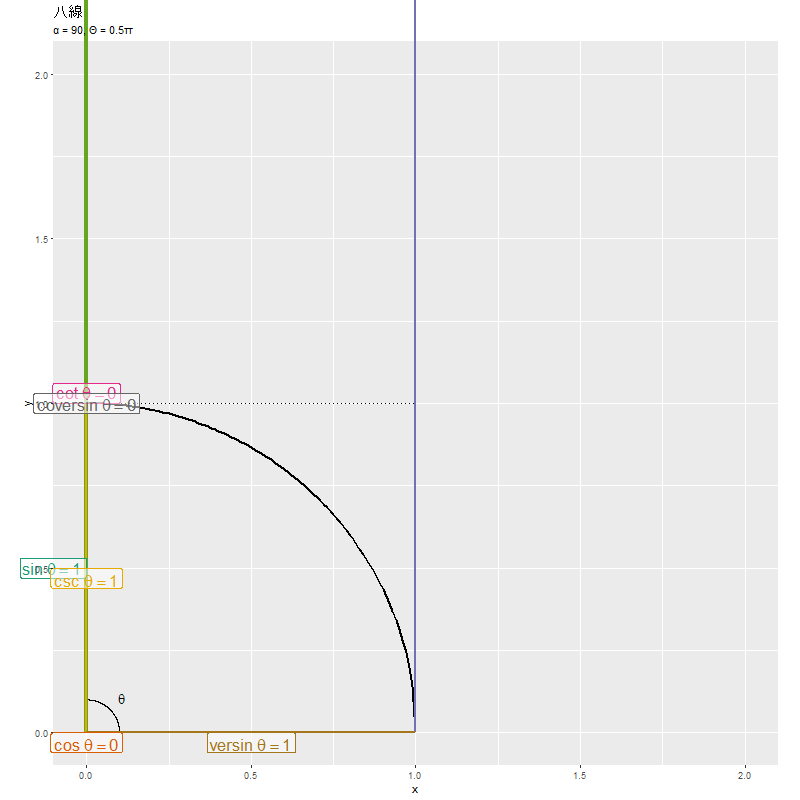
各線分の長さの変化が、「八線の計算」のグラフに対応します。ただし、単位円全体における推移のグラフです。
この記事では、日本古来の三角関数について確認しました。
参考書籍
- 『三角関数(改定第3版)』(Newton別冊)ニュートンプレス,2022年.
おわりに
年末年始に新しいことをしたいなと気まぐれに手に取ったのが三角関数のムック本だったので、これを機会にちょっと勉強してみようかと始めました。が、どうしてこうなった。へぇーで読み飛ばしていい昔話だと思うんですが、図を再現してみたくなってしまいました。
調べてみたら他にも色々あるみたいですね。知ってしまったからには他のもまとめてみたいですが、またの機会にします。それと、単位円バージョンもする必要がありますね。こっちは早くやりたいのですが、正解の例や図を見付けないと再現できないので、ぼちぼち調べます。
ちなみに私は、三角関数は早々に投げてしまってまともに勉強していないので、三角比と三角関数の違いも分からないレベルです。半年くらいかけてじっくり取り組みたいなと思っています、今のところは、三角関数カテゴリも作ったし。この記事がその始めの一歩です。
2022年12月30日は、Juice=Juiceの現リーダーの植村あかりさんの24歳のお誕生日です。
おめでとうございます!あーりーらしい新たなJuiceになってきて頼もしい限りです。ところで、グループリーダーの卒業発表月間な今日この頃なんですが、あーりーはどうなんでしょうか、、
【次の内容】
つづく?