はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、多次元混合ガウス分布(多変量混合正規分布)の定義を確認します。
【前の内容】
【他の記事一覧】
【この記事の内容】
多次元混合ガウス分布の定義式
多次元ガウス分布(Multivariate Gaussian Mixture Distribution)・多変量正規分布(Multivariate Normal Mixture Distribution)の定義を確認します。
定義式
混合ガウス分布は、複数のガウス分布を線形結合した分布です。ガウス分布については「多次元ガウス分布の定義式 - からっぽのしょこ」を参照してください。
多次元混合ガウス分布は、パラメータ$\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}$を用いて、次の式で定義されます。
ここで、$K$はクラスタ数、$\pi_k$はクラスタ$k$となる確率、$\boldsymbol{\mu}_k$はクラスタ$k$の平均ベクトル、$\boldsymbol{\Sigma}_k$は分散共分散行列です。
各クラスとなる確率をまとめたベクトル$\boldsymbol{\pi} = (\pi_1, \pi_2, \cdots, \pi_K)$を混合比率(混合パラメータ)と言います。各成分は0から1の値で、全ての成分の和が1になる必要があります。この条件を数式で表すと、$0 \leq \pi_k \leq 1$または$\pi_k \in (0, 1)$、$\sum_{k=1}^K \pi_k = 1$です。
全てのクラスタの平均ベクトルをまとめて$\boldsymbol{\mu} = \{\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \cdots, \boldsymbol{\mu}_K\}$、分散共分散行列をまとめて$\boldsymbol{\Sigma} = \{\boldsymbol{\Sigma}_1, \boldsymbol{\Sigma}_2, \cdots, \boldsymbol{\Sigma}_K\}$で表します。
$\mathbf{x}, \boldsymbol{\mu}_k$は$D$次元ベクトル、$\boldsymbol{\Sigma}_k$は$D \times D$の行列です。
$\sigma_{k,d}$はクラスタ$k$のときの$x_d$の標準偏差、$\sigma_{k,d}^2 = \sigma_{k,d,d}$は$x_d$の分散、$\sigma_{k,i,j} = \sigma_{k,j,i}$は$x_i, x_j$の共分散です。
$x_d$は実数をとり、$\mu_{k,d}$は実数、$\sigma_{k,d}, \sigma_{k,d}^2$は正の実数、$\sigma_{k,i,j}\ (i \neq j)$は実数、また$\boldsymbol{\Sigma}_k$は正定値行列を満たす必要があります。
混合ガウス分布は、混合比率$\boldsymbol{\pi}$を用いて$K$個のガウス分布の加重平均で定義されています。
多次元混合ガウス分布の確率変数$\mathbf{x}$は、割り当てられたクラスタを潜在変数$\mathbf{s}$で表すことで、次の式でも定義できます。
1 of K表現(one-hotベクトル)の潜在変数$\mathbf{s} = (s_1, s_2, \cdots, s_K)$を導入します。割り当てられたクラスタに対応する成分が1で、それ以外の成分が0である$K$次元ベクトル$\mathbf{s}$によってクラスタを表します。各成分が0か1の値をとり、(値が1なのは1つだけなので)全ての成分の和が1になる条件を数式で表すと、$s_k \in \{0, 1\}$、$\sum_{k=1}^K s_k = 1$です。
$\mathbf{s}$は、パラメータ$\boldsymbol{\pi}$を持つカテゴリ分布の確率変数として定義できます。確率$\pi_k$で$s_k = 1$(クラスタが$k$)になります。カテゴリ分布については「カテゴリ分布の定義式 - からっぽのしょこ」を参照してください。
0乗は1なので($a^0 = 1$なので)、$s_k\ (k = 1, \dots, K)$を指数として用いて総乗$\prod_k$の形にすることで、割り当てられたクラスタの分布のみを取り出すことができます。
クラスタが$k$のとき($s_k = 1$のとき)
となります。
つまり、クラスタが$k$のとき($s_k = 1$のとき)、$\mathbf{x}$はクラスタ$k$の分布に従います。
混合分布は複数の分布を用いて定義されていますが、確率変数は1つのクラスタに従うように設計されています。
ここまでは、混合ガウス分布の定義を数式から確認しました。次は、グラフから確認します。
グラフの確認
「K個のガウス分布」と「クラスタ数がKの混合ガウス分布」の関係をグラフで確認します。混合ガウス分布のグラフ作成については「分布の作図」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(mvnfast)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
混合ガウス分布のパラメータ$\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}$を指定します。
# 次元数を設定:(固定) D <- 2 # クラスタ数を指定 K <- 3 # 混合比率を指定 pi_k <- c(0.45, 0.25, 0.3) # K個の平均ベクトルを指定 mu_kd <- c( 0, 5, 5, -10, -10, -5 ) |> matrix(nrow = K, ncol = D, byrow = TRUE) # マトリクスに変換 # K個の分散共分散行列を指定 sigma_ddk <- c( 36, 10, 10, 25, 9, -1.3, -1.3, 16, 25, -3.2, -3.2, 16 ) |> array(dim = c(D, D, K)) # 3次元配列に変換 mu_kd; sigma_ddk
## [,1] [,2] ## [1,] 0 5 ## [2,] 5 -10 ## [3,] -10 -5 ## , , 1 ## ## [,1] [,2] ## [1,] 36 10 ## [2,] 10 25 ## ## , , 2 ## ## [,1] [,2] ## [1,] 9.0 -1.3 ## [2,] -1.3 16.0 ## ## , , 3 ## ## [,1] [,2] ## [1,] 25.0 -3.2 ## [2,] -3.2 16.0
次元数Dとクラスタ数K、各パラメータの値を指定します。
・K個のガウス分布の計算コード(クリックで展開)
設定したパラメータに応じて、混合ガウス分布の確率変数$\mathbf{x} = (x_1, x_2)$がとり得る値を作成します。
# 確率変数の値を作成 x_1_vals <- seq( from = min(mu_kd[, 1] - sqrt(sigma_ddk[1, 1, ]) * 3), to = max(mu_kd[, 1] + sqrt(sigma_ddk[1, 1, ]) * 3), length.out = 201 ) x_2_vals <- seq( from = min(mu_kd[, 2] - sqrt(sigma_ddk[2, 2, ]) * 3), to = max(mu_kd[, 2] + sqrt(sigma_ddk[2, 2, ]) * 3), length.out = 201 )
$x_1, x_2$の値(x軸・y軸の値)をx_1_vals, x_2_valsとします。この例ではそれぞれ、クラスタごとに平均を中心に標準偏差の3倍を範囲としたときの最小値から最大値を範囲とします。
クラスタごとに、$\mathbf{x}$の点ごとの確率密度を計算して、混合比率を掛けます。
# クラスタごとにガウス分布の確率密度を計算 dens_cluster_df <- tidyr::expand_grid( k = 1:K, # クラスタ番号 x_1 = x_1_vals, # x軸の値 x_2 = x_2_vals # y軸の値 ) |> # クラスタごとに格子点を複製 dplyr::group_by(k) |> # クラスタごとの計算用にグループ化 dplyr::mutate( dens_k = mvnfast::dmvn( X = cbind(x_1, x_2), mu = mu_kd[unique(k), ], sigma = sigma_ddk[, , unique(k)] ), # クラスタごとの確率密度 dens_k_weighted = dens_k * pi_k[unique(k)], # 重み付け確率密度 k = factor(k, levels = 1:K), # 色分け用に因子化 label_k = paste0( "list(", "k==", unique(k), ", mu[k]==(list(", paste0(mu_kd[unique(k), ], collapse = ", "), "))", ", Sigma[k]==(list(", paste0(sigma_ddk[, , unique(k)], collapse = ", "), "))", ")" ), # パラメータラベル label_k_weighted = paste0( "list(", "k==", unique(k), ", pi[k]==", pi_k[unique(k)], ", mu[k]==(list(", paste0(mu_kd[unique(k), ], collapse = ", "), "))", ", Sigma[k]==(list(", paste0(sigma_ddk[, , unique(k)], collapse = ", "), "))", ")" ) # パラメータラベル ) |> dplyr::ungroup() # グループ化を解除 dens_cluster_df
## # A tibble: 121,203 × 7 ## k x_1 x_2 dens_k dens_k_weighted label_k label_k_weighted ## <fct> <dbl> <dbl> <dbl> <dbl> <chr> <chr> ## 1 1 -25 -22 1.12e-10 5.05e-11 list(k==1, mu[k]… list(k==1, pi[k… ## 2 1 -25 -21.8 1.35e-10 6.10e-11 list(k==1, mu[k]… list(k==1, pi[k… ## 3 1 -25 -21.6 1.63e-10 7.35e-11 list(k==1, mu[k]… list(k==1, pi[k… ## 4 1 -25 -21.4 1.96e-10 8.84e-11 list(k==1, mu[k]… list(k==1, pi[k… ## 5 1 -25 -21.2 2.36e-10 1.06e-10 list(k==1, mu[k]… list(k==1, pi[k… ## 6 1 -25 -21.0 2.82e-10 1.27e-10 list(k==1, mu[k]… list(k==1, pi[k… ## 7 1 -25 -20.7 3.38e-10 1.52e-10 list(k==1, mu[k]… list(k==1, pi[k… ## 8 1 -25 -20.5 4.03e-10 1.81e-10 list(k==1, mu[k]… list(k==1, pi[k… ## 9 1 -25 -20.3 4.80e-10 2.16e-10 list(k==1, mu[k]… list(k==1, pi[k… ## 10 1 -25 -20.1 5.70e-10 2.56e-10 list(k==1, mu[k]… list(k==1, pi[k… ## # … with 121,193 more rows
クラスタごとに、確率密度と混合比率によって重み付けした確率密度を計算します。多次元ガウス分布の確率密度は、mvnfastパッケージのdmvn()で計算できます。
また、パラメータを表示するためのラベル(expression()の記法の文字列)を作成しておきます。
・K個のガウス分布の作図コード(クリックで展開)
パラメータの値を数式で表示するための文字列ベクトルを作成します。
# パラメータラベルを作成 param_label_cluster <- dens_cluster_df[["label_k"]] |> # ラベル列を抽出 unique() # 重複を削除 param_label_cluster
## [1] "list(k==1, mu[k]==(list(0, 5)), Sigma[k]==(list(36, 10, 10, 25)))" ## [2] "list(k==2, mu[k]==(list(5, -10)), Sigma[k]==(list(9, -1.3, -1.3, 16)))" ## [3] "list(k==3, mu[k]==(list(-10, -5)), Sigma[k]==(list(25, -3.2, -3.2, 16)))"
データフレームからラベル列を取り出して、unique()で重複を削除します。
$K$個のガウス分布のグラフを作成します。
# クラスタごとにガウス分布を作図 ggplot() + geom_contour(data = dens_cluster_df, mapping = aes(x = x_1, y = x_2, z = dens_k, color = k, linetype = "cluster"), size = 1) + # クラスタごとの確率密度 scale_color_hue(breaks = 1:K, labels = parse(text = param_label_cluster), name = "cluster") + # 線の色の凡例ラベル scale_linetype_manual(breaks = "cluster", values = "solid", labels = "cluster k distribution", name = "density") + # 線の種類の凡例ラベル coord_fixed(ratio = 1) + # アスペクト比 theme(legend.position = "right", legend.direction="vertical", legend.text.align = 0) + # 図の体裁 labs(title = "Gaussian Distribution", subtitle = parse(text = paste0("K==", K)), x = expression(x[1]), y = expression(x[2]))
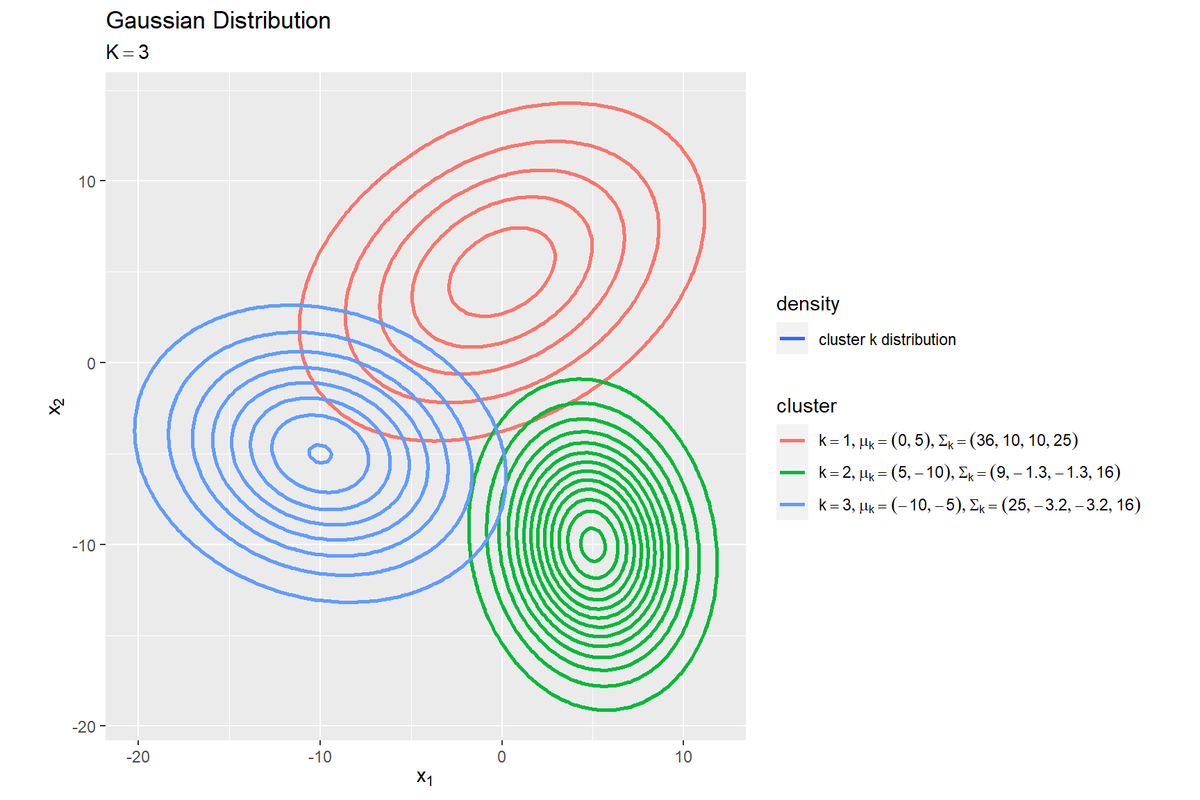
クラスタごとに色分けして描画します。
クラスタごとに1つの山になります。それぞれの体積が1(それぞれ積分すると1)になります。
・K個の重み付けガウス分布の作図コード(クリックで展開)
同様に、パラメータラベルを取り出します。
# パラメータラベルを作成 param_label_weighted <- dens_cluster_df[["label_k_weighted"]] |> # ラベル列を抽出 unique() # 重複を削除 param_label_weighted
## [1] "list(k==1, pi[k]==0.45, mu[k]==(list(0, 5)), Sigma[k]==(list(36, 10, 10, 25)))" ## [2] "list(k==2, pi[k]==0.25, mu[k]==(list(5, -10)), Sigma[k]==(list(9, -1.3, -1.3, 16)))" ## [3] "list(k==3, pi[k]==0.3, mu[k]==(list(-10, -5)), Sigma[k]==(list(25, -3.2, -3.2, 16)))"
共通の値で等高線を引くための数値ベクトルを作成します。
# 等高線を引く値を作成 break_vec <- ggplot2:::contour_breaks( c(min(dens_cluster_df[["dens_k_weighted"]]), max(dens_cluster_df[["dens_k_weighted"]])) ) break_vec
## [1] 0.0000 0.0005 0.0010 0.0015 0.0020 0.0025 0.0030 0.0035
geom_contour()で使われているcontour_breaks()で値を作成します(雰囲気で使っているので解説は省略します)。
$K$個の重み付けしたガウス分布のグラフを、元の分布と重ねて作成します。
# クラスタごとに重み付けしたガウス分布を作図 ggplot() + geom_contour(data = dens_cluster_df, mapping = aes(x = x_1, y = x_2, z = dens_k, color = k, linetype = "cluster"), breaks = break_vec, size = 1) + # クラスタごとの確率密度 geom_contour(data = dens_cluster_df, mapping = aes(x = x_1, y = x_2, z = dens_k_weighted, color = k, linetype = "weighted"), breaks = break_vec, size = 1) + # クラスタごとの割り引き確率密度 scale_color_hue(breaks = 1:K, labels = parse(text = param_label_cluster), name = "cluster") + # 線の色の凡例ラベル scale_linetype_manual(breaks = c("cluster", "weighted"), values = c("dotdash", "solid"), labels = c("cluster k distribution", "weighted distribution"), name = "density") + # 線の種類 coord_fixed(ratio = 1) + # アスペクト比 theme(legend.position = "right", legend.direction="vertical", legend.text.align = 0) + # 図の体裁 guides(linetype = guide_legend(override.aes = list(size = 0.5))) + # 凡例の体裁 labs(title = "Gaussian Distribution", subtitle = parse(text = paste0("K==", K)), x = expression(x[1]), y = expression(x[2]))
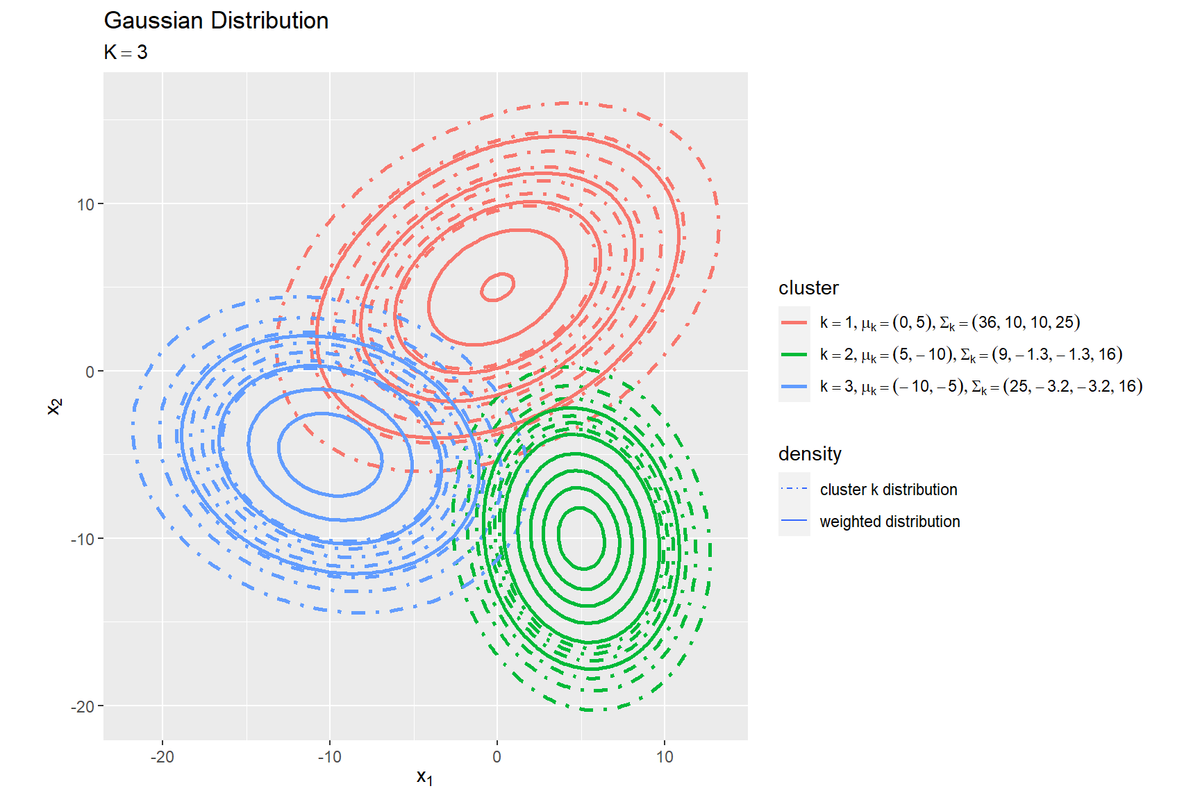
クラスタごとに色分けして、元の分布を点入りの破線で示します。
混合比率(各分布の重み)は0から1の値なので、それぞれ山が小さくなり(等高線の間隔が広く)ます。値を掛けただけなので、水平方向には変化しません。
混合比率を掛けたことで、各山の体積が混合比率に一致し、全ての山の体積の合計が1になります。
・混合ガウス分布の計算と作図コード(クリックで展開)
混合ガウス分布の確率密度を計算します。
# 混合ガウス分布の確率密度を計算 dens_mixture_df <- dens_cluster_df |> dplyr::group_by(x_1, x_2) |> # 点ごとの計算用にグループ化 dplyr::summarise(density = sum(dens_k_weighted), .groups = "drop") # K個の分布の加重平均を計算 dens_mixture_df
## # A tibble: 40,401 × 3 ## x_1 x_2 density ## <dbl> <dbl> <dbl> ## 1 -25 -22 3.28e-10 ## 2 -25 -21.8 4.19e-10 ## 3 -25 -21.6 5.33e-10 ## 4 -25 -21.4 6.77e-10 ## 5 -25 -21.2 8.58e-10 ## 6 -25 -21.0 1.09e- 9 ## 7 -25 -20.7 1.37e- 9 ## 8 -25 -20.5 1.72e- 9 ## 9 -25 -20.3 2.16e- 9 ## 10 -25 -20.1 2.71e- 9 ## # … with 40,391 more rows
x_1, x_2列でグループ化することでx_1_vals, x_2_valsの格子点($\mathbf{x}$の点)ごとに、重み付けした確率密度を合計します。
混合ガウス分布のパラメータラベルを作成します。
# パラメータラベルを作成 param_label_df <- tibble::tibble( x = -Inf, # x軸の値 y = Inf, # y軸の値 label = paste0( paste0("pi = (", paste0(pi_k, collapse = ", "), ")"), "\n", paste0("mu = (", paste0("(", apply(mu_kd, 1, paste0, collapse = ", "), ")", collapse = ", "), ")"), "\n", paste0("Sigma = (", paste0("(", apply(sigma_ddk, 3, paste0, collapse = ", "), ")", collapse = ", "), ")") ) # パラメータラベル ) param_label_df
## # A tibble: 1 × 3 ## x y label ## <dbl> <dbl> <chr> ## 1 -Inf Inf "pi = (0.45, 0.25, 0.3)\nmu = ((0, 5), (5, -10), (-10, -5))\nSigm…
混合ガウス分布のグラフを、$K$個のガウス分布と重ねて作成します。
# 混合ガウス分布を作図 ggplot() + geom_contour(data = dens_mixture_df, mapping = aes(x = x_1, y = x_2, z = density, linetype = "mixture"), color = "hotpink", size = 1) + # 混合分布の確率密度 geom_contour(data = dens_cluster_df, mapping = aes(x = x_1, y = x_2, z = dens_k_weighted, color = k, linetype = "weighted"), breaks = break_vec, size = 1) + # クラスタごとの割り引き確率密度 geom_label(data = param_label_df, mapping = aes(x = x, y = y, label = label), hjust = 0, vjust = 1, alpha = 0.5) + # パラメータラベル scale_color_hue(breaks = 1:K, labels = parse(text = param_label_weighted), name = "cluster") + # 線の色の凡例ラベル scale_linetype_manual(breaks = c("weighted", "mixture"), values = c("dashed", "solid"), labels = c("weighted distribution", "mixture distribution"), name = "density") + # 線の種類 coord_fixed(ratio = 1) + # アスペクト比 theme(legend.position = "right", legend.direction="vertical", legend.text.align = 0) + # 図の体裁 guides(linetype = guide_legend(override.aes = list(size = 0.5))) + # 凡例の体裁 labs(title = "Gaussian Mixture Distribution", subtitle = paste0("K = ", K), x = expression(x[1]), y = expression(x[2]))
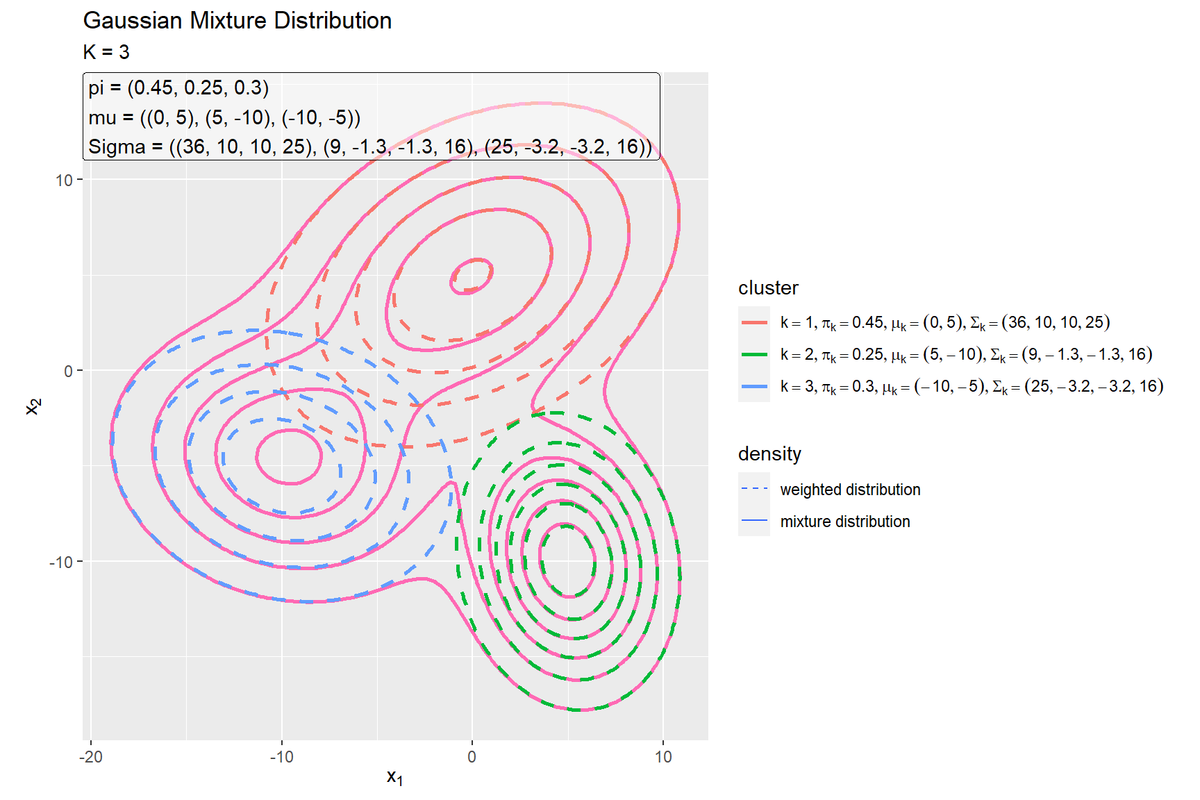
重み付けした分布を破線で示します。
$K$個の重み付けした分布に関して、x・y軸の値ごとに積み上げた形になります。
・混合ガウス分布の作図コード(クリックで展開)
最後に、混合ガウス分布だけのグラフを確認します。
# 混合ガウス分布を作図 ggplot() + geom_contour_filled(data = dens_mixture_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.5) + # 混合分布の確率密度 geom_label(data = param_label_df, mapping = aes(x = x, y = y, label = label), hjust = 0, vjust = 1, alpha = 0.5) + # パラメータラベル coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Gaussian Mixture Distribution", subtitle = paste0("K = ", K), fill = "density", x = expression(x[1]), y = expression(x[2]))
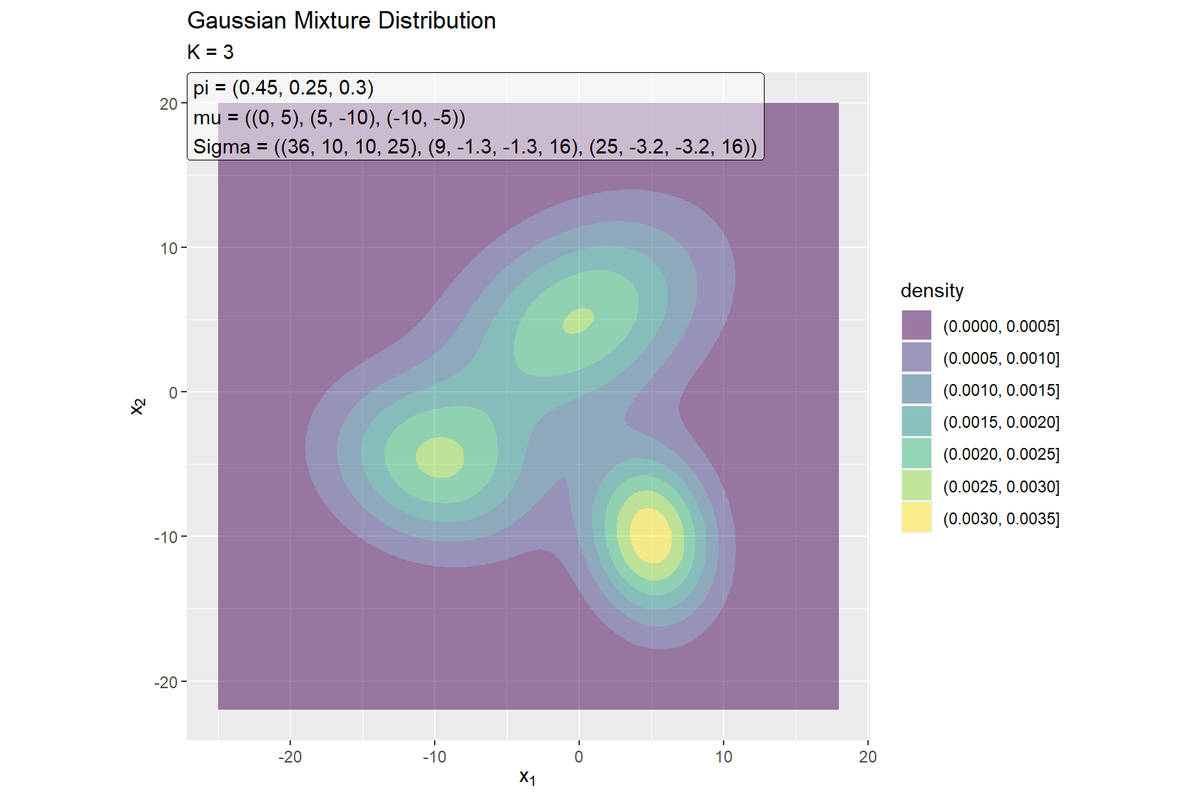
$K$個の山を持つ分布なのが分かります。ただし、クラスタ間において平均ベクトルが近い場合は、$K$個以下の山になることもあります。
この記事では、多次元混合ガウス分布の定義を確認しました。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
須山ベイズ本に登場する確率分布についてまとめるのが当面の目的なので、いくつか飛ばしていますしPython版は全然なのですが、この分布で一区切りの予定です。須山ベイズ本の解説記事の修正までを年内にやりたかったのですが、年度内には終わるかなぁ。
2022年12月27日は、カントリー・ガールズとJuice=Juiceの元メンバーの稲場愛香さんの25歳のお誕生日です。おめでとうございます!
ソロ活動も本格化してきてとても楽しみです。来年も頑張りまなかん❀゜。☆\(´ω ` )/☽
【次の内容】
つづく