はじめに

　gganimateパッケージについて理解したいシリーズです。
　この記事では、Elastic関数によるイージング処理を解説します。

【他の内容】

【目次】

はじめに
Elastic
おわりに

Elastic

　弾性イージング関数(Elastic Easing Function)とイージング処理についてアニメーションで確認します。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(gganimate)
library(tidyverse)

　基本的に、パッケージ名::関数名()の記法で書きます。ただし作図コードに関してはごちゃごちゃしてしまうので、ggplot2パッケージの関数は関数名のみで、gganimateパッケージの関数はパッケージ名を明示して書きます。

指数関数と正弦波の確認

　Elasticイージング関数(Elastic関数)は、指数イージング関数(Exponential Easing Function)に正弦波(Sine Curve)を含めることを考えます。

$f(x) = 2^{10 x - 10} (- \sin (x))$

　この関数をグラフで確認します。

・作図コード(クリックで展開)

　x軸の値と関数の出力(y軸の値)をデータフレームに格納します。

# x軸の値を作成
x_vec <- seq(from = -2.5, to = 2.5, by = 0.01)

# 指数関数と正弦波の積
tmp_df <- tibble::tibble(
  x = x_vec, 
  expo = 2^(10 * x - 10), 
  sine = -sin(x * 2 * pi / 3), 
  y = expo * sine
)

　このデータフレームはここでしか使いません。

　イージング関数として利用する範囲を示すのに利用するデータフレームを作成します。

# イージング関数として利用する領域
area_df <- tibble::tibble(
  x_from = c(0, 0, 1, 1), 
  y_from = c(0, 1, 1, 0), 
  x_to = c(0, 1, 1, 0), 
  y_to = c(1, 1, 0, 0)
)

　点 $(x, y)$ として、4つの点 $(0, 0)$ ・ $(0, 1)$ ・ $(1, 1)$ ・ $(1, 0)$ に対応します。

　指数関数と正弦波の積のグラフを作成します。

# 指数関数と正弦波の積を作図
ggplot(tmp_df, aes(x = x)) + 
  geom_line(mapping = aes(y = expo), color = "red", linetype = "dashed") + # 指数関数
  geom_line(mapping = aes(y = sine), color = "orange", linetype = "dashed") + # 正弦波
  geom_line(mapping = aes(y = y), color = "hotpink", size = 1) + # 元の関数
  geom_segment(data = area_df, mapping = aes(x = x_from, xend = x_to, y = y_from, yend = y_to), 
               color = "red", size = 1) + # 対象の領域
  coord_fixed(ratio = 1) + # アスペクト比
  ylim(c(-2, 2)) + # y軸の表示範囲
  labs(title = expression(f(x) == 2^(10 * x - 10) * (-sin(x))), 
       y = expression(f(x)))

　geom_segment()で領域を描きます。x, y引数に指定した点とxend, yend引数に指定した点を直線で繋ぎます。

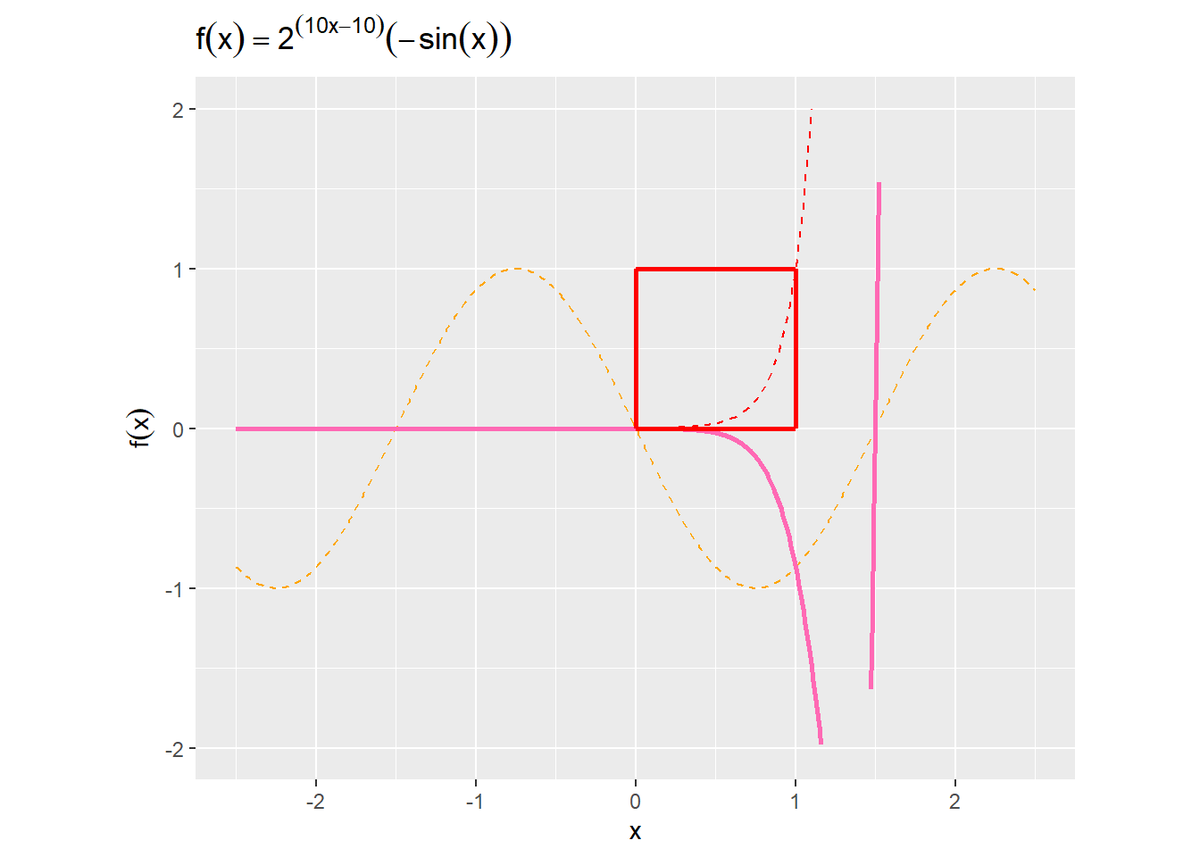
f:id:anemptyarchive:20220411193822p:plain — 指数関数と正弦波の積のグラフ

　Expo-in関数(赤色の破線)が0に近いときは(負の)正弦波のノイズ(オレンジ色の破線)の影響を受けず、値が大きくなるほど強く影響を受けているのが分かります。

　イージング関数では赤色の線で囲まれた縦横0から1の領域に注目し、点 $(0, 0)$ から点 $(1, 1)$ まで変化する関数である必要があります。
　そこで、次のように式を変形します。

$f(x) = 2^{10 x - 10} \left\{ - \sin \Bigl( (10 x - 10.75) \frac{2 \pi}{3} \Bigr) \right\}$

　(値の理由までは追求しませんが、波の幅を細かくするためとおそらく0から1に抑えるための設定です。)

　この関数のグラフを確認します。

・作図コード(クリックで展開)

# 指数関数と正弦波の積を計算
tmp_df <- tibble::tibble(
  x = x_vec, 
  expo = 2^(10 * x - 10), 
  sine = -sin((10 * x - 10.75) * 2 * pi / 3), 
  y = expo * sine
)

# 指数関数と正弦波の積を作図
ggplot(tmp_df, aes(x = x)) + 
  geom_line(mapping = aes(y = expo), color = "red", linetype = "dashed") + # 指数関数
  geom_line(mapping = aes(y = sine), color = "orange", linetype = "dashed") + # 正弦波
  geom_line(mapping = aes(y = expo * sine), color = "hotpink", size = 1) + # 元の関数
  geom_segment(data = area_df, mapping = aes(x = x_from, xend = x_to, y = y_from, yend = y_to), 
               color = "red", size = 1) + # 対象の領域
  coord_fixed(ratio = 1) + # アスペクト比
  xlim(c(-1, 1.5)) + # x軸の表示範囲
  ylim(c(-1, 1.5)) + # y軸の表示範囲
  labs(title = expression(f(x) == 2^(10 * x - 10) * (-1) * sin * bgroup("(", (10 * x - 10.75) * frac(2 * pi, 3), ")")), 
       y = expression(f(x))) # ラベル

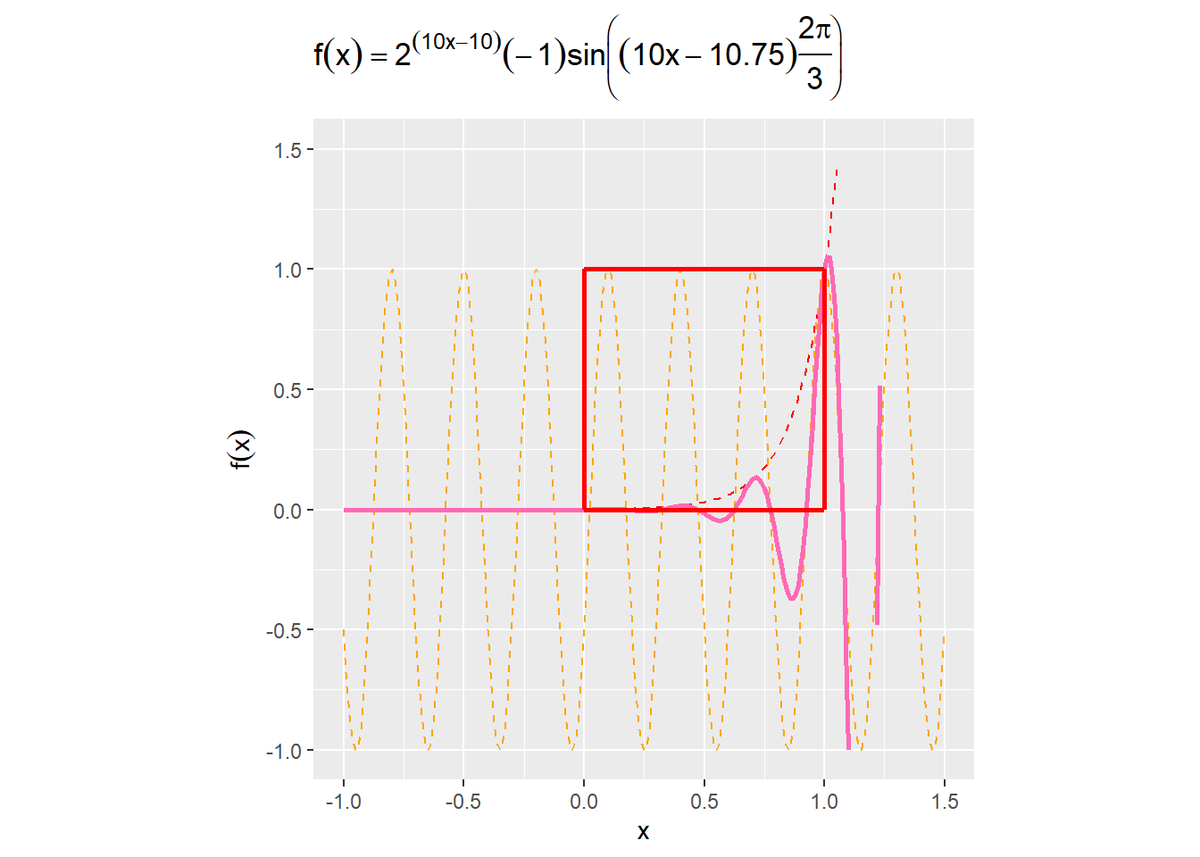
f:id:anemptyarchive:20220411193845p:plain — 指数関数と正弦波の積のグラフ

　ノイズの波(オレンジ色の破線)が細かくなったことで、tex:f(x)も波打つようになり、またほぼ点 $(0, 0)$ から点 $(1, 1)$ に変化する関数になりました。

# xが0のとき
x <- 0
2^(10 * x - 10) * (-sin((10 * x - 10.75) * 2 * pi / 3))

# xが1のとき
x <- 1
2^(10 * x - 10) * (-sin((10 * x - 10.75) * 2 * pi / 3))

## [1] -0.0004882812
## [1] 1

　この関数を利用します。ただし、0にならない点に注意して実装する必要があります。

In

　まずは、Elastic-inイージング関数を確認します。Inタイプは、始めの変化が小さく、時間が進むにつれて変化が大きくなります。

　Elastic-in関数は、次の式で定義されます。

$f_{in}(t) = - 2^{10 t - 10} \sin \Bigl( (10 t - 10.75) \frac{2 \pi}{3} \Bigr) \quad (0 \leq t \leq 1)$

　 $0 \leq t \leq 1$ のとき $f(t)$ がほぼ点 $(0, 0)$ から点 $(1, 1)$ に変化するのが先ほどのグラフからも分かります。

　この関数(y軸の値)を計算して、時間(x軸)の値と共にデータフレームに格納します。

# 時間変化の値を作成:(0 <= t <= 1)
t_vec <- seq(from = 0, to = 1, by = 0.01)

# Elastic-in
elastic_in_df <- tibble::tibble(
  t = t_vec, 
  y = dplyr::if_else(
    condition = t == 0, 
    true = 0, 
    false = -2^(10 * t - 10) * sin((10 * t - 10.75) * 2 * pi / 3)
  ), 
  easing_fnc = "elastic-in"
)
head(elastic_in_df)

## # A tibble: 6 x 3
##       t         y easing_fnc
##   <dbl>     <dbl> <chr>     
## 1  0     0        elastic-in
## 2  0.01 -0.000323 elastic-in
## 3  0.02 -0.000117 elastic-in
## 4  0.03  0.000126 elastic-in
## 5  0.04  0.000398 elastic-in
## 6  0.05  0.000691 elastic-in

　dplyrパッケージのif_else()を使って、t(列の値)が0のときy(列の値)を0にして、0以外のときは定義式の計算をします。
　また、他の関数と比較する際に利用するため、easing_fnc列として関数名を持たせておきます。

　作図用のデータフレームを作成します。

# イージング関数を指定
point_df <- elastic_in_df

# イージング曲線用のデータフレームを作成
line_df <- point_df %>% 
  dplyr::rename(x = t) # フレーム用の列をx軸用の列に変更

　作図コードを再利用しやすいように、グラフを描画する関数のデータフレームをpoint_dfとして複製します。この後作成する他の関数のデータフレームを指定すると、その関数のグラフを同じコードで描画できます(タイトルは書き換えます)。
　ここでは、時間(t列の値)の変化に応じてフレームを切り替えるアニメーションを作成します。アニメーション(フレーム切替)の影響を受けずにイージング曲線(折れ線グラフ)を描画するために、フレーム列(x軸の値の列)の名前を変更しておきます。

　Elastic-in関数のアニメーションを作成します。

# イージング関数を作図
anim <- ggplot(point_df, aes(x = t, y = y)) + 
  geom_line(data = line_df, mapping = aes(x = x, y = y), 
            color = "hotpink", size = 1) + # イージング曲線
  geom_vline(mapping = aes(xintercept = t), 
             color = "orange", size = 1, linetype = "dashed") + # 経過時間の線
  geom_hline(mapping = aes(yintercept = y), 
             color = "red", size = 1, linetype = "dashed") + # 変化量の線
  geom_point(mapping = aes(y = 0), color = "orange", size = 5) + # 経過時間の点
  geom_point(mapping = aes(x = 1), color = "red", size = 5) + # 変化量の点
  geom_point(color = "hotpink", size = 5) + # イージング曲線上の点
  gganimate::transition_reveal(along = t) + # フレーム
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Elastic-in Easing Function", 
       subtitle = "t = {round(frame_along, 2)}", 
       color = "easing function", 
       x = "time", y = expression(f(t))) # ラベル

# gif画像を作成
gganimate::animate(plot = anim, nframes = 101, fps = 50)

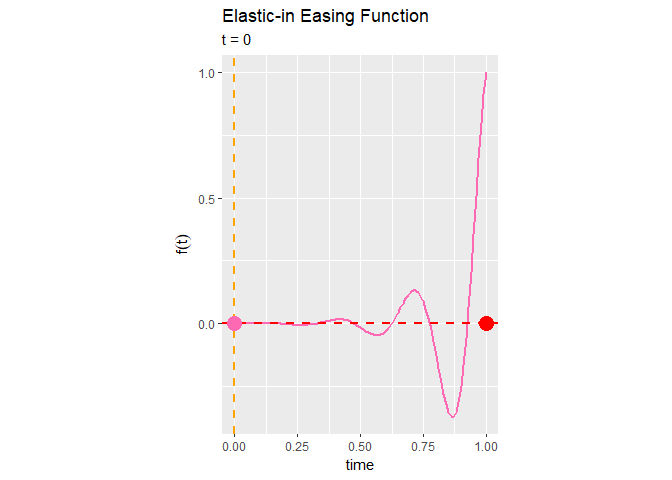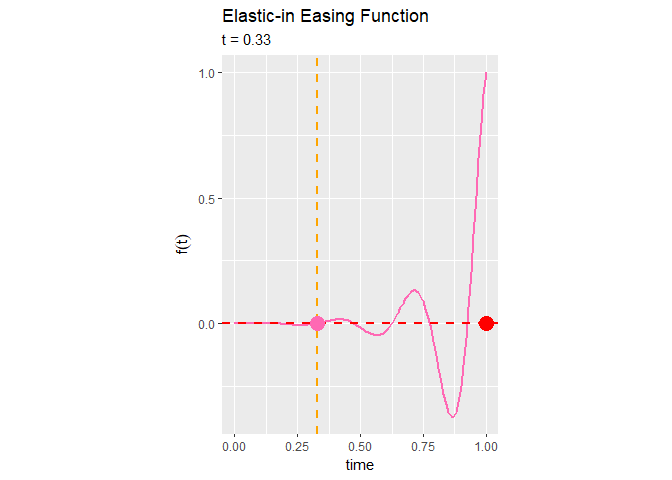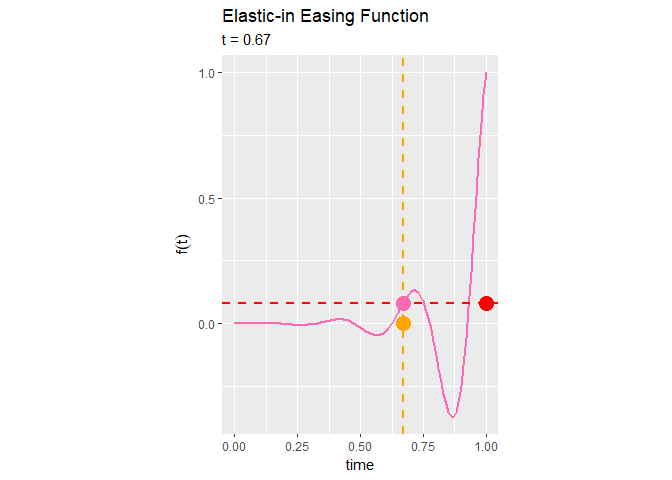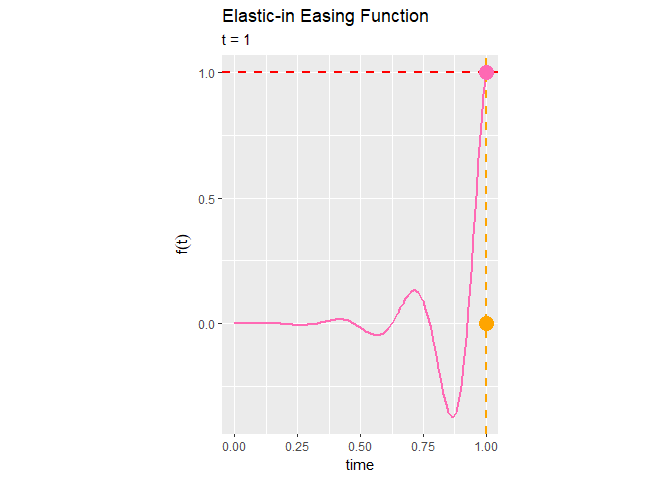
f:id:anemptyarchive:20220411193906g:plain — Elastic-in関数のグラフ

　x軸上を通過するオレンジ色の点は、経過時間を表します。この点(時間経過)は、常に一定に変化します。
　ピンク色の線は、イージング関数のグラフで、経過時間と移動量(アニメーションの変化)の関係を表します。イージング曲線上を通過するピンク色の点は、その時間における関数の値です。
　y軸に対して並行に移動する赤色の点は、イージング関数に従って変化する点で、イージング処理されたアニメーションの変化を表します。

　Elastic-in関数によるイージング処理は、始めはほとんど変化せず、徐々に0付近を上下しながら最後に急激に変化するのが分かります。

Out

　次は、Elastic-outイージング関数を確認します。Outタイプは、始めの変化が大きく、時間が進むにつれて変化が小さくなります。

　Elastic-out関数は、Inの関数を用いて次の式で定義されます。

$f_{out}(t) = 1 - f_{in}(1 - t) \quad (0 \leq t \leq 1)$

　時間 $t$ は0から1に変化するので、 $1 - t$ は0から1に変化します。この操作により、y軸に対してグラフが反転します。
　さらに、 $f_{in}(1 - t)$ は1から0に変化するので、 $1 - f_{in}(1 - t)$ は0から1に変化します。これにより、x軸に対してもグラフが反転した関数が得られます。

　この式を整理します。Inの式の $t$ を $t'$ で表し $1 - t$ に置き換えると

$\begin{aligned} f_{out}(t) &= 1 - \Bigl\{ - 2^{10 t' - 10} \sin \Bigl( (10 t' - 10.75) \frac{2 \pi}{3} \Bigr) \Bigr\} \\ &= 1 + 2^{10 (1 - t) - 10} \sin \Bigl( \{10 (1 - t) - 10.75\} \frac{2 \pi}{3} \Bigr) \\ &= 1 + 2^{- 10 t} \sin \Bigl( - (10 t + 0.75) \frac{2 \pi}{3} \Bigr) \\ &= 1 - 2^{- 10 t} \sin \Bigl( (10 t + 0.75) \frac{2 \pi}{3} \Bigr) \end{aligned}$

で計算できることが分かります。3行目から4行目では、 $\sin(- \theta) = - \sin(\theta)$ により式を変形しています。

　時間(x軸)の値とイージング関数(y軸)の値をデータフレームに格納します。

# Elastic-out
elastic_out_df <- tibble::tibble(
  t = t_vec, 
  y = dplyr::if_else(
    condition = t == 1, 
    true = 1, 
    false = 1 - 2^(-10 * t) * sin((10 * t + 0.75) * 2 * pi / 3)
  ), 
  easing_fnc = "elastic-out"
)
head(elastic_out_df)

## # A tibble: 6 x 3
##       t      y easing_fnc 
##   <dbl>  <dbl> <chr>      
## 1  0    0      elastic-out
## 2  0.01 0.0874 elastic-out
## 3  0.02 0.205  elastic-out
## 4  0.03 0.343  elastic-out
## 5  0.04 0.493  elastic-out
## 6  0.05 0.646  elastic-out

　Elastic-out関数のアニメーションを作成します。

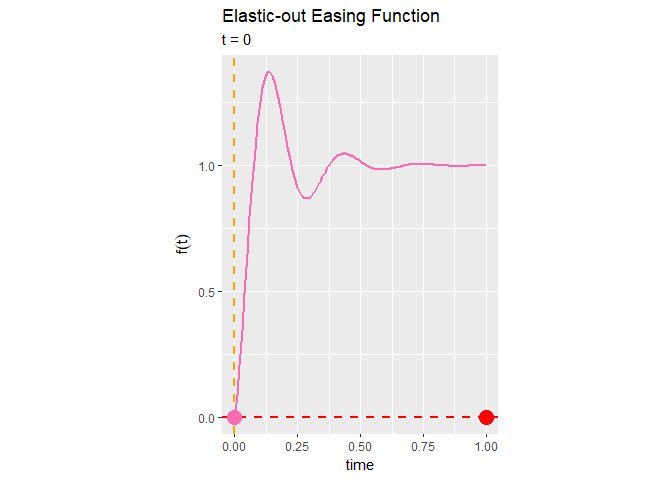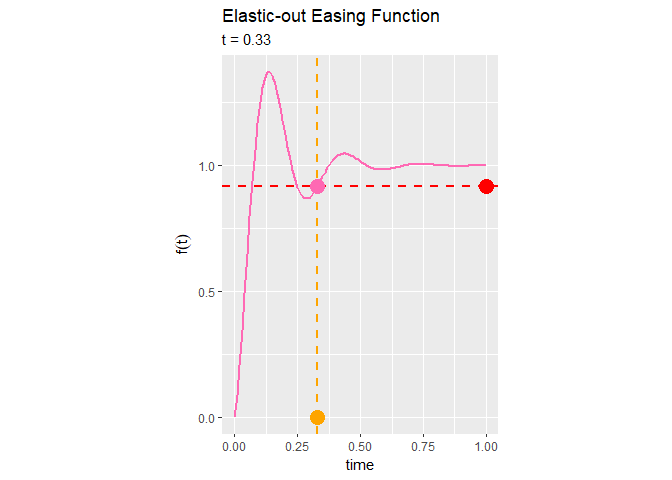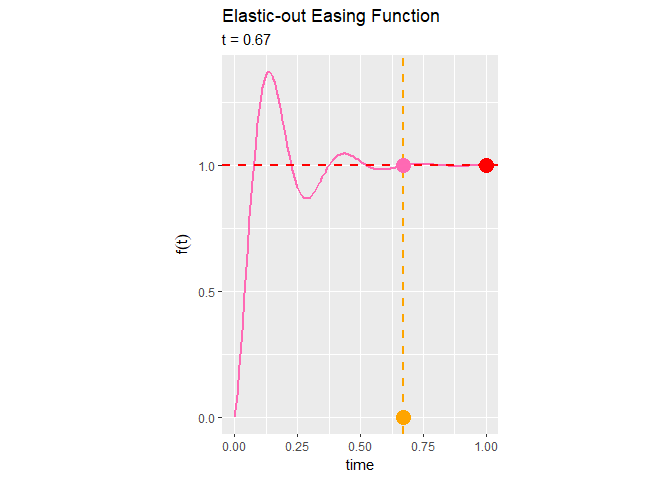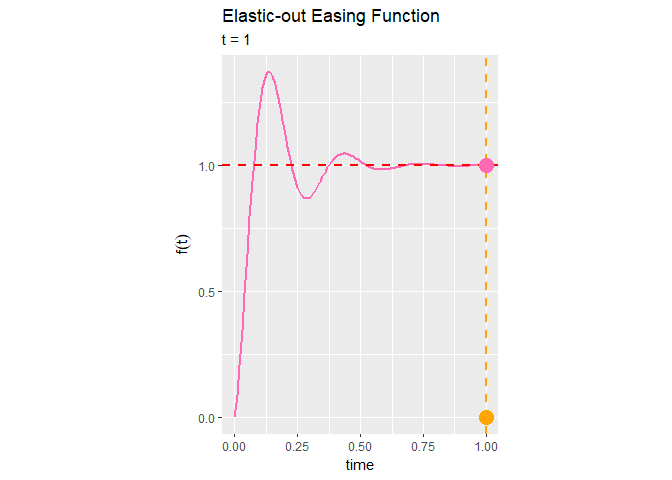
f:id:anemptyarchive:20220411193943g:plain — Elastic-out関数のグラフ

　Elastic-out関数によるイージング処理は、始めに急激に変化して1を超え、1付近を上下しながら徐々に変化が小さくなるのが分かります。

InOut

　続いて、Elastic-in-outイージング関数を確認します。InOutタイプは、始めと終わりの変化が小さく、中盤の変化が大きくなります。

　Elastic-in-out関数は、Inの関数とOutの関数を用いて次の式で定義されます。

$\begin{aligned} f_{inout}(t) = \begin{cases} \frac{1}{2} f_{in}(2 t) &\quad (0 \leq t < 0.5) \\ \frac{1}{2} (f_{out}(2 t - 1) + 1) &\quad (0.5 \leq t \leq 1) \end{cases} \end{aligned}$

　前半( $t$ が0から0.5の間)の変化ではInの関数で計算します。 $t$ を2倍にすることで0から1の範囲で関数の計算を行い、計算結果を2分の1にすることで出力を0から0.5の範囲に抑えます。
　後半( $t$ が0.5から1の間)の変化ではOutの関数で計算します。こちらも $2 t - 1$ にすることで0から1の範囲で関数の計算を行い、前半部分に対応する(2分の1になるので0.5の2倍の)1を足して、2分の1にすることで出力を0.5から1の範囲にします。

　それぞれ式を整理します。上の式(前半の式)は、Inの式の $t$ を $t'$ で表し $2 t$ に置き換えて

$\begin{aligned} \frac{1}{2} f_{in}(2 t) &= \frac{1}{2} \Bigl\{ - 2^{10 t' - 10} \sin \Bigl( (10 t' - 10.75) \frac{2 \pi}{3} \Bigr) \Bigr\} \\ &= \frac{1}{2} \Bigl[ - 2^{10 (2 t) - 10} \sin \Bigl( \{10 (2 t) - 10.75\} \frac{2 \pi}{3} \Bigr) \Bigr] \\ &= \frac{1}{2} \Bigl\{ - 2^{20 t - 10} \sin \Bigl( (20 t - 10.75) \frac{2 \pi}{3} \Bigr) \Bigr\} \\ &= - 2^{20 t - 11} \sin \Bigl( (20 t - 10.75) \frac{2 \pi}{3} \Bigr) \end{aligned}$

となります。3行目から4行目では、 $\frac{1}{x} = x^{-1}$ と $x^m x^n = x^{m+n}$ により式を変形しています。

　下の式(後半の式)は、Outの関数の $t$ を $t'$ で表し $2 t - 1$ に置き換えて

$\begin{aligned} \frac{1}{2} (f_{out}(2 t - 1) + 1) &= \frac{1}{2} \Bigl\{ 1 - 2^{- 10 t'} \sin \Bigl( (10 t' + 0.75) \frac{2 \pi}{3} \Bigr) + 1 \Bigr\} \\ &= \frac{1}{2} \Bigl[ 2 - 2^{- 10 (2 t - 1)} \sin \Bigl( \{10 (2 t - 1) + 0.75\} \frac{2 \pi}{3} \Bigr) \Bigr] \\ &= \frac{1}{2} \Bigl\{ 2 + 2^{- 20 t + 10} \sin \Bigl( (20 t - 9.25) \frac{2 \pi}{3} \Bigr) \Bigr\} \\ &= 1 + 2^{- 20 t + 9} \sin \Bigl( (20 t - 9.25) \frac{2 \pi}{3} \Bigr) \end{aligned}$

となります。

　よって、2つの式をまとめると

$\begin{aligned} f_{inout}(t) = \begin{cases} - 2^{20 t - 11} \sin \Bigl( (20 t - 10.75) \frac{2 \pi}{3} \Bigr) &\quad (0 \leq t < 0.5) \\ 1 + 2^{- 20 t + 9} \sin \Bigl( (20 t - 9.25) \frac{2 \pi}{3} \Bigr) &\quad (0.5 \leq t \leq 1) \end{cases} \end{aligned}$

で計算できます(ただし、参考にした実装例と計算式が違ったのでどこか計算が間違っているかも知れません)。参考(外部リンク)：「イージング関数チートシート」

　時間(x軸)の値とイージング関数(y軸)の値をデータフレームに格納します。

# Elastic-inout:(未完)
elastic_inout_df <- tibble::tibble(
  t = t_vec, 
  y = dplyr::case_when(
    t == 0 ~ 0, 
    t == 1 ~ 1, 
    t < 0.5 ~ -2^(20 * t - 11) * sin((20 * t - 10.75) * 2 * pi / 3), 
    t >= 0.5 ~ 1 + 2^(-20 * t + 9) * sin((20 * t - 9.25) * 2 * pi / 3)
  ), 
  easing_fnc = "elastic-in-out"
)
head(elastic_inout_df)

## # A tibble: 6 x 3
##       t          y easing_fnc    
##   <dbl>      <dbl> <chr>         
## 1  0     0         elastic-in-out
## 2  0.01 -0.0000586 elastic-in-out
## 3  0.02  0.000199  elastic-in-out
## 4  0.03  0.000495  elastic-in-out
## 5  0.04  0.000777  elastic-in-out
## 6  0.05  0.000977  elastic-in-out

　dplyrパッケージのcase_when()を使って、条件分岐して計算します。

　Elastic-in-out関数のアニメーションを作成します。

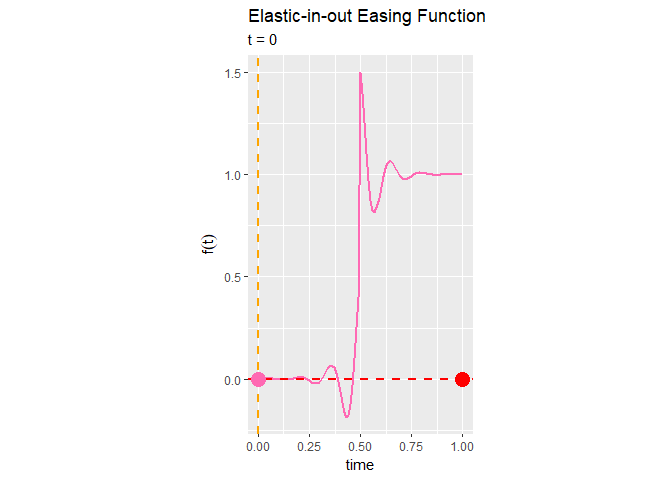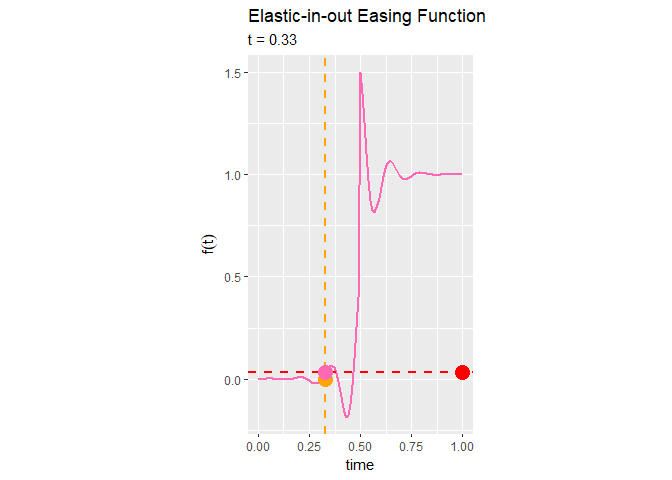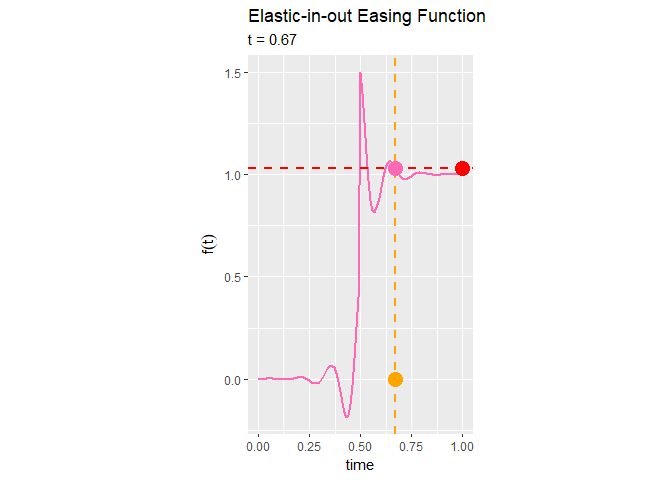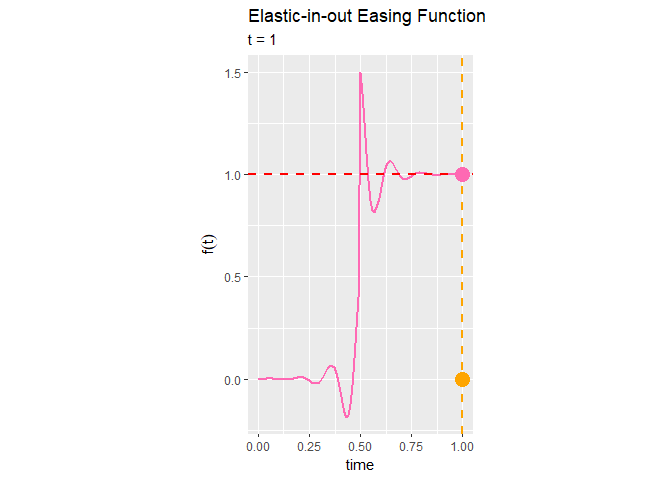
f:id:anemptyarchive:20220411194026g:plain — Elastic-in-out関数のグラフ：(未完)

　(やっぱりこれ点対称なグラフになっていないよね…)

　というわけで別の方法を試してみます。

# Elastic-in関数を作成
f_in <- function(t) {
  return(
    -2^(10 * t - 10) * sin((10 * t - 10.75) * 2 * pi / 3)
  )
}

# Elastic-in関数を作成
f_out <- function(t) {
  return(
    1 - 2^(-10 * t) * sin((10 * t + 0.75) * 2 * pi / 3)
  )
}

# Elastic-inout
elastic_inout_df <- tibble::tibble(
  t = t_vec, 
  y = dplyr::case_when(
    t == 0 ~ 0, 
    t == 1 ~ 1, 
    t < 0.5 ~ f_in(2 * t) * 0.5, 
    t >= 0.5 ~ (f_out(2 * t - 1) + 1) * 0.5
  ), 
  easing_fnc = "elastic-in-out"
)

　InとOutそれぞれの計算を行う関数を作成して、式を整理する前のInOutの定義式の計算をします。

　こちらの計算結果を使ってアニメーションを作成します。

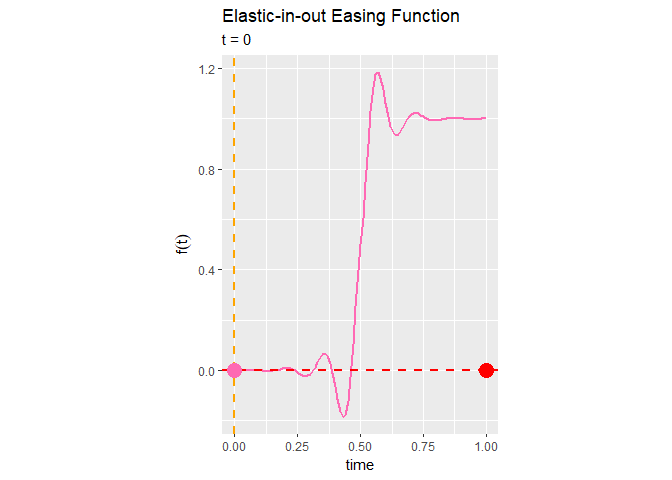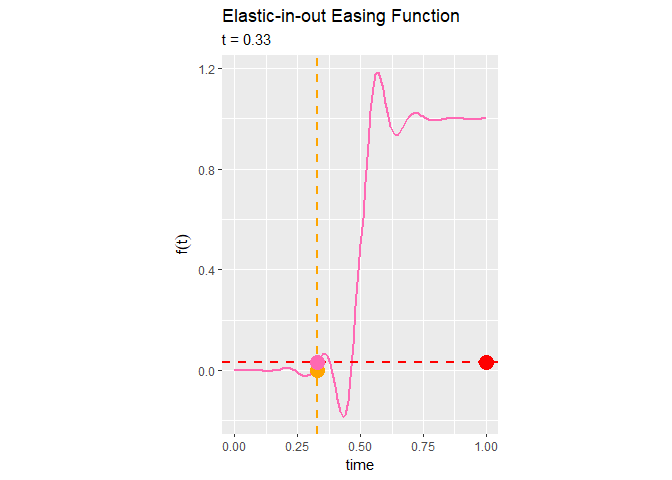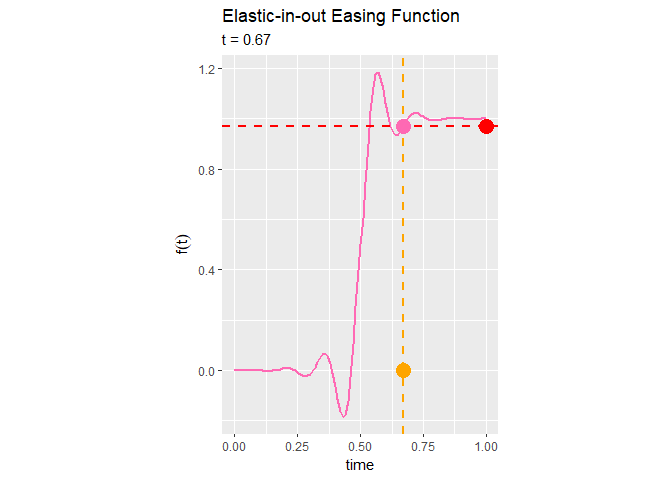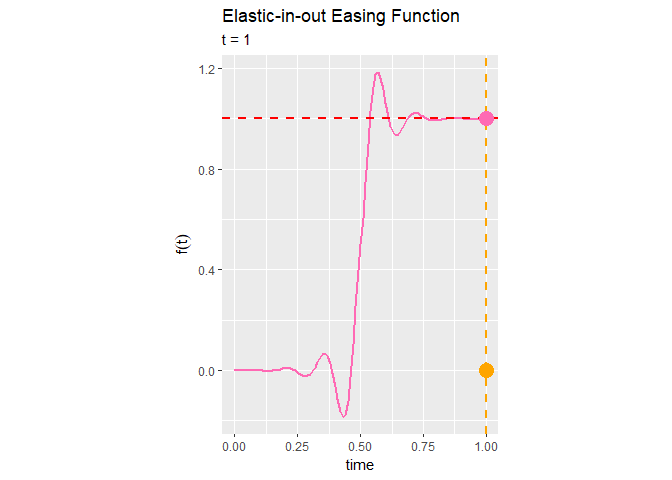
f:id:anemptyarchive:20220411215924g:plain — Elastic-in-out関数のグラフ

　Elastic-in-out関数によるイージング処理は、前半は0付近を上下し、中盤に急激に急激に変化し、後半は1付近を前後するのが分かります。

イージング処理の比較

　最後に、Linear関数と3つのElastic関数を比較します。

　これまでに確認したグラフを重ねて描画するため、データフレームを結合します。

# Linear
linear_df <- tibble::tibble(
  t = t_vec, 
  y = t, 
  easing_fnc = "linear"
)

# 比較対象を結合
easing_df <- rbind(
  linear_df, 
  elastic_in_df, 
  elastic_out_df, 
  elastic_inout_df
) %>% 
  dplyr::mutate(
    easing_fnc = factor(easing_fnc, level = c("linear", "elastic-in", "elastic-out", "elastic-in-out"))
  ) # 因子型に変換

# イージング曲線用のデータフレームを作成
line_df <- easing_df %>% 
  dplyr::rename(x = t) # フレーム用の列をx軸用の列に変更

# 確認
head(easing_df)

## # A tibble: 6 x 3
##       t     y easing_fnc
##   <dbl> <dbl> <fct>     
## 1  0     0    linear    
## 2  0.01  0.01 linear    
## 3  0.02  0.02 linear    
## 4  0.03  0.03 linear    
## 5  0.04  0.04 linear    
## 6  0.05  0.05 linear

　比較する関数のデータフレームを結合します。
　グラフを色分けするために、関数名の列を因子型に変換しておきます。factor()のレベル引数levelに関数名の順番を指定すると、凡例の並びや色付けを指定できます。

　イージング関数のアニメーションを作成します。

# イージング関数を作図
anim <- ggplot(easing_df, aes(x = t, y = y, color = easing_fnc)) + 
  geom_vline(mapping = aes(xintercept = t), 
             color = "pink", size = 1, linetype = "dashed") + # 経過時間の線
  geom_hline(mapping = aes(yintercept = y, color = easing_fnc), linetype = "dashed") + 
  geom_line(data = line_df, mapping = aes(x = x, y = y, color = easing_fnc), size = 1) + # イージング曲線
  geom_point(mapping = aes(x = 1), size = 5) + 
  geom_point(mapping = aes(y = 0), color = "pink", size = 5) + 
  geom_point(size = 5) + # イージング曲線上の点
  gganimate::transition_reveal(along = t) + # フレーム
  scale_color_manual(values = c("red", "limegreen", "orange", "mediumblue")) + # 点と線の色:(不必要)
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Elastic Easing Functions", 
       subtitle = "t = {round(frame_along, 2)}", 
       color = "easing function", 
       x = "time", y = expression(f(t))) # ラベル

# gif画像を作成
gganimate::animate(plot = anim, nframes = 101, fps = 50)

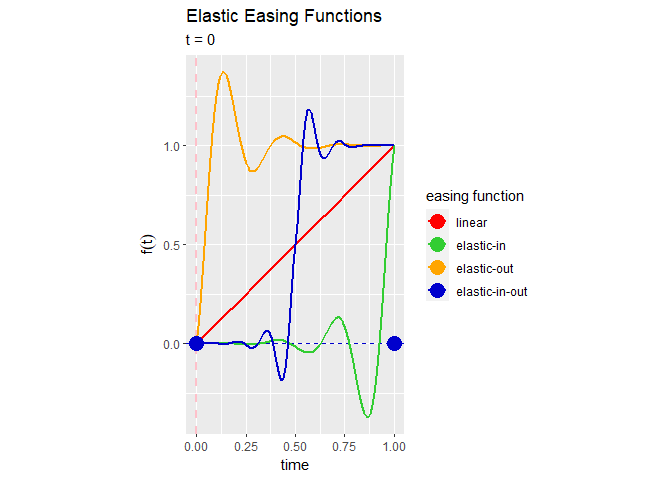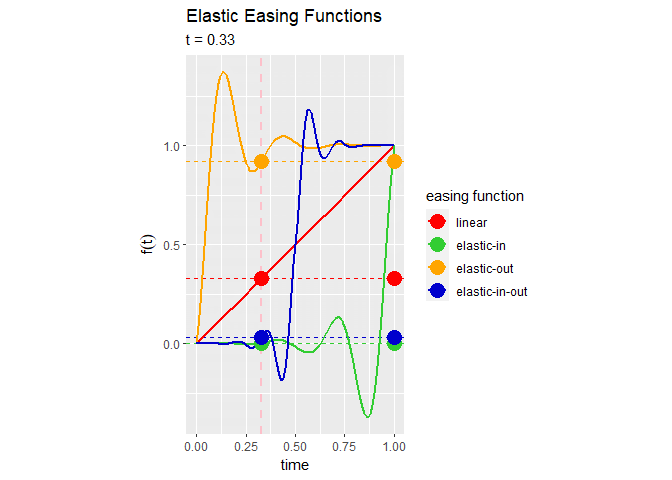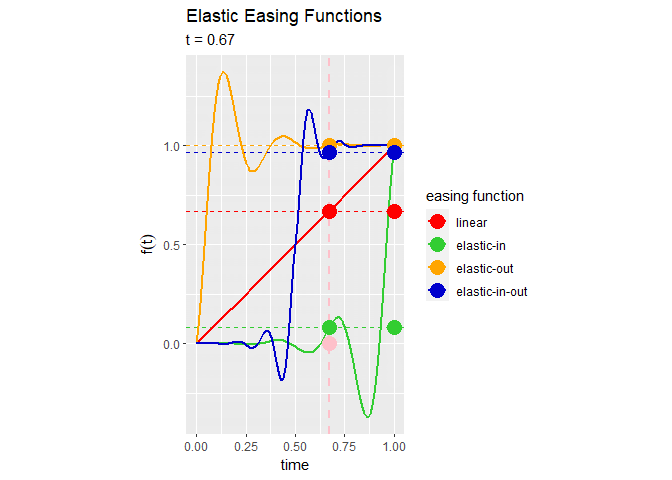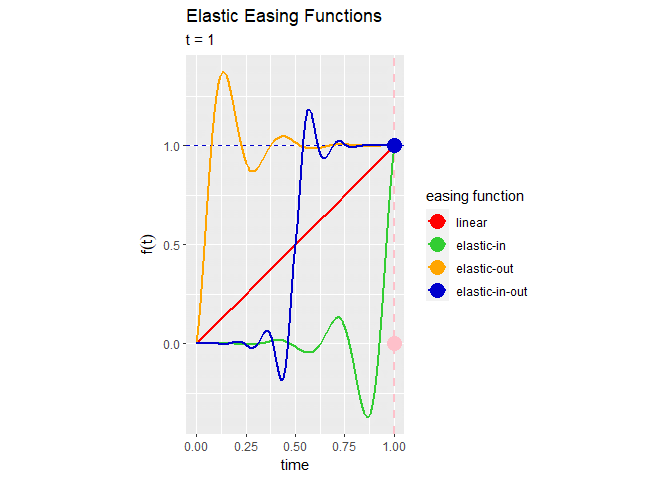
f:id:anemptyarchive:20220411220113g:plain — Elastic関数のグラフ

　InのグラフとOutのグラフが点 $(0.5, 0.5)$ で点対称になっている(はず)のが分かります。また、InOutのグラフがInとOutを繋げたグラフになっており、点 $(0.5, 0.5)$ でLinear関数と等しくなるのが分かります。

　続いて、垂直に移動する点で表現していたイージング処理された変化を、棒グラフで表現します。

# イージング関数の数を取得
fnc_size <- length(unique(easing_df[["easing_fnc"]]))

# イージングバー用のデータフレームを作成
bar_df <- easing_df %>% 
  dplyr::mutate(x = (rep(1:fnc_size, each = length(t_vec)) * 2 - 1) / (fnc_size * 2)) # x軸の値を等間隔に設定
head(bar_df)

## # A tibble: 6 x 4
##       t     y easing_fnc     x
##   <dbl> <dbl> <fct>      <dbl>
## 1  0     0    linear     0.125
## 2  0.01  0.01 linear     0.125
## 3  0.02  0.02 linear     0.125
## 4  0.03  0.03 linear     0.125
## 5  0.04  0.04 linear     0.125
## 6  0.05  0.05 linear     0.125

　バーを0から1の範囲で等間隔に配置するために、x軸の値を等間隔に設定します。

　棒グラフのアニメーションを作成します。

# イージング処理を作図
anim <- ggplot() + 
  geom_tile(data = bar_df, mapping = aes(x = x, y = y/2, height = y, fill = easing_fnc), 
           alpha = 0.7, width = 0.9/fnc_size) + # イージングバー
  geom_hline(data = easing_df, mapping = aes(yintercept = y, color = easing_fnc), 
             linetype = "dashed") + # 変化量の線
  geom_line(data = line_df, mapping = aes(x = x, y = y, color = easing_fnc)) + # イージング曲線
  geom_point(data = easing_df, mapping = aes(x = t, y = y, color = easing_fnc), 
             alpha = 0.5, size = 5) + # イージング曲線上の点
  gganimate::transition_reveal(along = t) + # フレーム
  scale_color_manual(values = c("red", "limegreen", "orange", "mediumblue")) + # 点と線の色:(不必要)
  scale_fill_manual(values = c("red", "limegreen", "orange", "mediumblue")) + # バーの色:(不必要)
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Elastic Easing Functions", 
       subtitle = "t = {round(frame_along, 2)}", 
       fill = "easing function", color = "easing function", 
       x = "time", y = expression(f(x))) # ラベル

# gif画像を作成
gganimate::animate(plot = anim, nframes = 101, fps = 50)

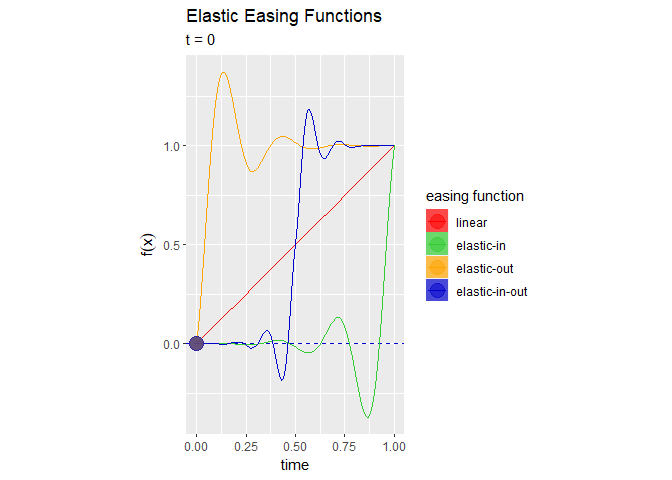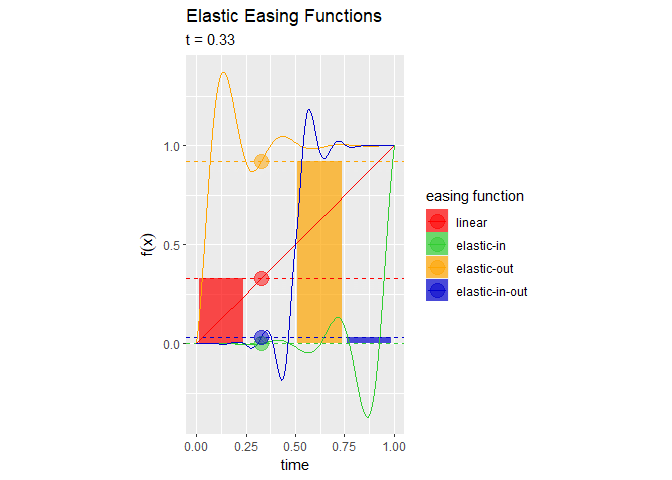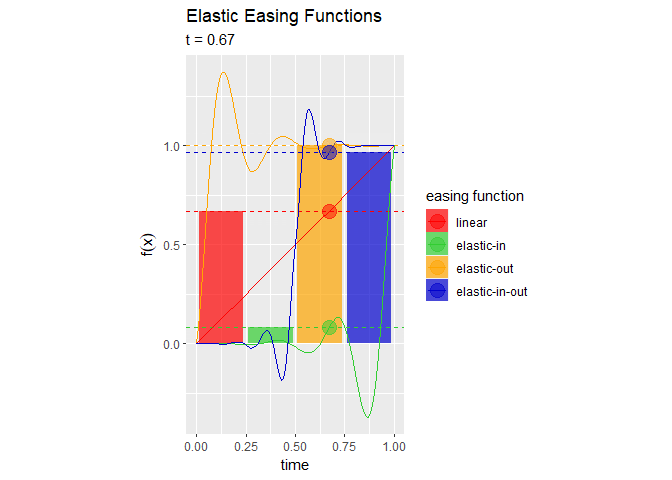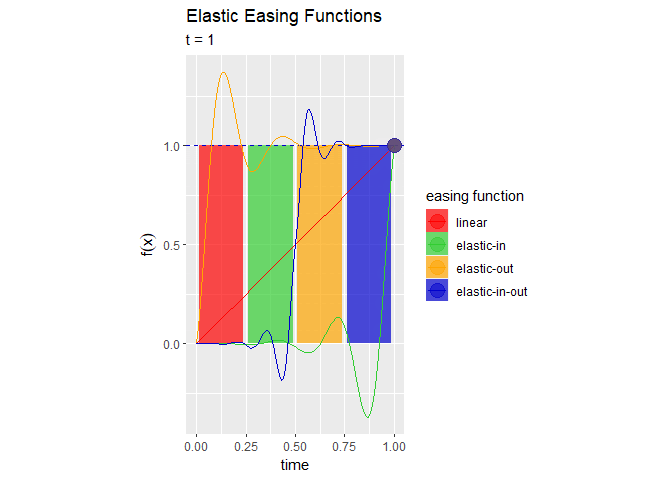
f:id:anemptyarchive:20220411220146g:plain — Elastic関数によるイージング処理

　イージング曲線上の点と対応するバーの高さが一致しているのが分かります。

　点の軌跡でイージング処理を可視化します。

　作図用にデータフレームを加工します。(それとは別に、時間の値を粗く(by = 0.1に)してデータを作り直しました。)

# イージング関数の数を取得
fnc_size <- length(unique(easing_df[["easing_fnc"]]))

# 移動点用のデータフレームを作成
point_df <- easing_df %>% 
  dplyr::mutate(
    x = rep(1:fnc_size, each = length(t_vec)), 
    frame = t
  ) %>% # プロット位置とフレーム列を追加
  dplyr::select(t, x, y, easing_fnc, frame) # 列を並べ替え

# 最初のフレームで描画するデータを確認
point_df %>% 
  dplyr::filter(frame == 0)

## # A tibble: 4 x 5
##       t     x     y easing_fnc     frame
##   <dbl> <int> <dbl> <fct>          <dbl>
## 1     0     1     0 linear             0
## 2     0     2     0 elastic-in         0
## 3     0     3     0 elastic-out        0
## 4     0     4     0 elastic-in-out     0

　点のプロット位置として、関数ごとにx軸の値を割り当てます。また、フレーム列として時間列の値を複製します。

　過去の点の位置を表示するために、データ(行)を複製したデータフレームを作成します。

# 点の軌跡用のデータフレームを作成
trace_point_df <- easing_df %>% 
  tibble::add_column(
    x = rep(1:fnc_size, each = length(t_vec)), 
    n = rep((length(t_vec)-1):0, times = fnc_size)
  ) %>% # 複製する数を追加
  tidyr::uncount(n) %>% # 過去フレーム用に複製
  dplyr::group_by(t, easing_fnc) %>% # 時間と関数でグループ化
  dplyr::mutate(
    idx = length(t_vec) + 1 - dplyr::row_number(), 
    frame = t_vec[idx]
  ) %>% # フレーム列を追加
  dplyr::ungroup() %>% # グループ化を解除
  dplyr::arrange(frame, x) %>% # 昇順に並び替え
  dplyr::select(t, x, y, easing_fnc, frame) # 利用する列を選択

# 第3フレームまでに描画するデータ
trace_point_df %>% 
  dplyr::filter(frame <= 0.2)

## # A tibble: 12 x 5
##        t     x         y easing_fnc     frame
##    <dbl> <int>     <dbl> <fct>          <dbl>
##  1   0       1  0        linear           0.1
##  2   0       2  0        elastic-in       0.1
##  3   0       3  0        elastic-out      0.1
##  4   0       4  0        elastic-in-out   0.1
##  5   0       1  0        linear           0.2
##  6   0.1     1  0.1      linear           0.2
##  7   0       2  0        elastic-in       0.2
##  8   0.1     2  0.00195  elastic-in       0.2
##  9   0       3  0        elastic-out      0.2
## 10   0.1     3  1.25     elastic-out      0.2
## 11   0       4  0        elastic-in-out   0.2
## 12   0.1     4 -0.000977 elastic-in-out   0.2

　この例だと、最初のフレーム(frame列が0)ではデータがなく、2番目のフレーム(frame列が0.1)では前の時間(t列が0)のデータ、3番目のフレーム(frame列が0.2)ではそれまでの時間(t列が0.2未満)のデータとなるようにします。

　横方向に点が移動するアニメーションを作成します。

# イージングされた点移動を作図
anim <- ggplot(point_df, aes(x = x, y = y, color = easing_fnc)) + 
  geom_hline(mapping = aes(yintercept = t), 
             color = "pink", size = 1, linetype = "dashed") + # 経過時間の線
  geom_point(size = 5, show.legend = FALSE) + # イージング移動点
  geom_point(data = trace_point_df, mapping = aes(x = x, y = y, color = easing_fnc), 
             size = 5, alpha = 0.2, show.legend = FALSE) + # 点の軌跡
  gganimate::transition_manual(frame = frame) + # フレーム
  scale_x_reverse(breaks = unique(point_df[["x"]]), labels = unique(point_df[["easing_fnc"]]), minor_breaks = FALSE) + # x軸目盛の反転
  scale_color_manual(values = c("red", "limegreen", "orange", "mediumblue")) + # 点と線の色:(不必要)
  scale_fill_manual(values = c("red", "limegreen", "orange", "mediumblue")) + # 点と線の色:(不必要)
  coord_flip() + # 軸の入れ替え
  labs(title = "Elastic Easing Functions", 
       subtitle = "t = {current_frame}", 
       x = "Easing Function", y = expression(f(t))) # ラベル

# gif画像を作成
gganimate::animate(plot = anim, nframes = length(t_vec)+10, fps = 10, end_pause = 10)

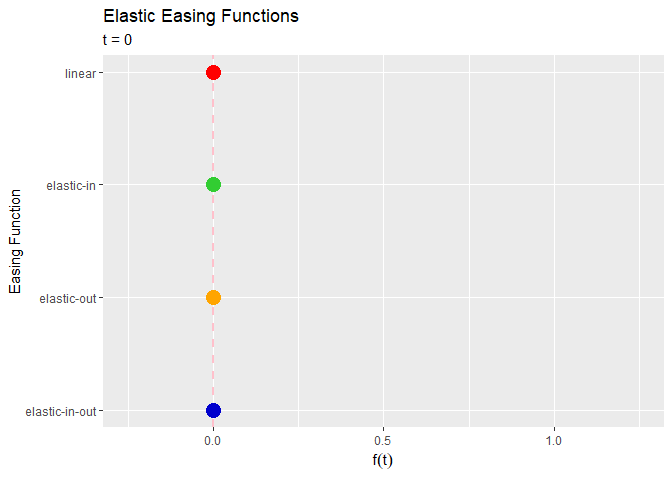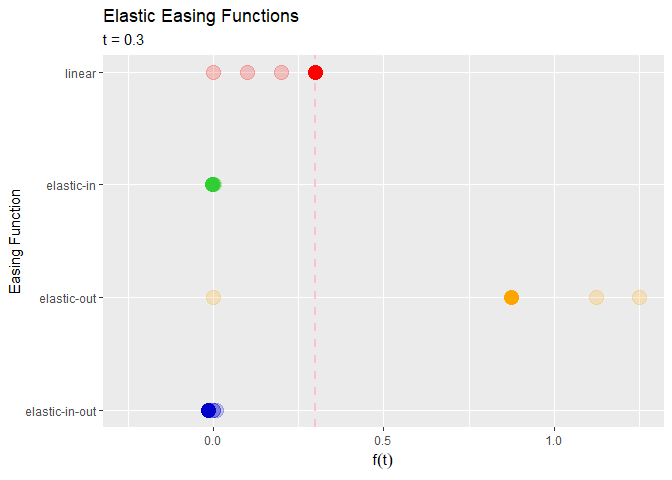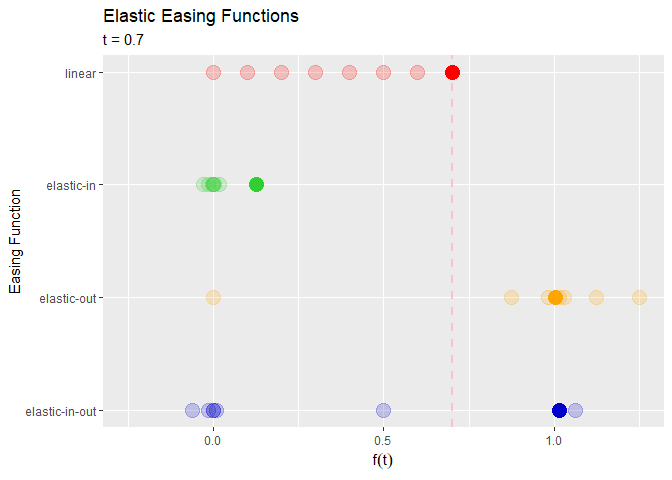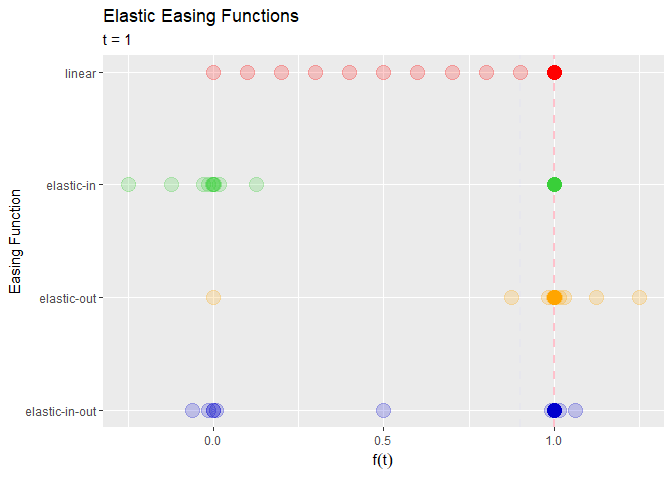
f:id:anemptyarchive:20220411220203g:plain — Elastic関数によるイージング処理

　coord_flip()でx軸とy軸を入れ変えているので、横方向がy軸になります。

　変化が遅い地点(時間)ほど点の跡が多く残ります。点の跡の偏りがイージング曲線に対応します。

　以上で、弾性イージング関数を確認しました。次は、バウンドイージング関数を確認します。

おわりに

　難しい数式ではないのですが1つ解けませんでした。

【次の内容】

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

Elastic関数によるイージング【gganimate】