はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、4.4節の内容です。1次元の確率分布のラプラス近似をPythonで実装します。
【数式読解編】
【他の節一覧】
【この節の内容】
4.4.0 ラプラス近似
1次元の場合のラプラス近似(ガウス分布による近似)を実装します。
利用するライブラリを読み込みます。
# 4.4.0項で利用するライブラリ import numpy as np from scipy import integrate from scipy.stats import norm # 1変量ガウス分布 import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
分布が近似される様子をアニメーションで確認するのにMatplotlibライブラリのanimationモジュールを利用します。不要であれば省略してください。
・真の分布の設定
まずは、この例で利用する分布の式を確認します。
この例では、次の式を真の関数とします。
$\sigma(x)$は、ロジスティックシグモイド関数で、次の式で定義されます。
関数$f(x)$を用いた次の式を真の分布とします。
真の分布$p(x)$を得るためには、$f(x)$の積分を求める必要があります。しかし$f(x)$の積分が得られない場合に、$p(x)$の近似分布$q(x)$を求めることにします。
ラプラス近似では、ガウス分布を用いて近似します。つまりここでは、$p(x)$に近似するガウス分布$q(x)$(のパラメータ)を求めます。
勾配法・ニュートン-ラフソン法、ラプラス近似では、負の対数$E(x)$の1階微分$\nabla E(x)$と2階微分$\nabla \nabla E(x)$を用います。それぞれ導出しますが、必要な式は後でまとめるので、ここは飛ばしても問題ありません。
・計算式の導出(クリックで展開)
$f(x)$の対数をとり符号を反転させた(-1を掛けた)ものを、負の対数$E(x)$で表します。
シグモイド関数の項を
とおいて、$E(x)$を$x$で微分します。
対数関数の微分$\frac{d \ln x}{d x} = \frac{1}{x}$、指数関数の微分$\frac{d \exp(x)}{d x} = \exp(x)$、合成関数の微分$\frac{d g(f(x))}{d x} = \frac{d g(f(x))}{d f(x)} \frac{d f(x)}{d x}$を行いました。
$\nabla E(x)$を更に$x$で微分します。
ロジスティックシグモイド関数の微分$\frac{d \sigma(x)}{d x} = \sigma(x) (1 - \sigma(x))$、指数関数の微分、合成関数の微分を行いました。ロジスティックシグモイド関数の微分については「Sigmoid関数の微分【PRMLのノート】 - からっぽのしょこ」を参照してください。
・利用する関数の作成
次に、最急降下法・ニュートン-ラフソン法、ラプラス近似などの計算に利用する関数を作成します。
ロジスティッシグモイド関数を作成します。
# ロジスティックシグモイド関数を作成 def sigmoid(x): return 1.0 / (1.0 + np.exp(-x))
ロジスティックシグモイド関数は次の式です。
真の関数$f(x)$と真の分布$p(x)$を作成します。
# 真の関数を指定 def f(x): return np.exp(-0.5 * x**2) * sigmoid(20.0 * x + 4.0) # 真の確率分布を指定 def p(x, f): # 正規化係数を計算 C = integrate.quad(f, np.min(x), np.max(x))[0] return f(x) / C
この例では、次の式を真の関数とします。
$f(x)$の積分
を正規化係数として、真の分布を次の式とします。
この分布(の正規化係数)は解析的に得られない(?)ため近似分布を求めるのでした。ここで作成するp()は、真の分布のグラフを描いて近似できているかを確認するのに使います(近似には使いません)。そのため、scipyの積分用の関数integrate.quad()を使って簡易的に(グラフの描画範囲で)正規化係数を計算します。
$f(x)$の負の対数$E(x)$と、$E(x)$の1階微分$\nabla E(x)$、2階微分$\nabla \nabla E(x)$の計算を行う関数を作成します。
# 真の関数の負の対数を指定 def E(x): return 0.5 * x**2 + np.log(1.0 + np.exp(-(20.0 * x + 4.0))) # 負の対数の1階微分を指定 def nabla_E(x): # 中間変数を計算 exp_x = np.exp(-(20.0 * x + 4.0)) y = sigmoid(20.0 * x + 4.0) return x - 20.0 * y * exp_x # 負の対数の2階微分を指定 def nabla2_E(x): # 中間変数を計算 exp_x = np.exp(-(20.0 * x + 4.0)) y = sigmoid(20.0 * x + 4.0) return 1.0 + 400.0 * y**2 * exp_x
それぞれ次の式になります。
作図用の$x$の点を作成して、真の関数$f(x)$と分布$p(x)$を作図します。
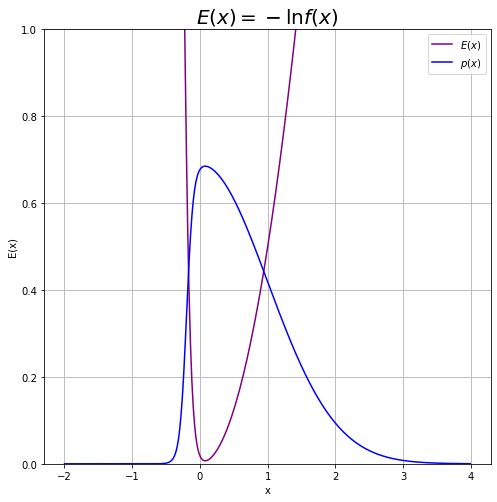
# 作図用のxの点を作成 x_vals = np.arange(-2.0, 4.0, 0.01) # 真の分布のグラフを作成 plt.figure(figsize=(8, 8)) plt.plot(x_vals, f(x_vals), color='purple', label='$f(x)$') # 真の関数 plt.plot(x_vals, p(x_vals, f), color='blue', label='$p(x)$') # 真の分布 plt.xlabel('x') plt.ylabel('f(x), p(x)') plt.title('$f(x) = \exp(- 0.5 x^2) \sigma(20 x + 4)$', fontsize=20) plt.legend() plt.grid() plt.show()

正規化したことで$f(x)$より$p(x)$の方がy軸の値が小さくなっていますが、同様の形状をしているのが分かります。
例えば、2つの点$x_1, x_2$について、$f(x_1) < f(x_2)$であれば$p(x_1) < p(x_2)$になります。この関係を、比例の記号$\propto$を使って$p(x) \propto f(x)$で表しています。
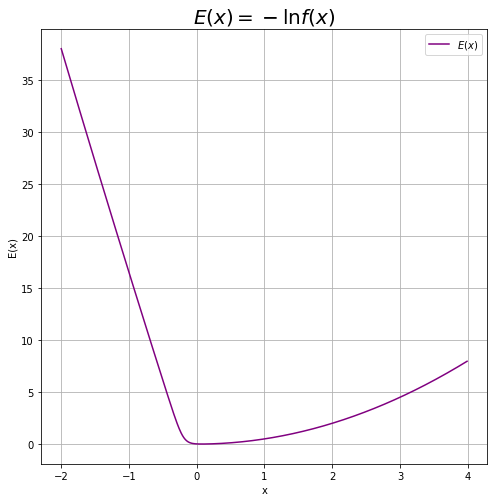
$f(x)$の負の対数$E(x)$を作図します。
# 負の対数のグラフを作成 plt.figure(figsize=(8, 8)) plt.plot(x_vals, E(x_vals), color='purple', label='$E(x)$') # 負の対数 #plt.plot(x_vals, nabla_E(x_vals), color='purple', linestyle='--', label='$\\nabla E(x)$') # 1階微分 #plt.plot(x_vals, nabla2_E(x_vals), color='purple', linestyle=':', label='$\\nabla^2 E(x)$') # 2階微分 #plt.plot(x_vals, p(x_vals, f), color='blue', label='$p(x)$') # 真の分布 plt.xlabel('x') plt.ylabel('E(x)') plt.title('$E(x) = - \ln f(x)$', fontsize=20) plt.legend() plt.grid() #plt.ylim(0.0, 1.0) plt.show()
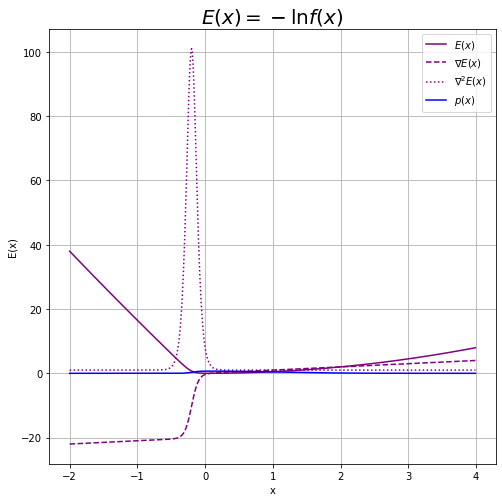
ラプラス近似では、真の分布$p(x)$を近似するのに、$p(x)$が最大となる値を求める必要があります。$p(x)$が最大になる値は、最頻値(モード)と言います。
しかし、真の分布(青色の曲線)は分からないので、真の関数$f(x)$のモードを求めます。また、「真の関数が最大となる値」は「負の対数が最小になる値」と同じです。
そこでこの例では、最急降下法またはニュートン-ラフソン法を用いて負の対数(紫色の実線の曲線)が最小となる値を求めます。
負の対数の1階微分(紫色の破線)$\nabla E(x)$や2階微分(紫色の点線)$\nabla \nabla E(x)$については、最後に確認します。
・最頻値の探索
では、近似分布を得るための処理を確認していきます。
最急降下法またはニュートン-ラフソン法により、負の対数が最小(真の分布の確率密度が最大)となる$x$の値$x_0$を求めます。
# 試行回数を指定 max_iter = 100 # 最急降下法の学習係数を指定 eta = 0.05 # xの初期値を指定 x = 3.0 # 最頻値を探索 trace_x = np.zeros(max_iter + 1) trace_x[0] = x for i in range(max_iter): # 負の対数の1階微分を計算 dy = nabla_E(x) # 負の対数の2階微分を計算 d2y = nabla2_E(x) # xを更新 x -= eta * dy # 最急降下法 #x -= dy / d2y # ニュートン-ラフソン法 # 値を記録 trace_x[i+1] = x.copy() # 最頻値を記録(近似分布の平均を設定) x0 = x.copy() print(x0)
0.07747958098531298
ニュートン-ラフソン法では、次の式で値を更新します(検索して出てくるのは$x^{(\mathrm{old})} - \frac{E(x)}{\nabla E(x)}$なんだけど?)。
最急降下法では、次の式で値を更新します。
$\eta$は、学習係数で、更新の幅を調整します。
収束した値を最頻値(モード)$x_0$とします。
更新値の推移をグラフで確認します。
# 更新値の推移を作図 plt.figure(figsize=(8, 8)) plt.plot(x_vals, E(x_vals), color='blue', label='$E(x)$') # 負の対数 plt.plot(trace_x, E(trace_x), c='chocolate', marker='o', mfc='orange', mec='orange', label='$x^{(t)}$') # xの推移 plt.scatter(x0, E(x0), color='red', marker='x', s=200, label='$x^{(' + str(max_iter) +')}$') # 最頻値の推定値 #plt.plot(x_vals, f(x_vals), color='blue', label='$E(x)$') # 真の関数 #plt.scatter(x0, f(x0), color='red', marker='x', s=200, label='$x^{(' + str(max_iter) +')}$') # xの推移:(真の関数) #plt.plot(trace_x, f(trace_x), c='chocolate', marker='o', mfc='orange', mec='orange', label='$x^{(t)}$') # 最頻値の推定値:(真の関数) plt.xlabel('x') plt.ylabel('E(x)') plt.suptitle('Newton-Raphson Method', fontsize=20) plt.title('iter:' + str(max_iter) + ', x=' + str(np.round(x, 3)), loc='left') plt.legend() plt.grid() plt.show()
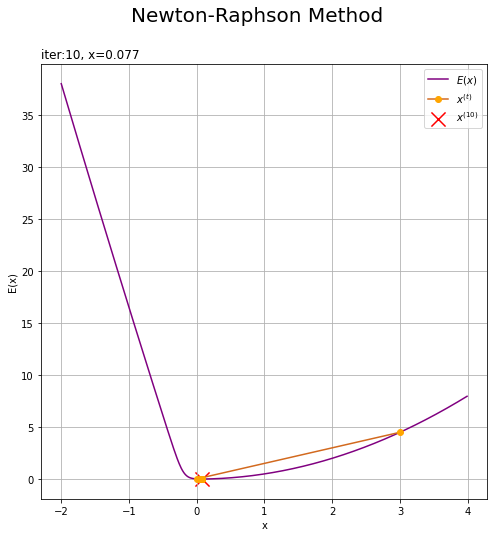
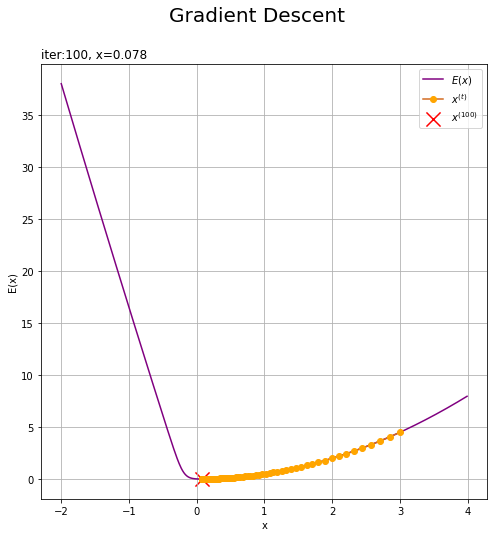
この例だと、ニュートン-ラフソン法の方が早く収束しました。初期値や学習係数の設定によって結果は変わりますが、ここではこれ以上言及しません。詳しくは「ステップ29:勾配降下法とニュートン法の比較【ゼロつく3のノート(数学)】 - からっぽのしょこ」を参考にしてください。
以降は最急降下法による結果を用います。
・近似分布の計算
モードが得られたので、近似分布を計算します。
# 近似分布の平均を指定(手計算) #x0 = 0.06 # 近似分布の精度(負の対数の2階微分)を計算 A = nabla2_E(x0) print(A) # 近似分布の確率密度を計算 laplace_dens = norm.pdf(x=x_vals, loc=x0, scale=np.sqrt(1.0 / A))
2.5303534746545844
ラプラス近似による近似分布は、平均$x_0$・精度$A$のガウス分布になります。
精度は
で計算します。また精度は分散の逆数なので、標準偏差は$\sqrt{\frac{1}{A}}$です。
1変量ガウス分布の確率密度は、scipyのnorm.pdf()で計算できます。平均の引数locにx0、標準偏差の引数scaleに平方根をとった精度の逆数np.sqrt(1.0 / A)を指定します。
真の分布$p(x)$と近似分布$q(x)$を重ねて作図します。
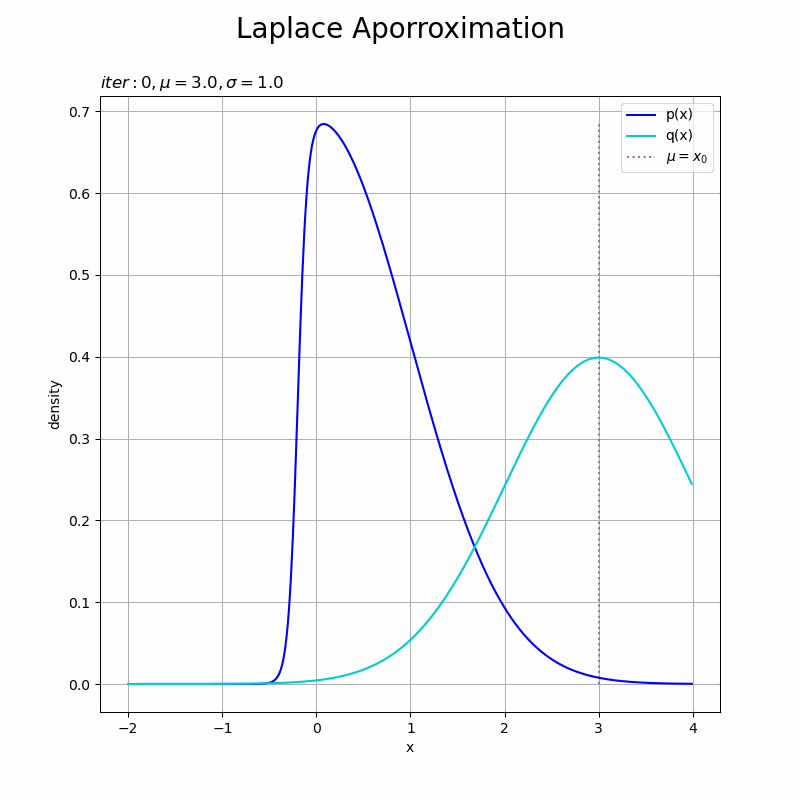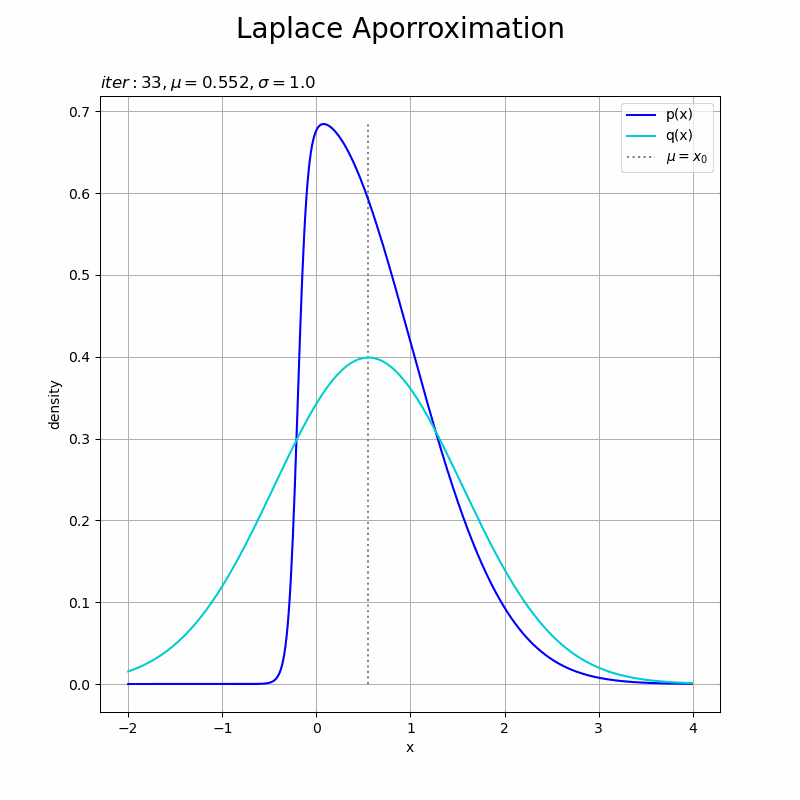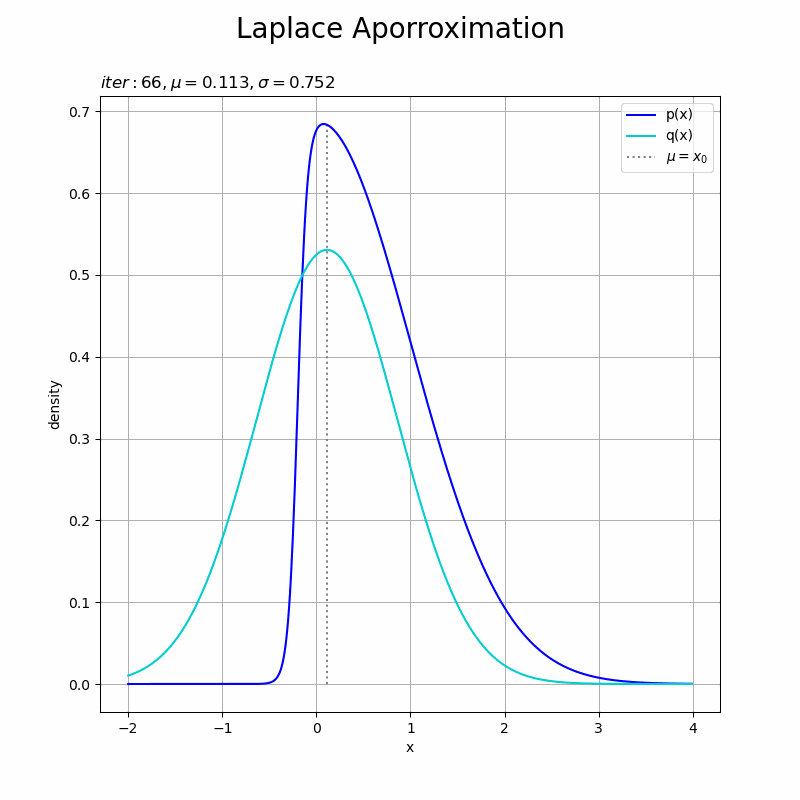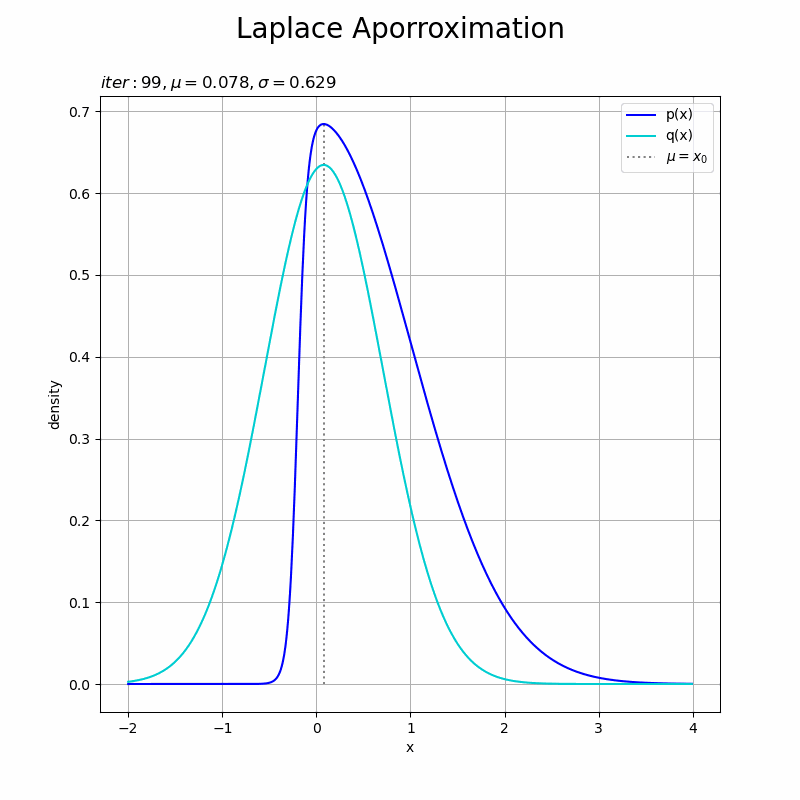
# 近似分布のグラフを作成 plt.figure(figsize=(8, 8)) plt.plot(x_vals, p(x_vals, f), color='blue', label='p(x)') # 真の分布 plt.plot(x_vals, laplace_dens, color='darkturquoise', label='q(x)') # 近似分布 plt.vlines(x=x0, ymin=0.0, ymax=np.max([p(x_vals, f), laplace_dens]), colors='gray', linestyle=':', label='$\mu = x_0$') # 最頻値の推定値 plt.xlabel('x') plt.ylabel('density') plt.suptitle('Laplace Aporroximation', fontsize=20) plt.title('$\mu=' + str(np.round(x0, 2)) + ', \sigma=' + str(np.round(np.sqrt(1.0 / A), 2)) + '$', loc='left') plt.legend() plt.grid() plt.show()

(目で見る感じ最大値が一致してるっぽいので)近似できているとしましょう。(本の図と少しズレてるのだがなぜ?)
真の分布と近似分布の負の対数のグラフを確認します。
# 負の対数のグラフを作成 plt.figure(figsize=(8, 8)) plt.plot(x_vals, -np.log(p(x_vals, f)), color='blue', label='$- \ln p(x)$') # 真の分布の対数 plt.plot(x_vals, -np.log(laplace_dens), color='darkturquoise', label='$- \ln q(x)$') # 近似分布の対数 plt.xlabel('x') plt.ylabel('log density') plt.title('Negative logarithm', fontsize=20) plt.legend() plt.grid() plt.show()

以上で、ラプラス近似による近似分布を実装できました。
近似分布の推移をアニメーションで確認します。
・作図コード(クリックで展開)
# 図を初期化 fig = plt.figure(figsize=(8, 8)) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目のxの値を取得(近似分布の平均を設定) x0 = trace_x[i] # 近似分布の精度を計算 A = nabla2_E(x0) # 近似分布の確率密度を計算 laplace_dens = norm.pdf(x=x_vals, loc=x0, scale=np.sqrt(1.0 / A)) # 近似分布のグラフを作成 plt.plot(x_vals, p(x_vals, f), color='blue', label='p(x)') # 真の分布 plt.plot(x_vals, laplace_dens, color='darkturquoise', label='q(x)') # 近似分布 plt.vlines(x=x0, ymin=0.0, ymax=np.max([p(x_vals, f), laplace_dens]), colors='gray', linestyle=':', label='$\mu = x_0$') # 最頻値の推定値 plt.xlabel('x') plt.ylabel('density') plt.suptitle('Laplace Aporroximation', fontsize=20) plt.title('$iter:' + str(i) + ', \mu=' + str(np.round(x0, 3)) + ', \sigma=' + str(np.round(np.sqrt(1.0 / A), 3)) + '$', loc='left') plt.legend() plt.grid() # gif画像を作成 anime_laplace = FuncAnimation(fig, update, frames=max_iter, interval=100) # gif画像を保存 anime_laplace.save('ch4_4_0_LaplaceApproximation.gif')
近似分布の平均は$\mu = x_0$なので、「最頻値の探索」でプロットした$x$の更新値の推移(オレンジ色の点)に従って分布が移動しています。
近似分布の標準偏差は$\sigma = \sqrt{\frac{1}{A}}$なので、「真の分布の設定」でプロットした負の対数の2階微分(紫色の点線)に従って分布の形状が変わります。最後に急激に変化しているのは、$x = 0$付近で紫色の点線の曲線が大きく変化している(大きな山になっている)ためです。
負の対数の1階微分$\nabla E(x)$と2階微分$\nabla \nabla E(x)$と、近似分布との関係を確認しましょう。
・作図コード(クリックで展開)
# 図を初期化 fig = plt.figure(figsize=(8, 8)) # x_valsからフレームに利用する間隔を指定 n = 3 # y軸の表示範囲を指定 y_min = -0.5 y_max = 1.5 # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目のxの値を取得(近似分布の平均を設定) x0 = x_vals[i*n] # 近似分布の精度を計算 A = nabla2_E(x0) # 近似分布の確率密度を計算 laplace_dens = norm.pdf(x=x_vals, loc=x0, scale=np.sqrt(1.0 / A)) # 近似分布のグラフを作成 plt.plot(x_vals, p(x_vals, f), color='blue', label='p(x)') # 真の分布 plt.plot(x_vals, laplace_dens, color='darkturquoise', label='q(x)') # 近似分布 plt.vlines(x=x0, ymin=y_min, ymax=y_max, colors='gray', linestyle=':', label='$\mu = x_0$') # 推定した最頻値 plt.scatter(x0, 0.0, color='gray') # 推定した最頻値 plt.plot(x_vals, nabla_E(x_vals), color='purple', linestyle='--', label='$\\nabla E(x)$') # 1階微分 plt.scatter(x0, nabla_E(x0), color='purple') # 1階微分 plt.plot(x_vals, np.sqrt(1.0 / nabla2_E(x_vals)), color='purple', linestyle=':', label='$\\sigma = \\sqrt{\\frac{1}{A}}$') # 標準偏差 plt.scatter(x0, np.sqrt(1.0 / nabla2_E(x0)), color='purple') # 標準偏差 plt.xlabel('x') plt.ylabel('density') plt.suptitle('Laplace Aporroximation', fontsize=20) plt.title('$\mu=' + str(np.round(x0, 3)) + ', \sigma=' + str(np.round(np.sqrt(1.0 / A), 3)) + '$', loc='left') plt.legend() plt.grid() plt.ylim(y_min, y_max) # gif画像を作成 anime_laplace = FuncAnimation(fig, update, frames=int(len(x_vals) / n), interval=100) # gif画像を保存 anime_laplace.save('ch4_4_0_LaplaceApproximation_check.gif')
(記事に添付できるサイズの問題で上の設定と下の図は少し異なります。)

紫色の破線は、$\nabla E(x)$です。$\nabla E(x) = 0$となる$x_0$が真の最頻値です。つまり、破線上を通る紫の点と、$x = 0$上を通る灰色の点が重なるとき、一番良く近似できていることになります。
紫色の点線は、$\nabla \nabla E(x)$(つまり精度$A$)の逆数の平方根で、各$x_0$における近似分布の標準偏差を表します。曲線が大きく変化するところで、近似分布(青緑色の曲線)の形状が変化するのを確認できます。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
負の対数の微分を計算するのに丸一日かかってしまった。2次元版もやるつもりでPythonで組んだんだけど、例として面白い関数を探すのが意外と難しい。どうしようか。
先日公開されたアルバム曲をどうぞ♪
【次節の内容】
なんとかやりました。