はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、4.3.2項を補足する内容です。Sigmoid関数を微分します。
【他の節一覧】
【この節の内容】
・Sigmoid関数の微分
Sigmoid関数(ロジスティックシグモイド関数)の微分を導出します。
Sigmoid関数は、入力を$x$、出力を$y$として、次の式で定義されます。
出力は、$0 < y < 1$の値になります。確率の定義を満たす値を出力するので、入力を確率値に変換したと解釈できます。
Sigmoid関数を微分します。
1行目から2行目では、分母全体を$f(x)$に対応させて、逆数の微分$\left\{\frac{1}{f(x)}\right\}' = - \frac{f'(x)}{f(x)^2}$を行っています。
2行目から3行目では、指数関数の微分$\{e^{cx}\}' = c e^{cx}$を行っています。
この式をさらに、扱いやすい形に整理します。
1行目の後の項の分子に、$0 = 1 - 1$を加えることで項を分割しています(値には影響していません)。
Sigmoid関数の定義式より、$y$に置き換えます。
Sigmoid関数の出力$y$を使った簡単な計算式が得られました。
Sigmoid関数とその微分をグラフで確認します。
# 利用するパッケージ library(tidyverse) # Sigmoid関数を計算 sigmoid_df <- tidyr::tibble( x = seq(-10, 10, by = 0.05), # 入力の範囲を指定 y = 1 / (1 + exp(-x)), # 出力 dy = y * (1 - y) # 微分 ) %>% tidyr::pivot_longer(cols = !x, names_to = "type", values_to = "value") # 縦長のデータフレームに変換 # Sigmoid関数を作図 ggplot(sigmoid_df, aes(x = x, y = value, color = type)) + geom_line() + labs(title = "Logistic Sigmoid Function")
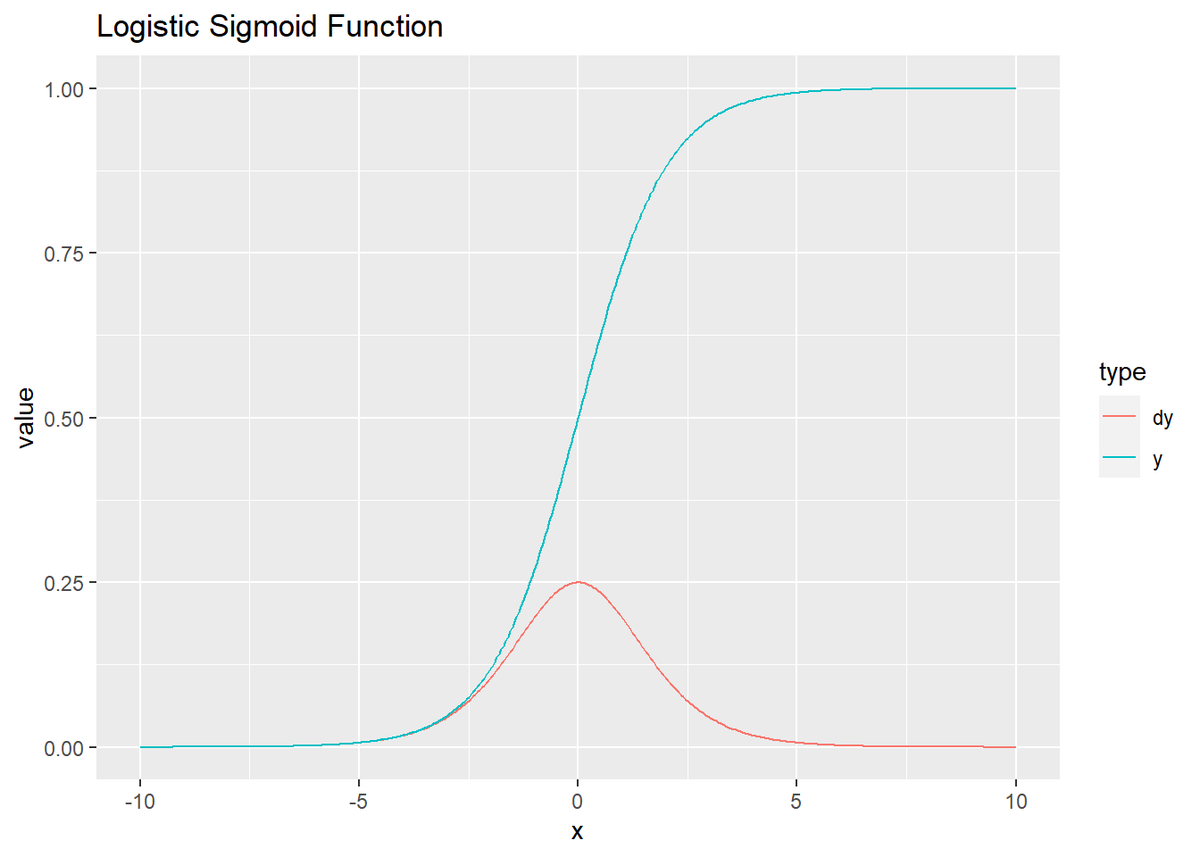
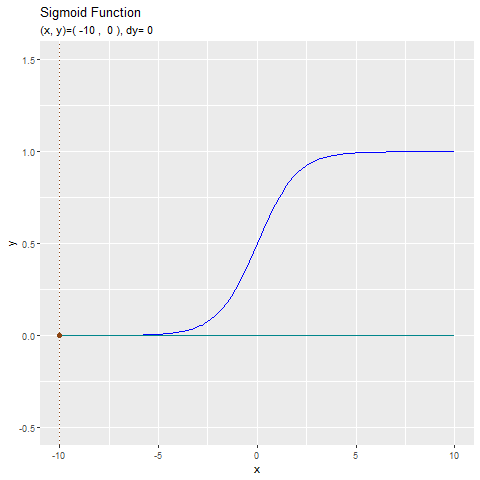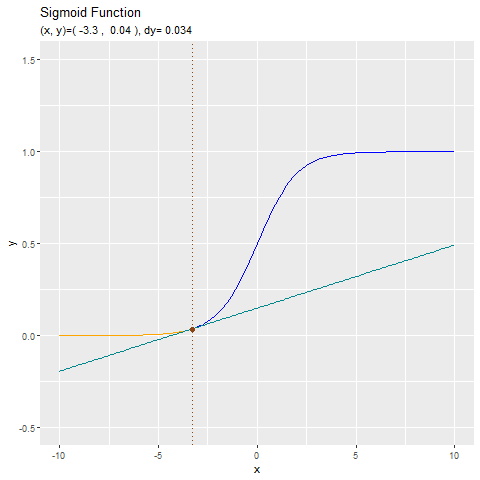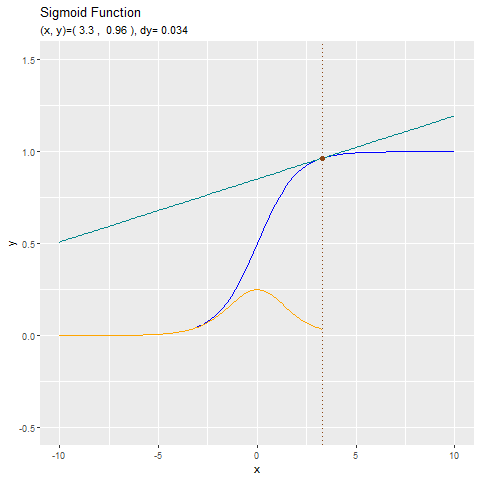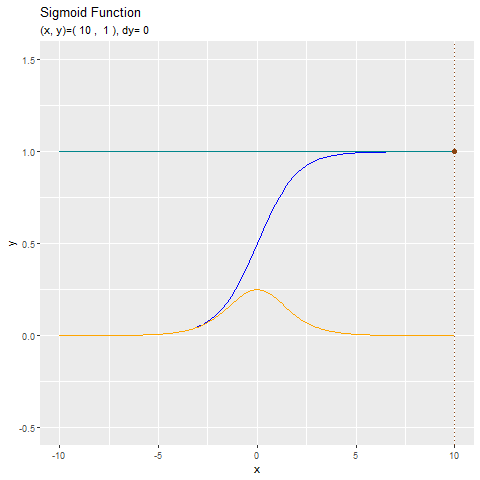
出力のグラフ(青色の曲線)が0から1の値になるのを確認できます。入力$a$の値が小さいと出力は0に近い値(ほぼ0)に、大きいと1に近い値(ほぼ1)になります。また、Sigmoid関数は単調増加するので、$x_1 < x_2$であれば$y_1 < y_2$となります。
微分のグラフ(赤色の曲線)は、出力が0から1へ大きく変化する$x = 0$をピークとする山なりの形になります。
導関数と接線の関係をアニメーションで確認します。
・コード(クリックで展開)
# 追加パッケージ library(gganimate) # 関数を指定 f <- function(x) { y <- 1 / (1 + exp(-x)) # Sigmoid #y <- (exp(x) - exp(-x)) / (exp(x) + exp(-x)) # tanh return(y) } # 導関数を指定 df <- function(y) { dy <- y * (1 - y) # Sigmoid #dy <- 1 - y^2 # tanh return(dy) } # x軸の値を作成 x_vals <- seq(-10, 10, by = 0.1) length(x_vals) # フレーム数 # Sigmoid関数を計算 sigmoid_df <- tidyr::tibble( x = x_vals, y = f(x) # 出力 ) # xの値ごとにグラフを計算 anime_diff_df <- tidyr::tibble() anime_tangentline_df <- tidyr::tibble() anime_tangentpoint_df <- tidyr::tibble() for(i in 1:length(x_vals)) { # 接点のx軸の値を取得 x_val <- x_vals[i] # 接点のy軸の値を計算 y_val <- f(x_val) # 接線の傾きを計算 dy_val <- df(y_val) # 接線の切片を計算 b_val <- y_val- dy_val * x_val # フレーム切替用のラベルを作成 label_txt <- paste( "(x, y)=(", round(x_val, 2), ", ", round(y_val, 2), "), dy=", round(dy_val, 3) ) # 導関数を計算 tmp_diff_df <- tidyr::tibble( x = x_vals[1:i], y = f(x), # 出力 dy = df(y), # 微分 label = as.factor(label_txt) ) anime_diff_df <- rbind(anime_diff_df, tmp_diff_df) # 接線を計算 tmp_tangentline_df <- tidyr::tibble( x = x_vals, y = dy_val * x + b_val, label = as.factor(label_txt) ) anime_tangentline_df <- rbind(anime_tangentline_df, tmp_tangentline_df) # 接点を格納 tmp_tangentpoint_df <- tidyr::tibble( x = x_val, y = y_val, label = as.factor(label_txt) ) anime_tangentpoint_df <- rbind(anime_tangentpoint_df, tmp_tangentpoint_df) } # 作図 anime_graph <- ggplot() + geom_line(data = sigmoid_df, aes(x = x, y = y, group = 1), color = "blue") + # 対象の関数 geom_line(data = anime_diff_df, aes(x = x, y = dy, group = 1), color = "orange") + # 導関数 geom_line(data = anime_tangentline_df, aes(x = x, y = y, group = 1), color = "turquoise4") + # 接線 geom_point(data = anime_tangentpoint_df, aes(x = x, y = y), color = "chocolate4", size = 2) + # 接点 geom_vline(data = anime_tangentpoint_df, aes(xintercept = x), color = "chocolate4", linetype = "dotted") + # 接線の垂線 gganimate::transition_manual(label) + # フレーム ylim(c(-0.5, 1.5)) + labs(title = "Sigmoid Function", subtitle = "{current_frame}") # gif画像として出力 gganimate::animate(anime_graph, nframes = length(x_vals), fps = 10)
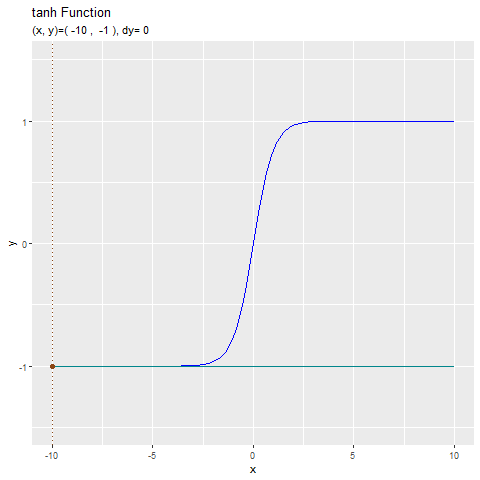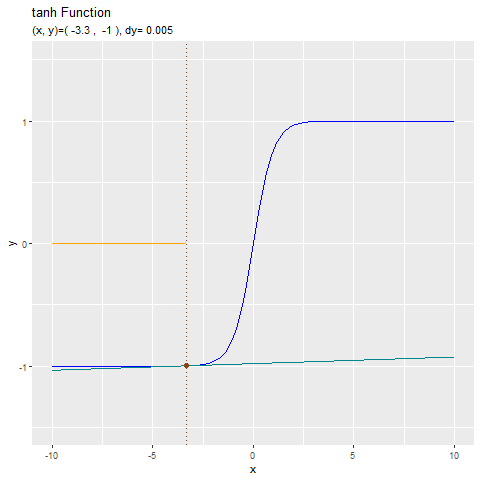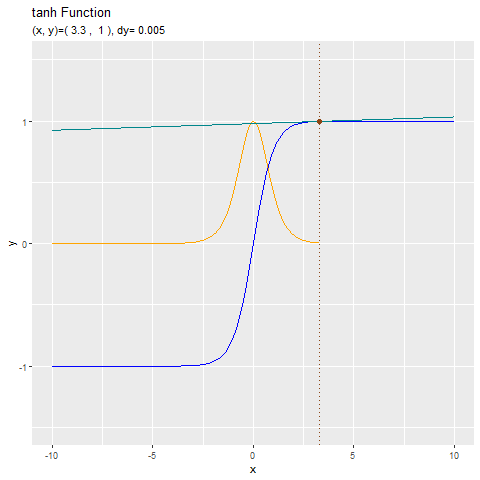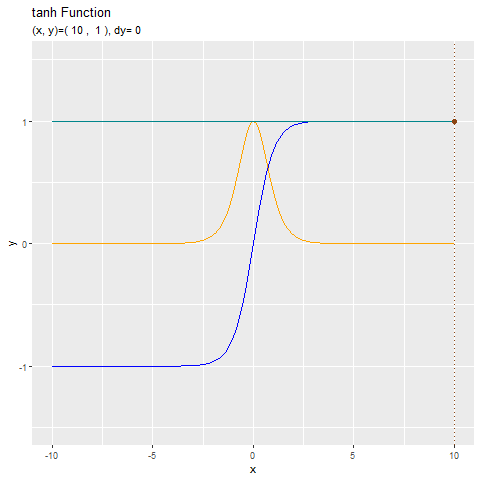
形が似ているtanh関数と合わせてどうぞ。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
ロジスティック回帰を理解するためのパーツを順調に揃えていってる感じがする。
先ほど公開されたモーニング娘。'21の新シングルのMVをどうぞ。
明るくて楽し気な曲も良いね。
【関連する内容】
同じ内容ですが、こちらは誤差逆伝播法で導出しています。