はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
ポアソン分布の計算とグラフの作成をPythonで行います。
【前の内容】
【他の記事一覧】
【この記事の内容】
ポアソン分布
ポアソン分布(Poisson Distribution)の計算と作図を行います。
利用するライブラリを読み込みます。
# 利用するライブラリ import numpy as np from scipy.stats import poisson # ポアソン分布 from scipy.special import gamma, loggamma # ガンマ関数, 対数ガンマ関数 import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
分布の変化をアニメーション(gif画像)で確認するのにmatplotlibライブラリのanimationモジュールを利用します。不要であれば省略してください。
定義式の確認
まずは、ポアソン分布の定義式を確認します。
ポアソン分布は、次の式で定義されます。
ここで、$x$は単位時間における事象の発生回数、$\lambda$は発生回数の期待値です。
確率変数の値$x$は0以上の整数となります。パラメータ$\lambda$は、$\lambda > 0$を満たす必要があります。
この式の対数をとると、次の式になります。
ポアソン分布の平均と分散は、どちらもパラメータ$\lambda$になります。
確率の計算
ポアソン分布に従う確率を計算する方法をいくつか確認します。
パラメータを設定します。
# パラメータを指定 lmd = 4.0 # 確率変数の値を指定 x = 2.0
ポアソン分布のパラメータ$\lambda > 0$、確率変数がとり得る値(非負の整数)$x$を指定します。設定した値に従う確率を計算します。lambdaは予約語のため変数名として使えないのでlmdとします。
まずは、定義式から確率を計算します。
# 定義式により確率を計算 prob = lmd**x / gamma(x + 1.0) * np.exp(-lmd) print(prob)
0.14652511110987343
ポアソン分布の定義式
で計算します。
階乗$x!$の計算は、ガンマ関数$\Gamma(x + 1) = x!$に置き換えて計算します。ガンマ関数は、SciPyライブラリのspecialモジュールのgamma()で計算できます。
対数をとった定義式から計算します。
# 対数をとった定義式により確率を計算 log_prob = x * np.log(lmd) - loggamma(x + 1.0) - lmd prob = np.exp(log_prob) print(prob, log_prob)
0.14652511110987343 -1.9205584583201643
対数をとった定義式
を計算します。計算結果の指数をとると確率が得られます。
指数と対数の性質より$\exp(\log x) = x$です。
次は、SciPyライブラリのモジュールを使って確率を計算します。
ポアソン分布のモジュールpoissonの確率メソッドpmf()を使って計算します。
# ポアソン分布の関数により確率を計算 prob = poisson.pmf(k=x, mu=lmd) print(prob)
0.14652511110987343
変数の引数kにx、パラメータの引数muにlmdを指定します。
logpmf()だと対数をとった確率を計算します。
# ポアソン分布の対数をとった関数により確率を計算 log_prob = poisson.logpmf(k=x, mu=lmd) prob = np.exp(log_prob) print(prob, log_prob)
0.14652511110987343 -1.9205584583201643
計算結果の指数をとると確率が得られます。
統計量の計算
ポアソン分布の平均と分散を計算します。
平均を計算します。
# 計算式により平均を計算 E_x = lmd print(E_x)
4.0
ポアソン分布の平均は$\lambda$です。
分散を計算します。
# 計算式により分散を計算 V_x = lmd print(V_x)
4.0
ポアソン分布の分散も$\lambda$です。
ポアソン分布のモジュールの平均メソッドmean()でも平均を計算できます。
# ポアソン分布の関数により平均を計算 E_x = poisson.mean(mu=lmd) print(E_x)
4.0
確率メソッドと同様に引数を指定します。
分散メソッドvar()で分散を計算します。
# ポアソン分布の関数により分散を計算 V_x = poisson.var(mu=lmd) print(V_x)
4.0
こちらも同様に引数を指定します。
分布の可視化
MatplotlibライブラリのPyPlotモジュールを利用してポアソン分布のグラフを作成します。
ポアソン分布の確率変数がとり得る値$x$ごとの確率を計算します。
# パラメータを指定 lmd = 4.0 # 作図用のxの点を作成 x_vals = np.arange(np.ceil(lmd) * 4.0) # ポアソン分布を計算 probability = poisson.pmf(k=x_vals, mu=lmd)
$x$がとり得る値を作成してx_valsとします。この例では、0からlmdの4倍を範囲とします。ただし、$x$は0以上の整数なので、np.ceil()でlmdを切り上げて使います。
x_valsの各要素に対応する確率を求めます。
ポアソン分布のグラフを作成します。
# ポアソン分布を作図 plt.figure(figsize=(12, 9)) # 図の設定 plt.bar(x=x_vals, height=probability, color='#00A968') # 棒グラフ plt.xlabel('x') # x軸ラベル plt.ylabel('probability') # y軸ラベル plt.suptitle('Poisson Distribution', fontsize=20) # 全体のタイトル plt.title('$\lambda=' + str(lmd) + '$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.grid() # グリッド線 plt.show() # 描画
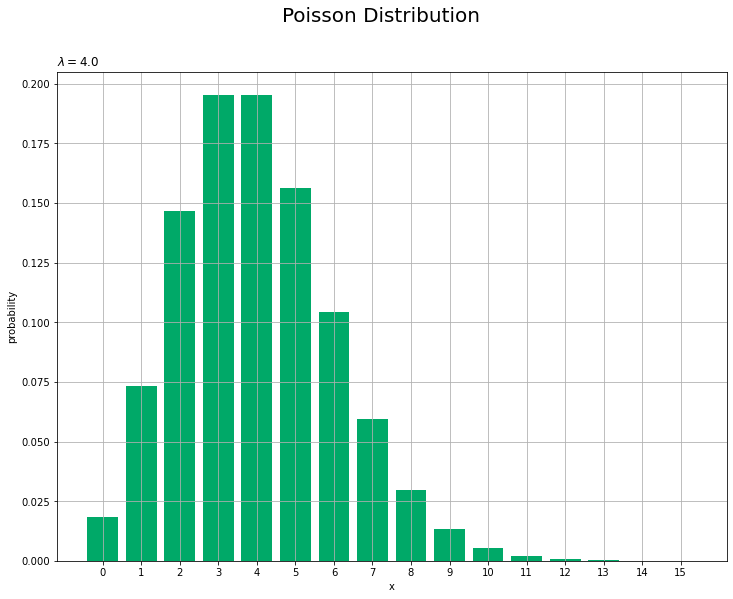
この分布に平均と標準偏差を重ねて表示します。
# 統計量を計算 E_x = lmd s_x = np.sqrt(lmd) # 統計量を重ねたポアソン分布を作図 plt.figure(figsize=(12, 9)) # 図の設定 plt.bar(x=x_vals, height=probability, color='#00A968') # 分布 plt.vlines(x=E_x, ymin=0.0, ymax=probability.max(), color='orange', linewidth=2.5, linestyle='--', label='$E[x]$') # 平均 plt.vlines(x=E_x - s_x, ymin=0.0, ymax=probability.max(), color='orange', linewidth=2.5, linestyle=':', label='$E[x] \pm \\sqrt{V[x]}$') # 平均 - 標準偏差 plt.vlines(x=E_x + s_x, ymin=0.0, ymax=probability.max(), color='orange', linewidth=2.5, linestyle=':') # 平均 + 標準偏差 plt.xlabel('x') # x軸ラベル plt.ylabel('probability') # y軸ラベル plt.suptitle('Poisson Distribution', fontsize=20)# 全体のタイトル plt.title('$\lambda=' + str(lmd) + '$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.legend() # 凡例 plt.grid() # グリッド線 plt.show() # 描画
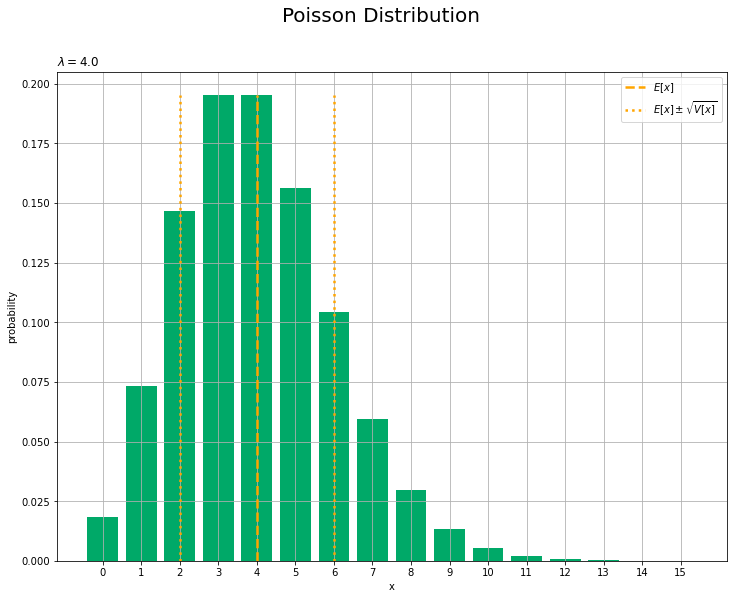
平均(破線)となる確率が最大なのを確認できます。また、点線で平均を中心に標準偏差の範囲を示しています。
ポアソン分布のグラフを描画できました。
パラメータと分布の形状の関係
パラメータが及ぼす分布への影響をアニメーション(gif画像)で可視化します。
パラメータ$\lambda$の値を少しずつ変更して、分布の変化をアニメーションで確認します。
・作図コード(クリックで展開)
# lambdaとして利用する値を指定 lambda_vals = np.arange(start=0.0, stop=10.1, step=0.1) print(len(lambda_vals)) # フレーム数 # 作図用のxの点を作成 x_vals = np.arange(np.ceil(lambda_vals.max()) * 2.0) # y軸(確率)の最大値を設定 prob_max = np.max(poisson.pmf(k=x_vals, mu=lambda_vals.min())) + 0.1 #prob_max = 0.5 # 図を初期化 fig = plt.figure(figsize=(12, 9)) # 図の設定 fig.suptitle('Poisson Distribution', fontsize=20)# 全体のタイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目のパラメータを取得 lmd = lambda_vals[i] # ポアソン分布を計算 probability = poisson.pmf(k=x_vals, mu=lmd) # ポアソン分布を作図 plt.bar(x=x_vals, height=probability, color='#00A968') # 棒グラフ plt.xlabel('x') # x軸ラベル plt.ylabel('probability') # y軸ラベル plt.title('$\lambda=' + str(np.round(lmd, 1)) + '$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.grid() # グリッド線 plt.ylim(ymin=0.0, ymax=prob_max) # y軸の表示範囲 # gif画像を作成 anime_prob = FuncAnimation(fig, update, frames=len(lambda_vals), interval=100) # gif画像を保存 anime_prob.save('Poisson_prob.gif')
101
$\lambda$がとり得る値を作成してlambda_valsとします。
lambda_valsの値ごとに作図します。
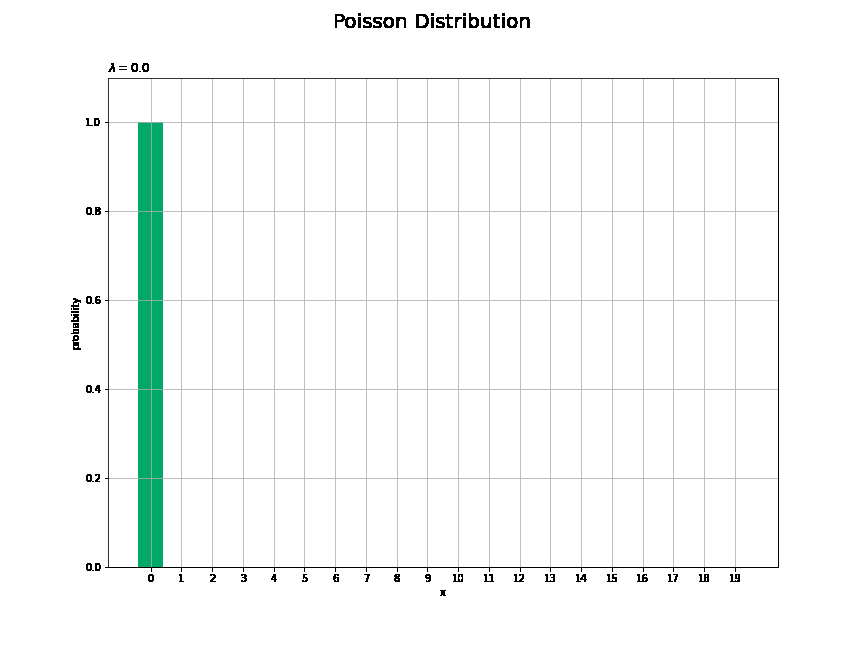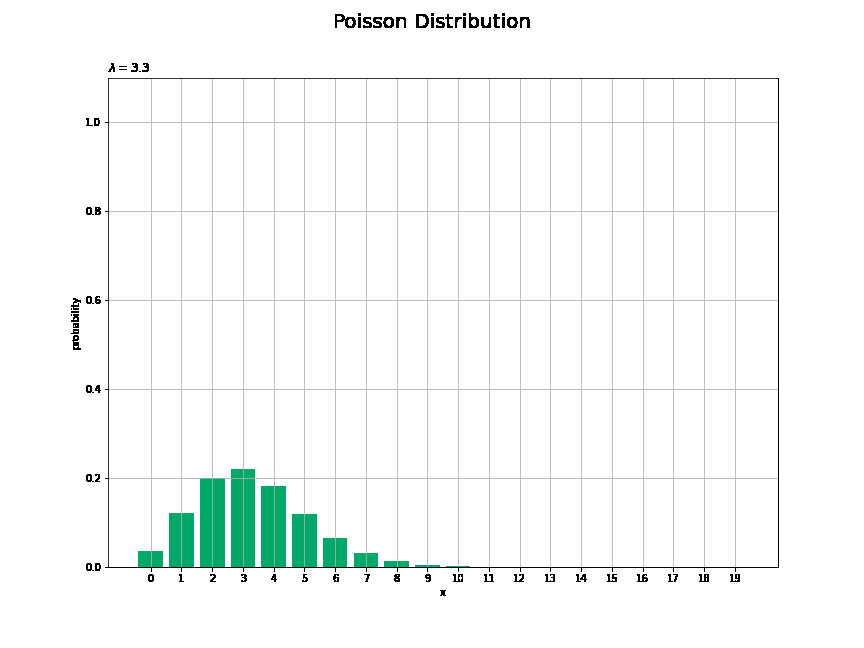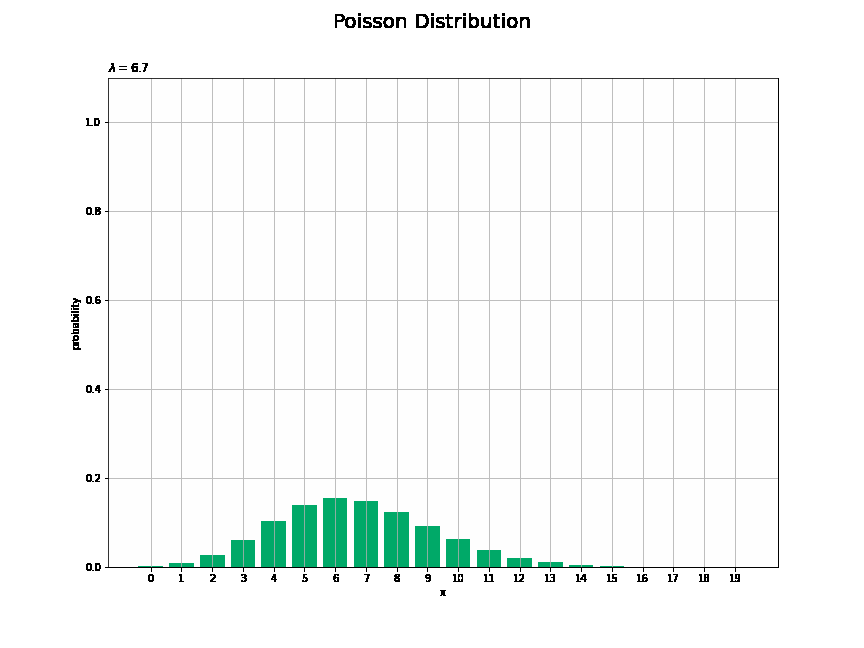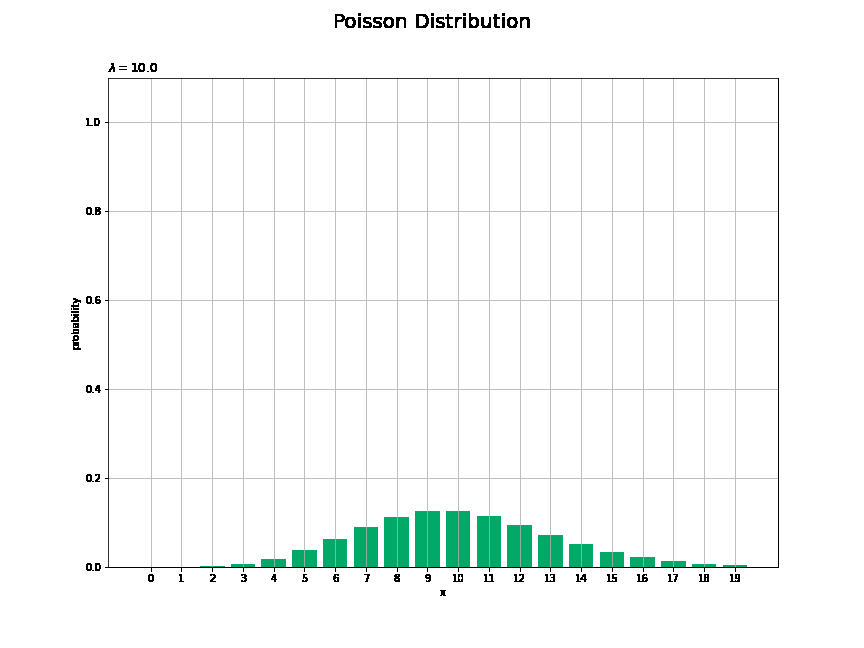
$\lambda$が大きくなるに従って、$x$が大きいほど確率が高くなる(山が右に移動する)のを確認できます。
乱数の生成
ポアソン分布の乱数を生成してヒストグラムを確認します。
パラメータを指定して、ポアソン分布に従う乱数を生成します。
# パラメータを指定 lmd = 4.0 # データ数(サンプルサイズ)を指定 N = 1000 # ポアソン分布に従う乱数を生成 x_n = np.random.poisson(lam=lmd, size=N) print(x_n[:10])
[3 1 5 4 3 2 1 6 2 5]
ポアソン分布の乱数は、NumPyライブラリのrandomモジュールのポアソン分布の乱数生成関数np.random.poisson()で生成できます。パラメータの引数lamにlmd、データ数(サンプルサイズ)の引数sizeにNを指定します。
サンプルを集計します。
# 作図用のxの点を作成 x_vals = np.arange(x_n.max() + 5.0) print(x_vals[:10]) # 乱数を集計 frequency = np.array([np.sum(x_n == m) for m in x_vals]) print(frequency[:10]) # ポアソン分布を計算 probability = poisson.pmf(k=x_vals, mu=lmd)
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
[ 11 80 140 208 210 145 103 57 22 14]
x_nに含まれる値がmの要素数は、np.sum(x_n == m)で得られます。
リスト内包表記を用いて、x_valsの全ての要素をカウントして配列に格納します。
ヒストグラムを作成します。
# サンプルのヒストグラムを作成 plt.figure(figsize=(12, 9)) # 図の設定 plt.bar(x=x_vals, height=frequency, color='#00A968') # ヒストグラム plt.xlabel('x') # x軸ラベル plt.ylabel('frequency') # y軸ラベル plt.suptitle('Poisson Distribution', fontsize=20)# 全体のタイトル plt.title('$\lambda=' + str(lmd) + ', N=' + str(N) + '=(' + ', '.join([str(f) for f in frequency]) + ')$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.grid() # グリッド線 plt.show() # 描画
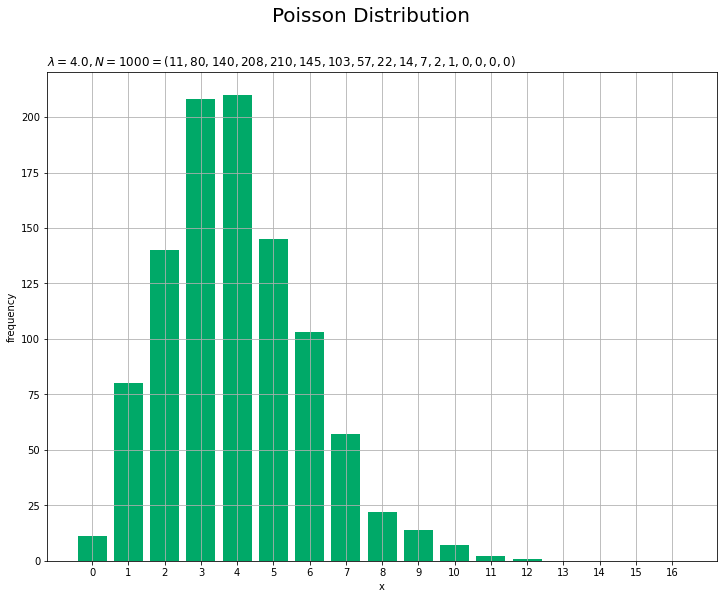
構成比を分布に重ねて描画します。
# サンプルの構成比を作図 plt.figure(figsize=(12, 9)) # 図の設定 plt.bar(x=x_vals, height=probability, color='white', edgecolor='green', linestyle='--') # 元の分布 plt.bar(x=x_vals, height=frequency / N, color='#00A968', alpha=0.8) # 構成比 plt.xlabel('x') # x軸ラベル plt.ylabel('proportion') # y軸ラベル plt.suptitle('Poisson Distribution', fontsize=20)# 全体のタイトル plt.title('$\lambda=' + str(lmd) + ', N=' + str(N) + '=(' + ', '.join([str(f) for f in frequency]) + ')$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.grid() # グリッド線 plt.show() # 描画
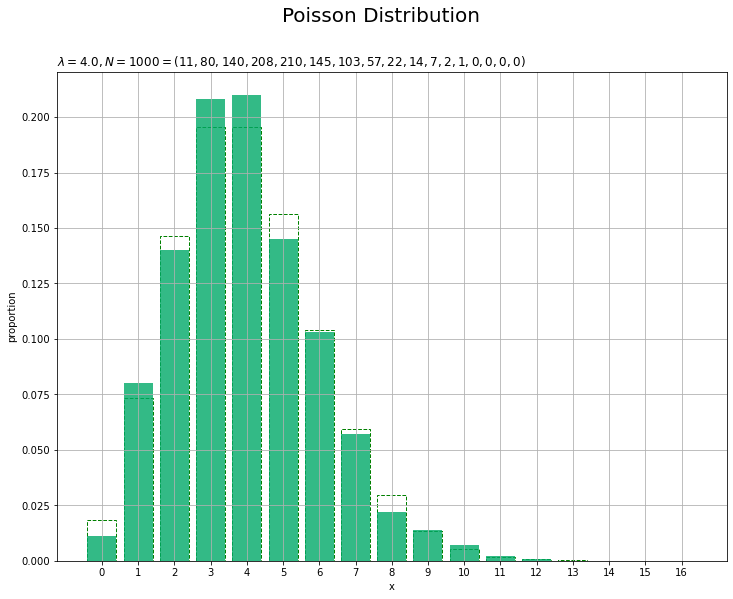
頻度frequencyをデータ数Nで割り、各値の構成比を計算します。
データ数が十分に増えると元の分布(破線のグラフ)のグラフに形が近づきます。
サンプルサイズとヒストグラムの変化をアニメーションで確認します。乱数を1つずつ取り出して作図します。
・作図コード(クリックで展開)
ヒストグラムのアニメーションを作成します。
# フレーム数を指定 N_frame = 150 # 図を初期化 fig = plt.figure(figsize=(10, 7.5)) # 図の設定 fig.suptitle('Poisson Distribution', fontsize=20)# 全体のタイトル # y軸(頻度)の最大値を設定 freq_max = np.max([np.sum(x_n[:N_frame] == m) for m in x_vals]) + 1.0 # 作図処理を関数として定義 def update(n): # 前フレームのグラフを初期化 plt.cla() # n個の乱数を集計 frequency = np.array([np.sum(x_n[:(n+1)] == m) for m in x_vals]) # サンプルのヒストグラムを作成 plt.bar(x=x_vals, height=frequency, color='#00A968', zorder=1) # ヒストグラム plt.scatter(x=x_n[n], y=0.0, s=100, c='orange', zorder=2) # サンプル plt.xlabel('x') # x軸ラベル plt.ylabel('frequency') # y軸ラベル plt.title('$\lambda=' + str(lmd) + ', N=' + str(n + 1) + '=(' + ', '.join([str(f) for f in frequency]) + ')$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.grid() # グリッド線 plt.ylim(ymin=-0.5, ymax=freq_max) # y軸の表示範囲 # gif画像を作成 anime_freq = FuncAnimation(fig, update, frames=N_frame, interval=100) # gif画像を保存 anime_freq.save('Poisson_freq.gif')
構成比のアニメーションを作成します。
## アニメーションによる可視化:(構成比) # フレーム数を指定 N_frame = 150 # 図を初期化 fig = plt.figure(figsize=(10, 7.5)) # 図の設定 fig.suptitle('Poisson Distribution', fontsize=20)# 全体のタイトル # y軸(割合)の最大値を設定 prop_max = np.max([np.sum(x_n[:N_frame] == m) for m in x_vals]) / N_frame + 0.1 # 作図処理を関数として定義 def update(n): # 前フレームのグラフを初期化 plt.cla() # n個の乱数を集計 frequency = np.array([np.sum(x_n[:(n+1)] == m) for m in x_vals]) # サンプルのヒストグラムを作成 plt.bar(x=x_vals, height=probability, color='white', edgecolor='green', linestyle='--', zorder=1) # 元の分布 plt.bar(x=x_vals, height=frequency / (n + 1), color='#00A968', alpha=0.8, zorder=2) # 構成比 plt.scatter(x=x_n[n], y=0.0, s=100, c='orange', zorder=3) # サンプル plt.xlabel('x') # x軸ラベル plt.ylabel('proportion') # y軸ラベル plt.title('$\lambda=' + str(lmd) + ', N=' + str(n + 1) + '=(' + ', '.join([str(f) for f in frequency]) + ')$', loc='left') # タイトル plt.xticks(ticks=x_vals) # x軸目盛 plt.grid() # グリッド線 plt.ylim(ymin=-0.01, ymax=prop_max) # y軸の表示範囲 # gif画像を作成 anime_prop = FuncAnimation(fig, update, frames=N_frame, interval=100) # gif画像を保存 anime_prop.save('Poisson_prop.gif')
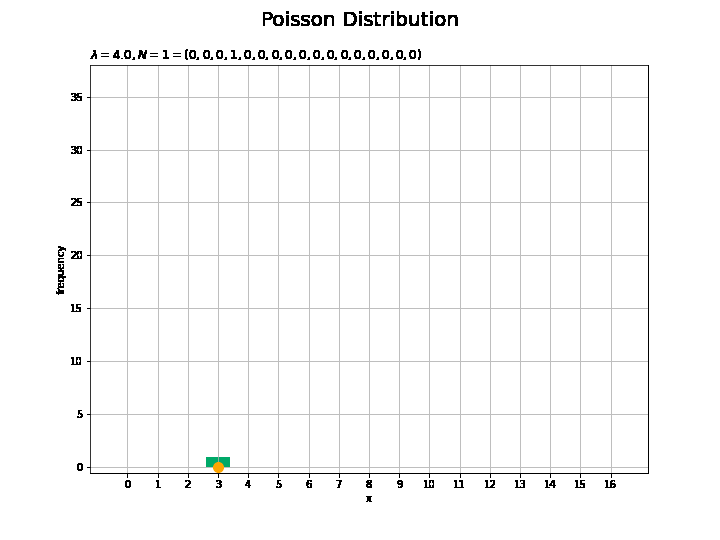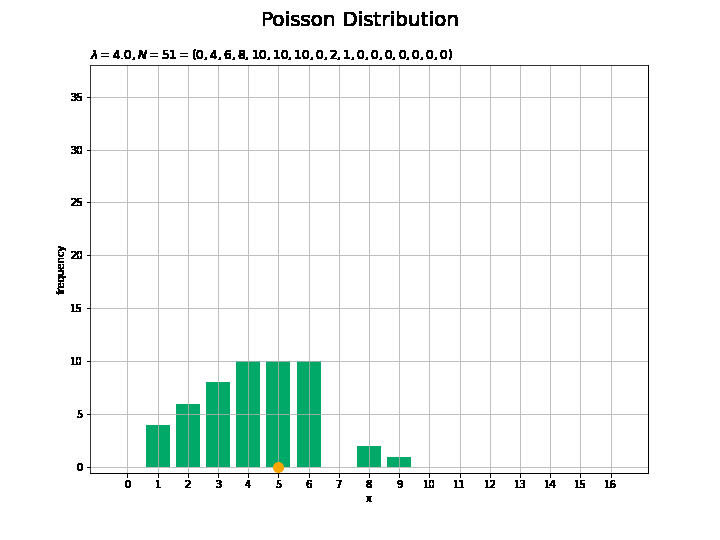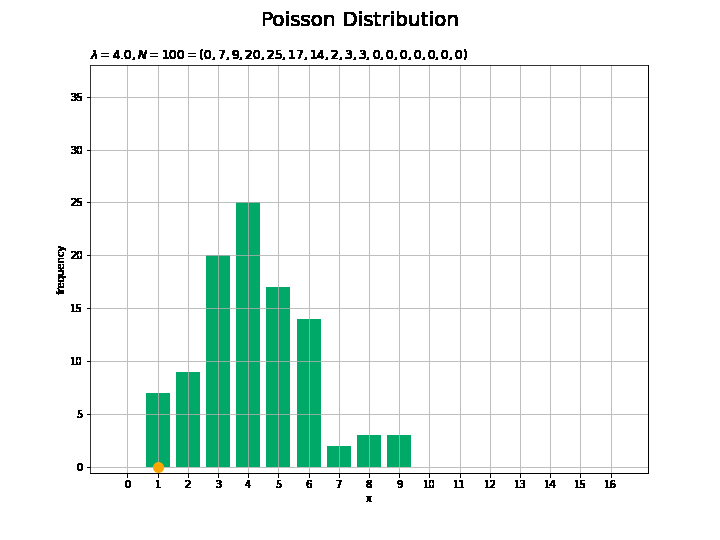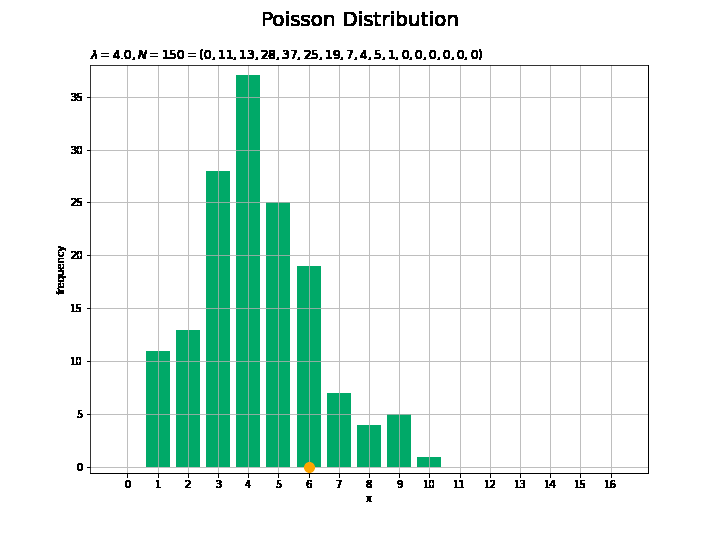
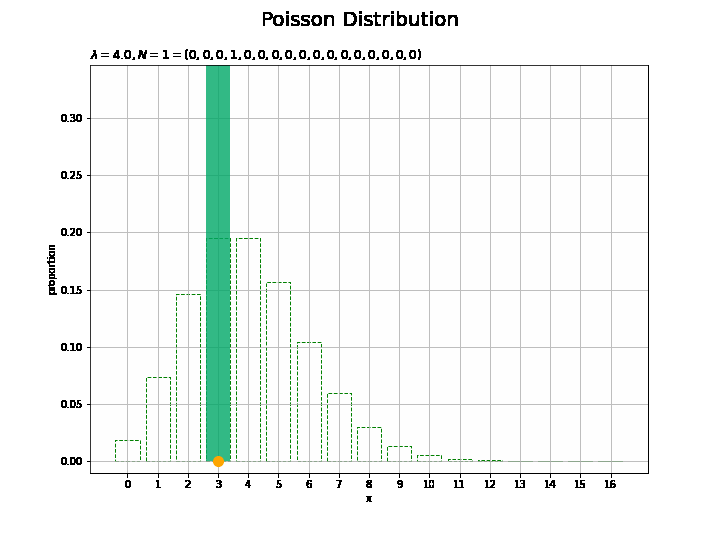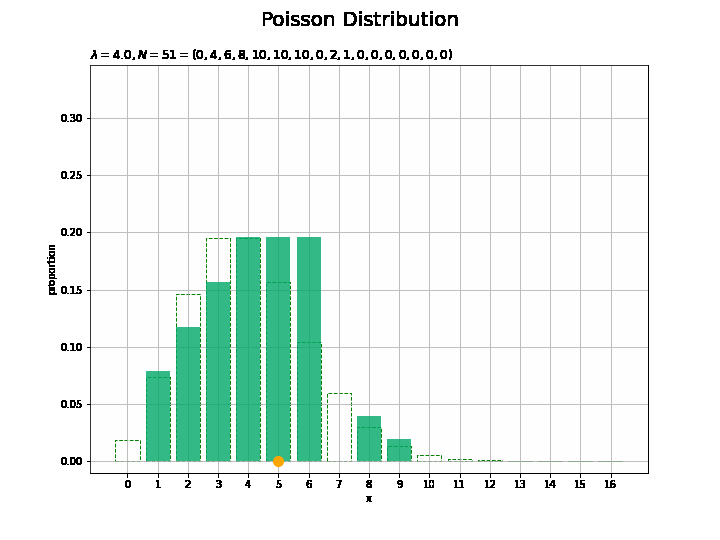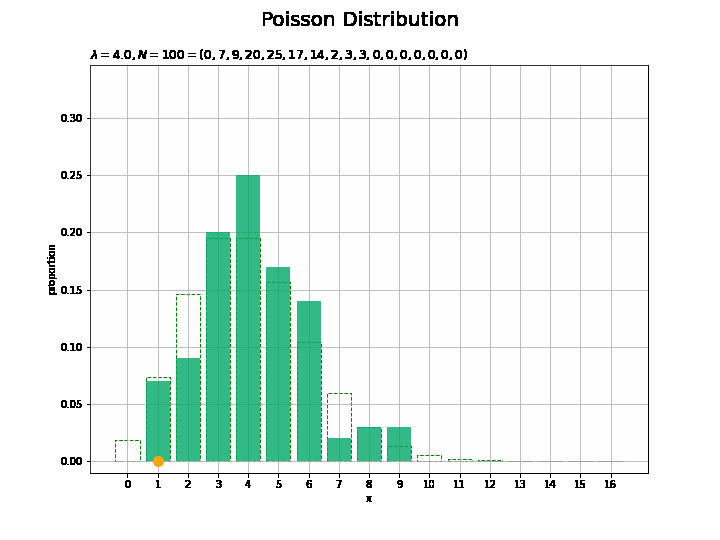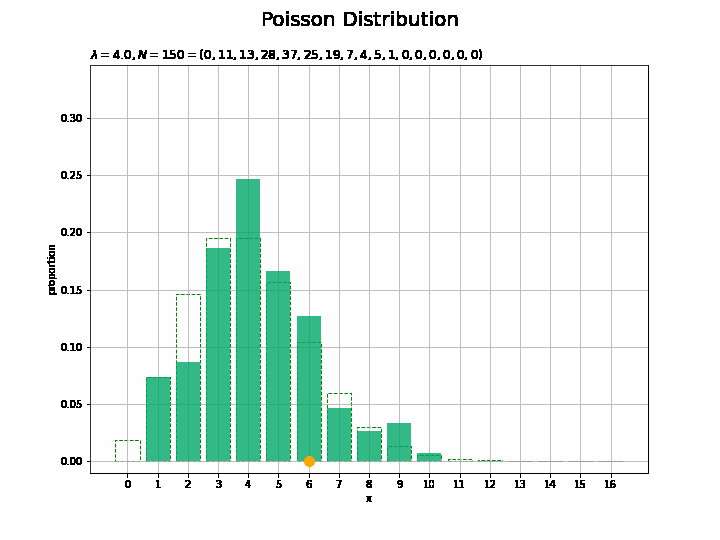
サンプルが増えるに従って、元の分布に近付くのを確認できます。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
飽きてない飽きてないぞ。
【次の内容】
つづく