はじめに
「プログラミング」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ実行結果を見ながら処理の意図を確認していきます。
この記事は、5.5.2項「Sigmoidレイヤ」の内容です。SigmoidレイヤをPythonで実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
5.5.2 Sigmoidレイヤの実装
シグモイド関数(Sigmoid関数)の順伝播と逆伝播の計算を行うSigmoidレイヤを実装します。シグモイド関数(順伝播)については「3.2.4:シグモイド関数の実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」、シグモイド関数の微分(逆伝播)については「シグモイド関数の逆伝播の導出【ゼロつく1のノート(数学)】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 5.5.2項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・数式の確認
まずは、Sigmoidレイヤの定義式を確認します。
順伝播では、入力を$\mathbf{X} = (x_{0,0}, \cdots, x_{N-1,H-1})$、出力を$\mathbf{Y} = (y_{0,0}, \cdots, y_{N-1,H-1})$として、行列の各項に対してシグモイド関数の計算をします。$N$はバッチサイズ(1試行当たりのデータ数)、$H$は中間層(次の層)のニューロン数です。また、Pythonのインデックスに合わせて添字を0から割り当てています。
順伝播の各出力(シグモイド関数の出力)$y_{n,h}$は、0から1の値に変換されます。
逆伝播では、「逆伝播の入力$\frac{\partial L}{\partial y_{n,h}}$」と「Sigmoidレイヤの微分$\frac{\partial y_{n,h}}{\partial x_{n,h}}$」の積$\frac{\partial L}{\partial x_{n,h}} = \frac{\partial L}{\partial y_{n,h}} \frac{\partial y_{n,h}}{\partial x_{n,h}}$を求めます。
$\frac{\partial L}{\partial x_{n,h}}$は、順伝播の入力$x_{n,k}$に関する損失$L$の微分であり、逆伝播の出力です。詳しくは「5.2:連鎖率【ゼロつく1のノート(数学)】 - からっぽのしょこ」を参照してください。
$\frac{\partial L}{\partial y_{n,h}}$は、順伝播の出力$y_{n,k}$に関する損失$L$の微分です。これは、次のレイヤの逆伝播で計算されるため、このレイヤでは計算しません。
$\frac{\partial y_{n,h}}{\partial x_{n,h}}$は、Sigmoid関数の入力$x_{n,h}$に関する出力$y_{n,h}$の微分であり、次の式で計算します。
$0 < y _{n,h} < 1$なので、$0 < 1 - y _{n,h} < 1$です。
したがって、逆伝播の出力$\frac{\partial L}{\partial x_{n,h}}$は、次の式で計算できます。
以上が、Sigmoidレイヤで行う計算です。
・処理の確認
次に、Sigmoidレイヤで行う処理を確認します。
・順伝播の計算
順伝播の入力$\mathbf{X}$を作成します。
# (仮の)順伝播の入力を作成 x = x = np.array([[1.0, -0.5], [0.0, 3.0]]) print(x)
[[ 1. -0.5]
[ 0. 3. ]]
ここでは簡単に、$2 \times 2$の2次元配列とします。
順伝播の式(5.9)を計算します。
# 順伝播を計算 y = 1 / (1 + np.exp(-x)) print(np.round(y, 3))
[[0.731 0.378]
[0.5 0.953]]
順伝播の出力が得られました。全ての項が0から1の値となります。yを次のレイヤ(Affineレイヤ)に入力します。
ここまでは、順伝播の処理を確認しました。続いて、逆伝播の処理を確認します。
・逆伝播の計算
逆伝播の入力$\frac{\partial L}{\partial \mathbf{Y}}$を作成します。
# (仮の)逆伝播の入力を作成 dy = np.ones_like(y) print(dy)
[[1. 1.]
[1. 1.]]
$\frac{\partial L}{\partial \mathbf{Y}}$は$\mathbf{Y}$と同じ形状です。ここでは簡単に、全ての要素を1とします。
逆伝播の式(5.12)を計算します。
# 逆伝播を計算 dx = dy * y * (1 - y) print(np.round(dx, 3))
[[0.197 0.235]
[0.25 0.045]]
逆伝播の出力が得られました。dxを前のレイヤ(Affineレイヤ)に入力します。
以上がSigmoidレイヤで行う処理です。
・実装
処理の確認ができたので、Sigmoidレイヤをクラスとして実装します。
# Sigmoidレイヤの実装 class Sigmoid: # 初期化メソッド def __init__(self): # 順伝播の出力を初期化 self.out = None # 順伝播メソッド def forward(self, x): # 順伝播を計算:式(5.9) out = 1 / (1 + np.exp(-x)) # 順伝播の出力を保存 self.out = out return out # 逆伝播メソッド def backward(self, dout): # 逆伝播を計算:式(5.12) dx = dout * self.out * (1.0 - self.out) return dx
順伝播の出力$\mathbf{Y}$は逆伝播の計算にも用いるので、順伝播の計算時に(順伝播メソッドの実行時に)計算結果をインスタンス変数outに保存しておきます。逆伝播メソッドでは、保存した値を用いて計算します。
実装したクラスを試してみましょう。
Sigmoidクラスのインスタンスを作成します。
# Sigmoidレイヤのインスタンスを作成
layer = Sigmoid()
順伝播の入力を作成して、順伝播の計算をします。
# (仮の)順伝播の入力を作成 x = np.array([[1.0, -0.5], [-2.0, 3.0]]) print(x) # 順伝播を計算 y = layer.forward(x) print(y)
[[ 1. -0.5]
[-2. 3. ]]
[[0.73105858 0.37754067]
[0.11920292 0.95257413]]
逆伝播の入力を作成して、逆伝播の計算をします。
# (仮の)逆伝播の入力を作成 dy = np.ones_like(y) print(dy) # 逆伝播を計算 dx = layer.backward(dy) print(dx)
[[1. 1.]
[1. 1.]]
[[0.19661193 0.23500371]
[0.10499359 0.04517666]]
Sigmoidレイヤを実装できました。
・グラフの確認
最後に、Sigmoidレイヤの順伝播と逆伝播をグラフで確認します。
Sigmoidクラスのインスタンスを作成します。
# Sigmoidレイヤのインスタンスを作成
layer = Sigmoid()
作図用に順伝播の各入力$x$がとり得る値を作成して、順伝播を計算します。
# 作図用の順伝播の入力を作成 x_vals = np.arange(-10.0, 10.0, 0.01) # 順伝播を計算 y_vals = layer.forward(x_vals) print(np.round(y_vals[:5], 5)) # 前から5つ print(np.round(y_vals[-5:], 5)) # 後から5つ
[5.e-05 5.e-05 5.e-05 5.e-05 5.e-05]
[0.99995 0.99995 0.99995 0.99995 0.99995]
順伝播のグラフを作成します。
# 順伝播のグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 plt.plot(x_vals, y_vals, label='forward') # 折れ線グラフ plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('Sigmoid Layer', fontsize=20) # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
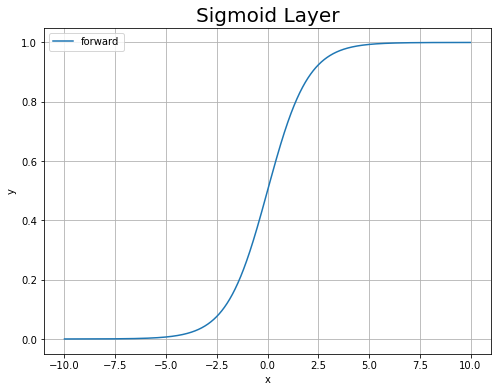
当然ですが、ソフトマックス関数のグラフになります。
作図用の逆伝播の入力を作成して、逆伝播を計算します。
# 作図用の逆伝播の入力を作成 dy_vals = np.ones_like(y_vals) # 逆伝播を計算 dx_vals = layer.backward(dy_vals) print(np.round(dx_vals[:5], 5)) # 前から5つ print(np.round(dx_vals[-5:], 5)) # 後から5つ
[5.e-05 5.e-05 5.e-05 5.e-05 5.e-05]
[5.e-05 5.e-05 5.e-05 5.e-05 5.e-05]
逆伝播の入力は全ての要素(点)が1です。
逆伝播のグラフを作成します。
# 逆伝播のグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 plt.plot(x_vals, dx_vals, label='backward') # 折れ線グラフ plt.xlabel('x') # x軸ラベル plt.ylabel('dx') # y軸ラベル plt.title('Sigmoid Layer', fontsize=20) # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
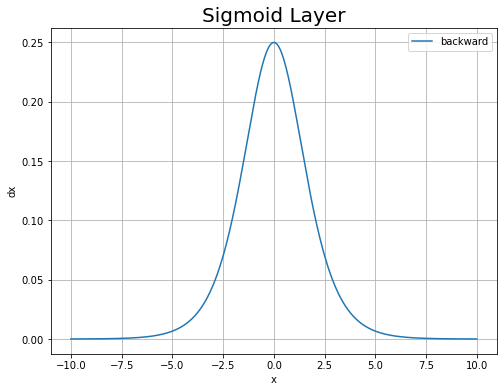
$x$が大きいまたは小さいほど、$\frac{\partial y}{\partial x}$が0に近付きます。
順伝播と逆伝播のグラフを重ねて描画します。
# Sigmoidレイヤのグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 plt.plot(x_vals, y_vals, label='forward') # シグモイド関数 plt.plot(x_vals, dx_vals, label='backward') # 勾配 plt.xlabel('x') # x軸ラベル plt.ylabel('y, dx') # y軸ラベル plt.title('Sigmoid Layer', fontsize=20) # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
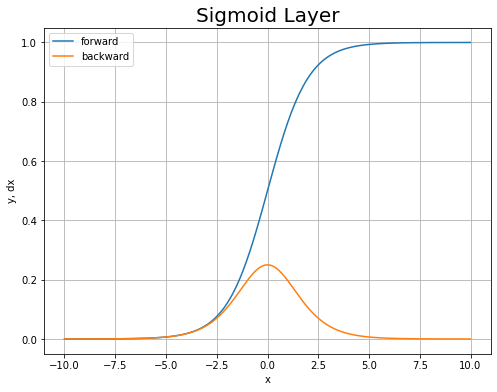
順伝播のグラフ(青線)において変化(傾き)の大きい-5から5の範囲で、逆伝播グラフ(オレンジ線)の値が大きくなっているのが分かります。
以上で、Sigmoidレイヤを実装できました。次は、Affineレイヤを実装します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
- サポートページ:Sigmoidレイヤのコード(https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/layers.py)
おわりに
加筆修正の際に記事を分割しました。
【次節の内容】