はじめに
「プログラミング」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ実行結果を見ながら処理の意図を確認していきます。
この記事は、5.6.3項「Softmax-with-Lossレイヤ」の内容です。ニューラルネットワークの学習時の最後のレイヤとして用いるソフトマックス関数と交差エントロピー誤差を合わせたSoftmax-with-LossレイヤをPythonで実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
5.6.3 Softmax-with-Lossレイヤの実装
ソフトマックス関数と交差エントロピー誤差の順伝播と逆伝播の計算を行うSoftmax-with-Lossレイヤを実装します。ソフトマックス関数については「3.5:ソフトマックス関数の実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」、「4.2.2-4:交差エントロピー誤差の実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」、交差エントロピー誤差については「4.2.2-4:交差エントロピー誤差の実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」、Softmax-with-Lossレイヤの逆伝播については「Softmax-with-Lossレイヤの逆伝播の導出【ゼロつく1のノート(数学)】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 5.6.3項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
この項では、3.5節の(バッチ対応版)ソフトマックス関数softmax()、4.2.4項の(バッチ対応版)交差エントロピー誤差cross_entropy_error()を利用します。そのため、関数定義を再度実行しておく必要があります。
または次の方法で、「deep-learning-from-scratch-master」フォルダ内の「common」フォルダの「functions.py」ファイルから実装済みの関数を読み込むこともできます。ファイルの読み込みについては「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
# 読み込み用の設定 import sys sys.path.append('../deep-learning-from-scratch-master') # パスを指定 # 実装済みの関数を読み込み #from common.functions import softmax # (バッチ対応版)ソフトマックス関数:3.5節 #from common.functions import cross_entropy_error # (バッチ対応版)交差エントロピー誤差:4.2.4項
・数式の確認
まずは、Softmax-with-Lossレイヤの定義式を確認します。
順伝播では、スコア(最終層の重み付き和)を入力$\mathbf{A} = (a_{0,0}, \cdots, a_{N-1,9})$、正規化されたスコアを中間変数$\mathbf{Y} = (y_{0,0}, \cdots, y_{N-1,9})$、交差エントロピー誤差を出力$L$とします。$N$はバッチサイズ(1試行当たりのデータ数)、$K$は分類するクラス数です。ここでは、クラス数を数字の種類数10とします。また、Pythonのインデックスに合わせて添字を0から割り当てています。
各データに関する入力$\mathbf{a}_n = (a_{n,0}, a_{n,1}, \cdots, a_{n,9})$を、ソフトマックス関数により$0 < y_{n,k} < 1,\ \sum_{k=0}^9 y_{n,k} = 1$となるように正規化して$\mathbf{y}_n = (y_{n,0}, y_{n,1}, \cdots, y_{n,9})$とします。ただし実装上は、オーバーフロー対策をした計算式(3.11)を用います(4.4.2項)。
また、$\mathbf{Y}$と教師データ$\mathbf{T} = (t_{0,0}, \cdots, t_{N-1,9})$を用いて、複数データに対する交差エントロピー誤差$L$を求めます。$\mathbf{t}_n = (t_{n,0}, t_{n,1}, \cdots, t_{n,9})$はone-hotベクトルです。
損失$L$は、学習時におけるニューラルネットワークの出力であり、現在のパラメータによるデータへの当てはまり具合を表します。
逆伝播では、「逆伝播の入力$\frac{\partial L}{\partial L} = 1$」と「Softmax-with-Lossレイヤの勾配$\frac{\partial L}{\partial \mathbf{A}}$」の積$\frac{\partial L}{\partial \mathbf{A}} = \frac{\partial L}{\partial L} \frac{\partial L}{\partial \mathbf{A}}$を求めます(5.2.2項)。
各入力$a_{n,k}$に関する出力$L$の微分$\frac{\partial L}{\partial a_{n,k}}$は、次の式で計算できます。
よって、入力$\mathbf{A}$に関する損失$L$の勾配$\frac{\partial L}{\partial \mathbf{A}}$は、次の行列になります。
ちなみに、バッチサイズが$N = 1$のとき本にある$\frac{\partial L}{\partial a_k} = y_k - t_k$の形になるのが分かります。
$y_k - t_k$は、推論結果と正解の差であり、誤差と言えます。この誤差を前のレイヤ・前のレイヤへと逆順に伝播していくことで各層のパラメータの勾配を求めていきます。これを誤差逆伝播法と言います。
以上が、Softmax-with-Lossレイヤので行う計算です。
・処理の確認
次に、Softmax-with-Lossレイヤで行う処理を確認します。
・順伝播の計算
順伝播の入力$\mathbf{X}$と教師ラベル$\mathbf{T}$を作成します。
# (仮の)入力を作成 A = np.array([ [1.0, 3.0, 5.0, 7.0, 9.0, 1.5, 3.5, 5.5, 7.5, 9.5], [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], [-10.0, -8.0, -6.0, -4.0,-2.0, 0.0, 2.0, 4.0, 6.0, 8.0] ]) print(A.shape) # (仮の)教師データを作成 T = np.array([ [0, 0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 1] ]) print(T.shape)
(3, 10)
(3, 10)
この例では、バッチサイズを3とします。$\mathbf{Y}$と$\mathbf{T}$は同じ形状です。
softmax()でソフトマックス関数による活性化(正規化)を行ってから、cross_entropy_error()で損失(交差エントロピー誤差)を計算します。
# ソフトマックス関数による活性化 Y = softmax(A) print(np.round(Y, 3)) print(np.sum(Y, axis=1)) # 正規化の確認 # 交差エントロピー誤差を計算 L = cross_entropy_error(Y, T) print(L)
[[0. 0.001 0.006 0.044 0.326 0. 0.001 0.01 0.073 0.538]
[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ]
[0. 0. 0. 0. 0. 0. 0.002 0.016 0.117 0.865]]
[1. 1. 1.]
2.355810776839421
順伝播の出力が得られました。
ここまでは、順伝播の処理を確認しました。続いて、逆伝播の処理を確認します。
・逆伝播の計算
「バッチサイズbatch_size」と「ニューラルネットワークの順伝播の出力Y」、「教師ラベルT」を用いて逆伝播を計算します。
# バッチサイズを取得 batch_size = T.shape[0] print(batch_size) # 逆伝播 dA = (Y - T) / batch_size print(np.round(dA, 2)) print(dA.shape)
3
[[ 0. 0. 0. 0.01 0.11 0. 0. -0.33 0.02 0.18]
[ 0.03 0.03 0.03 0.03 -0.3 0.03 0.03 0.03 0.03 0.03]
[ 0. 0. 0. 0. 0. 0. 0. 0.01 0.04 -0.05]]
(3, 10)
逆伝播の出力が得られました。dxを前のレイヤ(Affineレイヤ)に入力します。
以上がSoftmax-with-Lossレイヤで行う計算です。
・実装
処理の確認ができたので、Softmax-with-Lossレイヤをクラスとして実装します。
# Softmax-with-Lossレイヤの実装 class SoftmaxWithLoss: # 初期化メソッド def __init__(self): # 変数を初期化 self.loss = None # 交差エントロピー誤差 self.y = None # ニューラルネットワークの出力 self.t = None # 教師ラベル # 順伝播メソッド def forward(self, x, t): # 教師ラベルを保存 self.t = t # ソフトマックス関数による活性化(正規化) self.y = softmax(x) # 交差エントロピー誤差を計算 self.loss = cross_entropy_error(self.y, self.t) return self.loss # 逆伝播メソッド def backward(self, dout=1): # バッチサイズを取得 batch_size = self.t.shape[0] # 順伝播の入力の勾配を計算 dx = (self.y - self.t) / batch_size return dx
順伝播の中間変数$\mathbf{Y}$と教師ラベル$\mathbf{T}$は逆伝播の計算にも用いるので、順伝播の計算時に(順伝播メソッドの実行時に)それぞれインスタンス変数y, tに保存しておきます。逆伝播メソッドでは、保存した値を用いて計算します。
実装したクラスを試してみましょう。
SoftmaxWithLossクラスのインスタンスを作成します。
# Softmax-with-Lossレイヤのインスタンスを作成
layer = SoftmaxWithLoss()
先ほど作成した変数を使って、順伝播の計算をします。
# 順伝播を計算 L = layer.forward(A, T) print(np.round(layer.y, 2)) print(np.sum(layer.y, axis=1)) # 正規化の確認 print(layer.loss) print(L)
[[0. 0. 0.01 0.04 0.33 0. 0. 0.01 0.07 0.54]
[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ]
[0. 0. 0. 0. 0. 0. 0. 0.02 0.12 0.86]]
[1. 1. 1.]
2.355810776839421
2.355810776839421
当然ですが、順伝播メソッドlayer.forward()の返り値Lとインスタンス変数layer.lossは同じ値になります。
逆伝播を計算します。
# 逆伝播を計算 dA = layer.backward() print(np.round(dA, 3))
[[ 0. 0. 0.002 0.015 0.109 0. 0. -0.33 0.024 0.179] [ 0.033 0.033 0.033 0.033 -0.3 0.033 0.033 0.033 0.033 0.033] [ 0. 0. 0. 0. 0. 0. 0.001 0.005 0.039 -0.045]]
引数のdoutはデフォルト値が設定してあるので省略できます。
Softmax-with-Lossレイヤを実装できました。
・グラフの確認
最後に、Softmax-with-Lossレイヤの順伝播と逆伝播をグラフで確認します。3次元のグラフで可視化できるようにクラス数を2とします。3Dプロットについては「3Dプロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
ただし、cross_entropy_error()の実装を変更しておく必要があります。cross_entropy_error()では、$\log 0$の計算を回避するために微小な値1e-7を加えました。グラフを正しく作成するには、微小な値を加えず定義式の通りに計算する(実装を変更する)必要があります。
SoftmaxWithLossクラスのインスタンスを作成します。
# Softmax-with-Lossレイヤのインスタンスを作成
layer = SoftmaxWithLoss()
作図用と計算用の入力$\mathbf{x} = (x_0, x_1)$を作成します。
# 入力の値を作成 x_vals = np.arange(-20.0, 20.1, 2.0) # 作図用の入力を作成 X0_vals, X1_vals = np.meshgrid(x_vals, x_vals) # 計算用の入力を作成 X_vals = np.array([ X0_vals.flatten(), X1_vals.flatten() ]).T print(X_vals[:5]) print(X_vals.shape) # 作図用の入力の形状を保存 input_shape = X0_vals.shape print(input_shape)
[[-20. -20.]
[-18. -20.]
[-16. -20.]
[-14. -20.]
[-12. -20.]]
(441, 2)
(21, 21)
$x_0$と$x_1$がとり得る値を作成してx_valsとします。
$x_0$と$x_1$がx_valsの全ての組み合わせを持つようにnp.meshgrid()で作成して、それぞれX0_valsとX1_valsとします。
X0_vals, X1_valsを1列に並び替えて結合してX_valsとします。各行が1つの点$\mathbf{x}$に対応します。
また、各入力$x_0, x_1$の元の形状をinput_shapeとして保存しておきます。
教師ラベル$\mathbf{t} = (t_0, t_1)$を作成します。
# 教師ラベルを作成 t = np.array([1, 0])
ここでは、$t_0 = 1$とします。つまり、クラス0を正解とします。
X_valsの行(点)ごとに順伝播と逆伝播を計算して、それぞれリストに格納していきます。
# 作図用のリストを初期化 L_vals = [] dX_vals = [] # 点ごとに処理 for x in X_vals: # 順伝播を計算 L_vals.append(layer.forward(x, t)) # 逆伝播を計算 dX_vals.append(layer.backward()) print(np.round(L_vals[:5], 2)) print(np.round(dX_vals[:5], 2))
[0.69 0.13 0.02 0. 0. ]
[[-0.25 0.25]
[-0.06 0.06]
[-0.01 0.01]
[-0. 0. ]
[-0. 0. ]]
for文を使って1データ(1つの点)ごとに計算して、損失(順伝播の出力)をL_vals、$\mathbf{x}$の勾配(逆伝播の出力)をdX_valsにappend()メソッドで格納していきます。
計算結果をそれぞれNumPy配列に変換して、作図用に整形します。
# 順伝播の出力(損失)を整形 L_vals = np.array(L_vals).reshape(input_shape) print(L_vals.shape) # 逆伝播の出力(勾配)を整形 dX_vals = np.array(dX_vals) dX0_vals = dX_vals[:, 0].reshape(input_shape) dX1_vals = dX_vals[:, 1].reshape(input_shape) print(dX0_vals.shape) print(dX1_vals.shape)
(21, 21)
(21, 21)
(21, 21)
$\frac{\partial L}{\partial \mathbf{x}}$に対応するX_valsから$\frac{\partial L}{\partial x_0}$と$\frac{\partial L}{\partial x_1}$を取り出して、それぞれX0_vals, X1_valsと同じ形状にします。
順伝播のグラフを作成します。
# 順伝播のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, L_vals, label='forward') # ワイヤーフレーム図 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('loss') # z軸ラベル fig.suptitle('Softmax with Loss Layer', fontsize=20) # 全体のタイトル ax.set_title('t=' + str(t), loc='left') # タイトル ax.legend() # 凡例 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
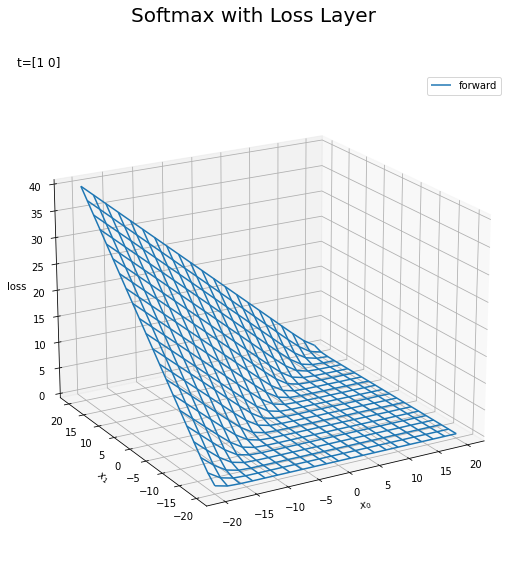
この例ではクラス0が正解なので、$x_0$と$x_1$を比較して、$x_0$が大きいほど損失$L$が小さくなります。
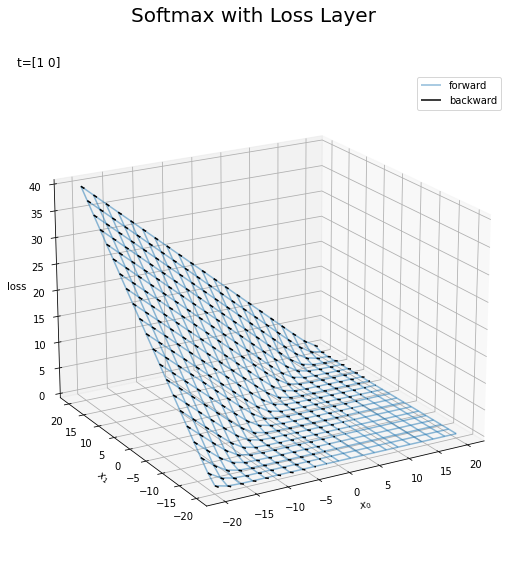
3Dのベクトル図を重ねて勾配を可視化します。ベクトル図については「矢印プロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
# z軸方向の勾配の値を計算 W_vals = np.sqrt(dX0_vals**2 + dX1_vals**2) + 1e-7 # 勾配を可視化 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, L_vals, alpha=0.5, label='forward') # 損失 #plt.contourf(X0_vals, X1_vals, L_vals, alpha=0.5, offset=0) # 塗りつぶし等高線図 ax.quiver(X0_vals, X1_vals, L_vals, -dX0_vals/W_vals, -dX1_vals/W_vals, -W_vals, color='black', pivot='tail', arrow_length_ratio=0.1, length=0.5, label='backward') # 勾配 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('loss') # z軸ラベル fig.suptitle('Softmax with Loss Layer', fontsize=20) # 全体のタイトル ax.set_title('t=' + str(t), loc='left') # タイトル ax.legend() # 凡例 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
2Dのベクトル図でも可視化してみます。
# 勾配を可視化 plt.figure(figsize=(8, 8)) # 図の設定 plt.contourf(X0_vals, X1_vals, L_vals, alpha=0.5) # 損失 plt.quiver(X0_vals, X1_vals, -dX0_vals, -dX1_vals) # 勾配 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.suptitle('Softmax with Loss Layer', fontsize=20) # 全体のタイトル plt.title('t=' + str(t), loc='left') # タイトル plt.grid() # グリッド線 plt.show()
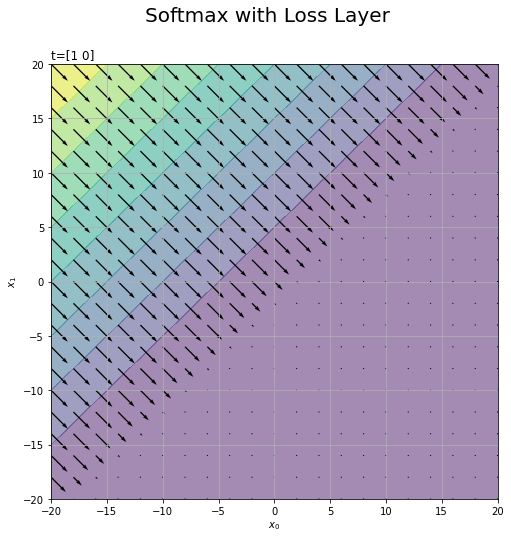
3Dプロットを真上から見た図に対応しています。
ここまでで、ニューラルネットワークに必要なレイヤを実装できました。次節では、これらを組み合わせてニューラルネットワークを実装します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
- サポートページ:Softmax-with-Lossレイヤのコード(https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/layers.py)
おわりに
これでパーツが揃った!ニューラルネットワークを組み立てるぞー。
- 2021.09.21:加筆修正しました。
【次節の内容】