はじめに
「機械学習・深層学習」初学者のための『ゼロから作るDeep Learning』の攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
ニューラルネットワーク内部の計算について、数学的背景の解説や計算式の導出を行い、また実際の計算結果やグラフで確認していきます。
この記事は、5.6節「Affineレイヤの実装」の内容です。重み付き和の計算過程を可視化することで理解を深めます。
【元の記事】
【他の記事一覧】
【この記事の内容】
Affineレイヤの順伝播の可視化
Affineレイヤの順伝播で行う重み付き和の計算過程を可視化して確認します。ここで行う処理は1層のニューラルネットワークと言えます。ただし話を簡単にするために、バイアスを省略します。Affineレイヤ(重み付き和)については「3.3-4:ニューラルネットワークの順伝播【ゼロつく1のノート(実装)】 - からっぽのしょこ」または「5.6.2:Affineレイヤの実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt
また、MNISTデータセットを読み込みます。詳しくは「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
# 読み込み用の設定 import sys sys.path.append('../deep-learning-from-scratch-master') # パスを指定 # load_mnist()を読み込み from dataset.mnist import load_mnist # MNISTデータセットを取得 (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=True, one_hot_label=False)
画像データ(入力データ)は、flatten引数で1行に並べ替えて、normalize引数で0から1の値に正規化しておきます。また、教師ラベルは、one_hot_labelをFalseにすることで、スカラにしておきます。
・入力の確認
まずは、入力データ(手書き数字)を可視化して確認します。
・1データの場合
訓練用の画像とラベルのデータセットx_train, t_trainから、データ番号を指定して1つの入力データ$\mathbf{x}_n = (x_{n,0}, x_{n,1}, \cdots, x_{n,783})$と教師ラベル$t_n$を取り出します。Pythonのインデックスに合わせて添字を0から割り当てています。
# データ番号を指定 n = 0 # 画像とラベルデータを取得 x = x_train[n] t = t_train[n] print(x[150:160]) print(x.shape) print(t)
[0. 0. 0.01176471 0.07058824 0.07058824 0.07058824
0.49411765 0.53333336 0.6862745 0.10196079]
(784,)
5
flatten=Trueを指定したので、各画像(入力)$\mathbf{x}_n$はピクセル数(要素数)$D = 28 * 28 = 784$のベクトル(1次元配列)です。
$\mathbf{x}_n$を手書き数字の形で描画します。
# 手書き数字を描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 6)) # 図の設定 ax.pcolor(x.reshape((28, 28))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_xticks(np.arange(28) + 0.5) # x軸の目盛位置 ax.set_xticklabels(np.arange(28)) # x軸目盛 ax.set_ylabel('d') # y軸ラベル ax.set_yticks(np.arange(28) + 0.5) # y軸の目盛位置 ax.set_yticklabels(np.arange(28)) # y軸目盛 ax.set_title('$t_n=' + str(t) + '$', loc='left') # タイトル fig.suptitle('$x_n$', fontsize=15) # 全体のタイトル ax.invert_yaxis() # y軸を反転 ax.set_aspect('equal', adjustable='box') # アスペクト比 plt.show()

xを$28 \times 28$の2次元配列に変換して作図します。
$\mathbf{x}_n$をそのまま(1次元配列の状態で)描画します。
# 処理上の入力データを描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 0.3)) # 図の設定 ax.pcolor(x.reshape((1, 784))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('n') # y軸ラベル ax.set_yticks([0.5]) # y軸の目盛位置 ax.set_yticklabels([0]) # y軸目盛 ax.set_title('$t_n=' + str(t) + '$', loc='left') # タイトル fig.suptitle('$x_n$', fontsize=15, y=3) # 全体のタイトル ax.invert_yaxis() # y軸を反転 plt.show()

元の画像の0行目のピクセルの右隣に1行目のピクセルが並び、その右隣に2行目・・・と28行分のピクセルが並んでいます。(x軸の目盛位置の調整はほとんど影響しないので省略しました。)
(畳み込みニューラルネットワークではない)ニューラルネットワークではこの状態で処理(計算)されます。縦方向の繋がりが断ち切られて処理されるのが分かります。
・バッチデータの場合
先ほどは、1つのデータを取り出しました。今度は、バッチサイズ$N$を指定して、バッチデータとして入力データ$\mathbf{X} = (x_{0,0}, \cdots x_{N-1, 783})$と教師ラベル$\mathbf{t} = (t_0, t_1, \cdots, t_{N-1})$を取り出します。
# バッチサイズを指定 N = 9 # 画像とラベルデータを取得 X = x_train[:N] T = t_train[:N] print(X[:, 150:155]) print(X.shape) print(T) print(T.shape)
[[0. 0. 0.01176471 0.07058824 0.07058824]
[0. 0. 0. 0. 0.1882353 ]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0.1254902 0.92941177 0.99215686 0.9882353 ]
[0. 0.14901961 0.16862746 0.4117647 1. ]
[0. 0. 0.01960784 0.24705882 0.77254903]]
(9, 784)
[5 0 4 1 9 2 1 3 1]
(9,)
$\mathbf{X}$は$N \times D$の行列(2次元配列)であり、各行が1つの入力(画像)データ$\mathbf{x}_n$です。
$\mathbf{X}$をデータごとに手書き数字の形で描画します。
# データごとに手書き数字を描画 fig, axs = plt.subplots(nrows=3, ncols=3, figsize=(9, 9)) # 図の設定 for n, ax in enumerate(axs.flat): ax.pcolor(X[n].reshape((28, 28))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('d') # y軸ラベル ax.label_outer() # 外側のラベルのみ表示 ax.set_title('$n=' + str(n) + ', t_n=' + str(T[n]) + '$', loc='left') # タイトル ax.set_aspect('equal', adjustable='box') # アスペクト比 ax.invert_yaxis() # y軸を反転 fig.suptitle('$X$', fontsize=15) # 全体のタイトル plt.show()

x[n]で、各データを取り出して順番に作図します。
バッチサイズNに応じて、plt.subplots()の行数と列数の引数nrows, ncolsを指定する必要があります。
(軸目盛の表示設定ax.invert_yaxis()が、全ての図でいるときと、最後だけでいいときがあってよく分からない。)
$\mathbf{X}$をそのまま描画します。
# 処理上の入力データを描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 3)) # 図の設定 ax.pcolor(X) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('n') # y軸ラベル ax.set_yticks(np.arange(N) + 0.5) # y軸の目盛位置 ax.set_yticklabels(np.arange(N)) # y軸目盛 #ax.set_yticklabels(['$' + str(n) + '\ (t_n=' + str(T[n]) + ')$' for n in range(N)]) # y軸目盛:(正解ラベルを表示) ax.set_title('t=' + str(T), loc='left') # タイトル fig.suptitle('$X$', fontsize=15) # 全体のタイトル ax.invert_yaxis() # y軸を反転 plt.show()
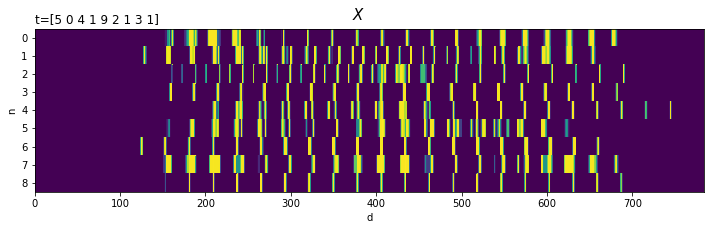
この形状でも、データ(数字)ごとに傾向が異なるのが分かります。
データを確認するため、同じ数字だけを取り出して可視化してみましょう。
・作図コード(クリックで展開)
# バッチサイズを指定 N = 9 # 数字を指定 k = 6 # 指定した数字の画像とラベルデータを取得 X = x_train[t_train == k][:N] T = t_train[t_train == k][:N] print(X[:, 150:155]) print(X.shape) print(T) print(T.shape)
[[0. 0. 0.14901961 0.69803923 0.9882353 ]
[0. 0. 0. 0. 0.29411766]
[0. 0. 0.21176471 0.92156863 0.8 ]
[0. 0. 0. 0.2901961 0.9490196 ]
[0. 0. 0.12941177 0.63529414 0.99215686]
[0. 0. 0. 0. 0.12156863]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0.07450981]
[0. 0. 0. 0. 0.5019608 ]]
(9, 784)
[6 6 6 6 6 6 6 6 6]
(9,)
t_train == kの結果を添字として使うことで、Trueの要素(t_trainの値がkに指定した値の要素)のみ取り出せます。
Xを手書き数字の形で描画します。
# データごとに手書き数字を描画 fig, axs = plt.subplots(nrows=3, ncols=3, figsize=(9, 9), sharex=True, sharey=True) # 図の設定 for n, ax in enumerate(axs.flat): ax.pcolor(X[n].reshape((28, 28))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('d') # y軸ラベル ax.label_outer() # 外側のラベルのみ表示 ax.set_title('n=' + str(n), loc='left') # タイトル ax.set_aspect('equal', adjustable='box') # アスペクト比 fig.suptitle('$X\ (t=' + str(k) + ')$', fontsize=20) # 全体のタイトル ax.invert_yaxis() # y軸を反転 plt.show()
Xをそのまま描画します。
# 処理上の入力データを描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 3)) # 図の設定 ax.pcolor(X) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('n') # y軸ラベル ax.set_yticks(np.arange(N) + 0.5) # y軸の目盛位置 ax.set_yticklabels(np.arange(N)) # y軸目盛 ax.set_title('$X\ (t=' + str(k) + ')$', fontsize=15) # タイトル ax.invert_yaxis() # y軸を反転 plt.show()
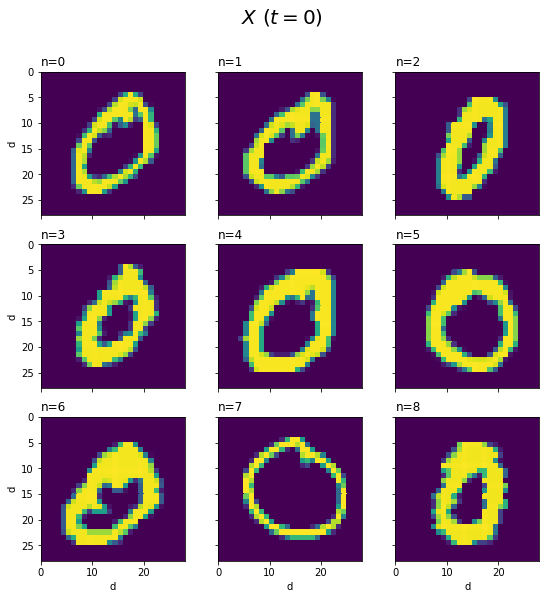




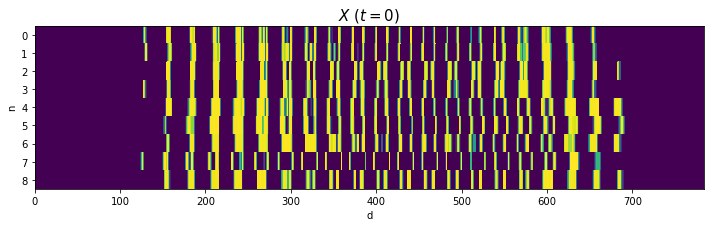
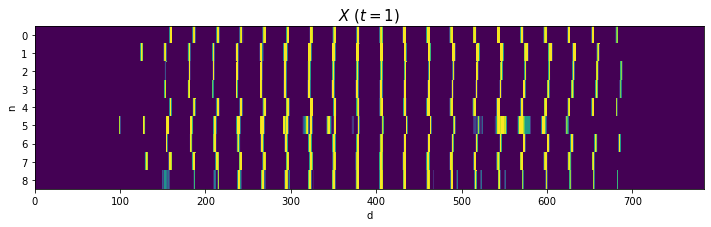
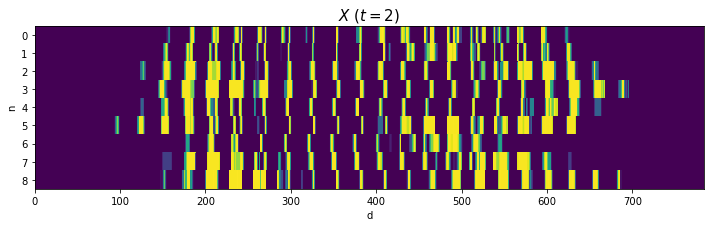
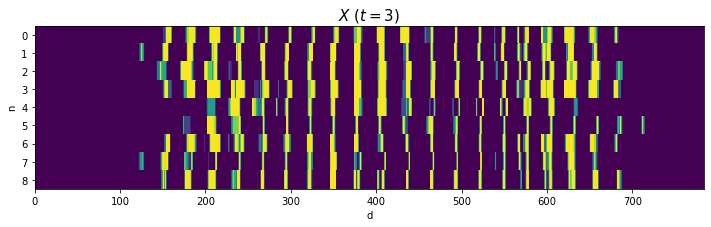
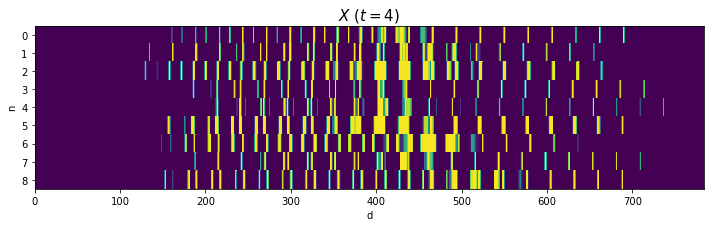





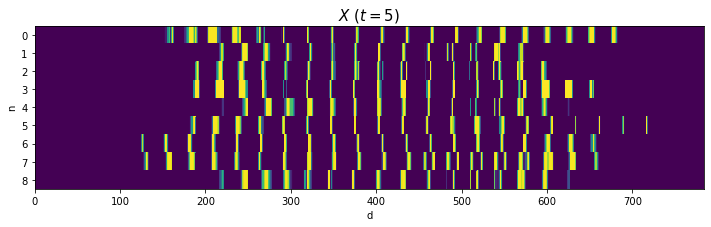
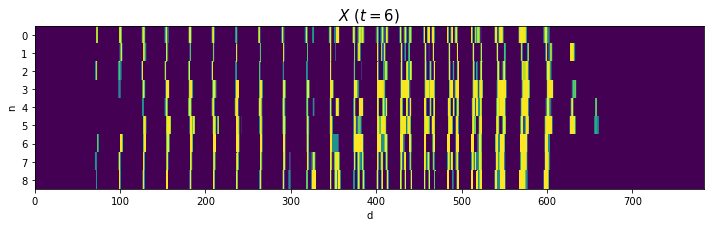
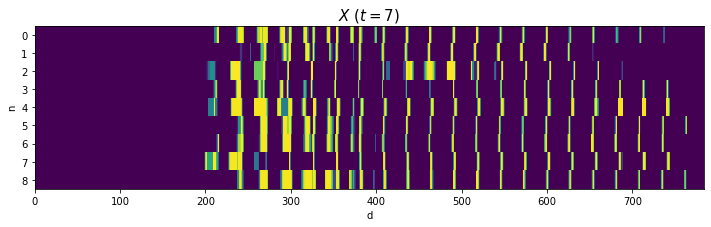
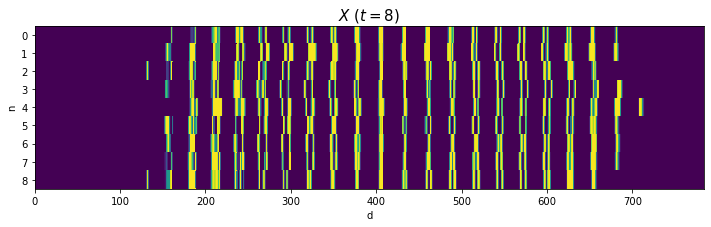
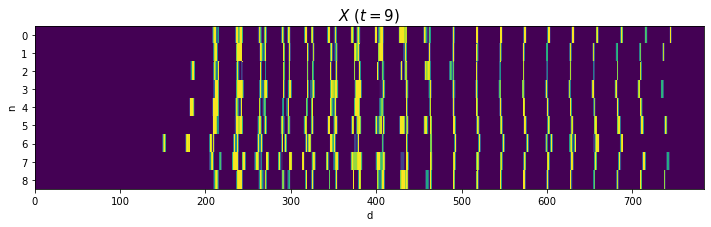
2と4はバラツキが大きいですが、それなりに共通した形ですね(?)。0や8のように2本に枝分かれする文字は、ハの字型になっていますね。
(あと、思っていたより字が汚いですよね。だからこそベンチマークになるのでしょうが。)
・重みの設定
次は、重みを可視化します。ただし、ここでは簡易的に重みを設定します。
重み$\mathbf{W} = (w_{0,0}, \cdots, w_{783,9})$を作成します。この例では、データセット全体における「数字ごとの平均値」を重みとして利用することにします。
# 重みを作成 W = np.zeros((784, 10)) for k in range(10): W[:, k] = np.mean(x_train[t_train == k], axis=0) print(W[150:155, :5]) print(W.shape)
[[0.09442687 0.01412742 0.36298302 0.3829734 0.06451192]
[0.17172489 0.04140154 0.46316317 0.48024842 0.0734271 ]
[0.27210975 0.10478874 0.54724389 0.55877799 0.07602418]
[0.38963154 0.20477685 0.61027074 0.61324334 0.06785146]
[0.49186763 0.29759428 0.64457238 0.62329566 0.06074872]]
(784, 10)
$\mathbf{W}$は$D \times K$の行列です。$K$は、クラス数で、ここでは数字の種類数の10です。
$\mathbf{W}$の各列が、各クラスの重みに対応しています。
x_trainから数字kのデータを取り出して、np.mean(axis=0)でピクセルごとに平均を求め、W[:, k]でWのk列目に代入します。式にすると$w_{d,k} = \frac{1}{N} \sum_{n=0}^{N-1} x_{n,d}$です(ただしこの$N$はデータセット全体における数字$k$の数です)。
本来の重みは負の値もとりますが、この例では$0 \leq x_{n,d} \leq 1$の平均値なので、$0 \leq w_{d,k} \leq 1$です。
$\mathbf{W}$をクラス(列)ごとに手書き数字に対応した形で描画します。
# クラスごとに重みを描画 fig, axs = plt.subplots(nrows=3, ncols=4, figsize=(12, 9), sharex=True, sharey=True) # 図の設定 for k in range(10): ax = axs.flat[k] # k番目のクラスの図 ax.pcolor(W[:, k].reshape((28, 28))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('d') # y軸ラベル ax.label_outer() # 外側のラベルのみ表示 ax.set_title('k=' + str(k), loc='left') # タイトル ax.set_aspect('equal', adjustable='box') # アスペクト比 fig.suptitle('$W$', fontsize=20) # 全体のタイトル ax.invert_yaxis() # y軸を反転 plt.show()
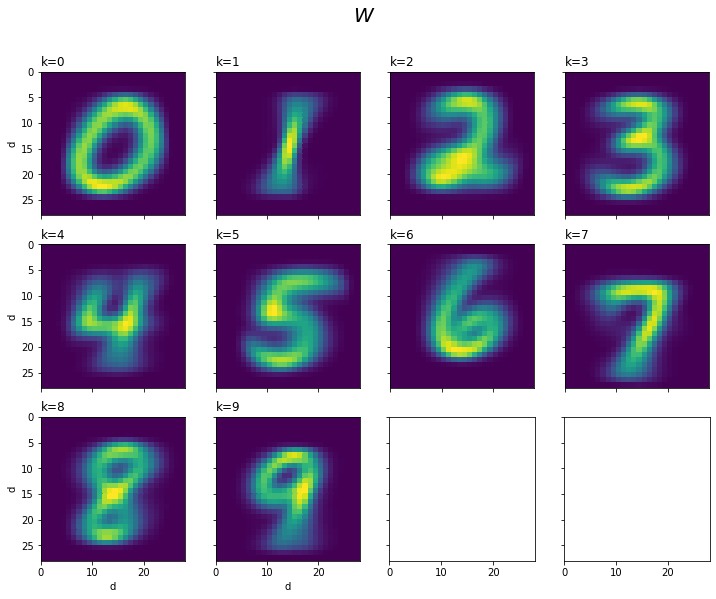
各クラス(数字)を象徴する(?)ピクセルほど値が大きくなり(色が黄色に近付き)ます。
(あの不揃いな字も平均するとキレイになるのね。)
$\mathbf{W}$をそのまま描画します。
# 処理上の重みを描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(3, 12)) # 図の設定 ax.pcolor(W) # ヒートマップ ax.set_xlabel('k') # x軸ラベル ax.set_xticks(np.arange(10) + 0.5) # x軸の目盛位置 ax.set_xticklabels(np.arange(10)) # x軸目盛 ax.set_ylabel('d') # y軸ラベル ax.set_title('$W$', fontsize=20) # タイトル ax.invert_yaxis() # y軸を反転 plt.show()

クラスごとに傾向が似ていたリ似ていなかったりしますね。(似ていると、この後で行う分類が難しくなります。)
・重み付け
入力と重みを用意できたので重み付き和の計算といきたいところですが、その前に重み付けした入力を確認しておきます。
・1データの場合
重み付き和$\mathbf{z}_n$は、次の式で計算します。
$1 \times D$と$D \times K$の行列の積とみると、$\mathbf{z}_n$は$1 \times K$のベクトルになるのが分かります。
$k$番目の項$z_{n,k}$は、次の計算です。
つまり、$\mathbf{z}_n$の各項$z_{n,k}$は、$\mathbf{x}_n$と「$\mathbf{W}$の$k$列目$(w_{d,0}, w_{d,1}, \cdots, w_{d,783})^{\mathrm{T}}$」の内積です($\mathrm{T}$は転置行列を表す記号で、このベクトルが縦ベクトルであることを表していますが、ここでは特に重要ではありません)。
ここでは、各入力$x_{n,d}$に対応する重み$w_{d,k}$を掛けた「$x_{n,0} w_{0,k}$から$x_{n,783} w_{783,k}$」を手書き数字の要領で可視化します。
・作図コード(クリックで展開)
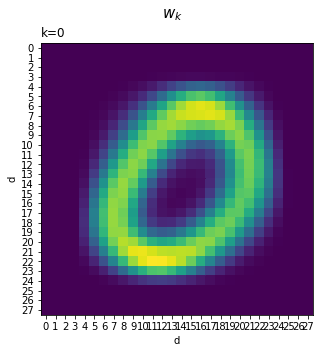
クラス$k$に関する重み$(w_{0,k}, w_{1,k}, \cdots, w_{783,k})^{\mathrm{T}}$を入力に対応する形で描画します。
# クラス番号を指定 k = 0 # クラスkの重みを描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 5)) # 図の設定 ax.pcolor(W[:, k].reshape((28, 28))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_xticks(np.arange(28) + 0.5) # x軸の目盛位置 ax.set_xticklabels(np.arange(28)) # x軸目盛 ax.set_ylabel('d') # y軸ラベル ax.set_yticks(np.arange(28) + 0.5) # y軸の目盛位置 ax.set_yticklabels(np.arange(28)) # y軸目盛 ax.set_title('k=' + str(k), loc='left') # タイトル fig.suptitle('$w_k$', fontsize=15) # 全体のタイトル ax.invert_yaxis() # y軸を反転 ax.set_aspect('equal', adjustable='box') # アスペクト比 plt.show()
同じピクセルの入力と各クラスの重みを掛けます。それが$x_{n,d} w_{d,k}$です。
要素ごとに重み付けした入力$(x_{n,0} w_{0,k}, x_{n,2} w_{2,k}, \cdots, x_{n,783} w_{783,k})$を描画します。
# クラスkの重み付けした手書き数字を描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 5)) # 図の設定 ax.pcolor((x * W[:, k]).reshape((28, 28))) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_xticks(np.arange(28) + 0.5) # x軸の目盛位置 ax.set_xticklabels(np.arange(28)) # x軸目盛 ax.set_ylabel('d') # y軸ラベル ax.set_yticks(np.arange(28) + 0.5) # y軸の目盛位置 ax.set_yticklabels(np.arange(28)) # y軸目盛 ax.set_title('$t_n=' + str(t) + ', k=' + str(k) + '$', loc='left') # タイトル fig.suptitle('$x_n * w_k$', fontsize=15) # 全体のタイトル ax.invert_yaxis() # y軸を反転 ax.set_aspect('equal', adjustable='box') # アスペクト比 plt.show()

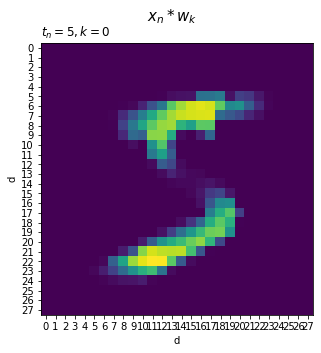
(タイトルに関して、クラス$k$に関する重みを$\mathbf{w}_k$で表しましたが、今後この表記は登場しません。また、要素ごとの積は6.1節で登場するアダマール積$\odot$を使って表記すべきですが、簡易的に$*$を使っています。)
入力の各要素$x_{n,d}$の値が、重み$w_{d,k}$によって調整されているのが分かります。
このピクセルの総和が重み付き和$z_{n,k}$です。
同様の計算を全てのクラスで行い手書き数字の形で描画します。
# データ番号を指定 n = 0 # 画像とラベルデータを取得 x = x_train[n] t = t_train[n] # 図の設定 fig, axs = plt.subplots(nrows=3, ncols=4, figsize=(12, 9), sharex=True, sharey=True) # クラスごとに重み付き入力を描画 for k in range(10): ax = axs.flat[k] ax.pcolor((x * W[:, k]).reshape((28, 28))) # 重み付けした入力データ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('d') # y軸ラベル ax.label_outer() # 外側のラベルのみ表示 ax.set_title('$k=' + str(k) + ', z_k=' + str(np.round(np.sum(x * W[:, k]), 1)) + '$', loc='left') # タイトル ax.set_aspect('equal', adjustable='box') # アスペクト比 # 入力データを作図 ax = axs.flat[11] ax.pcolor(x.reshape((28, 28))) # 元の入力データ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('d') # y軸ラベル ax.label_outer() # 外側のラベルのみ表示 ax.set_title('$t_n=' + str(t) + '$', loc='left') # タイトル ax.set_aspect('equal', adjustable='box') # アスペクト比 fig.suptitle('$x_n * W$', fontsize=20) # 全体のタイトル ax.invert_yaxis() # y軸を反転 plt.show()
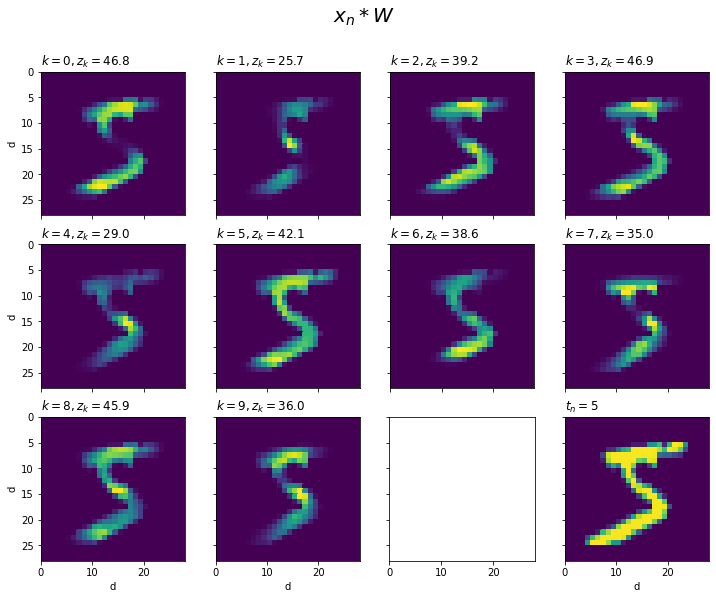
x * W[:, k]で、入力xに各クラスの重みW[:, k]を順番に掛けて作図します。
参考のため、最後の図には$\mathbf{x}_n$をそのまま表示しています。
各図(クラス)の784個のピクセル(要素)$x_{n,d} w_{d,k}$の総和が$z_{n,k}$です。
$x_{n,d}$は、ピクセル$d$に書かれている度合いでした。また、$w_{d,k}$は、書かれている数字$k$におけるピクセル$d$の重要度と言える値でした。よって、「$x_{n,d}$が大きくかつ$w_{d,k}$も大きい」と$z_{n,k}$が大きくなります。逆に、「$x_{n,d}$が大きくても$w_{d,k}$が小さい」または「$x_{n,d}$小さいと$w_{d,k}$が大きくても」$z_{n,k}$は小さくなります。つまり、入力$x_{n,d}$を重要度$w_{d,k}$で調整していると言えます。
図を見ると、入力の字と重みの字が重なる部分が多いクラスほど$z_{n,k}$が大きくなるのが分かります。
そのままの形状でも描画します。
# 処理上の重み付き入力を描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 3)) # 図の設定 ax.pcolor(x.reshape((1, 784)) * W.T) # ヒートマップ ax.set_xlabel('d') # x軸ラベル ax.set_ylabel('k') # y軸ラベル ax.set_yticks(np.arange(10) + 0.5) # y軸の目盛位置 ax.set_yticklabels(np.arange(10)) # y軸目盛 ax.set_title('$t_n=' + str(t) + '$', loc='left') # タイトル fig.suptitle('$x_n * W$', fontsize=15) # 全体のタイトル ax.invert_yaxis() # y軸を反転 plt.show()

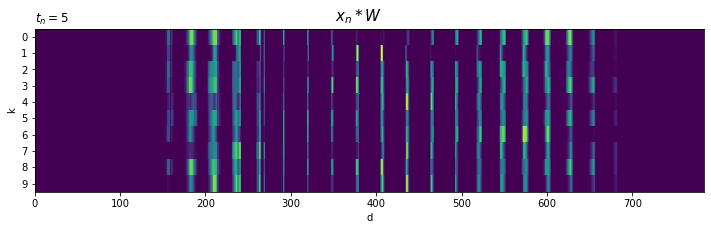
クラスごとに、注目しているピクセルが異なるのが分かります。
・重み付き和の計算
では、重み付き和を計算します。この計算結果がAffineレイヤの順伝播の出力です。
・1データの場合
まずは、1データの場合を確認します。
# データ番号を指定 n = 0 # 画像とラベルデータを取得 x = x_train[n] t = t_train[n]
ドット積np.dot()で重み付き和$\mathbf{z}_n$を計算します。
# 重み付き和を計算 z = np.dot(x.reshape((1, 784)), W) print(np.round(z, 1)) print(z.shape)
[[46.8 25.7 39.2 46.9 29. 42.1 38.6 35. 45.9 36. ]]
(1, 10)
reshape()は不要ですが一応明示的に書いておきます。
$\mathbf{z}_n$を描画します。
# 重み付き和を描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 2)) # 図の設定 ax.pcolor(z) # ヒートマップ ax.set_xlabel('k') # x軸ラベル ax.set_xticks(np.arange(10) + 0.5) # x軸目盛の位置 ax.set_xticklabels(np.arange(10)) # x軸目盛 ax.set_ylabel('n') # y軸ラベル ax.set_yticks([0.5]) # y軸目盛の位置 ax.set_yticklabels([0]) # y軸目盛 ax.set_title('$n=' + str(n) + ', t_n=' + str(t) + '$', loc='left') # タイトル fig.suptitle('$z_n = x_n \cdot W$', fontsize=20) # 全体のタイトル ax.invert_yaxis() # y軸を反転 ax.set_aspect('equal', adjustable='box') # アスペクト比 plt.show()

0番目の入力データ$\mathbf{x}_0$だと、クラス$k = 0, 3, 5$に対応する出力$z_{0,0}, z_{0,3}, z_{0,5}$が大きくなりました。
・バッチデータの場合
同様に、バッチデータでも重み付き和$\mathbf{Z} = (z_{0.0}, \cdots, z_{N-1,9})$を計算します。
# バッチサイズを指定 N = 20 # 画像とラベルデータを取得 X = x_train[:N] T = t_train[:N] #重み付き和を計算 Z = np.dot(X, W) print(np.round(Z[:5], 1)) print(Z.shape)
[[46.8 25.7 39.2 46.9 29. 42.1 38.6 35. 45.9 36. ]
[72.3 21.3 39.8 41.4 31.2 42.9 41.3 32.7 43.8 35. ]
[21.5 5.8 20. 19.6 24.9 16.5 20.1 15.6 20.1 21. ]
[21.2 29.6 30.9 27.2 20.9 22. 21.5 19.2 35.3 21.2]
[34.8 24.9 32.1 31.5 40.8 32. 33.1 37.3 41.6 45.9]]
(20, 10)
バッチデータの場合は次の計算をします。
$\mathbf{Z}$は、$N \times D$と$D \times K$の行列の積なので、$N \times K$の行列になります。
例えば、$z_{3,5}$は「3番目の入力データ$\mathbf{x}_3$」と「クラス5に関する重み($\mathbf{W}$の5列目)」の内積$\sum_{d=0}^{783} x_{3,d} w_{d,5}$です。1データのときと同様に、データごとに各クラスの重みを掛けて総和を求めています。
$\mathbf{Z}$を描画します。
# 重み付き和を描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 8)) # 図の設定 ax.pcolor(Z) # ヒートマップ ax.set_xlabel('k') # x軸ラベル ax.set_xticks(np.arange(10) + 0.5) # x軸目盛位置 ax.set_xticklabels(np.arange(10)) # x軸目盛 ax.set_ylabel('n') # y軸ラベル ax.set_yticks(np.arange(N) + 0.5) # y軸目盛の位置 #ax.set_yticklabels(np.arange(N)) # y軸目盛 ax.set_yticklabels(['$' + str(n) + '\ (t_n=' + str(T[n]) + ')$' for n in range(N)]) # y軸目盛:(正解ラベルを表示) ax.set_title('t=' + str(T), loc='left') # タイトル fig.suptitle('$Z = X \cdot W$', fontsize=20) # 全体のタイトル ax.invert_yaxis() # y軸を反転 ax.set_aspect('equal', adjustable='box') # アスペクト比 plt.show()
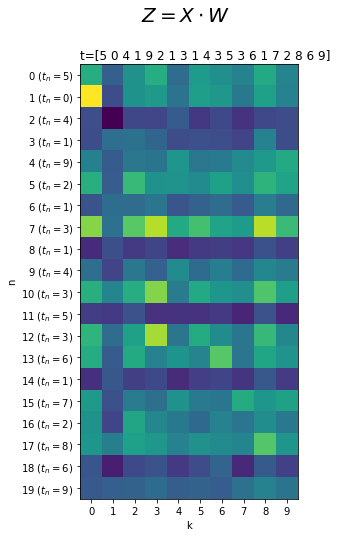
$N$個の重み付き和$\mathbf{z}_n$が行方向に並んでいるのが分かります。
ただし、$\mathbf{Z}$の全ての要素における最小値と最大値によって色付けされるためくっきりしない感じになっています。そこで、データごとに正規化してデータ間の作図上の影響を減らしてみます。
・ソフトマックス関数による活性化
最後に、重み付き和をソフトマックス関数(Softmax関数)で正規化します。つまり、1層のニューラルネットワークの出力と言えます。ソフトマックス関数については「3.5:ソフトマックス関数の実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」を参照してください。
・バッチデータの場合
$\mathbf{z}_n$ごとにソフトマックス関数の計算をします。
# ソフトマックス関数による活性化(正規化) Y = np.exp(Z) / np.sum(np.exp(Z), axis=1, keepdims=True) print(np.round(Y[:5], 3)) print(Y.shape)
[[0.403 0. 0. 0.427 0. 0.004 0. 0. 0.165 0. ]
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[0.033 0. 0.007 0.005 0.92 0. 0.008 0. 0.008 0.02 ]
[0. 0.003 0.013 0. 0. 0. 0. 0. 0.984 0. ]
[0. 0. 0. 0. 0.007 0. 0. 0. 0.013 0.98 ]]
(20, 10)
$\mathbf{Z}$の各要素を次の式で計算して、$\mathbf{Y} = (y_{0,0}, \cdots, y_{N-1,9})$とします。
出力は、$0 < y_{n,k} < 1,\ \sum_{k=0}^9 y_{n,k} = 1$になるのでした。
$\mathbf{Y}$を描画します。
# 出力データを描画 fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 8)) # 図の設定 ax.pcolor(Y) # ヒートマップ ax.set_xlabel('k') # x軸ラベル ax.set_xticks(np.arange(10) + 0.5) # x軸目盛位置 ax.set_xticklabels(np.arange(10)) # x軸目盛 ax.set_ylabel('n') # y軸ラベル ax.set_yticks(np.arange(N) + 0.5) # y軸目盛の位置 #ax.set_yticklabels(np.arange(N)) # y軸目盛 ax.set_yticklabels(['$' + str(n) + '\ (t_n=' + str(T[n]) + ')$' for n in range(N)]) # y軸目盛:(正解ラベルを表示) ax.set_title('t=' + str(T), loc='left') # タイトル fig.suptitle('$Y = h(X \cdot W)$', fontsize=15) # 全体のタイトル ax.invert_yaxis() # y軸を反転 ax.set_aspect('equal', adjustable='box') # アスペクト比 plt.show()

推論結果がくっきりしましたね(こんなに変化するとは知らなかった。極端に大きくなる指数関数のグラフを見ると明らかなのかな?)。
結果をみると、クラス8が最大になっているデータが多いですね。(この例の重みの設定だと、8が他の数字と被るピクセルが多くて反応しやすいんですかね。あ、そこでクラス8のバイアス$b_8$を負の値にして、$z_{n,k}$を調整するみたいな役割なのかな。)
一応、推論結果(分類結果)と教師データを比較してみましょう。
# 推論結果を表示 print(np.argmax(Z, axis=1)) print(T) # 推論結果を比較 print(np.argmax(Z, axis=1) == T) # 正解率を計算 print(np.sum(np.argmax(Z, axis=1) == T) / N)
[3 0 4 8 9 2 8 8 8 4 3 2 3 6 8 7 2 8 6 8]
[5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7 2 8 6 9]
[False True True False True True False False False True True False
True True False True True True True False]
0.6
Affineレイヤの出力Zの代わりに、Softmaxレイヤの出力Yを使っても同じ結果になります。
以上で、Affineレイヤの順伝播(重み付き和)の計算を確認できました。逆伝播では、逆伝播の入力と転置した重みを使って同様の計算が行われます。
順伝播では、重みというフィルターに入力を通すことで、クラスごとに伝播する量を調整して出力したと言えます。逆伝播でも、同じフィルター(重み)に逆伝播の入力を通すことで、クラスごとに同じ量を調整して出力します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
Affineレイヤについてもう少し踏み込もうとAffine変換を調べるも関連が分からずに悩んでけど、関係ないんかーい。
重み付き和については別の本を進めているときにイメージが深まったので、この機会に言語化しました。
2021年9月29日は、モーニング娘。の10期メンバーの加入10周年の日です!!!!
デビュー曲と最近の曲をどうぞ。
10期最高伝説!!!!
まーちゃんが卒業、とても悲しい。ソロになっても楽しく歌っていられる世界であってほしいな。
【関連する記事】